A Novel Categorical Approach to Semantics of Relational First-Order Logic

Abstract

We present a categorical formalization of a variant of first-order logic. Unlike other texts on this topic, the goal of this paper is to give a very transparent and self-contained account without requiring more background than basic logic and set theory. Our focus is to show how the semantics of first-order formulas can be derived from their usual deduction rules. For understanding the core ideas, it is not necessary to investigate the internal term structure of atomic formulas, thus we abstract atomic formulas to (syntactically opaque) relations; in this sense, our variant of first-order logic is “relational”. While the derived semantics is based on categorical principles (even the duality that arises from a symmetry between two ways of looking at something where there is no reason to choose one over the other), it is nevertheless “constructive” in that it describes explicit computations of the truth values of formulas. We demonstrate this by modeling the categorical semantics in the RISCAL (RISC Algorithm Language) system which allows us to validate the core propositions by automatically checking them in finite models.

1. Introduction

Most introductions to first-order logic first define the syntax of formulas, then formalize their meaning in the form established in the 1930s by Tarski [1] (essentially what we call today in programming language theory a “denotational semantics” [2]), then introduce a deduction calculus, and finally show the soundness and completeness of this calculus concerning the semantics: if a formula can be derived in the calculus, it is true according to the semantics, and vice versa. These relationships between truth and derivability have to be established because there is no self-evident link between the semantics of a formula and the deduction rules associated with it. Historically, deduction came first; the soundness of a deduction calculus was established by showing that it could not lead to apparent inconsistencies, i.e. that both a formula and its negation could not be derived in a deduction system. It was Tarski who first gave meaning to formulas that was independent of deduction.

However, as it did since the 1940s to many other mathematical areas, category theory [3,4,5,6,7], the general theory of mathematical structures, can bring and provide an alternative light also to first-order logic. It does so by considering logical notions as special instances of “universal” constructions, where a value of interest is determined

• first, by depicting the core property that the value shall satisfy; and
• second, by giving a criterion how to choose a canonical value from all values that satisfy the property.

It was eventually recognized that by such universal constructions the semantics of the connectives of propositional logic could be determined directly from their associated introduction and elimination rules. However, it took until the late 1960s until Lawvere gained the fundamental insight that this idea could be also applied to the quantifiers of first-order logic [8], thus establishing a direct relationship between its semantics and its proof calculus.

However, this insight has not yet obtained a foothold in basic texts on logic and its basic education. The main reason may be that the corresponding material is found mostly in texts on category theory and its applications where it is dispersed among examples of the application of categorical notions without a clear central presentation. Furthermore, the general treatment of first-order logic with terms and variables requires a complex mathematical apparatus [9] which is much beyond the scope of basic introductions. Reasonably compact introductions can be found, e.g., in Section 2.1.10 of [10], in [11], in Section 1.6 of [12] (however, in the context of type theory rather than classical first-order logic), in Section 9.5 of [3] (the treatment of quantifiers only), and in Section 7.1.12 of [7] (again only the treatment of quantifiers).

The goal of this paper is to give a compact introduction to a categorical version of first-order logic that is fully self-contained, only introduces the categorical notions relevant for the stated purpose, and presents them from the point of view of the intended application. For this purpose, it elaborates a simple but completely formalized syntactic and semantic framework of first-order logic that represents the background of the discussion, without gaps and inconsistencies. As a deliberate decision, this framework does not address the syntax and semantics of terms but abstracts atomic formulas to opaque relations; this allows for focusing the discussion on the essentials. However, to describe a reasonably close relative of first-order logic, this framework is (in contrast to other presentations) not based on relations of fixed arity, i.e., with a fixed number of variables; instead, we consider relations of infinite arity, i.e., with infinitely many variables. However, only finitely many variables may influence the truth value of the relation, which represents the effect that a classical atomic formula can only reference a finite number of variables. The overall result is a slick and elegant presentation. Because the duality has many manifestations in logic and it is agreed by all hands that a duality is like a “giant symmetry”—a symmetry between theories, we focus on this concept in our approach. For the implementation, we use the RISCAL—the RISC Algorithm Language [13], which is a specification language with an associated software system for describing mathematical algorithms, formally specifying their behavior based on mathematical theories, and validating the correctness of algorithms, specifications, and theories by the execution/evaluation of their formal semantics. The term “algorithm language” indicates that RISCAL is intended to model, rather than low-level code, algorithms (as can be found in textbooks on discrete mathematics) in a high-level language, and specifying the behavior of these algorithms by formal contacts. RISCAL has been developed to validate the correctness of mathematical theories, specifications, and programs, by checking instances of these artifacts on finite domains; applications of RISCAL are for instance in discrete mathematics, number theory, and computer algebra. Software based on formal logic plays an ever-increasing role in areas where a mathematically precise understanding of a subject domain and sound rules for reasoning about the properties of this domain are essential. A prime example is the formal modeling, specification, and verification of computer programs and computing systems, but there are many other applications in areas such as knowledge-based systems, computer mathematics, or the semantic web [14]. Furthermore, the intent of all our projects (namely LogTechEdu, SemTech [15], and others listed in Funding section) is to further advance education in computer science and related topics. In academical courses for computer science and mathematics, by utilizing the power of modern software based on formal logic and semantics, students shall engage with the material they encounter by actively producing the problem solutions rather than just passively taking them from the lecturer.

The remainder of this paper is structured as follows: in Section 2, we define a term-free variant of first-order logic and give it a semantics in the usual style based on set-theoretic notions. In Section 3, we introduce those categorical notions that are necessary for understanding the following elaboration and discuss their relationships. The core of this paper is Section 4 where we elaborate the categorical formulation of the semantics of our variant of first-order logic. In Section 5, we demonstrate that these semantics are constructive by modeling it in the RISCAL system [13], which allows us to automatically check the core propositions in particular finite models. Section 6 concludes our presentation and gives an outlook on our future work.

2. A Relational First-Order Logic

In this section, we introduce a simplified variant of first-order logic that abstracts from the syntactic structure of atomic formulas and thus copes without the concept of terms, constants, function symbols, predicate symbols, and all of the associated semantic apparatus. Towards this goal, atomic formulas are replaced by relations over assignments (maps of variables to values) that are constrained to only depend on a finite number of variables; we will call such relations “predicates”. Consequently, the semantics of every non-atomic formula is also a relation (i.e., a predicate, as mentioned).

We begin with some standard notions. First, we specify variables and the values that variables hold.

Axiom 1

(Variables and Values). Let $\mathit{Var}$ denote an arbitrary infinite and enumerable set; we call the elements of this set variables. Furthermore, let $\mathit{Val}$ denote an arbitrary non-empty set; we call the elements of these set values.

Next, we define assignments.

Definition 1

(Assignments). We define $\mathit{Ass}:=\mathit{Var}\to \mathit{Val}$ as the set of all mappings of variables to values (a function space); we call the elements of this set assignments. Thus, for every assignment $a\in \mathit{Ass}$ and every variable $x\in \mathit{Var}$, we have $a\left(x\right)\in \mathit{Val}$.

We note that assignment is similar to a concept of state in theory of formal semantics of programming languages (see, e.g., [16]) where the state is a function from variables to values: to each variable, the state associates its current value.

Definition 2

(Updates). Let $a\in \mathit{Ass}$ be an assignment, $x\in \mathit{Var}$ a variable, and $v\in \mathit{Val}$ a value. We define the update assignment $a[x\mapsto v]\in \mathit{Ass}$ as follows:

$$\begin{array}{cc}\hfill a[x\mapsto v]\left(y\right)& :=\left\{\begin{array}{cc}v,\hfill & \mathit{if}x=y;\hfill \\ a\left[x\right],\hfill & \mathit{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

Consequently, $a[x\mapsto v]$ is identical to a except that it maps variable x to value v.

Based on this, we can formulate the following updating properties.

Proposition 1

(Update Properties). Let $a\in \mathit{Ass}$ be an assignment, $x,y\in \mathit{Var}$ variables, and $v,v_1,v_2\in \mathit{Val}$ values. Then, we have the following properties:

$$\begin{array}{cc}\hfill a[x\mapsto a(x\left)\right]& =a,\hfill \\ \hfill a[x\mapsto v_1][x\mapsto v_2]& =a[x\mapsto v_2],\hfill \\ \hfill x\ne y\Rightarrow a[x\mapsto v_1][y\mapsto v_2]& =a[y\mapsto v_2][x\mapsto v_1].\hfill \end{array}$$

Proof. 

Directly from the definitions. □

The properties of assignments listed above (and only these) will be of importance in the subsequent proofs.

Now, we turn to the fundamental semantic notions.

Definition 3

(Relations). We define $\mathit{Rel}:=\mathcal{P}\left(\mathit{Ass}\right)$ as the set of all sets of assignments; we call the elements of this set “relations”. Consequently, a relation is a set of assignments.

Definition 4

(Variable Independence). We state that relation $R\in \mathit{Rel}$ is independent of variable $x\in \mathit{Var}$, written as $R⫫x$, if and only if the following holds:

$$\forall a\in \mathit{Ass},v_1,v_2\in \mathit{Val}.a[x\mapsto v_1]\in R\iff a[x\mapsto v_2]\in R.$$

Consequently, if $R⫫x$, the value of x in any assignment a does not influence whether a is in R. We say that R depends on x if $R⫫x$ does not hold.

We transfer the central syntactic property of atomic formulas (they can only refer to finitely many variables) to its semantic counterpart.

Definition 5

(Predicates). A relation $R\in \mathit{Rel}$ is a predicate, if it only depends on finitely many variables. We denote by $\mathit{Pred}$ the set of all predicates and by ${\mathit{Pred}}_x:=\{P\in \mathit{Pred}|P⫫x\}$ the subset of all predicates that are independent of x.

Now, we are ready to introduce the central entities of our paper. First, we give a definition of the abstract syntax of formulas.

Definition 6

(Abstract Syntax of Formulas). We define $For$ as that smallest set of abstract syntax trees in which every element $F\in \mathit{For}$ is generated by an application of a rule of the following context-free grammar (where $P\in \mathit{Pred}$ denotes an arbitrary predicate and $x\in \mathit{Var}$ denotes an arbitrary variable):

$$\begin{array}{cc}\hfill F& ::=P|\top |\perp \hfill \\ \hfill & |\neg F|F_1\wedge F_2|F_1\vee F_2|F_1\to F_2|F_1\leftrightarrow F_2\hfill \\ \hfill & |\forall x.F|\exists x.F\hfill \end{array}$$

We call the elements of this set formulas.

In this definition, the role of a classic atomic predicate $p(t_1,\dots ,t_n)$ with argument terms $t_1,\dots ,t_k$ in which n variables $x_1,\dots ,x_n$ occur freely is abstracted to a predicate P that depends on variables $x_1,\dots ,x_n$.

Now, we establish the relationship between the syntax and semantics of formulas.

Definition 7

(Semantics of Formulas). Let $F\in \mathit{For}$ be a formula. We define the relation $〚F〛\in \mathit{Rel}$, called the semantics of F, by induction on the structure of F:

$$\begin{array}{cc}\hfill 〚P〛& :=\{a\in \mathit{Ass}|a\in P\}\hfill \\ \hfill 〚\top 〛& :=\{a\in \mathit{Ass}|\mathit{true}\}\hfill \\ \hfill 〚\perp 〛& :=\{a\in \mathit{Ass}|\mathit{false}\}\hfill \\ \hfill 〚\neg F〛& :=\{a\in \mathit{Ass}|a\notin 〚F〛\}\hfill \\ \hfill 〚F_1\wedge F_2〛& :=\{a\in \mathit{Ass}|a\in 〚F_1〛\mathit{and}a\in 〚F_2〛\}\hfill \\ \hfill 〚F_1\vee F_2〛& :=\{a\in \mathit{Ass}|a\in 〚F_1〛\mathit{or}a\in 〚F_2〛\}\hfill \\ \hfill 〚F_1\to F_2〛& :=\{a\in \mathit{Asss}|a\notin 〚F_1〛\mathit{or}a\in 〚F_2〛\}\hfill \\ \hfill 〚F_1\leftrightarrow F_2〛& :=\{a\in \mathit{Ass}|\left(a\in 〚F_1〛\mathit{and}a\in 〚F_2〛\right)\mathit{or}\left(a\notin 〚F_1〛\mathit{and}a\notin 〚F_2〛\right)\}\hfill \\ \hfill 〚\forall x.F〛& :=\{a\in \mathit{Ass}|a[x\mapsto v]\in 〚F〛,\mathit{for}\mathit{all}v\in \mathit{Val}\}\hfill \\ \hfill 〚\exists x.F〛& :=\{a\in \mathit{Ass}|a[x\mapsto v]\in 〚F〛,\mathit{for}\mathit{some}v\in \mathit{Val}\}\hfill \end{array}$$

The above definition is well-defined in that every formula denotes a relation. To show that formulas indeed denote predicates, some more work is required.

Proposition 2

(Quantified Formulas and Variable Independence). For every variable $x\in \mathit{Var}$ and formula $F\in \mathit{For}$, we have $〚\forall x.F〛⫫x$ and $〚\exists x.F〛⫫x$, i.e., the semantics of quantified formulas do not depend on x.

Proof. 

We prove this proposition by reductio ad absurdum.

First, assume that $〚\forall x.F〛$ depends on x. Then, we have some assignment $a\in 〚\forall x.F〛$ and some values $v_1,v_2\in \mathit{Val}$ such that $a[x\mapsto v_1]\in 〚\forall x.F〛$ and $a[x\mapsto v_2]\notin 〚\forall x.F〛$. From $a[x\mapsto v_2]\notin 〚\forall x.F〛$ we have some $v\in \mathit{Val}$ with $a[x\mapsto v_2][x\mapsto v]\notin 〚F〛$ and thus $a[x\mapsto v]\notin 〚F〛$. However, $a[x\mapsto v_1]\in 〚\forall x.F〛$ implies $a[x\mapsto v_1][x\mapsto v]\in 〚F〛$ and thus $a[x\mapsto v]\in 〚F〛$, which represents a contradiction.

Now, assume that $〚\exists x.F〛$ depends on x. Then, we have some assignment $a\in 〚\exists x.F〛$ and some values $v_1,v_2\in \mathit{Val}$ such that $a[x\mapsto v_1]\in 〚\exists x.F〛$ and $a[x\mapsto v_2]\notin 〚\exists x.F〛$. From $a[x\mapsto v_1]\in 〚\exists x.F〛$, we have some $v\in \mathit{Val}$ with $a[x\mapsto v_1][x\mapsto v]\in 〚F〛$ and thus $a[x\mapsto v]\in 〚F〛$. However, $a[x\mapsto v_2]\notin 〚\exists x.F〛$ implies $a[x\mapsto v_2][x\mapsto v]\notin 〚F〛$ and thus $a[x\mapsto v]\notin 〚F〛$, which represents a contradiction. □

Proposition 3

(Formula Semantics and Predicates). For every formula $F\in \mathit{For}$, we have $〚F〛\in \mathit{Pred}$, i.e., the semantics of F is a predicate.

Proof. 

The proof proceeds by induction over the structure of F.

• If $F=P$, we have $〚F〛=\{a\in \mathit{Ass}|a\in P\}=P\in \mathit{Pred}$.
• If $F\in \{\top ,\perp \}$, there are no $x,a,v_1,v_2$ such that $a[x\mapsto v_1]\in 〚F〛$ and $a[x\mapsto v_2]\notin 〚F〛$ because, for $F=\top$, the second condition must be false and for $F=\perp$ the first one; thus, F does not depend on any variable.
• If $F=\neg F_1$, by the induction hypothesis, we may assume that $〚F_1〛$ depends only on the variables in some finite variable set X. From the definition of $〚F〛$, it is then easy to show that $〚\neg F_1〛$ also depends only on the variables in X.
• If $F\in \{F_1\wedge F_2,F_1\vee F_2,F_1\to F_2,F_1\leftrightarrow F_2\}$, we may assume by the induction hypothesis that $〚F_1〛$ depends only on the variables in some finite set $X_1$ while $P_2$ only depends on the variables in some finite set $X_2$. From the definition of $〚F〛$, it is then easy to show that $〚F〛$ depends only on the variables in the finite set $X_1\cup X_2$.
• If $F\in \{\forall x.F_1,\exists x.F_1\}$, we may assume by the induction hypothesis that $〚F_1〛$ only depends on the variables in some finite variable set X. We are now going to show that $〚F〛$ only depends on the variables in the finite set $X\backslash \left\{x\right\}$. Actually, we assume that this is not the case and show a contradiction. From this assumption and Proposition 2, we have a variable $y\ne x\wedge y\notin X$ on which F depends; thus, we have an assignment a and values $v_1,v_2$ such that $a[y\mapsto v_1]\in 〚F〛$ and $a[y\mapsto v_2]\notin 〚F〛$.
  If $F=\forall x.F_1$, from $a[y\mapsto v_2]\notin 〚F〛$, we have a $v\in \mathit{Val}$ with $a[y\mapsto v_2][x\mapsto v]\notin 〚F_1〛$ and thus (since $y\ne x$) $a[x\mapsto v][y\mapsto v_2]\notin 〚F_1〛$. From $a[y\mapsto v_1]\in 〚F〛$, we know $a[y\mapsto v_1][x\mapsto v]\in 〚F_1〛$ and thus $a[x\mapsto v][y\mapsto v_1]\in 〚F_1〛$. Thus, $〚F_1〛$ depends on a variable $y\notin X$ which contradicts the induction assumption.
  If $F=\exists x.F_1$, from $a[y\mapsto v_1]\in 〚F〛$, we have a $v\in \mathit{Val}$ with $a[y\mapsto v_1][x\mapsto v]\in 〚F_1〛$ and thus (since $y\ne x$) $a[x\mapsto v][y\mapsto v_1]\in 〚F_1〛$. From $a[y\mapsto v_2]\notin 〚F〛$ we know $a[y\mapsto v_2][x\mapsto v]\notin 〚F_1〛$ and thus $a[x\mapsto v][y\mapsto v_2]\notin 〚F_1〛$. Thus, $〚F_1〛$ depends on a variable $y\notin X$ which contradicts the induction assumption.

This completes our proof. □

In the following, we transfer the classical model-theoretic notions to our framework.

Definition 8

(Satisfaction). Let $a\in \mathit{Ass}$ be an assignment and $F\in \mathit{For}$ be a formula. We define $a\vDash F$ (read: a satisfies F) as follows:

$$a\vDash F:\iff a\in 〚F〛.$$

Definition 9

(Validity). Let $F\in \mathit{For}$ be a formula. We define $\vDash F$ (read: F is valid) as follows:

$$\vDash F:\iff \forall a\in \mathit{Ass}.a\vDash F.$$

Definition 10

(Logical Consequence). Let $F,G\in \mathit{For}$ be formulas. We define $F\vDash G$ (read: G is a logical consequence of F) as follows:

$$F\vDash G:\iff \forall a\in \mathit{Ass}.a\vDash F\Rightarrow a\vDash G.$$

Definition 11

(Logical Equivalence). Let $F,G\in \mathit{For}$ be formulas. We define $F\equiv G$ (read: F and G are logically equivalent) as follows:

$$F\equiv G:\iff \forall a\in \mathit{Ass}.a\vDash F\iff a\vDash G.$$

Proposition 4

(Logical Consequence and Logical Equivalence). Let $F,G\in \mathit{For}$ be formulas. Then, we have the following equivalences:

• $(F\vDash G)\iff (\vDash F\to G)$
• $(F\vDash G)\iff (〚F〛\subseteq 〚G〛)$
• $(F\equiv G)\iff (\vDash F\leftrightarrow G)$
• $(F\equiv G)\iff (〚F〛=〚G〛)$

Proof. 

Directly from the definitions. □

Thus, a logical consequence on the meta-level coincides with an implication on the formula level and with the subset relation on the semantic level. Furthermore, logical equivalence on the meta-level coincides with equivalence on the formula level and with the equality relation on the semantic level.

In the following, we establish a set-theoretic interpretation of the logical operations of our formula language.

Definition 12

(Complement). We define the complement $\overline{R}\in \mathit{Rel}$ of relation $R\in \mathit{Rel}$ as the relation $\overline{R}:=\mathit{Ass}\backslash R$. Consequently, an assignment is in $\overline{R}$ if and only if it is not in R.

Proposition 5

(Propositional Semantics as Set Operations). Let $F,F_1,F_2\in \mathit{For}$ be formulas. We then have the following equalities:

$$\begin{array}{cc}\hfill 〚P〛& =P\hfill \\ \hfill 〚\top 〛& =\mathit{Ass}\hfill \\ \hfill 〚\perp 〛& =\varnothing \hfill \\ \hfill 〚\neg F〛& =\overline{〚F〛}\hfill \\ \hfill 〚F_1\wedge F_2〛& =〚F_1〛\cap 〚F_2〛\hfill \\ \hfill 〚F_1\vee F_2〛& =〚F_1〛\cup 〚F_2〛\hfill \\ \hfill 〚F_1\to F_2〛& =\overline{〚F_1〛}\cup 〚F_2〛\hfill \\ \hfill 〚F_1\leftrightarrow F_2〛& =\left(〚F_1〛\cap 〚F_2〛\right)\cup \left(\overline{〚F_1〛}\cap \overline{〚F_2〛}\right)\hfill \end{array}$$

Proof. 

Directly from the definition of the semantics. □

While the above results are quite intuitive, a corresponding set-theoretic interpretation of quantified formulas is not. In the following, we only state the plain result without indication of how it can be intuitively understood; we will delegate this explanation to Section 4, where the categorical framework will provide us with adequate insight.

Proposition 6

(Quantifier Semantics as Set Operations). Let $F\in \mathit{For}$ be a formula. We then have the following equalities:

$$\begin{array}{cc}\hfill 〚\forall x.F〛& =\bigcup \{P\in \mathit{Pred}|P⫫x\wedge P\subseteq 〚F〛\},\hfill \\ \hfill 〚\exists x.F〛& =\bigcap \{P\in \mathit{Pred}|P⫫x\wedge 〚F〛\subseteq P\}.\hfill \end{array}$$

In other words, $〚\forall x.F〛$ is the weakest predicate P (“weakest” in the sense of the largest set) that is independent from x and that satisfies the property $P\subseteq 〚F〛$ while $〚\exists x.F〛$ is the strongest predicate P (“strongest” in the sense of the smallest set) that is independent of x and that satisfies the property $〚F〛\subseteq P$.

Proof. 

The proof is in two stages. First, we take an arbitrary assignment $a\in \mathit{Ass}$ and show

$$a\in 〚\forall x.F〛\iff \left(\exists P\in \mathit{Pred}.P⫫x\wedge P\subseteq 〚F〛\wedge a\in P\right)$$

⇒: We assume $a\in 〚\forall x.F〛$ and prove for $P:=〚\forall x.F〛$

$$\begin{array}{cc}\hfill & P\in \mathit{Pred}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & P⫫x\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & P\subseteq 〚F〛\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & a\in P\hfill \end{array}$$

(4)

From Proposition 3, we have (1). From Proposition 2, we have (2). From $a\in 〚\forall x.F〛$, we have (4). To show (3), we take arbitrary assignment $a_0\in P$ and show $a_0\in 〚F〛$. From $a_0\in P$, we know $a_0[x\mapsto v]\in 〚F〛$ for $v:=a_0\left(x\right)$. Since $a_0[x\mapsto a_0\left(x\right)]=a_0$, we thus know $a_0\in 〚F〛$.

⇐: We assume for some $P\in \mathit{Pred}$

$$\begin{array}{cc}\hfill & P⫫x\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & P\subseteq 〚F〛\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & a\in P\hfill \end{array}$$

(7)

and prove $a\in 〚\forall x.F〛$. For this, we take arbitrary $v\in \mathit{Val}$ and prove $a[x\mapsto v]\in 〚F〛$. From (6), it suffices to show $a[x\mapsto v]\in P$. From (5), we know

$$\begin{array}{c}\hfill \forall v_1,v_2\in \mathit{Val}.a[x\mapsto v_1]\in P\iff a[x\mapsto v_2]\in P\end{array}$$

(8)

From (7) and $a=a[x\mapsto a(x\left)\right]$, we know $a[x\mapsto v_0]\in P$ for $v_0:=a\left(x\right)$. Thus, with (8), we know $a[x\mapsto v]\in P$.

Now, we take arbitrary $a\in \mathit{Ass}$ and show

$$a\in 〚\exists x.F〛\iff \left(\forall P\in \mathit{Pred}.P⫫x\wedge 〚F〛\subseteq P\Rightarrow a\in P\right)$$

⇒: We assume $a\in 〚\exists x.F〛$ and take arbitrary but fixed $P\in \mathit{Pred}$ for which we assume

$$\begin{array}{cc}\hfill & P⫫x\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & 〚F〛\subseteq P\hfill \end{array}$$

(10)

Our goal is to show $a\in P$. From $a\in 〚\exists x.F〛$, we know $a[x\mapsto v]\in 〚F〛$ for some $v\in \mathit{Val}$. From (10), we thus know $a[x\mapsto v]\in P$. From (9), we thus know $a[x\mapsto a(x\left)\right]\in P$. Since $a[x\mapsto a(x\left)\right]=a$, we thus know $a\in P$.

⇐: We assume

$$\begin{array}{c}\hfill \forall P\in \mathit{Pred}.P⫫x\wedge 〚F〛\subseteq P\Rightarrow a\in P\end{array}$$

(11)

and prove $a\in 〚\exists x.F〛$. From (11) instantiated with $P:=〚\exists x.F〛$ and Propositions 3 and 2, it suffices to prove $〚F〛\subseteq 〚\exists x.F〛$. Take arbitrary assignment $a_0\in 〚F〛$. Since $a_0[x\mapsto a\left(x\right)]=a$, we thus have $a_0[x\mapsto v]\in 〚F〛$ for $v:=a\left(x\right)$ and thus $a_0\in 〚\exists x.F〛$. □

3. Category Theory

In this section, we discuss those aspects of category theory that are relevant for the subsequent categorical formulation of our relational first-order logic.

3.1. Basic Notions

We begin with the basic notions of category theory.

Definition 13

(Category). A category C is a triple $⟨O,A,\circ ⟩$ of the following components:

• A class O of elements called C-objects or just objects.
• A class A of elements called C-arrows or just arrows. Each arrow has a source object and a target object from O; we write $f:a\to b$ to indicate that f is an arrow with source a and target b. We write $C(a,b)$ to denote the class of all arrows of A with source a and target b (called the hom-class of all arrows from a to b). For every object x in O, A contains an arrow ${\mathit{id}}_x:x\to x$ called the identity arrow for x.
• A composition—binary operation ∘ defined on arrows. For all arrows $f:a\to b$ and $g:b\to c$, we have $(g\circ f):a\to c$. Furthermore, the composition satisfies the following axioms:

  -

  Associativity: $(h\circ g)\circ f=h\circ (g\circ f)$, for all arrows $f:a\to b$, $g:b\to c$, $h:c\to d$.

  -

  Identity: ${\mathit{id}}_b\circ f=f=f\circ {\mathit{id}}_a$, for all arrows $f:a\to b$.

Definition 14

(Isomorphism). Let C be a category and $a,b$ be C-objects $a,b$. Then, we have $a\simeq b$ (read: a and b are isomorphic) if there are C-arrows $f:a\to b$ and $g:b\to a$, called isomorphisms, such that $g\circ f={\mathit{id}}_a$ and $f\circ g={\mathit{id}}_b$.

Definition 15

(Subcategory). A category C is a subcategory of category $𝒟$ if every C-object is also a $𝒟$-object, every C-arrow is also a $𝒟$-arrow, every identity arrow in C is also an identity arrow in $𝒟$, and $g{\circ }_{C}f=g{\circ }_{D}f$ for all C-arrows $f:a\to b$ and $g:b\to c$, where ${\circ }_C$ denotes the composition in C and ${\circ }_D$ denotes the composition in $𝒟$.

3.2. Object Constructions

We are now introducing constructions of categorical objects that will subsequently play an important role in the categorical formulation of relational first-order logic.

Definition 16

(Initial and Final Objects). Let C be a category. A C-object 0 is initial if for every C-object a there exists exactly one arrow $0_a:0\to a$. A C-object 1 is final if for every C-object a there exists exactly one arrow $1_a:a\to 1$.

The following diagram illustrates the arrows of an initial object 0 and a final object 1 with respect to an arbitrary object a:

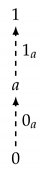
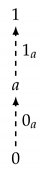
This construction of initial/final objects is “universal” in the sense that it describes a class of entities (objects and accompanying arrows) that share a common property and picks from this class an entity whose characterizing property is the existence of exactly one arrow from/to every entity of this class. This defines the entity uniquely up to isomorphism. Further instances of such constructions will be given later.

Definition 17

(Product and Coproduct). Let C be a category. Then, the triple $⟨a\times b,{\pi }_1,{\pi }_2⟩$ is a product of C-objects a and b if $a\times b$ is a C-object, the product object, with arrows ${\pi }_1:a\times b\to a$ and ${\pi }_2:a\times b\to b$, the projections, such that for every triple $⟨c,f,g⟩$ with C-object c and arrows $f:c\to a$ and $g:c\to b$ there exists exactly one arrow $⟨f,g⟩:c\to a\times b$ such that the following diagram commutes:

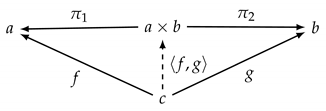
Dually, the triple $(a+b,{\iota }_1,{\iota }_2)$ is a coproduct of C-objects a and b if $a+b$ is a C-object, the coproduct object, with arrows ${\iota }_1:a\to a+b$ and ${\iota }_2:b\to a+b$, the injections, such that, for every triple $⟨c,f,g⟩$ with C-object c and arrows $f:a\to c$ and $g:b\to c$, there exists exactly one arrow $[f,g]:a+b\to c$ such that the following diagram commutes:

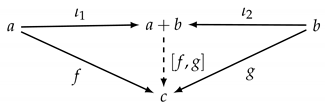
The product and the coproduct are thus defined by universal constructions analogous to those of the final and the initial element, respectively; thus, products and coproducts are also uniquely defined up to isomorphism.

Definition 18

(Product Arrow). Let C be a category with products $⟨a_1\times a_2,{\pi }_1,{\pi }_2⟩$ and $⟨b_1\times b_2,{\pi }_1^{\prime },{\pi }_2^{\prime }⟩$ and arrows $f:a_1\to b_1$ and $g:a_2\to b_2$, respectively. Then, the product arrow $f\times g:a_1\times a_2\to b_1\times b_2$ is the arrow $⟨f\circ {\pi }_1,g\circ {\pi }_2⟩$.

Definition 19

(Exponential). Let C be a category in which, for all C-objects, there exists a product object. Then, the tuple $⟨b^a,{\mathit{eval}}_{a,b}⟩$ is an exponential of C-objects a and b if $b^a$ is a C-object, the exponential object, with arrow ${\mathit{eval}}_{a,b}:b^a\times a\to b$, the evaluation arrow, such that for every C-object c with arrow $f:c\times a\to b$ there exists exactly one arrow ${\mathit{curry}}_f:c\to b^a$, the currying arrow, such that the following diagram commutes:

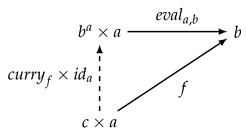
Since the exponential is also defined by a universal construction, it is uniquely defined up to isomorphism.

3.3. Functors and Adjunction

Moving on from individual categories, we will now discuss some concepts that address relationships between categories.

Definition 20

(Functor). Let C and $𝒟$ be categories. A functor $F:C\to 𝒟$ is a map that takes every C-object a to a $𝒟$-object $F\left(a\right)$ and every C-arrow $f:a\to b$ to a $𝒟$-arrow $F\left(f\right):F\left(a\right)\to F\left(b\right)$ such that

• $F\left({\mathit{id}}_a\right)={\mathit{id}}_{F\left(a\right)}$ for every C-object a, and
• $F\left(g{\circ }_{C}f\right)=F\left(g\right){\circ }_{D}F\left(f\right)$ for all C-arrows $f:a\to b$ and $g:b\to c$.

Definition 21

(Adjunction, Left, and Right Adjoint). Let C and $𝒟$ be categories with functors $F:C\to 𝒟$ and $G:𝒟\to C$. Then, we have $F⊣G$ (read: $⟨F,G⟩$ is an adjunction, F is a left adjoint of G, G is a right adjoint of F) if for every C-object a and $𝒟$-object b the arrow classes $𝒟\left(F\right(a),b)$ and $C(a,G(b\left)\right)$ are isomorphic, i.e., there exists a bijection between them. This is equivalent to saying that, for every C-object a and $𝒟$-object b, there exist two surjective mappings $s_1:𝒟(F\left(a\right),b)\to C(a,G\left(b\right))$ and $s_2:C(a,G\left(b\right))\to 𝒟(F\left(a\right),b)$, i.e.,

• for every $𝒟$-arrow $g:F\left(a\right)\to b$ we have a C-arrow $f:a\to G\left(b\right)$ with $s_2\left(f\right)=g$ and
• for every C-arrow $f:a\to G\left(b\right)$, we have a $𝒟$-arrow $g:F\left(a\right)\to b$ with $s_1\left(g\right)=f$.

Note. 

This equivalence is a consequence of the Cantor–Schröder–Bernstein theorem which states that there exists a bijective function between sets A and B if there exist injective functions $f:A\to B$ and $g:B\to A$. This implies that such a bijective function also exists if there exist surjective functions $f^{\prime }:A\to B$ and $g^{\prime }:B\to A$ because, from these, we can define the injective functions $f\left(a\right):=\mathit{such}b.g^{\prime }\left(b\right)=a$ and $g\left(b\right):=\mathit{such}a.f^{\prime }\left(a\right)=b$. While the theorem has been formulated for sets, it can also be generalized to classes.

The above formulation will become handy in proving that two functors represent an adjunction.

Proposition 7

(Equivalence of Adjunctions and Universals). Let C and $𝒟$ be categories with functors $F:C\to 𝒟$ and $G:𝒟\to C$. Then, the condition $F⊣G$ is equivalent to each of the following two conditions:

1. 

For every C-object a, there is a C-arrow $u:a\to G\left(F\right(a\left)\right)$, the “universal arrow”, such that, for every $𝒟$-object b and C-arrow $f:a\to G\left(b\right)$, there exists a $𝒟$-arrow $g_{b,f}:F\left(a\right)\to b$:

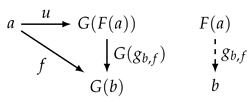
2. 

For every $𝒟$-object b, there is a C-arrow $v:F\left(G\right(b\left)\right)\to b$, the “couniversal arrow”, such that, for every C-object a and $𝒟$-arrow $g:F\left(a\right)\to b$, there is a C-arrow $f_{a,g}:a\to G\left(b\right)$:

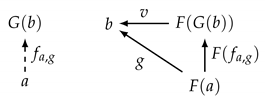
Proof. 

See the proof of Propositions 6 and 7 in [12]. □

3.4. Object Constructions by Adjunction

We conclude this section by demonstrating that the previously described object conjunctions can be also considered as applications of functors that are determined as left respectively right adjoints to certain basic functors.

Proposition 8

(Initial and Final Object by Adjunction). Let $\mathbf{1}$ be the “singleton” category with a single object ∗ (and consequently a single arrow ${\mathit{id}}_{\ast }:\ast \to \ast$); this category is uniquely defined up to isomorphism. Let C be a category with the constant functor $C:C\to \mathbf{1}$; in addition, this functor is uniquely defined up to isomorphism. Then, the following holds:

• Let C-object 0 be initial and the “initial object functor” $I_0:\mathbf{1}\to C$ be defined by $I_0(\ast ):=0$ and $I_0\left({\mathit{id}}_{\ast }\right):={\mathit{id}}_0$. Then, we have $I_0⊣C$, i.e., the initial object functor is a left adjoint of the constant functor.
• Let C-object 1 be final and the “final object functor” $F_1:\mathbf{1}\to C$ be defined by $F_1(\ast ):=1$ and $F_1\left({\mathit{id}}_{\ast }\right):={\mathit{id}}_1$. Then, we have $C⊣F_1$, i.e., the final object functor is a right adjoint of the constant functor.

Proof. 

For showing the first statement, we take the initial object 0 with initial object functor $I_0$. We show $I_0⊣C$, i.e., that $C(I_0(\ast ),a)$ and $\mathbf{1}(\ast ,C(a\left)\right)$ are isomorphic, for arbitrary C-object a. This follows from $\mathbf{1}(\ast ,C(a\left)\right)=\mathbf{1}(\ast ,\ast )$, $C(I_0(\ast ),a)=C(0,a)$, and the fact that there exists exactly one $\mathbf{1}$-arrow ${\mathit{id}}_{\ast }:\ast \to \ast$ and, since 0 is initial, exactly one C-arrow $f:0\to a$.

For showing the second statement, we take the final object 1 with final functor $F_1$. We prove $C⊣F_1$, i.e., that $\mathbf{1}\left(C\right(a),\ast )$ and $C(a,F_1(\ast ))$ are isomorphic, for arbitrary C-object a. This follows from $\mathbf{1}\left(C\right(a),\ast )=\mathbf{1}(\ast ,\ast )$, $C(a,F_1(\ast ))=C(a,1)$, and the fact that there exists exactly one $\mathbf{1}$-arrow ${\mathit{id}}_{\ast }:\ast \to \ast$ and, since 1 is final, exactly one C-arrow $f:a\to 1$. □

Proposition 9

(Product and Coproduct by Adjunction). Let C be a category. Let the “product category” $C\times C$ be the category whose objects $(a,b)$ are pairs of C-objects a and b, whose arrows $(f,g):(a,c)\to (b,d)$ are pairs of C-arrows $f:a\to b$ and $g:c\to d$, where the identity arrows are pairs of identity arrows, and where composition is component-wise composition. Let the “diagonal functor” $\Delta :C\to C\times C$ be defined by $\Delta \left(a\right)=(a,a)$ for every C-object a and $\Delta \left(f\right)=(f,f)$ for every C-arrow $f:a\to b$. Then, the following holds:

• Assume that every pair of C-objects a and b has a product $a\times b$ and let the “product functor” $P:C\times C\to C$ be defined by $P(a,b):=a\times b$. Then, we have $\Delta ⊣P$, i.e., the product functor is a right adjoint of the diagonal functor.
• Assume that every pair of C-objects a and b has a coproduct $a+b$ and let the “coproduct functor” $C:C\to C\times C$ be defined by $C(a,b):=a+b$. Then, we have $C⊣\Delta$, i.e., the coproduct functor is a left adjoint of the diagonal functor.

Proof. 

For showing the first statement, we take arbitrary category C and functor P satisfying the stated assumption. We show $\Delta ⊣P$, i.e., that, for arbitrary C-objects $p,a,b$, the arrow classes $(C\times C)(\Delta (p),(a,b\left)\right)$ and $C(p,P(a,b\left)\right)$ are isomorphic. Since $\Delta \left(p\right)=(p,p)$ and $P(a,b)=a\times b$, it suffices to find surjections $s_1:(C\times C)((p,p),(a,b))\to C(p,a\times b)$ and $s_2:C(p,a\times b)\to (C\times C)((p,p),(a,b))$. First, we define $s_1(f,g):=⟨f,g⟩$ where $⟨f,g⟩:p\to a\times b$ is the unique C-arrow given to us by Definition 17 with property $f={\pi }_1\circ ⟨f,g⟩$ and $g={\pi }_2\circ ⟨f,g⟩$. Now, we show that, for every C-arrow $h:p\to a\times b$, there exist some C-arrows $f:p\to a$ and $g:p\to b$ with $s_1(f,g)=h$. We take $f:={\pi }_1\circ h$ and $g:={\pi }_2\circ h$. Due to the uniqueness of $⟨f,g⟩$, the equalities $f={\pi }_1\circ h$ and $g={\pi }_2\circ h$ imply $h=⟨f,g⟩$ and thus $s_1(f,g)=h$. Second, we define $s_2\left(h\right):=({\pi }_1\circ h,{\pi }_2\circ h)$. Now, we show that, for every $(C\times C)$-arrow $(f,g):(p,p)\to (a,b)$, i.e., for all C-arrows $f:p\to a$ and $g:p\to b$, there exists some C-arrow $h:p\to a\times b$ with $s_2\left(h\right)=(f,g)$, i.e., ${\pi }_1\circ h=f$ and ${\pi }_2\circ h=g$. Definition 17 can be used to define h.

For showing the second statement, we take arbitrary category C and functor C satisfying the stated assumption. We prove $C⊣\Delta$, i.e., that, for arbitrary C-objects $a,b,c$, the arrow classes $C\left(C\right(a,b),c)$ and $(C\times C)\left(\right(a,b),\Delta (c\left)\right)$ are isomorphic. Since $C(a,b)=a+b$ and $\Delta \left(c\right)=(c,c)$, it suffices to find surjections $s_1:C(a+b,c)\to (C\times C)((a,b),(c,c))$ and $s_2:(C\times C)((a,b),(c,c))\to C(a+b,c)$. First, we define $s_1\left(h\right):=(h\circ {\iota }_1,h\circ {\iota }_2)$. Now, we prove that for every $(C\times C)$-arrow $(f,g):(a,b)\to (c,c)$, i.e., for all C-arrows $f:a\to c$ and $g:b\to c$, there exists some C-arrow $h:a+b\to c$ with $s_1\left(h\right)=(f,g)$, i.e., $h\circ {\iota }_1=f$ and $h\circ {\iota }_2=g$. Definition 17 can be used to define h. Second, we define $s_2(f,g):=[f,g]$ where $[f,g]:a+b\to c$ is the unique C-arrow given to us by Definition 17 with property $f=[f,g]\circ {\iota }_1$ and $g=[f,g]\circ {\iota }_2$. Now, we show that, for every C-arrow $h:a+b\to c$, there exist some C-arrows $f:a\to c$ and $g:b\to c$ with $s_2(f,g)=h$. We take $f:=h\circ {\iota }_1$ and $g:=h\circ {\iota }_2$. Due to the uniqueness of $[f,g]$, the equalities $f=h\circ {\iota }_1$ and $g=h\circ {\iota }_2$ imply $h=[f,g]$ and thus $s_2(f,g)=h$. □

Proposition 10

(Exponential by Adjunction). Let C be a category in which, for every pair of C-objects a and b, there exists a product object $b\times a$ and an exponential object $b^a$. For every C-object a, let the “(unary) product functor” $P_a:C\to C$ be defined by $P_a\left(b\right):=b\times a$ and the “(unary) exponential functor” $E_a:C\to C$ be defined by $E_a\left(b\right):=b^a$. Then, we have $P_a⊣E_a$, i.e., the exponential functor is a right adjoint of the product functor.

Proof. 

We take arbitrary category C, C-object a, and functors $P_a$ and $E_a$ satisfying the assumption. We show $P_a⊣E_a$, i.e., that, for arbitrary C-objects $b,c$, the arrow classes $C(P_a\left(c\right),b)$ and $C(c,E_a\left(b\right))$ are isomorphic. Since $P_a\left(b\right)=b\times a$ and $E_a\left(b\right)=b^a$, it suffices to find surjections $s_1:C(c\times a,b)\to C(c,b^a)$ and $s_2:C(c,b^a)\to C(c\times a,b)$. First, we define $s_1\left(f\right):={\mathit{curry}}_f$. Now, we show that, for every C-arrow $g:c\to b^a$, there exists some C-arrow $f:c\times a\to b$ with $s_1\left(f\right)=g$, i.e., ${\mathit{curry}}_f=g$. We define $f:={\mathit{eval}}_{a,b}\circ (g\times {\mathit{id}}_a)$ and show ${\mathit{curry}}_f=g$. From the definition of f, we know that the C-arrow $g:c\to b^a$ satisfies the equality $f={\mathit{eval}}_{a,b}\circ (g\times {\mathit{id}}_a)$. However, Definition 19 implies that the only such C-arrow is ${\mathit{curry}}_f$; thus, ${\mathit{curry}}_f=g$. Second, we define $s_2\left(g\right):={\mathit{eval}}_{a,b}\circ (g\times {\mathit{id}}_a)$. Now, we show that, for every C-arrow $f:c\times a\to b$, there exists some C-arrow $g:c\to b^a$ with $s_2\left(g\right)=f$, i.e., ${\mathit{eval}}_{a,b}\circ (g\times {\mathit{id}}_a)=f$. We define $g:={\mathit{curry}}_f$ from which Definition 19 proves the goal. □

We are now ready to discuss the central aspects of categorical logic.

4. A Categorical Semantics

Based on the concepts introduced in the previous sections, this section elaborates a categorical semantics of our relational version of first-order logic. We advise the reader to consult Figure 1 to grasp the overall framework and the relationship between its various categories and functors.

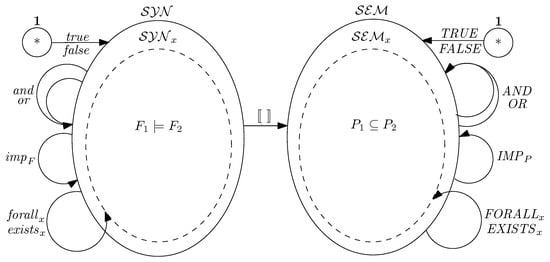
Figure 1. A Categorical Semantics of Relational First-Order Logic.

4.1. Syntactic Category and Formula Functors

We start by introducing the “syntactic category” $\mathcal{S}\mathcal{Y}\mathcal{N}=⟨\mathit{For},A,\circ ⟩$ as follows:

• The objects of this category are the formulas in the set $\mathit{For}$ which was introduced in Definition 6.
• The arrow class A consists of all pairs $⟨F_1,F_2⟩$ of formulas $F_1,F_2$ for which $F_1\vDash F_2$ holds, i.e., for which $F_2$ is a logical consequence of $F_1$, as described in Definition 8. The source object of such an arrow is $F_1$, and its target object is $F_2$. The existence of an arrow $f:F_1\to F_2$ thus indicates $F_1\vDash F_2$. The identity ${\mathit{id}}_F:F\to F$ indicates the fact $F\vDash F$.
• The composition ∘ denotes relational composition: for all arrows $f:F_1\to F_2$ and $g:F_2\to F_3$, and the existence of the arrow $(g\circ f):F_1\to F_3$ indicates the transitivity of the relation ⊧.

For every variable x, ${\mathcal{S}\mathcal{Y}\mathcal{N}}_x$ is that subcategory of $\mathcal{S}\mathcal{Y}\mathcal{N}$ whose objects are formulas whose semantics are independent of x (see Definition 4).

For reasons explained below, we will exclude from the syntactic category negations and equivalences, i.e., formulas of form $(\neg F)$ and $(F_1\leftrightarrow F_2)$. We may do so by considering them as the following syntactic shortcuts:

$$\begin{array}{cc}\hfill (\neg F)& \equiv (F\to \perp ),\hfill \\ \hfill (F_1\leftrightarrow F_2)& \equiv (F_1\to F_2)\wedge (F_2\to F_1).\hfill \end{array}$$

The validity of these shortcuts can be easily shown by proving the corresponding logical equivalences. Consequently, negations and equivalences need subsequently not be considered any more and their semantics need not be explicitly defined.

For the other kinds of formulas, we introduce the following (families of) “formula functors” where $\mathbf{1}$ is the “singleton” category with a single object ∗ (see Proposition 8):

$$\begin{array}{cc}\hfill \mathit{true}& :\mathbf{1}\to \mathcal{S}\mathcal{Y}\mathcal{N}\hfill \\ \hfill \mathit{false}& :\mathbf{1}\to \mathcal{S}\mathcal{Y}\mathcal{N}\hfill \\ \hfill \mathit{and}& :\mathcal{S}\mathcal{Y}\mathcal{N}\times \mathcal{S}\mathcal{Y}\mathcal{N}\to \mathcal{S}\mathcal{Y}\mathcal{N}\hfill \\ \hfill \mathit{or}& :\mathcal{S}\mathcal{Y}\mathcal{N}\times \mathcal{S}\mathcal{Y}\mathcal{N}\to \mathcal{S}\mathcal{Y}\mathcal{N}\hfill \\ \hfill {\mathit{imp}}_{F\in \mathit{For}}& :\mathcal{S}\mathcal{Y}\mathcal{N}\to \mathcal{S}\mathcal{Y}\mathcal{N}\hfill \\ \hfill {\mathit{forall}}_{x\in \mathit{Var}}& :\mathcal{S}\mathcal{Y}\mathcal{N}\to {\mathcal{S}\mathcal{Y}\mathcal{N}}_x\hfill \\ \hfill {\mathit{exists}}_{x\in \mathit{Var}}& :\mathcal{S}\mathcal{Y}\mathcal{N}\to {\mathcal{S}\mathcal{Y}\mathcal{N}}_x\hfill \end{array}$$

These functors map formulas to formulas, and logical consequences to logical consequences. The formula mappings are naturally defined as follows:

$$\begin{array}{cc}\hfill \mathit{true}(\ast )& :=\top \hfill \\ \hfill \mathit{false}(\ast )& :=\perp \hfill \\ \hfill \mathit{and}(F_1,F_2)& :=F_1\wedge F_2\hfill \\ \hfill \mathit{or}(F_1,F_2)& :=F_1\vee F_2\hfill \\ \hfill {\mathit{imp}}_{F_1}\left(F_2\right)& :=F_1\to F_2\hfill \\ \hfill {\mathit{forall}}_x\left(F\right)& :=\forall x.F\hfill \\ \hfill {\mathit{exists}}_x\left(F\right)& :=\exists x.F\hfill \end{array}$$

As for the mapping of consequences, we notice that all functors are covariant in their $\mathcal{S}\mathcal{Y}\mathcal{N}$ arguments. It is exactly for this reason that negation and equivalence (which do not allow covariance in their arguments) are not modeled as formula functors and that implication (which is only covariant in its second argument) is not modeled by a binary functor but by a family of unary functors.

Thus, we have for all formulas $F,F_1,F_2,G,G_1,G_2$ and every variable x the following (easy to prove) properties:

$$\begin{array}{cc}\hfill & (F_1\vDash G_1)\wedge (F_2\vDash G_2)\Rightarrow \mathit{and}(F_1,F_2)\vDash \mathit{and}(G_1,G_2)\hfill \\ \hfill & (F_1\vDash G_1)\wedge (F_2\vDash G_2)\Rightarrow \mathit{or}(F_1,F_2)\vDash \mathit{or}(G_1,G_2)\hfill \\ \hfill & (F_2\vDash G_2)\Rightarrow {\mathit{imp}}_{F_1}\left(F_2\right)\vDash {\mathit{imp}}_{F_1}\left(G_2\right)\hfill \\ \hfill & (F\vDash G)\Rightarrow {\mathit{forall}}_x\left(F\right)\vDash {\mathit{forall}}_x\left(G\right)\hfill \\ \hfill & (F\vDash G)\Rightarrow {\mathit{exists}}_x\left(F\right)\vDash {\mathit{exists}}_x\left(G\right)\hfill \end{array}$$

Therefore, the object maps of these functors naturally induce the necessary logical consequences.

4.2. Semantic Category and Predicate Functors

Next, we introduce the “semantic category” $\mathcal{S}\mathcal{E}\mathcal{M}=⟨\mathit{Pred},B,\circ ⟩$ as follows:

• The objects of this category are the predicates in the set $\mathit{Pred}$ which was introduced in Definition 5 (thus $\mathcal{S}\mathcal{E}\mathcal{M}$-objects are relations, i.e., sets).
• The arrow class B consists of all pairs $⟨P_1,P_2⟩$ of predicates $P_1,P_2$ for which $P_1\subseteq P_2$ holds, i.e., for which $P_1$ is a subset of $P_2$. The source object of such an arrow is $P_1$, its target object is $P_2$. The existence of an arrow $f:P_1\to P_2$ thus indicates $P_1\subseteq P_2$. The identity ${\mathit{id}}_P:P\to P$ indicates the fact $P\subseteq P$.
• The composition ∘ denotes relational composition: for all arrows $f:P_1\to P_2$ and $g:P_2\to P_3$, the existence of the arrow $(g\circ f):P_1\to P_3$ indicates the transitivity of the relation ⊆.

For every variable x, ${\mathcal{S}\mathcal{E}\mathcal{M}}_x$ is the subcategory of $\mathcal{S}\mathcal{E}\mathcal{M}$ whose objects are predicates that are independent of x (see Definition 4).

Corresponding to the various kinds of formula constructions, we will have the following “predicate functors” (respectively families of functors):

$$\begin{array}{cc}\hfill \mathit{TRUE}& :\mathbf{1}\to \mathcal{S}\mathcal{E}\mathcal{M}\hfill \\ \hfill \mathit{FALSE}& :\mathbf{1}\to \mathcal{S}\mathcal{E}\mathcal{M}\hfill \\ \hfill \mathit{AND}& :\mathcal{S}\mathcal{E}\mathcal{M}\times \mathcal{S}\mathcal{E}\mathcal{M}\to \mathcal{S}\mathcal{E}\mathcal{M}\hfill \\ \hfill \mathit{OR}& :\mathcal{S}\mathcal{E}\mathcal{M}\times \mathcal{S}\mathcal{E}\mathcal{M}\to \mathcal{S}\mathcal{E}\mathcal{M}\hfill \\ \hfill {\mathit{IMP}}_{P\in \mathit{Pred}}& :\mathcal{S}\mathcal{E}\mathcal{M}\to \mathcal{S}\mathcal{E}\mathcal{M}\hfill \\ \hfill {\mathit{FORALL}}_{x\in \mathit{Var}}& :\mathcal{S}\mathcal{E}\mathcal{M}\to {\mathcal{S}\mathcal{E}\mathcal{M}}_x\hfill \\ \hfill {\mathit{EXISTS}}_{x\in \mathit{Var}}& :\mathcal{S}\mathcal{E}\mathcal{M}\to {\mathcal{S}\mathcal{E}\mathcal{M}}_x\hfill \end{array}$$

These functors map predicates to predicates and subset relations to subset relations (their detailed definitions will be given later). As we will see, these functors are covariant in their $\mathcal{S}\mathcal{E}\mathcal{M}$-arguments, i.e., we have for all predicates $P,P_1,P_2,Q,Q_1,Q_2$ and every variable x the following properties:

$$\begin{array}{cc}\hfill & (P_1\subseteq Q_1)\wedge (P_2\subseteq Q_2)\Rightarrow \mathit{AND}(P_1,P_2)\subseteq \mathit{AND}(Q_1,Q_2)\hfill \\ \hfill & (P_1\subseteq Q_1)\wedge (P_2\subseteq Q_2)\Rightarrow \mathit{OR}(P_1,P_2)\subseteq \mathit{OR}(Q_1,Q_2)\hfill \\ \hfill & (P_2\subseteq Q_2)\Rightarrow {\mathit{IMP}}_{P_1}\left(P_2\right)\subseteq {\mathit{IMP}}_{P_1}\left(Q_2\right)\hfill \\ \hfill & (P\subseteq Q)\Rightarrow {\mathit{FORALL}}_x\left(P\right)\subseteq {\mathit{FORALL}}_x\left(Q\right)\hfill \\ \hfill & (P\subseteq Q)\Rightarrow {\mathit{EXISTS}}_x\left(P\right)\subseteq {\mathit{EXISTS}}_x\left(Q\right)\hfill \end{array}$$

Therefore, the object maps of these functors (defined by the respective predicate operations) naturally induce appropriate arrow maps (the corresponding subset relations).

4.3. The Semantic Functor

Now, we introduce the “semantic functor”

$$〚〛:\mathcal{S}\mathcal{Y}\mathcal{N}\to \mathcal{S}\mathcal{E}\mathcal{M}$$

defined as follows:

• For every $\mathcal{S}\mathcal{Y}\mathcal{N}$-object F, i.e., formula F, $〚F〛$ denotes the semantics of F as defined in Definition 7, which according to Proposition 3 is a predicate, i.e., indeed a $\mathcal{S}\mathcal{E}\mathcal{M}$-object.
• For every $\mathcal{S}\mathcal{Y}\mathcal{N}$-arrow $f:F_1\to F_2$, i.e., every pair of formulas $F_1$ and $F_2$ with $F_1\vDash F_2$, we have the $\mathcal{S}\mathcal{E}\mathcal{M}$-arrow $〚f〛:〚F_1〛\to 〚F_2〛$, i.e., the fact $〚F_1〛\subseteq 〚F_2〛$, which is a direct consequence of Definition 10 which introduces the ⊧ relation.

This semantic functor establishes the relationship between the previously introduced formula functors and predicate functors by the following identities on $\mathcal{S}\mathcal{E}\mathcal{M}$-objects, i.e., predicate identities that will hold for all formulas $F,F_1,F_2$ and every variable x:

$$\begin{array}{cc}\hfill & 〚\mathit{true}(\ast )〛=\mathit{TRUE}(\ast )\hfill \\ \hfill & 〚\mathit{false}(\ast )〛=\mathit{FALSE}(\ast )\hfill \\ \hfill & 〚\mathit{and}(F_1,F_2)〛=\mathit{AND}(〚F_1〛,〚F_2〛)\hfill \\ \hfill & 〚\mathit{or}(F_1,F_2)〛=\mathit{OR}(〚F_1〛,〚F_2〛)\hfill \\ \hfill & 〚{\mathit{imp}}_{F_1}\left(F_2\right)〛={\mathit{IMP}}_{〚F_1〛}(〚F_2〛)\hfill \\ \hfill & 〚{\mathit{forall}}_x\left(F\right)〛={\mathit{FORALL}}_x(〚F〛)\hfill \\ \hfill & 〚{\mathit{exists}}_x\left(F\right)〛={\mathit{EXISTS}}_x(〚F〛)\hfill \end{array}$$

4.4. Categorical Semantics of First-Order Relational Logic

We are now going to elaborate in detail the semantic functors from which all of the above can be shown; this elaboration is inspired from and indeed directly derived from the well-known logical inference rules of first-order logic. The resulting definitions are based on the categorical notions introduced in Section 3, i.e., final and initial objects, products and coproducts, exponentials, and left and right adjoints, respectively. This gives us for every logical operation a “universal” definition of its semantics. Nevertheless, this semantics is also “constructive” in the sense that it is explicitly defined from well-known set-theoretic operations.

4.4.1. Logical Constants

The role of the logical constants in reasoning is exhibited by the following two “rules” which follow directly from Definition 8 (these rules are propositions that are valid for every formula F; they mimic the corresponding inference rules of first-order logic):

$$\begin{array}{c}\hfill F\vDash \top \perp \vDash F\end{array}$$

In other words, ⊤ is a logical consequence of every formula F, i.e., ⊤ is the “weakest” formula. Dually, every formula F is a logical consequence of ⊥, i.e., ⊥ is the “strongest” formula. This implies that $\mathit{true}(\ast )=\top$ is the final object of category $\mathcal{S}\mathcal{Y}\mathcal{N}$ and $\mathit{false}(\ast )=\perp$ is its initial one (see Definition 16). Then, Proposition 8 implies $C_{\mathcal{S}\mathcal{Y}\mathcal{N}}⊣\mathit{true}$ and $\mathit{false}⊣C_{\mathcal{S}\mathcal{Y}\mathcal{N}}$, i.e., functor $\mathit{true}$ is the right adjoint of the constant functor $C_{\mathcal{S}\mathcal{Y}\mathcal{N}}:\mathcal{S}\mathcal{Y}\mathcal{N}\to \mathbf{1}$ while functor $\mathit{false}$ is its left one.

Correspondingly, $\mathit{TRUE}(\ast )$ is the final object of category $\mathcal{S}\mathcal{E}\mathcal{M}$ (the “weakest” predicate, i.e., the predicate which is a superset of every predicate) and $\mathit{FALSE}(\ast )$ is its initial object (the “strongest” predicate, i.e., the predicate which is a subset of every predicate). By Proposition 8, we then have $C_{\mathcal{S}\mathcal{E}\mathcal{M}}⊣\mathit{TRUE}$ and $\mathit{FALSE}⊣C_{\mathcal{S}\mathcal{E}\mathcal{M}}$, i.e., functor $\mathit{TRUE}$ is the right adjoint of the constant functor $C_{\mathcal{S}\mathcal{E}\mathcal{M}}:\mathcal{S}\mathcal{E}\mathcal{M}\to \mathbf{1}$ while functor $\mathit{FALSE}$ is its left one.

Therefore, corresponding to the above rules for formulas, we have the following rules for every predicate P:

$$\begin{array}{c}\hfill P\subseteq \mathit{TRUE}(\ast )\mathit{FALSE}(\ast )\subseteq P\end{array}$$

Since final and initial objects are unique, these rules actually represent implicit but unique definitions of $\mathit{TRUE}(\ast )$ and $\mathit{FALSE}(\ast )$ which can be explicitly written as

$$\begin{array}{c}\hfill \mathit{TRUE}(\ast ):=\bigcup \left\{P\right|P\in \mathit{Pred}\}\mathit{FALSE}(\ast ):=\bigcap \{P|P\in \mathit{Pred}\}\end{array}$$

i.e., $\mathit{TRUE}(\ast )$ is the union of all predicates and $\mathit{FALSE}(\ast )$ is their intersection. Thus, we have derived alternative characterizations $〚\top 〛=\mathit{TRUE}(\ast )$ and $〚\perp 〛=\mathit{FALSE}(\ast )$ that are both constructive and universal (Proposition 5 gives us $〚\top 〛=\mathit{Ass}$ and $〚\perp 〛=\varnothing$ from which it is easy to verify these equalities).

4.4.2. Conjunction and Disjunction

The role of conjunction in reasoning is exhibited by the following rules for arbitrary formulas $F_1,F_2,F$ (the first two ones mimic the logical inference rules of “elimination”, and the last one mimics the inference rule of “introduction”):

$$\begin{array}{c}{F}_1\wedge F_2\vDash F_1\\ F_1\wedge F_2\vDash F_2\\ (F\vDash F_1)\wedge (F\vDash F_2)\Rightarrow (F\vDash F_1\wedge F_2)\end{array}$$

Dually, we have the following rules for disjunction:

$$\begin{array}{c}{F}_1\vDash F_1\vee F_2\\ F_2\vDash F_1\vee F_2\\ (F_1\vDash F)\wedge (F_2\vDash F)\Rightarrow (F_1\vee F_2\vDash F)\end{array}$$

These rules (whose soundness can be established with the help of Definition 8) state that $(F_1\wedge F_2)$ is the “weakest” formula F for which both $(F\vDash F_1)$ and $(F\vDash F_2)$ hold and that $(F_1\vee F_2)$ is the “strongest” formula F for which both $(F_1\vDash F)$ and $(F_2\vDash F)$ hold. Thus, $\mathit{and}(F_1,F_2)=(F_1\wedge F_2)$ is the product of the $\mathcal{S}\mathcal{Y}\mathcal{N}$-objects $F_1$ and $F_2$ and $\mathit{or}(F_1,F_2)=(F_1\vee F_2)$ is their coproduct (see Definition 17). Furthermore, by Proposition 9, we have ${\Delta }_{\mathcal{S}\mathcal{Y}\mathcal{N}}⊣\mathit{and}$ and $\mathit{or}⊣{\Delta }_{\mathcal{S}\mathcal{Y}\mathcal{N}}$ i.e., functor $\mathit{and}$ is the right adjoint of the diagonal functor ${\Delta }_{\mathcal{S}\mathcal{Y}\mathcal{N}}:\mathcal{S}\mathcal{Y}\mathcal{N}\to \mathcal{S}\mathcal{Y}\mathcal{N}\times \mathcal{S}\mathcal{Y}\mathcal{N}$ while functor $\mathit{or}$ is its left one.

Correspondingly $\mathit{AND}(P_1,P_2)$ is the product of the $\mathcal{S}\mathcal{E}\mathcal{M}$-objects $P_1$ and $P_2$ (the “weakest” predicate P for which both $(P\subseteq P_1)$ and $(P\subseteq P_2)$ hold) and $\mathit{OR}(P_1,P_2)$ is their coproduct (the “strongest” predicate P for which $(P_1\subseteq P)$ and $(P_2\subseteq P)$ hold). By Proposition 9, we then have ${\Delta }_{\mathcal{S}\mathcal{E}\mathcal{M}}⊣\mathit{AND}$ and $\mathit{OR}⊣{\Delta }_{\mathcal{S}\mathcal{E}\mathcal{M}}$ i.e., functor $\mathit{AND}$ is the right adjoint of the diagonal functor ${\Delta }_{\mathcal{S}\mathcal{E}\mathcal{M}}:\mathcal{S}\mathcal{E}\mathcal{M}\to \mathcal{S}\mathcal{E}\mathcal{M}\times \mathcal{S}\mathcal{E}\mathcal{M}$, while functor $\mathit{OR}$ is its left one.

Thus, we have, corresponding to the rules for formulas, the following rules for all predicates $P_1,P_2,P$:

$$\begin{array}{c}\mathit{AND}(P_1,P_2)\subseteq P_1\\ \mathit{AND}(P_1,P_2)\subseteq P_2\\ (P\subseteq P_1)\wedge (P\subseteq P_2)\Rightarrow (P\subseteq \mathit{AND}(P_1,P_2))\end{array}$$

Dually, we have

$$\begin{array}{c}{P}_1\subseteq \mathit{OR}(P_1,P_2)\\ P_2\subseteq \mathit{OR}(P_1,P_2)\\ (P_1\subseteq P)\wedge (P_2\subseteq P)\Rightarrow (\mathit{OR}(P_1,P_2)\subseteq P)\end{array}$$

Since products and coproducts are uniquely defined, these rules actually represent implicit but unique definitions of $\mathit{AND}(P_1,P_2)$ and $\mathit{OR}(P_1,P_2)$ which can be explicitly written as follows:

$$\begin{array}{cc}\hfill \mathit{AND}(P_1,P_2)& :=\bigcup \{P\in \mathit{Pred}|P\subseteq P_1\wedge P\subseteq P_2\}\hfill \\ \hfill \mathit{OR}(P_1,P_2)& :=\bigcap \{P\in \mathit{Pred}|P_1\subseteq P\wedge P_2\subseteq P\}\hfill \end{array}$$

This gives us alternative characterizations $〚F_1\wedge F_2〛=〚F_1〛\cup 〚F_2〛=\mathit{AND}(〚F_1〛,〚F_2〛)$ and $〚F_1\vee F_2〛=〚F_1〛\cup 〚F_2〛=\mathit{OR}(〚F_1〛,〚F_2〛)$ that are both constructive and universal (Proposition 5 implies $〚F_1\wedge F_2〛=〚F_1〛\cap 〚F_2〛$ and $〚F_1\vee F_2〛=〚F_1〛\cup 〚F_2〛$ from which it is not difficult to verify these equalities).

4.4.3. Implication

The role of implication in reasoning is exhibited by the following rules for arbitrary formulas $F_1,F_2,F$ (the first rule mimics the logical inference rules of “implication elimination” or “modus ponens”, the last one mimics the inference rule of “implication introduction”):

$$\begin{array}{c}(F_1\to F_2)\wedge F_1\vDash F_2\\ (F\wedge F_1\vDash F_2)\Rightarrow (F\vDash F_1\to F_2)\end{array}$$

These rules (whose soundness can be established with the help of Definition 8) state that $(F_1\to F_2)$ is the “weakest” formula F for which $(F\wedge F_1\vDash F_2)$ holds. Thus, ${\mathit{imp}}_{F_1}\left(F_2\right)=(F_1\to F_2)$ is the exponential of the $\mathcal{S}\mathcal{Y}\mathcal{N}$-objects $F_1$ and $F_2$ (see Definition 19). Proposition 10 then gives us ${\mathit{and}}_{F_1}⊣{\mathit{imp}}_{F_1}$, i.e., functor ${\mathit{imp}}_{F_1}$ is the right adjoint of the unary conjunction functor ${\mathit{and}}_{F_1}:\mathcal{S}\mathcal{Y}\mathcal{N}\to \mathcal{S}\mathcal{Y}\mathcal{N}\times \mathcal{S}\mathcal{Y}\mathcal{N}$ with object map ${\mathit{and}}_{F_1}\left(F_2\right):=\mathit{and}(F_1,F_2)=F_1\wedge F_2$.

Correspondingly, ${\mathit{IMP}}_{P_1}\left(P_2\right)$ is the product of the $\mathcal{S}\mathcal{E}\mathcal{M}$-objects $P_1$ and $P_2$ (the “weakest” predicate P for which $(P\cap P_1\subseteq P_2)$ holds; Proposition 10 then gives us ${\mathit{AND}}_{P_1}⊣{\mathit{IMP}}_{P_1}$, i.e., functor ${\mathit{IMP}}_{P_1}$ is the right adjoint of the unary functor ${\mathit{AND}}_{P_1}:\mathcal{S}\mathcal{E}\mathcal{M}\to \mathcal{S}\mathcal{E}\mathcal{M}\times \mathcal{S}\mathcal{E}\mathcal{M}$ with object map ${\mathit{AND}}_{P_1}\left(P_2\right):=\mathit{AND}(P_1,P_2)=P_1\cup P_2$.

Thus, corresponding to above rules for formulas, we have the following rules for all predicates $P_1,P_2,P$:

$$\begin{array}{c}{\mathit{IMP}}_{P_1}\left(P_2\right)\cap P_1\subseteq P_2\\ (P\cap P_1\subseteq P_2)\Rightarrow (P\subseteq {\mathit{IMP}}_{P_1}\left(P_2\right))\end{array}$$

Since exponentials are uniquely defined, these rules represent an implicit but unique definition of ${\mathit{IMP}}_{P_1}\left(P_2\right)$ which can be explicitly written as follows:

$$\begin{array}{cc}\hfill {\mathit{IMP}}_{P_1}\left(P_2\right)& :=\bigcup \{P\in \mathit{Pred}|P\cap P_1\subseteq P_2\}\hfill \end{array}$$

This gives us an alternative characterization $〚F_1\to F_2〛={\mathit{IMP}}_{〚F_1〛}(〚F_2〛)$ that is both constructive and universal (Proposition 5 implies $〚F_1\wedge F_2〛=\overline{〚F_1〛}\cup 〚F_2〛$ from which it is possible to verify this equality).

4.4.4. Universal and Existential Quantification

The role of universal quantification in reasoning is exhibited by the following rules for arbitrary formulas $F,G$ provided that the semantics $〚G〛$ of G do not depend on x (see Definition 4):

$$\begin{array}{c}\forall x.F\vDash F\\ (G\vDash F)\Rightarrow (G\vDash \forall x.F)\end{array}$$

The first rule mimics the logical inference rule of “universal elimination”, the second one mimics the inference rule of “universal introduction” (except that our version of first-order logic does not involve terms and variables and thus copes without variable substitutions). This pair of rules in a nutshell yields that $(\forall x.F)$ is the “weakest” formula G from which F is a logical consequence and whose semantics do not depend on x. Dually, we have for existential quantification the following pair of rules:

$$\begin{array}{c}F\vDash \exists x.F\\ (F\vDash G)\Rightarrow (\exists x.F\vDash G)\end{array}$$

These rules state that $(\exists x.F)$ is the “strongest” formula G that is a logical consequence of F and whose semantics $〚G〛$ does not depend on x.

We are now going to derive appropriate categorical characterizations of the corresponding functors ${\mathit{forall}}_{x\in \mathit{Var}}:\mathcal{S}\mathcal{Y}\mathcal{N}\to {\mathcal{S}\mathcal{Y}\mathcal{N}}_x$ and ${\mathit{exists}}_{x\in \mathit{Var}}:\mathcal{S}\mathcal{Y}\mathcal{N}\to {\mathcal{S}\mathcal{Y}\mathcal{N}}_x$ from the category $\mathcal{S}\mathcal{Y}\mathcal{N}$ of all formulas to the subcategory ${\mathcal{S}\mathcal{Y}\mathcal{N}}_x$ of all those formulas whose semantics do not depend on x. For this, we may notice that, from above rules, the relations $(G\vDash F)$ and $(F\vDash G)$ involve two kinds of relations, a more general relation F that may depend on x and a more special relation G that is independent of x. In order to bring all relations to the “same level”, we introduce a syntactic “injection” functor $I_x:{\mathcal{S}\mathcal{Y}\mathcal{N}}_x\to \mathcal{S}\mathcal{Y}\mathcal{N}$ whose maps are just identities, i.e., $I_x\left(G\right)=G$ and $I_x(f:F\to G)=f:F\to G$. This allows us to express above rules as

$$\begin{array}{c}{I}_x\left({\mathit{forall}}_x\left(F\right)\right)\vDash F\\ (I_x\left(G\right)\vDash F)\Rightarrow (G\vDash {\mathit{forall}}_x\left(F\right))\end{array}$$

and dually

$$\begin{array}{c}F\vDash I_x\left({\mathit{exists}}_x\left(F\right)\right)\\ (F\vDash I_x\left(G\right))\Rightarrow ({\mathit{exists}}_x\left(F\right)\vDash G)\end{array}$$

Now, the first set of rules matches the assumptions of the second part of Proposition 7 for $F:=I_x$ and $G:={\mathit{forall}}_x$ (considering that the satisfaction relation ⊧ denotes the existence of an arrow in categories $\mathcal{S}\mathcal{Y}\mathcal{N}$, respectively ${\mathcal{S}\mathcal{Y}\mathcal{N}}_x$); thus, we have $I_x⊣{\mathit{forall}}_x$. Likewise, the second set of rules matches the assumptions of the first part of that proposition for $F:={\mathit{exists}}_x$ and $G:=I_x$; thus, we have ${\mathit{exists}}_x⊣I_x$. Summarizing, the universal functor ${\mathit{forall}}_x$ is the right adjoint of the injection functor $I_x$ while the existential functor ${\mathit{exists}}_x$ is its left adjoint.

These considerations can be easily transferred to categorical characterizations of the corresponding functors ${\mathit{FORALL}}_{x\in \mathit{Var}}:\mathcal{S}\mathcal{E}\mathcal{M}\to {\mathcal{S}\mathcal{E}\mathcal{M}}_x$ and ${\mathit{EXISTS}}_{x\in \mathit{Var}}:\mathcal{S}\mathcal{E}\mathcal{M}\to {\mathcal{S}\mathcal{E}\mathcal{M}}_x$ from the category $\mathcal{S}\mathcal{E}\mathcal{M}$ of all predicates to the subcategory ${\mathcal{S}\mathcal{E}\mathcal{M}}_x$ of all those predicates that do not depend on x with the semantic “injection” functor $J_x:{\mathcal{S}\mathcal{E}\mathcal{M}}_x\to \mathcal{S}\mathcal{E}\mathcal{M}$ whose maps are just identities, i.e., $J_x\left(Q\right)=Q$ and $J_x(f:P\to Q)=f:P\to Q$. We then have

$$\begin{array}{c}{J}_x\left({\mathit{FORALL}}_x\left(P\right)\right)\subseteq P\\ (J_x\left(Q\right)\subseteq P)\Rightarrow (Q\subseteq {\mathit{FORALL}}_x\left(P\right))\end{array}$$

and dually

$$\begin{array}{c}P\subseteq J_x\left({\mathit{EXISTS}}_x\left(P\right)\right)\\ (P\subseteq J_x\left(Q\right))\Rightarrow ({\mathit{EXISTS}}_x\left(P\right)\subseteq Q)\end{array}$$

Now, the first set of rules matches the assumptions of the second part of Proposition 7 for $F:=J_x$ and $G:={\mathit{FORALL}}_x$ (considering that the subset relation ⊆ denotes the existence of an arrow in categories $\mathcal{S}\mathcal{E}\mathcal{M}$, respectively ${\mathcal{S}\mathcal{E}\mathcal{M}}_x$); thus, we have $J_x⊣{\mathit{FORALL}}_x$. Likewise, the second set of rules matches the assumptions of the first part of that proposition for $F:={\mathit{EXISTS}}_x$ and $G:=J_x$; thus, we have ${\mathit{EXISTS}}_x⊣J_x$. Summarizing, the universal functor ${\mathit{FORALL}}_x$ is the right adjoint of the injection functor $J_x$ while the existential functor ${\mathit{EXISTS}}_x$ is its left adjoint.

The above rules say that ${\mathit{FORALL}}_x\left(P\right)$ is the weakest predicate Q that does not depend on x for which $(J_x\left(Q\right)\subseteq Q)$ holds while ${\mathit{EXISTS}}_x\left(P\right)$ is the strongest predicate Q that does not depend on x for which $(Q\subseteq J_x\left(Q\right))$ holds. Since left and right adjoints are uniquely defined, these rules represent implicit but unique definitions of ${\mathit{FORALL}}_x\left(P\right)$ and ${\mathit{EXISTS}}_x\left(P\right)$ which can be explicitly written as follows:

$$\begin{array}{cc}\hfill {\mathit{FORALL}}_x\left(P\right)& :=\bigcup \{Q\in {\mathit{Pred}}_x|J_x\left(Q\right)\subseteq P\}\hfill \\ \hfill {\mathit{EXISTS}}_x\left(P\right)& :=\bigcap \{Q\in {\mathit{Pred}}_x|P\subseteq J_x\left(Q\right)\}\hfill \end{array}$$

From $J_x\left(Q\right)=Q$ and $Q\in {\mathit{Pred}}_x\iff Q\in \mathit{Pred}\wedge Q⫫x$ (see Definition 5), this can also be written as follows:

$$\begin{array}{cc}\hfill {\mathit{FORALL}}_x\left(P\right)& :=\bigcup \{Q\in \mathit{Pred}|Q⫫x\wedge Q\subseteq P\}\hfill \\ \hfill {\mathit{EXISTS}}_x\left(P\right)& :=\bigcap \{Q\in \mathit{Pred}|Q⫫x\wedge P\subseteq Q\}\hfill \end{array}$$

Thus, we have derived alternative characterizations $〚\forall x.F〛={\mathit{FORALL}}_x(〚F〛)$ and $〚\exists x.F〛={\mathit{EXISTS}}_x(〚F〛)$ that are both constructive and universal. This is exactly the characterization whose correctness we have proved in Proposition 6.

5. An Implementation of the Categorical Semantics

In this section, we describe how the constructions that we have theoretically modeled in Section 2 can be actually implemented. For this purpose, we use RISCAL (RISCAL is developed at JKU, Linz, Austria, https://www3.risc.jku.at/research/formal/software/RISCAL/, see [13]), the RISC Algorithm Language [13,17], a specification language, and an associated software system for modeling mathematical theories and algorithms in a specification language based on first-order logic and set theory. The language is based on a type system where all types have finite sizes (specified by the user); this allows for fully automatically deciding formulas and verifying the correctness of algorithms for all possible inputs. To this end, the system translates every syntactic phrase into an executable form of its denotational semantics; the RISCAL model checker evaluates these semantics to determine the results of algorithms and the truth values of formulas such as the postconditions of algorithms. Since the domains of RISCAL models have (parameterized but) finite size, the validity of all theorems and the correctness of all algorithms can be fully automatically checked; the system has been mainly employed in educational scenarios [18,19]. Figure 2 gives a screenshot of the software with the RISCAL model that is going to be discussed below.

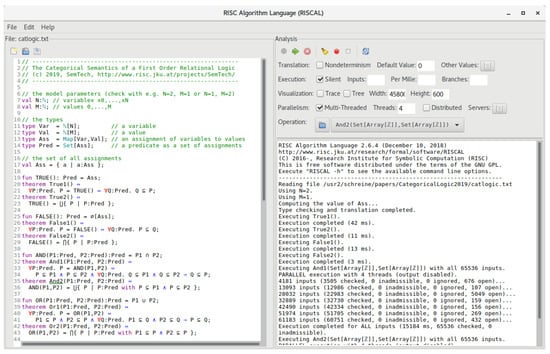
Figure 2. The RISCAL Software.

Figure 3 and Figure 4 list a RISCAL model of the categorical semantics over a domain of $N+1$ variables (identified with the natural numbers $0,\dots ,N$) with $M+1$ values, for arbitrary model parameters $N,M\in {\mathbb{N}}_0$; all theorems over these domains are decidable and can be checked by RISCAL. The RISCAL definition of domains, functions, and predicates closely correspond to those given in this paper; in particular, we have a domain Pred of predicates (since the number of variables is finite, by definition all relations are predicates) and predicate functions TRUE, FALSE, AND, OR, IMP, FORALL, EXISTS. Different from the categorical formulation, IMP is a binary function, not a family of unary functions; likewise, FORALL and EXISTS are binary functions whose first argument is a variable. Furthermore, we introduce functions NOT and EQUIV for the semantics of negation and conjunction and show by theorems Not and Equiv that they can be reduced to the other functions.

Figure 3. A RISCAL Model of the Categorical Semantics (Part 1).

Figure 4. A RISCAL Model of the Categorical Semantics (Part 2).

All other logical operations are first defined in their usual set-theoretic form. Subsequently, we describe their categorical semantics by a pair of theorems: the first theorem claims that the set-theoretic semantics is equivalent to an implicit definition of the categorical semantics while the second theorem claims equivalence to the corresponding constructive definition. Choosing small parameter values $N=2$ and $M=1$ (i.e., relations with variables $x_0,x_1,x_2$ and values $0,1$), RISCAL can easily check the validity of all claims, as demonstrated by the following output:

RISC Algorithm Language 2.6.4 (10 December 2018)

http://www.risc.jku.at/research/formal/software/RISCAL

(C) 2016-, Research Institute for Symbolic Computation (RISC)

This is free software distributed under the terms of the GNU GPL.

Execute "RISCAL -h" to see the available command line options.

-----------------------------------------------------------------

Reading file /usr2/schreine/papers/CategoricalLogic2019/catlogic.txt

Using N=2.

Using M=1.

Computing the value of Ass...

Computing the value of TRUE...

Computing the value of FALSE...

Type checking and translation completed.

Executing True1().

Execution completed (3 ms).

Executing True2().

Execution completed (1 ms).

Executing False1().

Execution completed (0 ms).

Executing False2().

Execution completed (1 ms).

Executing And1(Set[Array[ℤ]],Set[Array[ℤ]]) with all 65536 inputs.

PARALLEL execution with 4 threads (output disabled).

...

Execution completed for ALL inputs (18,373 ms, 65,536 checked, 0 inadmissible).

Executing And2(Set[Array[ℤ]],Set[Array[ℤ]]) with all 65,536 inputs.

PARALLEL execution with 4 threads (output disabled).

46273 inputs (36446 checked, 0 inadmissible, 0 ignored, 9827 open)...

Execution completed for ALL inputs (3576 ms, 65536 checked, 0 inadmissible).

Executing Or1(Set[Array[ℤ]],Set[Array[ℤ]]) with all 65536 inputs.

PARALLEL execution with 4 threads (output disabled).

...

Execution completed for ALL inputs (26,889 ms, 65,536 checked, 0 inadmissible).

Executing Or2(Set[Array[ℤ]],Set[Array[ℤ]]) with all 65,536 inputs.

PARALLEL execution with 4 threads (output disabled).

42,676 inputs (32,887 checked, 0 inadmissible, 0 ignored, 9789 open)...

Execution completed for ALL inputs (3907 ms, 65,536 checked, 0 inadmissible).

Executing Imp1(Set[Array[ℤ]],Set[Array[ℤ]]) with all 65,536 inputs.

PARALLEL execution with 4 threads (output disabled).

...

Execution completed for ALL inputs (48,592 ms, 65,536 checked, 0 inadmissible).

Executing Imp2(Set[Array[ℤ]],Set[Array[ℤ]]) with all 65,536 inputs.

PARALLEL execution with 4 threads (output disabled).

...

Execution completed for ALL inputs (9462 ms, 65,536 checked, 0 inadmissible).

Executing Not(Set[Array[ℤ]]) with all 256 inputs.

PARALLEL execution with 4 threads (output disabled).

Execution completed for ALL inputs (28 ms, 256 checked, 0 inadmissible).

Executing Equiv(Set[Array[ℤ]],Set[Array[ℤ]]) with all 65,536 inputs.

PARALLEL execution with 4 threads (output disabled).

Execution completed for ALL inputs (354 ms, 65,536 checked, 0 inadmissible).

Executing Forall1(ℤ,Set[Array[ℤ]]) with all 768 inputs.

PARALLEL execution with 4 threads (output disabled).

Execution completed for ALL inputs (1315 ms, 768 checked, 0 inadmissible).

Executing Forall2(ℤ,Set[Array[ℤ]]) with all 768 inputs.

PARALLEL execution with 4 threads (output disabled).

Execution completed for ALL inputs (512 ms, 768 checked, 0 inadmissible).

Executing Exists1(ℤ,Set[Array[ℤ]]) with all 768 inputs.

PARALLEL execution with 4 threads (output disabled).

Execution completed for ALL inputs (1299 ms, 768 checked, 0 inadmissible).

Executing Exists2(ℤ,Set[Array[ℤ]]) with all 768 inputs.

PARALLEL execution with 4 threads (output disabled).

Execution completed for ALL inputs (461 ms, 768 checked, 0 inadmissible).

These values are, however, the largest ones with which model checking is realistically feasible; choosing, for example, $N=3$ and $M=2$ gives for the checking theorem And1 about $4\times {10}^9$ possible inputs whose checking on a single processor core would take RISCAL more than two decades.

6. Conclusions

In this paper, we developed a novel categorical interpretation of the semantics of a relational (term-less) variant of first-order logic [20] with the goal to aid the intuitive understanding of these formulas and to lay the seed of tools that illustrate the meaning of these formulas by the visualization of their semantics. The main advantage of this formulation is the (in comparison to other previous approaches) much more explicit illustration of the various logical constructions (connectives and quantifiers) as categorical notions; this may provide an alternative route to teaching semantics for first-order logic. Furthermore, since this categorical semantics is constructive, we could directly implement (and thus validate) it in the RISCAL software.

We hope that this paper, by its self-contained nature and by focusing on the core principles of categorical logic rather than attempting an exhaustive treatment, contributes to the more widespread dissemination of categorical ideas to students and researchers of logic, its applications, and its automation; in particular, it may provide an alternative view on the semantics of first-order logic by complementing the classical formulation and thus help to gain deeper insights.

It remains to be shown, however, whether and how this view can be indeed helpful and illuminating in educational scenarios, i.e., in courses on logic and its applications. In previous works [21,22,23,24], we have strived to improve the understanding of the formal semantics of programming languages by developing corresponding tools with appropriate visualization techniques, partially also based on categorical principles. Other work of ours [25] has extended this work towards the visualization of the semantics of first-order formulas by pruned evaluation trees, however, based on the classical formulation. Future work of us will investigate how the categorical principles outlined in this paper can be transferred to corresponding novel tools and visualization techniques for education in semantics and logic—for instance, in describing software component systems whose semantics are described both from the categorical and the logical side, or elaborating a precise logical definition of contracts that have to be satisfied for a successful composition of components.