Construction of S-Box Based on Chaotic Map and Algebraic Structures

Abstract

The Advanced Encryption Standard (AES) is widely used in different kinds of security applications. The substitution box (S-box) is the main component of many modern symmetric encryption ciphers that provides confusion between the secret key and ciphertext. The S-box component that is used in AES is fixed. If we construct this component dynamically, the encryption strength of AES would be greater than before. In this manuscript, we used chaotic logistic map, Mobius transformation and symmetric group $S_{256}$ to construct S-box for AES. The idea behind the proposed work is to make supplementary safe S-box. The presented S-box is analyzed for the following analyses: linear approximation probability (LP), nonlinearity (NL), differential approximation probability (DP), strict avalanche criterion (SAC), and bit independence criterion (BIC). The analyses show that the proposed technique is useful in generating high resistance S-box to known attacks.

1. Introduction

The concept of substitution box (S-box) was first given by Claude Shannon in 1949 [1] after that this component got the attention of many researchers. The S-box has wide usage in secure communication, and it is the core component in popular block ciphers such as data encryption standard (DES), international data encryption algorithm (IDEA) and advanced encryption standard (AES) [2] etc. Most of the time, the strength of any cryptosystem [3,4,5,6,7,8] depends on the resistance of S-boxes against known attacks, which is why, to design a robust cipher, the synthesis of strong S-boxes is required. The strength of S-box [9,10,11,12,13,14] usually depends on some algebraic and statistical criteria, such as linear and differential analyses, strict avalanche criterion (SAC) to measure maximal confusion ability between key and cipher text, bit independence criteria to know the dependency of plaintext, and ciphertext bits. Linear and differential cryptanalysis shows that it is essential to propose dominant ciphers that can resist renown attacks. The AES is largely acknowledged as a valid cryptosystem. One of the vital components of AES is its S-box, which is constructed based on the inversion of $GF\left(2^8\right)$ elements and an affine transformation. Due to AES popularity in the communication systems, S-box got more attention.

In the past 10 to 15 years, some cryptosystems have been constructed by chaotic maps [15,16,17,18,19,20,21] to provide more secure encryption techniques. The safety of secret data can be achieved using dynamical chaotic systems in chaos-based secure communication [22,23,24,25,26,27,28]. The inclusion of chaotic maps in vulnerable schemes can make them more secure against renowned attacks. The pseudo random number generator for symmetric key encryption ciphers and one-way functions are two basic techniques for the execution of data protection. The ability of dynamical systems to induce nonlinearity can be used to synthesize S-boxes, and the analyses of these kinds of boxes were very good against different types of attacks.

The structure of the article is as follows: Section 2 presents the preliminaries. Section 3 consists of the construction methodology for proposed S-box. In Section 4, we presented the analysis to measure the resistance of the presented box against linear and differential types of attacks. Section 5 is the conclusion.

2. Preliminaries

The proposed work is based on the action of general linear group and chaotic logistic map. There are few works on the general linear group for the construction of S-boxes in the literature. In this section, we briefly present the basics of these two modules to be used later in the section for proposed S-box generation.

2.1. General Linear Group

The group that we will use is the action of projective linear group $PGL(2,GF\left(2^8\right))$ on Galois field $GF\left(2^8\right)$, and construct a nonlinear vector corresponding to a particular type of linear fractional transformation $(180z+144)/(83z+4)$ with the condition that $180\times 4-144\times 83\ne 0$.

$$f:PGL(2,GF\left(2^8\right))\times GF\left(2^8\right)\to GF\left(2^8\right)\cup \infty$$

(1)

$$f\left(z\right)=\left(\right(180z+144)/(83z+4\left)\right)$$

(2)

where $180,144,83,4\in GF\left(2^8\right)$

2.2. Logistic Map

The logistic map is a model of population growth given as [29]:

$$y_{k+1}=p\ast y_k\ast (1-y_k)$$

(3)

where $0<p<4$, $y_0\in \left[0,1\right]$. Furthermore, the chaotic range for logistic map lies where $p\in \left[3.6,4\right]$. p is a positive constant and is known as biotic potential, which is responsible for the chaotic behavior. While it had proposed by John Von Neumann in 1947, there are two logistic map sequences which we are using in proposed work, with initial parameters as $y_0$ and $y_1$ with $p_0$ and $p_1$.

Chaos has several benefits when applied in secure communication. It has been shown that chaotic security algorithms have commended many advantages such as high security, speed, reasonable computational overheads, and computational power over the traditional algorithms. One of the most notable features is the sensitivity of the initial conditions. The values of the iterations are very sensitive and change significantly by a tiny change in the initial conditions of either p or y.

Figure 1 illustrates the idea of sensitivity of initial conditions. Figure 1a shows the values of the first 100 iterations against the initial parameters of $p=3.7$ and $y_0=0.5$. Figure 1b shows the values of the 100 iterations generated after first 300 iterations against the initial parameters of $p=3.700000000$ and $y_0=0.5$ in red color and the values of the 100 iterations generated after first 300 iterations against the initial parameters of $p=3.700000001$ and $y_0=0.5$ in blue color. It can be seen that the two graphs are significantly different to each other despite a tiny difference in the initial condition of p. Similarly, Figure 1c shows the values of the 100 iterations generated after first 300 iterations against the initial parameters of $p=3.7$ and $y_0=0.50000000$ in red color and the values of the 100 iterations generated after first 300 iterations against the initial parameters of $p=3.7$ and $y_0=y_0=0.50000000$ in blue color. It can be seen that the two graphs are significantly different to each other despite a tiny difference in the initial condition of $y_0$.

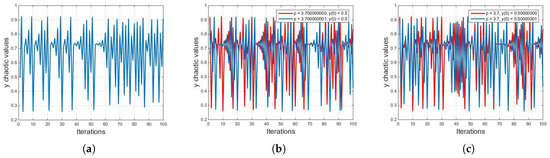
Figure 1. Illustration of sensitivity to initial conditions of logistic map. (a) values of the first 100 iterations against the initial parameters of $p=3.7$ and $y_0=0.5$, (b) comparison between the iteration values generated from two slightly different initial conditions of p, (c) comparison between the iteration values generated from two slightly different initial conditions of $y_0$.

3. Propose S-Box

We have divided the proposed algorithm for the construction of S-box into three steps, we shall construct the initial row vector with the help of linear fractional group technique for the construction of nonlinear vector; this is explained earlier. In step 2, we shall construct the intermediate S-box with the help of initial vector of step 1 and chaotic logistic map of Equation (3). In step 3, we shall take the output of step 2 as a seed and will apply a particular permutation of $S_{256}$ on it to get S-box with desire properties. The illustration of the proposed generation of S-box and explanation of steps is as follows:

3.1. Step 1: Application of General Linear Group

In first step we are going to apply the action of projective linear group $PGL(2,GF\left(2^8\right))$ on Galois field $GF\left(2^8\right)$ as mentioned earlier. The methodology is explained in Table 1 and Galois field element representation corresponding to a particular primitive irreducible polynomial can also be shown. The output of this first step in form of 16 × 16 S-box is shown in Table 2.

Table 1. Construction of S-box using fractional transformation.

z	$\mathit{f}\left(\mathit{z}\right)=\frac{(\mathit{az}+\mathit{b})}{(\mathit{cz}+\mathit{d})}$	Here We Are Taking ${\mathit{\zeta }}^{{\mathit{i}}_{\mathit{i}}}$ and ${\mathit{\zeta }}^{{\mathit{j}}_{\mathit{j}}}$ from Table 2	S-Box Elements
0	$f\left(0\right)=\frac{\left(180\right(0)+144)}{\left(83\right(0)+4)}$	$f\left(0\right)=\frac{{\Delta }^i}{{\Delta }^j}$	255
1	$f\left(1\right)=\frac{\left(180\right(1)+144)}{\left(83\right(1)+4)}$	$f\left(1\right)=\frac{{\Delta }^{i_2}}{{\Delta }^{j_2}}$	125
⋮	⋮	⋮
254	$f\left(254\right)=\frac{\left(180\right(254)+144)}{\left(83\right(254)+4)}$	$f\left(254\right)=\frac{{\Delta }^{i_{254}}}{{\Delta }^{j_{254}}}$	106
255	$f\left(255\right)=\frac{\left(180\right(255)+144)}{\left(83\right(255)+4)}$	$f\left(255\right)=\frac{{\Delta }^{i_{255}}}{{\Delta }^{j_{255}}}$	95

Table 2. Initial vector corresponding to $a=183$, $b=144$, $c=83$ and $d=4$ of Mobius transformation in matrix form.

255	125	26	23	249	72	44	32	33	34	202	30	191	186	248	211
166	189	195	62	242	150	253	45	165	239	143	169	2	103	183	65
86	130	91	40	219	223	60	210	168	73	115	139	154	175	187	75
124	39	152	218	131	251	185	81	28	157	109	12	6	13	224	226
135	230	188	164	149	128	116	228	217	173	212	8	84	80	243	93
20	146	194	36	42	35	79	77	179	9	151	85	172	52	118	222
15	14	101	18	112	117	55	92	48	178	22	25	54	231	4	16
138	64	160	134	46	200	120	238	137	114	108	241	61	153	50	3
132	78	163	110	90	201	129	47	236	53	104	246	49	41	100	158
232	68	21	159	141	227	197	208	245	38	215	156	70	133	43	127
198	180	74	190	89	37	69	209	98	136	29	182	87	126	207	237
51	122	155	204	192	247	206	59	24	82	63	83	17	107	184	142
205	167	19	121	216	177	96	66	105	123	229	113	214	11	234	94
0	221	240	220	31	196	119	161	252	181	148	99	111	56	97	244
67	250	199	57	254	7	203	145	171	225	140	193	213	102	174	1
58	10	88	147	233	170	5	176	71	235	27	144	162	76	106	95

The purpose of step 1 is to destroy the linear structure of Galois field $GF\left(2^8\right)$, because $GF\left(2^8\right)$ is basically a cyclic group and it is very easy to generate all its elements with the help of root of primitive irreducible polynomial of degree 8. The process of cyclic generation of Galois field elements is a linear operation. We have made this operation nonlinear with the help of linear fractional transformation. A minimum requirement to make a linear operation into nonlinear operation is affine transformation but here we are going beyond this because affine transformation is a particular case of linear fractional transformation.

In Figure 2, we have shown the nonlinearity of the initial vector and compared it with a linear initial vector. It can be seen that red line presents a linear vector from 0 to 255 and green line shows that nonlinear vector of step 1, which we shall use for the construction of S-box. This nonlinearity of the initial vector will play an important role in improving the confusion creating capacity of the proposed S-box.

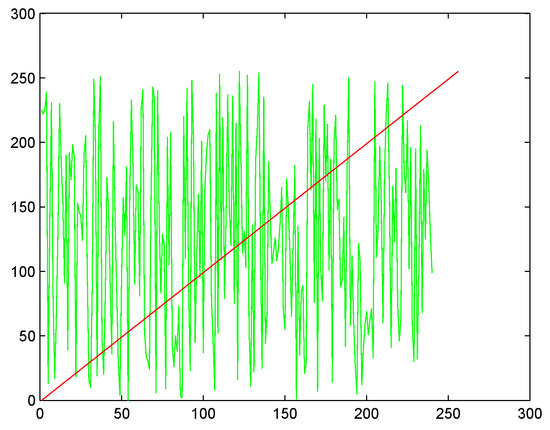
Figure 2. Uncertainty of the initial vector.

3.2. Step 2: Applying Logistic Chaotic Map

In this step, we need the following stuff:

(a) Initial vector of step 1 as a basic seed, which is shown in Table 2. Let the initial seed be represented as K with size 1 × 256.

(b) Define the two chaotic logistic map sequences as defined in Equation (3) with appropriate initial conditions.

(c) Initial parameters for first logistic map are as follows $p=3.99234589$ and $y_0=0.5$. The first logistic map sequence is represented as $f_1$. The length of this sequence is 256.

(d) Initial parameters for second logistic map are as follows $p=3.99777777$ and $y_0=0.6$. The second logistic map sequence is represented as y. The length of this sequence is also 256.

(e) Define $f_2=y_{155}$, that is $f_2$ has a single value of second chaotic sequence which is placed at 155th position.

(f) Define a function $pos\_min$ as shown in Algorithm 1. It consists of two steps; in step 1, “ones(1,256)” will give us a row vector with 256 values, all with a value of $f_2$. In step 2, the position at where the minimum difference lies will be set as an output.

(g) Use the initial seed of S-box generated with the help of general linear group shown in Table 2 and the logistic map, we will get the vector $K_1$. The whole process of getting the output of this step is depicted in Algorithm 2 and the output of this step is shown in Table 3.

Algorithm 1 To find the positions at where the minimum difference lies

Inputs: Two distinct logistic chaotic map sequences, $f_1$, y and $f_2$. Output: Position location, $pos\_min$.  1: $\mathbf{function}[pos\_min]=find\_pos\_min(f_1,f_2)$  2:  $f=f_2\ast ones(1,256)$  3:  $diff=abs\left(minus(f_1,f)\right)$  4:  $pos\_min=find(diff==min(diff\left)\right)$  5: $\mathbf{End}$

Algorithm 2 To generate S-box with the input seeds of logistic map and general linear group

Inputs: Initial vector K of Table 1 (which is a substitution box), functions for logistic map and $pos\_min$. Outputs: Substitution box, $K_1$.  1: $i=1$  2: while $i<257$ do  3:  $[pos\_min]=find\_pos\_min(f_1,y))$  4:  $p=0$  5:  for $j\leftarrow 1:length\left(V\right)$ do  6:   if $pos\_min==V\left(j\right)$ then  7:    $p=1$  8:   end if  9:  end for  10:  if $p==0$ then  11:   $V\left(i\right)=pos\_min$  12:   $K_1\left(i\right)=K(pos\_min)$  13:   $x_1=0.9\times x_1+0.1\times K(pos\_min)/255$  14:   $y=logistic(k_1,x_1)$  15:   $f_2=y\left(155\right)$  16:   $i=i+1$  17:  else  18:   $x_0=0.9\times x_0+0.1\times K(pos-min)/255$  19:   $f_1=logistic(k_0,x_0)$  20:  end if  21: end while

Table 3. Output of step 2.

Rows/Columns	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	84	44	60	125	119	238	63	110	207	22	191	187	48	252	202	93
1	181	50	57	118	151	56	92	192	86	229	171	19	113	10	233	24
2	242	161	139	27	13	126	170	21	134	122	17	20	34	216	159	40
3	138	201	107	100	152	0	81	127	42	213	65	128	251	197	237	172
4	136	95	221	102	165	45	49	135	190	85	99	222	41	162	80	32
5	106	137	164	109	72	53	43	12	89	101	26	38	74	124	71	158
6	16	54	163	147	209	64	120	160	66	186	97	239	166	112	178	8
7	47	37	3	133	2	108	247	223	206	250	114	76	15	211	155	231
8	123	88	248	203	115	208	210	245	1	195	144	154	156	196	230	96
9	79	182	67	117	111	168	183	142	232	175	157	131	193	220	184	189
10	146	148	35	87	91	31	77	61	236	4	167	234	205	33	52	94
11	73	212	9	83	214	227	145	200	51	62	149	30	59	11	103	98
12	70	194	14	243	235	199	169	174	68	5	224	140	218	179	255	246
13	254	215	188	39	75	23	82	253	29	173	78	143	153	249	28	225
14	180	58	150	244	176	217	105	204	116	46	69	185	130	219	177	6
15	198	228	141	132	104	121	18	7	226	240	90	129	241	25	55	36

3.3. Step 3: Application of Permutation to Get S-Box

In step 3 we shall choose a particular permutation $\mu \in S_{256}$ as shown in Table 4, and then apply it on Table 3 $\in GF\left(2^8\right)$ elements as follows;

$$S-box:S_{256}\times GF\left(2^8\right)\to GF\left(2^8\right).$$

(4)

$$\mu (a_0,a_1,a_2,\dots ,a_{255})=(a_{\mu \left(0\right)},a_{\mu \left(1\right)},a_{\mu \left(2\right)},\dots ,a_{\mu \left(255\right)}),$$

(5)

where $(a_0,a_1,a_2,\dots ,a_{255}),(a_{\mu \left(0\right)},a_{\mu \left(1\right)},a_{\mu \left(2\right)},\dots ,a_{\mu \left(255\right)})\in GF\left(2^8\right)$. $\mu \in S_{256}$ will change the position of elements of Table 3 in the form of proposed S-box, which is given in Table 5.

Table 4. Particular permutation $\mu$ of symmetric group of permutation $S_{256}$.

Rows/Columns	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	94	30	171	84	96	215	28	246	3	216	245	255	152	86	31	180
1	118	208	184	237	204	112	185	109	183	182	76	159	19	149	44	239
2	123	173	103	12	195	154	63	244	256	188	65	130	18	194	38	72
3	162	45	78	137	119	83	165	98	27	142	249	125	100	238	120	199
4	9	7	20	200	174	42	243	136	91	102	52	139	242	117	213	59
5	60	47	232	43	145	181	114	167	229	8	150	221	172	132	23	210
6	192	231	35	69	22	115	201	151	247	193	222	39	54	178	56	85
7	138	104	214	48	107	175	240	108	16	21	17	141	62	88	74	14
8	61	248	226	144	90	95	71	202	10	81	53	163	110	254	75	32
9	11	224	101	129	177	253	111	37	24	33	140	131	113	2	155	206
10	68	197	66	147	6	79	189	25	187	49	134	5	64	146	241	70
11	217	168	124	205	158	170	143	209	207	191	223	196	15	51	50	169
12	153	73	36	160	127	219	87	122	135	55	97	41	190	233	126	157
13	13	133	121	235	1	252	93	34	251	211	212	179	92	106	67	82
14	29	99	234	148	227	176	225	203	40	198	105	220	58	4	250	166
15	186	26	218	156	161	236	164	57	128	46	89	228	230	77	116	80

Table 5. The proposed S-box.

Rows/Columns	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	75	220	207	219	234	91	95	101	136	1	79	27	254	231	59	206
1	114	34	113	221	250	209	71	232	61	228	42	63	180	44	202	96
2	175	253	163	14	142	159	239	116	140	45	109	233	201	240	137	133
3	4	103	11	99	144	166	5	178	7	130	32	106	123	15	170	205
4	17	35	28	146	147	94	210	40	194	155	230	171	25	107	31	36
5	195	225	0	125	8	252	169	211	90	115	190	153	82	84	208	119
6	224	127	58	251	67	85	139	37	69	249	2	223	192	156	183	56
7	193	43	64	55	162	181	152	237	188	174	242	9	128	255	235	226
8	117	20	131	124	215	167	68	135	100	47	222	157	76	213	145	203
9	72	33	87	244	10	26	160	48	70	126	184	132	246	214	19	243
10	104	138	154	18	81	6	12	212	98	227	60	74	161	165	108	217
11	111	112	143	93	53	229	86	57	92	198	236	122	77	218	62	16
12	186	216	13	30	148	46	172	102	120	245	204	151	83	189	51	50
13	200	158	173	78	80	3	238	22	73	141	199	185	38	97	149	182
14	105	248	176	129	89	241	54	164	179	150	39	121	118	197	24	247
15	52	41	49	21	191	110	66	88	65	177	29	23	168	196	187	134

4. Analyses for Evaluating the Strength of S-Box

In the analyses section we shall determine the cryptographic strength of the propose S-box with some suitable measures. To find the S-box with fitting confusion creating strength many standard evaluating analyses are presented in literature such as DP, SAC, BIC, Nonlinearity, and LP. We shall also use these criteria to test the security of proposed S-box.

4.1. Nonlinearity

Definition 1.

Let$f\left(x\right):GF\left(2^n\right)\to GF\left(2\right)$be an n Boolean function, the nonlinearity of$f\left(x\right)$can take the form,

$$H_f=mi{n}_{l\in L_n}{d}_H(f,l)$$

(6)

where,$L_n$is a set of the whole linear and affine functions,$d_H(f,l)$denotes the Hamming distance between f and l.

The nonlinearity denoted by the Walsh spectrum can take the form,

$$N_f=2^{-n}(1-ma{x}_{\omega \in GF\left(2^n\right)}\left|S_{⟨f⟩}\left(\omega \right)\right|)$$

(7)

The cyclic spectrum of the function $f\left(x\right)$ is,

$$S_{⟨f⟩}\left(\omega \right)=2^{-n}{\displaystyle \sum _{x\in GF\left(2^n\right)}}{(-1)}^{f\left(x\right)\oplus x.\omega }$$

(8)

where, $\omega \in GF\left(2^n\right)$, and $x.\omega$ denotes the dot product of x and w. The larger the nonlinearity $N_f$ of the function f, the stronger the ability of its resistance to the linear attacks, and vice versa.

The results of nonlinearity of proposed algorithm are shown in Table 6, with the help of these results we can say that the nonlinearity of the nonlinear values of the substitution box created by the chaos-based scheme shaped in the reading are 112, 112, 112, 112, 112, 112, 112, 112. Nonlinearity average value, minimum value and maximum value are 112, 112, and 112, respectively.

Table 6. Nonlinearity of proposed S-box.

${\mathit{ftn}}_0$	${\mathit{ftn}}_1$	${\mathit{ftn}}_2$	${\mathit{ftn}}_3$	${\mathit{ftn}}_4$	${\mathit{ftn}}_5$	${\mathit{ftn}}_6$	${\mathit{ftn}}_7$
112	112	112	112	112	112	112	112

4.2. Strict Avalanche Criterion

SAC describes a fact that when one bit in the input of Boolean function changes, the changing probability of every bit in its output is $1/2$. In practical application, a correlation matrix, the construction method is always constructed to test the SAC property of the Boolean function. The results of SAC are shown in Table 7. In Table 7, we have shown the eight different Boolean functions corresponding to S-box. It can be observed that the values are approximately equal to 0.5, which is very good for cryptographic uncertainty. Therefore, the proposed nonlinear component satisfies this criterion with approximately optimal values.

Table 7. SAC of proposed S-box.

0.515625	0.515625	0.453125	0.484375	0.562500	0.500000	0.453125	0.453125
0.468750	0.484375	0.562500	0.453125	0.5000	0.531250	0.500000	0.484375
0.515625	0.515625	0.500000	0.500000	0.4608750	0.500000	0.531250	0.562500
0.531250	0.531250	0.468750	0.531250	0.453125	0.546875	0.500000	0.500000
0.453125	0.500000	0.453125	0.500000	0.515625	0.531250	0.546875	0.500000
0.453125	0.515625	0.515625	0.546875	0.468750	0.531250	0.531250	0.468750
0.531250	0.531250	0.468750	0.531250	0.515625	0.484375	0.531250	0.468750
0.515625	0.562500	0.515625	0.531250	0.531250	0.515625	0.484375	0.484375

4.3. Bit Independent Criterion

Given a Boolean function $f_j$, $f_k$ is a two bits output of an S-box, if $f_j\oplus f_k$ is highly nonlinear and meets the SAC, the correlation coefficient of each output bit pair may be close to 0 when one input bit is inversed. Thus, we can check the BIC of the S-box by verifying whether $f_j\oplus f_k$ $(j\ne k)$ of any two output bits of the S-box meets the nonlinearity and SAC. According to the description of BIC, an $8\times 8$ S-box produced by our procedure is checked. The results show the exclusive-or sum of all pairs of output bits of this S-box is highly nonlinear and approximately fulfill SAC.

In Table 8, we have shown the results of bit independence criterion (BIC) for SAC. This analysis is very important to know the confusion strength of any nonlinear algorithm. The requirement of this analysis is that all values should be approximately equal to 0.5, and it can be observed that the whole table is between 0.490234 and 0.525391. It means our S-box fulfills this criterion with very close readings.

Table 8. Bit independence criterion for SAC.

——	0.515625	0.486328	0.517578	0.500000	0.515625	0.509766	0.494141
0.515625	——	519531	0.490234	0.511719	0.480469	0.501953	0.496094
0.486328	0.519531	——	0.496094	0.525391	0.490234	0.507813	0.507813
0.517578	0.490234	0.496094	——	0.494141	0.513672	0.505859	0.511719
0.500000	0.511719	0.525391	0.494141	——	0.505859	0.494141	0.517578
0.515625	0.480469	0.490234	0.513672	0.505859	——	0.509766	0.515625
0.509766	0.501953	0.507813	0.505859	0.494141	0.509766	——	0.494141
0.494141	0.496094	0.507813	0.511719	0.517578	0.515625	0.494141	——

In Table 9, we presented the BIC for nonlinearity for proposed box. It can be observed that all the values are 112 which is maximum possible nonlinearity for a secure S-box.

Table 9. Bit independence criterion for nonlinearity.

0	112	112	112	112	112	112	112
112	0	112	112	112	112	112	112
112	112	0	112	112	112	112	112
112	112	112	0	112	112	112	112
112	112	112	112	0	112	112	112
112	112	112	112	112	0	112	112
112	112	112	112	112	112	0	112
112	112	112	112	112	112	112	0

4.4. Differential Approximation Probability

The Differential approximation probability $D{P}_f$ can reflect the $XOR$ distribution of the input and output of the Boolean function, i.e., the maximum likelihood of outputting $\Delta y$, when the input is $\Delta x$,

$$D{P}_f=ma{x}_{\Delta x\ne 0,\Delta y}\left(\frac{\left\{x\in X\left|f\right(x)\oplus f(x\oplus \Delta x)=\Delta y\right\}}{2^n}\right)$$

(9)

where, X denotes a set of all possible inputs, $2^n$ is the number of elements in the set.

The smaller the $D{P}_f$, the stronger the ability of the S-box for fighting against differential cryptanalysis attacks, and vice versa. In Table 10, the results of differential approximation probabilities are presented. It can be observed that all the values are 0.015625 and same which is equal to AES S-box strength, this shows that our S-box is good against the differential type of attacks.

Table 10. Differential approximation probability of proposed S-box.

Rows/Columns	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
1	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
2	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
3	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
4	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
5	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
6	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
7	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
8	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
9	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
10	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
11	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
12	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
13	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
14	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156
15	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156	0.0156

4.5. Linear Approximation Probability

Given two randomly selected masks $\Gamma x$ and $\Gamma y$, we used $\Gamma x$ to calculate the mask of all possible values of an input x, and use $\Gamma y$ to calculate the mask of the output values $S\left(x\right)$ of the corresponding S-box. After masking the input and the output values, and the maximum number of the same results is called the maximum linear approximation that can be computed by the following equation:

$$L{P}_f=ma{x}_{\Gamma x,\Gamma y\ne 0}\left|\frac{\left\{x|x.\Gamma x=S(x).\Gamma y\right\}}{2^n}-\frac{1}{2}\right|$$

(10)

where, $\Gamma x$ and $\Gamma y$ are the mask values of the input and output, respectively, X is a set of all possible input values of x, the elements of which is $2^n$.

The smaller the LP, the stronger the ability of the S-box for fighting against linear cryptanalysis attacks, vise-versa.

5. Conclusions

In this manuscript, we have shown the usage of logistic chaotic map, symmetric group of permutation and projective general linear group action to get high-quality S-box for encryption algorithms. The method presented assurances the success of the SAC, nonlinearity, BIC with an optimal reading and at the same time guarantying an extremely good differential and linear probability. In Table 11, it can be seen that strength of proposed S-box is comparable with well-known prevailing S-boxes. So, one can use the proposed S-box for secure communication in any block cipher encryption algorithm. Moreover, the proposed method can construct 256! S-boxes based on the permutation of $S_{256}$. The S-box which we have constructed in this paper is an example and a member of combination of eight output bits of AES S-box.

Table 11. Comparison of the chaotic and non-chaotic S-boxes with proposed S-box.

S-Boxes/Analyses	Minimum Nonlinearity	SAC Offset	Minimum BIC-Nonlinearity	DP	LP
Ref [2]	112	0.02637	112	0.015625	0.0625
Ref [9], S-box1	112	0.02579	112	0.015625	0.0625
Ref [12]	112	0.02502	112	0.015625	0.0625
Ref [13]	100	0.03125	100	0.0290525	0.070557
Ref [14]	104	0.02007	96	0.0390625	0.148438
Ref [25]	108	0.01833	104	0.03125	0.09375
Ref [9], S-box2	107.5	0.4971	103.85	NA	NA
Ref [9], S-box3	104	0.4531	112	NA	NA
Proposed	112	0.01567	112	0.01562	0.0625