Abstract
While the observation of magnetic monopoles has defied all experimental attempts in high-energy physics and astrophysics, sound theoretical approaches predict that they should exist, and they have indeed been observed as quasiparticle excitations in certain condensed-matter systems. This indicates that, even though they are not ubiquitous contrary to electrons, it is possible to get them as excitations above a background. In this report, we show that phonons or lattice shear strain generate topological monopoles in some low-dimensional quantum antiferromagnets. For the Heisenberg ladder, phonons are found to generate topological monopoles with nonzero density due to quantum spin fluctuations. For the four-leg Heisenberg tube, longitudinal shear stress generates topological monopoles with density proportional to the strain deformation. The present theory is based on mapping the spin degrees of freedom onto spinless fermions using the generalized Jordan–Wigner transformation in dimensions higher than one. The effective magnetic field generated by the motion of the spinless fermions has nonzero divergence when phonons or shear stress are present. A possible material where the present kind of monopoles could be observed is BiCuPO.
Keywords:
topological monopoles; quantum antiferromagnets; Heisenberg model; Jordan–Wigner transformation; spin ladders; magnetic monopoles PACS:
75.10.Jm; 75.30.-m; 75.30.Kz
1. introduction
Magnetic monopoles have not yet been observed experimentally, even though the amount of theoretical evidence, based on some of the most beautiful mathematics, is impressive. Magnetic monopoles, originally predicted by Dirac [1], have attracted significant attention, and have been the subject of numerous works. One of the interesting consequences of these monopoles is the explanation of the quantization of the electric charge. That is, all existing stable ubiquitous charges in nature are either positive or negative multiples of an electron’s charge, but fractional charges are confined in nuclei. Another sweet consequence of the potential existence of magnetic monopoles is the restoration of electricity–magnetism duality symmetry.
Magnetic monopoles have also been proposed in gauge theories and unification theories of (high-energy) physics, where symmetry breaking plays a predominant role [2,3,4,5]. Recently, Gould and Rajantie [6] investigated the cross section for pair production of magnetic monopoles in heavy-ion collisions and neutron stars. The search for magnetic monopoles has not been limited to high-energy physics or astrophysics, but interestingly they have been claimed to exist in systems where Bose–Einstein condensation occurs. Indeed, Ray et al. [7] reported the observation of magnetic monopoles in a spin-1 Bose–Einstein condensate. It is thus legitimate to ask if they can occur in spin-1/2 systems.
Spin excitations can be treated as either fermions or hard-core bosons. Excitations in an ordered antiferromagnet are known to be magnons, which are well described by hard-core bosons within the spin-wave theory. In the latter, spin operators are mapped onto constrained bosonic operators. Also, triplons in disordered dimerized systems can be described using boson operators [8]. Recently, Ollikainen et al. [9] reported on the experimental realization of a Dirac monopole as a result of the decay of an isolated monopole in a spin-1 Bose–Einstein condensate. The scenario of finding magnetic monopoles as excitations above a given background manifold was proposed to occur in spin-ice materials by Castelnovo, Moessner, and Sondhi [10]. They pointed out that Coulomb’s law for magnetic monopoles is able to reproduce well the physical properties of the spin ice materials DyTiO and HoTiO. Fennell et al. [11] used neutron scattering to establish that HoTiO exhibits an almost ideal magnetic Coulomb phase, which they interpreted as the quasiparticle vacuum for Castelnovo et al.’s magnetic monopoles. Morris et al. [12] reported the presence of Dirac strings (monopoles) in the spin-ice material DyTiO using diffuse neutron scattering. They also found that a gas of magnetic monopoles interacting according to Coulomb’s law is able to account for the heat capacity of this magnetic ice material.
It is also well known that spin-1/2 operators, and by the same token spin excitations, can be mapped onto spinless fermions using the Jordan–Wigner (JW) transformation in one dimension and its generalized analogs in higher dimensions [13,14]. In this report, we address the issue of whether topological monopoles occur or not in spin-1/2 quantum antiferromagnets. The spin- Heisenberg model in dimensions higher than one transforms onto a system of interacting JW spinless fermions coupled to gauge fields generated by these fermions themselves. These gauge fields create effective magnetic fields. We report on the conditions under which these effective magnetic fields are caused by topological monopoles. We studied two simple lattices—namely, the Heisenberg two-leg ladder made of two coupled chains, and the Heisenberg tube made of four coupled chains. We found that topological monopoles occur in the two-leg ladder in the presence of transverse phonons, and longitudinal shear stress generates them in the Heisenberg tube. It is also interesting to note that quantum spin fluctuations are needed for the topological charges in the two-leg ladder, but these charges can exist in the Heisenberg tube under longitudinal stress even if long-range antiferromagnetic order sets in. In both cases, the effective magnetic field has nonzero divergence, implying the occurrence of a nonzero density of topological charges. We predict that any magnetic frustration resulting from the geometry of chemical bonds should also generate nonzero densities of monopoles in materials which can be modeled by coupled ladders. While the present findings do not necessary imply the existence of real magnetic monopoles, we speculate that the mechanism (phonons and shear stress) leading to the present topological monopoles could suggest a mechanism for the generation of real magnetic monopoles in the universe. We speculate that real magnetic monopoles in the universe could be brought into evidence by gravitational waves or spacetime deformations. This could present an alternative explanation which is not based on the dynamo theory for the origin of the anomalously long-lived magnetic fields in astrophysical bodies [15].
This paper is organized as follows. In Section 2, we show that topological monopoles can be generated in the two-leg Heisenberg ladder when coupled to transverse phonons. For the four-leg Heisenberg tube considered in Section 3, magnetic monopoles are shown to exist as a consequence of longitudinal shear stress. Conclusions are drawn in Section 4.
2. Two-Leg Ladders
To highlight the importance of geometry and dimensionality for the existence of topological monopoles in quantum antiferromagnets, we begin our investigation with the simplest lattice geometry where magnetic flux can occur, namely the Heisenberg ladder. We show that monopoles can be generated for this lattice in the presence of transverse phonons. The Hamiltonian for the ladder antiferromagnet (Figure 1) reads as:
where J and are positive coupling constants along the chains and rungs, respectively. The chains are labeled by the index , and the sites along each chain by the label i, which runs over the N sites of each chain. The generalized JW transformation [13,16] for the ladder,
maps the term of Hamiltonian (1) onto a Hamiltonian of spinless fermions coupled to a “vector” potential A [13]:
with
() is the annihilation (creation) operator of a spinless fermion at site . is the occupation number operator. Note that the phase difference along the rung is found to be depending on the direction of hopping. This phase disappears from the Hamiltonian because and , which effectively leads to . Identities analogous to these ones simplify the phase difference for hopping along the chains as well. The As in (4) designate the components of the vector potential to which the spinless fermions couple. An effective magnetic field is defined using this vector potential [14]; . Given the fact that the JW fermions are confined to move only within the ladder, the only nonzero component of the magnetic field is ; note that the z-axis is chosen to be perpendicular to the ladder. The partial derivatives in the curl are finite differences because the smallest plaquettes around which the JW fermions move are made of primitive unit square cells, and it is therefore meaningless to consider the continuum limit in this lattice model. Inspection of Equation (4) tells us that the only nonzero component of the gauge field is the component along the x-axis, which assumes the values and on chains 1 and 2 of the ladder, respectively. This implies that only has a dependence along the y direction. The components of A along y and z directions are identically zero. In this context, the curl of A yields
a result which is derived assuming that the lattice parameter a is unity (), and using finite difference for the partial derivative.
Figure 1.
The two-leg ladder lattice is shown.
Alternatively, one can derive the expression of B in (5) using the magnetic flux through an elementary plaquette of the ladder, consisting of a single unit square cell. This flux is given by the phase difference as we go once around this elementary plaquette, which has area . Using (5) one finds for this flux. Writing , and replacing the integral by yields the same result for as in (5). means the integration is carried over the surface area of a single plaquette, and designates an element of this area, with direction perpendicular to the plaquette.
The effective magnetic field in Equation (5) does not have the dimension of true magnetic fields because the JW fermions, which generate it when orbiting around unit plaquettes, do not carry an electric charge. Any magnetic charge found here is thus only a topological charge.
After we have defined the magnetic field in which the JW fermions move on the ladder, it is legitimate to ask whether this magnetic field is caused by some kind of topological monopole. To check this, we calculate the divergence of B, which gives because there is no z dependence in B and the x- and y-components are zero. This shows that the topological charge density is zero, implying the absence of any topological monopoles in the Heisenberg ladder. This result concerns a plane Heisenberg ladder. Consider now a Heisenberg ladder in the presence of transverse phonons. The case of such phonons with wavevector is shown in Figure 2 in order to illustrate the appearance of the additional component at site i. The transverse displacement causes a staggered inclination of the plaquettes by angle . The magnetic field, which is perpendicular to the plaquette at any site and any time, is also inclined by the same angle with respect to the z axis. The x-component that has an x dependence will give a nonzero contribution to the divergence of the magnetic field. For a finite inclination , the magnetic field is indeed
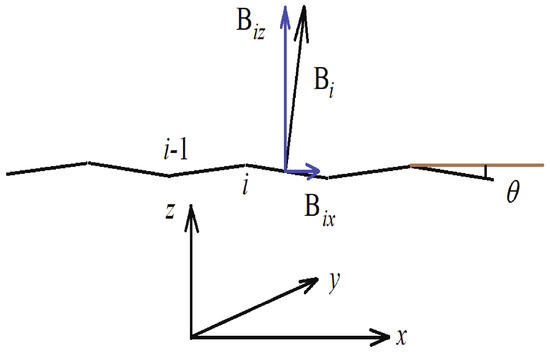
Figure 2.
The two-leg ladder in the presence of transverse phonons. The view of the -plane is shown.
Given that there is still no z-dependence, the divergence of yields
If we assume that a real two-leg system is characterized by long-range antiferromagnetic order (we also assume that inter-ladder couplings are negligible in the calculation of the above magnetic field), and replace the number operators by their thermal averages, then the divergence vanishes. However, quantum fluctuations caused by spin flips, which give rise to spin waves, will create nonzero density of topological monopoles. The density of monopoles in this case will also have space and time dependence because of the dynamics of the transverse phonons. To summarize this part of the present report, we conclude that two ingredients are needed for the creation of topological monopoles in the two-leg Heisenberg antiferromagnet: the first is the coupling to transverse phonons and the second is the quantum spin fluctuations that yield spin waves.
3. The Heisenberg Rectangular Tube
3.1. Tube without Shear Strain
As mentioned earlier, the divergence of the effective magnetic field for the plane Heisenberg ladder is zero because of the lack of any z dependence in this magnetic field. We saw that coupling to transverse phonons and spin waves combine to generate a nonzero density of topological monopoles. We also found that coupling two ladders to form a four-leg Heisenberg tube presents a field with nonzero divergence; so topological monopoles. The legs of the tube are labeled 1, 2, 3, and 4, and sites on each leg are labeled with index i (Figure 3). The Heisenberg Hamiltonian in this case assumes the form
where is the chain label, and i is the site index on each chain.
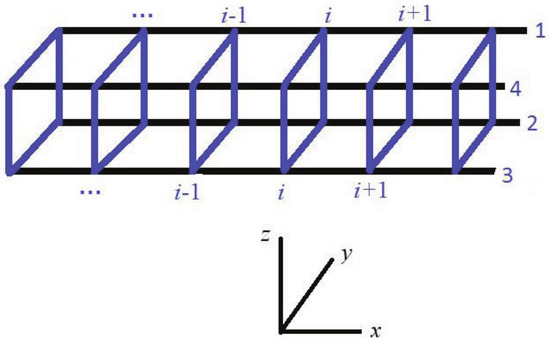
Figure 3.
The four-leg Heisenberg tube.
The generalized JW transformation for this system is found by adapting the three-dimensional JW transformation of Reference [14]:
Note that these phases are required for the preservation of the spin operators’ commutation relations. Using (9), the Hamiltonian (8) takes on the expression
with
In (10), designates the z–z Ising interaction, which is phase-free. Next, we calculate the phase difference for JW fermions moving around elementary plaquettes that are perpendicular to the x, y, or z directions. Equating these phase differences to the flux of the effective magnetic field B that the motion of the spinless fermions causes, one finds the following for the x, y, and z components of at position i:
The index i in is now the label for the whole unit cell between i and in the tube. This means that has no dependence on the chain labels. Note that in deriving the expressions (12) for the magnetic field, the lattice parameter is set to be 1 in the flux , where is an element of surface area. The divergence of this magnetic field vanishes. Indeed,
To get (13), the divergence terms were calculated as finite differences; that is, along the x direction ; . Along the y axis, there are only two contributions to the magnetic field, which are for the elementary plaquette delimited by chains 1 and 2, and for the plaquette delimited by chains 4 and 3. So, the component of the divergence along this direction is simply the difference between these two terms divided by the lattice parameter : . Similarly, the partial derivative with respect to z is .
3.2. The Heisenberg Tube with Shear Strain
The result in (13) implies that the density of topological monopoles is zero in the Heisenberg tube. An important observation in Equation (13) is that the vanishing of the divergence of B does not occur because of the vanishing of the contribution from each term , with . It rather occurs because of cancellations between terms contributed by derivatives along different directions. Let us consider a situation where one of the elementary plaquettes is not perpendicular to at least one of the other two plaquettes. Then the magnetic field perpendicular to that plaquette will have two projections on two of the three axes of the reference frame. The divergence will depend on the angle between the normal to this plaquette and one of the axes of the reference frame.
We assume that due to some shear force, the two upper chains (1 and 4) of the tube are slightly displaced with respect to the two lower chains 2 and 3. Consequently, the plaquette is not perpendicular to the x axis, and the effective magnetic field that results from the motion of a JW fermion on this plaquette will form an angle with the x axis. The contribution to the x component of the field is now multiplied by , and a contribution in adds up to the z component of the field. If the lateral displacement of the tube due to the shear force is u, then . The y component remains unaffected. The components of the magnetic field at site i (distance along the tube) are:
Notice that if , Equation (14) reduce to (12) in the absence of shear force. For a nonzero small , we write , and . In this case, Equation (14) may be written as
To second-order in displacement, the divergence of the magnetic field at distance along the tube is nonzero, and reads as
In deriving (16), for differentiation with respect to z we used the finite differences and , and for differentiation with respect to x the finite differences and , where a is the lattice parameter assumed to be the same in all three directions, set equal to 1.
It is enlightening to find that the topological monopoles proposed to occur here are a consequence of some sort of magnetic frustration induced by the shear force. Frustration is also a key element in the occurrence of magnetic monopoles in spin ice materials, which crystallize in the the highly frustrated pyrochlore lattice [10,11,12].
Next, suppose that a three-dimensional material is made of weakly coupled Heisenberg tubes such that long-range antiferromagnetic order sets in. Let m designate the absolute value of magnetization. Then, the thermal averages of the occupation numbers are , and if we assume that magnetization is up at sites (i,1) and (i,3), and down at sites (i,2) and (i,4) due to the staggered character of the antiferromagnetic order. Keeping only the first order in and approximating the right-hand side of Equation (16) using thermal averaging leads to
Equation (17) implies that the Heisenberg tube is made of a succession of adjacent magnetic monopoles of opposite charges. For constant magnetization m and uniform displacement u, the magnetic monopoles give rise to a magnetic field that satisfies Coulomb’s law, with a staggered density of monopoles. In the absence of shear displacement (i.e., ), or AF order (i.e., ), this density vanishes, leading to the disappearance of monopoles.
4. Conclusions
In summary, we show that topological monopoles may occur in quantum antiferromagnets. We examined the Heisenberg two-leg ladder and four-leg tube. We found that spin fluctuations and coupling to transverse phonons are required for the realization of such monopoles in the two-leg ladder. For the four-leg tube, longitudinal shear deformation is required for their establishment. The JW transformation is used to map the spin degrees of freedom in these spin-1/2 antiferromagnets onto spinless fermions. The Heisenberg Hamiltonian transforms onto the Hamiltonian of interacting fermions moving in a vector field. The divergence of the effective magnetic field is nonzero when transverse phonons are taken into account for the ladder, and a longitudinal shear deformation is considered along the tube. The case of a three-dimensional system of weakly coupled tubes with antiferromagnetic order is considered to illustrate the production of a finite staggered density of magnetic monopoles along each tube. We propose that a possible material where the present monopoles can be produced is BiCuPO [17,18].
The magnetic monopoles encountered here do not require Dirac strings, and are thus potential candidates for fundamental magnetic monopoles. This scenario is appealing because it does not exclude the idea that magnetic monopoles are somewhere in the universe, perhaps even everywhere around us, but in order to observe them, they have to be excited out of their background. In spin antiferromagnets, the magnetic frustration or shear stress is able to generate monopoles, but in the universe, we speculate that space-time gravity-induced deformations resulting from the motion and collisions of large astronomical objects could lead to the generation of magnetic monopoles. The latter could be responsible for the observed large-scale galactic and intergalactic magnetic fields [15]. The results of this work could also perhaps shed some light on the mechanism generating the monopoles in spin ice materials, which are characterized by strong magnetic frustration.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dirac, P.A.M. Quantized singularities in the electromagnetic field. Proc. R. Soc. 1931, 133. [Google Scholar] [CrossRef]
- Rajantie, A. Magnetic monopoles from gauge theory phase transitions. Phys. Rev. D 2003, 68. [Google Scholar] [CrossRef]
- Pati, J.; Salam, A. Lepton number as the fourth “color”. Phys. Rev. D 1974, 10, 275–289. [Google Scholar] [CrossRef]
- Baez, J.C.; Huerta, J. The algebra of grand unified theories. Bull. Am. Math. Soc. 2010, 47, 483–552. [Google Scholar] [CrossRef]
- Goddard, P.; Olive, D.I. Magnetic monopoles in gauge field theories. Rep. Prog. Phys. 1978, 41, 1357–1437. [Google Scholar] [CrossRef]
- Gould, O.; Rajantie, A. Magnetic monopole mass bounds from heavy-ion collisions and neutron stars. Phys. Rev. Lett. 2017, 119. [Google Scholar] [CrossRef] [PubMed]
- Ray, M.W.; Ruokokoski, E.; Tiurev, K.; Möttönen, M.; Hall, D.S. Observation of isolated monopoles in a quantum field. Science 2015, 348, 544–547. [Google Scholar] [CrossRef] [PubMed]
- Giamarchi, T.; Rüegg, C.; Tchernyshyov, O. Bose–Einstein condensation in magnetic insulators. Nat. Phys. 2008, 4, 198–204. [Google Scholar] [CrossRef]
- Ollikainen, T.; Tiurev, K.; Blinova, A.; Lee, W.; Hall, D.S.; Möttönen, M. Experimental realization of a dirac monopole through the decay of an isolated monopole. Phys. Rev. X 2017, 7. [Google Scholar] [CrossRef]
- Castelnovo, C.; Moessner, R.; Sondhi, S.L. Magnetic monopoles in spin ice. Nature 2008, 451, 42–45. [Google Scholar] [CrossRef] [PubMed]
- Fennell, T.; Deen, P.P.; Wildes, A.R.; Schmalzl, K.; Prabhakaran, D.; Boothroyd, A.T.; Aldus, R.J.; McMorrow, D.F.; Bramwell, S.T. Magnetic coulomb phase in the spin ice Ho2Ti2O7. Science 2009, 326, 415–417. [Google Scholar] [CrossRef] [PubMed]
- Morris, D.J.P.; Tennant, D.A.; Grigera, S.A.; Klemke, B.; Castelnovo, C.; Moessner, R.; Czternasty, C.; Meissner, M.; Rule, K.C.; Hoffmann, J.-U.; et al. Dirac strings and magnetic Mmonopoles in the spin ice Dy2Ti2O7. Science 2009, 326, 411–414. [Google Scholar] [CrossRef] [PubMed]
- Azzouz, M. Interchain-coupling effect on the one-dimensional spin-1/2 antiferromagnetic Heisenberg model. Phys. Rev. B 1993, 48, 6136–6140. [Google Scholar] [CrossRef]
- Bock, B.; Azzouz, M. Generalization of the Jordan-Wigner transformation in three dimensions and its application to the Heisenberg bilayer antiferromagnet. Phys. Rev. B 2001, 64. [Google Scholar] [CrossRef]
- Widrow, L.M. Origin of galactic and extragalactic magnetic fields. Rev. Mod. Phys. 2002, 74. [Google Scholar] [CrossRef]
- Azzouz, M.; Chen, L.; Moukouri, S. Calculation of the singlet-triplet gap of the antiferromagnetic Heisenberg model on a ladder. Phys. Rev. B 1994, 50, 6233–6237. [Google Scholar] [CrossRef]
- Koteswararao, B.; Salunke, S.; Mahajan, A.V.; Dasgupta, I.; Bobroff, J. Spin-gap behavior in the two-leg spin-ladder BiCu2PO6. Phys. Rev. B 2007, 76. [Google Scholar] [CrossRef]
- Kohama, Y.; Wang, S.; Uchida, A.; Prsa, K.; Zvyagin, S.; Skourski, Y.; McDonald, R.D.; Balicas, L.; Ronnow, H.M.; Rüegg, C.; et al. Anisotropic cascade of field-induced phase transitions in the frustrated spin-ladder system BiCu2PO6. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).