Hysteretic Loops in Correlation with the Maximum Dissipated Energy, for Linear Dynamic Systems

Abstract

This paper presents the outcomes of the theoretical and experimental research carried out on a real model at natural scale using Voigt–Kelvin linear viscoelastic type m, c, and k models excited by a harmonic force F(t) = F₀ sinωt, where F₀ is the amplitude of the harmonic force and ω is the excitation angular frequency. The linear viscous-elastic rheological system (m, c, k) is characterized by the fact that the c linear viscous damping—and, consequently, the fraction of the critical damping ζ—may be changed so that the dissipated energy can reach maximum $W_d^{\max }$ values. The optimization condition between the $W_d^{\max }$ maximum dissipated energy and the amortization ${\zeta }^0=\pm \left(1-{\Omega }^2\right)/2\Omega$ modifies the structure of the relation F = F(x), which describes the elliptical hysteresis loop F–x in the sense that it has its large axis making an angle less than 90° with respect to the x-axis in $\Omega <1$ ante-resonance, and an angle greater than 90° in post-resonance for $\Omega >1$. The elliptical Q–x hysteretic loops are tilted with their large axis only at angles below 90°. It can be noticed that the equality between the arias of the hysteretic loop, in the two representations systems Q–x and F–x, is verified, both being equal with the maximum dissipated energy $W_d^{\max }$.

1. Introduction

For the vibration-driven technological processes with excitation harmonic forces, Voigt–Kelvin linear rheological models are adopted with the discretionary variation of the amortization or of the fraction of the critical amortization $\zeta =c/2\sqrt{k/m}$.

The functional optimization of the vibration-driven processes consists of reaching a maximum $W_d^{\max }$ dissipated energy for $\zeta ={\zeta }^0$ in direct correlation with the area of the elliptical hysteretic loop. By locating suitable transducers on the physical system, the elliptical hysteretic loops can be determined in such a manner that allows the assessment of their areas, respectively the maximum dissipated energy for a dynamic system may be assessed with rigidity k and amplitude A of the instantaneous displacement $x=A\sin \left(\omega t-\phi \right)$, where φ is the phase angle.

Depending on the optimization requirement, in order to achieve a maximum dissipation, i.e., $W_d^{\max }$, can be determined the pairs of values ${\zeta }_{optim}={\zeta }^0$ for which are established the calculus relations of the significant parameters. Thus, the functional relations were established for A = A(ω), amplitude, the $W_d=W_d\left(\zeta ,\Omega \right)$ dissipated energy, the viscoelastic force $Q=c\dot{x}+kx=Q\left(x\right)$, and the excitation force F = F(x). The correlations between the maximum dissipated energy and the areas of the elliptical hysteretic loops are reflected in the graphical representations for the case of operation in ante-resonance at $\Omega <1$ and respectively for the case of post-resonance at $\Omega >1$ [1,2,3].

Experimental research carried out so far has mainly highlighted the positioning of hysteretic loops as an ante-resonance regime for testing elastomeric devices. The results highlighted in this field, both linearly and nonlinearly, are presented in papers published by various researchers from Italy, France, USA, and Romania [4,5,6,7,8,9,10]. Interpretation of experimental results and behavioral modeling of elastomeric device behavior are addressed in published reference works [11,12,13,14,15,16,17,18]. To highlight the post-resonance regime, interesting and useful research is contained in some published papers cited in the literature [19,20,21,22,23].

In this paper are highlighted the hysteretic loops families of the elastomeric devices that were designed, manufactured and tested, for a viaduct on the “Transilvania” Motorway, in Romania. Thus, based on dynamic testing devices and realized within ICECON Bucharest (Romania), there were determined the characeristic shapes of the hysteretic loops for the three dynamic regimmes, namely: ante-resonance, resonance, and post-resonance.

The characteristic function for dissipated energy was also established, highlighting its modification in relation to the fraction of critical damping ζ as a system parameter.

The novelty of the approach consists of the fact that for the elastomeric isolator system/device are highlighted the dissipative characteristics, the hysteretic loop orientation, as well as the dissipated energy variation depending on the parameter ζ, which can take different values in relation to mass m, elasticity k, and linear dissipation c. The graphical representation of the hysteretic loop in accordance with the dissipated energy allowed a clearer, more operational and efficient highlighting of the dynamic behavior during the tests, with meaningful and eloquent conclusions.

2. Parameter Analysis

The dynamic linear models m, c, and k, produced by the harmonic force F(t) = F₀ sinωt and with the reaction force Q(t) in the liniar viscoelastic system, c, k, is presented in Figure 1.

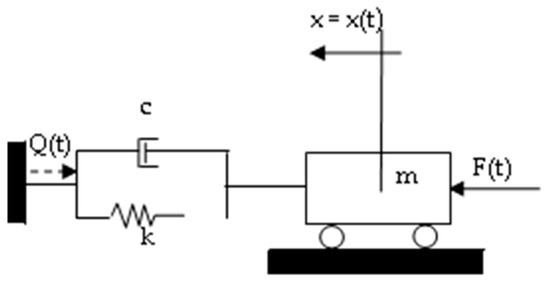
Figure 1. Linear dynamic model m, c, and k.

The movement equation at the dynamic balance is

$$m\ddot{x}+c\dot{x}+kx=F_0\sin \omega t.$$

(1)

The solution of Equation (1) is

$$x=A\sin \left(\omega t-\phi \right),$$

(2)

where A is the amplitude of the instantaneous displacement x = x(t), $\phi$ is the phase shift between the instantaneous displacement x(t) and the excitation force F(t).

It is introduced the notation: $\Omega =\frac{\omega }{{\omega }_n}$, where ${\omega }_n=\sqrt{\frac{k}{m}}$, so that the variable $\Omega$ to be used as excitation relative pulsation.

2.1. Amplitude of Displacement

An amplitude of the instantaneous displacement x = x(t) may be expressed by the A(ω) or A(Ω) relation, as follows:

$$A\left(\omega \right)=\frac{F_0}{\sqrt{{\left(k-m{\omega }^2\right)}^2+c^2{\omega }^2}},$$

(3)

or

$$A\left(\omega \right)=\frac{F_0}{k}\frac{1}{\sqrt{{\left(1-{\mathsf{\Omega }}^2\right)}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2}}.$$

(4)

2.2. De-Phasing between Force and Displacement

The de-phasing φ between the excitation force F = F(t) and the instantaneous displacement x = x(t) may be calculated as follows:

$${tg\phi |}_{\omega }=\frac{c\omega }{k-m{\omega }^2},$$

(5)

or

$${tg\phi |}_{\Omega }=\frac{2\zeta \Omega }{1-{\Omega }^2}.$$

(6)

2.3. Dissipated Energy

The dissipated energy W_d may be expressed according to $\Omega$ and $\zeta$ as follows:

$$W_d=W_d\left(\mathsf{\Omega },\zeta \right)=W_0\frac{2\zeta \mathsf{\Omega }}{{\left(1-{\mathsf{\Omega }}^2\right)}^2+{\left(2\zeta \mathsf{\Omega }\right)}^2},$$

(7)

where $W_0=\pi \frac{F_0}{k}$.

From the condition of maximum W_d, which is $\frac{d{W}_d}{d\zeta }=0$, it emerges that ${\zeta }^0=\pm \frac{1-{\Omega }^2}{2\Omega }$, so that the maximum dissipated energy $W_d^{\max }$ becomes

$$W_d^{\max }=W_0\frac{1}{2\left(1-{\Omega }^2\right)}=W_0\frac{1}{2\left(2\zeta \Omega \right)}.$$

(8)

It can be noticed that for certain values of $\Omega$ it correspond the values of ${\zeta }^0$ for which the dissipated energy is at maximum. The representation of $W_d\left(\zeta \right)$, so that the variation domain of $\zeta$ to be included ${\zeta }^0$, leads to a curve with a maximum point, having the coordinates ${\zeta }^0$ at $W_d^{\max }$. For the discrete values of $\Omega$, a family of parametrical curves of $W_d\left(\Omega ,\zeta \right)$ can be obtained.

2.4. Equation of the F–x Elliptic Hysteretic Loop

Phase $\omega t$ is eliminated between x = x(t) and F = F(t) as follows:

$$\{\begin{array}{c}x=A\sin \omega t\cos \phi -A\sin \phi \cos \omega t\\ F=F_0\sin \omega t\end{array},$$

(9)

where $\sin \omega t=\frac{F}{F_0}$, $\cos \omega t=\pm \sqrt{1-\frac{F^2}{F_0^2}}$, resulting

$$\frac{x}{A}=\frac{F}{F_0}\cos \phi \mp \sin \phi \sqrt{1-\frac{F^2}{F_0^2}}.$$

(10)

If we note the dimensionless sizes $\frac{x}{A}=X$ and $\frac{F}{F_0}=\Phi$, then relation (10) becomes

$$X=\Phi \cos \phi \mp \sin \phi \sqrt{1-{\Phi }^2}.$$

(11)

From of equation (11) $\mathsf{\Phi }$ emerges as

$$\Phi =X\cos \phi \pm \sin \phi \sqrt{1-X^2},$$

(12)

where $\sin \phi =\frac{c\omega }{\sqrt{{\left(k-m{\omega }^2\right)}^2+c^2{\omega }^2}}$ and $\cos \phi =\frac{k-m{\omega }^2}{\sqrt{{\left(k-m{\omega }^2\right)}^2+c^2{\omega }^2}}$.

By replacing $\frac{x}{A}=X$, $\frac{F}{F_0}=\Phi$, $\sin \phi$, and $\cos \phi$ in relation (12), the expression of force F emerges according to pulsation $\omega$, rigidity k, and amortization c as follows:

$$F\left(x\right)=F\left(x,\omega \right)=\left(k-m{\omega }^2\right)x\pm c\omega \sqrt{A^2\left(\omega \right)-x^2},$$

(13)

or in terms of $\Omega$ and $\zeta$ measures we have

$$F\left(x,\Omega \right)=k\left[\left(1-{\Omega }^2\right)x\pm 2\zeta \Omega \sqrt{A^2\left(\Omega \right)-x^2}\right].$$

(14)

For the condition that the dissipated energy to be maximum, $W_d=W_d^{\max }$ at ${\zeta }_{optim}={\zeta }^0$.

(a)

For the ante-resonance regime $\Omega <1$ at ${\zeta }_a^0=\frac{1-{\Omega }^2}{2\Omega }$, obtaining

$$F\left(x,\Omega \right)=\left(1-{\Omega }^2\right)\hspace{0.17em}k\left[x\pm \sqrt{A^2\left(\Omega \right)-x^2}\right],$$

(15)

or

$$F\left(x,\zeta ,\Omega \right)=2{\zeta }_a^0\Omega \hspace{0.17em}k\left[x\pm \sqrt{A^2\left(\Omega ,{\zeta }_a^0\right)-x^2}\right].$$

(16)

(b)

For the post-resonance regime $\Omega >1$ at ${\zeta }_p^0=-\frac{1-{\Omega }^2}{2\Omega }$ the following is obtained:

$$F\left(x,\Omega \right)=\left(1-{\Omega }^2\right)\hspace{0.17em}k\left[x\pm \sqrt{A^2\left(\Omega \right)-x^2}\right],$$

(17)

or

$$F\left(x,\zeta ,\mathsf{\Omega }\right)=-2{\zeta }_p^0\mathsf{\Omega }k\left[x\pm \sqrt{A^2\left(\mathsf{\Omega },{\zeta }_p^0\right)-x^2}\right].$$

(18)

where

$$A\left(\Omega \right)=\pm \frac{F_0}{k}\frac{1}{\left(1-{\Omega }^2\right)\sqrt{2}},$$

(19)

or

$$A\left(\Omega ,{\zeta }_{a,p}^0\right)=\pm \frac{F_0}{k}\frac{1}{2{\zeta }_{a,p}^0\Omega \sqrt{2}}.$$

(20)

2.5. Equation of the Hysteretic Loop Q–x

The instantaneous viscous-elastic force $Q\left(t\right)=c\dot{x}+kx$ may be expressed from the dynamic equilibrium equation. Thus, it can be expressed $m\ddot{x}+c\dot{x}+kx=F\left(t\right)$ or

$$m\ddot{x}+Q\left(t\right)=F\left(t\right),$$

(21)

from where Q(t) emerges as $Q\left(t\right)=F\left(t\right)-m\ddot{x}$, or in relation with x = x(t), it is obtained

$$Q\left(x\right)=F\left(x\right)-m\left(-{\omega }^{2}x\right).$$

(22)

In Equation (22) we insert the expression of force $F\left(x\right)=F\left(x,\omega \right)$ from (13) and have

$$Q\left(x\right)=Q\left(x,\omega \right)=kx\pm c\omega \sqrt{A^2\left(\omega \right)-x^2},$$

(23)

and in relation with $\Omega$ Equation (23) becomes

$$Q\left(x\right)=Q\left(x,\omega \right)=k\left[x\pm 2\zeta \Omega \sqrt{A^2\left(\Omega \right)-x^2}\right].$$

(24)

It is found that the family of ellipses according to Equation (24) is characterized by the fact that all ellipses have their major axis in the quadrant (0, π/2) with positive angular coefficient $tg\alpha =k>0$ for any value $\Omega >0$, where $\alpha$ is the angle between the ellipse axis and the Ox axis [24].

3. Elliptic Hysteretic Loops for the Ante-Resonance Regime ($\Omega <1$)

For a dynamic system where m = 10⁴ kg, k = 2⋅10⁷ N/m at the relative pulses Ω₁ = 0.8 with ${\zeta }_{optim}={\zeta }_1^0=0.225$; Ω₂ = 0.6 with ${\zeta }_{optim}={\zeta }_2^0=0.53$; and Ω₃ = 0.5 with ${\zeta }_{optim}={\zeta }_3^0=0.75$, the representation of the elliptical hysteretic loops Q–x and F–x, according to the graph of function W_d = W(ζ), as shown in Figure 2, Figure 3 and Figure 4. In each figure functions F(x) and Q(x) are represented based on Equations (16) and (24), respectively, corresponding to the representation of function W_d^max = W(ζ), given by Equation (8). Thus, it is found that for the maximum value of the dissipated energy W_d^max according to ${\Omega }_i<1$ and ${\zeta }_{optim}={\zeta }_i^0$, i = 1, 2, 3, the areas of the ellipses F–x and Q–x are maximum and equal [25,26,27,28,29]

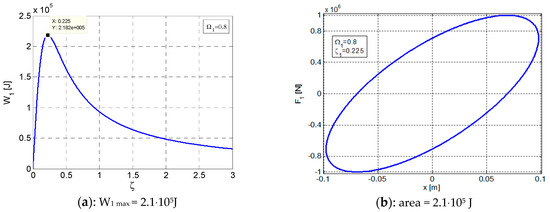
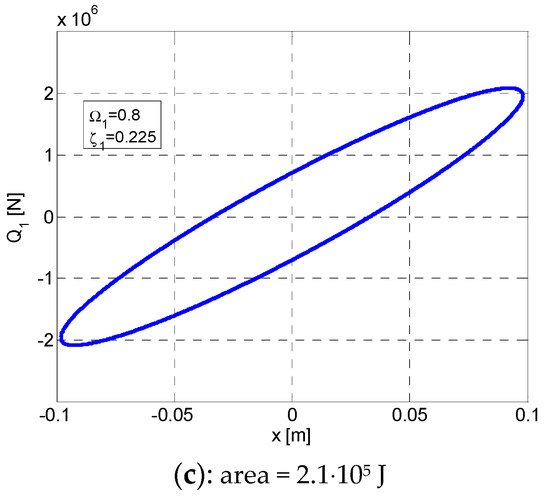
Figure 2. Variation curves in ante-resonance for W₁^max at Ω₁ = 0.8 and ζ₁ = 0.225. (a) Variation of W₁ according to ζ. (b) Elliptic hysteretic loop F₁–x. (c) Elliptic hysteretic loop Q₁–x. x = [−0.08701 ÷ +0.08701].

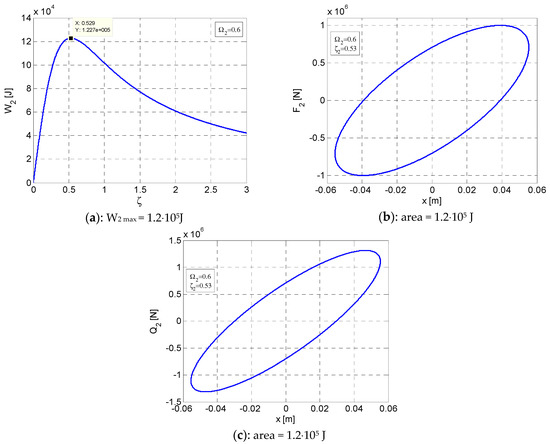
Figure 3. Variation curves in ante-resonance for W₂^max at Ω₂ = 0.6 and ζ₂ = 0.53. (a) Variation of W₂ according to ζ. (b) Elliptic hysteretic loop F₂–x. (c) Elliptic hysteretic loop Q₂–x. x = [−0.05542 ÷ +0.05542].

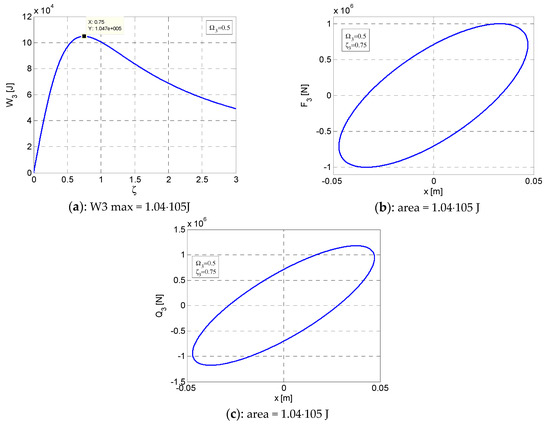
Figure 4. Variation curves in ante-resonance for W₃^max at Ω₃ = 0.5 and ζ₃ = 0.75. (a) Variation of W₃ according to ζ. (b) Elliptic hysteretic loop F₃–x. (c) Elliptic hysteretic loop Q₃–x. x = [−0.04715 ÷ +0.04715].

We specify the fact that the fraction of the critical amortization ${\zeta }_{ef}$, in this case for W_d ^max, may be defined as follows:

$${\zeta }_{ef}=\frac{W_d^{\max }}{4\pi \frac{1}{2}k{A}^2\left(\omega ,{\zeta }^0\right)},$$

(25)

and taking into account Equations (8) and (20), we have

$${\zeta }_{ef}={\zeta }^0\Omega .$$

(26)

It can be observed that only at a resonance, when ${\Omega }_i=1$, it results ${\zeta }_{ef}={\zeta }^0$.

In Figure 2, Figure 3, Figure 4 and Figure 5, the functions W_i = W_i(ζ), F_i–x, and Q_i–x are represented for ${\zeta }_{optim}={\zeta }_i^0$ in which W_i = W_d ^max(ζ⁰) and ${\Omega }_i$ where i = 1, 2, 3.

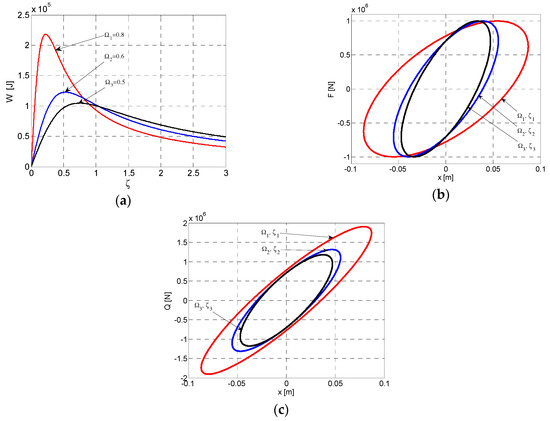
Figure 5. Families of curves in ante-resonance for W₁^max, W₂^max, and W₃^max. (a) Families of curves W according to the current variable ζ and the discreet variable Ω. (b) The family of elliptical hysteretic loops F–x according to the current variable x and the pair of discreet variables Ω, ζ. (c) The family of elliptical hysteretic loops Q–x according to the current variable x and the pair of discreet variables Ω, ζ.

4. Elliptic Hysteretic Loops for the Post-Resonance Regime ($\Omega >1$)

In the case of the above described system, for Ω₄ = 1.31 with ${\zeta }_4^0=0.28$; Ω₅ = 1.66 with ${\zeta }_5^0=0.53$; Ω₆ = 2 with ${\zeta }_6^0=0.75$, and Ω₇ = 2.32 with ${\zeta }_7^0=0.95$, in the Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 there were represented the functions W_i(ζ) and Q_i(x) were i = 4,5,6,7.

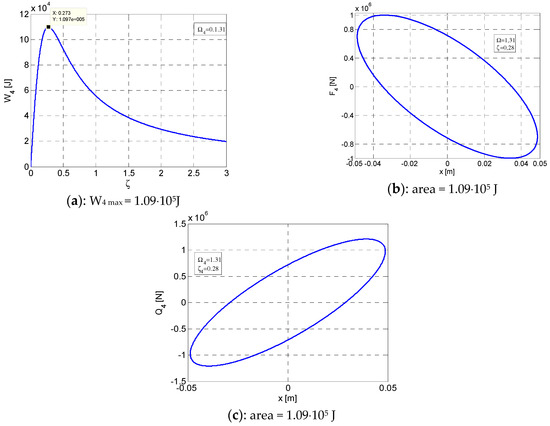
Figure 6. Variation curves in post-resonance for W₄^max at Ω₄ = 1.31 and ζ₄ = 0.28. (a) Variation of W₄ according to ζ. (b) Elliptic hysteretic loop F₄–x. (c) Elliptic hysteretic loop Q₄–x. x = [−0.04878 ÷ +0.04878].

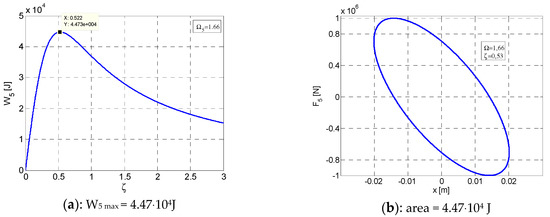
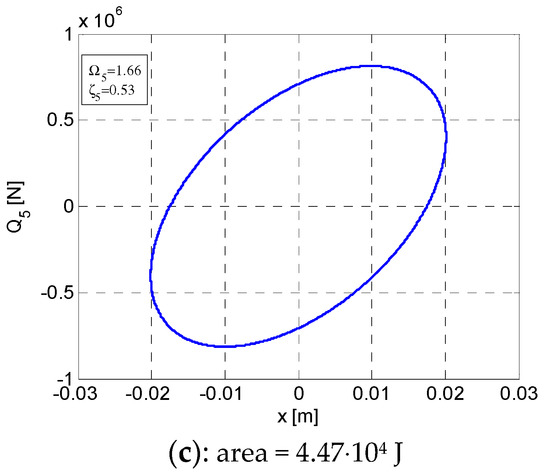
Figure 7. Variation curves in post-resonance for W₅^max at Ω₅ = 1.66 and ζ₅ = 0.53. (a) Variation of W₅ according to ζ. (b) Elliptic hysteretic loop F₅–x. (c) Elliptic hysteretic loop Q₅–x. x = [−0.02012 ÷ +0.02012].

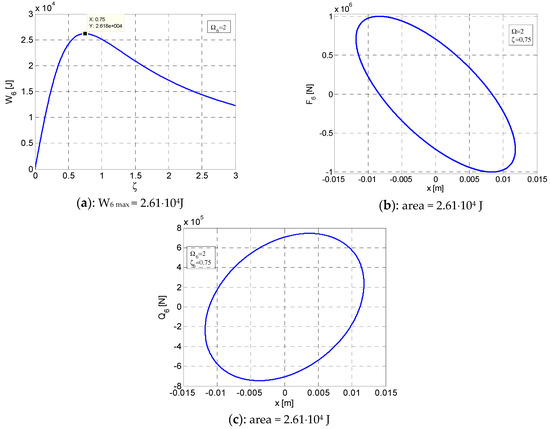
Figure 8. Variation curves in post-resonance for W₆^max at Ω₆ = 2 and ζ₆ = 0.75. (a) Variation of W₆ according to ζ. (b) Elliptic hysteretic loop F₆–x. (c) Elliptic hysteretic loop Q₆–x. x = [−0.01179 ÷ +0.01179].

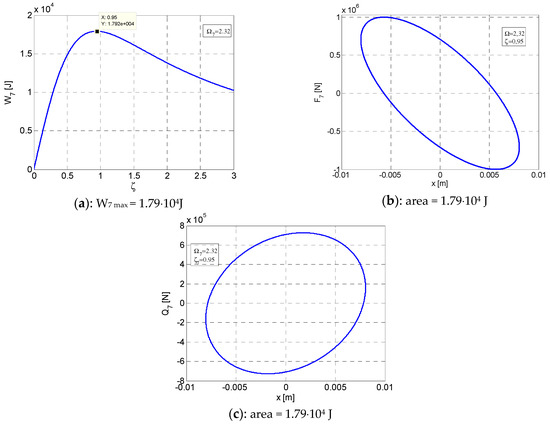
Figure 9. Variation curves in post-resonance for W₇^max at Ω₇ = 2.32 and ζ₇ = 0.95. (a) Variation of W₇ according to ζ. (b) Elliptic hysteretic loop F₇–x. (c) Elliptic hysteretic loop Q₇–x. x = [−0.008045 ÷ +0.008045].

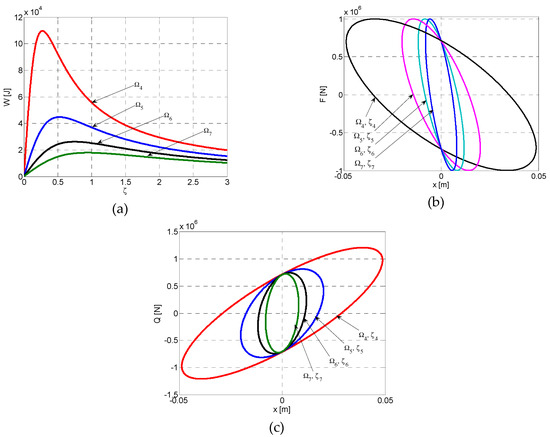
Figure 10. Families of curves in post-resonance for the maximum values of the dissipated energy W₄, W₅, W₆, and W₇ at parameters (Ω₄, ζ₄), (Ω₅, ζ₅), (Ω₆, ζ₆), and (Ω₇, ζ₇). (a) Families of curves W parametrized by the discreet variable Ω. (b) The family of elliptical hysteretic loops F–x for the pair of variables Ω, ζ. (c) The family of elliptical hysteretic loops Q–x for the pair of variables Ω, ζ.

5. Conclusions

The dynamic linear system m, c, and k excited by a harmonic perturbatory force is assessed dynamic regimes of ante-resonance $\Omega <1$ and and post-resonance $\Omega >1$ for values of the viscous dumping $\zeta ={\zeta }_{optim}={\zeta }^0$, for which the dissipated energy is maximum: $W_d=W^{\max }\left({\zeta }^0\right)$.

(a)

For this, there are established the functional relations of the perturbatory force F = F(x) in relation with the instantaneous displacement x = x(t), of the viscoelastic force Q = Q(t) in relation with x = x(t), of the viscoelastic force Q = Q(x) in relation with x = x(t), and of the dissipated energy in relation with the variation of the viscous dumping $\zeta$, namely W_d = W(ζ);

(b)

In this context, based on the graphical representations, it was possible to emphasize the fact that the ellipses F–x are rotating in relation to the origin of the axis system, according to the dynamic regime $\Omega <1$ or $\Omega >1$. The axis of the ellipse F–x rotation is caused by the inertial effect that is produced by the presence of the factor $1-{\Omega }^2$ in the expression of the function F = F(x);

(c)

The representation of the function Q = Q(x) highlights the that it constantly maintains an angle of inclination of the ellipse Q–x, axis, with a positive slope;

(d)

It can be noticed that the areas of the hysteretic loops F–x and Q–x are equal between them and equal with the maximum value of the dissipated energy W^max (${\zeta }^0$) for ${\zeta }^0=\frac{1-{\Omega }^2}{2\Omega }$.

(e)

The effective critical dumping ${\zeta }_{ef}$ depends both on the value of ${\zeta }^0$ as well as on the relative pulsation $\Omega <1$, for ante-resonance or $\Omega >1$, for post-resonance. In the case of the resonance regime, for $\Omega =1$, then ${\zeta }_{ef}={\zeta }^0$ is a sole situation that enables the assessment of the fraction from the optimal critical amortization ${\zeta }^0$.

The concordant graphical representations eloquently demonstrated the fact that for the dynamic regimes defined by the relative pulsation $\Omega$, the dissipative effects of the linear viscous-elastic systems may be analyzed, in experimental conditions defined by specific requirements.

The obtained results are based on the experimental tests performed on dynamic testing systems using real manufactured products. The tests were carried out in laboratories specialized in the testing of anti-vibration and anti-seismic devices, and the devices, belonging to recognized laboratories or manufacturing companies such as SISMALAB (Italy), EUCENTRE (Italy), DIS (Reno, USA), ALGA (Italy), and ICECON (Romania).

Based on the researches and the results presented in this paper, were designed and manufactured the elastomeric anti-seismic devices used for a viaduct with a length of 200 m, on the “Transilvania” Motorway, constructed by the Bechtel company (USA), in Romania.

The experimental tests performed in order to determine the hysterical loop families were conducted within the ICECON Romanian Research Institute for Construction Equipment and Technology – ICECON, using both anti-vibration and anti-seismic devices.

The assessment system using specialized tests was based on the Romanian Patent No. 80484/1982 “Stand for the measurement of the mechanical characteristics of rubber”, whose owner is the author of this paper.