Abstract
Shortest-path network interdiction, where a defender strategically allocates interdiction resource on the arcs or nodes in a network and an attacker traverses the capacitated network along a shortest s-t path from a source to a terminus, is an important research problem with potential real-world impact. In this paper, based on game-theoretic methodologies, we consider a novel stochastic extension of the shortest-path network interdiction problem with goal threshold, abbreviated as SSPIT. The attacker attempts to minimize the length of the shortest path, while the defender attempts to force it to exceed a specific threshold with the least resource consumption. In our model, threshold constraint is introduced as a trade-off between utility maximization and resource consumption, and stochastic cases with some known probability p of successful interdiction are considered. Existing algorithms do not perform well when dealing with threshold and stochastic constraints. To address the NP-hard problem, SSPIT-D, a decomposition approach based on Benders decomposition, was adopted. To optimize the master problem and subproblem iteration, an efficient dual subgraph interdiction algorithm SSPIT-S and a local research based better-response algorithm SSPIT-DL were designed, adding to the SSPIT-D. Numerical experiments on networks of different sizes and attributes were used to illustrate and validate the decomposition approach. The results showed that the dual subgraph and better-response procedure can significantly improve the efficiency and scalability of the decomposition algorithm. In addition, the improved enhancement algorithms are less sensitive and robust to parameters. Furthermore, the application in a real-world road network demonstrates the scalability of our decomposition approach.
1. Introduction
Networks are becoming increasingly important in modern life. The Internet, transportation systems, communication systems, and power distribution systems are all networks; even social systems can also be thought of as networks [1]. All of these networks are subject to competition between intended network users and adversaries who intend to interfere with that use, for instance, preventing illegal drug smuggling on the transportation network [2], identifying critical transmission-system components of power grid networks [3], stopping the spread of negative influence on a social network [4]. These competitive defence and attack problems that occur on networks can be modeled as network interdictions [5,6]. Network interdiction is a special class of adversarial network flow problems, which is widely studied in the fields of combinatorial optimization, computer science, artificial intelligence, and operations research. Usually, it involves two players who compete in a special case of a Stackelberg min–max or max–min game [7]. One player attempts to optimize their objective over the network, such as the shortest path, the maximum flow or the minimum cost flow. The opposing player aims to alter the network to maximally impair the attacker’s objective, for example by destroying arcs to maximize the attacker’s shortest path.
Most of the standard interdiction problems proposed in the literature can be considered as a special case of Stackelberg games [8], which involve a leader and a follower operating in turn with full knowledge of each other’s actions. The terms of “attacker” and “defender” are more commonly used in the context of security and antiterrorism applications, where the attacker plays the role of a malicious intelligent adversary seeking to impede a defender. It is worth noting that the terms of attacker, follower, and intruder can be used interchangeably in this paper. Similarly, the terms of defender, leader, and interdictor can be used interchangeably as well.
Considering cases where interdiction resources are vital and expensive, such as drones for wildlife protection in developing countries or missile strike in military operations, optimization of resource allocation must be taken into account. When preplanning for extremely expensive interdiction resources, decision makers must accept a trade-off between cost and effectiveness. In practice, when maximizing the expected interdiction performance requires excessive resources, decision makers tend to reduce the adversary’s network capacity to a specific threshold rather than demanding maximization. However, known frameworks can hardly address the cases where the goal of interdiction is restricted to a specified level. Therefore, we propose an alternative threshold model to balance the utility maximization and the resource consumption. By relaxing the maximization restraint to a specific goal threshold, we can greatly reduce the required resources while achieving a satisfying performance.
In an interdiction, the defender cannot guarantee that the interdiction action will be effective, which introduces uncertainty into the interdiction problems. For example, the deployed sensors can only discover the intruders with a certain probability. In this paper, we associate each defender’s interdiction action with a probability of success and assume that this probability is known to both players. This assumption is reasonable because many parameters of the interdiction resources, such as sensors, are publicly available. In this way, the deterministic interdiction model is transformed into a stochastic model.
In this paper, we introduce the game theory framework and model the novel stochastic shortest-path network interdiction with the goal threshold problem as a Stackelberg leader–follower game, where the defender acts as leader and the attacker acts as follower. The defender acts first and allocates interdiction sources to the arcs or nodes on the network to prolong the expected attacker’s shortest-path to a certain threshold, e.g., the allocation of sensors or checkpoints. The attacker can observe the defender’s strategy and chooses the expected shortest path to traverse the network from the source to the destination.
The widely studied k-most-vital-arcs-problem can be seen as a simplified type of network interdiction problem. Khachiyan et al. [9] proved that the k-most-vital-arcs-problem is NP-hard and strengthened the NP-hardness results by deriving inapproximability bounds for two variants of the problem. Wood [10] proved that the shortest-path network interdiction problem is NP-complete even for the simplest special case. The Stochastic Shortest Path network Interdiction with goal Threshold (SSPIT) model incorporates threshold constraint and randomness based on Israeli and Wood’s model [11], which makes it even more difficult to solve. Thus, the new SSPIT model is at least NP-complete [12]. In our SSPIT model, the defender’s strategy space grows exponentially with the number of resources available, whereas the attacker’s strategy space grows exponentially with the size of the network [13]. Take a fully connected graph with 20 nodes and 190 edges as an example; the number of defender actions for deploy 10 unit interdiction resources is , while the number of possible attacker paths without any cycles is . Real-world networks are significantly larger. For example, the entire Chicago sketch road network contains 933 nodes and 2950 arcs, and the defender’s resources available are also many more.
Therefore, we introduced a decomposition approach based on Benders decomposition [14] and reformulated the SSPIT problem as a bi-level mixed-integer problem SSPIT-D to help solve the NP-hard SSPIT problem. The higher level is a resource allocation problem for the defender, while the lower level is a shortest-path problem to be solved by the attacker. To enhance the efficiency and scalability of the basic decomposition algorithm SSPIT-D, we designed (i) an efficient dual subgraph interdiction master problem and (ii) a better-response subproblem using a local-search procedure. The subgraph procedure based algorithm SSPIT-S and the better response based algorithm SSPIT-DL can extract more constraints in each iteration and reduce the number of iterations required. The combination of the two algorithms SSPIT-SL can further improve the scalability and robustness.
The rest of this paper is organized as follows. Section 2 presents the related work. In Section 3, we illustrate our stochastic shortest-path network interdiction model and formulate the model using game theoretical methods. The algorithmic framework based on the decomposition approach and two improvement procedures are elaborated on in Section 4. Section 5 shows the computational empirical results and discussion. Finally, Section 6 provides the concluding remarks and suggestions for future work.
2. Related Work
The past decades have seen an accelerated development within network interdiction. Recently, network interdiction models have been widely applied to diverse areas involving competition, such as supply chain networks [15], counter-terrorism operations [16], facilities fortification [17], nuclear-weapons project interdiction [18], transportation networks [19], and electrical grid analysis [3,20]. The shortest-path network interdiction is a typical representative network interdiction problem [11]. The attacker attempts to traverse along the shortest path from the source to the destination, while the defender attempts to maximize the shortest path by interdicting some arcs or nodes with limited resource.
Shortest-path network interdiction problems can be naturally modeled as a bi-level optimization problem with opposing objective functions [21], with reference to Equation (1). The bi-level formulation takes full advantage of the special structural properties of network flows [22] and is inherently suitable for the Stackelberg game model with max–min conflict. Altner et al. [12] presented two polynomially separable valid inequalities for the network interdiction problem, and analyzed the integrality gaps and approximability of the bi-level mixed-integer program.
Shortest-path network interdiction problems can be extended for various application scenarios [23]. Wei et al. [24] introduced a threshold on the capacity of a network and proposed algorithms based on decomposition and duality formulation to optimize the interdictor’s resource consumption. However, the algorithms cannot scale up to large networks and are sensitive to network parameters. In Fulkerson and Harding’s model [25], the length of interdicted arcs increased linearly with the resource allocated. In our paper, we assume a certain amount of increment that would be added on the interdicted arcs. Israeli and Wood [11] also considered the network interdiction problem with binary interdiction allocations, while in reality, the interdiction actions may fail due to the restricted capability of facilities and staff.
The above studies are limited to deterministic models. In this paper, we introduce the probability of success in deploying resources and build a new stochastic model. For an interdicted arc or node, the deployed resource has a certain probability to actually take effect, and only a successful interdiction could induce a penalty on the attacker. For example, the deployed sensors can only probabilistically detect attackers when they traverse the covered arcs. The SSPIT model proposed in this paper can be seen as a stochastic extension of shortest-path network interdiction with goal threshold.
Stochastic models deal with the uncertainty that arises in network interdiction problems. Network interdiction problems are further complicated in the presence of uncertainty. Cormican et al. [26] incorporated the uncertainty of interdiction actions into the maximum flow interdiction problem. In their stochastic model, the network data are known with certainty, while each interdiction action is successful only with some probability, which is similar to the stochastic case considered in our paper. Pan and Morton [27] considered the case where the evader’s origin–destination pair is known to the interdictor only through a probability distribution. They use the L-shaped resource-directed decomposition method as the core solution technique and develop a class of step inequalities to tighten the mixed-integer master problem. In this paper, we introduce the artificial source and destination to convert the multiple sources and multiple destinations network to a single source and single destination network. Gutfraind et al. [28] proposed a Markov chain approach to model the stochastic interdiction behaviors, which achieves increased realism while remaining analytically penetrable. Stochastic models are more realistic to real-world scenarios and can invariably address the uncertainty in the network structure and evader behavior. Johnson et al. [29] further provided algorithms for optimal sensor placement in several classes of special graphs and approximation results for general graphs, assuming that the evaders are deterministic, Markov chain-based, reactive, and unreactive. Similar to our model, Bertsimas et al. [30] also introduced the randomized network interdiction problem, which allows the interdictor to use randomness to select arcs to be removed. They modeled the problem in both arc-based and path-based formulations.
The stochastic network interdiction problem directly leads to the robustness requirement. Decomposition algorithms are inherently sensitive to the parameters. In this paper, the proposed dual subgraph algorithm can significantly reduce the sensitivity of the algorithm to parameters. Many researchers study network flow problems in an uncertain environment from the viewpoint of robust optimization. Bertsimas et al. [31] introduced the robust and adaptive versions of the maximum flow problem and minimum cut problems in networks with node and arc failures, and established structural and computational results. The attacker may not be fully rational, and thus a deterministic strategy may lead to arbitrarily bad results. Hao et al. [32] studied the sensitivities of the optimal defender budget allocation and found that the allocation is sensitive to the percentage of nonstrategic attacker. Matuschke et al. [33] presented a new robust optimization model for the problem of maximizing the amount of flow surviving the attack of an interdictor, which can be used to model a large variety of network routing problems. Information asymmetries arise when the two opposing players have different perceptions of network parameters, such as the lengths of arcs. Bayrak and Bailey [34] examined shortest-path network interdiction under information asymmetries. The correct data values are known to the interdictor, while the evader only has estimates of these values. Computational results demonstrate improvements in the objective function values over the shortest-path network interdiction problem with symmetric information. Yates and Sanjeevi [35] modified the interdiction model to permit the allocation of static and dynamic sensors, and introduced a novel influence model for dynamic, network-patrolling sensors.
Multiobjective optimization problems are also an interesting domain for network interdiction. Our SSPIT model achieves a trade-off between resource consumption and interdiction effects by introducing threshold constraints, which can be seen as a simplified way of multiobjective optimization. Multiobjective Interdiction models aim to find all Pareto-optimal solutions in terms of the interdiction performance and the interdiction cost [36]. In addition, Ramirez-Marquez et al. [37] presented for the first time a multiobjective optimization algorithm for the multiobjective maximizing the shortest-path problem. They developed an evolutionary algorithm to approximate the optimal Pareto set of network strategies based on a Monte Carlo simulation. Xiao et al. [38] developed a subgraph sequence algorithm to identify the efficient frontier through a sequence of single-objective problems enumerating all possible budgets, and analyzed the saturation point of interdiction investment.
Network interdiction problems have been addressed in the field of game theory as well. Washburn and Wood [39] modeled the network interdiction problems as two-person zero-sum games where the defender attempts to detect the attacker by choosing optimal interdiction strategies on arcs. Game theory can extend the network interdiction model to more complicated settings and offers a principled way to achieve effective randomization. The solution concept of various equilibriums, such as the Nash equilibrium and strong Stackelberg equilibrium, can provide randomized mixed strategies to further increase the uncertainty the attacker faces. Our interdiction model is most similar to that of security games [40], where the defender allocates security resources strategically to protect targets against the adversary. Jain et al. [41] presented a scalable optimal solution technique for network-based security domains based on a double-oracle frame. Jain et al. [13] used warm starts and greedy responses to further improve the efficiency of the double-oracle framework. The double oracle framework inspired us to adopt a better-response algorithm based on the local search procedure, so that we can further reduce the number of iterations required by the decomposition algorithm. Although the research in the field of security games has achieved considerable success, most studies in Stackelberg security game are still target-structured, which fails to portray the network-featured actions of both players. The scope of research on the network-structured security domains is still limited.
Since the shortest-path interdiction problem is NP-hard, intelligent heuristics algorithms can be introduced to approximate the solution with respect to the above exact algorithms. Rocco et al. [42] introduced an evolutionary optimization approach that can be readily applied to solve deterministic network interdiction problems. Janjarassuk and Nakrachata-Amon [43] proposed a simulated annealing algorithm to solve the stochastic network interdiction problem. Compared with the exact algorithms, approximate algorithms are easier to solve and suitable for assisting exact algorithms to accelerate convergence [44].
3. Basic System Model
3.1. Problem Definition
The stochastic shortest-path network interdiction with goal threshold (SSPIT) problem can be molded as a Stackelberg leader–follower sequential game. The defender, as a leader, first uses available resources to interdict some subset of the network’s arcs or nodes. The attacker, as a follower, can observe the defender’s deployed strategy and then selects a shortest s-t path to traverse the network. The goal of the defender is to minimize resource consumption while forcing the attacker’s shortest path to exceed a specific threshold. We assume the interdiction game is under prefect information, i.e., the network topology, attributes and the capacity of the deployed resource are known to both the attacker and the defender. The assumption is reasonable, because defenders are generally publicly available and the malicious attacker can conduct surveillance in various ways to obtain sufficient information. In addition, we also assume that the attacker is perfectly rational, i.e., with full knowledge of the defender’s allocation strategy, the attacker acts with the best response.
To describe the new SSPIT problem formally, we adopted the notation introduced by Israeli and Wood [11]. See the complete notation in Table 1. The SSPIT problem is defined on a directed graph , where represents the vertex set and represents the arc set, either directed or undirected. We denote and as the number of nodes and arcs, respectively. The node set N includes a special source node and special termination nodes . Here, we assume that the source and termination nodes on the graph are unique. This assumption can be released to multiple sources and multiple destinations, as we will show later. Each arc is associated with a nominal length . Note that though the datum associated with arc is the length of the arc , in practice, the “length” is usually the time to traverse from i to j. We chose lengths for the convenience of computation as lengths are additive over a path. In cases of multiple arcs between two nodes i and j, all arcs other than the shortest can be discarded. Successful interdiction action increases the length of arc k to , where is the interdiction increment. In our stochastic setting, can be a binary random variable; if an interdiction fails, takes a value of 0; if it succeeds, takes a higher increase length. The probability of interdiction success on arc k is . If the value of is sufficiently large, the interdicted arc is considered completely destroyed and impassable, which can be removed from G. is the available resource or cost required to interdict arc k. represents the arc set directed out of (into) node i. Note that and are all non-negative scalar.

Table 1.
Notations for SSPIT problem.
We define as the interdiction variable, where when arc k is interdicted by the leader; otherwise, . Similarly, we define as the response variable, where when the follower travels arc k; otherwise, . Note that and are all binary variables.
The basic formulation of shortest-path network interdiction proposed by Israeli and Wood [11] is as follows:
where , R is the total resource budget.
3.2. Utility and Equilibrium
In network interdiction games, the strategy of the attacker corresponds to feasible paths from source node s to termination node t, while the strategy of the defender corresponds to the allocations of resources to the arcs or nodes in the network.
The attacker intends to traverse from the source node s to the termination node t along the path with the expected shortest path. If arc k is interdicted by the defender, i.e., , the expected length of arc k is considering the success probability . If arc k is not interdicted by the defender, i.e., , the length remains . In combination with the attacker’s traversing decision variable , the length of a feasible attacker traversing path, that is, the expected utility of the attacker is:
The attacker’s decision variable is constrained by the network flow to form a s-t path. Thus, the optimal utility of the attacker () is given in Equation (2):
By solving Equation (2), we obtain the attacker’s best response . Given the attacker’s best response , the defender can choose the interdiction arcs to minimize the resource consumption while ensuring the shortest path exceeds the threshold . The defender’s resource allocation problem is as follows:
Network-structured interdiction games are mostly zero-sum. In the zero-sum game, the sum of both players’ payoffs is always zero for any strategy profile. In the zero-sum game, the Nash equilibrium, the maximin and the minimax all would give the same solution, which is a critical property for theoretical analysis and computational standpoints. Our SSPIT model is also a one shot two-player zero-sum game on the network where the attacker’s action is the s-t path on the network, while the defender allocates limited resources to interdict a limited subset of the arcs or nodes.
The widely used solution concept for simultaneous-move and non-cooperative games is Nash equilibrium (NE), an outcome where no player has an incentive to deviate by playing a different strategy, as defined in Definition 1.
Definition 1.
(Nash Equilibrium) A pair of strategy forms a Nash equilibrium, if and only if:
- The defender plays a best response:;
- The attacker plays a best response:.
Specifically, We define the Nash equilibrium of SSPIT problem in Definition 2 below.
Definition 2.
(Subgame Perfect Nash Equilibrium) A pair of strategy forms a subgame perfect Nash equilibrium for the sequential SSPIT game, if and only if:
- The attacker plays a best response:;
- The attacker plays a best response:.
SSPIT is a Stackelberg leader–follower game. The defender chooses their strategy first, then the attacker chooses a strategy after observing the defender’s strategy. In this manner, the standard solution concept is a Strong Stackelberg equilibrium (SSE) [45]. SSE is not worse than NE though, counterintuitively, as the leader can at least commit to the NE solution. Let denote the attacker’s response function against defender’s strategy . We define the Strong Stackelberg Equilibrium as follows:
Definition 3.
(Strong Stackelberg Equilibrium) A pair of strategies forms a strong Stackelberg Equilibrium if they satisfy the following:
- 1.
- The defender (leader) plays a best response:
- 2.
- The attacker (follower) plays a best response:
- 3.
- The attacker breaks ties in favor of the defender:, where is the set of follower’s best responses to .
The maximin formulation naturally returns the SSE solution, and the SSE in our zero-sum model is equivalent to NE in terms of the leader’s strategy. In a word, with the nature of zero-sum, the NE, the SSE, and the minimax solution coincide with each other; thus, the SSE can be obtained by the following minimax formulation:
Computing the NE solution for a large-scale network turns out to be an extreme challenge, due to the exponentially growing resource allocations for the defender and the feasible s-t paths for the attacker. Thus, we introduced a novel decomposition framework to obtain the minimax based solution with finite iterations.
3.3. Formulation
Based on the maximin formulation Equation (4) and integrating the threshold constraint, the basic SSPIT model is formulated as follows in Equation (5):
Here, and denote the n-dimensional binary vectors with respective components and , . The objective function Equation (5a) minimizes the resource consumption required. Equation (5b) ensures that the shortest path of the original network exceeds the threshold . The network flow balance constraint Equation (5c) ensures that forms a valid path. Equation (5d) depicts the defender’s decision variable and the attacker’s decision variable . Since the model is totally unimodular, the binary constraints can be replaced by .
In fact, if each simple path between s and t in network G can be enumerated explicitly, another formulation of MIRGT can be constructed as follows:
where .
A path is a sequence of arcs where the head of one arc is the same as the tail of the next. denotes the arc–path incidence vector corresponding to a s-t path . implies that arc k is in the path ; otherwise, . Y is the set of which denotes the collection of arc–path incidence vectors corresponding to all simple s-t paths in G. For simplicity, we refer to as a “path”, Y as “a set of paths”, and as the interdicted path length of arc path . The validity of the SSPIT–Matrix lies in the fact that once the shortest path exceeds the threshold, all paths will exceed the threshold. Thus, when the network is small, the model can be solved efficiently with plenty of simple path enumerating algorithms. However, as the number of feasible paths in graphs grows exponentially with the number of nodes, it is impractical to generate all the feasible s-t paths for most real world networks, which makes solving the SSPIT–Matrix problem either inefficient or even impossible. Therefore, it is necessary to design new scalable algorithms to tackle large-scale networks.
4. Solution Methodology
The SSPIT model of Equation (5) is a bi-level optimization program with the leader’s decision transparent to the follower. The higher level is the defender’s resource allocation problem, while the lower level is the attacker’s shortest s-t path problem. The basic formulation of Equation (5) has an exponentially large number of constraints. In this section, we first propose a Benders decomposition based constraint generation decomposition approach. Then, a dual subgraph interdiction procedure and a local-search procedure are introduced to further improve the efficiency and scalability of the algorithm. Figure 1 depicts the framework of the decomposition proposed and two novel enhanced procedures. The main iteration loop of the decomposition algorithm is shown in the dashed box, and the leftmost and the rightmost boxes correspond to the enhancement procedure of the master problem and the subproblem, respectively.
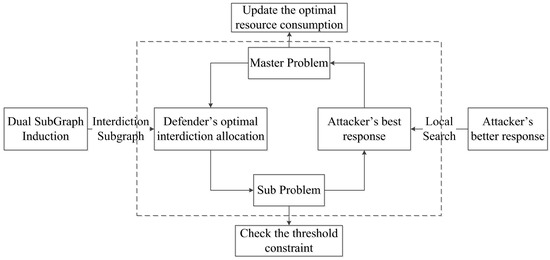
Figure 1.
Framework of decomposition algorithms and enhancement.
4.1. Benders Decomposition Reformulation
Note that when is fixed, the inner problem of SSPIT model 5 becomes a much easier optimization problem, i.e., given a fixed network interdiction condition, the problem is to find the expected shortest s-t path. Using projection, or partitioning, it is computationally efficient to solve in x-space rather than in -space. Thus, we introduced Benders decomposition to solve SSPIT.
Benders decomposition is an efficient way to solve large-scale optimization problems. The main idea of Benders decomposition is to separate the mixed decision variables into two-stage variables, which generates two relatively independent problems denoted as the Master problem and the subproblem, respectively. The two separated problems are much easier to solve alone or in combination. The Benders decomposition approach alternately solves the subproblem and the master problem and iteratively updates the master problem with the results of the subproblem until a convergence condition is satisfied. Based on Benders decomposition, the decomposition formulation of SSPIT is reformulated as a [Master()]–[Sub()] problem as follows in Equations (7)–(8):
Notice that in [Master()] and in [Sub()] are each fixed and known during their respective solutions. The decomposition algorithm seeks to solve [Master()]–[Sub()] by sequentially generating a fraction of the simple s-t paths within iterations. Let denote a specific defender interdiction plan and denote an optimal attacker response against . The set keeps track of the interdiction/response pair with and .
The basic decomposition algorithm for SSPIT problems based on Benders decomposition denoted as SSPIT-D is proposed in Algorithm 1.
| Algorithm 1 Basic Decomposition algorithm for SSPIT |
| Input: An instance of SSPIT Output: An optimal defender’s interdiction plan
|
The main logic of Algorithm 1 is as follows. The value of the threshold needs to be checked before the algorithm starts. Let () denote solution for [Sub()] when (), where and are the lengths of the shortest paths of G without and with full interdiction, respectively. Assume that the threshold value is between the upper and lower limits, i.e., . When , unlike full interdiction, it is not necessary to interdict all simple paths in G to achieve the goal threshold. The subproblem can constantly add new paths to the master problem until the master cannot find any better interdiction strategy. Generally speaking, the iteration will end before all simple paths are enumerated, i.e., . In each iteration, we only need to solve the master problem [Master()], which has a much smaller number of constraints and is much easier to solve than [SSPIT-Matrix]. When , the threshold cannot be reached, we can only try to maximize the shortest path. It should be noted that in the worst case, there is a possibility that the iteration will end with .
We introduced a simple instance of SSPIT to illustrate the basic Benders decomposition algorithm in Figure 2. After checking the threshold compared with the upper bound of interdicted shortest path, the subproblem [Sub()] first finds the attackers’ shortest path with length 18, as shown in Figure 2a; then, the master problem [Master()] returns an interdiction strategy to interdict arcs using 3 resources to guarantee the shortest-path threshold restriction, as shown by the dotted line in Figure 2b. In the next iteration, the [Sub()] finds a new best response shortest path with length 20 to the current interdiction strategy as shown in Figure 2c; then, the [Master()] returns a new interdiction strategy , which interdicts arcs using 5 resources, as shown in Figure 2d. In this case, the attacker’s expected shortest path of the interdicted network is 22.8. which satisfies the threshold constraint. Thus, the optimal interdiction strategy for the defender is to allocate 5 resources to interdict arcs , while the attacker’s best response travelling path is with expected shortest length 22.8.
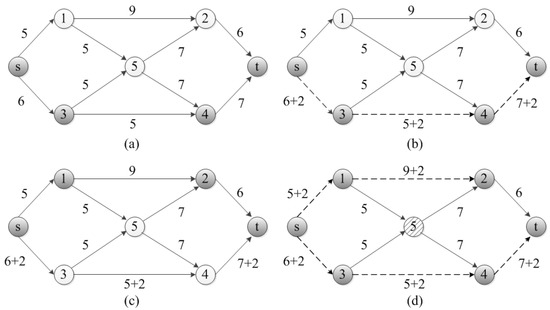
Figure 2.
A simple instance of stochastic shortest-path network interdiction with goal threshold (SSPIT) for illustration. s and t are the source and sink nodes, respectively. The nominal length of each arc is marked in addition to the arcs. The threshold is set to 22. The resource required to interdict each arc is assumed as 1, and the probability of successful interdiction is 0.8. Successful interdiction increases the length of the arc by 2, additionally. The interdicted arcs are indicated by dotted lines.
The decomposition algorithm can be regarded as a row generation algorithm in which one iteratively adds only those constraints which are violated by the current solution. The attacker strategy space is a capacity-constrained network path; hence, the attacker’s strategy space is a convex hull represented by network flow constraints. The subproblem [Sub(] solves an extreme point of the attacker’s strategy space, which returns an s-t path in this case.
Theorem 1.
The basic decomposition algorithm SSPIT-D correctly solves SSPIT in finite iterations.
Proof.
Let denote the collection of all simple arc s-t paths in G whose lengths are shorter than . By solving [Sub()], the algorithm can find a new path with the shortest interdicted length against the current interdiction plan . If it fails, i.e., , then the length of path under current interdiction plan is not less than the threshold , which is guaranteed by constraints in [Master()]. Meanwhile, the is also the shortest path under the current , which is guaranteed by the [Sub()]. Therefore, there are no other s-t arc paths whose expected path length does not meet the threshold constraint. The interdiction goal threshold is achieved and the algorithm terminates.
The master problem [Master()] can ensure that all path lengths in current exceed the threshold under current , which is obviously guaranteed by the threshold constraints Equation (7b).
Usually, some arcs may be shared between simple paths in the graph, and thus, the current interdiction strategy may also cause some other paths () to meet the threshold constraint after interdiction.
As a result, in each iteration, at least one new arc path will be added to the master problem. For a graph G, the number of simple s-t paths is finite, denoted as . Hence, the iteration will end in less than rounds. □
The basic decomposition algorithm performs poorly, and is especially sensitive to parameters. Generally, there are two ways to improve the performance: Reducing the number of iterations and improving the efficiency of solving problems in a single iteration. Solving the master problem of Equation (7) at each iteration requires much more computational effort than solving the subproblem of Equation (8), as the latter can be seen as a shortest-path problem. Therefore, we can improve the scalability and robustness of the basic decomposition algorithm using the following two ways:
- Improve the efficiency of solving the master problem to reduce the time of each iteration;
- Reduce the number of iterations required for convergence to reduce calls to the master problem.
4.2. Speed up the Mater Problem
Inspired by the double oracle framework in security games, which starts with a small restricted version of the original game and iteratively adds the best-response oracle to the current solution, we proposed a subgraph-based algorithm to reduce the number of iterations and improve the performance of the master problem. As shown in the illustrated instance of Figure 2, node 5 is irrelevant in the iterated decomposition solution process. The smaller scale network , where node 5 and its associated arcs are removed as shown in Figure 2d, has the same interdiction properties as the original network.
4.2.1. Optimal Interdiction Subgraph
Definition 4.
(Induced Subgraph) For a given graph , , the edge-induced subgraph by is the subgraph that:
- ;
The interdiction subgraph is the subgraph induced by a edge incidence interdiction vector , and given the optimal interdiction strategy , we can define the Optimal interdiction subgraph as follows:
Definition 5.
(Optimal interdiction subgraph) For a given graph , let be the optimal interdiction strategy, and . The subgraph induced by is the Optimal interdiction subgraph of G.
To further illustrate these definitions above, see the simple instance introduced in Figure 2. The [Sub()] first finds the attacker’s shortest-path response (Figure 2a), and there is , which can induce a interdiction subgraph shown by the dark nodes in Figure 2b. In this case, the master problem [Master()] returns an interdiction strategy to interdict arcs . Then, the [Sub()] finds a new best response shortest path , we have the new arcs set , and a new interdiction subgraph is induced by the updated , which is shown by the dark nodes in Figure 2d. Hence, the optimal interdiction subgraph induced by has the same interdiction properties as the original network but is easier to solve.
The intuition for the correctness of our subgraph decomposition algorithm is as follows. Once the algorithm converges, the current solution must be an equilibrium of the game, as each player’s strategy is the best response to the other’s current strategy (See Definition 1). In fact, the subproblem searches through all possible strategies and cannot find any better strategies. Furthermore, the algorithm must converge, because at worst, the subgraph will be exactly equal to the original, which is consistent with the basic decomposition model.
Theorem 2.
The optimal solution of the SSPIT problem on the interdiction subgraph is an upper bound of its solution on the original . The two are equal if and only if the interdiction subgraph is the optimal interdiction subgraph.
Proof.
Denote P and as the shortest path length after interdiction in G and , respectively. As , it is obvious that . According to the definition of optimal interdiction subgraph (Definition 5), the shortest path of G that satisfies the threshold constraint must be in , then ; if not, , which is a contradiction. □
As a rule of thumb, the parts involved in the shortest or near-shortest path are usually limited, i.e., the size of is usually much smaller than the size of original G. Hence, according to Theorem 2, we can obtain the upper bound through interdiction subgraph G’. Once we get the optimal interdiction subgraph, we get the optimal solution. In a word, we perform the master problem on the subgraphs which are iteratively generated instead of on the original network, until the interdiction subgraph is optimal.
4.2.2. Dual Reformulation
Note that if we fixed , the inner optimization problem of Equations (5b)–(5d) is simply the follower’s shortest-path problem with goal threshold, which is formulated as a minimum-cost flow model with one unit flow flowing from the source node s to the sink node t. Arc has the length if not interdicted (), and if successfully interdicted (). Such a special max–min and shortest-path structure of the shortest-path interdiction problem inspired us with a stochastic dual formulation by:
Denoting as the dual variables associated with the network flow-balance constraint Equation (5c) of SSPIT, we have the following MIP in Equation (9):
The dual decision variable denotes the length of the shortest path from source node s to target node i when . The decision variable determines whether interdiction is conducted on arc k with a success probability . The objective function of Equation (9a) is still to minimize the defender’s resource consumption. The threshold constraint is added in constraint Equation (9b) using the dual variable . Constraint Equation (9c) coupled with the original Equation (5b) captures Bellman’s equations for the shortest-path problem:
The dual model of Equation (9) can be solved directly using classic branch and bound approaches for MIP, which is potentially the simplest way to solve SSPIT model Equation (5). However, the LP relaxation of the dual model can be weak, especially when the values of interdiction increment parameters become quite large relative to the nominal arc lengths . For the case of complete interdiction, where the interdiction actions can completely remove an arc from the network, the dual model of Equation (9) performs poorly. More valid inequalities should be introduced to tighten the LP relaxation.
Pan and Morton [27] reported that the decomposition-based algorithm outperforms direct application of an MIP dual solver to a variant of the stochastic model. This contrasts with the situation in the deterministic setting because of the stochastic nature of the problem.
The matrix form of Equation (9) can be represented as follows in Equation (11):
where , is the vertex-edge incidence matrix; ; are each dimensional vectors; is the dimensional dual vector; and denotes the threshold.
When the size of the network is relatively small, it is more computationally efficient to solve the dual form. Thus, integrating the dual form into the master problem based on the subgraph will be a potential way to effectively improve the efficiency and scalability of the basic decomposition algorithm. The mathematical representation of the proposed interdiction subgraph-based decomposition algorithm is shown below:
where denotes the interdiction subgraph induced by the arc set .
Referring to the formula [DualMaster]–[Sub(] (Equations (12)–(13)), the subgraph decomposition algorithm for SSPIT problems based on interdiction subgraph denoted as SSPIT-S is proposed in Algorithm 2.
| Algorithm 2 Subgraph Decomposition algorithm for SSPIT |
| Input: An instance of SSPIT Output: An optimal defender’s interdiction plan
|
Theorem 3.
Algorithm SSPIT-S correctly solves SSPIT, and the number of iterations does not exceed algorithm SSPIT-D.
Proof.
With the iteration of the algorithm, once the optimal threshold shortest path in G is included in , it can be known from Theorem 2 that the solution of [DualMaster()] is equivalent to the solution of the original problem SSPIT. The [Sub()] is inherently consistent with the original SSPIT. Then, there is ). If not, i.e., , then the iteration continues and a new threshold shortest path is added to the subgraph until it contains the optimal path. Therefore, the algorithm SSPIT-S can obtain the optimal solution of SSPIT.
Denote and as the number of iterations required for convergence of algorithms SSPIT-D and SSPIT-S, respectively. Each time the two algorithms arrive at the step of solving [Sub()], the attacker reacts with a new best response against the current defender’s interdiction strategy . In SSPIT-D, the new arc path is directly added into path set for the master problem. However, in SSPIT-S, the path is used to update and induce an interdiction subgraph; the master problem [DualMaster()] calculates the interdiction strategy on the subgraph instead of tightly restricted . Let and be the arc set of and , respectively, and similarly let and be the set of all simple s-t path in and , respectively. For subgraph , induced by , according to Definition 4, there is , and thus, . Consequently, in one iteration, the algorithm SSPIT-S can interdict more possible simple paths than algorithm SSPIT-D, which could potentially reduce the number of iterations required as the total number of interdicted paths is constant, and thus, , i.e., the number of iterations of SSPIT-S is less than or equal to SSPIT-D. □
In practice, the subgraph-based algorithm SSPIT-S can significantly reduce the iterations required for convergence. Given the set and the current shortest path, there may be some shorter arcs in , which could be combined with the previous path to form a new alternate shortest path with high probability. Since the master problem of SSPIT-S is performed on the subgraph, algorithm SSPIT-S can avoid unnecessary iterations used to generate these shortest paths. In addition, the interdiction subgraph is typically smaller in size than the original, which makes the problem much easier to solve.
The subgraph-inducing procedure extracts columns and rows from the adjacency matrix of and, at worst, the subgraph is the original graph . Therefore, the complexity of the subgraph-inducing procedure is , where is the number of nodes in G. In practice, as the number of nodes in subgraph is usually limited relative to the original graph G, the procedure is acceptable.
4.3. Speed up the Subproblem
In the basic decomposition Algorithm 1, the subproblem produces one single optimal response pair in each iteration. Intuitively, if the subproblem [Sub()] could provide multiple optimal or suboptimal shortest paths in one iteration, it will help to reduce the number of iterations required for convergence. We adopted a better-response subproblem using the local-search procedure to enumerate all the shortest s-t paths and even other suboptimal shortest paths when solving the [Sub()] problem (Equation (8)) for a given ; then, we added the resulting multiple pairs () into the [Master()] problem, where denotes an optimal or suboptimal response to . When the better-response subproblem fails to generate new paths, the original subproblem is invoked.
Definition 6.
(Local-Search) Given , the standard shortest-path tree T (which contains all the shortest paths from source node s to any other nodes) can be built using classic algorithms. Denote as the shortest s-t path; and similarly denote as the shortest path. Then, , there are such additional paths whose path length also does not exceeded the threshold. The additional paths can be represented in form with the corresponding pair () given . The process to generate all these extra paths is defined as the local-search procedure.
For the local-search() procedure, we built the shortest path tree T using the Dijkstra algorithm. It is well known that generating the shortest path tree from s to all other nodes in G is not much more complicated than searching for a single shortest s-t path. The local search iteratively searches for a neighbor path . Here, we say that path is a neighbor path within distance l of path P if can be obtained by replacing a subpath of P with another path of length no longer than l, l can be obtained from the difference between the current shortest path and the threshold, e.g., . Each pair () returning from from local search() is introduced to , which yields one more subpath to be included in the master problem.
Denote as the path set generated by the procedure of local search() for subgraph . According to Definition 6, is established, which ensures that the local-search procedure does not compromise the validity of SSPIT algorithms above. Hence, the procedure can be used to further reduce iterations. We denoted the local-search enhanced algorithms as SSPIT-DL and SSPIT-SL for SSPIT-D and SSPIT-S, respectively.
The improved subgraph decomposition algorithm based on the local-search algorithm (SSPIT-SL) is detailed in Algorithm 3.
| Algorithm 3 Improved subgraph decomposition algorithm based on local-search. |
| Input: An instance of SSPIT Output: An optimal defender’s interdiction plan
|
It is worth noting that on one hand, the better-response procedure can add more paths to be interdicted, while on the other hand, the adopted shortest-path tree generation algorithm would also affect the efficiency of the enhanced algorithms, especially when the network scale is huge.
4.4. Variants for SSPIT Problem
In this section, we introduce some variants for interdiction problems and show how to convert them into basic SSPIT models.
4.4.1. SSPIT with Multiple Sources and Multiple Destinations
The models discussed in the previous section only consider the case of two designated vertices, i.e.. the single source node s and the single destinations node t. When the source–destinations pair is not specified, the defender is unaware of which source and destinations the attacker will choose. The attacker’s path-selection manner is usually assumed to follow a probability distribution. Hence, the attacker can take a random walk from source to destinations. In this paper, we consider the worst case for path selection and leave the robustness study for a random manner to the future.
The multiple sources and multiple destinations network can be easily converted to a single source and single destination network by introducing an artificial source and destination. The artificial source node is connected to each of the original sources, and the artificial destination node is connected to each of the original destinations. The length of the newly added artificial arcs is 0. None of these artificial arcs connected to the and may be interdicted. All of the original sources and destinations could be viewed as intermediate nodes, and the new converted network has a single source and a single destination . Figure 3 illustrates the above conversion process with a simple instance.
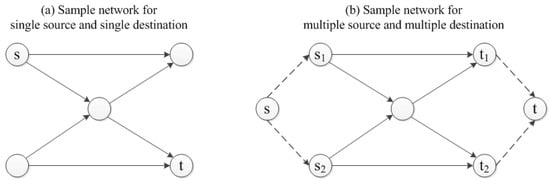
Figure 3.
A sample network with single source s and single destination t is shown in (a); the multiple sources and multiple destinations sample network can be converted to a single source and single destination network by adding an artificial source node to all the source nodes, an artificial destination node to all the destination nodes as shown in (b). The new joint arcs are indicated by dashed lines.
4.4.2. Nodal Interdiction for SSPIT
The SSPIT models discussed above focus primarily on arcs or edges, while the nodes or vertices should ALSO be included as candidates for resource allocation. Traditionally, a node-splitting technique is introduced which replaces each candidate target node i in the original network with two artificial nodes, and , and a link from to . The interdiction on candidate node i can be interpreted as interdiction on artificial arc . Figure 4 shows a sample of the node-splitting transformation.
Figure 4.
Sample of node-splitting transformation, the candidate nodes are split into two with an artificial arc to be interdicted instead.
Unfortunately, the node-splitting approach is not proper for larger-size networks. In the worst case of node-only interdiction, the approach would double the number of nodes and add m arcs to the original network. Here, we introduce a conversion constraint Equation (14) to convert the arcs interdiction to node interdiction for node-only interdiction and node–arc-mixed interdiction:
The additional constraint Equation (14) states that the outgoing arcs of a node are interdicted if and only if the node itself is interdicted. In other words, if node i is interdicted, all outgoing arcs incident to i are also interdicted. Here, we abandon the incoming constraint. as it is redundant.
5. Computational Experiments
We experimentally evaluated the performance of our methodologies proposed both on simulated networks as well as on real-world road networks.
We first identified the four algorithms that needed to be tested and analyzed the effectiveness of the two enhanced components in algorithm runtime and number of iterations. Secondly, we adopted three types of simulated networks with different topologies to verify the scalability of the proposed algorithms. The network topology greatly affects the efficiency of the decomposition algorithms, especially the extraction of subgraphs and the efficiency of local search. These different types of networks also indicate the potential applications of our models in other areas, such as social networks. Since the grid network is more similar to the road network and the influence of parameters is more obvious, we then continued to evaluate the parameter sensitivity and robustness of the enhancement algorithms on the grid network. Finally, we adopted two real-world road networks to further verify that our improved decomposition algorithm is scalable enough to be applied to the real world.
5.1. Test Problems and Environment
The test problems of artificially generated graphs are:
- Random Network:The Erdös–Rényi model [46] generates a random graph given node set N and the fixed connection probability p between any nodes. Obviously, the number of edges of the generated graph is not fixed.
- Small-world Network:The Kleinberg model [47] generates a adjacency matrix of a range dependent graph, where n is the number of nodes in the lattice; p is the maximum distance of short-range connection; q is the number of random connections to add per node; and is the clustering exponent.
- Regular Grid Network:The regular grid network model generates simulated grid networks with m rows and n columns, respectively. Each node at grid position has a probability p to connect to neighbor nodes at grid positions , , , , , , , and if a node exists at that particular position. Nodes and are set as the source and destination nodes, respectively.
The integer normal length , the interdiction increment , and the resource consumption are assumed to be uniformly distributed on , , and , respectively. The interdiction probability p is inversely linearly proportional to the node degrees as the increase in the attacker’s choice of arcs will reduce the probability that the defender detects him. In each test, we created 10 instances with different values of , and r parameters randomly.
The real-world test data [48] come from:
The real-world tested networks are assumed to be undirected. The length of arc is an approximate integer of the real road distance, while the resource consumption is linearly proportional to the node degrees.
The algorithms presented above are coded using the MATLAB toolbox YALMIP [49] and the COMPLEX 12.6 callable library. The tests were executed on a Windows 7 computer with Intel(R) Core(TM) i7-4770M CPU @ 3.40 Ghz with 8 GB RAM.
5.2. Analysis of Components of SSPIT
In this section, we evaluate the performance boost provided by the subgraph procedure and local-search procedure. Specifically, we evaluated the use of the subgraph and better-response procedure independently as well as in conjunction. These results are shown in Figure 6. We used random grid networks since they mimic the connectivity properties of urban road networks more. Additionally, SSPIT-D was established as the baseline; SSPIT-DL was enhanced by the better-response procedure using local search without the subgraph procedure; SSPIT-S was enhanced by the subgraph procedure using local search without the better-response procedure; and SSPIT-SL combined the two enhancements.
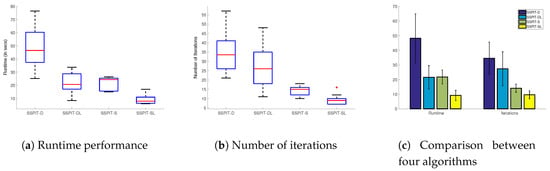
Figure 6.
The contributions of the subgraph procedure and better-response procedure. SSPIT-D was used as a baseline.
All data points were averaged over 20 samples on a random regular grid network with and a fixed . The box plots in Figure 6a,b detail the runtime and iteration performance of the four decomposition algorithms. The x-axis shows the different methodologies for the decomposition algorithm, and the y-axis shows the runtime in seconds in Figure 6a and the number of iterations in Figure 6b.
Figure 6c compares the four decomposition algorithms from the runtime and the number of iterations. The first set of data for Figure 6c compares the average runtime of the four algorithms. Here, the baseline SSPIT-D took 48.3 seconds; SSPIT-DL decreased the runtime to 21.5, while SSPIT-S decreased the runtime to 21.8. The combination of two enhancements SSPIT-SL further reduced runtime to 9.2. Similarly, the second set of data for Figure 6c compares the average number of iterations. Here, the baseline SSPIT-D took 35 iterations; SSPIT-D decreased the iterations to 27, while SSPIT-S decreased the iterations to 14. SSPIT-SL had the smallest number of iterations of 10. These results show that both the subgraph procedure and the better-response procedure can effectively reduce the runtime and number of iterations. For both procedures, the subgraph procedure is more effective at reducing the number of iterations, while the better-response procedure’s data variance is significantly larger, which implies that SSPIT-DL is more unstable. The combination of the two provides a boost in performance, which makes SSPIT-SL even more effective.
5.3. Scalability in Simulation
This section evaluates the performance of the four proposed algorithms as the network types and attributions are varied. These results are averaged over 10 samples.
The two enhanced procedures proposed are closely related to the topology of the network. To illustrate the impact, we selected three representative types of networks (i.e., random network, small world network, and grid network) and investigated the performance of different algorithms for the SSPIT problem as the network type varies.
Figure 7a,b presents the results of ER random networks of different sizes varying the number of nodes with arc connection probability of 0.5 (Random ER network: , N is the number of nodes). These results show that all four decomposition algorithms performed well in scalability for the ER network. As the size of the ER network expands, the three enhanced algorithms gradually outperform the basic SSPIT-D algorithm, in which the performance of SSPIT-S is better. In terms of iterations, the average number of iteration of the two algorithms related to the better-response procedure, i.e., SSPIT-DL and SSPIT-SL, is higher than those of the remaining two, which implies that the better-response procedure is not suitable for the ER network model. Thus, the experiment result shows that the subgraph procedure enhanced algorithm SSPIT-S provides the most improvement.
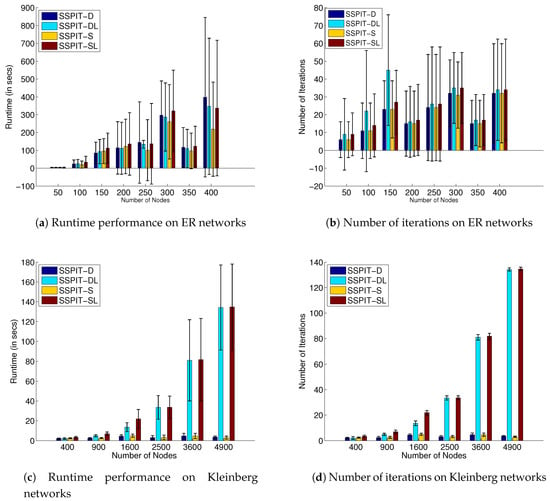
Figure 7.
Computational results for four decomposition algorithms on ER networks and Kleinberg networks of different sizes. (a,b) are the results for the ER networks, and (c,d) are the results for the Kleinberg networks.
Figure 7c,d presents the results of Kleinberg networks of different sizes (Random Kleinberg network: , N is the number of nodes). The Kleinberg model is a variant of the well-known two-dimensional Newman and Watts’s NW small world; hence, we introduced it to illustrate the potential applications of the proposed algorithms on social networks. The probability that two nodes have a long hop connection is determined by the Manhattan distance between them. All nodes are spatially evenly distributed. We generated random Kleinberg networks with different sizes with network attributes of .
Basically, all the algorithms performed well on the Kleinberg small-world networks. As the size of the Kleinberg network grows, the runtime of SSPIT-DL and SSPIT-SL enhanced by the better-response procedure increases significantly, while the runtime of the basic algorithm SSPIT-D and subgraph-enhanced algorithm SSPIT-S without better response remains at a lower level. As we mentioned earlier, the adopted shortest-path tree generation algorithm would affect the efficiency, especially when the network scale is huge. In Kleinberg networks, long-range arcs are dominated in long distances. The destination node can be reached by several hop arcs starting from the source node in a high probability, which makes the crucial arcs relatively fixed, thereby reducing the runtime and iterations substantially. The large clustering coefficient and shorter average distance features of small-world networks are beneficial to the solution of the decomposition-based algorithm. Overall, the four algorithms can be solved in several iterations, with a slightly larger number of SSPIT-DL and SSPIT-SL. In addition, the existence of long-rang arcs makes the extraction of the subgraph more straightforward, and the number of arcs associated with interdiction in the entire network is limited. In general, the basic decomposition algorithm SSPIT-D and the subgraph procedure enhanced algorithm SSPIT-S provide the most improvement.
Table 2 presents the results of regular grid networks of different sizes . The results showed that SSPIT-SL is the fastest among the four decomposition algorithms. When the network size grows, algorithms SSPIT-S and SSPIT-SL are much faster than the SSPIT-D and SSPIT-DL by a wide margin.

Table 2.
Computational results on regular grid networks.
Compared with the basic decomposition algorithm SSPIT-D, the other three algorithms have a smaller number of iterations in average, which is consistent with the theoretical analysis above. As shown in Section 5.2, both the better-response procedure and subgraph procedure can actually reduce the iterations required for convergence. The algorithm SSPIT-SL combines the two improved procedures to further reduce the iterations and improve the efficiency and scalability of the algorithm.
5.4. Sensitivity Analysis of Parameters on Algorithms
This section evaluates the performance of the four decomposition algorithms as the value of parameters is varied. As mentioned above, different values of parameters affect the performance of the decomposition algorithms. These tests are conducted on a regular grid network for convenience. SSPIT-SL is statistically significantly () faster than the basic SSPIT-D for large values.
5.4.1. Vary Interdiction Increment
We first investigated the performance of four decomposition algorithms as the interdiction increments of varied. We fixed the other attributes and varied the value of . is established as a baseline, and for each of the other values of , we took the same threshold of the baseline and the mean of its own upper and lower bounds and calculated the algorithms’ runtime and number of iterations in the two cases, respectively. The results are shown in Figure 8.
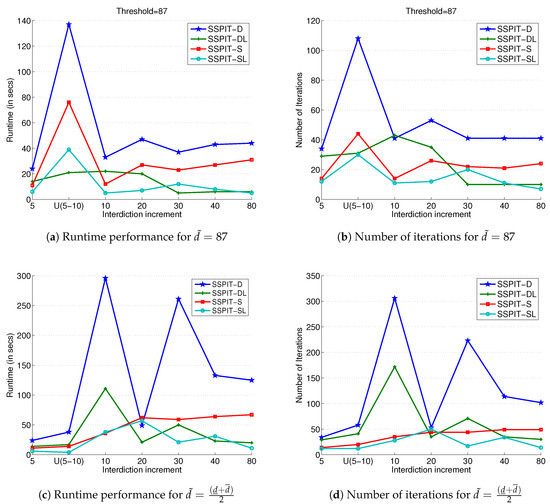
Figure 8.
Computational results varying with interdiction increment . (a,b) are the results for threshold taken from baseline , while (c,d) are the results for threshold .
For a fixed threshold , as the value of increases, the runtime of the case of reaches the peak. According to Figure 8a,b, SSPIT-D and SSPIT-S are more susceptible to the value of in the case of a small threshold. This indicates that the better-response algorithm based on a local-search procedure is more robust against the interdiction increment . In the case where , the enhanced three algorithms still outperform the basic algorithm SSPIT-D. As the value of increases, SSPIT-DL and SSPIT-SL are more robust. Hence, the better = response procedure can effectively deal with large interdiction increments, and together with the subgraph procedure, it can further improve the robustness of the decomposition algorithms.
5.4.2. Vary Interdiction Goal Threshold
Using the same grid network described above, we also tested the four decomposition based algorithms under different goal thresholds. Figure 9 presents the results when varying the value of threshold. Figure 9a,b depict the trends in the runtime and number of iterations as the threshold increases, respectively.
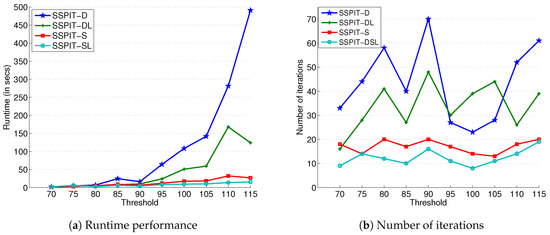
Figure 9.
Computational results varying with interdiction goal threshold for a regular grid network with and .
As shown in Figure 9, the basic algorithm SSPIT-D is quite sensitive to the threshold. As the value of the threshold increases, the runtime increases sharply and the number of iterations fluctuates drastically. The algorithm SSPIT-DL, which is enhanced by the better-response procedure, is less affected by the threshold. SSPIT-S and SSPIT-SL are more robust to different threshold values. Before the median of threshold 90, the running time of algorithms increased slightly. Subsequently, the runtime of SSPIT-D and SSPIT-DL climbed significantly, whereas the runtime of SSPIT-S and SSPIT-SL still maintained a gradual growth rate. All four algorithms reached a peak in the number of iterations near the median and the upper threshold. Increasing the threshold allowed more combinations of arcs to be interdicted, which leads to more feasible solutions for the master problem. After reaching a certain level, the crucial arcs are selected, and interdicting these arcs also ensures the satisfaction of the subsequent threshold. Meanwhile, when the threshold is approaching its upper bound, more arcs need to be considered. The subgraph procedure can efficiently extract subgraphs containing these crucial arcs that are closely related to interdiction, thereby reducing the number of iterations and speeding up the solution.
In summary, the subgraph procedure can significantly reduce the sensitivity of decomposition algorithms to the threshold. Combined with the better-response procedure, the solving ability and robustness of the decomposition approach are further improved.
5.4.3. Vary Probability of Successful Interdiction
We now present the results when varying the value of success interdiction probability in Table 3 using the same grid network above.

Table 3.
Computational results varing with interdiction success probability .
It can be concluded from Table 3 that the decomposition approach is more robust in terms of than the interdiction increment and the goal threshold. We observed a similar performance trend: the SSPIT-D and SSPIT-DL are much similar, while the SSPIT-S and SSPIT-SL are much similar. Still, SSPIT-SL outperforms the other three, which further indicates the effectiveness of the two procedures in enhancing the robustness of the decomposition approach.
5.5. Test on Real Data
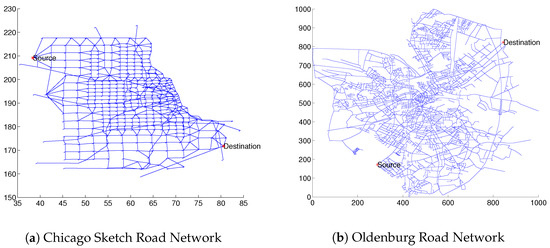
We also tested the efficiency and scalability of the decomposition approach on real-world urban road network data. The interdiction increment is set to multiplied by a certain factor. The interdiction resource for each arc is set as the starting node’s degree. The source and destination nodes are marked in Figure 5.
We first used the Chicago sketch road network as shown in Figure 5a for its similarity with the grid network. The results are shown in Table 4. It can be observed that the density of real networks is smaller than that of the regular grid network. Hence, the basic SSPIT-D algorithm is much easier to solve on real networks. As we mentioned above, the better-response procedure which uses a local-search procedure becomes time-consuming as the number of nodes N grows. Recall that the complexity of the better-response procedure is . However, the subgraph-enhanced algorithm SSPIT-S performs better than the other three, which significantly improves the efficiency of the decomposition approach, especially for the case of large increments.

Table 4.
Computational results on the Chicago Sketch Road Network.
The network size of the Chicago sketch is medium, so we used another much larger transportation network, the Oldenburg road network, as shown in Figure 5b, to further verify the scalability of the decomposition approach. The results are shown in Table 5.

Table 5.
Computational results on the Oldenburg Road Network.
The four algorithms exhibited similar properties as before. The algorithm SSPIT-DL enhanced by the better-response procedure is difficult to solve in a limited time, as the interdiction increment and threshold increase. Though the basic decomposition algorithm SSPIT-D shows acceptable performance, the subgraph procedure enhanced algorithm SSPIT-S can further improve the scalability and efficiency. For example, it took SSPIT-S only about 37 seconds to find the optimal solution to force the attacker’s shortest path to exceed 7000 using the fewest resources. Thus, we can draw a conclusion that SSPIT-S is now scalable enough to be applied and used in the real world.
6. Conclusions and Future Work
In this paper, we defined a novel variant of the shortest-path network interdiction problem, SSPIT, which takes into account the uncertainty of the interdiction action and the goal threshold constraint. An attacker attempts to traverse the network from the source node s to the destination node t along the shortest path, while the defender attempts to force the attacker’s shortest path to exceed a given threshold by interdicting some of the arcs or nodes. The interdiction action itself has a certain chance of success p. The goal threshold constraint is introduced as a common trade-off between utility maximization and resource consumption. By incorporating the probabilistic interdiction likelihood and threshold constraint into network interdiction, we presented a novel model named stochastic shortest-path Interdiction with goal threshold and presented SSPIT-D, a basic decomposition framework based on Benders decomposition to tackle the NP-hard SSPIT problem. However, the basic decomposition algorithm performs poorly and is especially sensitive to parameters. Inspired by the double oracle framework in security games, we further improved efficiency and scalability in two ways. First, the interdiction subgraph was induced by the set of response paths generated by the subproblem until the optimal interdiction subgraph was included. Duality also played a key role in reformulating a nested max–min or min–max model as a non-nested MIP. Thus, we designed an efficient dual subgraph interdiction procedure to help to solve master problems. Second, a better-response algorithm using a local-search procedure was proposed. The better response can extract more constraints from the subproblem. When the better response fails to return feasible paths, the original best-response subproblem is invoked, which guarantees each iteration adds as many feasible paths as possible to the master problem. Numerical experiments showed that the dual subgraph and better-response procedure can significantly improve the efficiency and scalability of the decomposition algorithm. In addition, the basic decomposition algorithm SSPIT-D is sensitive to the attributes and sizes of networks. The two procedures can significantly improve the robustness of the decomposition approach. Furthermore, we verified the scalability of our proposed algorithms on much larger real-world road networks. The algorithm SSPIT-S can provide solutions for large real-world transportation networks providing orders-of magnitude speedups. The scalability of our decomposition approach now makes it feasible for it to be used in real-world networked domains.
It is noteworthy that the SSPIT model is arguably appropriately conservative, i.e., it optimizes for the worst case. In fact, the defender may be unsure how the attacker will behave. Depending on the attacker’s behavior model and the defender’s goal, more different interdiction models can be built. Algorithms like the regret-minimization method can be introduced to provide a more robust solution for the shortest-path network interdiction games. We also hope to extend our research to a random strategy where the defender can further expand their leadership advantage by adopting a mixed strategy. For another major category of network interdiction problems, the network flow interdiction game, the number of feasible flows is infinite. This is significantly different from the shortest-path interdiction game in this paper. New theories are needed to prove the convergence of the decomposition problem. We believe that the computational game theory can provide useful enlightenment, which is a promising perspective to solve such Stackelberg games.
Author Contributions
X.W. and K.X. developed the theoretical concepts and wrote the theoretical sections. X.W., P.J., Q.Y., and Y.Z. wrote the experimental sections. All the authors contributed (wrote, reviewed, and supervised) to the final manuscript.
Funding
This work was supported by the National Science Foundation of China (NSFC) under granting No. 61473300 and Hunan Provincial Natural Science Foundation of China under granting No.2016JJ4006.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Washburn, A. Network Interdiction. In Two-Person Zero-Sum Games; Springer: Berlin, Germany, 2014; pp. 123–141. [Google Scholar]
- Zhang, J.; Zhuang, J.; Behlendorf, B. Stochastic shortest path network interdiction with a case study of Arizona–Mexico border. Reliab. Eng. Syst. Saf. 2018, 179, 62–73. [Google Scholar] [CrossRef]
- Salmeron, J.; Wood, K.; Baldick, R. Worst-case interdiction analysis of large-scale electric power grids. IEEE Trans. Power Syst. 2009, 24, 96–104. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Y.; Yang, S. Efficient influence maximization in social networks. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 199–208. [Google Scholar]
- Smith, J.C.; Prince, M.; Geunes, J. Modern Network Interdiction Problems and Algorithms. In Handbook of Combinatorial Optimization; Springer: Berlin, Germany, 2013; pp. 1949–1987. [Google Scholar]
- Collado, R.A.; Papp, D. Network Interdiction–Models, Applications, Unexplored Directions; Rutcor Res Rep, RRR4; Rutgers University: New Brunswick, NJ, USA, 2012. [Google Scholar]
- Smith, J.C.; Lim, C. Algorithms for network interdiction and fortification games. In Pareto Optimality, Game Theory and Equilibria; Springer: Berlin, Germany, 2008; pp. 609–644. [Google Scholar] [CrossRef]
- Von Stackelberg, H. The Theory of the Market Economy; Oxford University Press: Oxford, UK, 1952. [Google Scholar]
- Khachiyan, L.; Boros, E.; Borys, K.; Elbassioni, K.; Gurvich, V.; Rudolf, G.; Zhao, J. On short paths interdiction problems: Total and node-wise limited interdiction. Theory Comput. Syst. 2008, 43, 204–233. [Google Scholar] [CrossRef]
- Wood, R.K. Deterministic network interdiction. Math. Comput. Modell. 1993, 17, 1–18. [Google Scholar] [CrossRef]
- Israeli, E.; Wood, R.K. Shortest-path network interdiction. Networks 2002, 40, 97–111. [Google Scholar] [CrossRef]
- Altner, D.S.; Ergun, Ö.; Uhan, N.A. The maximum flow network interdiction problem: valid inequalities, integrality gaps, and approximability. Oper. Res. Lett. 2010, 38, 33–38. [Google Scholar] [CrossRef]
- Jain, M.; Conitzer, V.; Tambe, M. Security scheduling for real-world networks. In Proceedings of the 2013 International Conference on Autonomous Agents and Multi-Agent Systems, Saint Paul, MN, USA, 6–10 May 2013; pp. 215–222. [Google Scholar]
- Geoffrion, A.M. Generalized benders decomposition. J. Optim. Theory Appl. 1972, 10, 237–260. [Google Scholar] [CrossRef]
- Snyder, L.V.; Atan, Z.; Peng, P.; Rong, Y.; Schmitt, A.J.; Sinsoysal, B. OR/MS models for supply chain disruptions: A review. IIE Trans. 2016, 48, 89–109. [Google Scholar] [CrossRef]
- Hausken, K.; Zhuang, J. Defending against a stockpiling terrorist. Eng. Econ. 2011, 56, 321–353. [Google Scholar]
- Scaparra, M.P.; Church, R.L. A bilevel mixed-integer program for critical infrastructure protection planning. Comput. Oper. Res. 2008, 35, 1905–1923. [Google Scholar] [CrossRef]
- Brown, G.G.; Carlyle, W.M.; Harney, R.C.; Skroch, E.M.; Wood, R.K. Interdicting a nuclear-weapons project. Oper. Res. 2009, 57, 866–877. [Google Scholar] [CrossRef]
- Lusby, R.M.; Larsen, J.; Bull, S. A survey on robustness in railway planning. Eur. J. Oper. Res. 2018, 266, 1–15. [Google Scholar] [CrossRef]
- Sundar, K.; Coffrin, C.; Nagarajan, H.; Bent, R. Probabilistic Interdiction for Power Systems. arXiv, 2017; arXiv:1704.05391. [Google Scholar]
- Liu, D.; Toroporov, V.V.; Querin, O.M.; Barton, D.C. Bilevel optimization of blended composite wing panels. J. Aircr. 2011, 48, 107–118. [Google Scholar] [CrossRef]
- Ahuja, R.K. Network Flows: Theory, Algorithms, and Applications; Pearson Education: Upper Saddle River, NJ, USA, 2017. [Google Scholar]
- Gutin, E.; Kuhn, D.; Wiesemann, W. Interdiction games on Markovian PERT networks. Manag. Sci. 2014, 61, 999–1017. [Google Scholar] [CrossRef]
- Wei, X.; Zhu, C.; Xiao, K.; Yin, Q.; Zha, Y. Shortest Path Network Interdiction with Goal Threshold. IEEE Access 2018, 6, 29332–29343. [Google Scholar] [CrossRef]
- Fulkerson, D.R.; Harding, G.C. Maximizing the minimum source-sink path subject to a budget constraint. Math. Program. 1977, 13, 116–118. [Google Scholar] [CrossRef]
- Cormican, K.J.; Morton, D.P.; Wood, R.K. Stochastic network interdiction. Oper. Res. 1998, 46, 184–197. [Google Scholar] [CrossRef]
- Pan, F.; Morton, D.P. Minimizing a stochastic maximum-reliability path. Networks 2008, 52, 111–119. [Google Scholar] [CrossRef]
- Gutfraind, A.; Hagberg, A.A.; Izraelevitz, D.; Pan, F. Interdiction of a Markovian evader. arXiv, 2010; arXiv:1009.0556. [Google Scholar]
- Johnson, M.P.; Gutfraind, A.; Ahmadizadeh, K. Evader interdiction: algorithms, complexity and collateral damage. Ann. Oper. Res. 2014, 222, 341–359. [Google Scholar] [CrossRef]
- Bertsimas, D.; Nasrabadi, E.; Orlin, J.B. On the power of randomization in network interdiction. Oper. Res. Lett. 2016, 44, 114–120. [Google Scholar] [CrossRef]
- Bertsimas, D.; Nasrabadi, E.; Stiller, S. Robust and adaptive network flows. Oper. Res. 2013, 61, 1218–1242. [Google Scholar] [CrossRef]
- Hao, M.; Zhuang, J.; Jin, S. Robustness of Optimal Defensive Resource Allocations in the Face of Less Fully Rational Attacker. 2009, pp. 886–891. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.490.7426&rep=rep1&type=pdf (accessed on 1 January 2019).
- Matuschke, J.; McCormick, S.T.; Oriolo, G.; Peis, B.; Skutella, M. Protection of flows under targeted attacks. Oper. Res. Lett. 2017, 45, 53–59. [Google Scholar] [CrossRef][Green Version]
- Bayrak, H.; Bailey, M.D. Shortest path network interdiction with asymmetric information. Networks 2008, 52, 133–140. [Google Scholar] [CrossRef]
- Yates, J.; Sanjeevi, S. A length-based, multiple-resource formulation for shortest path network interdiction problems in the transportation sector. Int. J. Critical Infrastruct. Prot. 2013, 6, 107–119. [Google Scholar] [CrossRef]
- Pardalos, P.M.; Migdalas, A.; Pitsoulis, L. Pareto Optimality, Game Theory and Equilibria; Springer Science & Business Media: Berlin, Germany, 2008; Volume 17. [Google Scholar]
- Rocco S, C.M.; Ramirez-Marquezb, J.E. A bi-objective approach for shortest-path network interdiction. Comput. Ind. Eng. 2010, 59, 232–240. [Google Scholar] [CrossRef]
- Xiao, K.; Zhu, C.; Zhang, W.; Wei, X.; Hu, S. Stackelberg network interdiction game: nodal model and algorithm. In Proceedings of the 2014 5th International Conference on Game Theory for Networks (GAMENETS), Beijing, China, 25–27 November 2014; pp. 1–5. [Google Scholar]
- Washburn, A.; Wood, K. Two-person zero-sum games for network interdiction. Oper. Res. 1995, 43, 243–251. [Google Scholar] [CrossRef]
- Zhang, Y.; An, B.; Tran-Thanh, L.; Wang, Z.; Gan, J.; Jennings, N.R. Optimal escape interdiction on transportation networks. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Melbourne, Australia, 19–25 August 2017. [Google Scholar]
- Jain, M.; Korzhyk, D.; Vaněk, O.; Conitzer, V.; Pěchouček, M.; Tambe, M. A double oracle algorithm for zero-sum security games on graphs. In Proceedings of the The 10th International Conference on Autonomous Agents and Multiagent Systems, Taipei, Taiwan, 2–6 May 2011; pp. 327–334. [Google Scholar]
- Rocco S, C.M.; Ramirez-Marquezb, J.E. Deterministic network interdiction optimization via an evolutionary approach. Reliab. Eng. Syst. Saf. 2009, 94, 568–576. [Google Scholar] [CrossRef]
- Janjarassuk, U.; Nakrachata-Amon, T. A simulated annealing algorithm to the stochastic network interdiction problem. In Proceedings of the 2015 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 6–9 December 2015; pp. 230–233. [Google Scholar]
- Yates, J.; Lakshmanan, K. A constrained binary knapsack approximation for shortest path network interdiction. Comput. Ind. Eng. 2011, 61, 981–992. [Google Scholar] [CrossRef]
- Leitmann, G. On generalized Stackelberg strategies. J. Optim. Theory Appl. 1978, 26, 637–643. [Google Scholar] [CrossRef]
- Erdos, P.; Renyi, A. On random graphs I. Publ. Math. Debr. 1959, 6, 290–297. [Google Scholar]
- Kleinberg, J.M. Navigation in a small world. Nature 2000, 406, 845. [Google Scholar] [CrossRef]
- Bar-Gera, H. Transportation Networks for Research Core Team. Transportation Network Test Problems. Available online: https://github.com/bstabler/TransportationNetworks (accessed on 10 September 2018).
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No.04CH37508), New Orleans, LA, USA, 2–4 September 2004; pp. 284–289. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).