Abstract
Let G be a simple undirected graph containing n vertices. Assume G is connected. Let be the distance matrix, be the distance Laplacian, be the distance signless Laplacian, and be the diagonal matrix of the vertex transmissions, respectively. Furthermore, we denote by the generalized distance matrix, i.e., , where . In this paper, we establish some new sharp bounds for the generalized distance spectral radius of G, making use of some graph parameters like the order n, the diameter, the minimum degree, the second minimum degree, the transmission degree, the second transmission degree and the parameter , improving some bounds recently given in the literature. We also characterize the extremal graphs attaining these bounds. As an special cases of our results, we will be able to cover some of the bounds recently given in the literature for the case of distance matrix and distance signless Laplacian matrix. We also obtain new bounds for the k-th generalized distance eigenvalue.
Keywords:
distance matrix (spectrum); distance signlees Laplacian matrix (spectrum); (generalized) distance matrix; spectral radius; transmission regular graph MSC:
Primary: 05C50, 05C12; Secondary: 15A18
1. Introduction
We will consider simple finite graphs in this paper. A (simple) graph is denoted by , where represents its vertex set and represents its edge set. The order of G is the number of vertices represented by and its size is the number of edges represented by . The neighborhood of a vertex v consists of the set of vertices that are adjacent to it. The degree or simply is the number of vertices in . In a regular graph, all its vertices have the same degree. Let be the distance between two vertices . It is defined as the length of a shortest path. is called the distance matrix of G. is the complement of the graph G. It has the same vertex set with G but its edge set consists of the edges not present in G. Moreover, the complete graph , the complete bipartite graph , the path , and the cycle are defined in the conventional way.
The transmission of a vertex v is the sum of the distances from v to all other vertices in G, i.e., A graph G is said to be k-transmission regular if for each . The transmission (also called the Wiener index) of a graph G, denoted by , is the sum of distances between all unordered pairs of vertices in G. We have .
For a vertex , is also referred to as the transmission degree, or shortly . The sequence of transmission degrees is the transmission degree sequence of the graph. is called the second transmission degree of .
Distance matrix and its spectrum has been studied extensively in the literature, see e.g., [6]. Compared to adjacency matrix, distance matrix encapsulates more information such as a wide range of walk-related parameters, which can be applicable in thermodynamic calculations and have some biological applications in terms of molecular characterization. It is known that embedding theory and molecular stability have to do with graph distance matrix.
Almost all results obtained for the distance matrix of trees were extended to the case of weighted trees by Bapat [12] and Bapat et al. [13]. Not only different classes of graphs but the definition of distance matrix has been extended. Indeed, Bapat et al. [14] generalized the concept of the distance matrix to that of q-analogue of the distance matrix. Let be the diagonal matrix of vertex transmissions of G. The works [7,8,9] introduced the distance Laplacian and the distance signless Laplacian matrix for a connected graph G. The matrix is referred to as the distance Laplacian matrix of G, while the matrix is the distance signless Laplacian matrix of G. Spectral properties of and have been extensively studied since then.
Let A be the adjacency matrix and be the degree matrix G. is the signless Laplacian matrix of G. This matrix has been put forth by Cvetkovic in [16] and since then studied extensively by many researchers. For detailed coverage of this research see [17,18,19,20] and the references therein. To digging out the contribution of these summands in , Nikiforov in [33] proposed to study the -adjacency matrix of a graph G given by , where . We see that is a convex combination of the matrices A and . Since and , the matrix can underpin a unified theory of A and . Motivated by [33], Cui et al. [15] introduced the convex combinations of and . The matrix , is called generalized distance matrix of G. Therefore the generalized distance matrix can be applied to the study of other less general constructions. This not only gives new results for several matrices simultaneously, but also serves the unification of known theorems.
Since the matrix is real and symmetric, its eigenvalues can be arranged as: where is referred to as the generalized distance spectral radius of . For simplicity, is the shorthand for . By the Perron-Frobenius theorem, is unique and it has a unique generalized distance Perron vector, X, which is positive. This is due to the fact that is non-negative and irreducible.
A column vector is a function defined on . We have for all i. Moreover,
and has an eigenvector X if and only if and
They are often referred to as the -eigenequations of G. If has at least one non-negative element and it is normalized, then in the light of the Rayleigh’s principle, it can be seen that
where the equality holds if and only if X becomes the generalized distance Perron vector of G.
Spectral graph theory has been an active research field for the past decades, in which for example distance signless Laplacian spectrum has been intensively explored. The work [41] identified the graphs with minimum distance signless Laplacian spectral radius among some special classes of graphs. The unique graphs with minimum and second-minimum distance signless Laplacian spectral radii among all bicyclic graphs of the same order are identified in [40]. In [24], the authors show some bounding inequalities for distance signless Laplacian spectral radius by utilizing vertex transmissions. In [26], chromatic number is used to derive a lower bound for distance signless Laplacian spectral radius. The distance signless Laplacian spectrum has varies connections with other interesting graph topics such as chromatic number [10]; domination and independence numbers [21], Estrada indices [4,5,22,23,34,35,36,38], cospectrality [11,42], multiplicity of the distance (signless) Laplacian eigenvalues [25,29,30] and many more, see e.g., [1,2,3,27,28,32].
The rest of the paper is organized as follows. In Section 2, we obtain some bounds for the generalized distance spectral radius of graphs using the diameter, the order, the minimum degree, the second minimum degree, the transmission degree, the second transmission degree and the parameter . We then characterize the extremal graphs. In Section 3, we are devoted to derive new upper and lower bounds for the k-th generalized distance eigenvalue of the graph G using signless Laplacian eigenvalues and the -adjacency eigenvalues.
2. Bounds on Generalized Distance Spectral Radius
In this section, we obtain bounds for the generalized distance spectral radius, in terms of the diameter, the order, the minimum degree, the second minimum degree, the transmission degree, the second transmission degree and the parameter .
The following lemma can be found in [31].
Lemma 1.
If A is an non-negative matrix with the spectral radius and row sums , then
Moreover, if A is irreducible, then both of the equalities holds if and only if the row sums of A are all equal.
The following gives an upper bound for , in terms of the order n, the diameter d and the minimum degree of the graph G.
Theorem 1.
Let G be a connected graph of order n having diameter d and minimum degree δ. Then
with equality if and only if G is a regular graph with diameter .
Proof.
First, it is easily seen that,
Let . For a matrix A denote its largest eigenvalue. We have
Applying Equation (2), the inequality follows.
Suppose that G is regular graph with diameter less than or equal to two, then all coordinates of the generalized distance Perron vector of G are equal. If , then and . Thus equality in (1) holds. If , we get , and the equality in (1) holds. Note that the equality in (1) holds if and only if all coordinates the generalized distance Perron vector are equal, and hence has equal row sums.
Conversely, suppose that equality in (1) holds. This will force inequalities above to become equations. Then we get hence all the transmissions of the vertices are equal and so G is a transmission regular graph. If , then from the above argument, for every vertex , there is exactly one vertex with , and thus , and for a vertex of eccentricity 2,
implying that , giving that . But the is not transmission regular graph. Therefore, G turns out to be regular and its diameter can not be greater than 2. □
Taking in Theorem 1, we immediately get the following bound for the distance signless Laplacian spectral radius , which was proved recently in [27].
Corollary 1.
([27], Theorem 2.6) Let G be a connected graph of order , with minimum degree , second minimum degree and diameter d. Then
with equality if and only if G is (transmission) regular graph of diameter .
Proof.
As , letting in Theorem 1, we have
and the result follows. □
Next, the generalized distance spectral radius of a connected graph and its complement is characterized in terms of a Nordhaus-Gaddum type inequality.
Corollary 2.
Let G be a graph of order n, such that both G and its complement are connected. Let δ and Δ be the minimum degree and the maximum degree of , respectively. Then
where and are the diameters of G and respectively.
Proof.
Let denote the minimum degree of . Then , and by Theorem 1, we have
□
The following gives an upper bound for , in terms of the order n, the minimum degree and the second minimum degree of the graph G.
Theorem 2.
Let G be a connected graph of order n having minimum degree and second minimum degree . Then for , we have
where and . Also equality holds if and only if G is a regular graph with diameter at most two.
Proof.
Let be the generalized distance Perron vector of graph G and let and . From the ith equation of , we obtain
Similarly, from the jth equation of , we obtain
Now, by (2), we have,
Multiplying the corresponding sides of these inequalities and using the fact that for all k, we obtain
where , , which in turn gives
Now, using , the result follows.
Suppose that equality occurs in (3), then equality occurs in each of the above inequalities. If equality occurs in (4) and (5), the we obtain , for all giving that G is a transmission regular graph. Also, equality in (2), similar to that of Theorem 1, gives that G is a graph of diameter at most two and equality in gives that G is a regular graph. Combining all these it follows that equality occurs in (3) if G is a regular graph of diameter at most two.
Conversely, if G is a connected -regular graph of diameter at most two, then . Also
That completes the proof. □
Remark 1.
For any connected graph G of order n having minimum degree δ, the upper bound given by Theorem 2 is better than the upper bound given by Theorem 1. As
where
The following gives an upper bound for by using quantities like transmission degrees as well as second transmission degrees.
Theorem 3.
If the transmission degree sequence and the second transmission degree sequence of G are and respectively, then
where is an unknown parameter. Equality occurs if and only if G is a transmission regular graph.
Proof.
Let be the generalized distance Perron vector of G and Since
we have
Now, we consider a simple quadratic function of
Considering the ith equation, we have
It is easy to see that the inequalities below are true
Hence, we have
From this the result follows.
Now, suppose that equality occurs in (6), then each of the above inequalities in the above argument occur as equalities. Since each of the inequalities
and
occur as equalities if and only if G is a transmission regular graph. It follows that equality occurs in (6) if and only if G is a transmission regular graph. That completes the proof. □
The following upper bound for the generalized distance spectral radius was obtained in [15]:
with equality if and only if is same for i.
Remark 2.
For a connected graph G having transmission degree sequence and the second transmission degree sequence , provided that for all i, we have
Therefore, the upper bound given by Theorem 3 is better than the upper bound given by (7).
If, in particular we take the parameter in Theorem 3 equal to the vertex covering number , the edge covering number, the clique number , the independence number, the domination number, the generalized distance rank, minimum transmission degree, maximum transmission degree, etc., then Theorem 3 gives an upper bound for , in terms of the vertex covering number , the edge covering number, the clique number , the independence number, the domination number, the generalized distance rank, minimum transmission degree, maximum transmission degree, etc.
Let be the minimum among the entries of the generalized distance Perron vector of the graph G. Proceeding similar to Theorem 3, we obtain the following lower bound for , in terms of the transmission degrees, the second transmission degrees and a parameter .
Theorem 4.
If the transmission degree sequence and the second transmission degree sequence of G are and , respectively, then
where is an unknown parameter. Equality occurs if and only if G is a transmission regular graph.
Proof.
Similar to the proof of Theorem 3 and is omitted. □
The following lower bound for the generalized distance spectral radius was obtained in [15]:
with equality if and only if is same for i.
Similar to Remark 2, it can be seen that the lower bound given by Theorem 4 is better than the lower bound given by (8) for all graphs G with , for all i.
Again, if in particular we take the parameter in Theorem 4 equal to the vertex covering number , the edge covering number, the clique number , the independence number, the domination number, the generalized distance rank, minimum transmission degree, maximum transmission degree, etc, then Theorem 4 gives a lower bound for , in terms of the vertex covering number , the edge covering number, the clique number , the independence number, the domination number, the generalized distance rank, minimum transmission degree, maximum transmission degree, etc.
is referred to as join of and . It is defined by joining every vertex in to every vertex in .
Example 1.
(a) Let be the cycle of order 4. One can easily see that is a 4-transmission regular graph and the generalized distance spectrum of is . Hence, . Moreover, the transmission degree sequence and the second transmission degree sequence of are and , respectively. Now, putting in the given bound of Theorem 3, we can see that the equality holds:
(b) Let be the wheel graph of order . It is well known that The distance signless Laplacian matrix of is
Hence the distance signless Laplacian spectrum of is , and then the distance signless Laplacian spectral radius is . Also, the transmission degree sequence and the second transmission degree sequence of are and , respectively. As , taking and in the given bound of Theorem 3, we immediately get the following upper bound for the distance signless Laplacian spectral radius :
which implies that
3. Bounds for the k-th Generalized Distance Eigenvalue
In this section, we discuss the relationship between the generalized distance eigenvalues and the other graph parameters.
The following lemma can be found in [37].
Lemma 2.
Let X and Y be Hermitian matrices of order n such that , and denote the eigenvalues of a matrix M by .Then
where is the ith largest eigenvalue of the matrix M. Any equality above holds if and only if a unit vector can be an eigenvector corresponding to each of the three eigenvalues.
The following gives a relation between the generalized distance eigenvalues of the graph G of diameter 2 and the signless Laplacain eigenvalues of the complement of the graph G. It also gives a relation between generalized distance eigenvalues of the graph G of diameter greater than or equal to 3 with the -adjacency eigenvalues of the complement of the graph G.
Theorem 5.
Let G be a connected graph of order having diameter d. Let be the complement of G and let be the signless Laplacian eigenvalues of . If , then for all , we have
Equality occurs on the right if and only if and G is a transmission regular graph and on the left if and only if and G is a transmission regular graph.
If , then for all , we have
where is the α-adjacency matrix of and with a symmetric matrix of order n having , is the distance between the vertices , and , .
Proof.
Let G be a connected graph of order having diameter d. Let be the diagonal matrix of vertex degrees of . Suppose that diameter d of G is two, then transmission degree , for all then the distance matrix of G can be written as , where A and are the adjacency matrices of G and , respectively. We have
where I is the identity matrix and J is the all one matrix of order n. Taking , , in the first inequality of Lemma 2 and using the fact that it follows that
Again, taking , and in the second inequality of Lemma 2, it follows that
Combining (9) and (10) the first inequality follows. Equality occurs in first inequality if and only if equality occurs in (9) and (10). Suppose that equality occurs in (9), then by Lemma 2, the eigenvalues and of the matrices and Y have the same unit eigenvector. Since is the unit eigenvector of Y for the eigenvalue , it follows that equality occurs in (9) if and only if is the unit eigenvector for each of the matrices and Y. This gives that G is a transmission regular graph and is a regular graph. Since a graph of diameter 2 is regular if and only if it is transmission regular and complement of a regular graph is regular. Using the fact that for a connected graph G the unit vector is an eigenvector for the eigenvalue if and only if G is transmission regular graph, it follows that equality occurs in first inequality if and only if and G is a transmission regular graph.
Suppose that equality occurs in (10), then again by Lemma 2, the eigenvalues and 0 of the matrices and Y have the same unit eigenvector . Since , it follows that . Using the fact that the matrix J is symmetric(so its normalized eigenvectors are orthogonal [43]), we conclude that the vector belongs to the set of eigenvectors of the matrix J and so of the matrices . Now, is an eigenvector of the matrices and X, gives that G is a regular graph. Since for a regular graph of diameter 2 any eigenvector of and is orthogonal to , it follows that equality occurs in (10) if and only if and G is a regular graph.
If , we define the matrix of order n, where , is the distance between the vertices and . The transmission of a vertex can be written as , where , is the contribution from the vertices which are at distance more than two from . For , we have
where is the -adjacency matrix of and . Taking , and in the first inequality of Lemma 2 and using the fact that it follows that
Again, taking , and in the first inequality of Lemma 2, we obtain
Similarly, taking , and and then , and in the second inequality of Lemma 2, we obtain
It can be seen that the matrix defined in Theorem 5 is positive semi-definite for all . Therefore, we have the following observation from Theorem 5.
Corollary 3.
Let G be a connected graph of order having diameter . If , then
where is the α-adjacency matrix of .
It is clear from Corollary 3 that for , any lower bound for the -adjacency gives a lower bound for and conversely any upper bound for ∂ gives an upper bound for . We note that Theorem 5 generalizes one of the Theorems (namely Theorem 3.8) given in [8].
Example 2.
(a) Let be a cycle of order . It is well known (see [7]) that is a k-transmission regular graph with if n is even and if n is odd. Let . It is clear that the distance spectrum of the graph is . Also, since is a 4-transmission regular graph, then and so . Hence the generalized distance spectrum of is . Moreover, the signless Laplacian spectrum of is . Since the diameter of is 2, hence, applying Theorem 5, for , we have,
which shows that the equality occurs on right for and transmission regular graph .
Also, for , we have
which shows that the equality occurs on left for and transmission regular graph .
(b) Let be a cycle of order 6. It is clear that the distance spectrum of the graph is . Since is a 9-transmission regular graph, then and so . Hence, the generalized distance spectrum of is . Also, the α-adjacency spectrum of is . Let be the matrix defined by the Theorem 5, hence the spectrum of is Since diameter of the graph is 3, hence, applying Theorem 5, for , we have
Also for we have
We need the following lemma proved by Hoffman and Wielandt [39].
Lemma 3.
Suppose we have . Here, all these matrices are symmetric and have order n. Suppose they have the eigenvalues and where respectively arranged in non-increasing order. Therefore,
The following gives relation between generalized distance spectrum and distance spectrum for a simple connected graph G. We use to denote the set of For each subset S of we use to denote
Theorem 6.
Let G be a connected graph of order n and let be the eigenvalues of the distance matrix of . Then for each non-empty subset of , we have the following inequalities:
Proof.
Since , then by the fact that we get By Cauchy-Schwarz inequality, we further have that
Therefore
By Lemma 3, we have that
Again by Cauchy-Schwarz inequality, we have that
Therefore, we have the following inequality
Solving the quadratic inequality for so we complete the proof. □
Notice that and by Lemma 3, we also have We can similarly prove the following theorem.
Theorem 7.
Let G be a connected graph of order n. Then for each non-empty subset of , we have:
We conclude by giving the following bounds for the k-th largest generalized distance eigenvalue of a graph.
Theorem 8.
Assume G is connected and is of order n. Suppose it has diameter d and δ is its minimum degree. Let
Then for
Proof.
First we prove the upper bound. It is clear that
Let Then
which implies
Now, we prove the lower bound. Let . Then we have
Hence
and we get the left-hand side of the inequality (13). □
By a chemical tree, we mean a tree which has all vertices of degree less than or equal to 4.
Example 3.
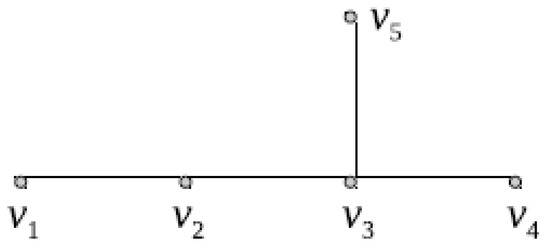
In Figure 1, we depicted a chemical tree of order .

Figure 1.
A chemical tree T.
The distance matrix of T is
Let be the distance eigenvalues of the tree T. Then one can easily see that , , , and . Note that, as , taking in Theorem 8, then for we get , for any . For example, and .
4. Conclusions
Motivated by an article entitled “Merging the A- and Q-spectral theories” by V. Nikiforov [33], recently, Cui et al. [15] dealt with the integration of spectra of distance matrix and distance signless Laplacian through elegant convex combinations accommodating vertex transmissions as well as distance matrix. For , the generalized distance matrix is known as . Our results shed light on some properties of and contribute to establishing new inequalities (such as lower and upper bounds) connecting varied interesting graph invariants. We established some bounds for the generalized distance spectral radius for a connected graph using various identities like the number of vertices n, the diameter, the minimum degree, the second minimum degree, the transmission degree, the second transmission degree and the parameter , improving some bounds recently given in the literature. We also characterized the extremal graphs attaining these bounds. Notice that the current work mainly focuses to determine some bounds for the spectral radius (largest eigenvalue) of the generalized distance matrix. It would be interesting to derive some bounds for other important eigenvalues such as the smallest eigenvalue as well as the second largest eigenvalue of this matrix.
Author Contributions
Conceptualization, A.A., M.B. and H.A.G.; formal analysis, A.A., M.B., H.A.G. and Y.S.; writing—original draft preparation, A.A., M.B. and H.A.G.; writing—review and editing, A.A., M.B., H.A.G. and Y.S.; project administration, A.A.; funding acquisition, Y.S.
Funding
Y. Shang was supported by UoA Flexible Fund No. 201920A1001 from Northumbria University.
Acknowledgments
The authors would like to thank the academic editor and the four anonymous referees for their constructive comments that helped improve the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alhevaz, A.; Baghipur, M.; Ganie, H.A.; Pirzada, S. Brouwer type conjecture for the eigenvalues of distance signless Laplacian matrix of a graph. Linear Multilinear Algebra 2019. [Google Scholar] [CrossRef]
- Alhevaz, A.; Baghipur, M.; Hashemi, E. Further results on the distance signless Laplacian spectrum of graphs. Asian-Eur. J. Math. 2018, 11, 1850066. [Google Scholar] [CrossRef]
- Alhevaz, A.; Baghipur, M.; Hashemi, E.; Ramane, H.S. On the distance signless Laplacian spectrum of graphs. Bull. Malay. Math. Sci. Soc. 2019, 42, 2603–2621. [Google Scholar] [CrossRef]
- Alhevaz, A.; Baghipur, M.; Paul, S. On the distance signless Laplacian spectral radius and the distance signless Laplacian energy of graphs. Discrete Math. Algorithms Appl. 2018, 10, 1850035. [Google Scholar] [CrossRef]
- Alhevaz, A.; Baghipur, M.; Pirzada, S. On distance signless Laplacian Estrada index and energy of graphs. Kragujevac J. Math. 2021, 45, 837–858. [Google Scholar]
- Aouchiche, M.; Hansen, P. Distance spectra of graphs: A survey. Linear Algebra Appl. 2014, 458, 301–386. [Google Scholar] [CrossRef]
- Aouchiche, M.; Hansen, P. Two Laplacians for the distance matrix of a graph. Linear Algebra Appl. 2013, 439, 21–33. [Google Scholar] [CrossRef]
- Aouchiche, M.; Hansen, P. On the distance signless Laplacian of a graph. Linear Multilinear Algebra 2016, 64, 1113–1123. [Google Scholar] [CrossRef]
- Aouchiche, M.; Hansen, P. Some properties of distance Laplacian spectra of a graph. Czechoslovak Math. J. 2014, 64, 751–761. [Google Scholar] [CrossRef]
- Aouchiche, M.; Hansen, P. Distance Laplacian eigenvalues and chromatic number in graphs. Filomat 2017, 31, 2545–2555. [Google Scholar] [CrossRef]
- Aouchiche, M.; Hansen, P. Cospectrality of graphs with respect to distance matrices. Appl. Math. Comput. 2018, 325, 309–321. [Google Scholar] [CrossRef]
- Bapat, R.B. Determinant of the distance matrix of a tree with matrix weights. Linear Algebra Appl. 2006, 416, 2–7. [Google Scholar] [CrossRef]
- Bapat, R.B.; Kirkland, S.J.; Neumann, M. On distance matrices and Laplacians. Linear Algebra Appl. 2005, 401, 193–209. [Google Scholar] [CrossRef]
- Bapat, R.B.; Lal, A.K.; Pati, S. A q-analogue of the distance matrix of a tree. Linear Algebra Appl. 2006, 416, 799–814. [Google Scholar] [CrossRef]
- Cui, S.Y.; He, J.X.; Tian, G.X. The generalized distance matrix. Linear Algebra Appl. 2019, 563, 1–23. [Google Scholar] [CrossRef]
- Cvetković, D. Signless Laplacians and line graphs. Bull. Acad. Serbe Sci. Arts Cl. Sci. Math. Natur. Sci. Math. 2005, 131, 85–92. [Google Scholar] [CrossRef]
- Cvetković, D. New theorems for signless Laplacians eigenvalues. Bull. Acad. Serbe Sci. Arts Cl. Sci. Math. Natur. Sci. Math. 2008, 137, 131–146. [Google Scholar]
- Cvetković, D.; Simić, S.K. Towards a spectral theory of graphs based on the signless Laplacian I. Publ. Inst. Math. (Beograd) 2009, 85, 19–33. [Google Scholar] [CrossRef]
- Cvetković, D.; Simić, S.K. Towards a spectral theory of graphs based on the signless Laplacian II. Linear Algebra Appl. 2010, 432, 2257–2272. [Google Scholar] [CrossRef]
- Cvetković, D.; Simić, S.K. Towards a spectral theory of graphs based on the signless Laplacian III. Appl. Anal. Discrete Math. 2010, 4, 156–166. [Google Scholar]
- Das, K.C.; Aouchiche, M.; Hansen, P. On distance Laplacian and distance signless Laplacian eigenvalues of graphs. Linear Multilinear Algebra 2019, 67, 2307–2324. [Google Scholar] [CrossRef]
- Das, K.C.; Aouchiche, M.; Hansen, P. On (distance) Laplacian energy and (distance) signless Laplacian energy of graphs. Discrete Appl. Math. 2018, 243, 172–185. [Google Scholar] [CrossRef]
- Diaz, R.C.; Rojo, O. Sharp upper bounds on the distance energies of a graph. Linear Algebra Appl. 2018, 545, 55–75. [Google Scholar] [CrossRef]
- Duan, X.; Zhou, B. Sharp bounds on the spectral radius of a nonnegative matrix. Linear Algebra Appl. 2013, 439, 2961–2970. [Google Scholar] [CrossRef]
- Fernandes, R.; de Freitas, M.A.A.; da Silva, C.M., Jr.; Del-Vecchio, R.R. Multiplicities of distance Laplacian eigenvalues and forbidden subgraphs. Linear Algebra Appl. 2018, 541, 81–93. [Google Scholar] [CrossRef]
- Li, X.; Fan, Y.; Zha, S. A lower bound for the distance signless Laplacian spectral radius of graphs in terms of chromatic number. J. Math. Res. Appl. 2014, 34, 289–294. [Google Scholar]
- Li, D.; Wang, G.; Meng, J. On the distance signless Laplacian spectral radius of graphs and digraphs. Electr. J. Linear Algebra 2017, 32, 438–446. [Google Scholar] [CrossRef]
- Liu, S.; Shu, J. On the largest distance (signless Laplacian) eigenvalue of non-transmission-regular graphs. Electr. J. Linear Algebra 2018, 34, 459–471. [Google Scholar] [CrossRef]
- Lu, L.; Huang, Q.; Huang, X. On graphs with distance Laplacian spectral radius of multiplicity n − 3. Linear Algebra Appl. 2017, 530, 485–499. [Google Scholar] [CrossRef]
- Lu, L.; Huang, Q.; Huang, X. On graphs whose smallest distance (signless Laplacian) eigenvalue has large multiplicity. Linear Multilinear Algebra 2018, 66, 2218–2231. [Google Scholar] [CrossRef]
- Minć, H. Nonnegative Matrices; John Wiley & Sons: New York, NY, USA, 1988. [Google Scholar]
- Lin, H.; Zhou, B. The distance spectral radius of trees. Linear Multilinear Algebra 2019, 67, 370–390. [Google Scholar] [CrossRef]
- Nikiforov, V. Merging the A- and Q-spectral theories. Appl. Anal. Discrete Math. 2017, 11, 81–107. [Google Scholar] [CrossRef]
- Shang, Y. Distance Estrada index of random graphs. Linear Multilinear Algebra 2015, 63, 466–471. [Google Scholar] [CrossRef]
- Shang, Y. Estimating the distance Estrada index. Kuwait J. Sci. 2016, 43, 14–19. [Google Scholar]
- Shang, Y. Bounds of distance Estrada index of graphs. Ars Combin. 2016, 128, 287–294. [Google Scholar]
- So, W. Commutativity and spectra of Hermitian matrices. Linear Algebra Appl. 1994, 212–213, 121–129. [Google Scholar] [CrossRef]
- Yang, J.; You, L.; Gutman, I. Bounds on the distance Laplacian energy of graphs. Kragujevac J. Math. 2013, 37, 245–255. [Google Scholar]
- Wilkinson, J.H. The Algebraic Eigenvalue Problem; Oxford University Press: New York, NY, USA, 1965. [Google Scholar]
- Xing, R.; Zhou, B. On the distance and distance signless Laplacian spectral radii of bicyclic graphs. Linear Algebra Appl. 2013, 439, 3955–3963. [Google Scholar] [CrossRef]
- Xing, R.; Zhou, B.; Li, J. On the distance signless Laplacian spectral radius of graphs. Linear Multilinear Algebra 2014, 62, 1377–1387. [Google Scholar] [CrossRef]
- Xue, J.; Liu, S.; Shu, J. The complements of path and cycle are determined by their distance (signless) Laplacian spectra. Appl. Math. Comput. 2018, 328, 137–143. [Google Scholar] [CrossRef]
- Zhang, F. Matrix Theory: Basic Results and Techniques; Springer: New York, NY, USA, 1999. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).