Abstract
The self-similarity in space and time (hereafter self-similarity), either deterministic or statistical, is characterized by similarity exponents and a function of scaled variable, called the scaling function. In the present paper, we address mainly the self-similarity in the limit of early stage, as opposed to the latter one, and also consider the scaling functions that decay or grow algebraically, as opposed to the rapidly decaying functions such as Gaussian or error function. In particular, in the case of simple diffusion, our symmetry analysis shows a mathematical mechanism by which the rapidly decaying scaling functions are generated by other polynomial scaling functions. While the former is adapted to the self-similarity in the late-stage processes, the latter is adapted to the early stages. This paper sheds some light on the internal structure of the family of self-similarities generated by a simple diffusion equation. Then, we present an example of self-similarity for the late stage whose scaling function has power-law tail, and also several cases of self-similarity for the early stages. These examples show the utility of self-similarity to a wider range of phenomena other than the late stage behaviors with rapidly decaying scaling functions.
1. Introduction
When the evolution of state shows some scaling behavior involving both space and time without fixed characteristic length or time, it is said to have self-similarity in space and time (hereafter, “self-similarity” for short) [1]. Self-similarity is a symmetry of the time-dependent fields which remain invariant under certain scale transformations of space and time. Similarity and dimensional methods in mechanics has long been known ([2] and references therein). Dynamical critical phenomena [3] or the late-stage dynamics of the first-order transition [4] are among the typical examples that have been studied a lot. Deterministic cases have also been actively studied (e.g., see the book [1]). The self-similarity is represented by some scaled variables, scaling exponents, and scaling functions. Among the simplest examples of self-similarity is the smearing Gaussian distribution governed by a diffusion equation, where the diffusing field evolves, for example, in the form , where is the scaling function for the scaled variable, , and is the scaling exponent, being in this case. Such symmetry object, scaling function, can have different types, and one of our main goals is to relate the scaling functions of different types.
Thus far, most studies on the self-similarity in physics have focused on the late-stage evolution, i.e., well after the initial transient, and at the same time focused on the case where the scaling function or its derivative decays rapidly, i.e., faster than any power-law as a function of the scaled variable. The basic reason for this is the fact that the group velocity in the parabolic or hyperbolic evolution equation is vanishing or finite at large length scale. This implies that the self-similarity with algebraic asymptotes of the scaling function is reduced to static (with steady flux) algebraic tails in the far field. As such far field condition has been rarely prepared physically, we have not paid much attention to the self-similarity with power-low asymptotes in the scaling function.
Self-similarity does not exclusively occur in the late stage, where the spatial scale is also large. Self-similarity as the short-time limit has not drawn much attention thus far, to the authors’ knowledge. In this limit, the local region is infinitely magnified by the scaled variable. Then, the scaling functions are not constrained to decay rapidly but they can even grow algebraically for large values of scaled variable.
In this paper, we first analyze the internal symmetry properties in the family of scaling functions for the 1D diffusion system (Section 2). Through the equation governing the scaling function and its adjoint equation together with the operator of “Wick rotation”, the scaling functions with rapidly decaying asymptote, which are suitable for the late-stage self-similarity, are related to the polynomial scaling functions, suitable for the short-time self-similarity. Secondly, we present some examples of self-similarity having the scaling functions with algebraic asymptote (Section 3): The first example is the late-stage self-similarity having an algebraically decaying scaling function which we think to be realizable in the permeative relaxation process of hydrogel. The other examples are the short-time self-similarity of 1D diffusion from parabolic or cusp-like initial field configuration and the short-time self-similarity of 1D linearized capillary-driven thin-film equation. Through these studies, we shed light on the family of self-similarity behaviors and the relationship among them. In Section 4, we briefly discuss the generalizability of the results obtained in this paper.
2. Symmetry Properties in the Family of Scaling Functions for the 1D Diffusion Process
2.1. Scaling Functions
For the 1D diffusion, , different approaches have been developed (see, for example, [5]). Here, we focus on the solutions with self-similarity in space and time.
where the scaling function should obey
The index p has been adjusted so that corresponds to the Gaussian scaling function. The even and odd solutions, and , respectively, are given in Appendix A with some explicit form for several p values. Here, we note only those properties that are relevant for the discussion below: For non-integer values of p, the solution behaves asymptotically with power law, , for . The special cases are: (i) the solutions with rapidly decaying derivatives for non-negative integer p with even [odd] parities when p is even [odd]; and (ii) the polynomial solutions for negative integer p with even [odd] parities when p is odd [even]. Surprisingly, (i) and (ii) are related to each other, as shown below. For the diffusion equation or heat equation, the general similarity solutions have been studied in detail (see, for example, [6]). However, the focus has not been put on the relationship among the solutions.
2.2. Symmetry in the Family of Scaling Functions
We noticed the two independent ways to relate the operators defined by Equation (2) for and their adjoint ones, , defined by
The first relation between and is nothing but the definition of adjoint, i.e., the “integration by parts” identity,
Equation (4) means that satisfying and satisfying are mutually the integrating factor of the other. In fact, if we have such , the solution of can be constituted from the vanishing condition of the right-hand side of Equation (4). The latter condition leads to
where and are the integration constants, and the integration pathway is assumed to be properly chosen to avoid the poles of the integrand. The second relation between and is through a kind of Wick rotation:
where the operator J is defined such that for any object including s as a variable. The identity in Equation (6) can be verified by elementary calculus.
The presence of two different pathways connecting the family with that of reveals the intra-relationship among the scaling functions , which is mediated by . Figure 1 schematically shows this mechanism:
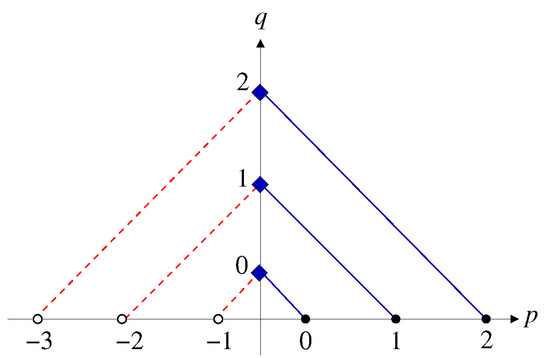
Figure 1.
Diagram showing the relations among the solutions of and those of See the main text.
A solution of (e.g., ) gives the solution of with (e.g., ) through . Once satisfying is given, the solution of with (e.g., ) is constructed by Equation (5) with and being replaced by and , respectively.
While the above symmetry property applies for any real index p, the cases of particular interest are when are polynomial with non-negative integers . Such can generate, through , the whose derivative decays rapidly as the term in Equation (5). Such polynomial solution has its origin in the adjoint equation , which can in turn be reduced to the Hermite equation by changing variable, . This type of analysis may shed some light on the internal structure of the family of dynamical similarities of a system of evolution, although for the moment being limited to a particular case. In Section 3.2, we study the case where is or as short-time self-similar evolution. The above-mentioned symmetry connects these scaling functions to the rapidly decaying ones and in the notation used in Appendix A.
3. Self-Similarity in Space and Time with Scaling Function Having Algebraic Tail
As mentioned above, we should realize that, when the scaling function of self-similarity has algebraic tails as function of the scaled variable, these algebraic asymptotes must be realized in the initial field configuration. For example, in Equation (2) for the 1D diffusion equation, the algebraic tail issues from the last two terms in , whose balance implies . Indeed, if we put for in Equation (1), we have . This consequence is intuitively understandable because most of the evolution system of our interest spreads mainly locally, being unable to update substantially the configurations far apart. Below, we present some examples of self-similarity having algebraic spatial tail. One is for the late stage and the other two are for the short-time limit.
3.1. Late-Stage Self-Similarity in Space and Time of Gel Network
It is generally difficult to prepare an algebraic static asymptotes over a large spatial range. This may be the reason the self-similarity having algebraic tails has been scarcely studied in physical application. Below, we present an example that an algebraic tail is nevertheless thinkable. The system considered is an aqueous gel, i.e., a soft solid consisting of a very fine permeable network saturated with water. Such a system responds as if it were an incompressible isotropic elastic body at short-time scale while its permeative relaxation under an osmotic pressure gradient is very slow. As the setup, we suppose a uniform 3D aqueous gel having a small water-filled hole around the center, . The hole’s radius is . For , the gel is in uniform equilibrium under no stress and, at , we quickly inject a small amount of water into the hole. The injection makes expand the holes from radius to . Soon after the injection, a quick elastic re-equilibration without permeation will take place, where each material point on the gel network has been pushed off radially. We denote by the initial radial displacement of the material point which has been at the radius . This displacement must satisfy because the gel network behaves incompressible at short timescale (where we assume ). Thus, we can prepare an algebraic initial configuration, , which is exact in the limit of for . The subsequent very slow permeative relaxation obeys the standard elasto-hydrodynamic model [7], which gives the following time evolution equation for the radial displacement field :
where D is the (cooperative) diffusion constant , with f, , and K being, respectively, the permeative friction coefficient between the gel network and solvent, the shear modulus, and the bulk (osmotic) modulus of the gel [8]. Hereafter, we use the units such that . In the late-stage, , at large distance , Equation (7) allows the similarity solutions of the form, , where is compatible with our initial condition. See Appendix B for the details including the analytical solutions. Figure 2 shows the evolution of self-similarity solution, , at and . We see there that the algebraic tail of the radial displacement at large r remains unchanged until the time .
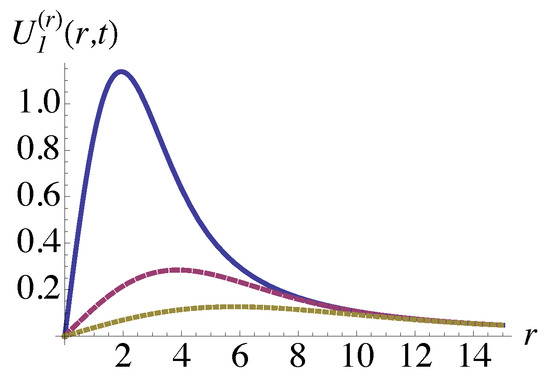
Figure 2.
Radial displacement of the gel. The radial displacement, is shown vs. r for the various time, (blue), 4 (magenta), and 9 (yellow). The vertical scale has been arbitrarily chosen and is supposed to be infinitesimal. For , the displacement, , retains a time-independent tail, . While the finiteness of should modify the radial displacements at small scale, , it does not influence the fate of the algebraic tail.
3.2. Self-Similarity in Space and Time in the Short-Time Limit of 1D Diffusion
Parabolic or wedge-shaped apexes are among the most generic local configurations that we encounter as the initial conditions of diffusion. While the former is generic form around the smooth extrema, the latter should be realized when some spatially localized source is removed after having established the wedge-shaped steady state profile. We discuss the simple case of one-dimension, but the generalization to higher dimensions is straightforward. In Figure 3a,b, the parabolic and wedge-like initial conditions are shown by solid curves, respectively. Their functional forms are and .
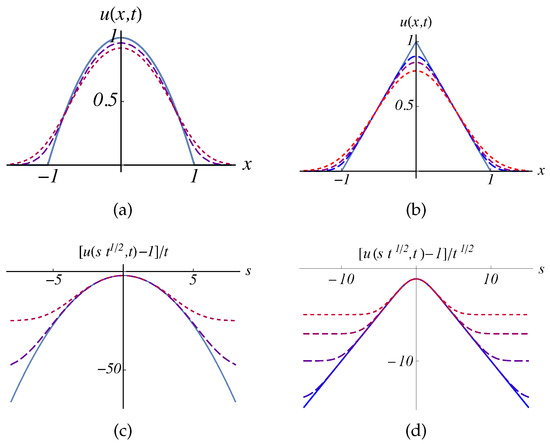
Figure 3.
(a,b) Initial conditions (solid curves) as well as the short-time evolution at and (dashed curves in (a)) and at and (dashed curves in (b)), respectively, are shown versus the unscaled variables. The initial condition has and the support, (c,d) The scaling function and the short-time evolution are represented using the scaled variables: (c) replots the evolution in (a) using and and compares with while (d) replots the evolution in (b) using with s and compares with .
The time evolution in the early stage is also shown in the same figure. In Figure 3c,d, the same evolutions are replotted by the scaled variables. In both cases, parabolic or wedge-like apexes, we can see that, the earlier is the time, the wider is the range of the scaled variable s that fits the scaling function.
As discussed below, the self-similarity in Figure 3a,c should be distinguished from the spreading of a Gaussian peak.
The short-time self-similarity serves to determine the kinetic parameters in the evolution equations. In the above example, the knowledge of the parabolic scaling function allows fitting the smooth apex of in Figure 3a with , which then gives the diffusion coefficient D among other parameters. An important point is that the peak curvature A remains constant in the short-time self-similarity, as opposed to the late-stage self-similarity. In the latter framework, the Gaussian scaling function fitted to the initial parabolic apex predicts the decrement of the curvature linear in time. Figure 4 compares the two approaches. While the short-time self-similarity (lower dashed curve) keeps the initial curvature at the apex and fits well to the true evolution (solid curve), the late-stage self-similarity (upper dashed curve) fails to fit the apex curvature. After preparing the first version of our paper [9], we noticed Christov and Stone [10] published at the same period, where the authors addressed the issue of early-stage vs. late-stage.
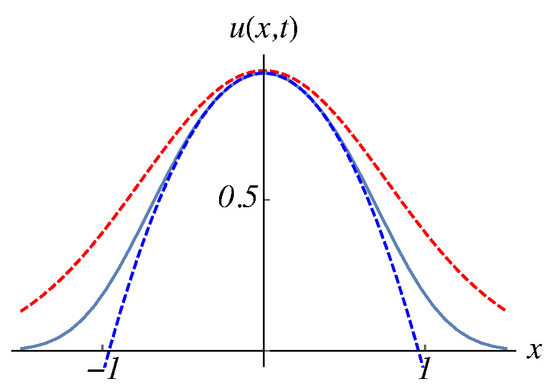
Figure 4.
The early stage profile at calculated from the truncated parabolic initial condition (solid curve) is compared with the short-time self-similarity prediction (lower dashed curve) and with the late-stage one (upper dashed curve).
3.3. Short-Time Self-Similarity in Space and Time of Capillary-Driven Thin-Film Equation
The capillary evolution of the profile of the free surface of a thin viscous liquid film occurs as the quasi-static balance between the Laplace pressure and the viscous force due to the flow (see [11] and the references cited therein). The time evolution of the height profile function, obeys the fourth-order partial differential equation:
The system allows the self-similarity, , where the scaling function with should obey
Most generally the solution or its derivative do not decay rapidly for a given value of . Equation (9) under a given allows two independent even solutions of which one solution can have the power-low asymptote . In [11], the special case corresponding to with rapidly decaying derivative has been analyzed. As in the case of diffusion, the scaling function with power-law asymptote implies the static algebraic asymptote in space, (), because the algebraic asymptote of issues from the balance of the last two terms on the left-hand side of Equation (9), which in turn implies . Figure 5 shows, in the scaled coordinates, the evolution from the wedge-like initial configuration, which corresponds to .
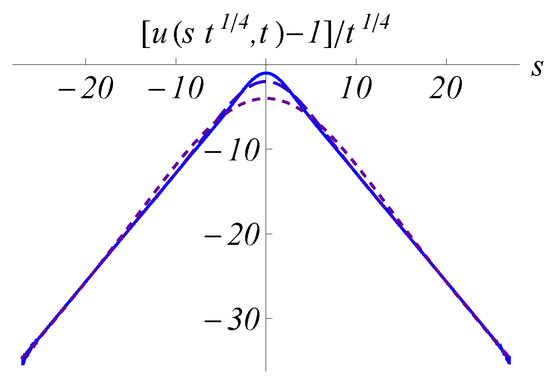
Figure 5.
Short-time self-similarity evolution with algebraic asymptote of capillary-driven thin-film equation. From the initial profile (this cannot be shown on this plane), the solution for Equation (8) at (solid curve), (long dashed curve) and (short dashed curve) are presented using the scaled variables. The scaling function, which is numerically obtained by solving Equation (9) with , is almost indistinguishable with the earliest profile (solid curve).
Unlike the simple diffusion, identifying the solution with algebraic asymptote requires a tuning of the ratio (e.g., at for Figure 5) because the other solution of the same parity grows with faster than any power-laws. Zhang and Lister [12], in their study of the rupture of thin film by the van der Waals interaction, discussed how the inclusion of nonlinearity in the evolution equation selects the value of the exponent to some discrete ones.
4. Conclusions
The fact that solutions to many differential equations enjoy the property of self-similarity is well known for about hundred years (see, e.g., the book by Sedov [2]). In this paper, we show the existence of transformation that internally relates among the solution family of the scaling function (Figure 1). The concrete transformation consists of an integrating factor, which is the solution of adjoint equation and a Wick-rotation type transformation.
To the authors’ knowledge, this type of symmetry has not been reported before. How general is such structure for the evolution systems other than the diffusion remains a future problem. The existence of such transformation might not be specific for the differential equations of scaling functions. However, it is physically interesting and new that this transformation relates the self-similar relaxation process with flux-free boundary on the one hand (i.e., with ) and the self-similar process with steady flux at boundary on the other hand ( with ).
We show the utility of the self-similarity in space and time to analyze the early stage of diffusive processes including the pure diffusion as well as the thin-film equation. These types of self-similarity focus on the local process in space-time and, therefore, are distinguished from the late-stage ones. The merit of the short-time similarity is that, even if the whole system has characteristic lengths or times, the self-similarity in the local space-time region works at the scale which is far below those characteristic scales. In Section 3, we show the utility of the scaling functions that decay or grow algebraically. The short-time self-similarity of diffusion from smooth peak or wedge-like apex are new physical results, and so is the short-time self-similar solution of the surface diffusion. Unlike that of Benzaquen et al. [11], the latter solution has algebraic tails. Generically, one can prepare any algebraically decaying tail as initial condition for which the approach taken in Section 3.2 will be useful, or at least usable. In the application of self-similar solution with algebraic tail to the relaxation of gel (Section 3.1), we bring a new physical idea of combining the elastic aspect of gel, which is described by hyperbolic or elliptic equations, and the diffusive aspect, which obeys parabolic equations. By the former aspect, we can prepare an algebraic tail, and afterwards the gel shows self-similar relaxation having algebraic tail.
In some fields of research [2], the main idea of considering scaling relations is the use of these relations for constructing unknown solutions to the equations whose physical behavior is yet to be clarified. In the present paper, we do the opposite. We take simple equations with well or less known solutions and state that, for some specially constructed initial conditions, scaling with respect to space and time variables occurs. In the future, these two approaches might meet, where the internal relationship among the solution family will help to understand the global picture.
Lastly, the application might not be limited to the linear systems. One apparent example is the Burgers equation, since this equation can be reduced to the diffusion equation through the Cole–Hopf transformation if the boundary conditions are compatible [13]. Other type of generalization remains as an open question. When some mathematical objects represents well some physical phenomena, the mathematical relationship among the former might well have some physical consequences in the latter. We would like to know in the future the meaning of the transformation in Section 2 in physics terms.
Author Contributions
Conceptualization, K.S. and T.F.; methodology, K.S.; investigation, T.F.; original draft preparation, K.S.; writing—review and editing, K.S.
Funding
This research received no external funding.
Acknowledgments
T.F. thanks the laboratory MSC of Université Paris-Diderot for the hospitality during his short stay. K.S. thanks Antoine Fruleux for the discussion at the early stage of this work. We thank the anonymous referees for their critical comments and some reference. K.S. enjoyed the support by the Conformational Flexibility research group.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Family of Scaling Functions for the Self-Similarity Solution of 1D Diffusion Equation
When q is non-negative integer, the adjoint equation has a polynomial solution, up to a multiplicative constant, where is the qth-order Hermite polynomial function. By the symmetry presented in the main text, the polynomial solution of with is . For non-integer or negative values of , the symmetric solution satisfying , and is and the antisymmetric solution satisfying , and is , where is the confluent hypergeometric function of the first kind [14,15].

Table A1.
Examples of scaling functions for some integer p.
Table A1.
Examples of scaling functions for some integer p.
| p | ||
|---|---|---|
| −3 | ||
| −2 | ||
| −1 | ||
| 0 | (*) | |
| 1 | (*) | |
| 2 | (*) |
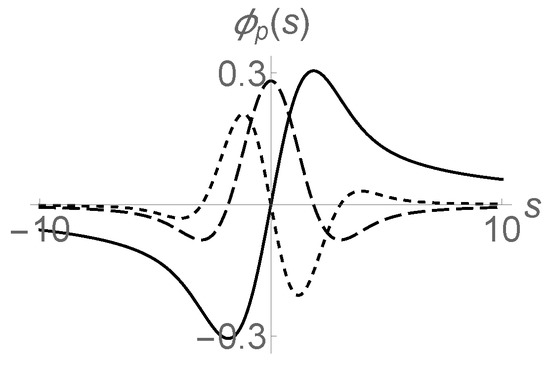
Figure A1.
Examples of the scaling functions satisfying Equation (2) with power-law asymptotes. (solid curve), (coarse dashed curve), and (fine dashed curve). For , these functions decays as with and 2, respectively.
Appendix B. Spacetime Self-Similarity Solution of Equation (7)
Into Equation (7), we substitute the form of the radial displacement,
We then obtain the ordinary differential equation for with :
In addition to the far field condition, , we impose the boundary condition at , which is compatible with the homogeneous dilatation around the origin. In terms of the displacement vector field , the homogeneous dilatation reads for with being a function of time. We then impose Under these boundary conditions, the solutions of Equation (A1) is written in terms of the confluent hypergeometric function [14,15]. The solution reads
This solution behaves as for and for . Because for , we choose , then we have
References
- Barenblatt, G.I. Scaling, Self-Similarity, and Intermediate Asymptotics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Sedov, L. Similarity and Dimensional Methods in Mechanics; Academic Press: Cambridge, MA, USA, 1959. [Google Scholar]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435–479. [Google Scholar] [CrossRef]
- Gunton, J.; Droz, M. Introduction to the Theory of Metastable and Unstable States; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Mansfield, E.L. The Nonclassical Group Analysis of the Heat Equation. J. Math. Anal. Appl. 1999, 231, 526–542. [Google Scholar] [CrossRef]
- Bluman, G.W.; Cole, J.D. The General Similarity Solution of the Heat Equation. J. Math. Mech. 1969, 18, 1025–1042. [Google Scholar]
- Tanaka, T.; Hocker, L.O.; Benedek, G.B. Spectrum of light scattered from a viscoelastic gel. J. Chem. Phys. 1973, 59, 5151–5159. [Google Scholar] [CrossRef]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Sekimoto, K.; Fujita, T. Family of self-similar solutions of diffusion equation—Structure and Properties. arXiv 2012, arXiv:math.AP/1211.0935. [Google Scholar]
- Christov, I.C.; Stone, H.A. Resolving a paradox of anomalous scalings in the diffusion of granular materials. Proc. Natl. Acad. Sci. USA 2012, 109, 16012–16017. [Google Scholar] [CrossRef] [PubMed]
- Benzaquen, M.; Salez, T.; Raphaël, E. Intermediate asymptotics of the capillary-driven thin-film equation. Eur. Phys. J. E 2013, 36, 82. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zhang, W.W.; Lister, J.R. Similarity solutions for van der Waals rupture of a thin film on a solid substrate. Phys. Fluids 1999, 11, 2454–2462. [Google Scholar] [CrossRef]
- Hopf, E. The partial differential equation yt + yyx = μxx. Commun. Pure Appl. Math. 1950, 3, 201–230. [Google Scholar] [CrossRef]
- Weisstein, E.W. “|Confluent Hypergeometric Function of the First Kind.” from MathWorld—A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/ConfluentHypergeometricFunctionoftheFirstKind.html (accessed on 28 October 2019).
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; National Bureau of Standards Applied Mathematics Series; Dover: London, UK, 1965; Volume 55, p. 503. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).