Topological Design Methods for Mecanum Wheel Configurations of an Omnidirectional Mobile Robot
Abstract
1. Introduction
2. Kinematics Model of an Omnidirectional Mobile Robot with n Mecanum Wheels
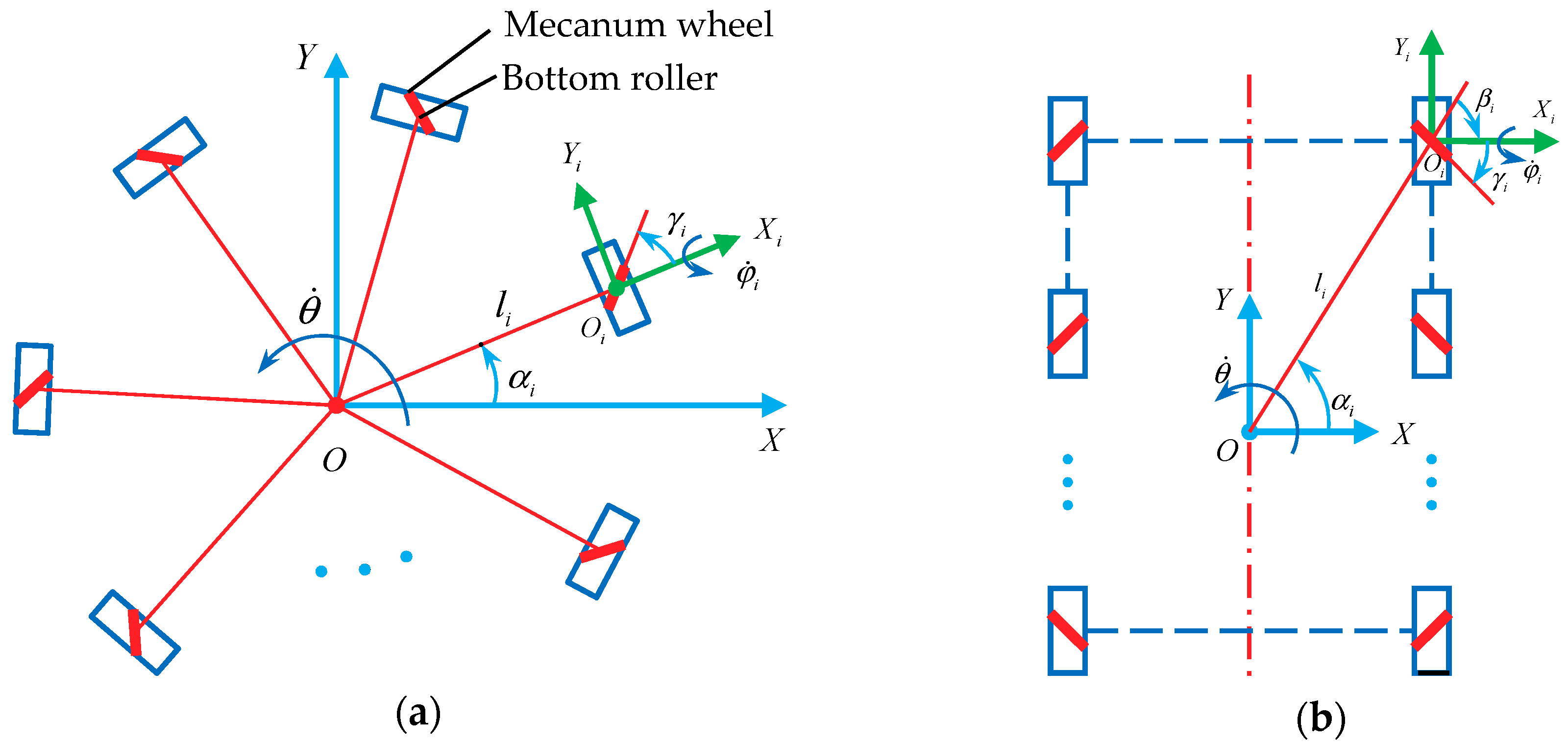
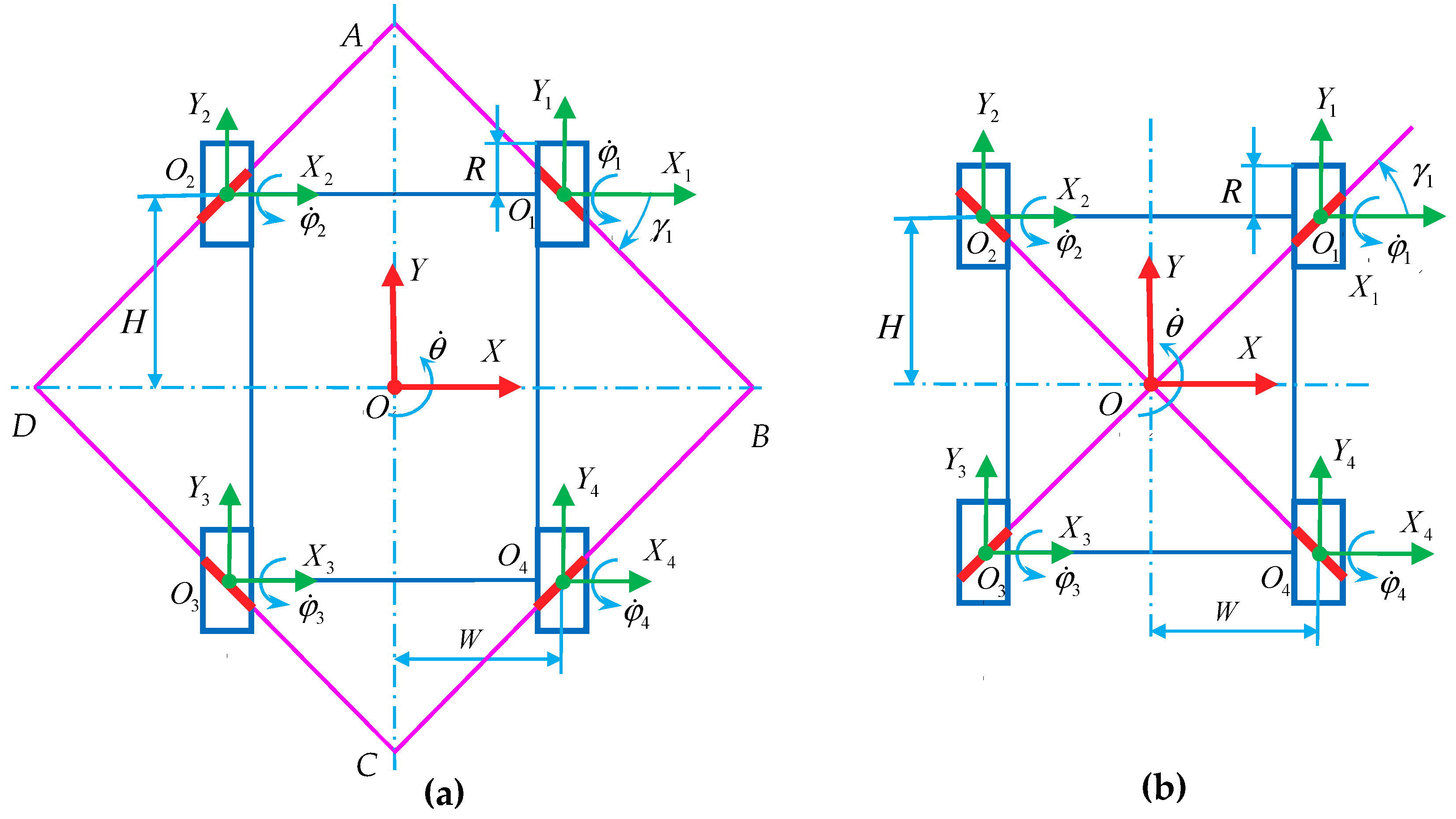
2.1. Mecanum Wheel Configurations of the Single Omnidirectional Mobile Robot
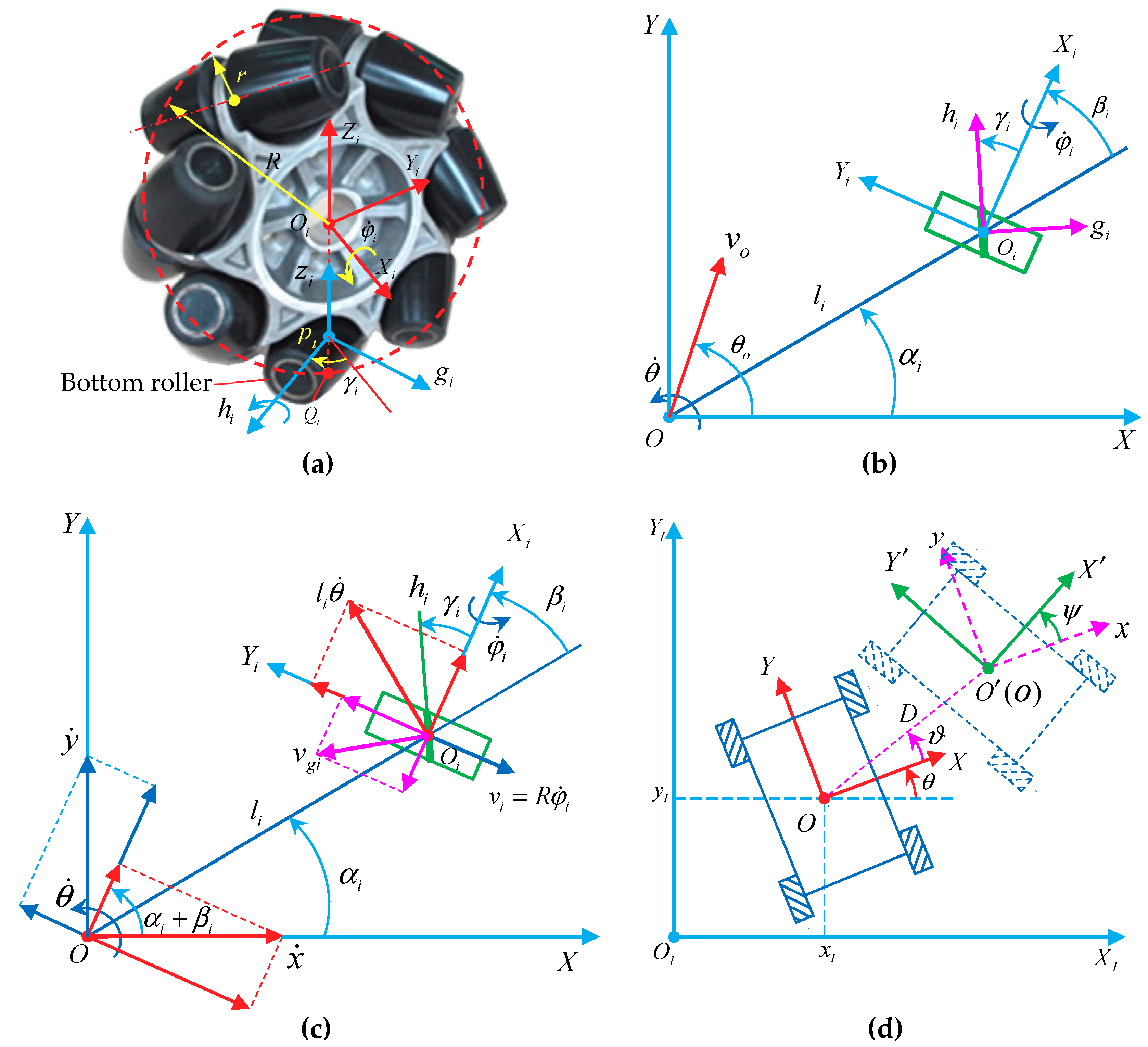
2.2. Kinematics Constraint Model of a Single Mecanum Wheel and Kinematics Model of an n-Mecanum-Wheel Robot
3. Bottom-Roller Axle Intersections Approach for Judging Robot’s Omnidirectional Mobility
3.1. Conditions for Omnidirectional Motion of a Mecanum-Wheeled Mobile Robot System
3.2. Relation Between the Roller Axle Intersection Points Number on Three Mecanum Wheels and the Column Rank of the Jacobian Matrix
3.2.1. No Intersection of the Three Bottom-Rollers Axles
3.2.2. The Axles of the Three Bottom-Rollers Intersect at One Point
3.2.3. The Axles of the Three Bottom-Rollers Intersect at Two Points
3.2.4. The Axles of the Three Bottom-Rollers Intersect at Three Points
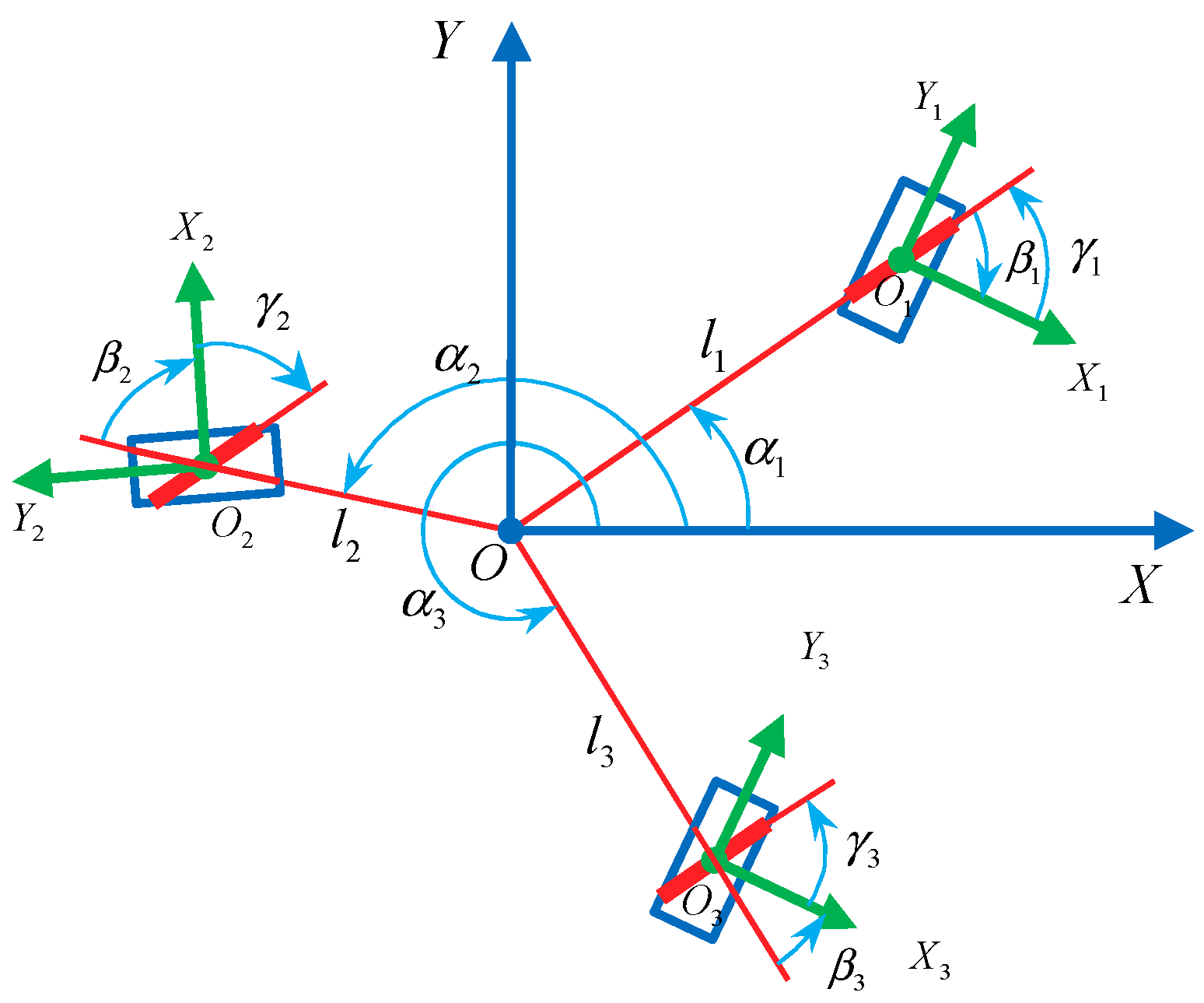
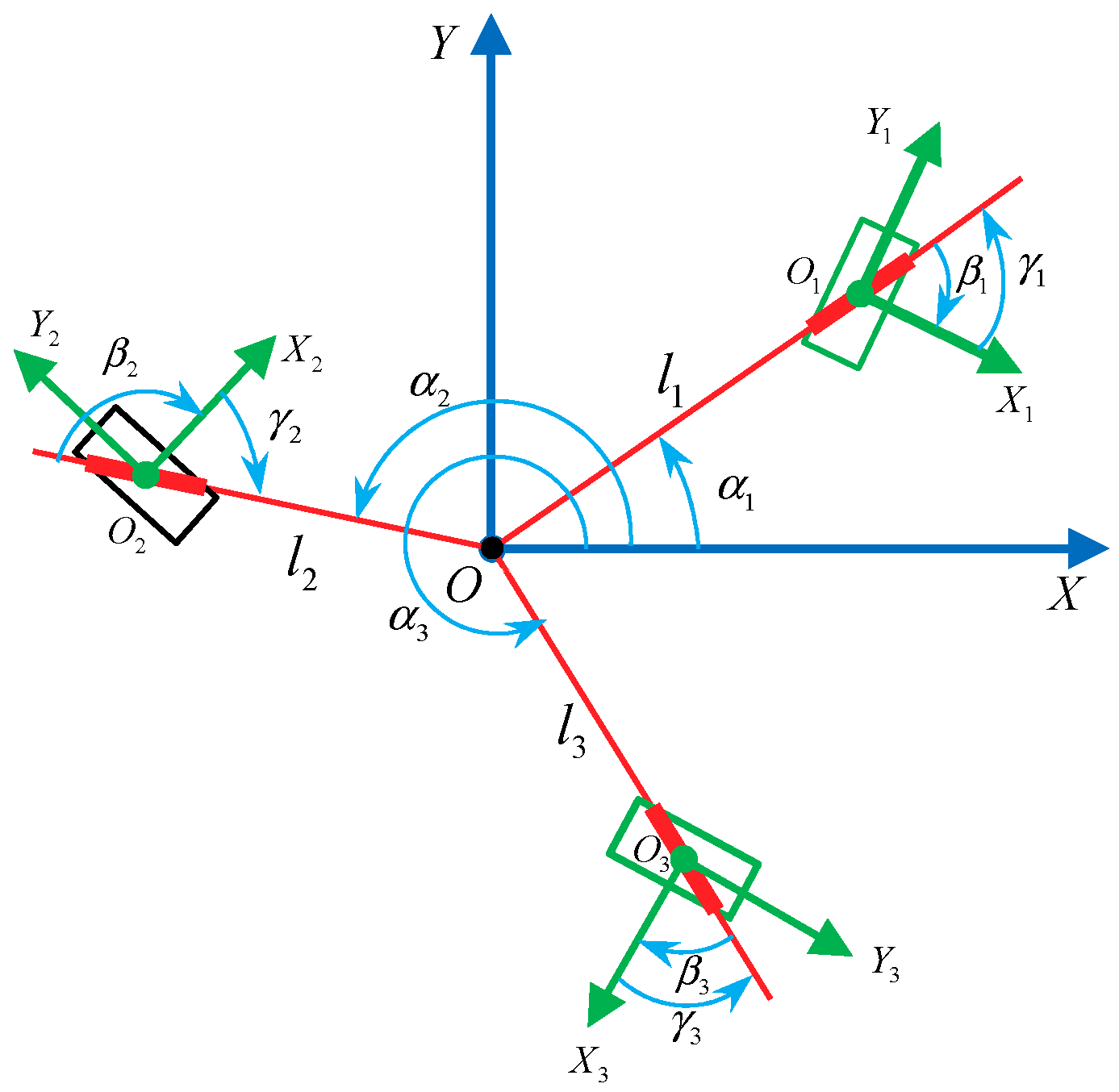
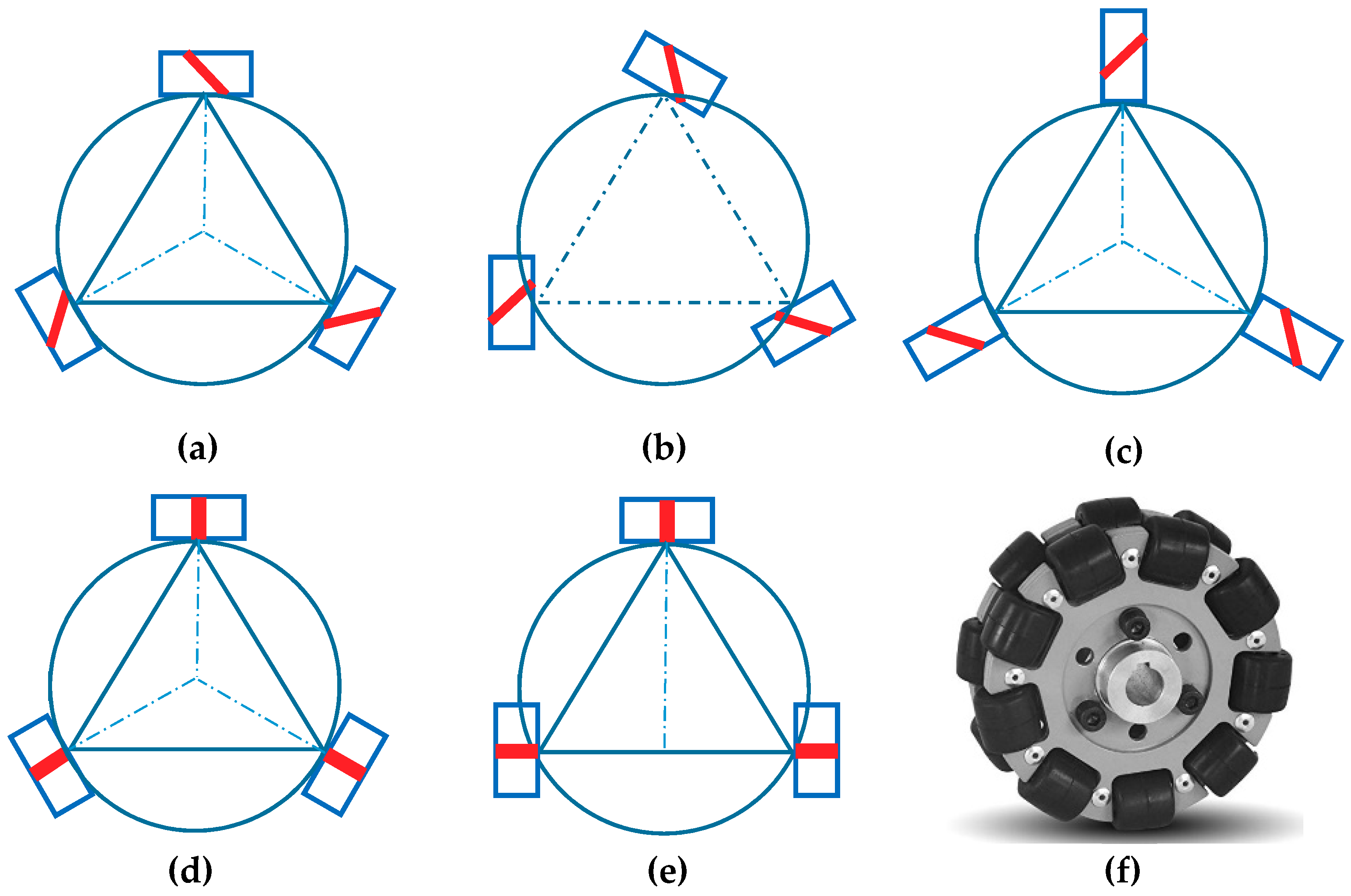
3.3. Three-Mecanum-Wheel Configurations of the Mobile Robot
4. Symmetrical Wheel Configurations of the Four-Mecanum-Wheel Mobile Robot
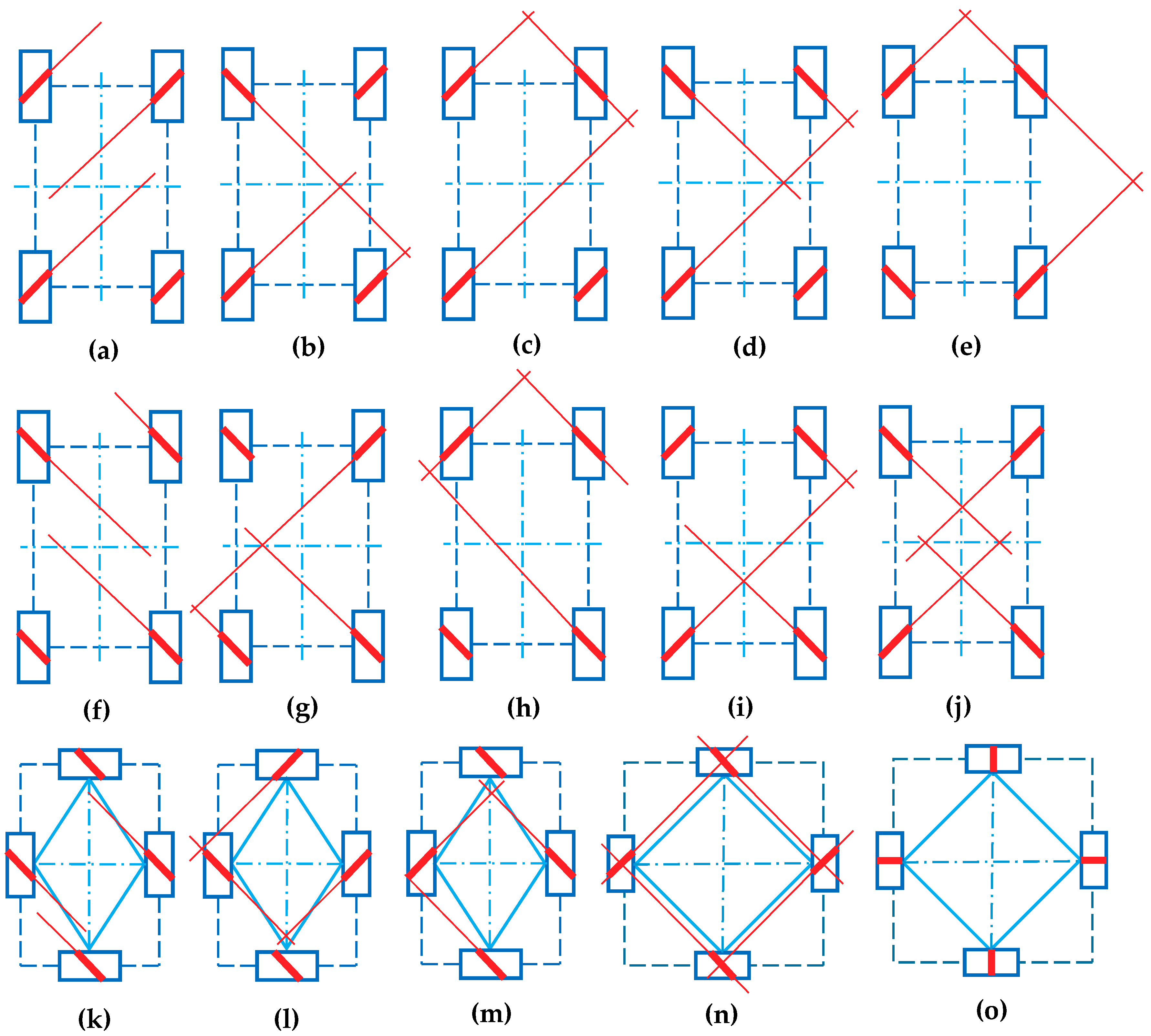
4.1. Judging the Four-Mecanum-Wheel Configurations by a Bottom-Roller Axle Intersections Approach
4.2. Theoretical Verification for the Symmetrical Rectangular Configurations with Four Mecanum Wheels
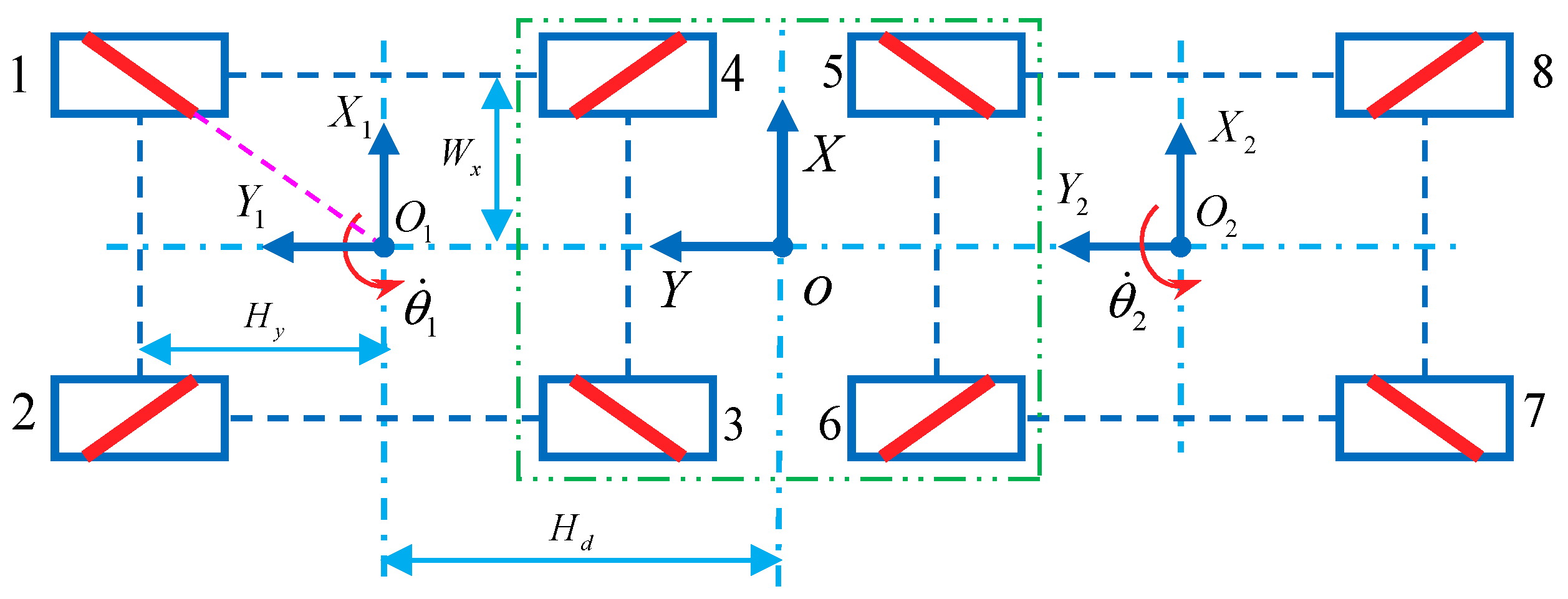
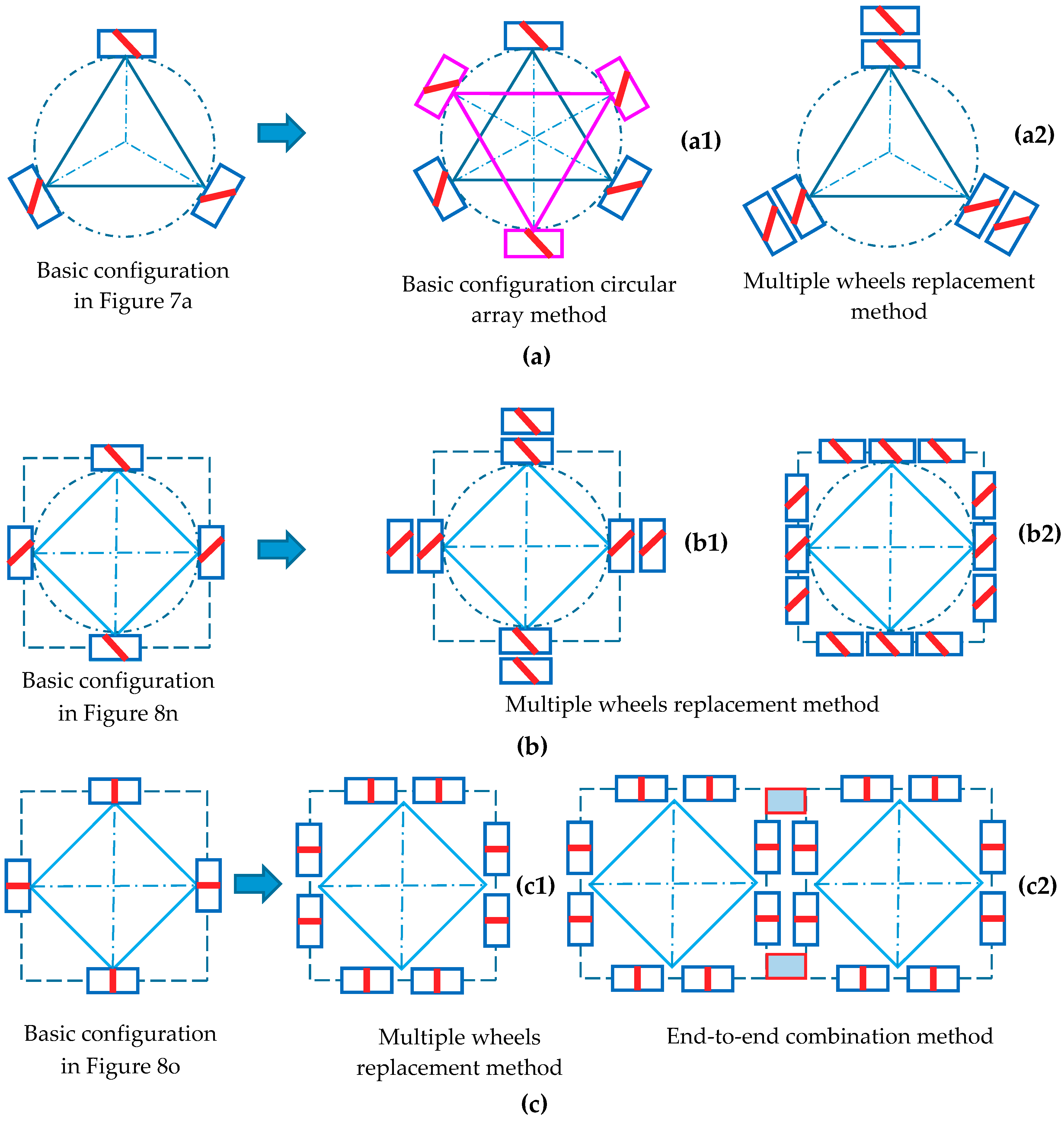
5. Design Method of Mecanum Wheel Configurations for the Omnidirectional Mobile Robot
5.1. Sub-Configuration Judgment Method for Judging the Omnidirectional Motion Capacity of the Wheel Combination Configurations
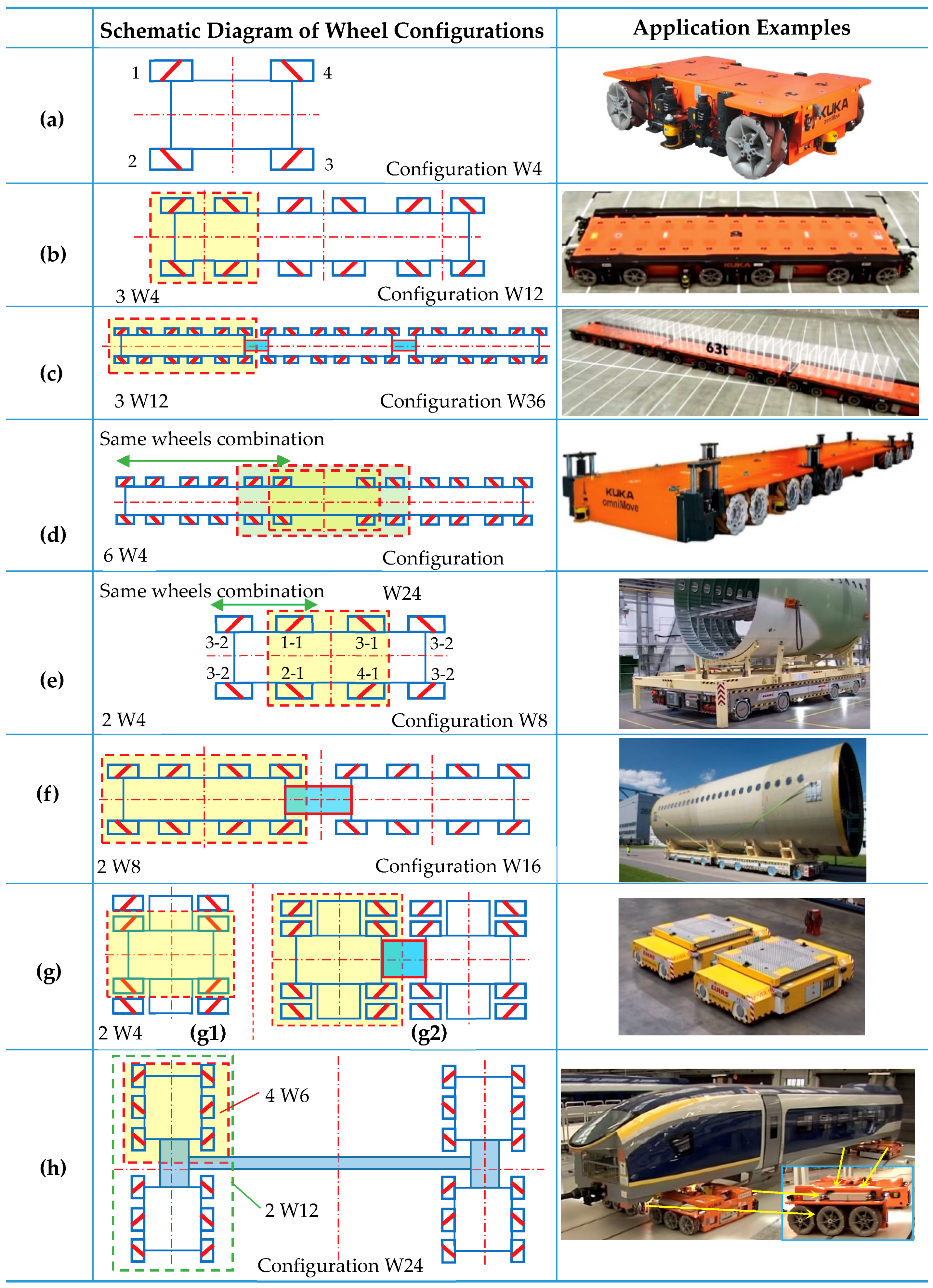
5.2. Analysis of Mecanum Wheel Configurations and Combination Configurations for Common Omnidirectional Mobile Robots
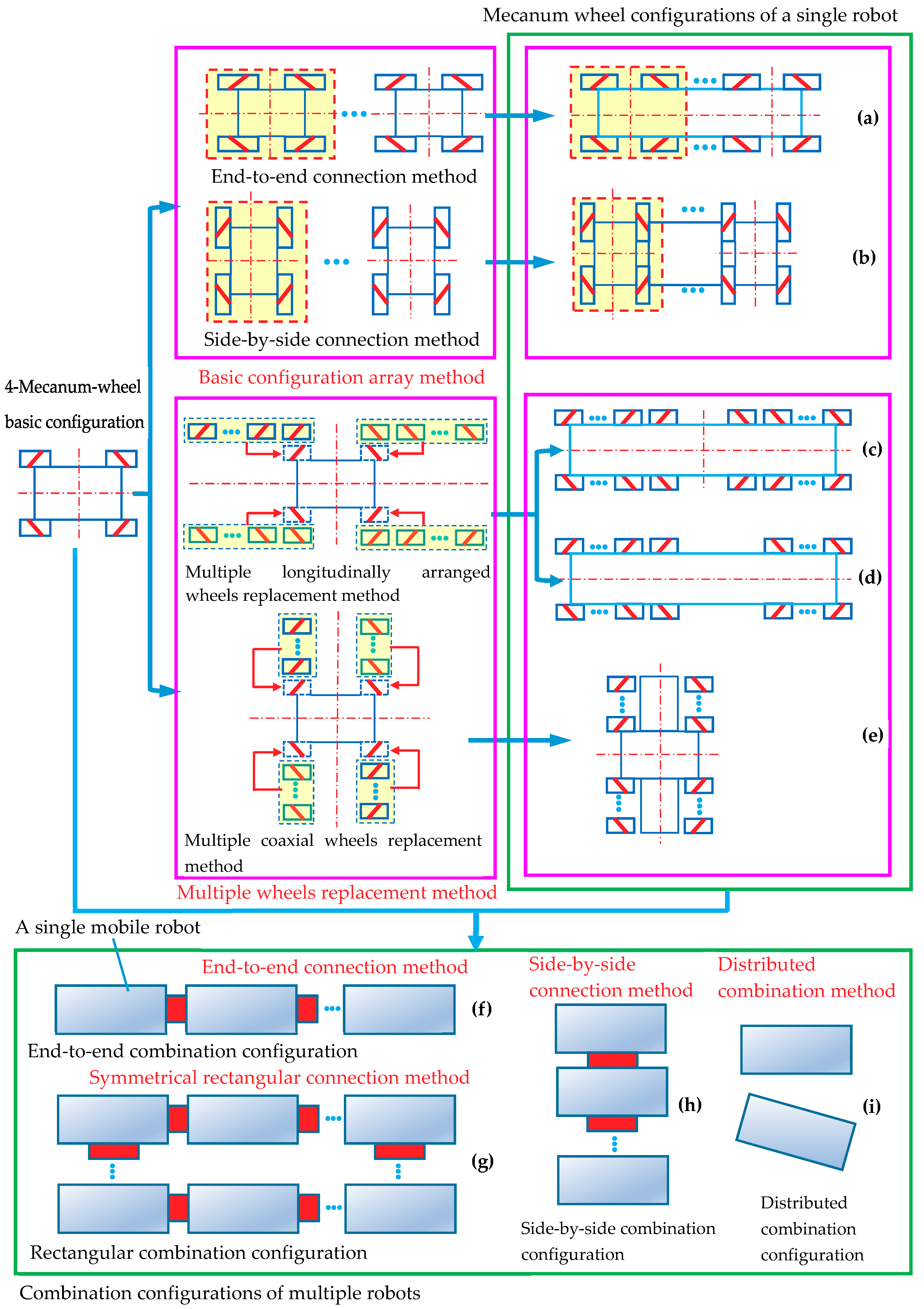
5.3. Topological Design Methods of Multi-Mecanum Wheel Configuration for Omnidirectional Mobile Robot
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gfrerrer, A. Geometry and kinematics of the Mecanum wheel. Comput. Aided Geom. Des. 2008, 25, 784–791. [Google Scholar] [CrossRef]
- Doroftei, I.; Grosu, V.; Spinu, V. Omnidirectional mobile robot-design and implementation. In Bioinspiration and Robotics: Walking and Climbing Robots; Habib, M.K., Ed.; I-Tech Education and Publishing: Rijeka, Croatia, 2007; pp. 511–528. [Google Scholar]
- Alvito, P.; Marques, C.; Carriço, P.; Freire, J. A Robotic Platform for the Social Robot Project. In Proceedings of the 23rd IEEE International Symposium on Robot and Human Interactive Communication (ROMAN 2014) Workshop on Interactive Robots for Aging and/or Impaired People, Edinburgh, UK, 25–29 August 2014. [Google Scholar]
- Sanbot Max. Available online: http://en.sanbot.com/product/sanbot-max/specification (accessed on 20 May 2019).
- Qian, J.; Zi, B.; Wang, D.; Ma, Y.; Zhang, D. The design and development of an omni-directional mobile robot oriented to an intelligent manufacturing system. Sensors 2017, 17, 2073. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Hu, J.; Li, J.; Liu, R.; Shu, M.; Yang, Y. An INS-UWB based collision avoidance system for AGV. Algorithms 2019, 12, 40. [Google Scholar] [CrossRef]
- Adăscăliţei, F.; Doroftei, I. Practical applications for mobile robots based on mecanum wheels-a systematic survey. In Proceedings of the 3rd International Conference on Innovations, Recent Trends and Challenges in Mechatronics, Mechanical Engineering and New High-Tech Products Development(MECAHITECH’11), Bucharest, Romania, 22–23 September 2011; pp. 112–123. [Google Scholar]
- Heß, D.; Künemund, F.; Röhrig, C. Linux based control framework for Mecanum based omnidirectional automated guided vehicles. In Proceedings of the World Congress on Engineering and Computer Science 2013, San Francisco, CA, USA, 23–25 October 2013. [Google Scholar]
- MC Drive Parade. Available online: https://www.youtube.com/watch?v=yf8x2egJRZ4 (accessed on 20 August 2010).
- KUKA omniMove. Available online: https://www.kuka.com/en-us/products/mobility/mobile-platforms/kuka-omnimove (accessed on 20 May 2019).
- Hryniewicz, P.; Gwiazda, A.; Banaś, W.; Sękala, A.; Foit, K. Modelling of a mecanum wheel taking into account the geometry of road rollers. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Sibiu, Romania, 14–17 June 2017; p. 012060. [Google Scholar]
- Airbus Rolls Out Its Second A350 XWB Composite Fuselage Demonstrator. Available online: https://www.airbus.com/newsroom/news/en/2009/08/airbus-rolls-out-its-second-a350-xwb-composite-fuselage-demonstrator.html (accessed on 7 August 2009).
- Automation, K.-R. KUKA omniMove at Siemens Plant Krefeld. Available online: https://www.youtube.com/watch?v=EvOrFgSmQoc (accessed on 2 October 2014).
- He, C.; Wu, D.; Chen, K.; Liu, F.; Fan, N. Analysis of the Mecanum wheel arrangement of an omnidirectional vehicle. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 5329–5340. [Google Scholar] [CrossRef]
- Muir, P.F.; Neuman, C.P. Kinematic modeling of wheeled mobile robots. J. Robot. Syst. 1987, 4, 281–340. [Google Scholar] [CrossRef]
- Muir, P.F. Modeling and Control of Wheeled Mobile Robots; Carnegie Mellon University: Pittsburgh, PA, USA, 1988. [Google Scholar]
- Angeles, J. Fundamentals of Robotic Mechanical Systems: Theory, Methods, and Algorithms, 4th ed.; Springer: Cham, Switzerland, 2002. [Google Scholar] [CrossRef]
- Campion, G.; Bastin, G.; D’Andrea-Novel, B. Structural properties and classification of kinematic and dynamic models of wheeled mobile robots. In Proceedings of the 1993 IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; pp. 462–469. [Google Scholar]
- Gracia, L.; Tornero, J. A new geometric approach to characterize the singularity of wheeled mobile robots. Robotica 2007, 25, 627–638. [Google Scholar] [CrossRef]
- Gracia, L.; Tornero, J. Kinematic modeling of wheeled mobile robots with slip. Adv. Robot. 2007, 21, 1253–1279. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Zhang, J.; Su, Q.; Gao, J. Research on motion characteristic of omnidirectional robot based on mecanum wheel. In Proceedings of the 2010 International Conference on Digital Manufacturing & Automation, Washington, DC, USA, 18–20 December 2010; pp. 237–241. [Google Scholar]
- Wang, S.; Zhang, Y.; Nie, B.; Xia, Y. Research on steering motion of omnidirectional platform based on Mecanum wheel. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Inner Mongolia, China, 15–17 July 2011; pp. 5177–5180. [Google Scholar]
- Wang, Y.; Chang, D. Motion Performance Analysis and Layout Selection for Motion System with Four Mecanum Wheels. J. Mech. Eng. 2009, 45, 307–310, 316. [Google Scholar] [CrossRef]
- Wang, Y.; Chang, D. Motion restricted condition and singular configuration for mecanum wheeled omni-directional motion system. J. Shanghai Univ. (Natl. Sci.) 2009, 15, 181–185. [Google Scholar]
- Mishra, S.; Sharma, M.; Mohan, S. Behavioural Fault tolerant control of an Omni directional Mobile Robot with Four mecanum Wheels. Def. Sci. J. 2019, 69, 353–360. [Google Scholar] [CrossRef]
- Gao, P.; Peng, J.; Yu, W.; Li, S.; Qin, X. Design and Motion Analysis of a Mecanum Three-Round Omni-Directional Mobile Platform. J. Northwest. Polytech. Univ. 2017, 35, 857–862. [Google Scholar]
- Zhang, Y.N.; Wang, S.S.; Zhang, J.; Song, J. Research on motion characteristic of omnidirectional device based on Mecanum wheel. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011; pp. 6094–6097. [Google Scholar]
- Indiveri, G. Swedish wheeled omnidirectional mobile robots: Kinematics analysis and control. IEEE Trans. Robot. 2009, 25, 164–171. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X.; Yang, X.; Hu, F.; Jiang, A.; Yang, C. Trajectory tracking of an omni-directional wheeled mobile robot using a model predictive control strategy. Appl. Sci. 2018, 8, 231. [Google Scholar] [CrossRef]
- Li, J.; Zhang, L. The Teleoperation System of Service Robot Based on Cloud Services. J. Comput. 2017, 28, 231–245. [Google Scholar]
- Li, Y.W.; Dai, S.M.; Shi, Y.; Zhao, L.L.; Ding, M.H. Navigation simulation of a Mecanum wheel mobile robot based on an improved A* algorithm in Unity3D. Sensors 2019, 19, 2976. [Google Scholar] [CrossRef] [PubMed]
- 44 MC DRIVE TP200 700 TDE. Available online: https://www.youtube.com/watch?v=iir0CINszQo (accessed on 24 October 2010).
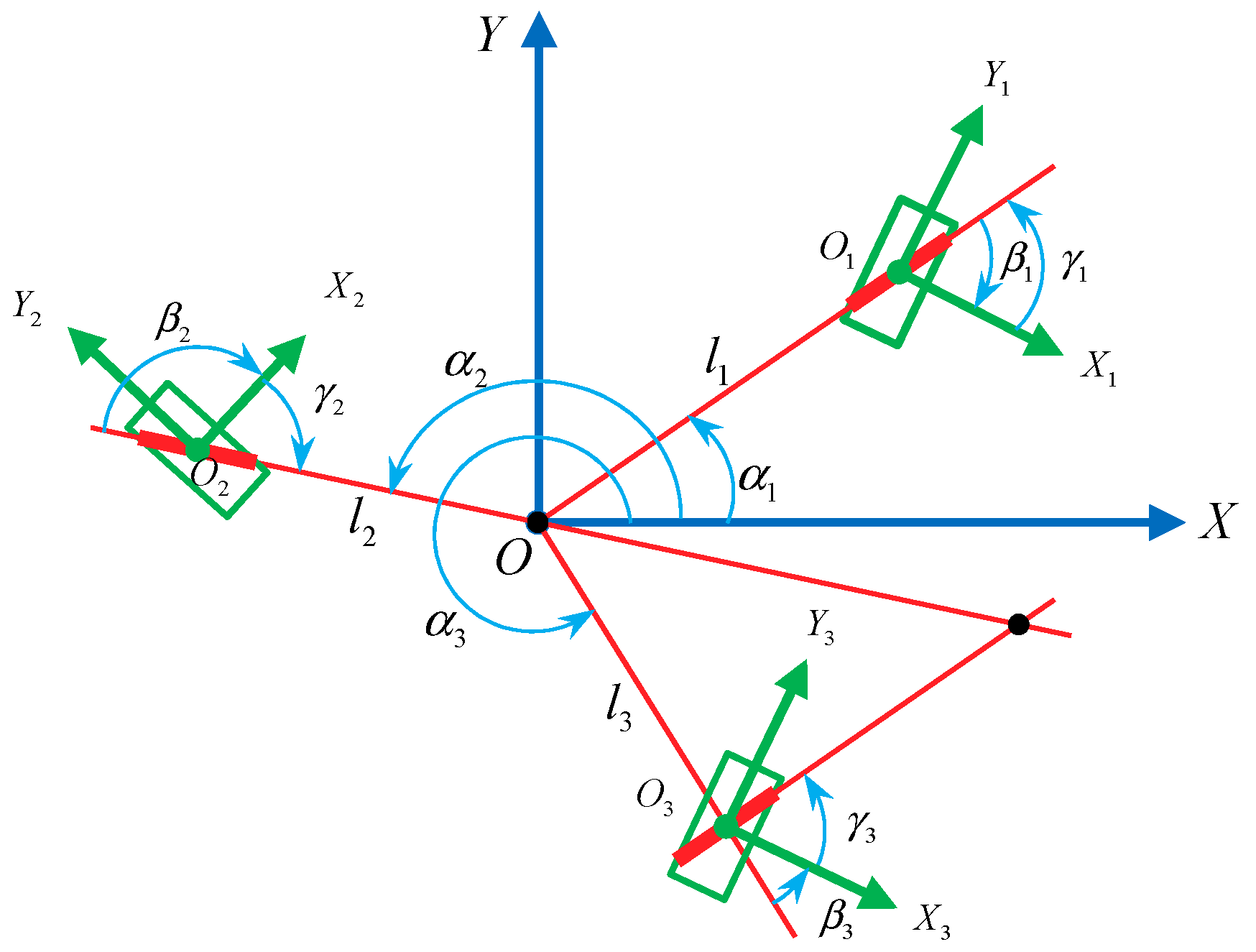
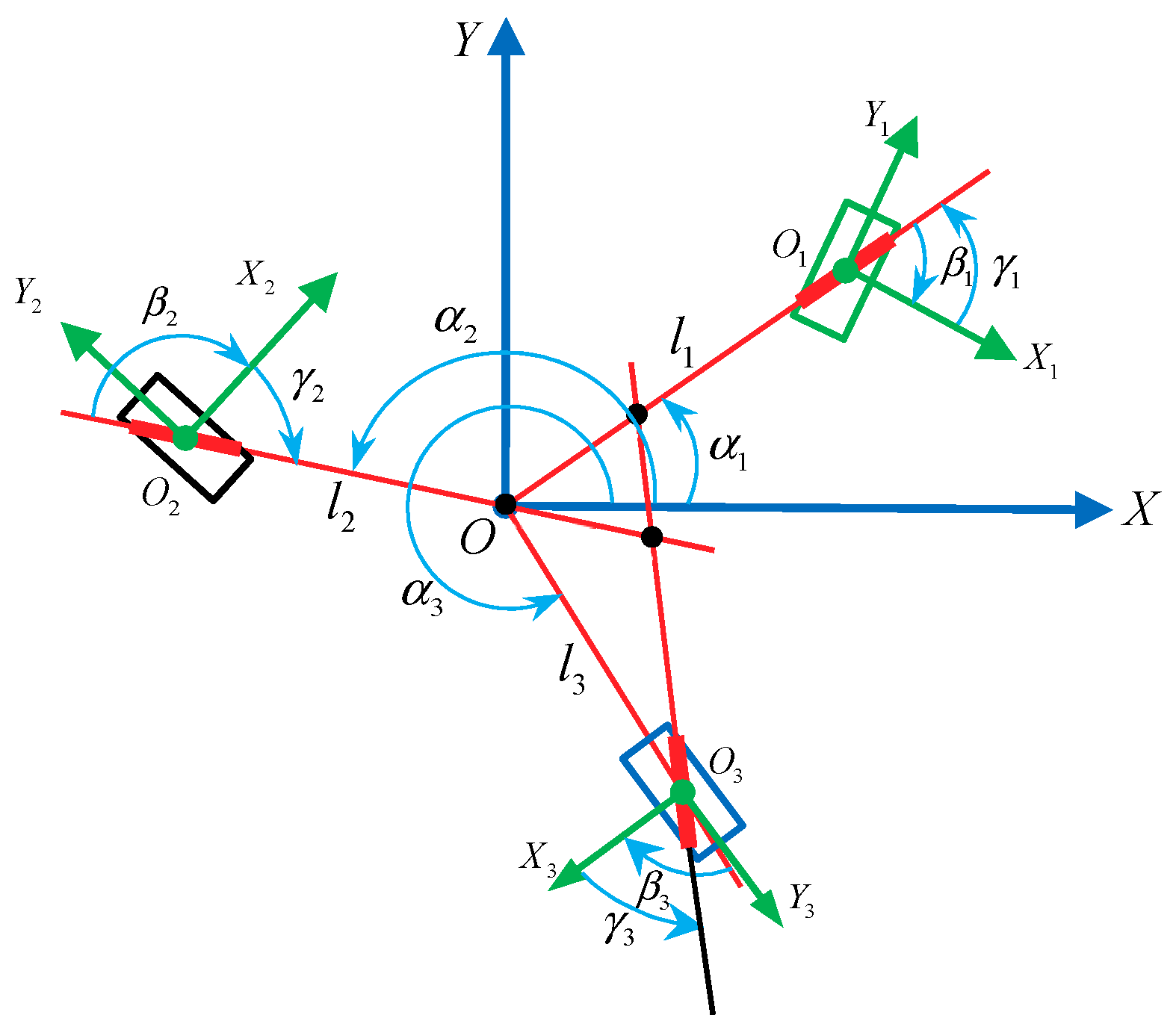
| Serial Number | |||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 |
| Serial Number | |||
|---|---|---|---|
| 1 | − | ||
| 2 | −180°− | ||
| 3 | − |
| Serial Number | |||
|---|---|---|---|
| 1 | − | ||
| 2 | −180°− | ||
| 3 |
| Serial Number | |||
|---|---|---|---|
| 1 | − | ||
| `2 | −180°− | ||
| 3 |
| Number of Intersection Points | Typical Configurations | Column Full Rank |
|---|---|---|
| 0 | 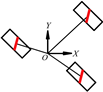 | No |
| 1 | 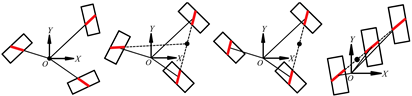 | No |
| 2 | 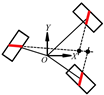 | Yes |
| 3 | 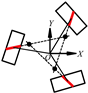 | Yes |
| Configurations in Figure 8 | a | b | c | d | e | f | g | h | i | J | k | l | m | n |
| Intersections | 0 | 2 | 2 | 2 | 2 | 0 | 2 | 2 | 2 | 2 | 0 | 2 | 2 | 2 |
| Column rank | 2 | 3 | 3 | 3 | 3 | 2 | 3 | 3 | 3 | 3 | 2 | 3 | 3 | 3 |
| Column full Rank | N | Y | Y | Y | Y | N | Y | Y | Y | Y/N | N | Y | Y | Y |
| Omnidirectional motion capacity | n | B | B | B | G | n | B | B | B | G/n | n | B | B | G |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Dai, S.; Zhao, L.; Yan, X.; Shi, Y. Topological Design Methods for Mecanum Wheel Configurations of an Omnidirectional Mobile Robot. Symmetry 2019, 11, 1268. https://doi.org/10.3390/sym11101268
Li Y, Dai S, Zhao L, Yan X, Shi Y. Topological Design Methods for Mecanum Wheel Configurations of an Omnidirectional Mobile Robot. Symmetry. 2019; 11(10):1268. https://doi.org/10.3390/sym11101268
Chicago/Turabian StyleLi, Yunwang, Sumei Dai, Lala Zhao, Xucong Yan, and Yong Shi. 2019. "Topological Design Methods for Mecanum Wheel Configurations of an Omnidirectional Mobile Robot" Symmetry 11, no. 10: 1268. https://doi.org/10.3390/sym11101268
APA StyleLi, Y., Dai, S., Zhao, L., Yan, X., & Shi, Y. (2019). Topological Design Methods for Mecanum Wheel Configurations of an Omnidirectional Mobile Robot. Symmetry, 11(10), 1268. https://doi.org/10.3390/sym11101268





