1. Introduction
The arch is a constructive and structural element whose origin must be sought in the Chaldean architecture of the third millennium BC [
1]. Its fundamental development was in the architecture of the great Roman constructions, which surpassed the rigid Greek lintel architecture and allowed them to build immense structures such as thermal baths, bridges and aqueducts [
2]. In Rome, the usual arch was the semicircular one, that is to say the arch formed by a semicircle in which its center is at the height of the imposts, the reason why its rise is equal to the half of its clear span or springing line [
3]. The variants of the semicircular arch, also used by the Romans, are the stilted arch, whose rise is greater than the half of the clear span; and the segmental arch, which differs from the semicircular arch in that the centre of the circumference is below the line of imposts, so that the circumference is no longer tangent to the walls or pillars where the arch starts.
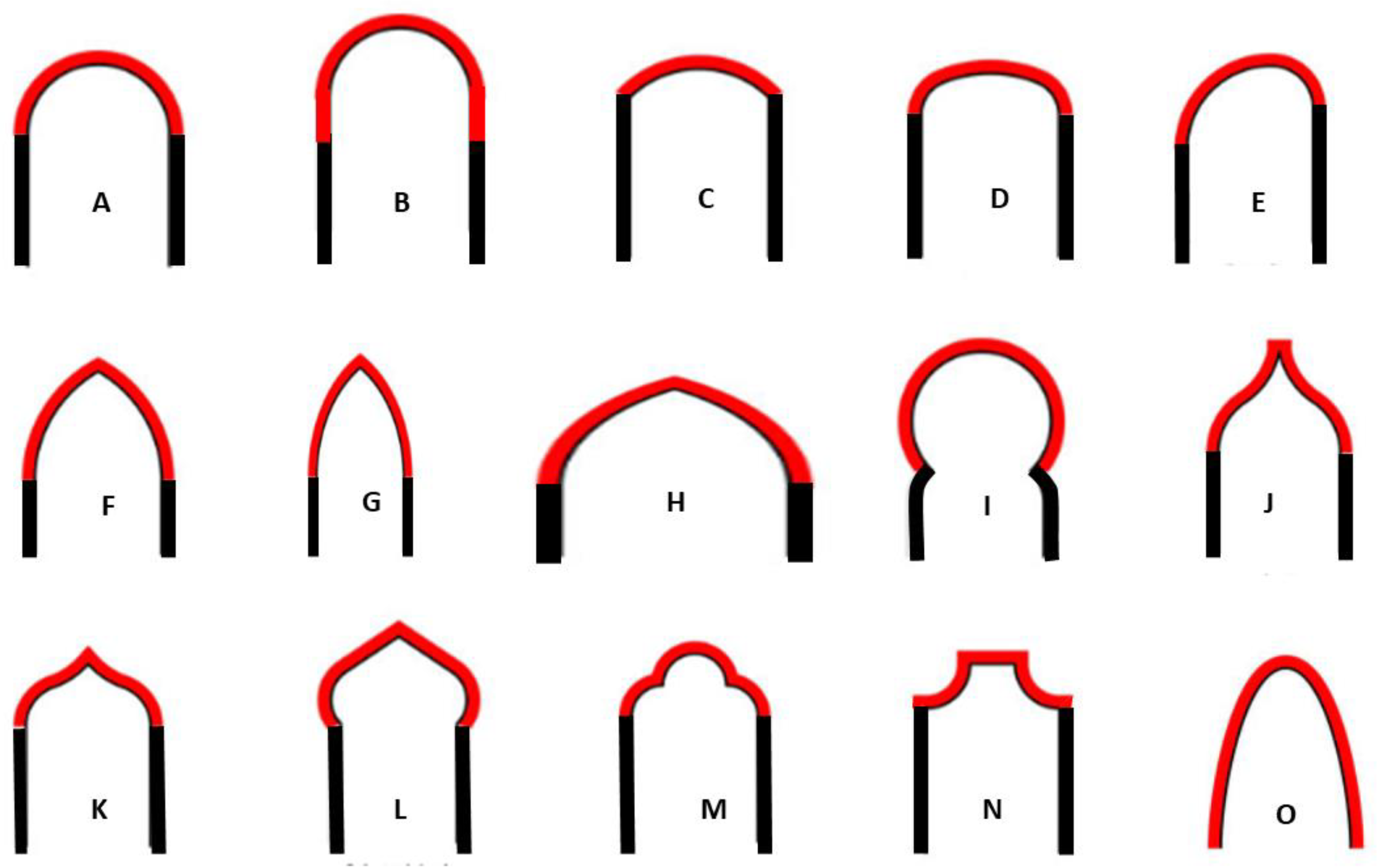
The semicircular arch with its respective types, see
Figure 1A, such as the stilted arch,
Figure 1B, the segmental arch,
Figure 1C, or the arch which is attached to the barrel vault of a nave to reinforce it and divides it into sections, were also characteristic of Romanesque architecture [
4]. However, it lost importance in the Gothic, which gave way to the three-pointed arch,
Figure 1E, with its different variants, as an acute arch,
Figure 1G, or the depressed arch,
Figure 1H [
5].
At the end of the Gothic, a new arch spread with force until well into the Renaissance and even in the Baroque: The basket-handle arch [
6],
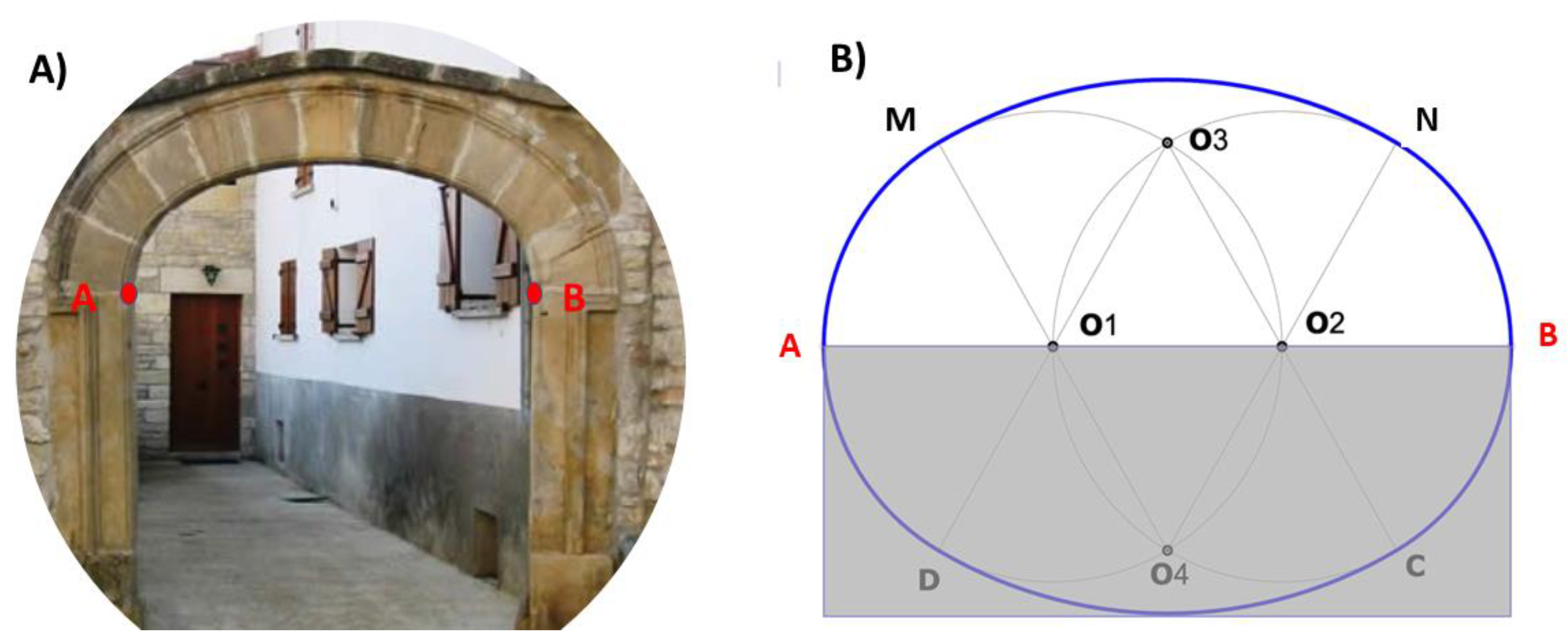
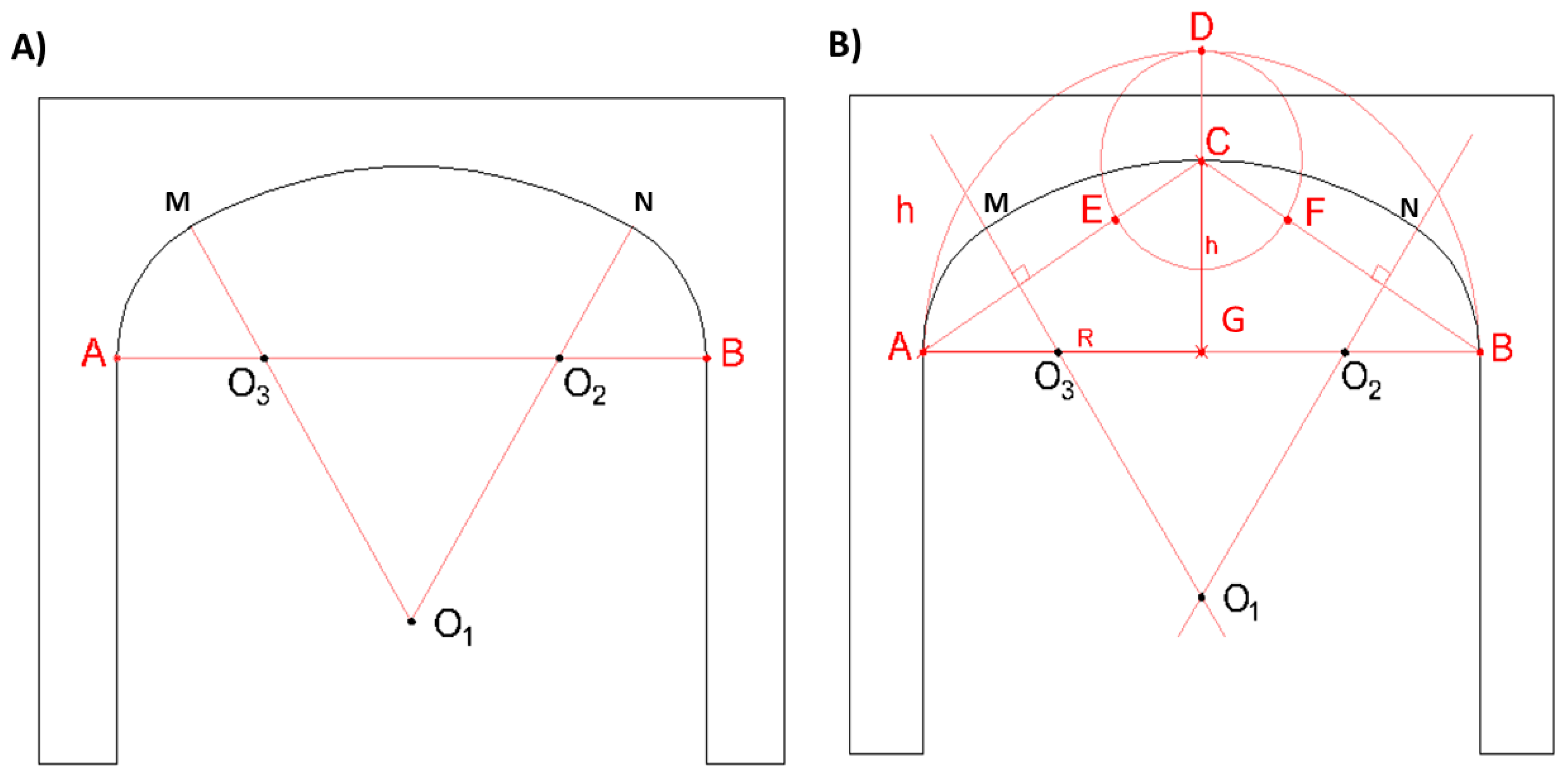
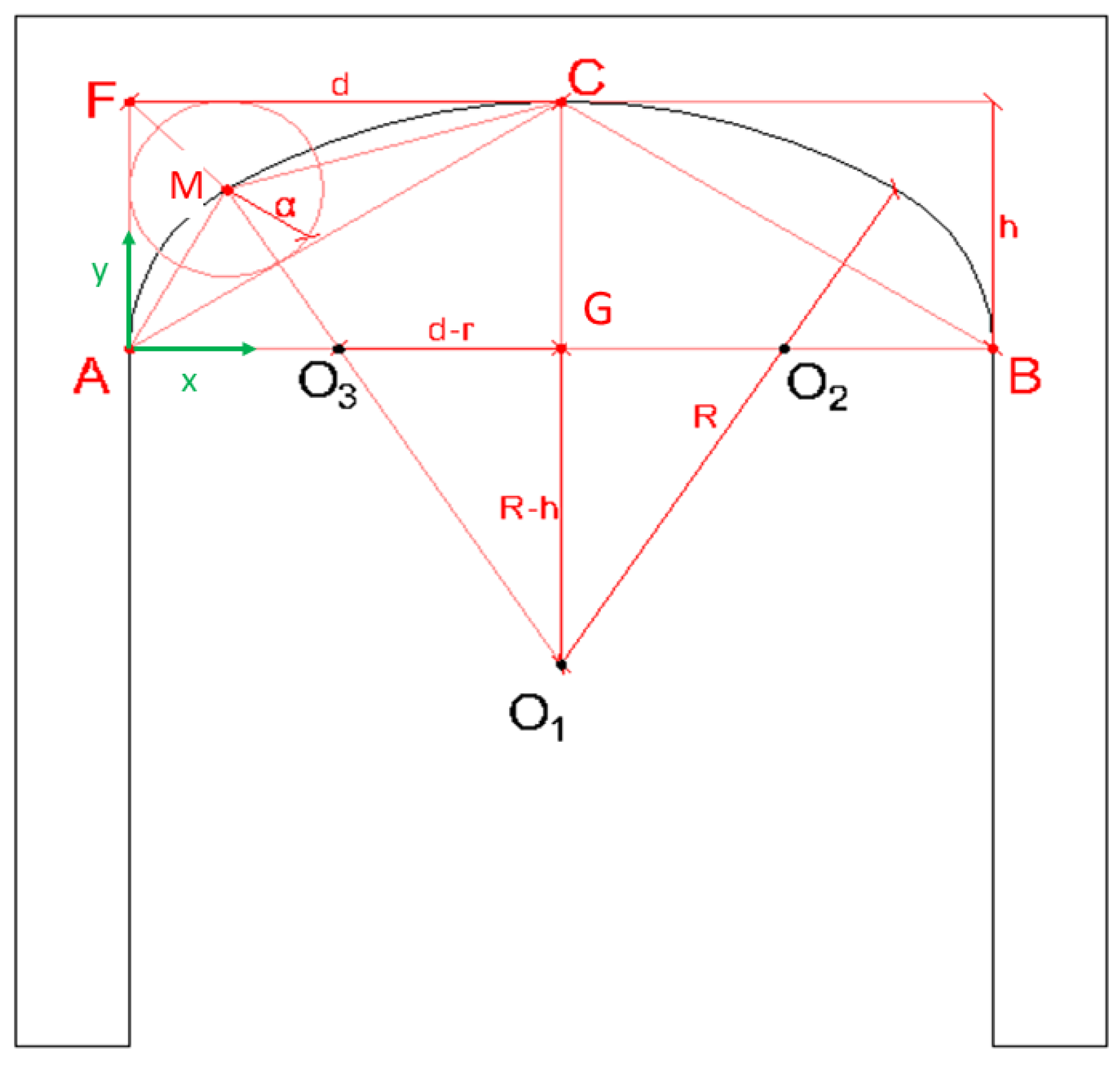
Figure 1D. The basket-handle arch is a symmetrical arch composed of a succession of circumferential arches tangent to each other and with the supports, see
Figure 2A.
It is important to emphasize that there are aesthetic conditions that have sometimes made the rules and procedures inspired by nature, e.g., trunks, and branches that simulate arches or vaults [
7]. Other examples of arches should be cited, such as the Sicilian-Catalan arch (closely related to the main topic of the research), or the Ottoman arch,
Figure 1K, fundamental in the history of such a technical element. Examples of these arches can be found in the literature, especially for bridges, e.g., Malabadi Bridge [
8]. It should be noted that the arches have generally been made with stone masonry, but there are examples made of wood, as the decorative elements in churches, especially the Catholic one, e.g., Borgund church (Norway) [
9,
10].
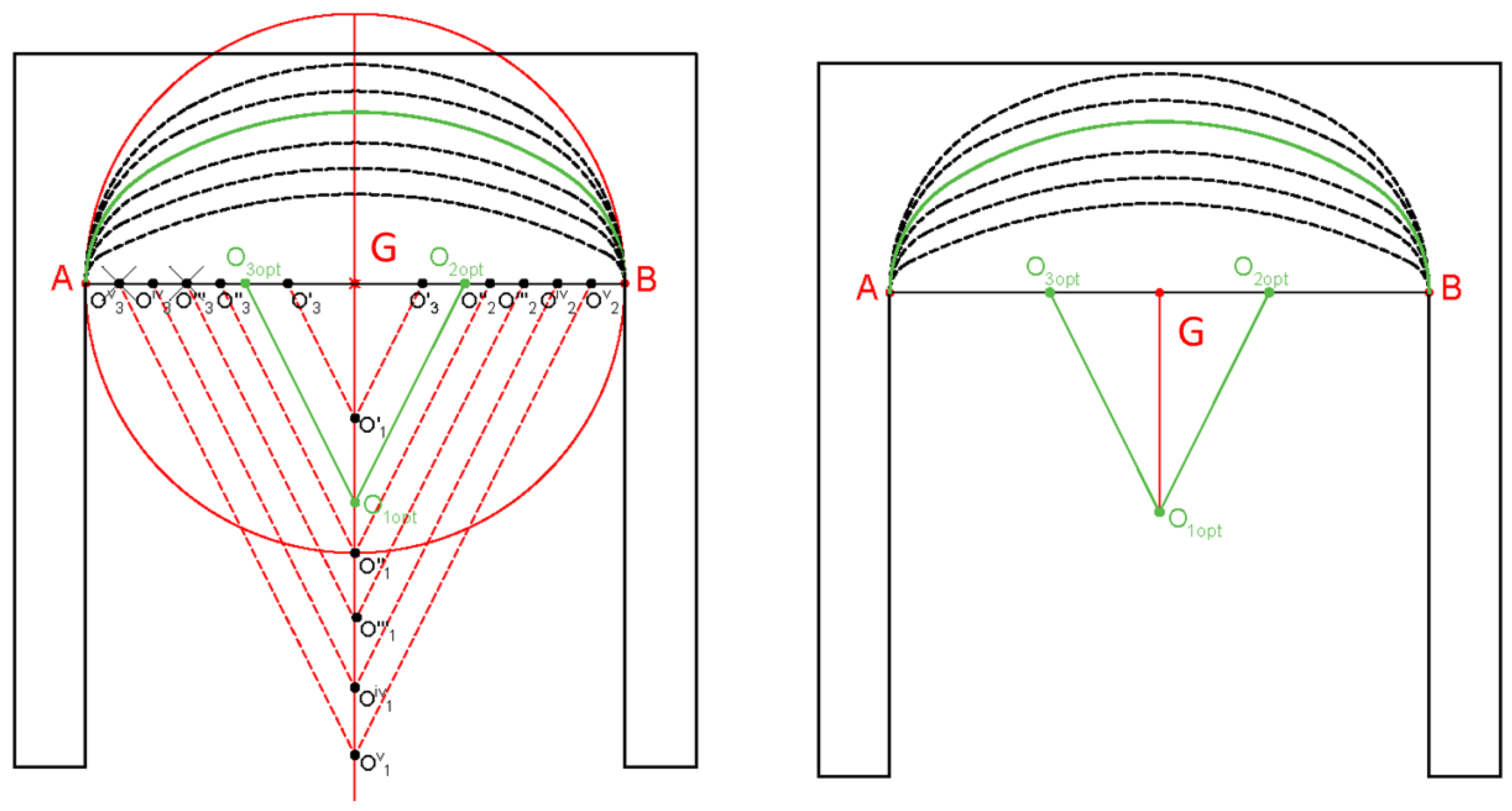
The most standard the basket-handle arch is made up of three circumferential arches, although arches of five, seven and nine centers can also be formed. The number of arches is as many as the smaller the rise in relation to the clear span, in any case, the number of arches of circumference is always odd. The basket-handle arch is precisely the upper half of an oval (
Figure 2B).
The basket-handle arch was widely used in Spain at the end of the Gothic style and in the
Plateresque style, where there are interesting examples both in gates of emblematic buildings and in the anonymous architecture of towns and villages [
11]. In the facades of the great
Plateresque buildings, there are important examples such as in the universities of Alcala and Salamanca, see
Figure 3. In the American Spanish territories, the
Plateresque style spread and therefore, there are examples of this architectural style.
In France, great examples can be found in the four rooms that form a cross on the famous open staircase of the Château de Chambord, the largest of the Loire castles (
Figure 3), or inside the cathedral of de Rodez (
Figure 4A). Another example is the gateway to Chenonceau (
Figure 4B), another of the Loire castles.
The basket-handle arch is sometimes combined with the ogee or inflected arch, widely used in 14th and 15th century architecture [
12], which is a pointed arch made up of four circumferential arches, two interior arches with a concave shape and two upper convex arches. Among the many examples, there is the gate of the Monastery of San Antonio el Real, by the architect Juan Guas, located in Segovia,
Figure 5A. It is also the case to integrate in the same façade the basket-handle, the ogee and the gothic arches as, for example, in the Monastery of Santa Clara located in Palencia (Spain),
Figure 5B).
The basket-handle arch was also used in Baroque architecture on both sides of the Atlantic. For example, the sumptuous arches of Blenheim Palace, a monumental country residence located at Woodstock in Oxfordshire County, England, which is the residence of the Dukes of Marlborough, built between 1705 and 1722, see
Figure 6A. In Spanish America, there are many examples from both the
Plateresque and
Baroque periods where the arches of the Primate Cathedral of Mexico City can be cited, see
Figure 6B.
With the recovery of the historical styles of the late nineteenth and early twentieth centuries, again the basket-handle arches are found as, in the Plaza de España in Seville (Spain), where they appear on marble columns with Corinthian capitals in the outer archery and on brick cores in the porches of those arches (
Figure 7). Likewise, in Modernism, in its formal search for a new architecture, it recovers the arc of the basket-handle arch as opposed to the semicircular arch used, almost exclusively, in the neoclassical period that precedes it (
Figure 8). Therefore, not only monumental examples are given because, in reality, the element arch is a widely used constructive technology, even in the ordinary architecture.
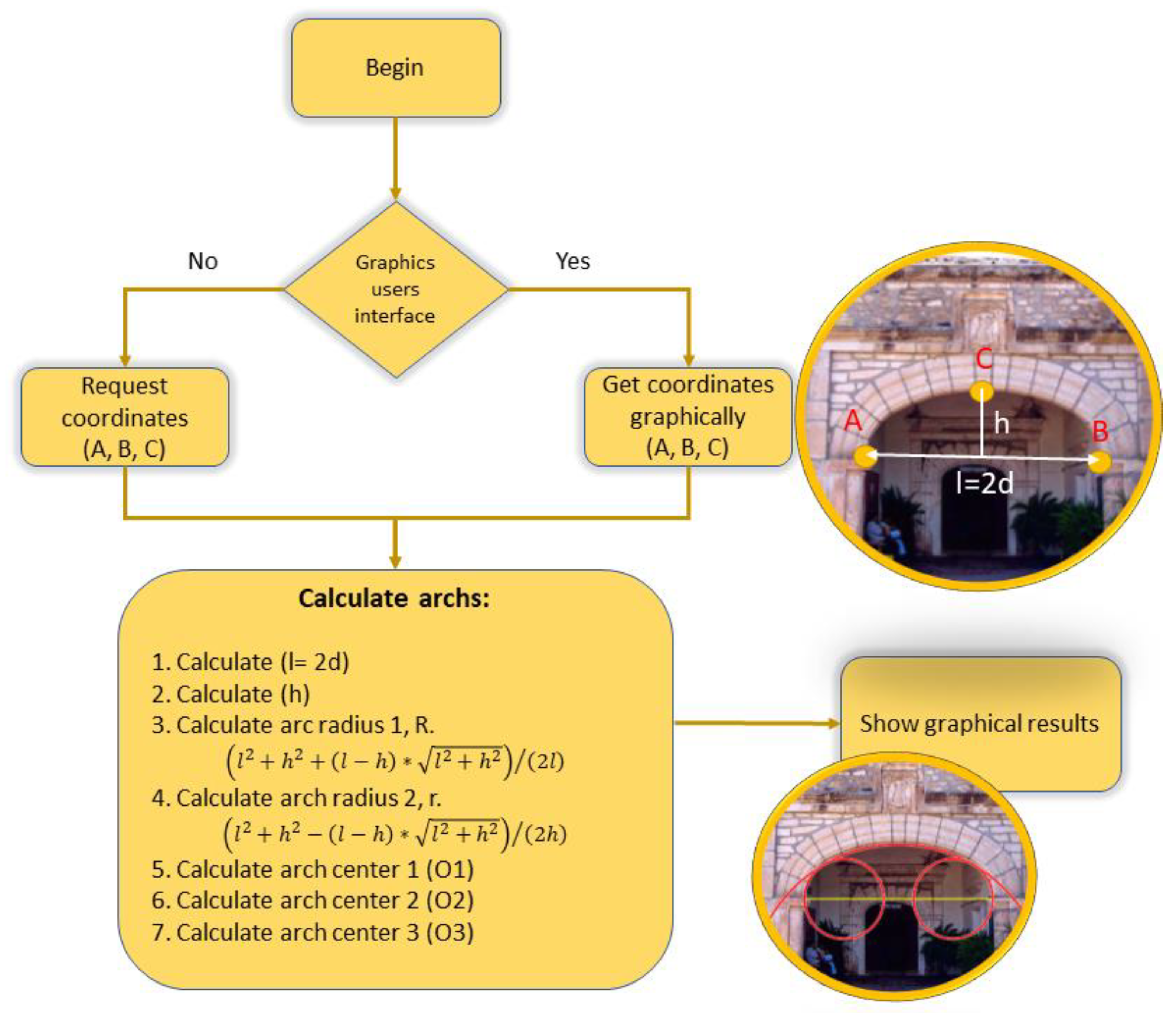
The design of a basket-handle arch does not present any difficulty as is seen below. However, there is no consensus on which is the optimal basket-handle arch. The objective of this work is to review the state of the art in the execution of the basket-handle of three arches, define which is the optimal arch geometry as a structural element in the construction, calculate the numerical solution and program it for its calculation and verification of existing arches.
2. Basket-Handle Arch in Architecture
The geometric approach to the design and construction of safe factory buildings has been used since ancient times by master builders in buildings, such as the Pantheon in Rome or Gothic cathedrals [
13,
14]. The Theory of Structures aims at the project of safe constructions. Considering only equilibrium solutions that respect the essential characteristic of the material, in that it only resists compressions, it has proven to be the most suitable for the analysis and design of masonry structures [
15]. Heyman’s modern theory, based on equilibrium, is the most effective for understanding masonry constructions or structures where equilibrium states depend on geometry [
15].
In the case of the analysis of masonry arches, it is necessary to assume three main conditions [
14]: Masonry has no tensile strength; it can withstand infinite compression; and there will be no slippage between the pieces that make up the arch, due to the high friction coefficient between the stones. Several studies provide additional background on limit analysis for masonry arches [
16].
The basic element of a masonry structure is the arch. Analyzing the equilibrium, a geometric place is found where the centers of thrust form a line, line of thrusts, whose shape depends on the geometry of the arch, the loads and the joints between the pieces. The solution for a stable arch is not unique, since there are infinite lines of thrust that can be contained within all the pieces that make it up. Thus, the equilibrium of the arch can be shown by the line of thrust, which is a theoretical line representing the path of the resulting compressive forces. The concept was first formulated in the 19th century by Moseley in 1833 [
13,
14,
15,
16,
17] and redefined at the beginning of the 20th century by Milankovich in 1907 [
14,
15,
16,
17,
18].
The analysis of limit states, using thrust lines, can establish the relative stability of the structures, as well as the possible collapse mechanisms. The development of interactive tools based on the analysis of thrust lines for masonry structures, using graphical computation, allows establishing the relationship between the structural behaviour of an arch and its geometry [
18].
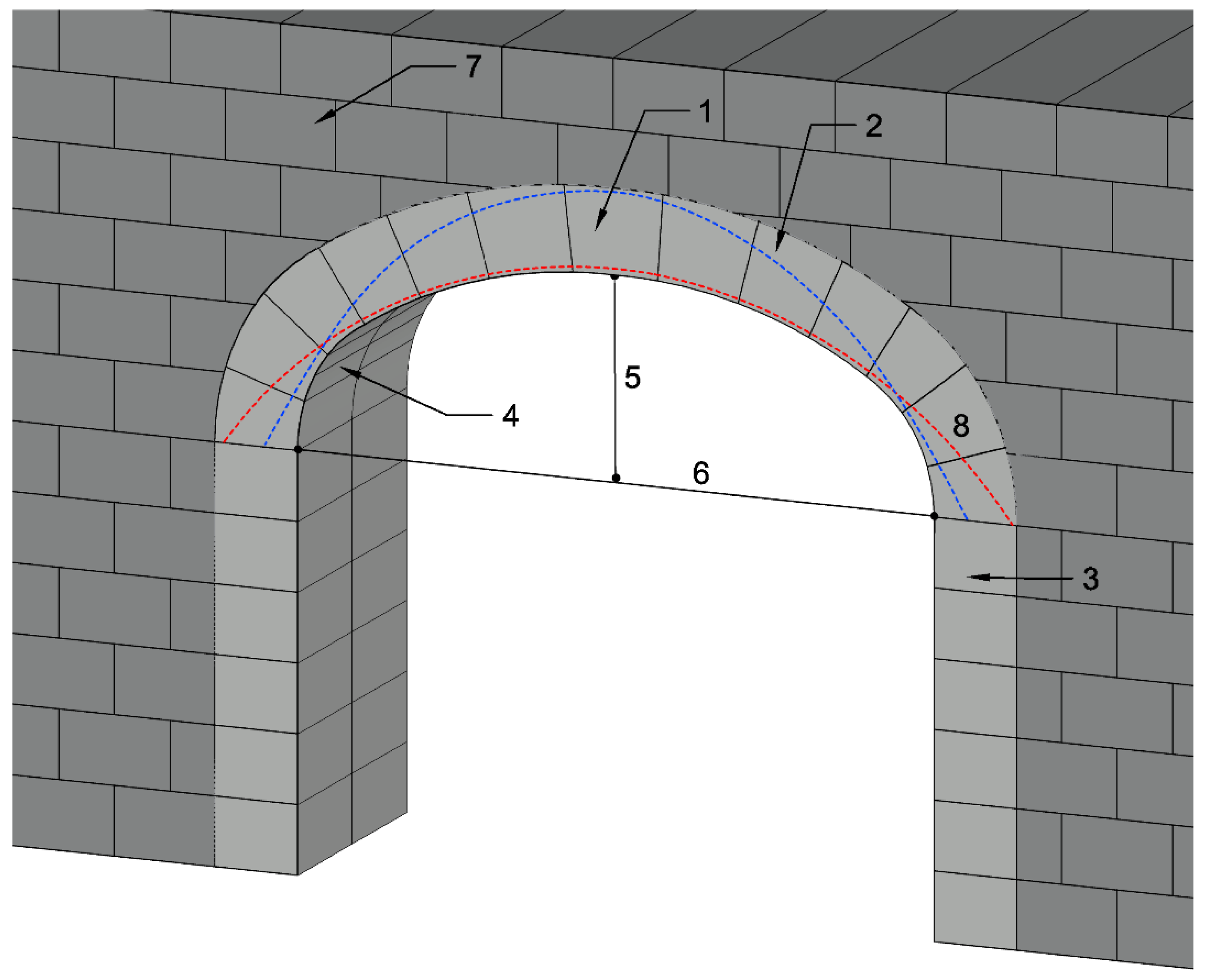
The inclined thrust existing in each element of the arch translates into one vertical (due to weight) and one horizontal (thrust of the arch). There is a maximum thrust corresponding to the most stretched line (
Figure 9). The thrust is maximum when the line is tangent to the intrados in correspondence with the section of the keystone of the arch, and is inserted into the abutments or imposts [
19], see
Figure 9 in red. The minimum line of thrust corresponds to the one that is tangent to the back of the arch, see
Figure 9 in blue.
In an arch it is considered that there are no moments in the junctions between stones, being supported on each other, nor in the extreme supports. The only force to be of concern is the horizontal thrust of the arch, since the horizontal thrust of a bow is greater, the greater the relationship between the springing line of the arch and the rise. The stilted arches can give horizontal thrusts smaller than segmental arches.
In ancient architecture, the thrust forms a polygon in whose vertices are applied on the weights of each voussoir (see
Figure 9, pieces of stone that make up the arch), can be considered as a system of articulated bars. In the case of a symmetrical arch, the horizontal thrust of its centre corresponds to the reaction in the support, being null in the centre when balancing the two halves of the arch (two unstable semi-arches are transformed into a stable arch) [
12,
13,
14,
15,
16]. The problem is to know the thrust of the arch in position, magnitude and direction, and then verify by static, the stability of the arch springer. In the case of monolithic stone springer, the result of the reaction is the composition between the horizontal thrust and its weight. In order to avoid slipping and to avoid that the resultant one is in the line of the angle, the stones that compose the abutment were inclined to a certain angle in a coincident way with the angle of friction of the material. This solution was used in very stretched arches.
The normal way was to have staggered abutments, or formed by pieces of the increasing section towards the base of the same one, to obtain that the resulting one remained inside when the push was excessive (low arches) or to load the abutments with weights in order to avoid the turn.
When friction is high (µ > 0.7), as is the case with limestone including marble, the stones that make up the arch (voussoir) do not slide between them, and the supports receive high compressive loads that can induce plastic deformations [
20]. Basket-handle arches are lowered arches, which would collapse due to the sinking of the keystone (central part of the arch, see
Figure 8), and the tilting of the lower sides towards the outside of the arch, a problem that can be solved by filling or solidifying this area. It should be noted that of the infinite possible directions of the arch’s fracture, the vertical is the most crucial as it results in the greatest minimum thickness value of an elliptical arch needed to support its own weight. In addition, in the case of mortars joining the elements that make up the arch perpendicular to the line of intrados, the fracture pattern is the greater value of the minimum thickness allowed [
21]. According to this, for a semi arch of clear span or width 2d, height h and thickness t, exposed to its own weight, the minimum thickness obtained to maintain the equilibrium corresponds to the lowest ratio h/2d. That is, the lowered arches, among which is the basket-handle arch, and the greatest thickness would be obtained for the stilted arches. For the arch as a structural element, higher safety factor values are obtained in the lowered arches [
22].
From the equilibrium analysis of an arch under external loads, it can be deduced that of the probable thrust lines that satisfy these conditions, the one closest to the geometric axis corresponds to the one that generates the lowest values of the bending moment and shear force in the transversal sections., Thus, it generates a better and uniform distribution of the compressive efforts transmitted through the section itself. It is possible to calculate the safety of the arches, establishing a factor of the degree of safety of the structure, based on the line of thrust contained inside the arch. Heyman suggested reducing the thickness of the arch by changing the extrados and intrados profiles in a homothetic way until they touch the line of thrust. The result is an ideal arch, of reduced thickness, contained within the real arch. The relationship between the thickness of the actual arch and the thickness of the ideal arch that defined it as the safety geometric factor (hreal/hideal) of the structure. This factor gives an idea of the safety of the arches. To calculate the exact value of the geometric safety factor can be arduous, but it is possible to obtain a lower limit easily, for example for a factor of 2, it is expected to be enough to be able to draw a line of thrusts inside the central half of the arch.
The inverse approach to that proposed by Heyman, is based on obtaining the ideal arch in which the line of thrust moves up and down, until it becomes tangent to the curve intrados and extrados of the real arch at least one point, while remaining within its profile [
22]. The result is a region that represents the domain of all probable thrust lines, parallel to those provided by the analysis, wholly contained within the thickness of the arch. By doing so, the safety geometric factor, calculated as the ratio between the actual arch thickness and the ideal arch, measured in the vertical direction, can be denoted as the “full safety range factor”. Heyman’s geometrical factor is a number that increases as the thickness of the arch decreases and is between 1 and infinite, this value being the maximum safety value because the line of thrust coincides exactly with the geometrical axis of the arch in this case. While the full range factor ranges from 0 (maximum risk, unstable arch) to 1 (maximum stability arch). This maximum safety condition means that the shape of such an arch (i.e., its geometric axis) matches exactly the load funicular, i.e., the shape of an inverted catenary. The arch safety evaluation methodology, based on a purely geometric formulation, makes it possible to determine that the thrust line of an arch of constant thickness, subject to its own weight, coincides with its geometric axis, only if the shape of the axis corresponds exactly to an inverted catenary corresponding to the load funicular. In this case, the loads are evenly distributed within the structure and each cross section is requested only by the axial compressive force. With this in mind, the ideal arch within the real one is the domain that contains exactly all states of equilibrium, i.e., all thrust lines parallel to those provided by the analysis.
For an arch to collapse, the structure must allow a mechanism to form. For some types of arches, such as lintels and flying buttresses (as rampant arches), it is not possible to find any disposition of articulations leading to the formation of a mechanism, which makes them safe arches from this point of view [
23]. Sometimes, the problem is to support a certain load. In this case, the arch should not collapse when it is possible to draw two straight lines that join the supports with the point of application of the load. This is the case of very thick lowered arches as the segmental arches or also, the flying buttresses performed as rampant arches.
It is also interesting to note that the minimum actual arch thickness is calculated considering the minimum vertical thickness between all thicknesses measured in correspondence with the lines of action of the loads passing through the centroids of the elements. In doing so, the verification procedure can be applied to arcs of any geometry, even those comprising of variable thicknesses. In nearly complete or complete arches, it is concluded that the greater the thickness of an arch, the greater its safety factor. This is due to the line of thrust that best fits within the profile of an arch if its thickness is greater. However, for arcs with small circular segment values, which are considered very safe arcs because their safety factor is close to 1, the increase in thickness does not correlate to an effective increase in the safety factor.
Most studies on the equilibrium limit analysis of the masonry arch adopt a geometric formulation, based on the determination of the line of thrust, and only a few use energy methods. More recently, there has been the problem of determining the minimum thickness that an arch must have to support its own weight. For a semicircular arch of inner radius R and thickness t, the ratio providing the minimum thickness was given by Pierre Couplet in 1730 [
21], where t/R = 0.101. It was later demonstrated that when a radial rupture occurs in a masonry arch, it is the line of thrust that is tangent to the hinge, not the force of the thrust [
24]. Coulomb in 1773 concluded that the failure mechanism in a masonry arch is the generation of hinges in its interior and not the sliding, and seeks to determine the point at which it occurs, determining the maximum and minimum limits of the thrust force at the coronation of the arch necessary to maintain equilibrium [
25]. At the beginning of the 19th century, Joaquín Monasterio determined the value of the minimum thickness of the arches based on Coulomb’s static theory and concluded that the minimum thickness of a semicircular arch should satisfy the ratio 0.1053 < t/R < 0.1176, improving the conservative result of Coulomb mentioned above [
21].
The thrust line, or resistance line, is defined as the geometric location of the points of application of the resulting thrust force that develops in any cross section of the arch. The minimum line of thrust is the one applied to the extrados of the crown and the base of the arch. A distinction is made between the thrust line and the funicular of forces generated from the lines of action of the thrust forces acting on the joints between the blocks of masonry. The study of the minimum necessary thickness of an arc, analyzing its limit equilibrium using variational formulation and the principles of potential energy, showed that s vertical rupture in a semi-cylindrical arc, subjected to its own weight and horizontal acceleration due to earthquake, was easier to produce than a radial rupture [
26]. Recent research at MIT on interactive analysis of structural forces provides new graphical tools for understanding the behavior of arches. The key mathematical principle is the use of graphical analysis to determine possible equilibrium states [
18]. Graphical methods can be complex, however provide good but conservative results [
27].
In summary, the methods of analysis of masonry arches mainly consider three types of equations for structural analysis, i.e., those referring to: Equilibrium (static), geometry (compatibility) and materials (stresses). In the case of historical arches, only the first two are necessary since the sections are considered to be subject to stresses lower than the maximum that the materials can withstand (the stones that compose the masonry blocks).
6. Discussion
In the study of the arches, the problem that is posed is that of supporting a certain load. In this case, the arch will not collapse when it is possible to draw two straight lines that join the supports with the point of application of the load, hence the appearance of the very thick lowered arch and the buttresses. The buttresses were built mainly to support the horizontal thrust of the vaults covering the naves of Gothic churches or cathedrals [
23]. Thus, from an inclined beam to a wall as a buttress and then to lighten the structure to the so-called ramp arch [
23]. This is a slender two-arch structure characterized by a higher support on one side than the other, see
Figure 1E. In elliptical arches in general and in the basket-handle arches in particular, the minimum thickness necessary to support its own weight is slightly greater when it is assumed that the plane of rupture is vertical at the point where the mechanism occurs, and that the structure collapses.
The study of the relationship between the thickness of the arch and its radius is a function of the relationship between the rise (h) and the half of the clear span of the arch (d) (
Figure 12). It was concluded that for elliptical arcs (d/h = 0.5), the smallest minimum thickness required was obtained when the rupture was vertical [
26]. Thus, if the arch is built with voussoirs, so that the union of the voussoirs follows the line of the intrados of the arch, the plane of rupture begins radially in the intrados and propagates as vertical towards the extrados, while the point where the mechanism is generated does not change [
26]. In the structural study of masonry arches, three types of analysis are considered: Equilibrium (static), geometry (compatibility) and materials (tensions). In the case of historical arches, only the first two are useful, as it is considered that the sections are subjected to stresses lower than the maximum that the materials (rocks) can withstand.
On the other hand, arches in architecture not only fulfil a structural function, but have been traditionally used as an aesthetic element. Therefore, it has been important to maintain the proportions between the clear span and the rise of the arch. Some authors have argued that the relationship between the central arch and the lateral arch should be the maximum [
29]. In this study, it has been shown, through the analysis of case studies of historic buildings, that the relationship between the central arch and the lateral arch is the opposite, the minimum.
It is necessary to point out the limitation or drawback of this study. The photographs with metric quality were not available. However, this can be solved, for example, with close range photogrammetry with metric quality obtaining, for example, orthophotographs.
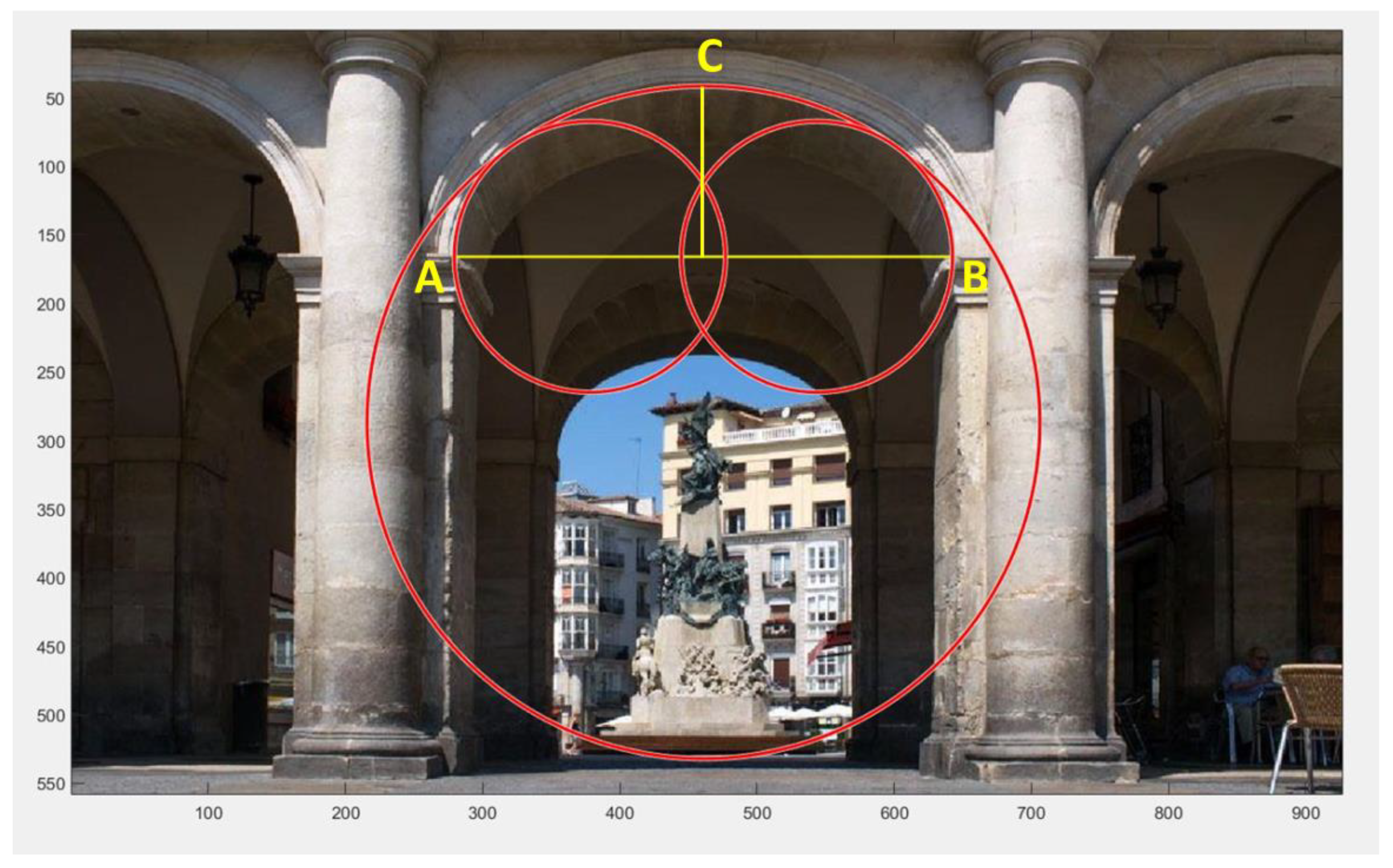
In many of the cases studied, it has been possible to verify first, if they are basket-handle arches of three centers, and second, if the proportion used fulfills the hypothesis raised in this study. It is also necessary to highlight that in those cases in which the solution proposed in this study has not been reached, it has been observed that it is very close. Therefore, it is considered that the study has been valid for arches of this type, basket-handle arches or three centers arches.