Abstract
Fuzzy Petri net (FPN) is a powerful tool to execute the fault diagnosis function for various industrial applications. One of the most popular approaches for fault diagnosis is to calculate the corresponding algebra forms which record flow information and three parameters of value of all places and transitions of the FPN model. However, with the rapid growth of the complexity of the real system, the scale of the corresponding FPN is also increased sharply. It indicates that the complexity of the fault diagnosis algorithm is also raised due to the increased scale of vectors and matrix. Focusing on this situation, a bidirectional adaptive fault diagnosis algorithm is presented in this article to reduce the complexity of the fault diagnosis process via removing irrelevant places and transitions of the large-scale FPN, followed by the correctness and algorithm complexity of the proposed approach that are also discussed in detail. A practical example is utilized to show the feasibility and efficacy of the proposed method. The results of the experiments illustrated that the proposed algorithm owns the ability to simplify the inference process and to reduce the algorithm complexity due to the removal of unnecessary places and transitions in the reasoning path of the appointed output place.
1. Introduction
With the increasing complexity of real systems, multifarious mechanisms have been presented to implement the inference process: expert system [1,2,3,4], Bayesian network [5], neural fuzzy system [6,7,8,9,10,11], multi-class diagnostic technique [12], Petri net (PN) [13,14], fuzzy Petri net (FPN) [15,16,17], etc. Among these techniques, FPN inherits the graphical nature and mathematical foundation of PN and represents the fuzzy production rule (FPR) accurately. Besides that, FPN can implement the dynamic inference process using different reasoning mechanisms. Owing to the advantages above, FPN has been applied in various fields to implement inference [18,19,20,21,22,23].
Ever since Looney (1998) proposed the forward fuzzy reasoning method using FPN for rule-based decision making [24], it has received much attention in the field of fault diagnosis to implement reasoning by FPN [25]. According to the existing literature, the main approach of fault diagnosis using FPN could be classified into two type: inference utilizing reachability tree-based analysis strategy and reasoning using the algebraic forms. Based on the former method, various reasoning algorithms based on fuzzy Petri net were proposed to implement knowledge representation and forward/backward inference [26,27,28,29]. The first strategy has some benefits as it can generate the reachability tree easily and analyze the reasoning process clearly. However, this approach still has some drawbacks such as difficulty utilizing the parallel reasoning ability and modeling large-scale knowledge-based systems (KBS). Thus, to make the most of the parallel operational ability of FPN, the second method, namely reasoning mechanism using the algebraic forms, was proposed to analyze and implement the reasoning process. Gao et al. proposed a parallel reasoning algorithm using max-algebra, and they presented an improved reasoning algorithm based on the novel fuzzy reasoning Petri net (FRPN) to represent and reason the KBS with the negative literals [30,31]. In addition, there are other similar algorithms that have been proposed by other researchers [32,33,34]. Although fault diagnosis algorithms using FPN have been known to be successful, the existing algorithms are facing an enormous challenge called state explosion issue where the scale of FPN would increase with the rapid growth of the scale of KBS. The side-effect of the state explosion issue is to make the scale of related vectors and matrix of FPN using the second fault diagnosis mechanism by algebra forms increase sharply. It further indicates that the complexity and difficulty of the corresponding fault diagnosis algorithm is also increasing.
Focusing on the problematic issues, a bidirectional adaptive fault diagnosis algorithm by FPN is proposed to optimize and simplify the reasoning process based on our previous work, to generate an equivalent FPN model for the corresponding large-scale knowledge-based systems and to decompose the large scale FPN into a series of sub-FPNs surrounding the inner-inference-paths among fuzzy Petri nets [35,36]. The main thinking of the proposed algorithm is to reduce the complexity of fault diagnosis processing by removing the unnecessary places and transitions in the inference path of the appointed output place. To realize this presented function, the proposed algorithm has three phases: (1) using a backward reasoning mechanism to seek the unconcerned places and transitions; (2) implementing delete row or column commands to compress the dimension of the operational matrices; and (3) executing the forward reasoning strategy to calculate the truth degree of the goal on the simplified FPN. A practical example of turbine fault diagnosis system is employed to provide the feasibility and efficacy of the proposed method. The results of the experiments prove the proposed algorithm can select the optimum reasoning path of the appointed output place.
The rest of this article is organized as follows: Section 2 introduces the basis of FPN. Section 3 presents the proposed algorithm in detail. Section 4 analyzes the correctness and complexity of the proposed algorithm. Section 5 illustrates the feasibly and validity of the proposed algorithm via a case study. Section 6 concludes this article.
2. Fuzzy Petri Net
In this section, the formality and relevant notions of FPN are discussed. Following that, the corresponding operators in the inference process are also generated.
2.1. Fuzzy Petri Net and Related Definitions
Focusing on the fault diagnosis issue, an FPN formalism is proposed in this article based on [37].
Definition 1.
Fuzzy Petri Net.
The FPN is represented as an 8-tuple: , where
- 1.
- is a finite set of places. Moreover,indicates a place vector, where. Ifis the goal place or a place which has a direct or indirect relationship with the goal place,. Else,.
- 2.
- is a finite set of transitions. Moreover,indicates a transit vector, where. Ifis the transition which has a direct or indirect relationship of the goal place,. Else,.
- 3.
- is an input matrix. Here,records whether a directed arc fromtoexists, where
- 4.
- is an output matrix. Here,records whether a directed arc fromtoexists, where
- 5.
- is a vector of fuzzy marking, wheremeans the truth degree of corresponding place. The initial truth degree vector is denoted by.
- 6.
- ,is the threshold of. Moreover,is a threshold vector, where;
- 7.
- is the weight of the arc fromto.indicates how much the placeimpacts its following transition;
- 8.
- is the belief strength, whereindicates how much of a transitionimpacts its output places.
Definition 2.
Pre-set and Post-set.
For an FPN,is the pre-set or input set ofandis the post-set or output set of, where.is a flow relationship.
Definition 3.
Input place and Output place.
If, placeis an input place.
If, placeis an output place.
Definition 4.
Enable and fired.
For a transition, if there exists, transitionis enabled in the condition of markingand denoted by. Moreover, if transitionis enabled in the condition of making, then a new markingcould be obtained afterfired and denoted by.
Additional, an input strength vectoris defined asto records the input strength value of each place, where,.
Definition 5.
Incidence Matrix, Input Weight Matrix, and Output Belief Strength Matrix.
Incidence matrixis defined as, where,
Input Weight Matrixis defined as, whereis the weight fromto. If, there are. Else,.
Output Belief Strength Matrixis defined as, whereis thebelief strengthfromto. If, there are. Else,.
2.2. Proposed Operators of the Proposed Algorithm
In the proposed algorithm, to delete the row or column in the operational matrices, the operators of these delete rows and columns are defined as follows.
Definition 6.
Operators of Delete Rows and Columns.
Assume vectoris the vector to record the locations of rows which need to be deleted. Operatoris designed to delete the appointed rows.
Assume vectoris the vector to record the locations of columns which need to be deleted. Operatoris designed to delete the appointed columns.
Definition 7.
Three operators of Max Algebra.
where,are the-dimensional matrices.
whereare the-dimensional matrices, respectively.
. If. Else,.
3. Bidirectional Adaptive Reasoning Algorithm
An acyclic net is a net which does not have a loop or circuit structure. According to reference [38,39], there does not exist circularity structure in the practically KBS. Based on this finding, the research focuses on how to implement the inference on the acyclic FPN. Thus, the proposed algorithm would only just consider the situation of the acyclic FPN model.
The related concepts of the proposed algorithm are listed as follows. (The assumption is that the FPN model has its own places and transitions in the reasoning process.)
3.1. The Proposed Algorithm
In the algorithm, to compress the scale of the operational matrices, a bidirectional reasoning algorithm is presented with combined highlights and a forward reasoning strategy with backward reasoning mechanism. The backward reasoning mechanism is employed to seek the unnecessary places and transitions to the forward reasoning strategy which is used to calculate the truth degree of the goal on the simplified FPN. The entire flowchart is drawn as shown in Figure 1.
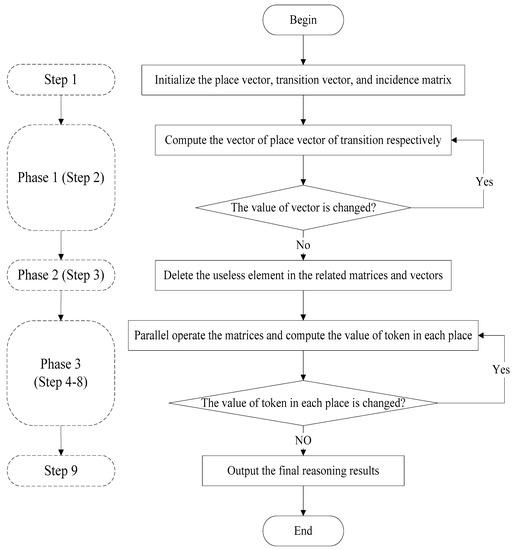
Figure 1.
Flowchart of the Proposed Algorithm.
According to the flowchart in Figure 1, it is easy to find that the entire algorithm could be divided into three phases. The Phases 1 and 2 execute the backward searching to find and remove the unnecessary places and transitions of the goal output place. Phase 3 executes the forward searching to calculate the truth degree of goal place based on the obtained simplest inference-path based on the Phases 1 and 2.
3.2. Implementation Steps
The implementation of the proposed algorithm could be separated into nine steps:
Step 1: Initialize the place vector, transition vector, and incidence matrix.
In the initial place vector , if place is the goal place, mark the correspondence as 1. Else, is marked as 0. Moreover, each element of the initial transition vector is marked as 0, where .
Step 2: Assume .
First, calculate , , and repeatedly until is satisfied.
Then, execute . (In vector , one represents the related places or transition of the goal place.)
Step 3: Make all locations of elements whose value is 0 in , and the location of elements whose value is 0 in . Then, using the proposed operators of delete rows and columns to update the input weighted matrix , output belief strength matrix , threshold vector , and fuzzy marking vector .
Step 4: Assume , . Then, execute .
Step 5: Execute , and judge whether . If it is true, it reveals that a new transition can be enabled in the reasoning process. Then, execute . Else, and move to Step 9.
Step 6: Execute , and judge whether . Then, Fire the related transition. Else, move to Step 9.
Step 7: Execute , where represents the belief strength of output place with the fired transition in Step 6.
Step 8: Execute to get the latest update belief strength of all places. Then, judge whether . If it is true, move to Step 9. Else, move to Step 4.
Step 9: The whole reasoning process is stopped, and the final result is recorded in .
4. Analysis
This section presents the theoretical analysis of the proposed algorithm from two different viewpoints: correctness and algorithm complexity.
4.1. Correctness
The analysis of correctness of the proposed algorithm is organized and based on two phases: backward reasoning phase and forward reasoning phase.
In the backward reasoning phase, means that is the goal in the initial place vector.
When , perform , . If and , then can be obtained ( means ). Then, is used to add the input transition of goal place into the transition vector .
In , is analyzed first. Assume , where . If and , then can be obtained where means . Hence, the function of is to add the input place of input transition of conclusion place into the vector . Furthermore, reflects the set of related places of the goal place .
In the repeated part of Figure 1, with the increasing of , the equations and , can also be easily understood based on the thinking of the situation .
Based on the analysis above, the correctness of backward reasoning phase has been proven. In comparison to the backward reasoning phase, the forward reasoning phase uses four equations to implement the reasoning process.
When , . is the input strength of each transition. Then, . is used to judge whether a new transition exists in the reasoning path. In addition, if there is a new transition, the equation will be used to update the newest data.
. is used to judge which transitions can be enabled. After firing the transition, is used to record the belief strength of output place related to the fired transition. To sum up, these equations in the forward reasoning phase are used to judge the transition that can be fired and implement the reasoning process step by step.
After analyzing the function of each equation in these phases, the correctness of the proposed algorithm has been proven.
4.2. Algorithm Complexity
The algorithm complexity is presented in two phases.
In the backward reasoning phase, the algorithm is used to analyze the worst situation where only one transition is added into the transition vector each time. In the repeat, no transition can be added into . exists at this time. Thus, the biggest circle number is . Accordingly, the matrix can implement parallel analysis and computation and the algorithm complexity of backward reasoning phase is .
After implementing the backward reasoning mechanism, the dimensions of the operational matrices are reduced to from , where are the number of irrelevant places or transitions.
In the forward reasoning phase, the algorithm complexity is related to the dimension of operational matrices. Thus, the algorithm complexity of forward reasoning algorithm is .
To conclude this section, the proposed algorithm is summarized into two situations as follows.
- In the worst situation, all places and transitions appear in the reasoning path. This means that the backward reasoning mechanism is out of work. The algorithm complexity of the proposed algorithm is .
- In other situations, the number of unconcerned places and transitions are and , and the algorithm complexity of the proposed algorithm is .
5. Case Study
In this section, a numerical case study is reported to demonstrate the whole reasoning process of the present reasoning algorithm, particularly the potential of the proposed method for simplifying the inference process and reducing the algorithm complexity based different appointed output places.
In the experiment, the FPN models adopted in this study should meet three requirements to reflect the algorithm feasibility. First, three types of FPN models are included in the model. Second, the model should contain two or more of the final conclusions (i.e., output places). Third, other special cases, such as a certain place where a pre-set is greater than or equal to two transitions or a subsequent place that is greater than or equal to two transitions, is considered. This study accordingly uses the fault diagnosis case for an integrated manufacturing system in the literature [26] to demonstrate the proposed decomposition of the algorithm.
The corresponding FPN model is generated as shown in Figure 2 and the meaning of each place is listed in Table 1.
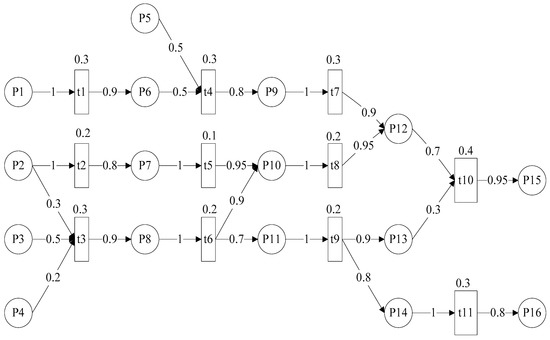
Figure 2.
The Fuzzy Petri net (FPN) of case study.

Table 1.
The meaning of each place of Figure 2.
5.1. Relevant Experimental Data of the Case Study
Assume the initial marking vector is defined as follows.
The and of the case study are illustrated as follows.
5.2. Experiments
According to the case study, two experiments are designed based on different appointed goal output place. In Experiment 1, the goal output place is . In Experiment 2, the goal output place is changed to .
5.2.1. Experiment One
Experiment 1 aims at trying to get the truth degree of in Figure 2.
The initial place vector and transition vector are demonstrated as follows.
After performing the backward reasoning phase, the relevant vectors and matrices are gained as follows.
According to the , the reasoning path of goal place is demonstrated as shown in Figure 3 after deleting the irrelevant element in FPN.
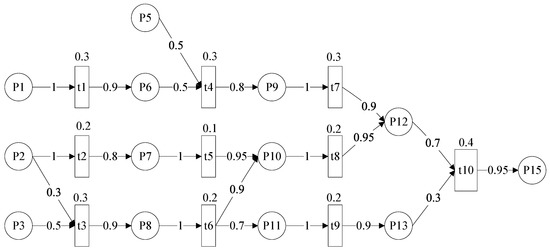
Figure 3.
The reasoning path of goal place .
After executing Phases 1 and 2 of the proposed algorithm, the subnet of the goal output place is obtained as shown in Figure 3. The related data (including vectors and matrices) are also modified based on the result of previous phases. The simplified data are given below.
Based on the modified data, the details of performing the forward reasoning strategy are demonstrated, as shown in Table 2 and Table 3, respectively.

Table 2.
The recovery procedure of output strength vector of Experiment 1.

Table 3.
The forward reasoning process of Experiment 1.
According to Table 3, it is easy to get that the final truth degree of is 0.582415 after repeating the inference process five times.
5.2.2. Experiment Two
Experiment 2 is meant to try to calculate the truth degree of another output place by using the same FPN model shown in Figure 2.
The initial place vector , transition vector are demonstrated as follows.
After performing the backward reasoning phase, the relevant vectors and matrices are gained as follows.
According to the , the reasoning path of goal place is demonstrated as shown in Figure 4 after deleting the irrelevant element in FPN.
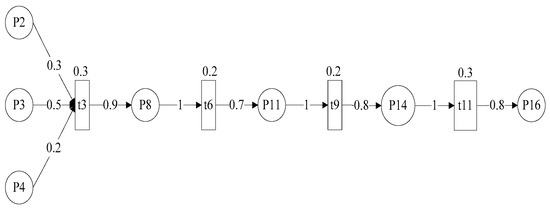
Figure 4.
The reasoning path of goal place .
After executing Phases 1 and 2 of the proposed algorithm, the subnet of the goal output place is obtained as shown in Figure 4. The related data (including vectors and matrices) are also modified based on the result of previous phases. The simplified data are given below.
Based on the modified data, the details of the forward reasoning are demonstrated, as shown in Table 4 and Table 5, respectively.

Table 4.
The recovery procedure of output strength vector of Experiment 2.

Table 5.
The forward reasoning process of Experiment 2.
According to Table 5, it is easy to get that the final truth degree of is 0.300384 after repeating the inference process five times.
5.3. Analysis of Experiments 1 and 2
The two experiments used the same FPN model to calculate the truth degree of different output places. Although these inferences are implemented under the same framework, the details of the inference are different. Table 6 illustrates the comparison of the two experiments from the viewpoint of the related operational matrices.

Table 6.
Comparison of Experiments.
In Table 6, it easily found that the scale of the operational matrices is compressed. In the case of Experiment 2, the scale of the original matrices and are 16 × 11 and is 11 × 16. In the backward reasoning phase, these matrices are unitized to seek the reasoning path for the goal place. Then, irrelevant places and transitions are deleted by implementing operators. Finally, the dimensions of related matrices are reduced from 14 × 10 and 10 × 14 to 7 × 4 and 4 × 6, because the forward reasoning phase is executed in the individual reasoning path as shown in Figure 4.
In the existing literature, the fault diagnosis mechanism using FPN algebra is that all elements (including places and transitions) of the FPN model are used to execute the fault diagnosis. However, with the rapidly increasing scale of FPN, the number of unrelated places and transitions of the goal outplace in a large-scale FPN is also increased. Hence, the biggest feature of the proposed algorithm is that the complexity of inference is adjusted by different goal places because of the removal of unnecessary places and transitions of the goal output places. The case study is a typical instance to indicate this advantage. Although these two experiments are implemented on the same FPN, the scales of related matrices are compressed from 16 × 11 and 11 × 16 to 7 × 4 and 4 × 7 based on the different reasoning paths.
In summary, the proposed mechanism will adjust the dimension of the related operational matrices and vectors in the reasoning process automatically because the individual reasoning path will be recognized based on different goal places. By implementing the fault diagnosis using large-scale FPNs, the inference process is more flexible and closer to human thinking
6. Conclusions
Focusing on the side-effect of state explosion issue of FPN, a bidirectional adaptive fault diagnosis algorithm has been presented in this paper to control the dimensions of the operational matrices and simplify the reasoning process by removing the irrelated elements (i.e., places and transitions) in a large-scale FPN model. In the proposed algorithm, the algorithm was implemented in three phases. Firstly, backward reasoning mechanism was executed to find the unconcerned places and transitions. Secondly, the delete row and column commands were used to compress the dimensional of the corresponding operational matrices. Finally, forward reasoning was implemented to calculate the truth degree of the goal place. After undergoing the three phases, a theoretical analysis was carried out to prove the feasibly and validity of the proposed algorithm from two aspects: correctness and algorithm complexity. Using the analysis, a case study of fault diagnosis was used to illustrate the whole implementation process. From the results of two experiments, it is easy to find that the proposed algorithm can overcome the state explosion issue effectively because the places and transitions that are not involved in the reasoning path will be removed automatically.
Author Contributions
K.-Q.Z. conceived and designed the experiments; W.-H.G. performed the experiments; L.-P.M. analyzed the data; K.-Q.Z. and A.M.Z. wrote the paper.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Nos. 61741205, 61462029 and 61363073), the Research Foundation of Education Bureau of Hunan Province, China (No. 16C1314) and Post-doctoral Science Foundation of Central South University (No. 175605).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Burrell, P.; Inman, D. An expert system for the analysis of faults in an electricity supply network: Problems and achievements. Comput. Ind. 1998, 37, 113–123. [Google Scholar] [CrossRef]
- Liu, S.C.; Liu, S.Y. An efficient expert system for machine fault diagnosis. Int. J. Adv. Manuf. Technol. 2003, 21, 691–698. [Google Scholar] [CrossRef]
- Liu, H.; Gegov, A.; Cocea, M. Rule-based systems: A granular computing perspective. Granul. Comput. 2016, 1, 259–274. [Google Scholar] [CrossRef]
- Ahmad, S.S.S.; Pedrycz, W. The development of granular rule-based systems: A study in structural model compression. Granul. Comput. 2017, 2, 1–12. [Google Scholar] [CrossRef]
- Huang, Y.; McMurran, R.; Dhadyalla, G.; Jones, R.P. Probability based vehicle fault diagnosis: Bayesian network method. J. Intell. Manuf. 2008, 19, 301–311. [Google Scholar] [CrossRef]
- Alessandri, A. Fault diagnosis for nonlinear systems using a bank of neural estimators. Comput. Ind. 2003, 52, 271–289. [Google Scholar] [CrossRef]
- Chen, K.Y.; Lim, C.P.; Lai, W.K. Application of a neural fuzzy system with rule extraction to fault detection and diagnosis. J. Intell. Manuf. 2005, 16, 679–691. [Google Scholar] [CrossRef]
- Lai, Y.F.; Chen, M.Y.; Chiang, H.S. Constructing the lie detection system with fuzzy reasoning approach. Granul. Comput. 2017, 3, 169–176. [Google Scholar] [CrossRef]
- Lukovac, V.; Pamučar, D.; Popović, M.; Đorović, B. Portfolio model for analyzing human resources: An approach based on neuro-fuzzy modeling and the simulated annealing algorithm. Expert Syst. Appl. 2017, 90, 318–331. [Google Scholar] [CrossRef]
- Pamučar, D.; Ljubojević, S.; Kostadinović, D.; Đorović, B. Cost and risk aggregation in multi-objective route planning for hazardous materials transportation—A neuro-fuzzy and artificial bee colony approach. Expert Syst. Appl. 2016, 65, 1–15. [Google Scholar] [CrossRef]
- Pamučar, D.; Vasin, L.; Atanasković, P.; Miličić, M. Planning the City Logistics Terminal Location by Applying the Green-Median Model and Type-2 Neurofuzzy Network. Comput. Intell. Neurosci. 2016, 2016, 6972818. [Google Scholar]
- Mortada, M.A.; Yacout, S.; Lakis, A. Fault diagnosis in power transformers using multi-class logical analysis of data. J. Intell. Manuf. 2013, 25, 1429–1439. [Google Scholar] [CrossRef]
- Reyes, A.; Yu, H.; Kelleher, G.; Lloyd, S. Integrating Petri Nets and hybrid heuristic search for the scheduling of FMS. Comput. Ind. 2002, 47, 123–138. [Google Scholar] [CrossRef]
- Cecil, J.A.; Srihari, K.; Emerson, C.R. A review of Petri-net applications in manufacturing. Int. J. Adv. Manuf. Technol. 1992, 7, 168–177. [Google Scholar] [CrossRef]
- Luo, X.; Kezunovic, M. Implementing fuzzy Reasoning Petri-Nets for fault section estimation. IEEE Trans. Power Deliv. 2008, 23, 676–685. [Google Scholar] [CrossRef]
- Hu, H.; Li, Z.; Al-Ahmari, A. Reversed fuzzy Petri nets and their application for fault diagnosis. Comput. Ind. Eng. 2011, 60, 505–510. [Google Scholar] [CrossRef]
- Yang, B.; Li, H. A novel dynamic timed fuzzy Petri nets modeling method with applications to industrial processes. Expert Syst. Appl. 2018, 97, 276–289. [Google Scholar] [CrossRef]
- Pan, H.L.; Jiang, W.R.; He, H.H. The Fault Diagnosis Model of Flexible Manufacturing System Workflow Based on Adaptive Weighted Fuzzy Petri Net. Adv. Sci. Lett. 2012, 11, 811–814. [Google Scholar] [CrossRef]
- Amin, M.; Shebl, D. Reasoning dynamic fuzzy systems based on adaptive fuzzy higher order Petri nets. Inf. Sci. 2014, 286, 161–172. [Google Scholar] [CrossRef]
- Liang, W.; An, R. Unobservable fuzzy petri net diagnosis technique. Aircr. Eng. Aerosp. Technol. 2013, 85, 215–221. [Google Scholar]
- Liu, H.C.; Lin QL Ren, M.L. Fault diagnosis and cause analysis using fuzzy evidential reasoning approach and dynamic adaptive fuzzy Petri nets. Comput. Ind. Eng. 2013, 66, 899–908. [Google Scholar] [CrossRef]
- Wang, W.M.; Peng, X.; Zhu, G.N.; Hu, J.; Peng, Y.H. Dynamic representation of fuzzy knowledge based on fuzzy petri net and genetic-particle swarm optimization. Expert Syst. Appl. 2014, 41, 1369–1376. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Tian, G. Determining Truth Degrees of Input Places in Fuzzy Petri Nets. IEEE Trans. Syst. Man Cyber. Syst. 2017, 47, 3425–3431. [Google Scholar] [CrossRef]
- Looney, C. G Fuzzy Petri nets for rule-based decision making. IEEE Trans. Syst. Man Cyber. 1988, 18, 178–183. [Google Scholar] [CrossRef]
- Zhou, K.Q.; Zain, A.M. Fuzzy Petri Nets and Industrial Applications: A Review. Artif. Intell. Rev. 2016, 45, 405–446. [Google Scholar] [CrossRef]
- Chen, S.M. Weighted fuzzy reasoning using Weighted Fuzzy Petri Nets. IEEE Trans. Knowl. Data Eng. 2002, 14, 386–397. [Google Scholar] [CrossRef]
- Liu, Z.; Li, H.; Zhou, P. Towards timed fuzzy Petri net algorithms for chemical abnormality monitoring. Expert Syst. Appl. 2011, 38, 9724–9728. [Google Scholar] [CrossRef]
- Wai, R.J.; Liu, C.M. Design of dynamic petri recurrent fuzzy neural network and its application to path-tracking control of nonholonomic mobile robot. IEEE Trans. Ind. Electron. 2009, 56, 2667–2683. [Google Scholar]
- Chen, S.M.; Ke, J.S.; Chang, J.F. Knowledge representation using fuzzy Petri nets. IEEE Trans. Knowl. Data Eng. 1990, 2, 311–319. [Google Scholar] [CrossRef]
- Gao, M.M.; Wu, Z.M.; Zhou, M.C. A Petri net-based formal reasoning algorithm for fuzzy production rule-based systems. IEEE Int. Conf. Syst. Man Cyber. 2000, 4, 3093–3097. [Google Scholar]
- Gao, M.M.; Zhou, M.C.; Huang, X.G.; Wu, Z.M. Fuzzy reasoning Petri nets. IEEE Trans. Syst. Man Cyber. Part A Syst. Hum. 2003, 33, 314–324. [Google Scholar]
- Liu, H.C.; Luan, X.; Li, Z.; Wu, J. Linguistic Petri Nets Based on Cloud Model Theory for Knowledge Representation and Reasoning. IEEE Trans. Knowl. Data Eng. 2018, 30, 717–728. [Google Scholar] [CrossRef]
- Guo, Y.; Meng, X.; Wang, D.; Meng, T.; Liu, S.; He, R. Comprehensive risk evaluation of long-distance oil and gas transportation pipelines using a fuzzy petri net model. J. Nat. Gas Sci. Eng. 2016, 33, 18–29. [Google Scholar] [CrossRef]
- Li, H.; You, J.X.; Liu, H.C.; Tian, G. Acquiring and Sharing Tacit Knowledge Based on Interval 2-Tuple Linguistic Assessments and Extended Fuzzy Petri Nets. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2018, 26, 43–65. [Google Scholar] [CrossRef]
- Zhou, K.Q.; Zain, A.M.; Mo, L.P. A decomposition algorithm of fuzzy Petri net using an index function and incidence matrix. Expert Syst. Appl. 2015, 42, 3980–3990. [Google Scholar] [CrossRef]
- Zhou K, Q.; Mo L, P.; Jin, J.; Zain, A.M. An equivalent generating algorithm to model fuzzy Petri net for knowledge-based system. J. Intell. Manuf. 2017, 1–12. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Li, Z.; Tian, G. Fuzzy Petri nets for knowledge representation and reasoning: A literature review. Eng. Appl. Artif. Intell. 2017, 60, 45–56. [Google Scholar] [CrossRef]
- Zhang, J.H.; Xia, J.J.; Garibaldi, J.M.; Groumpos, P.P.; Wang, R.B. Modeling and control of operator functional state in a unified framework of fuzzy inference petri nets. Comput. Methods Prog. Biomed. 2017, 144, 147–163. [Google Scholar] [CrossRef] [PubMed]
- Nazareth, D.L. Investigating the applicability of Petri nets for rule-based system verification. IEEE Trans. Knowl. Data Eng. 1993, 5, 402–415. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).