Local Casimir Effect for a Scalar Field in Presence of a Point Impurity

Abstract

The Casimir effect for a scalar field in presence of delta-type potentials has been investigated for a long time in the case of surface delta functions, modelling semi-transparent boundaries. More recently Albeverio, Cacciapuoti, Cognola, Spreafico and Zerbini have considered some configurations involving delta-type potentials concentrated at points of ${\mathbb{R}}^3$; in particular, the case with an isolated point singularity at the origin can be formulated as a field theory on ${\mathbb{R}}^3\backslash \left\{\mathbf{0}\right\}$, with self-adjoint boundary conditions at the origin for the Laplacian. However, the above authors have discussed only global aspects of the Casimir effect, focusing their attention on the vacuum expectation value (VEV) of the total energy. In the present paper we analyze the local Casimir effect with a point delta-type potential, computing the renormalized VEV of the stress-energy tensor at any point of ${\mathbb{R}}^3\backslash \left\{\mathbf{0}\right\}$; for this purpose we follow the zeta regularization approach, in the formulation already employed for different configurations in previous works of ours.

1. Introduction

The main characters in investigations on vacuum effects of the Casimir type are the boundary conditions assumed for the quantum field and/or the external potential possibly acting on the field itself [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. The boundary conditions are typically employed to account for the presence of perfectly conducting walls, or perfectly reflecting mirrors. On the other hand, the interpretation of the external potentials depends essentially on their structure; in many cases these potentials can be viewed as modelling some type of confinement, softer than the one given by sharp boundaries.

Nowadays, a quite remarkable literature is available, regarding Casimir-type settings with external delta-type potentials. Such models can be viewed as limit cases of configurations with sharply peaked (but regular) potentials.

Most of the literature considers the case of surface delta functions, concentrated on supports of co-dimension 1; these are commonly interpreted as semi-transparent walls, inducing a partial confinement of the quantum field. The first ones to investigate a Casimir configuration of this kind were probably Mamaev and Trunov [16], who computed the renormalized VEV of the energy density for a massive scalar field in presence of delta potentials concentrated on two parallel plates. Variations of the same model, concerning both a scalar and a spinor field, were later examined by Bordag, Hennig and Robaschik in [17]. In the last two decades, there has been a renewed interest on surface delta potentials: see, e.g., [18,19,20,21,22,23,24,25,26,27].

The Casimir effect in presence of point delta-type potentials (concentrated on supports of co-dimension 3) has been studied only in more recent times, and the existing literature is not so wide; these configurations are typically interpreted in terms of point-like impurities. In [28], Spreafico and Zerbini proposed a general setting to renormalize the relative partition function of a finite-temperature quantum field theory (on flat or even on curved, ultrastatic spacetimes with noncompact spatial section); in this work the authors discussed, as an application, the total Casimir energy at finite or zero temperature for a massless scalar field (in flat spacetime), in presence of one or two point-like impurities. In [29] Albeverio, Cognola, Spreafico and Zerbini computed the renormalized, relative partition function and the Casimir force for a massless scalar field in presence of an infinite conducting plate and of a point-like impurity, placed outside the plate. A similar analysis was performed in [30] by Albeverio, Cacciapuoti and Spreafico, who determined the renormalized, relative partition function for a massless scalar field in presence of a point-like impurity and of a Coulomb potential centered at the same point.

From a mathematical point of view, the description of delta-type potentials can be given in terms of suitable boundary conditions across the support of the delta functions, defining a self-adjoint realization of the Laplace operator. This approach has been developed for delta functions concentrated on surfaces, curves or points in ${\mathbb{R}}^3$. Therefore, a problem involving $-\Delta$ (the opposite of the Laplacian) plus a delta-type potential is reformulated with full analytical rigor as a problem in the region outside the singularity, where the fundamental operator is $-\Delta$ with the above mentioned boundary conditions. When this setting was originally devised, the interest in delta-type potentials was not motivated by their action on quantum fields but, rather, by non-relativistic quantum mechanics; the aim was to define rigorously Schrödinger operators with delta-type potentials and to develop, in particular, the corresponding scattering theory. Of course, the operator $-\Delta$ plus a delta-type potential has a different status in quantum field theory, where it can appear in the spatial part of the field equations.

In the case of a point delta-type potential on ${\mathbb{R}}^3$, the rigorous definition of the corresponding operator in terms of boundary conditions for the Laplacian was first given in a seminal paper of Berezin and Faddeev [31]; a standard reference on this topic, using systematically the language of Sobolev spaces, is the book by Albeverio et al. [32]. To implement this setting, a price must be paid: one must think the potential as the product of the point delta function by an infinitesimally small coupling constant. It is customary to interpret the infinitesimal nature of this constant as the effect of some “renormalization” of the interaction, an idea suggested by the construction of [31].

Before proceeding, let us mention that general delta-type potentials have also been treated within the framework of much more general mathematical theories; in particular, they have been described in terms of singular perturbations of self-adjoint operators in scales of Hilbert spaces by Albeverio et al. [33,34] and by means of Krein-like resolvent formulas by Posilicano et al. [35,36].

In the present work, we analyze the Casimir physics of a massless scalar field in presence of a point-like impurity. This configuration is closely related to the settings of [28,29,30]; however these papers discussed only global observables, like the total energy. On the contrary, our analysis is focused on local aspects; more precisely, we compute the renormalized VEV of the stress-energy tensor at any space point outside the impurity. To treat the point delta-type potential, we stick to the standard setting of [31,32]. Besides, to renormalize the stress-energy VEV we follow the local zeta regularization approach; here, a regularization is introduced for the field theory depending an a complex parameter, and the renormalization of local observables is defined in terms of the analytic continuation with respect to this parameter.

Zeta regularization is an elegant strategy to give meaning to the divergent expressions appearing in naïve manipulations of quantum field theory; its application to the local observables of quantum fields was proposed by Dowker and Critchley [37], Hawking [38] and Wald [39], and especially supported by Actor, Cognola, Dowker, Elizalde, Moretti, Zerbini et al., who must be credited with developing this idea in a systematic way (see [40,41,42,43] and the references cited therein). The same ideas have become more popular in the treatment of global observables (such as the total energy), resulting into an abundant literature (see, e.g., [44,45,46] and references therein); notably, global zeta regularization appears in all the previously cited works on field theory with point-like singularities. In our recent book [47], we have proposed a formulation of the local (and global) zeta techniques for a scalar field, based on canonical quantization and on the introduction of a suitably regularized field operator depending on a parameter $u\in \mathbb{C}$; the renormalization of local (or global) observables is defined in terms of the analytic continuation to a neighborhood of the point $u=0$, formally corresponding to the unregularized field operator.

From the very beginning of zeta regularization theory, it was understood that the analytic continuation required by this approach is deeply related to certain integral kernels associated to the fundamental operator of the field theory, i.e., $-\Delta$ plus the possibly given external potential. Here we mention, in particular, the Dirichlet and heat kernels which correspond, respectively, to the complex powers and to the exponential of the fundamental operator; these facts are relevant even for the results described in the present paper.

Let us describe the organization of the present work. In Section 2 we summarize the local zeta regularization scheme for the stress-energy VEV of a scalar field and its connection to the above mentioned kernels, following systematically [47]; in particular, we introduce the fundamental operator $\mathcal{A}$ associated to the field equation and account for the possibility to replace it with the modified version ${\mathcal{A}}_{\epsilon }:=\mathcal{A}+{\epsilon }^2$ (depending on the “infrared cutoff” $\epsilon >0$, which should be ultimately sent to zero). In Section 3 we consider on ${\mathbb{R}}^3$ the operator $-\Delta$ plus a point delta-type potential concentrated at the origin; following [32], we review the rigorous description of this configuration in terms of the fundamental operator $\mathcal{A}=-\Delta$ on $\Omega :={\mathbb{R}}^3\backslash \left\{\mathbf{0}\right\}$ (with suitable boundary conditions at the origin) and introduce as well its modified version ${\mathcal{A}}_{\epsilon }$. In Section 4 we report an explicit expression for the heat kernel of ${\mathcal{A}}_{\epsilon }$, following trivially from a result of [48] on the same kernel for $\mathcal{A}$; this expression is rephrased in Section 5 in terms of a system of spherical coordinates, to be used on $\Omega$ up to the end of the paper.

In Section 6 we determine the zeta-regularized stress-energy VEV $⟨0|{\widehat{T}}_{\mu \nu }^{u,\epsilon }|0⟩$ for our field theory with point singularity; more precisely, we derive an integral representation for this VEV using the previously mentioned expression for the heat kernel and some known relations involving the Dirichlet kernel of ${\mathcal{A}}_{\epsilon }$. This representation of the stress-energy VEV, depending on the regulating parameter $u\in \mathbb{C}$ and on the infrared cutoff $\epsilon >0$, is reformulated in Section 7 in terms of Bessel functions; this also allows to determine the analytic continuation of the map $u\mapsto ⟨0|{\widehat{T}}_{\mu \nu }^{u,\epsilon }|0⟩$ to a meromorphic function on the whole complex plane, possessing a simple pole at $u=0$. We compute the regular part of $⟨0|{\widehat{T}}_{\mu \nu }^{u,\epsilon }|0⟩$ at this point in Section 8 and subsequently evaluate the limit $\epsilon \to 0^{+}$ of the resulting expression in Section 9; according to a general prescription of [47], these operations determine the renormalized stress-energy VEV $⟨0|{\widehat{T}}_{\mu \nu }{|0⟩}_{ren}$. The final expressions thus obtained for the non-vanishing components of $⟨0|{\widehat{T}}_{\mu \nu }{|0⟩}_{ren}$ are reported in the conclusive Section 10; therein, we also analyze the asymptotic behavior of the renormalized stress-energy VEV in various regimes, discussing especially the expansions for small and large distances from the point impurity (see, respectively, Section 10.1 and Section 10.2).

Some of the computations required by this paper were assisted by the symbolic mode of Mathematica.

2. The General Setting

Quantum field theory and the fundamental operator. In the present section we briefly recall the general setting of [47] for the quantum theory of a scalar field on a space domain with boundary conditions, possibly in presence of a static external potential; this formulation will be methodically employed in the sequel.

We use natural units, so that $c=1$ and $\hslash =1$, and work in $(1+3)$-dimensional Minkowski spacetime; this is identified with ${\mathbb{R}}^4=\mathbb{R}\times {\mathbb{R}}^3$ using a set of inertial coordinates

$$x={\left(x^{\mu }\right)}_{\mu =0,1,2,3}\equiv (x^0,{(x^i)}_{i=1,2,3})\equiv (t,\mathbf{x}),$$

(1)

so that the spacetime line element reads

$$d{s}^2={\eta }_{\mu \nu }d{x}^{\mu }d{x}^{\nu },\left({\eta }_{\mu \nu }\right):=\mathrm{diag}(-1,1,1,1).$$

(2)

We assume that, in this coordinate system, the spatial domain for the field consists of a fixed open subset $\Omega$ of ${\mathbb{R}}^3$.

To proceed, we consider a canonically quantized, neutral scalar field $\widehat{\varphi }:\mathbb{R}\times \Omega \to {\mathcal{L}}_{sa}\left(\mathfrak{F}\right)$, $(t,\mathbf{x})\mapsto \widehat{\varphi }(t,\mathbf{x})$ ($\mathfrak{F}$ is the Fock space and ${\mathcal{L}}_{sa}\left(\mathfrak{F}\right)$ are the self-adjoint operators on it); this can interact with a static background potential $V:\Omega \to \mathbb{R}$, $\mathbf{x}\mapsto V\left(\mathbf{x}\right)$. We indicate with $|0⟩\in \mathfrak{F}$ the vacuum state and we systematically use the acronym VEV for “vacuum expectation value”. We assume the field $\widehat{\varphi }$ to fulfill the Klein-Gordon-like equation

$$(-{\partial }_{tt}-\Delta +V)\widehat{\varphi }=0,$$

(3)

with given boundary conditions on $\partial \Omega$ (here and in the sequel, $\Delta$ is the 3-dimensional Laplacian). The operator

$$\mathcal{A}:=-\Delta +V$$

(4)

with the prescribed boundary conditions will be called the fundamental operator of the system. We require $\mathcal{A}$ to be a self-adjoint, non-negative operator in $L^2(\Omega )$; obviously enough, “$\mathcal{A}$ non-negative” means that $\mathcal{A}$ has spectrum $\sigma \left(\mathcal{A}\right)\subset [0,+\infty )$. These conditions of self-adjointness and non-negativity are in fact limitations about the admissible boundary conditions and potentials.

The operator $\mathcal{A}$ considered in this work corresponds, morally, to a delta-type potential placed at the origin $\mathbf{x}=\mathbf{0}$, multiplied by an infinitesimally small coupling constant. According to the already cited paper of Berezin and Faddeev [31], this configuration can be described rigorously in terms of the space domain $\Omega :={\mathbb{R}}^3\backslash \left\{\mathbf{0}\right\}$, defining $\mathcal{A}$ to be the operator $-\Delta$ on $\Omega$ with suitable boundary conditions at the origin (and with no external potential V); the basic features of $\mathcal{A}$ will be reviewed in Section 3. In the remainder of the present Section 2 we will not focus on this specific configuration, referring again to a general field theory as in [47].

Zeta regularization and renormalization of the stress-energy VEV. A quantum field theory of the type considered in [47] is typically affected by ultraviolet divergences: these appear in the computation of VEVs for many significant observables, in particular for the stress-energy tensor. To treat these divergences, one can first regularize the field operator, and then set up a suitable renormalization procedure; the zeta approach employed in [47] and in the present work is a technique allowing to achieve these goals.

The field regularization illustrated in [47] requires a self-adjoint, strictly positive operator on $L^2(\Omega )$; the last condition means that the spectrum of the operator must be contained in $[{\epsilon }^2,+\infty )$ for some $\epsilon >0$. When the fundamental operator $\mathcal{A}$ is strictly positive, it can be used directly for the purpose of regularization; however, in many interesting cases (including the one considered in the present work), the spectrum $\sigma \left(\mathcal{A}\right)$ contains a right neighborhood of the zero. In these cases, one can replace $\mathcal{A}$ with the modified fundamental operator

$${\mathcal{A}}_{\epsilon }:=\mathcal{A}+{\epsilon }^2(\epsilon >0)$$

(5)

and ultimately take the limit $\epsilon \to 0^{+}$. The parameter $\epsilon$ introduced in Equation (5) can be interpreted as an infrared cutoff; note that $\epsilon$ is dimensionally a mass in our units with $c=\hslash =1$.

After defining the operator (5), we introduce the zeta-regularized field operator

$${\widehat{\varphi }}_{ϵ}^u:={\left({\kappa }^{-2}{\mathcal{A}}_{\epsilon }\right)}^{-u/4}\widehat{\varphi },$$

(6)

where $u\in \mathbb{C}$ is the regulating parameter and $\kappa >0$ is a “mass scale” parameter; note that ${\widehat{\varphi }}_{ϵ}^u{|}_{u=0}=\widehat{\varphi }$, at least formally. We use the above regularized field operator to define the zeta-regularized stress-energy tensor

$${\widehat{T}}_{\mu \nu }^{u,\epsilon }:=\left(1-2\xi \right){\partial }_{\mu }{\widehat{\varphi }}_{ϵ}^u\circ {\partial }_{\nu }{\widehat{\varphi }}_{ϵ}^u-\left(\frac{1}{2}-2\xi \right){\eta }_{\mu \nu }\left({\partial }^{\varrho }{\widehat{\varphi }}_{ϵ}^u{\partial }_{\varrho }{\widehat{\varphi }}_{ϵ}^u+V{({\widehat{\varphi }}_{ϵ}^u)}^2\right)-2\xi {\widehat{\varphi }}_{ϵ}^u\circ {\partial }_{\mu \nu }{\widehat{\varphi }}_{ϵ}^u.$$

(7)

Here: $\xi \in \mathbb{R}$ is an assigned dimensionless parameter; $A\circ B:=(1/2)(AB+BA)$ for all linear operators $A,B$ on $\mathfrak{F}$; all the bilinear terms in ${\widehat{\varphi }}_{ϵ}^u$ are evaluated on the diagonal (e.g., ${\partial }_{\mu }{\widehat{\varphi }}_{ϵ}^u\circ {\partial }_{\nu }{\widehat{\varphi }}_{ϵ}^u$ indicates the map $x\in \mathbb{R}\times \Omega \mapsto {\partial }_{\mu }{\widehat{\varphi }}_{ϵ}^u\left(x\right)\circ {\partial }_{\nu }{\widehat{\varphi }}_{ϵ}^u\left(x\right)$); $V{({\widehat{\varphi }}_{ϵ}^u)}^2$ stands for the map $x\equiv (t,\mathbf{x})\mapsto V\left(\mathbf{x}\right){\widehat{\varphi }}_{ϵ}^u{\left(x\right)}^2$.

The VEV $⟨0|{\widehat{T}}_{\mu \nu }^{u,\epsilon }|0⟩$ is well defined and analytic for $\epsilon >0$ and $Reu$ large enough; when the map $u\mapsto ⟨0|{\widehat{T}}_{\mu \nu }^{u,\epsilon }|0⟩$ can be analytically continued to a neighborhood of $u=0$ (possibly, with a singularity at 0), we define the renormalized stress-energy VEV as [47]

$$⟨0|{\widehat{T}}_{\mu \nu }{|0⟩}_{ren}:=\underset{\epsilon \to 0^{+}}{lim}RP{|}_{u=0}⟨0|{\widehat{T}}_{\mu \nu }^{u,\epsilon }|0⟩,$$

(8)

where $RP$ indicates the regular part of the Laurent expansion near $u=0$ (Consider a complex-valued analytic function $u\mapsto \mathcal{F}\left(u\right)$, defined in a complex neighborhood of $u=0$ except, possibly, the origin; then, $\mathcal{F}$ has Laurent expansion $\mathcal{F}\left(u\right)={\sum }_{k=-\infty }^{+\infty }{\mathcal{F}}_k{u}^k$. We define the regular part of $\mathcal{F}$ near $u=0$ to be $\left(RP\mathcal{F}\right)\left(u\right):={\sum }_{k=0}^{+\infty }{\mathcal{F}}_k{u}^k$; in particular, $RP{|}_{u=0}\mathcal{F}={\mathcal{F}}_0$). In Equation (8), taking the regular part in u amounts to renormalize the ultraviolet divergences, which are the harder problem to be solved; then the cutoff $\epsilon$ associated to the milder, infrared pathologies is simply removed taking its zero limit.

For a discussion on the role of the parameter $\xi$ appearing in Equation (7) and in the related VEVs we refer to [47] (see, especially, Appendix A and references therein). Here we limit ourselves to mention that the conformal invariance properties of the stress-energy tensor can be discussed and yield a natural decomposition of the form

$$⟨0|{\widehat{T}}_{\mu \nu }{|0⟩}_{ren}=T_{\mu \nu }^{(◊)}+\left(\xi -{\xi }_c\right)T_{\mu \nu }^{(\blacksquare )},{\xi }_c:=\frac{1}{6}.$$

(9)

The functions $T_{\mu \nu }^{(◊)}$, $T_{\mu \nu }^{(\blacksquare )}$ in Equation (9) are referred to, respectively, as the conformal and non-conformal parts of the stress-energy VEV (and ${\xi }_c$ is called the critical value). Of course, if we have $⟨0|{\widehat{T}}_{\mu \nu }{|0⟩}_{ren}$ for any value of $\xi$, we obtain its conformal and non-conformal parts with the prescriptions $T_{\mu \nu }^{(◊)}=⟨0|{\widehat{T}}_{\mu \nu }{|0⟩}_{ren}{|}_{\xi ={\xi }_c}$ and $T_{\mu \nu }^{(\blacksquare )}=\frac{1}{{\xi }_c}(T_{\mu \nu }^{(◊)}-⟨0|{\widehat{T}}_{\mu \nu }{|0⟩}_{ren}{|}_{\xi =0})$.

Integral kernels. For the implementation of the previous scheme, it is essential to point out the relations between the regularized stress-energy VEV and some integral kernels [47]; in order to illustrate them, it is convenient to recall some basic facts about such kernels.

In general, given a linear operator $\mathcal{B}:f\mapsto \mathcal{B}f$ acting on $L^2(\Omega )$, the integral kernel of $\mathcal{B}$ is the unique (generalized) function $\Omega \times \Omega \to \mathbb{C}$, $(\mathbf{x},\mathbf{y})\mapsto \mathcal{B}(\mathbf{x},\mathbf{y})$ such that $\left(\mathcal{B}f\right)\left(\mathbf{x}\right)={\int }_{\Omega }d\mathbf{y}\mathcal{B}(\mathbf{x},\mathbf{y})f\left(\mathbf{y}\right)$ ($\mathbf{x}\in \Omega$).

In particular, let $\mathcal{A}$ be a strictly positive self-adjoint operator in $L^2(\Omega )$ and consider the complex power ${\mathcal{A}}^{-s}$, with exponent $s\in \mathbb{C}$; the corresponding kernel $(\mathbf{x},\mathbf{y})\mapsto {\mathcal{A}}^{-s}(\mathbf{x},\mathbf{y})$ is called the s-th Dirichlet kernel of $\mathcal{A}$. For $\mathcal{A}$ strictly positive (or even non negative), we can define the corresponding heat semigroup ${\left(e^{-\mathfrak{t}\mathcal{A}}\right)}_{\mathfrak{t}\in [0,+\infty )}$; the mapping $(\mathfrak{t},\mathbf{x},\mathbf{y})\mapsto e^{-\mathfrak{t}\mathcal{A}}(\mathbf{x},\mathbf{y})$ is called the heat kernel of $\mathcal{A}$ (the variable $\mathfrak{t}$ must not be confused with the time coordinate t). The Mellin-type integral representation ${\mathcal{A}}^{-s}(\mathbf{x},\mathbf{y})=$$\Gamma {\left(s\right)}^{-1}{\int }_0^{+\infty }d\mathfrak{t}{\mathfrak{t}}^{s-1}{e}^{-\mathfrak{t}\mathcal{A}}(\mathbf{x},\mathbf{y})$ holds true for all $s\in \mathbb{C}$ such that the previous integral converges.

Now, let us return to the quantum field theory of the previous paragraphs; this has important connections with the Dirichlet and heat kernels of the operator $\mathcal{A}={\mathcal{A}}_{\epsilon }$. In fact, it can be shown that the components of the regularized stress-energy VEV are completely determined by the Dirichlet kernel ${\mathcal{A}}_{\epsilon }^{-s}(\mathbf{x},\mathbf{y})$ via the following relations, where $i,j,\ell \in \{1,2,3\}$ are spatial indexes and summation over repeated indexes is understood:

$$\begin{array}{c}{\displaystyle ⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{x}\right)|0⟩=}\\ {\displaystyle {\kappa }^u{\left[\left(\frac{1}{4}+\xi \right){\mathcal{A}}_{\epsilon }^{-\frac{u-1}{2}}(\mathbf{x},\mathbf{y})+\left(\frac{1}{4}-\xi \right)\left({\partial }^{x^{\ell }}{\partial }_{y^{\ell }}+V\left(\mathbf{x}\right)\right){\mathcal{A}}_{\epsilon }^{-\frac{u+1}{2}}(\mathbf{x},\mathbf{y})\right]}_{\mathbf{y}=\mathbf{x}};}\end{array}$$

(10)

$$⟨0|{\widehat{T}}_{i0}^{u,\epsilon }\left(\mathbf{x}\right)|0⟩=⟨0|{\widehat{T}}_{0i}^{u,\epsilon }\left(\mathbf{x}\right)|0⟩=0;$$

(11)

$$\begin{array}{c}{\displaystyle ⟨0|{\widehat{T}}_{ij}^{u,\epsilon }\left(\mathbf{x}\right)|0⟩=⟨0|{\widehat{T}}_{ji}^{u,\epsilon }\left(\mathbf{x}\right)|0⟩=}\\ {\displaystyle {\kappa }^u\left[\left(\frac{1}{4}-\xi \right){\eta }_{ij}\left({\mathcal{A}}_{\epsilon }^{-\frac{u-1}{2}}(\mathbf{x},\mathbf{y})-\left({\partial }^{x^{\ell }}{\partial }_{y^{\ell }}+V\left(\mathbf{x}\right)\right){\mathcal{A}}_{\epsilon }^{-\frac{u+1}{2}}(\mathbf{x},\mathbf{y})\right)+\right.}\\ {\displaystyle {\left.+\left(\left(\frac{1}{2}-\xi \right){\partial }_{x^i{y}^j}-\xi {\partial }_{x^i{x}^j}\right){\mathcal{A}}_{\epsilon }^{-\frac{u+1}{2}}(\mathbf{x},\mathbf{y})\right]}_{\mathbf{y}=\mathbf{x}}}\end{array}$$

(12)

($⟨0|{\widehat{T}}_{\mu \nu }^{u,\epsilon }\left(\mathbf{x}\right)|0⟩$ is short for $⟨0|{\widehat{T}}_{\mu \nu }^{u,\epsilon }(t,\mathbf{x})|0⟩$; indeed, the VEV does not depend on the time coordinate t). In a number of interesting cases, explicit expressions are available for the heat kernel $e^{-\mathfrak{t}\mathcal{A}}(\mathbf{x},\mathbf{y})$ of the fundamental operator $\mathcal{A}$. Recalling Equation (5), we obtain from here the heat kernel of the modified fundamental operator ${\mathcal{A}}_{\epsilon }$ via the identity

$$e^{-\mathfrak{t}{\mathcal{A}}_{\epsilon }}(\mathbf{x},\mathbf{y})=e^{-{\epsilon }^2\mathfrak{t}}{e}^{-\mathfrak{t}\mathcal{A}}(\mathbf{x},\mathbf{y}).$$

(13)

Subsequently, we can determine the Dirichlet kernels appearing in Equations (10)–(12) via the Mellin relation

$${\mathcal{A}}_{\epsilon }^{-s}(\mathbf{x},\mathbf{y})=\frac{1}{\Gamma \left(s\right)}{\int }_0^{+\infty }d\mathfrak{t}{\mathfrak{t}}^{s-1}{e}^{-\mathfrak{t}{\mathcal{A}}_{\epsilon }}(\mathbf{x},\mathbf{y}).$$

(14)

Curvilinear coordinates. In order to fit the symmetries of the specific problem under analysis, it is often useful to consider on $\Omega$ a set of curvilinear coordinates $\mathbf{q}\equiv {\left(q^i\right)}_{i=1,2,3}$ in place of the Cartesian coordinates $\mathbf{x}=\left(x^i\right)$; this induces a set of coordinates $q\equiv \left(q^{\mu }\right)\equiv (t,\mathbf{q})$ on Minkowski spacetime. The line elements of $\Omega$ and of Minkowski spacetime read, respectively,

$$d{\ell }^2=a_{ij}\left(\mathbf{q}\right)d{q}^{i}d{q}^j,d{s}^2=-d{t}^2+d{\ell }^2=g_{\mu \nu }\left(q\right)d{q}^{\mu }d{q}^{\nu },$$

(15)

where $a_{ij}\left(\mathbf{q}\right)$ is a suitable symmetric and positive definite matrix, while

$$g_{00}\left(q\right):=-1,g_{0i}\left(q\right)=g_{i0}\left(q\right):=0,g_{ij}\left(q\right):=a_{ij}\left(\mathbf{q}\right).$$

(16)

For the components of the stress-energy tensor in the spacetime coordinates $q^{\mu }$ we have an expression similar to (7), with ${\eta }_{\mu \nu }$ and the second order derivatives ${\partial }_{\mu \nu }$ replaced, respectively, by the metric coefficients $g_{\mu \nu }\left(\mathbf{q}\right)$ and by the corresponding covariant derivatives ${\nabla }_{\mu \nu }$ ( recall that the first order covariant derivatives ${\nabla }_{\mu }$ coincide with the ordinary derivatives ${\partial }_{\mu }$ on scalar functions).

Obviously enough, a function $\mathbf{x}\mapsto f\left(\mathbf{x}\right)$ on $\Omega$ or $(\mathbf{x},\mathbf{y})\mapsto h(\mathbf{x},\mathbf{y})$ on $\Omega \times \Omega$ induces a function of the curvilinear coordinates $\mathbf{q}$ of $\mathbf{x}$ and $\mathbf{p}$ of $\mathbf{y}$; we indicate the latter function with the slightly abusive notation $\mathbf{q}\mapsto f\left(\mathbf{q}\right)$ or $(\mathbf{q},\mathbf{p})\mapsto h(\mathbf{q},\mathbf{p})$. Keeping this in mind, we can write the following analogues of Equations (10)–(12) [47]:

$$\begin{array}{c}{\displaystyle ⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩=}\\ {\displaystyle {\kappa }^u{\left[\left(\frac{1}{4}+\xi \right){\mathcal{A}}_{\epsilon }^{-\frac{u-1}{2}}(\mathbf{q},\mathbf{p})+\left(\frac{1}{4}-\xi \right)\left({\partial }^{q^{\ell }}{\partial }_{p^{\ell }}+V\left(\mathbf{q}\right)\right){\mathcal{A}}_{\epsilon }^{-\frac{u+1}{2}}(\mathbf{q},\mathbf{p})\right]}_{\mathbf{p}=\mathbf{q}};}\end{array}$$

(17)

$$⟨0|{\widehat{T}}_{i0}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩=⟨0|{\widehat{T}}_{0i}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩=0;$$

(18)

$$\begin{array}{c}{\displaystyle ⟨0|{\widehat{T}}_{ij}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩=⟨0|{\widehat{T}}_{ji}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩=}\\ {\displaystyle {\kappa }^u\left[\left(\frac{1}{4}-\xi \right)a_{ij}\left(\mathbf{q}\right)\left({\mathcal{A}}_{\epsilon }^{-\frac{u-1}{2}}(\mathbf{q},\mathbf{p})-\left({\partial }^{q^{\ell }}{\partial }_{p^{\ell }}+V\left(\mathbf{q}\right)\right){\mathcal{A}}_{\epsilon }^{-\frac{u+1}{2}}(\mathbf{q},\mathbf{p})\right)+\right.}\\ {\displaystyle {\left.+\left(\left(\frac{1}{2}-\xi \right){\partial }_{q^i{p}^j}-\xi D_{q^i{q}^j}\right){\mathcal{A}}_{\epsilon }^{-\frac{u+1}{2}}(\mathbf{q},\mathbf{p})\right]}_{\mathbf{p}=\mathbf{q}}.}\end{array}$$

(19)

In the above, $D_{q^i{q}^j}$ are the covariant derivatives of second order corresponding to the metric coefficients $a_{ij}\left(\mathbf{q}\right)$ of the given curvilinear coordinates on $\Omega$; let us recall that, for any scalar function f on $\Omega$, we have

$$D_{q^i{q}^j}f={\partial }_{q^i{q}^j}f-{\gamma }_{ij}^k\left(\mathbf{q}\right){\partial }_{q^k}f$$

(20)

where ${\gamma }_{ij}^k$ are the Christoffel symbols for the spatial metric $a_{ij}$, i.e., ${\gamma }_{ij}^k=\frac{1}{2}{a}^{k\ell }({\partial }_i{a}_{\ell j}+{\partial }_j{a}_{i\ell }-{\partial }_{\ell }{a}_{ij})$. Of course, the analogues of Equations (13) and (14) in curvilinear coordinates are

$$e^{-\mathfrak{t}{\mathcal{A}}_{\epsilon }}(\mathbf{q},\mathbf{p})=e^{-{\epsilon }^2\mathfrak{t}}{e}^{-\mathfrak{t}\mathcal{A}}(\mathbf{q},\mathbf{p}),$$

(21)

$${\mathcal{A}}_{\epsilon }^{-s}(\mathbf{q},\mathbf{p})=\frac{1}{\Gamma \left(s\right)}{\int }_0^{+\infty }d\mathfrak{t}{\mathfrak{t}}^{s-1}{e}^{-\mathfrak{t}{\mathcal{A}}_{\epsilon }}(\mathbf{q},\mathbf{p}).$$

(22)

3. The Fundamental Operator for a Point Impurity

The precise definition of the operator $\mathcal{A}$ corresponding to a delta-type potential is a non-trivial problem, whose treatment depends crucially on the co-dimension of the support of the delta-type potential. As already indicated, the case of a point impurity in spatial dimension $d=3$ (with support of co-dimension 3) was first treated in a mathematically precise setting by Berezin and Faddeev in [31]. These authors proposed an approach to define the operator

$$“\mathcal{A}:=-\Delta +\left(\beta +\frac{{\beta }^2}{4\pi \lambda }\right){\delta }_{\mathbf{0}}”,$$

(23)

where ${\delta }_{\mathbf{0}}$ is the Dirac delta at the origin, $\lambda \in \mathbb{R}\backslash \left\{0\right\}$ is a fixed parameter and $\beta$ is infinitesimally small; we already mentioned that the infinitesimal nature of the coupling constant can be interpreted as the effect of a renormalization. The approach of [31] was refined in many subsequent works; here we mention, in particular, the book [32] by Albeverio et al. (see also the vast literature cited therein). The present variable $\lambda$ is connected to the variable $\alpha$ of [32] by the relation $\lambda =1/\left(4\pi \alpha \right)$.

According to the references mentioned above, the heuristic expression (23) has a rigorous counterpart based on the space domain

$$\Omega :={\mathbb{R}}^3\backslash \left\{\mathbf{0}\right\}$$

(24)

and on the Laplacian on this domain, with an appropriate boundary condition at the origin.

To define precisely this counterpart, from now on we intend the derivatives, the Laplacian, etc. of functions on ${\mathbb{R}}^3$ (or on $\Omega$) in the sense of the Schwartz distribution theory. We indicate with $H^2\left({\mathbb{R}}^3\right)$ the Sobolev space of complex-valued functions on ${\mathbb{R}}^3$ whose (distributional) derivatives up to second order are in $L^2\left({\mathbb{R}}^3\right)$; we recall that $H^2\left({\mathbb{R}}^3\right)$ is embedded in the space $C_B\left({\mathbb{R}}^3\right)$ of bounded, continuous functions on ${\mathbb{R}}^3$ [49].

To go on, for each $z\in \mathbb{C}\backslash [0,+\infty )$ we consider the function

$${\mathcal{G}}_z:\Omega \to \mathbb{C},{\mathcal{G}}_z\left(\mathbf{x}\right):=\frac{e^{i\sqrt{z}|\mathbf{x}|}}{4\pi |\mathbf{x}|}.$$

(25)

Here and in the following, we consider the principal determination of the argument for complex numbers, i.e., $arg:\mathbb{C}\backslash [0,+\infty )\to (0,2\pi )$; furthermore, for any $z\in \mathbb{C}\backslash [0,+\infty )$, we always write $\sqrt{z}$ to indicate the square root determined by this choice of the argument, i.e., the one with $\mathrm{Im}\sqrt{z}>0$ .

Note that ${\mathcal{G}}_z\in L^2(\Omega )$ and that $(-\Delta -z){\mathcal{G}}_z=0$ everywhere in $\Omega$ (however, one has $(-\Delta -z){\mathcal{G}}_z={\delta }_{\mathbf{0}}$ in ${\mathbb{R}}^3$ which shows, in particular, that ${\mathcal{G}}_z$ does not belong to $H^2\left({\mathbb{R}}^3\right)$). Then, after fixing $\lambda \in \mathbb{R}$ we set

$$\begin{array}{c}{\displaystyle \mathrm{Dom}\mathcal{A}:=\left\{\psi \in L^2(\Omega )\left|\exists z\in \mathbb{C}\backslash [0,+\infty ),\phi \in H^2\left({\mathbb{R}}^3\right)\mathrm{s}.\mathrm{t}.\psi =\phi +\frac{4\pi \lambda }{1-i\sqrt{z}\lambda }\phi \left(\mathbf{0}\right){\mathcal{G}}_z\right.\right\},}\\ {\displaystyle \mathcal{A}:=(-\Delta )\upharpoonright \mathrm{D}\mathrm{o}\mathrm{m}\mathcal{A}\subset L^2(\Omega )\to L^2(\Omega ).}\end{array}$$

(26)

Let us point out some known facts about the operator $\mathcal{A}$ defined above.

(i)

The condition characterizing a function $\psi$ in the domain of $\mathcal{A}$ is in fact a boundary condition at the origin $\mathbf{x}=\mathbf{0}$: $\psi$ is required to be the sum of a function $\phi \in H^2\left({\mathbb{R}}^3\right)\subset C_B\left({\mathbb{R}}^3\right)$, well defined even at the origin, and of another function diverging at the origin, with the peculiar form $\frac{4\pi \lambda }{1-i\sqrt{z}\lambda }\phi \left(\mathbf{0}\right){\mathcal{G}}_z$ . In addition, for any fixed $z\in \mathbb{C}\backslash [0,+\infty )$, this decomposition of $\psi$ is shown to be unique [32,36].

(ii)

Consider a function $\psi \in \mathrm{Dom}\mathcal{A}$ and its decomposition as in (26), based on some pair $(z,\phi )$. For any $z^{\prime }\in \mathbb{C}\backslash [0,+\infty )$, $\psi$ has a similar representation based on the pair $(z^{\prime },{\phi }^{\prime })$, where ${\phi }^{\prime }=\phi +\frac{4\pi \lambda }{1-i\sqrt{z}\lambda }\phi \left(\mathbf{0}\right)({\mathcal{G}}_z-{\mathcal{G}}_{z^{\prime }})$. Let us remark that the difference ${\mathcal{G}}_z-{\mathcal{G}}_{z^{\prime }}$ does indeed belong to the Sobolev space $H^2\left({\mathbb{R}}^3\right)$, despite the fact that ${\mathcal{G}}_z$ and ${\mathcal{G}}_{z^{\prime }}$ are both singular at the origin; to prove this claim it suffices to recall that ${\mathcal{G}}_{z^{\prime }}\in L^2(\Omega )\simeq L^2\left({\mathbb{R}}^3\right)$ and to use the resolvent-type identity ${\mathcal{G}}_z-{\mathcal{G}}_{z^{\prime }}=(z^{\prime }-z)R_0\left(z\right){\mathcal{G}}_{z^{\prime }}$ (see, e.g., Lemma 2.1 of [36]), where the bounded operator $R_0\left(z\right):L^2\left({\mathbb{R}}^3\right)\to H^2\left({\mathbb{R}}^3\right)$ is the resolvent associated to the free Laplacian $(-\Delta )\upharpoonright H^2\left({\mathbb{R}}^3\right)$ .

(iii)

Consider again a decomposition as in (26) for a function $\psi \in \mathrm{Dom}\mathcal{A}$; recalling that $(-\Delta -z){\mathcal{G}}_z=0$, we have $(-\Delta -z)\psi =(-\Delta -z)\phi$ in $\Omega$. This identity if often used in manipulations involving $\mathcal{A}$; incidentally, the expression on the right-hand side is in $L^2(\Omega )$ (since $\phi \in H^2\left({\mathbb{R}}^3\right)$), which ensures $(-\Delta -z)\psi$ and $-\Delta \psi =\mathcal{A}\psi$ to be as well in $L^2(\Omega )$, as stated in Equation (26).

The analysis performed in [31,32] shows that the setting on $\Omega$ based on the operator (26) is morally equivalent (for $\lambda \ne 0$) to the configuration suggested by Equation (23). Let us remark that the prescription (26) with $\lambda =0$ gives

$$\mathrm{Dom}\mathcal{A}{|}_{\lambda =0}=H^2\left({\mathbb{R}}^3\right);$$

(27)

this shows, in particular, that the fundamental operator $\mathcal{A}$ coincides with the free Laplacian $(-\Delta )\upharpoonright H^2\left({\mathbb{R}}^3\right)$ for $\lambda =0$.

Concerning the spectrum of $\mathcal{A}$, we refer to Theorem 1.1.4 of [32].

For each $\lambda \in \mathbb{R}$, the continuous spectrum of $\mathcal{A}$ is in fact absolutely continuous and

$${\sigma }_c\left(\mathcal{A}\right)={\sigma }_{ac}\left(\mathcal{A}\right)=[0,+\infty );$$

(28)

in this regard, let us mention that the scattering theory for $\mathcal{A}$ developed in Section I.1.4 of the cited book allows to interpret $-\lambda$ as the $s=0$, partial wave scattering length. Referring to the point spectrum of $\mathcal{A}$, we have

$${\sigma }_p\left(\mathcal{A}\right)=\left\{\begin{array}{cc}{\displaystyle \varnothing }\hfill & {\displaystyle \mathrm{if}\lambda ⩾0,}\hfill \\ {\displaystyle \{-1/{\lambda }^2\}}\hfill & {\displaystyle \mathrm{if}\lambda <0.}\hfill \end{array}\right.$$

(29)

The appearance of a negative eigenvalue for $\lambda <0$ prevents the perturbed operator $\mathcal{A}$ from fulfilling the basic assumption of non-negativity, which is necessary in order to set up a field theory in the framework of [47]; for this reason, throughout this work we restrict the attention to the sole case

$$\lambda ⩾0,$$

(30)

where $\sigma \left(\mathcal{A}\right)=[0,+\infty )$.

From here to the end of the paper, Ω is the space domain (24) and $\mathcal{A}$ is the operator (26) for some fixed $\lambda ⩾0$. We consider a field theory on $\Omega$, with fundamental operator $\mathcal{A}$; since $\mathcal{A}$ is just the (opposite of the) Laplacian on this domain, we will apply the setting of Section 2 with $V\left(\mathbf{x}\right)=0$ for all $\mathbf{x}\in \Omega$. Of course, the equivalent of this statement in any curvilinear coordinate system $\mathbf{q}$ for $\Omega$ is

$$V\left(\mathbf{q}\right)=0.$$

(31)

Since $\sigma \left(\mathcal{A}\right)$ contains a right neighborhood of zero, following Equation (5), we will introduce an infrared cutoff $\epsilon >0$ and consider the modified fundamental operator ${\mathcal{A}}_{\epsilon }:=\mathcal{A}+{\epsilon }^2$ in place of $\mathcal{A}$; at the end of the paper (see, in particular, Section 9), $\epsilon$ will be sent to zero.

4. The Heat Kernel for a Point Impurity

The heat kernel of $\mathcal{A}$ has been computed in [48] (see, in particular, Equation (3.4) on page 228); from this result and from Equation (21) we obtain the following, for $\mathbf{x},\mathbf{y}\in \Omega$:

$$\begin{array}{c}{\displaystyle e^{-\mathfrak{t}{\mathcal{A}}_{\epsilon }}(\mathbf{x},\mathbf{y})=}\\ {\displaystyle \frac{e^{-{\epsilon }^2\mathfrak{t}}}{{\left(4\pi \mathfrak{t}\right)}^{3/2}}\left[e^{-\frac{{|\mathbf{x}-\mathbf{y}|}^2}{4\mathfrak{t}}}+\frac{2\mathfrak{t}}{|\mathbf{x}||\mathbf{y}|}\left(e^{-\frac{(|\mathbf{x}|+{|\mathbf{y}|)}^2}{4\mathfrak{t}}}-\frac{1}{\lambda }{\int }_0^{+\infty }dw{e}^{-\left(\frac{w}{\lambda }+\frac{{(w+|\mathbf{x}|+|\mathbf{y}|)}^2}{4\mathfrak{t}}\right)}\right)\right].}\end{array}$$

(32)

In passing, let us notice that the above expression for the heat kernel can be viewed as the sum of two distinct terms. The first one coincides with the standard heat kernel associated to the modified, free operator $-\Delta +{\epsilon }^2$ (indeed, let us recall that in spatial dimension $d=3$ the heat kernel associated to the operator $-\Delta +{\epsilon }^2$ on $H^2\left({\mathbb{R}}^3\right)$ has the form $e^{-\mathfrak{t}(-\Delta +{\epsilon }^2)}(\mathbf{x},\mathbf{y})=\frac{e^{-{\epsilon }^2\mathfrak{t}}}{{\left(4\pi \mathfrak{t}\right)}^{3/2}}{e}^{-\frac{{|\mathbf{x}-\mathbf{y}|}^2}{4\mathfrak{t}}}$, for $\mathbf{x},\mathbf{y}\in {\mathbb{R}}^3$); for this reason, the first term can be viewed as a “free-theory” contribution, which also appears when $\lambda =0$. The second term corresponds to the two addenda within the round brackets in Equation (32); this can be viewed as a “perturbative” contribution and it can be easily checked that it vanishes for $\lambda \to 0^{+}$.

5. Spherical Coordinates

To fit the symmetries of the problem under analysis, let us consider on $\Omega$ the standard spherical coordinates $\mathbf{q}=(r,\theta ,\phi )\in (0,+\infty )\times (0,\pi )\times (0,2\pi )$, which are related to the Cartesian coordinates $\mathbf{x}$ by

$$x^1=rsin\theta cos\phi ,x^2=rsin\theta sin\phi ,x^3=rcos\theta .$$

(33)

Of course, the metric coefficients in spherical coordinates are $\left(a_{ij}\left(\mathbf{q}\right)\right)=\mathrm{diag}(1,r^2,r^2{sin}^2\theta )$, and the corresponding Christoffel symbols are readily obtained. Now, let

$$\mathbf{q}=(r,\theta ,\phi ),\mathbf{p}=(r^{\prime },{\theta }^{\prime },{\phi }^{\prime });$$

(34)

then, the correspondent of Equation (32) in spherical coordinates reads

$$\begin{array}{c}{\displaystyle e^{-\mathfrak{t}{\mathcal{A}}_{\epsilon }}(\mathbf{q},\mathbf{p})=}\\ {\displaystyle \frac{e^{-\mathfrak{t}{\epsilon }^2}}{{\left(4\pi \mathfrak{t}\right)}^{3/2}}\left[e^{-\frac{r^2+{r^{\prime }}^2-2r{r}^{\prime }S(\theta ,{\theta }^{\prime },\phi -{\phi }^{\prime })}{4\mathfrak{t}}}+\frac{2\mathfrak{t}}{r{r}^{\prime }}\left(e^{-\frac{{(r+r^{\prime })}^2}{4\mathfrak{t}}}-\frac{1}{\lambda }{\int }_0^{+\infty }dw{e}^{-\left(\frac{w}{\lambda }+\frac{{(w+r+r^{\prime })}^2}{4\mathfrak{t}}\right)}\right)\right],}\end{array}$$

(35)

where

$$S(\theta ,{\theta }^{\prime },\phi -{\phi }^{\prime }):=cos(\theta -{\theta }^{\prime }){cos}^2\left(\frac{\phi -{\phi }^{\prime }}{2}\right)+cos(\theta +{\theta }^{\prime }){sin}^2\left(\frac{\phi -{\phi }^{\prime }}{2}\right).$$

(36)

note that $r^2+{r^{\prime }}^2-2r{r}^{\prime }S(\theta ,{\theta }^{\prime },\phi -{\phi }^{\prime })$ is just the expression of ${|\mathbf{x}-\mathbf{y}|}^2={|\mathbf{x}|}^2+{|\mathbf{y}|}^2-2\mathbf{x}·\mathbf{y}$ when $\mathbf{x},\mathbf{y}$ have spherical coordinates $\mathbf{q},\mathbf{p}$ as in Equation (34).

6. The Regularized Stress-Energy VEV

Let us keep the coordinate system and the notations of the previous section. We recall that, for (suitable) $s\in \mathbb{C}$, the s-th Dirichlet kernel ${\mathcal{A}}_{\epsilon }^{-s}(\mathbf{q},\mathbf{p})$ can be expressed via Equation (22); the integral over $\mathfrak{t}$ appearing therein involves the heat kernel $e^{-\mathfrak{t}{\mathcal{A}}_{\epsilon }}(\mathbf{q},\mathbf{p})$ given by Equations (35) and (36), which, in turn, comprises an integral over another variable w. In the end, we obtain an explicit representation for ${\mathcal{A}}_{\epsilon }^{-s}(\mathbf{q},\mathbf{p})$, containing integrals for $\mathfrak{t},w\in (0,+\infty )$.

It is readily inferred that the above mentioned integral representation of ${\mathcal{A}}_{\epsilon }^{-s}(\mathbf{q},\mathbf{p})$ is well defined, even along the diagonal $\mathbf{p}=\mathbf{q}$, for any $s\in \mathbb{C}$ with $\mathrm{Re}s>3/2$. Notice that, as usual, the restriction on $\mathrm{Re}s$ descends from the behavior of the integrand function for $\mathfrak{t}\to 0^{+}$. On the other hand, let us remark that the presence of the infrared cutoff parameter $\epsilon >0$ is essential in order to ensure the convergence of the integral for large values of $\mathfrak{t}$ (for any $s\in \mathbb{C}$).

By differentiation, we obtain analogous representations for the first order derivatives in $\mathbf{q},\mathbf{p}$ and for the second order covariant derivatives in $\mathbf{q}$ of the Dirichlet kernel; on the diagonal $\mathbf{p}=\mathbf{q}$, these representations always make sense for $\mathrm{Re}s$ sufficiently large.

To proceed, let us consider the relations (17)–(19) (and (31)), allowing to express the VEV of the zeta-regularized stress-energy tensor in terms of the Dirichlet kernel ${\mathcal{A}}_{\epsilon }^{-s}(\mathbf{q},\mathbf{p})$. Using the integral representations discussed formerly for the Dirichlet kernel ${\mathcal{A}}_{\epsilon }^{-s}(\mathbf{q},\mathbf{p})$ and for its derivatives, we obtain the forthcoming explicit expressions (37)–(40) for the non-vanishing components of the zeta-regularized stress-energy VEV. These expressions are derived introducing, for any fixed $r>0$, the new integration variables $v:=w/\left(2r\right)\in (0,+\infty )$ and $\tau :=\mathfrak{t}/r^2\in (0,+\infty )$:

$$\begin{array}{c}{\displaystyle ⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩=}\\ {\displaystyle \frac{{\kappa }^u}{{\left(4\pi \right)}^{3/2}\Gamma \left(\frac{u+1}{2}\right)r^{4-u}}{\int }_0^{+\infty }d\tau {\tau }^{\frac{u}{2}-3}{e}^{-{\epsilon }^2{r}^2\tau }[\left(\frac{1}{4}-2\xi \right)+\left(\frac{1}{4}+\xi \right)\frac{u}{2}+}\\ {\displaystyle +\left(\left(\frac{1}{2}-2\xi \right)\left({\tau }^2+1\right)+\left(\frac{1}{2}-4\xi \right)\tau +\left(\frac{1}{4}+\xi \right)\tau u\right)e^{-1/\tau }+}\\ {\displaystyle -\frac{2r}{\lambda }{\int }_0^{+\infty }dv{e}^{-\left(\frac{1}{\tau }{(v+1)}^2+\frac{2r}{\lambda }v\right)}\left(\left(\frac{1}{2}-2\xi \right){\left(\tau +v+1\right)}^2-\frac{\tau }{2}+\left(\frac{1}{4}+\xi \right)\tau u\right)];}\end{array}$$

(37)

$$\begin{array}{c}{\displaystyle ⟨0|{\widehat{T}}_{rr}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩=}\\ {\displaystyle \frac{{\kappa }^u}{{\left(4\pi \right)}^{3/2}\Gamma \left(\frac{u+1}{2}\right)r^{4-u}}{\int }_0^{+\infty }d\tau {\tau }^{\frac{u}{2}-3}{e}^{-{\epsilon }^2{r}^2\tau }[-\left(\frac{1}{4}-2\xi \right)+\left(\frac{1}{4}-\xi \right)\frac{u}{2}+}\\ {\displaystyle +\left(\left(\frac{1}{2}-4\xi \right){\tau }^2+\left(\frac{1}{2}-2\xi \right)(\tau +1)+\left(\frac{1}{4}-\xi \right)\tau u\right)e^{-1/\tau }+}\\ {\displaystyle -\frac{2r}{\lambda }{\int }_0^{+\infty }dv{e}^{-\left(\frac{1}{\tau }{(v+1)}^2+\frac{2r}{\lambda }v\right)}\left(\left(\frac{1}{2}-2\xi \right)\left({(\tau +v+1)}^2-\tau \right)-2\xi {\tau }^2+\left(\frac{1}{4}-\xi \right)\tau u\right)];}\end{array}$$

(38)

$$\begin{array}{c}{\displaystyle ⟨0|{\widehat{T}}_{\theta \theta }^{u,\epsilon }\left(\mathbf{q}\right)|0⟩=}\\ {\displaystyle \frac{{\kappa }^u}{{\left(4\pi \right)}^{3/2}\Gamma \left(\frac{u+1}{2}\right)r^{2-u}}{\int }_0^{+\infty }d\tau {\tau }^{\frac{u}{2}-3}{e}^{-{\epsilon }^2{r}^2\tau }[-\left(\frac{1}{4}-2\xi \right)+\left(\frac{1}{4}-\xi \right)\frac{u}{2}+}\\ {\displaystyle -\left(\left(\frac{1}{2}-4\xi \right)(\tau +1)\tau +\left(\frac{1}{2}-2\xi \right)(\tau +1)-\left(\frac{1}{4}-\xi \right)\tau u\right)e^{-1/\tau }+}\\ {\displaystyle +\frac{2r}{\lambda }{\int }_0^{+\infty }dv{e}^{-\left(\frac{1}{\tau }{(v+1)}^2+\frac{2r}{\lambda }v\right)}\left(\left(\frac{1}{2}-2\xi \right){(\tau +v+1)}^2-2\xi (\tau +v+1)\tau -\left(\frac{1}{4}-\xi \right)\tau u\right)].}\end{array}$$

(39)

Moreover, in compliance with the spherical symmetry of the problem under analysis, we have

$$⟨0|{\widehat{T}}_{\phi \phi }^{u,\epsilon }\left(\mathbf{q}\right)|0⟩={sin}^2\theta ⟨0|{\widehat{T}}_{\theta \theta }^{u,\epsilon }\left(\mathbf{q}\right)|0⟩.$$

(40)

Consistently with the facts mentioned before about the integral representation of the Dirichlet kernel (and of its derivatives), it can be checked by direct inspection that all the integrals appearing in Equations (37)–(39) are finite for any fixed $r,\epsilon >0$ and for all complex u with

$$\mathrm{Re}u>4;$$

(41)

moreover, the maps $u\mapsto ⟨0|{\widehat{T}}_{\mu \nu }^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$ ($\mu ,\nu \in \{0,r,\theta ,\phi \}$) described by Equations (37)–(40) are analytic in the region (41). In the following Section 7, we re-express the previous results in terms of Bessel functions; this automatically gives the analytic continuations of the maps $u\mapsto ⟨0|{\widehat{T}}_{\mu \nu }^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$, which are meromorphic functions on the whole complex plane with simple poles. Such continuations will be used in the subsequent Section 8 and Section 9 to determine the renormalized stress-energy VEV; for brevity, we shall give the details of these computations only for the map $u\mapsto ⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$, which is related to the energy density.

7. Expressing the Previous Results via Bessel Functions; Analytic Continuation

Let us consider the representation (37) for the component $⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$ of the regularized stress-energy VEV, involving integrals over the two variables $\tau ,v\in (0,+\infty )$. It can be easily checked that, for any $u\in \mathbb{C}$ with $\mathrm{Re}u>4$ (see Equation (41)), the order of integration over these variables can be interchanged due to Fubini’s theorem.

On the other hand, let us point out the following relations, descending from well-known integral representations for the Euler Gamma function $\Gamma$ and for the modified Bessel function of second kind $K_{\sigma }$ (see, respectively, Equations (5.9.1) and (10.32.10) of [50]):

$${\int }_0^{+\infty }d\tau {\tau }^{\sigma -1}{e}^{-a^2\tau }=a^{-2\sigma }\Gamma \left(\sigma \right)\mathrm{for}\mathrm{all}a>0,\sigma \in \mathbb{C}\mathrm{with}\mathrm{Re}\sigma >0;$$

(42)

$${\int }_0^{+\infty }d\tau {\tau }^{\sigma -1}{e}^{-a^2\tau -\frac{b^2}{\tau }}=2{\left(\frac{b}{a}\right)}^{\sigma }{K}_{-\sigma }\left(2ab\right)\mathrm{for}\mathrm{all}a,b>0,\sigma \in \mathbb{C}.$$

(43)

In view of the developments to be discussed in the forthcoming Section 8 and Section 9, for any $\sigma \in \mathbb{C}$ it is advantageous to consider in place of the Bessel function $K_{\sigma }$ the map

$${\mathfrak{K}}_{\sigma }:(0,+\infty )\to \mathbb{C},y\mapsto {\mathfrak{K}}_{\sigma }\left(y\right):=y^{\sigma }{K}_{\sigma }\left(y\right);$$

(44)

using this function, Equation (43) can be rephrased as

$${\int }_0^{+\infty }d\tau {\tau }^{\sigma -1}{e}^{-a^2\tau -\frac{b^2}{\tau }}=2^{\sigma +1}{b}^{2\sigma }{\mathfrak{K}}_{-\sigma }\left(2ab\right)\mathrm{for}\mathrm{all}a,b>0,\sigma \in \mathbb{C}.$$

(45)

Using Equations (42) and (45), by a few additional algebraic manipulations we obtain from Equation (37) that

$$\begin{array}{c}⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩=\frac{{\epsilon }^4\Gamma \left(\frac{u}{2}-2\right)}{{\left(4\pi \right)}^{3/2}\Gamma \left(\frac{u+1}{2}\right)}{\left(\frac{\kappa }{\epsilon }\right)}^u\left[\left(\frac{1}{4}-2\xi \right)+\left(\frac{1}{4}+\xi \right)\frac{u}{2}\right]+\\ {\displaystyle +\frac{2^{\frac{u}{2}}{\kappa }^u}{{\left(4\pi \right)}^{3/2}\Gamma \left(\frac{u+1}{2}\right)r^{4-u}}[\left(\frac{1}{4}-\xi \right){\mathfrak{K}}_{2-\frac{u}{2}}\left(2\epsilon r\right)+\left(\left(\frac{1}{2}-4\xi \right)+\left(\frac{1}{4}+\xi \right)u\right){\mathfrak{K}}_{1-\frac{u}{2}}\left(2\epsilon r\right)+}\\ {\displaystyle +\left(1-4\xi \right){\mathfrak{K}}_{-\frac{u}{2}}\left(2\epsilon r\right)-\frac{2r}{\lambda }{\int }_0^{+\infty }dv\frac{e^{-\frac{2r}{\lambda }v}}{{(v+1)}^{2-u}}(\left(1-4\xi \right){(v+1)}^2{\mathfrak{K}}_{-\frac{u}{2}}\left(2\epsilon r(v+1)\right)+}\\ {\displaystyle +\left((1-4\xi )(v+1)-\frac{1}{2}+\left(\frac{1}{4}+\xi \right)u\right){\mathfrak{K}}_{1-\frac{u}{2}}\left(2\epsilon r(v+1)\right)+\left(\frac{1}{4}-\xi \right){\mathfrak{K}}_{2-\frac{u}{2}}\left(2\epsilon r(v+1)\right)\left)\right].}\end{array}$$

(46)

Even though the above identity was derived under the restriction $\mathrm{Re}u>4$ on the regulating parameter u, we claim that Equation (46) automatically determines the analytic continuation of the map $u\mapsto ⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$ to a function which is meromorphic on the whole complex plane, with only simple poles. In the following items (i)–(iii) we briefly account for the last statement.

(i)

The reciprocal of the Euler Gamma function $\Gamma$ is analytic on the whole complex plane (see, e.g., §5.2(i) of [50]); so the Gamma’s in the denominators of Equation (46) give no problem from the viewpoint of analyticity.

(ii)

From the analyticity properties of the Gamma function (see, again, §5.2(i) of [50]) it can be readily inferred that the term in the first line of Equation (46) is a meromorphic function of u, with simple poles at

$$u\in \{4,2,0,-2,-4,...\},$$

(47)

(where the argument of the Gamma function in the numerator of the above mentioned term is a non-positive integer). In passing, let us remark that the expression under analysis does not depend on r or $\lambda$; indeed, this terms descends solely from the “free-theory” contribution to the heat kernel (see the comments below Equation (32)).

(iii)

Let us now consider the terms in the second, third and fourth line of Equation (46). From some basic properties of the modified Bessel function $K_{\sigma }$ (see, e.g., §10.25(ii), §10.38 and §10.40 of [50]) we infer that the function ${\mathfrak{K}}_{\sigma }$ defined in Equation (44) has the following regularity features: for any fixed $y\in (0,+\infty )$, the map $\sigma \mapsto {\mathfrak{K}}_{\sigma }\left(y\right)$ is analytic on the whole complex plane; for any fixed $\sigma \in \mathbb{C}$, both the maps $y\mapsto {\mathfrak{K}}_{\sigma }\left(y\right)$ and $y\mapsto (\partial {\mathfrak{K}}_{\sigma }/\partial \sigma )\left(y\right)$ are analytic (whence, in particular, continuous) for $y\in (0,+\infty )$ and they decay exponentially for $y\to +\infty$. The facts mentioned above about ${\mathfrak{K}}_{\sigma }$ and $\Gamma$ suffice to infer that the terms under analysis determine an analytic function of the regulating parameter u, defined on the whole complex plane.

Before proceeding, let us remark that analogous results can be derived for the analytic continuations of the maps $u\mapsto ⟨0|{\widehat{T}}_{\mu \nu }^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$, associated to the other components of the regularized stress-energy VEV. In the forthcoming Section 8 and Section 9 we determine the renormalized VEV of the stress-energy tensor, starting from these analytic continuations and implementing Equation (8) for $⟨0|{\widehat{T}}_{\mu \nu }\left(\mathbf{q}\right){|0⟩}_{ren}$.

8. Renormalization of Ultraviolet Divergences: The Regular Part at $\mathit{u}=\mathbf{0}$

The results reported in the previous section show, among other things, that the analytic continuations of the maps $u\mapsto ⟨0|{\widehat{T}}_{\mu \nu }^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$ possess a simple pole at the point $u=0$ (see, e.g., Equation (47)), of interest for renormalization. In the present section we proceed to determine the corresponding regular part at $u=0$, appearing in Equation (8) for the renormalized stress-energy VEV. As an example, we shall report here the details of the related computations only for the energy density component $RP{|}_{u=0}⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$ .

First of all, let us consider the expression (46) for $⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$ and recall once more the regularity properties of the various terms appearing therein (see items (i) and (ii) at the end of Section 7). In addition, let us notice that the following asymptotic expansions hold for $u\to 0$ (see §5 of [50]; here and in the following ${\gamma }_{EM}$ indicates the Euler-Mascheroni constant):

$$\begin{array}{c}{\displaystyle \Gamma \left(\frac{u}{2}-2\right)=\frac{1}{u}+\frac{1}{2}\left(\frac{3}{2}-{\gamma }_{EM}\right)+O\left(u\right);}\\ {\displaystyle \Gamma \left(\frac{u+1}{2}\right)=\sqrt{\pi }-\sqrt{\pi }\left(log2+\frac{{\gamma }_{EM}}{2}\right)u+O\left(u^2\right);}\\ {\displaystyle {\left(\frac{\kappa }{\epsilon }\right)}^u=1+ulog\left(\frac{\kappa }{\epsilon }\right)+O\left(u^2\right).}\end{array}$$

(48)

Keeping in mind all these facts, by simple computations we obtain from Equation (46)

$$\begin{array}{c}{\displaystyle RP{|}_{u=0}⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩=\frac{{\epsilon }^4}{8{\pi }^2}\left[\left(\frac{5}{16}-\xi \right)+\left(\frac{1}{4}-2\xi \right)log\left(\frac{2\kappa }{\epsilon }\right)\right]+}\\ {\displaystyle +\frac{1}{8{\pi }^2{r}^4}[\left(\frac{1}{4}-\xi \right){\mathfrak{K}}_2\left(2\epsilon r\right)+\left(\frac{1}{2}-4\xi \right){\mathfrak{K}}_1\left(2\epsilon r\right)+}\\ {\displaystyle +\left(1-4\xi \right){\mathfrak{K}}_0\left(2\epsilon r\right)-\frac{2r}{\lambda }{\int }_0^{+\infty }dv\frac{e^{-\frac{2r}{\lambda }v}}{{(v+1)}^2}(\left(1-4\xi \right){(v+1)}^2{\mathfrak{K}}_0\left(2\epsilon r(v+1)\right)+}\\ {\displaystyle +\left((1-4\xi )(v+1)-\frac{1}{2}\right){\mathfrak{K}}_1\left(2\epsilon r(v+1)\right)+\left(\frac{1}{4}-\xi \right){\mathfrak{K}}_2\left(2\epsilon r(v+1)\right)\left)\right].}\end{array}$$

(49)

In the first line of Equation (49), let us note the mass parameter $\kappa$ which has been introduced to regularize the field operator (see Equation (6)). Taking the regular part, as indicated in Equation (49), amounts to remove from the Laurent expansion for $⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$ at $u=0$ the pole term

$$\frac{{\epsilon }^4(1-8\xi )}{32{\pi }^2}\frac{1}{u}.$$

This is the same divergent contribution appearing in the computation of the renormalized energy density VEV for a scalar field of mass $\epsilon >0$ in empty space (with no external potentials or confining boundaries; in this case, $⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$ is just given by the first line of Equation (46)).

In the upcoming Section 9 we will send to zero the infrared cutoff parameter $\epsilon$; in view of this development, it is worthwhile to use the elementary identity

$$\frac{2r}{\lambda }{\int }_0^{+\infty }dv{e}^{-\frac{2r}{\lambda }v}=1$$

(50)

in order to re-write the third line of Equation (49). In this way we obtain the following, equivalent version of the cited equation:

$$\begin{array}{c}{\displaystyle RP{|}_{u=0}⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩=\frac{{\epsilon }^4}{8{\pi }^2}\left[\left(\frac{5}{16}-\xi \right)+\left(\frac{1}{4}-2\xi \right)log\left(\frac{2\kappa }{\epsilon }\right)\right]+}\\ {\displaystyle +\frac{1}{8{\pi }^2{r}^4}[\left(\frac{1}{4}-\xi \right){\mathfrak{K}}_2\left(2\epsilon r\right)+\left(\frac{1}{2}-4\xi \right){\mathfrak{K}}_1\left(2\epsilon r\right)+}\\ {\displaystyle +\frac{2r}{\lambda }{\int }_0^{+\infty }dv\frac{e^{-\frac{2r}{\lambda }v}}{{(v+1)}^2}(\left(1-4\xi \right){(v+1)}^2\left({\mathfrak{K}}_0\left(2\epsilon r\right)-{\mathfrak{K}}_0\left(2\epsilon r(v+1)\right)\right)+}\\ {\displaystyle -\left((1-4\xi )(v+1)-\frac{1}{2}\right){\mathfrak{K}}_1\left(2\epsilon r(v+1)\right)-\left(\frac{1}{4}-\xi \right){\mathfrak{K}}_2\left(2\epsilon r(v+1)\right)\left)\right].}\end{array}$$

(51)

Similar results can be derived for the regular parts at $u=0$ of the other components of the regularized stress-energy VEV. As shown in the next two sections, the dependence on $\kappa$ disappears from all components in the limit $\epsilon \to 0^{+}$.

9. Removal of the Infrared Cutoff: the Limit $\mathbf{\epsilon }\to {\mathbf{0}}^{+}$

We already pointed out that the expressions derived in the previous section for the regular part at $u=0$ of the regularized stress-energy VEV do still depend on the infrared cutoff parameter $\epsilon \in (0,+\infty )$. In this section, we compute the limit $\epsilon \to 0^{+}$ of the above cited expressions; in accordance with the general prescription (8) of Section 2, this determines the renormalized VEV of the stress-energy tensor. As usual, we illustrate for example the computation of the limit $\epsilon \to 0^{+}$ for $RP{|}_{u=0}⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$, ultimately yielding the renormalized energy density $⟨0|{\widehat{T}}_{00}\left(\mathbf{q}\right){|0⟩}_{ren}$.

For this purpose, let us first consider the expression (51) for $RP{|}_{u=0}⟨0|{\widehat{T}}_{00}^{u,\epsilon }\left(\mathbf{q}\right)|0⟩$. Recalling the asymptotic behavior of the Bessel function $K_{\sigma }$ near zero (see, e.g., Equations (10.30.2) and (10.30.3) on page 252 of [50]), it is easy to prove that the function ${\mathfrak{K}}_{\sigma }$ defined in Equation (44) fulfills the following relations (recall that ${\gamma }_{EM}$ is the Euler-Mascheroni constant):

$$\underset{y\to 0^{+}}{lim}{\mathfrak{K}}_{\sigma }\left(y\right)=2^{\sigma -1}\Gamma \left(\sigma \right)\mathrm{for}\mathrm{all}\sigma \in \mathbb{C}\mathrm{with}\mathrm{Re}\sigma >0;$$

(52)

$${\mathfrak{K}}_0\left(y\right)=-log(y/2)+{\gamma }_{EM}+O\left(y^{2}logy\right)\mathrm{for}y\to 0^{+}.$$

(53)

In particular, let us remark that Equation (52) gives

$$\underset{\epsilon \to 0^{+}}{lim}{\mathfrak{K}}_1\left(2\epsilon r\right)=1,\underset{\epsilon \to 0^{+}}{lim}{\mathfrak{K}}_1\left(2\epsilon r\right)=2\mathrm{for}\mathrm{all}r>0;$$

(54)

on the other hand, making reference to the expression in the third line of Equation (51), we can use Equation (53) to infer that

$$\underset{\epsilon \to 0^{+}}{lim}\left[{\mathfrak{K}}_0\left(2\epsilon r\right)-{\mathfrak{K}}_0\left(2\epsilon r(v+1)\right)\right]=log(v+1)\mathrm{for}\mathrm{all}r,v>0.$$

(55)

In addition, let us point out that by Lebesgue’s dominated convergence theorem the limit $\epsilon \to 0^{+}$ can be evaluated before performing the integrations over v in Equation (51).

Summing up, the above arguments allow us to derive the following explicit expression for the renormalized VEV of the energy density:

$$\begin{gathered} ⟨0|{\widehat{T}}_{00}\left(\mathbf{q}\right){|0⟩}_{ren}= \\ \frac{1}{8{\pi }^2{r}^4}\left[(1-6\xi )+\frac{2r}{\lambda }{\int }_0^{+\infty }dv\frac{e^{-\frac{2r}{\lambda }v}}{{(v+1)}^2}\left(\left(1-4\xi \right){(v+1)}^{2}log(v+1)-(1-4\xi )(v+1)+2\xi \right)\right]. \end{gathered}$$

(56)

To go on, it is useful to notice that the integral over $v\in (0,+\infty )$ appearing in Equation (56) can be re-expressed in terms of the exponential integral function ${\mathrm{E}}_1$ (see, e.g., Chapter 6 of [50]).

To be precise, let us introduce the function

$$\mathcal{E}:(0,+\infty )\to \mathbb{R},\rho \mapsto \mathcal{E}\left(\rho \right):=e^{\rho }{\mathrm{E}}_1\left(\rho \right).$$

(57)

Then, using a well-known integral representation for ${\mathrm{E}}_1$ (see, e.g., Equation (6.2.2) on page 150 of [50]), by a simple change of the integration variable we obtain

$$\mathcal{E}\left(\rho \right)={\int }_0^{+\infty }dv\frac{e^{-\rho v}}{v+1}\mathrm{for}\mathrm{all}\rho >0.$$

(58)

Moreover, keeping in mind Equation (57) for $\mathcal{E}$, by suitable integrations by parts of the integral in the right-hand side of the above relation (58) we can also prove the identities reported hereafter, for $\rho >0$:

$${\int }_0^{+\infty }dv{e}^{-\rho v}log(v+1)=\frac{1}{\rho }\mathcal{E}\left(\rho \right),{\int }_0^{+\infty }dv\frac{e^{-\rho v}}{{(v+1)}^2}=1-\rho \mathcal{E}\left(\rho \right).$$

(59)

We can use the results mentioned above to re-express Equation (56) as

$$⟨0|{\widehat{T}}_{00}\left(\mathbf{q}\right){|0⟩}_{ren}=\frac{1}{8{\pi }^2{r}^4}[(1-6\xi )+2\xi \rho +\left(\left(1-4\xi \right)(1-\rho )-2\xi {\rho }^2\right)\mathcal{E}\left(\rho \right)]{}_{\rho =2r/\lambda }.$$

(60)

Arguments analogous to those presented in this section can be employed to determine all the other components of the renormalized stress-energy VEV $⟨0|{\widehat{T}}_{\mu \nu }\left(\mathbf{q}\right){|0⟩}_{ren}$. In the upcoming, conclusive Section 10 we collect our final results for these quantities and discuss their asymptotic behaviors in various regimes.

10. The Renormalized Stress-Energy VEV

We now give the final form of our results separating the conformal and non-conformal parts of the renormalized stress-energy VEV, according to the general scheme of Section 2 (see, especially, Equation (9) and related comments). Using the spherical coordinates $\mathbf{q}=(r,\theta ,\phi )$, we have the relation

$$⟨0|{\widehat{T}}_{\mu \nu }\left(\mathbf{q}\right){|0⟩}_{ren}=T_{\mu \nu }^{(◊)}\left(\mathbf{q}\right)+\left(\xi -{\xi }_c\right)T_{\mu \nu }^{(\blacksquare )}\left(\mathbf{q}\right),{\xi }_c:=\frac{1}{6},$$

(61)

defining the conformal and non-conformal parts $T_{\mu \nu }^{(◊)}$ and $T_{\mu \nu }^{(\blacksquare )}$. The non-zero components in this representation are as follows:

$$\begin{array}{c}{\displaystyle T_{00}^{(◊)}\left(\mathbf{q}\right)=\frac{1}{24{\pi }^2{r}^4}{\left[\rho +\left(1-\rho -{\rho }^2\right)\mathcal{E}\left(\rho \right)\right]}_{\rho =2r/\lambda },}\\ {\displaystyle T_{00}^{(\blacksquare )}\left(\mathbf{q}\right)=-\frac{1}{4{\pi }^2{r}^4}{\left[3-\rho +\left(2-2\rho +{\rho }^2\right)\mathcal{E}\left(\rho \right)\right]}_{\rho =2r/\lambda };}\end{array}$$

(62)

$$\begin{array}{c}{\displaystyle T_{rr}^{(◊)}\left(\mathbf{q}\right)=\frac{1}{24{\pi }^2{r}^4}{\left[1-\left(1+\rho \right)\mathcal{E}\left(\rho \right)\right]}_{\rho =2r/\lambda },}\\ {\displaystyle T_{rr}^{(\blacksquare )}\left(\mathbf{q}\right)=-\frac{1}{2{\pi }^2{r}^4}{\left[1+\left(2-\rho \right)\mathcal{E}\left(\rho \right)\right]}_{\rho =2r/\lambda };}\end{array}$$

(63)

$$\begin{array}{c}{\displaystyle T_{\theta \theta }^{(◊)}\left(\mathbf{q}\right)=T_{\phi \phi }^{(◊)}\left(\mathbf{q}\right)/{sin}^2\theta =-\frac{1}{48{\pi }^2{r}^2}{\left[\left(1-\rho \right)-\left(2-{\rho }^2\right)\mathcal{E}\left(\rho \right)\right]}_{\rho =2r/\lambda },}\\ {\displaystyle T_{\theta \theta }^{(\blacksquare )}\left(\mathbf{q}\right)=T_{\phi \phi }^{(\blacksquare )}\left(\mathbf{q}\right)/{sin}^2\theta =\frac{1}{4{\pi }^2{r}^2}{\left[\left(4-\rho \right)+\left(4-3\rho +{\rho }^2\right)\mathcal{E}\left(\rho \right)\right]}_{\rho =2r/\lambda }.}\end{array}$$

(64)

From the explicit expressions reported above, it is evident that ${\lambda }^4{T}_{00}^{(◊)}$, ${\lambda }^4{T}_{rr}^{(◊)}$ and ${\lambda }^2{T}_{\theta \theta }^{(◊)}$ as well as their non-conformal counterparts depend solely on the dimensionless variable $\rho :=2r/\lambda$; the graphs of these functions of $\rho$ are reported in Figure 1, Figure 2 and Figure 3.

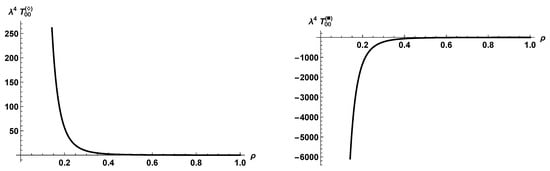
Figure 1. Graphs of ${\lambda }^4{T}_{00}^{(◊)}$ and ${\lambda }^4{T}_{00}^{(\blacksquare )}$ as functions of $\rho :=2r/\lambda$ .

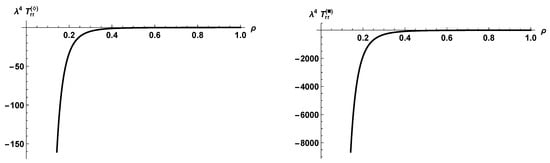
Figure 2. Graphs of ${\lambda }^4{T}_{rr}^{(◊)}$ and ${\lambda }^4{T}_{rr}^{(\blacksquare )}$ as functions of $\rho :=2r/\lambda$.

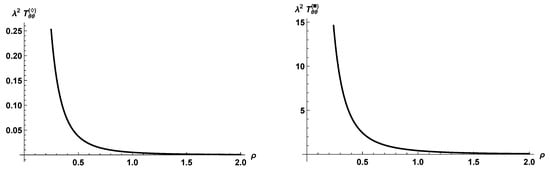
Figure 3. Graphs of ${\lambda }^2{T}_{\theta \theta }^{(◊)}$ and ${\lambda }^2{T}_{\theta \theta }^{(\blacksquare )}$ as functions of $\rho :=2r/\lambda$.

In the forthcoming Section 10.1 and Section 10.2, we derive the asymptotic expansions of $T_{\mu \nu }^{(◊)}\left(\mathbf{q}\right),T_{\mu \nu }^{(\blacksquare )}\left(\mathbf{q}\right)$ when $\rho :=2r/\lambda$ tends to $0^{+}$ and to $+\infty$. These expansions have a twofold interpretation: indeed, they determine the dominant contributions in the renormalized stress-energy VEV for small and large values of the radial coordinate r or, alternatively, for large and small values of the parameter $\lambda$.

10.1. Asymptotic Expansions for $\rho =2r/\lambda \to 0^{+}$

Let us consider Equation (57) for the map $\mathcal{E}$, involving the exponential integral function ${\mathrm{E}}_1$; using a well-known series representation for the latter (see, e.g., Equations (5.4.14) and (6.6.2) of [50]), it is easily shown that

$$\mathcal{E}\left(\rho \right)=-\sum _{n=0}^{+\infty }\left(log\rho +{\gamma }_{EM}-H_n\right)\frac{{\rho }^n}{n!}\mathrm{for}\mathrm{all}\rho >0$$

(65)

(as usual, ${\gamma }_{EM}$ is the Euler-Mascheroni constant; $H_n:={\sum }_{j=1}^{n}1/j$ is the n-th harmonic number).

Of course, the series representation (65) determines the asymptotic expansion of $\mathcal{E}\left(\rho \right)$ for $\rho \to 0^{+}$. In particular, this allows us to infer the following relations, for $\rho =2r/\lambda \to 0^{+}$:

$$\begin{array}{c}{\displaystyle T_{00}^{(◊)}\left(\mathbf{q}\right)=-\frac{1}{24{\pi }^2{r}^4}\left[log\rho +{\gamma }_{EM}+O\left(\rho \right)\right],}\\ {\displaystyle T_{00}^{(\blacksquare )}\left(\mathbf{q}\right)=\frac{1}{2{\pi }^2{r}^4}(log\rho +{\gamma }_{EM}-\frac{3}{2}+O\left(\rho \right));}\end{array}$$

(66)

$$\begin{array}{c}{\displaystyle T_{rr}^{(◊)}\left(\mathbf{q}\right)=\frac{1}{24{\pi }^2{r}^4}\left[log\rho +{\gamma }_{EM}+1+O\left(\rho \right)\right],}\\ {\displaystyle T_{rr}^{(\blacksquare )}\left(\mathbf{q}\right)=-\frac{1}{{\pi }^2{r}^4}(log\rho +{\gamma }_{EM}-\frac{1}{2}+O\left(\rho \right));}\end{array}$$

(67)

$$\begin{array}{c}{\displaystyle T_{\theta \theta }^{(◊)}\left(\mathbf{q}\right)=-\frac{1}{24{\pi }^2{r}^2}(log\rho +{\gamma }_{EM}+\frac{1}{2}+O\left(\rho \right)),}\\ {\displaystyle T_{\theta \theta }^{(\blacksquare )}\left(\mathbf{q}\right)=-\frac{1}{{\pi }^2{r}^2}\left[log\rho +{\gamma }_{EM}-1+O\left(\rho \right)\right].}\end{array}$$

(68)

The above relations show that all the non-vanishing components of the renormalized stress-energy VEV diverge near the origin $r=0$, where the point impurity is placed. In particular, Equation (66) makes patent the fact that the renormalized energy density $⟨0|{\widehat{T}}_{00}\left(\mathbf{q}\right){|0⟩}_{ren}$ possesses a non-integrable singularity at $r=0$; in consequence of this, it is not possible to define the total energy for the configuration under analysis simply by integration over $\Omega ={\mathbb{R}}^3\backslash \left\{\mathbf{0}\right\}$ of $⟨0|{\widehat{T}}_{00}\left(\mathbf{q}\right){|0⟩}_{ren}$. Here, we limit ourselves to mention that the appearance of problematic features of the above kind is rather typical in Casimir-type computations. (See, e.g., [47]. In general, the strategy to obtain the renormalized total energy VEV consists in exchanging the order of the operations involved: one first integrates the regularized energy density and then takes the regular part at $u=0$. §3.5 of the cited book contains some comments on this subject.)

10.2. Asymptotic Expansions for $\rho =2r/\lambda \to +\infty$

Recalling again Equation (57) for $\mathcal{E}$ and using a known asymptotic expansion of the exponential integral function ${\mathrm{E}}_1$ for large values of the argument (see, e.g., Ex. 2.2 on page 112 of [51]), for any $M\in \mathbb{N}$ we get

$$\mathcal{E}\left(\rho \right)=\frac{1}{\rho }\sum _{m=0}^M\frac{{(-1)}^{m}m!}{{\rho }^m}+O\left(\frac{1}{{\rho }^{M+2}}\right)\mathrm{for}\rho \to +\infty .$$

(69)

The above result allows us to derive the following asymptotic relations, for $\rho =2r/\lambda \to +\infty$:

$$\begin{array}{c}{\displaystyle T_{00}^{(◊)}\left(\mathbf{q}\right)=\frac{1}{8{\pi }^2{r}^4}\left[\frac{1}{{\rho }^2}-\frac{16}{3{\rho }^3}+\frac{30}{{\rho }^4}-\frac{192}{{\rho }^5}+O\left(\frac{1}{{\rho }^6}\right)\right],}\\ {\displaystyle T_{00}^{(\blacksquare )}\left(\mathbf{q}\right)=-\frac{3}{2{\pi }^2{r}^4}\left[\frac{1}{\rho }-\frac{2}{{\rho }^2}+\frac{20}{3{\rho }^3}-\frac{28}{{\rho }^4}+O\left(\frac{1}{{\rho }^5}\right)\right];}\end{array}$$

(70)

$$\begin{array}{c}{\displaystyle T_{rr}^{(◊)}\left(\mathbf{q}\right)=-\frac{1}{24{\pi }^2{r}^4}\left[\frac{1}{{\rho }^2}-\frac{4}{{\rho }^3}+\frac{36}{{\rho }^4}-\frac{96}{{\rho }^5}+O\left(\frac{1}{{\rho }^6}\right)\right],}\\ {\displaystyle T_{rr}^{(\blacksquare )}\left(\mathbf{q}\right)=-\frac{3}{2{\pi }^2{r}^4}\left[\frac{1}{\rho }-\frac{4}{3{\rho }^2}+\frac{10}{3{\rho }^3}-\frac{12}{{\rho }^4}+O\left(\frac{1}{{\rho }^5}\right)\right];}\end{array}$$

(71)

$$\begin{array}{c}{\displaystyle T_{\theta \theta }^{(◊)}\left(\mathbf{q}\right)=\frac{1}{12{\pi }^2{r}^2}\left[\frac{1}{{\rho }^2}-\frac{5}{{\rho }^3}+\frac{27}{{\rho }^4}-\frac{168}{{\rho }^5}+O\left(\frac{1}{{\rho }^6}\right)\right],}\\ {\displaystyle T_{\theta \theta }^{(\blacksquare )}\left(\mathbf{q}\right)=\frac{9}{4{\pi }^2{r}^2}\left[\frac{1}{\rho }-\frac{16}{9{\rho }^2}+\frac{50}{9{\rho }^3}-\frac{24}{{\rho }^4}+O\left(\frac{1}{{\rho }^5}\right)\right].}\end{array}$$

(72)

The above asymptotic expansions show that the renormalized stress-energy VEV vanishes quite rapidly for large values of r, that is for large distances from the impurity.

Apart from that, Equations (70)–(72) also allow us to infer that

$$\underset{\lambda \to 0^{+}}{lim}⟨0|{\widehat{T}}_{\mu \nu }\left(\mathbf{q}\right){|0⟩}_{ren}=0.$$

(73)

We recall that, for $\lambda =0$, the quantum field theory under analysis reduces to that of a free scalar field in empty Minkowski spacetime; in this regard, the identity (73) matches the physically sensible fact that the renormalized VEV of the stress-energy tensor vanishes identically when no potential (or no boundary) is present.