Abstract
The increased accessibility of drone technology and structure from motion 3D scene reconstruction have transformed the approach for mapping inaccessible slopes undergoing active rockfalls and generating virtual outcrop models (VOM). The Poggio Baldi landslide (Central Italy) and its natural laboratory offers the possibility to monitor and characterise the slope to define a workflow for rockfall hazard analysis. In this study, the analysis of multitemporal VOM (2016–2019) informed a rockfall trajectory analysis that was carried out with a physical-characteristic-based GIS model. The rockfall scenarios were reconstructed and then tested based on the remote sensing observations of the rock mass characteristics of both the main scarp and the rockfall fragment inventory deposited on the slope. The highest concentration of trajectory endpoints occurred at the very top of the debris talus, which was constrained by a narrow channel, while longer horizontal travel distances were allowed on the lower portion of the slope. To further improve the understanding of the Poggio Baldi landslide, a time-independent rockfall hazard analysis aiming to define the potential runout associated with several rock block volumetric classes is a critical component to any subsequent risk analysis in similar mountainous settings featuring marly–arenaceous multilayer sedimentary successions and reactivated main landslide scarps.
1. Introduction
Rockfall hazard is a well-known mass wasting phenomenon in mountainous regions. Notably, rockfalls have unusual properties, such as extreme velocity and a catastrophic nature, posing a very complex condition to act against. Due to this, in recent years new software and techniques for the study and simulation of this phenomenon have been developed. Some examples are provided in [,,], which showed the use of UAVs and GIS-based codes for runout simulations in the Central Apennines of Italy and East Spain, respectively. In [], the authors developed a new method to extract vegetation during simulations, while [] highlighted the identification of rockfall source areas at the regional scale through probabilistic analyses.
During a rockfall event, potential damages are associated with rocks reaching vulnerable elements during their descent down the slope [,,]. The volumes involved in a rockfall as well as its velocity and trajectories are the parameters that are directly related to the severity of the consequences of the event. The trajectories of the rock fragments depend on the slope geometry and the characteristics of the propagation zone, local asperities (i.e., jump features), and the mechanical characteristics of the exposed bedrock and soil cover. The quality of the results of rockfall analysis/simulations is directly related to the input parameters used. In particular, the geometry of the propagation area, the volume of the potential failing blocks, and the coefficient of restitution are key parameters during simulations []. The geometry of the propagation area and the coefficient of restitution can be interpreted using virtual outcrop models (VOMs) and field observations [,,,,,,], while the volume of blocks can be defined using geomechanical data or through the analysis and interrogation of past failures, when available [,]. In this context, one of the problems that often arises in rockfall simulations is the definition of rock block volumes when the structural condition varies within the slope [,]. In this study, we present a new approach to overcome this problem. A multitemporal remote sensing analysis of the slope was carried out to highlight different rockfall source sectors within the study area. In these sectors, we surveyed the discontinuity sets and their characteristics, such as spacing and persistence. These data were then used to calculate the volume of the potential rock blocks characterizing each area. Through this approach, it was possible to perform detailed rockfall simulations for each source area using specific structural/geomechanical data. The case example used for this purpose was the Poggio Baldi (PB) landslide in the Italian northern Apennines.
2. Study Area
The Poggio Baldi landslide (Figure 1) is in the Appennino Forlivese (Northern Apennines), in the vicinity of Poggio Baldi village. Poggio Baldi falls within the Foreste Casentinesi National Park in the Santa Sofia municipality (Forlì-Cesena FC, Emilia-Romagna). The landslide spans from 845 m asl at its main scarp to 467 m asl where the Bidente river cuts across the landslide body’s toe, and the road SS310 runs parallel to it. The Appennino Forlivese belongs to the Tosco-Emiliano sector of the Northern Apennines, a trust and fold orogenic belt verging N–E and oriented approximately WNW–ESE []. The Bidente river valley cuts into the Marnoso-Arenacea Formation (FMA). It is from the Miocene age [], and it is involved in a series of NW–SE oriented thrusts. The thrust front is cut by a series of high-angle direct faults nearly orthogonal to it. The FMA is composed of an alternation of sandstones and mudstones [,] showing well-defined and regular Bouma sequences, as described in []. The geomorphological setting is strongly controlled by the FMA lithologies combined with the geostructural evolution of the region. Along the Bidente river valley, the slope’s geometry is influenced by the juxtaposition of marl and sandstones. In the thrust back limb, strata are organized approximately in a monoclinal, gentle dipping structure (circa 30°) perpendicular to the main NW–SE thrust [].
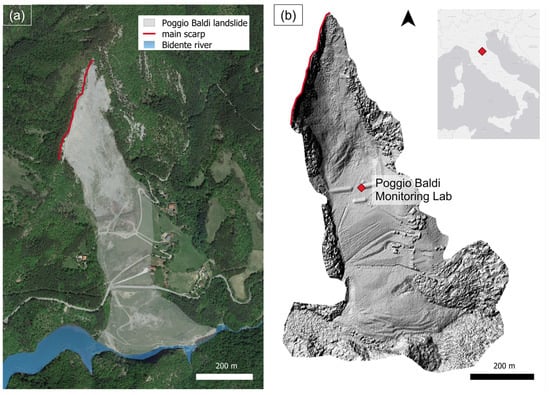
Figure 1.
Poggio Baldi landslide overview. The main subvertical landslide scar is highlighted in red (a). The location of the Poggio Baldi Monitoring Lab is also reported in the DEM (b).
The PB landslide is one of the largest slope instabilities of this Apennine sector. It mobilised nearly 4 × 106 m3 of rock, and it is still considered to be active, with a reactivation frequency of 100 years. Its main catastrophic events occurred in March 1914 and March 2010. The landslide’s initial activation is considered a large-scale wedge failure mechanism, which was inferred by the scarp geometry []. The latest reactivation occurred between 18 and 19 March 2010, when approximately 4 million cubic meters of material was mobilized, creating severe damage to several buildings and to the road SS310 [,]. After the development of tension cracks, the landslide body began to slowly move downward, reaching the Bidente river in 3 h, engulfing circa 16 × 104 m2 and damming the river, creating an ephemeral lake extending for 35 × 103 m2. The pluviometric archives report an unusual amount of rain and snow in the winter season before the reactivation; for this reason, it is considered to be one of the main triggers, in addition to the continuous ravelling of material from the summit of the scarp. The overload caused by the fallen blocks could have played a role in destabilizing the landslide body; some research estimated the increase in the material resting below the main 40 m scarp [].
According to [], this landslide can be classified as complex, a roto-translational slide evolved into an earthflow, with rockfall associated with the upper portion of the subvertical rock wall. The main scarp extends linearly for about 300 m, and its subvertical rock wall measures more than 100 m (Figure 2), with many suspended water conduits that seep through the rock mass and emerge within the rock wall. This is a highly unstable condition, leading to continuous rockfalls that have led to the deployment of several protection structures: three sand berms positioned at the toe of the debris body. In this study, we focus on the rockfall hazard posed by the continuous ravelling of rock blocks and its potential impact on human activities in the area affected by the rockfalls.

Figure 2.
Front view of the main Poggio Baldi landslide scarp. The three different members of the Marnoso-Arenacea Formation are distinguished by the different content ratios of marly and arenaceous strata.
In October 2021, the Poggio Baldi landslide became a permanent natural monitoring laboratory managed by the Department of Earth Sciences of Sapienza University of Rome. The lab employs the most advanced remote sensing tools to monitor the activity of the main rock scarp and the related debris talus at its toe. Over the years, many surveys and investigations have been carried out using modern remote sensing techniques (e.g., terrestrial laser scanning, drone photogrammetry, terrestrial InSAR, gigapixel imaging, and PhotoMonitoringTM) to acquire as much information as possible about active gravitational processes [,,].
3. Material and Methods
This paper aims to present a new method to study potential rockfall trajectories based on the identification of different source areas through the use of multitemporal remote sensing data and detailed structural analysis. Drone-based digital photogrammetry (DP) with structure from motion (SfM) techniques was exploited for the creation of slope VOMs. The geostructural characteristics of both the slope and the rock mass were extracted from both the generated point cloud and the orthomosaic. These were successively used to compute mean spacings and rock block volumes. Rock mass characterization and the rock block volumes were identified for each source sector to simulate the trajectories of falling blocks and define hazard zones. The results gathered by the presented approach were validated against past rockfall events recorded by different instruments over the years.
3.1. Virtual Outcrop Models
This section presents the VOMs that were built and exploited to detect rockfall and accumulation areas and derive the geostructural model. Digital photogrammetry (DP) from multitemporal drone surveys was implemented to derive three-dimensional point clouds and a high-resolution orthomosaic of the main rock scarp. The resulting point clouds were managed and processed within the software Cloud Compare []. The integration of information obtained from point clouds and the orthomosaic served the purpose of obtaining a reliable geostructural dataset (i.e., the discontinuity sets, their spacing, and the distribution of in situ rock blocks). Multitemporal surveys allowed us to identify and quantify rockfalls and subsequent debris accumulation.
Structure from motion (SfM) is a technique that is capable of reconstructing a high-resolution VOM of the object under investigation. It was developed during the 1990s [,,] based on the same stereoscopic principles of digital photogrammetry (DP), whereas the computer vision scientific community implemented most of the algorithms we use today [,,]. The SfM technique exploits the detection of homologous key points over large photographic datasets obtained with a large amount of redundancy and partial overlap among the pictures. This enables the reconstruction of sparse and dense point clouds and finally the 3D object []. This technique has made the use of DP easier and more attractive. In this study, a DJI Phantom 4 drone equipped with GPS, an IMU apparatus, and a 12.4 MPx onboard camera with a 1/2.32-inch sensor size and a 20 mm lens was used for the survey of the study area. The drone flights were made between 1:00 p.m. and 3:30 p.m. CET in April 2016 and May 2019. A total of 950 photographs were collected from different lines of sight, maintaining a constant distance from the outcrop. An overlap of about 70–80% was preserved between the frames. Both the reconstructed point clouds were georeferenced in the WGS84 UTM 32T coordinate system using a GNSS survey conducted during the April 2016 landslide survey, as described by []. Two dense point clouds (shown in Figure 3) were generated using the structure from motion (SfM) workflow implemented in the Agisoft LLC Metashape software [,,,,,,].

Figure 3.
SfM-based point clouds derived from the drone photogrammetric surveys. Campaigns were carried out in April 2016 (left) and May 2019 (right).
The photogrammetric point clouds (PCs) had totals of 26.6 × 106 and 73 × 106 points, respectively. Both point clouds were manually cleaned of vegetation points around the rocky scarp and the debris talus. The actual resolutions were established after cropping the rocky scarp, which were 220 pt/m2 and 657 pt/m2 for the 2016 and 2019 PCs, respectively. A preprocessing stage was carried out to standardise the PCs and make them comparable (i.e., a minimum distance between the nearest points at 0.1 m). The PCs were analysed and compared via CloudComapre® v.2.10.2 []. The pair of multitemporal point clouds were compared by taking advantage of the M3C2 algorithm [], taking care to account for the registration error, which had an RMSE equal to 0.2 m. This algorithm does not require interpolation but estimates the normal to the surface and the distance directly from the point cloud [,]. The three-dimensional comparison enabled us to identify specific sectors of the Poggio Baldi landslide reporting significant changes caused by rockfalls or deposition phenomena. In addition to the geometric localisation of these sectors, volume changes were measured with the 2.5D volume calculation algorithm embedded in CloudCompare® v. 2.10.2, which relies on the rasterization of clouds.
Following the point cloud reconstruction, an orthomosaic image of the rock scarp was computed from a set of overlapping drone images with the corresponding referencing information (Figure 4). It was derived from a process where several overlapping photos were stitched together with distortions removed to create a complete and continuous image representation of the rock scarp. An algorithm known as orthorectification was used to modify the photos based on the DSM information so that features were in their true locations. Finally, the orthorectified images were merged into a single orthomosaic, which was used to accurately measure distances and investigate fracture patterns.

Figure 4.
Orthomosaic extracted from the 2019 UAV survey.
The Poggio Baldi orthomosaic was derived from the drone images acquired during the May 2019 survey. After constructing the point cloud and the related DSM, a bounding box delimiting the rock scarp was defined before performing the orthorectification process. The final product covered a total area of about 40 × 103 m2 with a pixel size of 2.1 cm.
3.2. Slope Analysis
This section describes the remote-sensing-based approach that was used to characterize the rock-mass geostructural properties.
With the goal of extracting the main discontinuity features, we utilized the 3D discontinuity set extractor tool. As described in [,], the discontinuity set extractor (DSE) is a MATLABTM-based algorithm designed to extract a discontinuity’s geometrical properties from a laser or photogrammetric point cloud. The distinctive feature of DSE is its ability to exploit the real 3D information contained in each point and its corresponding neighbours to identify local differences in the geometry of the slope with no need to generate a mesh. The algorithm considers the points within a neighbouring space to compute best-fitting planes and attribute values directly to each point rather than the fitting patches. By using the raw data, the spatial orientation of each point is calculated only if it is coplanar with the adjacent points. This allows relative measurements to be obtained for each point rather than a single measurement for each surface identified in a 2.5D mesh. When the slope surface is primarily defined by discontinuity faces, the points in the cloud can be appropriately grouped into sets that define the predominant orientations and thus the discontinuity systems. Therefore, the joint sets are extracted in three main steps: (i) a local curvature computation using knn search [] and a PCA algorithm; (ii) a statical analysis using the 2D kernel density estimation function (kde2d) [] to define the main joint sets; and (iii) a cluster analysis through the DBSCAN algorithm [], which allows establishing points close enough to be considered a single surface.
Since point clouds are intrinsically non-uniform in terms of point density, a subsampling process was required. The selected minimum spatial distance between two adjacent points was set to 0.1 m. Therefore, this preprocessing step allowed uniform point densities throughout the rock scarp, thus reducing the problem of under- and over-represented surfaces (i.e., fewer points per area and more points per area, respectively) that would have biased the discontinuity extraction process. The discontinuity extraction was performed on the 2019 rock scarp point cloud following the modified approach implemented by [,]. Dominant densities were identified and removed, together with debris accumulations along the slope. The removal of the dominant joint set allowed the identification of the least represented surfaces. The value of the knn parameter was set to be equal to the mode of the k-nearest neighbours within an area of 1 m2. This value reflected the scale of the investigation and the need to overcome the complex local geological conditions (i.e., sandstone and marl–clay alternations), which determined the strong variations in the roughness of the exposed surfaces. Once the joint sets were extracted, the normal 3D spacing of each joint set was computed by analysing the relative position of each joint (considered to be nonpersistent) and measuring the orthogonal distances between them []. The mean normal spacing values were then exploited to compute the mean block volumes in each selected sector of interest []. Discontinuity systems that were only kinematically compatible with any type of failure were factors constraining the block volumes.
In addition to the three-dimensional analysis carried out by DSE, the orthomosaic was exploited by manually tracing the discontinuity planes in four selected representative areas of 400 m2 (20 × 20 m square) along the rock scarp. The vectorized fracture traces were subsequently analysed with the FracPaQ toolbox [] to quantify fracture patterns and spacings. FracPaQ is an open-source, cross-platform toolbox with a collection of MATLABTM programs designed to quantify fracture patterns in two dimensions from digital data, with user control over the output. Quantitative estimates for the attributes of individual fractures are returned as outputs. Since FracPaQ assumes that the input traces lie on a statistically flat surface, the investigated areas were adequately chosen within the source zones. Finally, to better constrain the bedding geometrical features, manual measurements of the orthomosaic were carried out. As a result, bedding spacings were integrated with the information derived from the 3D point cloud, thus constricting the mean block volumes.
Rockfall Hazard Analysis and Numerical Modelling
The volumes, trajectories, and velocities of rock fragments represent the main parameters that directly determine rockfall hazard []. From the different methods available to assess susceptibility and hazard for rockfall events [,,] and characterise the 3D rockfall events [], we selected a well-established strategy to quantify the probability for a rockfall to reach vulnerable elements and generate negative consequences. Probabilistic rockfall trajectory analysis tries to minimise both ontic and epistemic uncertainty by introducing a certain degree of variability in the inputs []. As described in [], the geometry of a slope plays a critical role in guiding a rockfall path down the slope. A digital elevation model of this geometry is the fundamental dataset that numerical simulations rely upon. Defining the characteristics in terms of the elasticity of the slope was of critical importance [,], and to achieve this the slope was divided into homogeneous areas exhibiting similar mechanical characteristics. The rockfall model was implemented using Rockyfor3D, and the outcomes of the simulation runs were postprocessed in GIS to be further investigated. The physical characteristics of the slope were assigned through the digital mapping of the slope domains, such as the average scree diameter, the outcropping bedrock, and the thickness of the debris cover; the mapping was validated through both the photointerpretation of the high-resolution images from the drone survey and the field observations. The values in terms of Rn were assigned following the guidelines given by [,], and the MOH values were modified according to expert judgement and the availability of the direct measurement of the scree geometry on the point cloud (2019).
The fundamental information needed to generate accurate rockfall models is the topographical representation of the slope. In the case of GIS-based methods, DEM provides the virtual surface from which to compute the types of motion (freefall, bounce, roll, or drag) of the falling rock blocks.
Rockyfor3D uses a three-dimensional rigid-body impact model that allows the calculation of the trajectories of single individually falling rocks with discrete geometry. This software can be used for regional, local, and slope-scale rockfall simulations []. The input parameters that define rock blocks are the release cell location, rock density, shape, volume, and initial vertical velocity. The local slope surface roughness is represented by a parameter defined as the height of a representative obstacle (MOH), expressed in m. Typical MOH values, as suggested by [], are represented by three statistical classes, rg70%, rg20%, and rg10%. During each rebound calculation, the MOH value in a cell is randomly chosen from the three representative values according to their probabilities of occurrence. Finally, the soil type is defined through a raster map identifying the type of bedrock exposed.
where MOH (mean obstacle height) or rg values are estimated, Dp is the penetration depth of the block, and R is the radius of the computed block. In RF3D the maximum penetration depth equals the radius of the falling block. In this study, we used a 3 × 3 m resolution DEM extracted from the 2019 SfM point cloud. The locations of the release points were selected based on 3D change detection. Field inspection and a geomorphological analysis of high-resolution aerial images were undertaken to define the slope roughness (MOH values) and soil type (Rn). The tangential coefficient of restitution (Rt) was automatically calculated by Rockyfor3D through the composition and size of the material covering the surface and the radius of the falling block []. The rock density, shape, and volume were defined by combining field and remote-sensed geostructural data. For modelling the upper scarp’s rockfalls in Poggio Baldi, we relied on a variety of remote sensing techniques, each contributing to constrain the numerical modelling. The positions of the source and deposition areas were extracted from the M3C2 analysis. The modelled scenarios were defined a priori based on the slope geomechanical analysis and the distribution of rockfall fragments along the slope. The M3C2 change detection was critical to select the objective source areas on the slope; the volumetric classes were chosen as the most representative for the analysis to be carried out. Although we consider this analysis to be time-independent, some considerations about the magnitude of the rockfall were simulated.
4. Results
In this section, the results obtained from the SfM-based point cloud, as well as from the orthomosaic processing, are presented with respect to three-dimensional changes and rock mass characterization. Furthermore, block volume estimations were exploited as inputs to model the rockfall-associated hazard.
4.1. Three-Dimensional Change Detection
The 3D change detection led us to identify geometrical differences that were representative of three years of gravitational processes in the study area. Sectors in which there were negative differences corresponded to loss areas (i.e., highly unstable areas subject to rockfalls). In contrast, areas in which there were positive differences corresponded to accumulation areas, which were located along the base of the scarp, consisting of heterogeneous debris that accumulated over time (Figure 5). The results revealed how four portions of the scarp were more affected by rockfalls. Hereafter, we refer to these most active sectors in terms of rock block release as Z1, Z2, Z3, and Z4, as reported by the white dashed polygons in Figure 5. Over the time span being considered, the four source zones discharged more than 3000 m3 of rock materials, which accumulated in the debris talus at its toe, as revealed by the 3D change detection (Table 1).
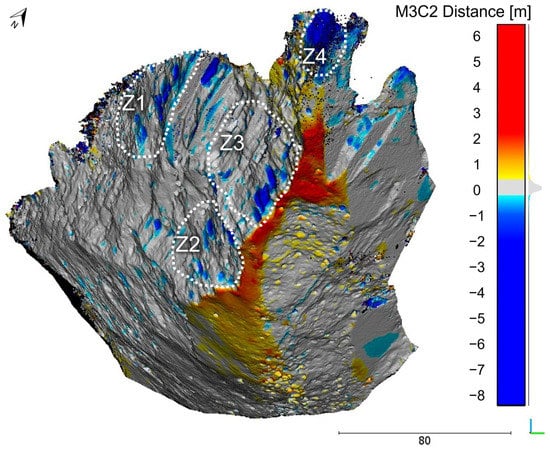
Figure 5.
Analysis of three-dimensional differences between the 2016 and 2019 SfM point clouds. White contour lines indicate sectors from which the largest volumes of rock have detached. The colour bar is saturated at ±8 m, and the detection threshold is set to ±0.3 m.

Table 1.
Surface and volume estimation related to rockfall processes that occurred between April 2016 and May 2019 at the Poggio Baldi rock scarp.
4.2. Geostructural Characterization
A 3D geostructural analysis carried out on clipped point clouds representative of the four source zones led us to group the exposed fracture planes into five different joint sets (Figure 6). Although within each of the individual zones along the scarp it was clear that there were five dominant discontinuity sets, some differences were observed concerning their principal orientation (Figure 7). Similarities appeared between Z1 and Z2 as well as between Z3 and Z4. Among the source zones, J3, which represents the north-dipping discontinuities, appeared to be the joint set that varied the most, whereas J1 (i.e., the slope face) resulted in the most dominant and conforming set (Table 2). The bedding strata, grouped as J2, were south dipping, with dip angles varying from 33 to 46 degrees.
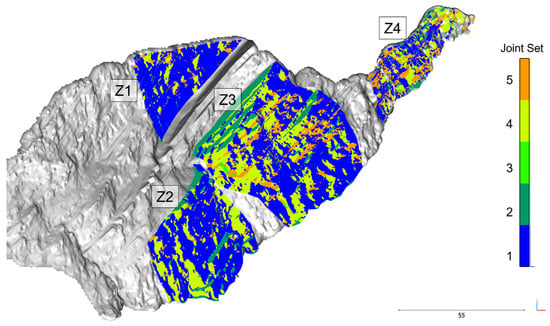
Figure 6.
Poggio Baldi rock scarp with discontinuity planes within each source sector coloured according to the assigned joint set.

Figure 7.
Stereoplot of discontinuity planes extracted utilizing DSE software at the selected source sectors.

Table 2.
Principal orientations of discontinuities extracted from source sectors in the 2019 SfM point cloud.
Joint spacings were estimated for each discontinuity set and each analysed sector. The distribution of the measured spacing values is depicted on the density plots (Figure 8) for each slope sector, assuming nonpersistent joints. Based on the spacing densities, J1, J4, and J5 had evenly distributed spacing values along the sectors, resulting in skewed peak densities around 1.5 m. J2 and J3, which were represented by a minor number of discontinuity planes with roughly distributed spacing values, resulted in wide density distributions characterised by long tails and no tight peaks. Following the distribution analysis, it is clear that the mean spacing of J2 derived from the 3D PC did not represent an accurate value, thus leading to the need to better constrain the bedding strata. The mean spacing values related to the density curves are summarised in Table 3.
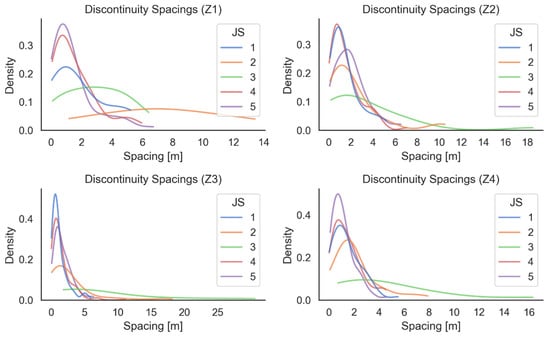
Figure 8.
Normal spacing value distributions of discontinuity planes by joint set and source zone.

Table 3.
Joint set normal mean spacings in the different source sectors.
In fact, the bedding strata of J2 were highly underestimated by the DSE analysis due to their orientation (orthogonal to the slope face) and the low presence of surfaces illuminated by daylight to be measured, thus affecting the three-dimensional geostructural results and all related analyses (e.g., joint spacings). To overcome this limitation, the discontinuity planes were also mapped in the orthomosaic within square boxes of 20 m per side (Figure 9). As a result, scalable vector graphics with discontinuity traces composed of one or more segments delimited by nodes were obtained, thus allowing the computation of quantitative patterns, with a focus on the bedding strata (Figure 10).

Figure 9.
Orthomosaic of the Poggio Baldi rock scarp, with 20 × 20 m frames for each source sector (top). Details of source sector frames (1, 2, 3, and 4), with the manually traced fractures in red (bottom).
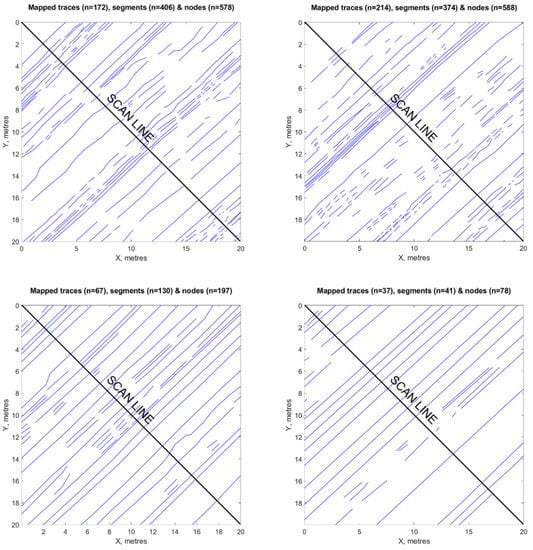
Figure 10.
Bedding strata were manually traced from the orthomosaic within the box of each source sector.
The resulting mean spacing values, gathered from both PC-based spacing distributions and orthophoto interpretations for each joint set and sector, are presented in Table 3. They provide clear evidence that the 2D-based discontinuity analysis returned far lower values of mean spacing for J2 (i.e., J2-OM in Table 3), which never exceeded 1.5 m. This contrasts with the results of the bedding spacings obtained from the 3D fracture analysis, which returned mean spacing values of up to 7 m.
After calculating the formed block based on the intersection of J1, J2, and J3, the resulting volumes (Figure 11) were determined for both the PC and the PC integrated with the orthomosaic (PC + OM) joint analysis. The mean volumes of the formed blocks obtained from the PC-based spacing corresponded to 39.75 m3, 10.93 m3, 26.01 m3, and 14.79 m3; while the PC + OM-based spacing analysis returned volumes of about 5.17 m3, 4.76 m3, 8.65 m3, and 9.48 m3 for sectors 1, 2, 3, and 4, respectively (Figure 11).
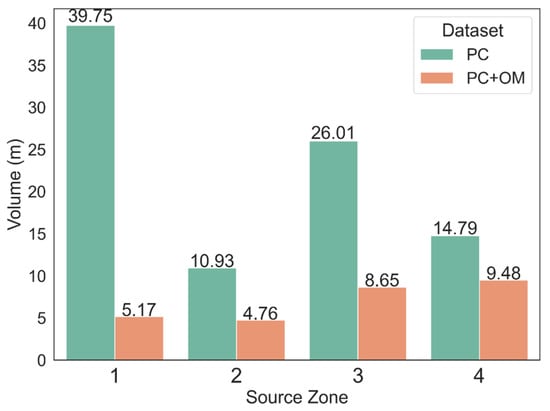
Figure 11.
Mean block volume estimation by source sector and dataset.
4.3. Three-Dimensional Rockfall Trajectory Analysis
Two accumulation zones, A and B, were identified (Figure 12a); accumulation zone A represents the area where most of the accumulation occurred (small volume blocks—Figure 5), while accumulation zone B represents the area where sparse higher-volume blocks can arrive, and it was defined by integrating the M3C2 analysis (Figure 5) with field and orthophoto observations. The accumulation zones and the rockfall fragment inventory were considered during the model’s calibration phases, offering a clear spatial distribution of the volumetric block classes. Finally, based on the GIS interpretation and field survey, a land-use map, with associated rockfall propagation characteristics, was created for use as an input for the subsequent RF3D analysis (Figure 12c). In Table 4, the parameters used in the formal RF3D simulations are provided.
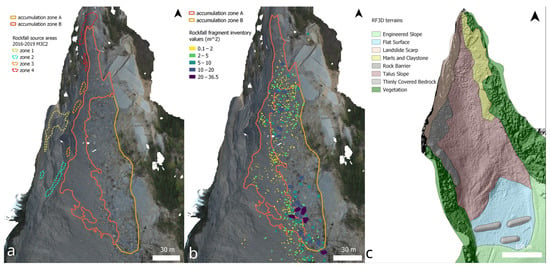
Figure 12.
Rockfall accumulation zones in the upper PB landslide. The source areas, as reported by the M3C2 analysis, are shown in panel (a). Panel (b) reports the superficial rockfall fragment inventory. The terrain subdivisions adopted for the RF3D modelling are reported in panel (c).

Table 4.
RF3D parameters.
The rockfall scenarios were hypothesised based on the formed rock block volume estimation, as reported in Figure 11.
In Figure 13, we report the spatial distribution of the intensity of deposited block, i.e., the number of blocks deposited. The NBD layer (number of blocks deposited) is compared against the target areas, where the warm colours represent the highest number of individual blocks that stopped in the pixel. In Table 5, the total number of source cells per Z is reported, given 10,000 simulated blocks per cell (i.e., the total number of rock blocks falling from each source area). According to the extensive research carried out by [,], the probabilistic models with the lowest and least frequent trajectories (outliers) were removed from the final results. Any value below the 1.5% threshold was considered unrealistic under the working assumptions of this simulation. Both NBD layers demonstrated how the runout of the simulated blocks was distributed well within the M3C2 2016–2019 boundaries; the highest concentration of trajectory endpoints occurred at the very top of the scarp, in the northernmost sector, constrained by the narrow channel, while on the lower portion of the slope the geometry allowed for longer horizontal travel distances. The general direction of the rockfall propagation was South-South-East. The rockfall simulation carried out with volumes extracted from the PC analysis showed that rock blocks reached the homogeneous scree of M3C2-extracted accumulation zone A and overflowed onto accumulation area B (Figure 13b). The simulation undertaken using the PC + OM dataset seemed to better replicate the target defined by M3C2-extracted accumulation zones A and B, with a good cover of accumulation zone A and few blocks reaching zone B (Figure 13a, in agreement with the results highlighted in Figure 5 and Figure 12b).
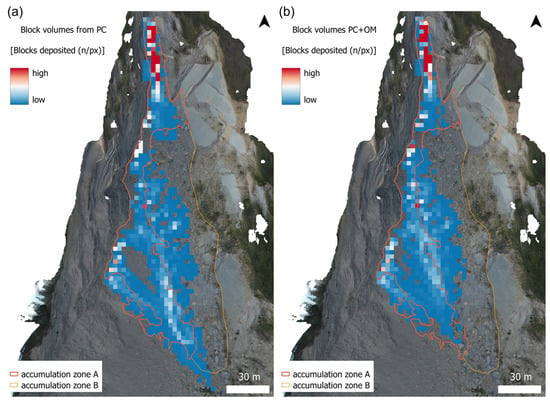
Figure 13.
RF3D results, as the number of blocks deposited per pixel. Panel (a) shows the simulation results obtained with the volume distribution of the PC analysis, while panel (b) shows the results from the PC + OM analysis. Refer to Table 5 for the simulation parameters.

Table 5.
Simulation characteristics for each source area, with 10,000 trajectories simulated per source pixel.
5. Discussion
Three-dimensional change detection was carried out between two photogrammetric georeferenced point clouds. The time span was about three years, from April 2016 to May 2019. From this multitemporal analysis, four active sectors of the rock scarp and a delimited accumulation area were identified, thus providing clear evidence of the state of activity of the landslide, which is releasing thousands of cubic meters of rockfalls per year, as also reported in []. With regards to the accumulation area, rockfalls tend to accrue along a channel developed at the edges of a residual debris pile related to the main March 2010 reactivation, which is currently slowly moving downslope []. This morphology is revealed by the vertical profiles shown in Figure 14. Furthermore, the 3D change detection provided an estimate of the volumes involved, which represents a proxy for the activity rate. Lost volumes within the four analysed sectors located over the rock scarp represent most of the total gained volume at the toe, thus revealing the main contribution of these areas in terms of rock block release. This agrees with the findings reported in []. Although critical for generating comprehensive landslide scenarios and specific volumetric classes to simulate during the trajectory analysis, the relatively short time span of the subsequent SfM surveys represents the largest obstacle to the definition of a frequency–magnitude relationship. Extrapolating a realistic trend seems to be impossible, given the available observations. It is strongly advised to interpret this study’s results in terms of a very likely scenario, the typical rockfall event for the Poggio Baldi slope, which does not necessarily investigate the whole spectrum of possible landslide scenarios.
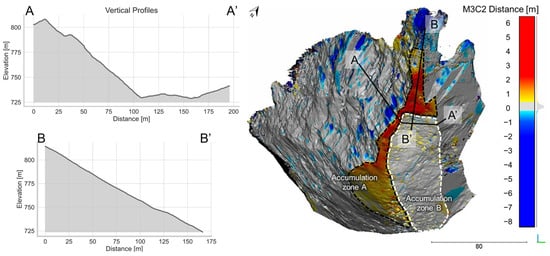
Figure 14.
Three-dimensional change detection of UAV-based point clouds in highlighted accumulation zones A and B (right side). Orthogonal vertical profiles showing the morphology of the slope (left side).
As a result, a further analysis was performed to investigate the potential block volume involved and the related runouts. For the former purpose, information about geometric parameters such as discontinuity sets and joint spacing were computed by integrating 2D and 3D UAV-derived remote sensing data. We stress that in the case of complex and heterogeneous lithologies, semi-automatic software needs to be integrated with expert-controlled tools to obtain accurate results []. Based on the 3D point cloud, five different joint sets and their spacing values were identified along the slope. For each studied sector, specific spacing values were derived from the 3D point cloud. However, due to the lack of daylight in the bedding strata, its automatically extracted spacing values appeared to be unrepresentative for the overall rock mass, and the relative block volume was overestimated. This was confirmed by the orthomosaic-based analysis, which revealed the true mean spacing value of the bedding within the investigated areas, which was significantly lower than the value derived from the automatic discontinuity extraction from the 3D point cloud (a difference of up to 6.2 m in zone 1, where sandstones prevail over marls). Hence, the potential formed block volumes computed by integrating both automatic and orthomosaic-based analysis spacing values appeared to be more consistent with the in situ rock blocks (Figure 15), which stand around 5.75 m3. The performed geostructural characterization highlighted how different members of the FMA, which correspond to different content ratios of marly and arenaceous strata, result in differently formed blocks along the slope. With this perspective, we stress the importance of performing sector-specific studies when heterogeneous rock masses must be characterized.

Figure 15.
Overview of the left part of the Poggio Baldi landslide rock scarp and details of typical in situ rock block dimensions measured from the point cloud (white box).
With regards to the rockfall simulation, the PC + OM dataset volume distribution successfully adhered to the available ground truth data, exhibiting a total runout distance and spread compliant with accumulation zones A and B. The PC volume distribution showed acceptable results concerning accumulation zone A, but an overflow on accumulation zone B. This was related to the relatively larger volume of the blocks, which was interpreted as overestimated when using automatic spacing extraction. The residual debris highlighted in Figure 14, vertical section A-A’, a mound of large rock fragments mixed with loose sediment, is an obstacle for the eastward propagation of rockfalls that was highlighted by both the M3C2 analysis and the RF3D results in Figure 13, and only a sparse number of higher-volume blocks reach this area (accumulation zone B). The main limitation of this approach is that it requires a very large set of multitemporal observations, which are most often not available, to perform adequately. Extremely rare rockfall events are challenging to record and describe. Hence, the balance between deterministic knowledge, input parameters, and the stochastic nature of rockfall modelling is of upmost importance, so the validity of such studies still largely relies on practitioners’ intuition and expert judgement. The justification for the adoption of this study’s workflow arises from the iterative model calibration process developed throughout the analysis, which provided runout characteristics that were in good agreement with the available high-resolution interpreted images.
The use of localised source areas rather than diffused hazard modelling offered higher control over the calibration of the model, as shown in Figure 15. Individual block detail provided a more rigorous comparison between the RF3D results, the rockfall fragment inventory, and the M3C2 target area. Rockfall hazard practitioners will understand the inherent challenges of defining the range of the MOH values accounting for the microroughness of the slope, which are usually obtained through time-consuming photointerpretation and manual point cloud measurements. In this study, we failed to find a suitable programmatic approach to characterise the obstacles on the slope and had to rely on manual measurements of the scree slope in the point clouds. The time-independent rockfall hazard analysis explored the effects of geomorphological processes affecting the main scarp and the whole landslide; the RF3D simulation results explored the behaviour of the rockfall activity, especially considering the constraints given by the source and accumulation areas highlighted by the M3C2 analysis. This provides a starting point for any further investigation regarding the magnitude–frequency relationship [] of the Poggio Baldi rockfall activity and future investigations in similar case studies characterized by complex geological/lithological settings.
6. Conclusions
Virtual outcrop models of the Poggio Baldi scarp area were successfully utilized to provide key data for the monitoring and assessment of rockfalls. By combining information derived from three-dimensional point clouds and the high-resolution orthomosaic, it was possible to extract and quantify fracture patterns that characterized the rock mass and defined block volumes. Multitemporal surveys allowed us to identify specific sectors of the slope where rockfalls occurred most frequently as well as the related accumulation zones at its toe. In addition, the overall lost and gained volumes were calculated to assess the activity of the slope.
To model the associated rockfall hazard, we simulated rockfall trajectories using the potential formed block volumes in each active sector of the slope. This was achieved utilizing joint spacing values resulting from the integration of 3D automatic extraction tools using point cloud data and 2D discontinuities that were manually extracted from the orthomosaic data. The use of both methods was required to provide more representative data due to the unreliable results gathered for bedding strata spacing in the automatic extraction procedure (not enough bedding surfaces illuminated by daylight were captured by the PC analysis), thus highlighting the need for expert judgement when using automatic tools for discontinuity set extraction. Subsequently, the potential formed blocks were used as input data for run-out modelling, which was validated based on the 3D change detection results.
The resulting rockfall conceptual model was tested by means of a 3D process-based probabilistic trajectory analysis; the parametrization of the model was informed by the geostructural analysis and the available remote sensing datasets and geomorphological observations. A time-independent rockfall hazard assessment demonstrated (i) the geometrical characteristics of the rockfalls affecting the different sectors of the main scarp, (ii) the benefits of differentiating the source areas based on 3D change detection, and (iii) the importance of using structure-derived data for more accurate modelling. Furthermore, the rockfall modelling coupled with the 3D change detection provided further insight into the actual time-dependent behaviour of the active processes on the Poggio Baldi slope. However, most of the information regarding the frequency–magnitude relationship of the Poggio Baldi rockfalls was extremely hard to interpret from the geomorphology of the landslide area, thus limiting the application of failure probability or frequency in rockfall hazard modelling.
In a more general perspective, we demonstrated that the availability of multitemporal data (3D models or images) of rock scarps may allow us to better calibrate simulations and, consequently, provide better designs for protection measures. Considering the drastically increased accessibility of tools for multitemporal data collection, we conclude that the systematic collection of virtual outcrop models of rock slopes may significantly support rockfall hazard practices.
Author Contributions
Conceptualization, C.R., G.M. and M.F.; methodology, C.R. and G.M.; formal analysis, C.R. and G.M.; investigation, C.R., G.M., M.F. and P.M.; data curation, C.R. and G.M.; writing—original draft preparation, C.R. and G.M.; writing—review and editing, M.F., M.E., J.C. and P.M.; supervision, P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research is a part of the project “Dipartimento di Eccellenza per le Scienze della Terra—Laboratorio naturale di Poggio Baldi” (Sapienza University of Rome—Years 2018–2022, P.I. Prof. Paolo Mazzanti). This work was also supported by NHAZCA Srl, a spin-off company of the University of Rome “Sapienza”, the Department of Earth Sciences of the University of Rome “Sapienza”, and the Parco Nazionale delle Foreste Casentinesi, Monte Falterona e Campigna.
Data Availability Statement
The data are contained within the article.
Acknowledgments
The authors wish to thank Roberto Fabbri, the Pro loco Corniolo-Campigna Association, and G. Pini for the logistic support provided during the field surveys.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sarro, R.; Riquelme, A.; García-Davalillo, J.C.; Mateos, R.M.; Tomás, R.; Pastor, J.L.; Cano, M.; Herrera, G. Rockfall Simulation Based on UAV Photogrammetry Data Obtained during an Emergency Declaration: Application at a Cultural Heritage Site. Remote Sens. 2018, 10, 1923. [Google Scholar] [CrossRef]
- Francioni, M.; Antonaci, F.; Sciarra, N.; Robiati, C.; Coggan, J.; Stead, D.; Calamita, F. Application of Unmanned Aerial Vehicle Data and Discrete Fracture Network Models for Improved Rockfall Simulations. Remote Sens. 2020, 12, 2053. [Google Scholar] [CrossRef]
- Schilirò, L.; Robiati, C.; Smeraglia, L.; Vinci, F.; Iannace, A.; Parente, M.; Tavani, S. An Integrated Approach for the Reconstruction of Rockfall Scenarios from UAV and Satellite-Based Data in the Sorrento Peninsula (Southern Italy). Eng. Geol. 2022, 308, 106795. [Google Scholar] [CrossRef]
- Bonneau, D.A.; DiFrancesco, P.-M.; Hutchinson, D.J. A Method for Vegetation Extraction in Mountainous Terrain for Rockfall Simulation. Remote Sens. Environ. 2020, 251, 112098. [Google Scholar] [CrossRef]
- Rossi, M.; Sarro, R.; Reichenbach, P.; Mateos, R.M. Probabilistic Identification of Rockfall Source Areas at Regional Scale in El Hierro (Canary Islands, Spain). Geomorphology 2021, 381, 107661. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Ghigi, S. Rockfall Hazard and Risk Assessment along a Transportation Corridor in the Nera Valley, Central Italy. Environ. Manag. 2004, 34, 191–208. [Google Scholar] [CrossRef]
- Michoud, C.; Derron, M.-H.; Horton, P.; Jaboyedoff, M.; Baillifard, F.-J.; Loye, A.; Nicolet, P.; Pedrazzini, A.; Queyrel, A. Rockfall Hazard and Risk Assessments along Roads at a Regional Scale: Example in Swiss Alps. Nat. Hazards Earth Syst. Sci. 2012, 12, 615–629. [Google Scholar] [CrossRef]
- Scavia, C.; Barbero, M.; Castelli, M.; Marchelli, M.; Peila, D.; Torsello, G.; Vallero, G. Evaluating Rockfall Risk: Some Critical Aspects. Geosciences 2020, 10, 98. [Google Scholar] [CrossRef]
- Gili, J.A.; Ruiz-Carulla, R.; Matas, G.; Moya, J.; Prades, A.; Corominas, J.; Lantada, N.; Núñez-Andrés, M.A.; Buill, F.; Puig, C.; et al. Rockfalls: Analysis of the Block Fragmentation through Field Experiments. Landslides 2022, 19, 1009–1029. [Google Scholar] [CrossRef]
- Gallo, I.G.; Martínez-Corbella, M.; Sarro, R.; Iovine, G.; López-Vinielles, J.; Hérnandez, M.; Robustelli, G.; Mateos, R.M.; García-Davalillo, J.C. An Integration of UAV-Based Photogrammetry and 3D Modelling for Rockfall Hazard Assessment: The Cárcavos Case in 2018 (Spain). Remote Sens. 2021, 13, 3450. [Google Scholar] [CrossRef]
- Robiati, C.; Eyre, M.; Vanneschi, C.; Francioni, M.; Venn, A.; Coggan, J. Application of Remote Sensing Data for Evaluation of Rockfall Potential within a Quarry Slope. ISPRS Int. J. Geo. Inf. 2019, 8, 367. [Google Scholar] [CrossRef]
- Onsel, I.E.; Donati, D.; Stead, D.; Chang, O. Applications of Virtual and Mixed Reality in Rock Engineering. In Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, Seattle, Washington, 17–20 June 2018. [Google Scholar]
- Lato, M.J.; Diederichs, M.S.; Hutchinson, D.J.; Harrap, R. Evaluating Roadside Rockmasses for Rockfall Hazards Using LiDAR Data: Optimizing Data Collection and Processing Protocols. Nat. Hazards 2012, 60, 831–864. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Oppikofer, T.; Abellán, A.; Derron, M.-H.; Loye, A.; Metzger, R.; Pedrazzini, A. Use of LIDAR in Landslide Investigations: A Review. Nat. Hazards 2012, 61, 5–28. [Google Scholar] [CrossRef]
- Abellán, A.; Oppikofer, T.; Jaboyedoff, M.; Rosser, N.J.; Lim, M.; Lato, M.J. Terrestrial Laser Scanning of Rock Slope Instabilities. Earth Surf. Process. Landf. 2014, 39, 80–97. [Google Scholar] [CrossRef]
- Eltner, A.; Kaiser, A.; Castillo, C.; Rock, G.; Neugirg, F.; Abellán, A. Image-Based Surface Reconstruction in Geomorphometry – Merits, Limits and Developments. Earth Surf. Dyn. 2016, 4, 359–389. [Google Scholar] [CrossRef]
- Bonneau, D.; DiFrancesco, P.-M.; Hutchinson, D.J. Surface Reconstruction for Three-Dimensional Rockfall Volumetric Analysis. ISPRS Int. J. Geo. Inf. 2019, 8, 548. [Google Scholar] [CrossRef]
- Sarro, R.; María Mateos, R.; Reichenbach, P.; Aguilera, H.; Riquelme, A.; Hernández-Gutiérrez, L.E.; Martín, A.; Barra, A.; Solari, L.; Monserrat, O.; et al. Geotechnics for Rockfall Assessment in the Volcanic Island of Gran Canaria (Canary Islands, Spain). J. Maps 2020, 16, 605–613. [Google Scholar] [CrossRef]
- Francioni, M.; Stead, D.; Sciarra, N.; Calamita, F. A New Approach for Defining Slope Mass Rating in Heterogeneous Sedimentary Rocks Using a Combined Remote Sensing GIS Approach. Bull. Eng. Geol. Environ. 2019, 78, 4253–4274. [Google Scholar] [CrossRef]
- McKenzie, D. Active Tectonics of the Mediterranean Region. Geophys. J. Int. 1972, 30, 109–185. [Google Scholar] [CrossRef]
- Martelli, L.; Camassi, R.; Catanzariti, R.; Fornaciari, L.; Spadafora, E. Explanatory Notes of the Geological Map of Italy, Scale 1:50,000, Sheet 265 “Bagno Di Romagna”; APAT and Geological Survey of Italy: Rome, Italy, 2002. [Google Scholar]
- Ricci Lucchi, F. The Miocene Marnoso-Arenacea Turbidites, Romagna and Umbria Apennines. Excursion N 7, Excursion Guidebook. In Proceedings of the 2nd International Association of Sedimentologists Regional Meeting, Bologna, Italy, 13–15 April 1981. [Google Scholar]
- Benini, A.; Farabegoli, E.; Martelli, L.; Severi, P. Stratigrafia e Paleogeografia Del Gruppo Di S. Sofia (Alto Appennino Forlivese). Mem. Descr. Della Carta Geol. d’Ital. 1992, 46, 231–243. [Google Scholar]
- Mutti, E.; Bernoulli, D.; Lucchi, F.R.; Tinterri, R. Turbidites and Turbidity Currents from Alpine ‘Flysch’ to the Exploration of Continental Margins. Sedimentology 2009, 56, 267–318. [Google Scholar] [CrossRef]
- Esposito, C.; Di Luzio, E.; Baleani, M.; Troiani, F.; Seta, M.D.; Bozzano, F.; Mazzanti, P. Fold architecture predisposing deep-seated gravitational slope deformations within a flysch sequence in the northern apennines (Italy). Geomorphology 2021, 380, 107629. [Google Scholar] [CrossRef]
- Bortolotti, V. Guide Geologiche Regionali. Appennino Tosco-Emiliano; BE-MA: Milano, Italy, 1992. [Google Scholar]
- Benini, A.; Biavati, G.; Generali, M.; Pizziolo, M. The Poggio Baldi Landslide (High Bidente Valley): Event and Post-Event Analysis and Geological Characterization. In Proceedings of the 7th EUREGEO–European Congress on Regional GEOscientific Cartography and Information Systems, Bologna, Italy, 12–15 June 2012; pp. 64–65. [Google Scholar]
- Mazzanti, P.; Bozzano, F.; Brunetti, A.; Caporossi, P.; Esposito, C.; Mugnozza, G.S. Experimental Landslide Monitoring Site of Poggio Baldi Landslide (Santa Sofia, N-Apennine, Italy). In Proceedings of the Advancing Culture of Living with Landslides; Mikoš, M., Arbanas, Ž., Yin, Y., Sassa, K., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 259–266. [Google Scholar]
- Varnes, D.J. Slope Movement Types and Processes. Spec. Rep. 1978, 176, 11–33. [Google Scholar]
- Mazzanti, P.; Caporossi, P.; Brunetti, A.; Mohammadi, F.I.; Bozzano, F. Short-Term Geomorphological Evolution of the Poggio Baldi Landslide Upper Scarp via 3D Change Detection. Landslides 2021, 18, 2367–2381. [Google Scholar] [CrossRef]
- Romeo, S.; Cosentino, A.; Giani, F.; Mastrantoni, G.; Mazzanti, P. Combining Ground Based Remote Sensing Tools for Rockfalls Assessment and Monitoring: The Poggio Baldi Landslide Natural Laboratory. Sensors 2021, 21, 2632. [Google Scholar] [CrossRef] [PubMed]
- Girardeau-Montaut, D. Détection de Changement Sur Des Données Géométriques Tridimensionnelles. Ph.D. Thesis, Télécom ParisTech, Paris, France, 2006. [Google Scholar]
- Spetsakis, M.E.; Aloimonos, J. (Yiannis) Structure from Motion Using Line Correspondences. Int. J. Comput. Vis. 1990, 4, 171–183. [Google Scholar] [CrossRef]
- Boufama, B.; Mohr, R.; Veillon, F. Euclidean Constraints for Uncalibrated Reconstruction. In Proceedings of the 1993 (4th) International Conference on Computer Vision, Berlin, Germany, 11–14 May 1993; pp. 466–470. [Google Scholar]
- Szeliski, R.; Kang, S.B. Recovering 3D Shape and Motion from Image Streams Using Nonlinear Least Squares. J. Vis. Commun. Image Represent. 1994, 5, 10–28. [Google Scholar] [CrossRef]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; Volume 1, pp. 519–528. [Google Scholar]
- James, M.R.; Robson, S. Straightforward Reconstruction of 3D Surfaces and Topography with a Camera: Accuracy and Geoscience Application. J. Geophys. Res. Earth Surf. 2012, 117, F03017. [Google Scholar] [CrossRef]
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3D Imaging; De Gruyter: Berlin, Germany, 2019; ISBN 978-3-11-060725-3. [Google Scholar]
- Carrivick, J.L.; Smith, M.W.; Quincey, D.J. Structure from Motion in the Geosciences; John and Wiley and Sons: Hoboken, NJ, USA, 2016; ISBN 978-1-118-89583-2. [Google Scholar]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the World from Internet Photo Collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef]
- Arya, S.; Mount, D.M.; Netanyahu, N.S.; Silverman, R.; Wu, A.Y. An Optimal Algorithm for Approximate Nearest Neighbor Searching Fixed Dimensions. J. ACM 1998, 45, 891–923. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D Comparison of Complex Topography with Terrestrial Laser Scanner: Application to the Rangitikei Canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Stumpf, A.; Malet, J.-P.; Allemand, P.; Pierrot-Deseilligny, M.; Skupinski, G. Ground-Based Multi-View Photogrammetry for the Monitoring of Landslide Deformation and Erosion. Geomorphology 2015, 231, 130–145. [Google Scholar] [CrossRef]
- Riquelme, A.J.; Abellán, A.; Tomás, R.; Jaboyedoff, M. A New Approach for Semi-Automatic Rock Mass Joints Recognition from 3D Point Clouds. Comput. Geosci. 2014, 68, 38–52. [Google Scholar] [CrossRef]
- Riquelme, A.; Cano, M.; Tomás, R.; Abellán, A. Identification of Rock Slope Discontinuity Sets from Laser Scanner and Photogrammetric Point Clouds: A Comparative Analysis. Procedia Eng. 2017, 191, 838–845. [Google Scholar] [CrossRef]
- Friedman, J.H. A Recursive Partitioning Decision Rule for Nonparametric Classification. IEEE Trans. Comput. 1977, 26, 404–408. [Google Scholar] [CrossRef]
- Botev, Z.I.; Grotowski, J.F.; Kroese, D.P. Kernel Density Estimation via Diffusion. Ann. Stat. 2010, 38, 2916–2957. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining; AAAI Press: Portland, Oregon, 1996; pp. 226–231. [Google Scholar]
- Farmakis, I.; Hutchinson, D.J. Semi-Automated Discontinuity Orientation Extraction in Complex Rock Masses Using Single-Scan LiDAR Data. Geophys. Res. Abstr. 2019, 21, 1. [Google Scholar]
- Farmakis, I.; Marinos, V.; Papathanassiou, G.; Karantanellis, E. Automated 3D Jointed Rock Mass Structural Analysis and Characterization Using LiDAR Terrestrial Laser Scanner for Rockfall Susceptibility Assessment: Perissa Area Case (Santorini). Geotech. Geol. Eng. 2020, 38, 3007–3024. [Google Scholar] [CrossRef]
- Riquelme, A.J.; Abellán, A.; Tomás, R. Discontinuity Spacing Analysis in Rock Masses Using 3D Point Clouds. Eng. Geol. 2015, 195, 185–195. [Google Scholar] [CrossRef]
- Palmstrom, A. Measurements of and Correlations between Block Size and Rock Quality Designation (RQD). Tunn. Undergr. Space Technol. 2005, 20, 362–377. [Google Scholar] [CrossRef]
- Healy, D.; Rizzo, R.E.; Cornwell, D.G.; Farrell, N.J.C.; Watkins, H.; Timms, N.E.; Gomez-Rivas, E.; Smith, M. FracPaQ: A MATLABTM Toolbox for the Quantification of Fracture Patterns. J. Struct. Geol. 2017, 95, 1–16. [Google Scholar] [CrossRef]
- Hantz, D.; Corominas, J.; Crosta, G.B.; Jaboyedoff, M. Definitions and Concepts for Quantitative Rockfall Hazard and Risk Analysis. Geosciences 2021, 11, 158. [Google Scholar] [CrossRef]
- Ferrari, F.; Giacomini, A.; Thoeni, K. Qualitative Rockfall Hazard Assessment: A Comprehensive Review of Current Practices. Rock Mech. Rock Eng. 2016, 49, 2865–2922. [Google Scholar] [CrossRef]
- Volkwein, A.; Schellenberg, K.; Labiouse, V.; Agliardi, F.; Berger, F.; Bourrier, F.; Dorren, L.K.A.; Gerber, W.; Jaboyedoff, M. Rockfall Characterisation and Structural Protection—A Review. Nat. Hazards Earth Syst. Sci. 2011, 11, 2617–2651. [Google Scholar] [CrossRef]
- Noël, F.; Cloutier, C.; Jaboyedoff, M.; Locat, J. Impact-Detection Algorithm That Uses Point Clouds as Topographic Inputs for 3D Rockfall Simulations. Geosciences 2021, 11, 188. [Google Scholar] [CrossRef]
- Dorren, L.K.A. A Review of Rockfall Mechanics and Modelling Approaches. Prog. Phys. Geogr. Earth Environ. 2003, 27, 69–87. [Google Scholar] [CrossRef]
- Ritchie, A.M. Evaluation of Rockfall and Its Control. Highw. Res. Rec. 1963, 17, 13–28. [Google Scholar]
- Mitchell, A.; Hungr, O. Theory and Calibration of the Pierre 2 Stochastic Rock Fall Dynamics Simulation Program. Can. Geotech. J. 2017, 54, 18–30. [Google Scholar] [CrossRef]
- Asteriou, P.; Tsiambaos, G. Effect of Impact Velocity, Block Mass and Hardness on the Coefficients of Restitution for Rockfall Analysis. Int. J. Rock Mech. Min. Sci. 2018, 106, 41–50. [Google Scholar] [CrossRef]
- Dorren, L.K.A. Rockyfor3D (v5. 2) Revealed–Transparent Description of the Complete 3D Rockfall Model; Int ecorisQ Association: Geneva, Switzerland, 2016; p. 32. [Google Scholar]
- Vanneschi, C.; Rindinella, A.; Salvini, R. Hazard Assessment of Rocky Slopes: An Integrated Photogrammetry–GIS Approach Including Fracture Density and Probability of Failure Data. Remote Sens. 2022, 14, 1438. [Google Scholar] [CrossRef]
- Moos, C.; Bontognali, Z.; Dorren, L.; Jaboyedoff, M.; Hantz, D. Estimating Rockfall and Block Volume Scenarios Based on a Straightforward Rockfall Frequency Model. Eng. Geol. 2022, 309, 106828. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).