The Prediction of Carbon Emission Information in Yangtze River Economic Zone by Deep Learning

Abstract

This study aimed to respond to the national “carbon peak” mid-and long-term policy plan, comprehensively promote energy conservation and emission reduction, and accurately manage and predict carbon emissions. Firstly, the proposed method analyzes the Yangtze River Economic Belt as well as its “carbon peak” and carbon emissions. Secondly, a support vector regression (SVR) machine prediction model is proposed for the carbon emission information prediction of the Yangtze River Economic Zone. This experiment uses a long short-term memory neural network (LSTM) to train the model and realize the experiment’s prediction of carbon emissions. Finally, this study obtained the fitting results of the prediction model and the training model, as well as the prediction results of the prediction model. Information indicators such as the scale of industry investment, labor efficiency output, and carbon emission intensity that affect carbon emissions in the “Yangtze River Economic Belt” basin can be used to accurately predict the carbon emissions information under this model. Therefore, the experiment shows that the SVR model for solving complex nonlinear problems can achieve a relatively excellent prediction effect under the training of LSTM. The deep learning model adopted herein realized the accurate prediction of carbon emission information in the Yangtze River Economic Zone and expanded the application space of deep learning. It provides a reference for the model in related fields of carbon emission information prediction, which has certain reference significance.

1. Introduction

In recent years, with the frequent occurrence of extremely severe weather due to global warming, countries around the world have begun to pay attention to the imbalance of carbon emissions caused by the emissions of greenhouse gases such as carbon dioxide (CO₂) [1]. Excessive CO₂ and other greenhouse gas emissions have caused irreparable damage to the environment [2]. Meanwhile, the process of social development cannot avoid the problem of carbon emissions, so the real-time prediction and monitoring of carbon emissions information has become extremely crucial [3]. Many scholars have performed a lot of research in the field of carbon emissions.

The earliest representative studies abroad mainly used the factor decomposition method, index decomposition method, input–output method, and combination model forecasting. Scholars have proposed an improved cuckoo optimization algorithm neural network (COANN) artificial neural network structure, which is optimized by the cuckoo algorithm (COA). The performance of COANN is evaluated by the mean square error (MSE), root mean square error (RMSE), mean absolute error (MAE), and correlation coefficient (CC) between the model output and the actual data set. The COANN prediction model can predict the world’s CO₂ emissions by 2050 [4]. Some researchers proposed a multi-objective predictive energy management strategy for residential grid-connected hybrid energy systems via machine learning technology. The strategy proposed includes three levels of control: 1—the logical level of management of computational load and accuracy; 2—on the dual prediction model of the residual causal expansion convolutional network, it is used for energy production and system power load; and 3—as well as multi-objective optimization for effective transactions, to provide energy for the public grid through battery charging scheduling [5]. It was proposed that energy efficiency on non-intrusive load monitoring (NILM) can save electricity by improving the awareness of behavior changes and reducing carbon dioxide emissions into the environment. In the data published in Malaysia from 1996 to 2018, a predictive model was established and scenario simulations were carried out. Malaysia’s public database was also sued for predicting the impact of CO₂ emissions and NILM on environmental degradation from 2019 to 2030 [6]. Some scholars have used Eviews software to analyze the carbon emission data of Beijing, Henan, Guangdong, and Zhejiang from 1997 to 2017. They also used differential stationary processing, moving average, and substituting strong impact points for data preprocessing. Through model identification, parameter estimation, and model testing, they established an integrated moving average autoregressive (ARIMA) models to predict carbon emissions in four regions [7]. It is believed that it is important to objectively evaluate the impact of relevant factors on carbon emissions. They proposed a modified production theory decomposition analysis (PDA) model under the semi-disposable hypothesis, and correspondingly decomposed the carbon emission changes of China’s thermal power generation industry [8]. Some scholars have used the Lasso regression model to screen out eight significant factors affecting carbon emissions, and used the BP neural network model to predict the carbon emissions of Jiangsu Province from 2019 to 2030. They used artificial neural networks (ANN) to develop carbon emission intensity prediction models for Australia, Brazil, China, India, and the United States. Nine parameters that play an important role in the intensity of carbon emissions were selected as input variables. After many iterations, the best model was selected for each country by predefined criteria. They used a 9–5–1 multilayer perceptron with a backpropagation algorithm to build, validate, and train the model. The results of the verification model show that the error between the predicted value and the actual value is approximately 0, and the proposed ANN model can accurately predict carbon emissions [9,10]. Wang et al. (2021) used the random forest (RF) machine learning algorithm to analyze the relationship between urban factors and carbon emissions using real data from Chinese cities [11]. Yan et al. (2021) proposed a new integrated inversion model. This model was used for the intelligent assessment and prediction of water, carbon, and ecological footprint based on integrated multi-task machine learning (MML) and multi-model stack (MMS) algorithms. The accuracy and generalization ability of the model is further explained through the three largest urban agglomerations in the middle reaches of the Yangtze River [12]. Huang et al. (2021) proposed a new method to simulate the dual relationship between emission inventory and pollution concentration for emission inventory estimation [13].

Deep learning has become the latest method and means of studying carbon emissions. At present, most studies use one algorithm to study carbon emissions, and do not consider the combination of multiple algorithms to study carbon emissions. Therefore, the prediction accuracy of the established model is key to measuring whether the algorithm is suitable for carbon emission prediction. Because the long short-term memory (LSTM) neural network is very effective in predicting time-dependent problems, the time factor has a greater impact on carbon emissions. In addition, the problem of carbon emissions is a complex non-linear problem. Additionally, a large amount of data need to be classified and processed. Due to the large error term in the LSTM prediction, slack variables are introduced into the SVR model. Slack variables are introduced to correct the larger prediction errors in the LSTM model, the LSTM-SVR hybrid model is established, and a better prediction effect is achieved. The innovation lies in the indexing of “carbon emissions” information and expanding the area of data availability. Meanwhile, the LSTM is revised by introducing slack variables into the SVR model. This research has a certain reference value for energy-saving development entities in the Yangtze River Economic Zone to implement energy-saving emission reduction and carbon emission refined control forecasts.

2. Related Concepts and Algorithm Analysis

2.1. Yangtze River Economic Belt

The Yangtze River Economic Belt comprises Guizhou, Sichuan, Yunnan, and Chongqing in the western region, and Hubei, Hunan, and Jiangxi provinces in the central region, and Anhui, Jiangsu, Zhejiang and Shanghai in the eastern region, with 11 provinces and cities. The Yangtze River Economic Belt covers an area of approximately 2.05 million square kilometers, has a total population of approximately 600 million, and represents 40% of the country’s GDP. It is regarded as a dynamic economic belt, second only to the coastal economic belt [14]. Its rapid economic development has been accompanied by increasingly prominent ecological and environmental problems in the Yangtze River Basin, such as soil erosion, floods, and ecological imbalances along the river. Due to the increasingly prominent environmental resource problems of the Yangtze River, the protection of its natural ecology has become ineffective, restricting the growth rate of the Yangtze River Economic Belt [15]. Figure 1 shows a sketch of the regional locations of provinces and cities in the Yangtze River Economic Belt.

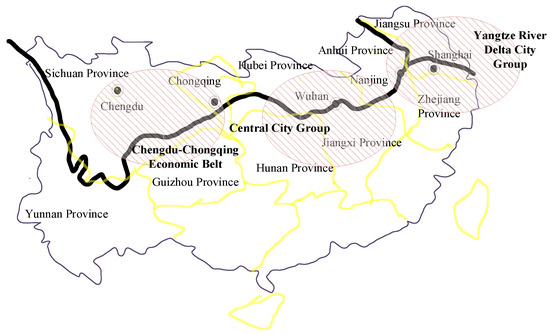
Figure 1. Sketch map of the geographic regions of provinces and cities in the Yangtze River Economic Belt.

2.2. Definition and Analysis of Carbon Sources

2.2.1. Definition

The “source” of greenhouse gases, in layman’s terms, is the activity of emitting gases into the atmosphere. “Greenhouse gases” can make the Earth’s surface temperature higher, generally by absorbing and re-emitting infrared radiation to play a role [16]. Greenhouse gases mainly include CO₂, ozone (O₃), and methane (CH₄). In addition, this also includes man-made greenhouse gases such as hydrofluorocarbons (HFCs) [17], of which CO₂ has the most obvious warming effect. The warming effects and life cycles of some greenhouse gases are shown in Figure 2.

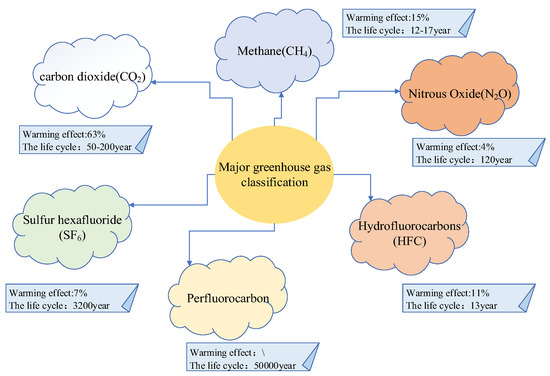
Figure 2. Diagram of the warming effects and life cycles of some greenhouse gases.

2.2.2. Analysis

“Carbon source”, as the name implies, is a gas component that increases the amount of CO₂ in the Earth’s atmosphere [18]. These gas components enter the atmosphere from the surface of the earth or are formed by the chemical conversion of CO₂ in the atmosphere. Corresponding to the “carbon source” is the “carbon sink”. Simply put, the “carbon sink” refers to the mechanism of removing greenhouse gases from the atmosphere, such as by means of the photosynthesis process of plants. From this point of view, the reduction in “carbon sinks” will also lead to an increase in carbon emissions [19]. The specific classification of “carbon sources” is shown in Figure 3.

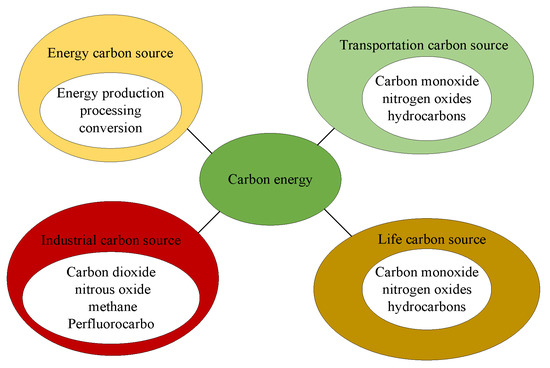
Figure 3. Schematic diagram of the classification of “carbon sources”.

2.2.3. Causes of Carbon Emissions

Carbon Emissions in the Process of Urbanization

The factors inducing high carbon emissions in the process of China’s urbanization can be divided into two categories. The first is that of economic factors such as the expansion of infrastructure construction, the growth of residents’ consumption, and the transformation of land use patterns. The other is the policy incentives that lead to phenomena such as short-lived construction, major demolition, and construction, and low-density urban sprawl. On the one hand, the new construction in the process of urbanization development constitutes an incremental part of carbon emissions. On the other hand, repeated construction and wasted building energy have aggravated high energy consumption and high carbon emissions in the process of urbanization. The combination of economic factors and policy factors in China’s urbanization has led to the phenomenon of high carbonization becoming more and more obvious. Firstly, industrial production has brought about an increase in carbon emissions. Rapid industrial development is the main driving force for China’s carbon emissions growth. In addition, the embodied carbon in China’s export trade plays an important role in the rise of China’s carbon emissions. China’s exports are dominated by processing trade, with high energy consumption, which is also one of the important factors that constitute China’s energy demand growth. Secondly, carbon emissions from the construction industry rapidly increased, and the increase in building areas also brought more carbon emissions. Finally, transportation carbon emissions have rapidly increased, and the increase in transportation demand has led to an upward trend in the total energy consumption of transportation and its share. In recent years, there have been significant changes in China’s transportation, road transportation infrastructure, and residents’ travel. With the acceleration of urban logistics circulation, the freight capacity of cities and towns has gradually strengthened. The urban expansion in the center will increase the distance traveled by residents, and the level of urban motorization will thus rapidly increase.

Carbon Emissions from Animals and Plants

The respiration of plants and animals produces CO₂. CO₂ generates organic matter and oxygen through photosynthesis. Carbon exists in the form of CO₂ in nature, and plant straw is a biological resource produced in the process of crop production. Burning plant straws will bring about a lot of carbon emissions.

2.3. Algorithmic Analysis of Carbon Emissions

Through the classification of “carbon sources”, it can be seen that CO₂ emissions involve a wide range and many uncertain factors. The amount of CO₂ cannot be directly obtained through the monitoring instrument. It needs to be calculated by methods. Common methods are subsequently explicated.

2.3.1. Oak Ridge National Laboratory (ORNL)

The Oak Ridge National Laboratory was established by the US Department of Energy in 1943 and is the world’s largest scientific energy research laboratory. In 1990, members of the laboratory proposed a method for CO₂ emissions from fossil fuel combustion:

Carbon emissions from coal = coal consumption × 0.982 × 0.733
Fuel oil carbon emissions = standard coal equivalent × 0.982 × 0.733 × 0.813
Gas carbon emissions = standard coal equivalent × 0.982 × 0.733 × 0.561

In the equation, 0.982 is the effective oxidation fraction, 0.733 is the carbon content per ton of standard coal, 0.813 means that under the premise of obtaining the same heat energy, the CO₂ released by fuel oil is 0.813 times the CO₂ released by coal, and 0.561 represents that when the same heat energy is obtained. The CO₂ released by natural gas is 0.561 times that of the CO₂ released by coal [20].

2.3.2. Logistic Model

Most economic indicators are increasing functions that change over time. Conditions such as the environment restrict their growth rate and will gradually slow down their growth rate. Most economic indicators show changes in graphs that resemble a flattened S-shaped curve (logistic curve). The relationship between carbon emissions and time is closely resembles an S-shaped curve [21].

2.3.3. System Dynamics Model

The system dynamics Stella software is used to construct the energy consumption model. The energy consumption model constructed by Stella software can obtain a simulation estimation model of energy consumption by inputting conditions such as GDP, population, and the proportion of output value of each industry. This model can effectively overcome errors caused by missing data [22].

The model obtains carbon emissions according to the following equation: carbon emissions = energy consumption x carbon emission factor × (1 − carbon sequestration rate) × oxidation rate.

2.3.4. Input–Output Analysis (IOA)

IOA combines input–output tables and uses mathematical methods to build models. IOA calculates carbon emissions by establishing relationships through models [23]. The principle is as follows:

First: Calculate the carbon emissions of energy consumption in various sectors.

• Calculate the direct carbon emission coefficient: $c{e}_j\left(\mathrm{direct}\right)=f_j·e_j$, where the energy carbon emission coefficient of the j sector is represented by $f_j$ as $\frac{\mathrm{t}\mathrm{C}{\mathrm{O}}_2}{tce}$, that is, the CO₂ emission per ton of energy, and $e_j$ is the energy consumption intensity of the j sector (10,000 tons of standard coal/CNY 10,000).
• Calculate the indirect carbon emission coefficient: $c{e}_j(\mathrm{indirect})=f_j\left({\displaystyle \sum _{i=1}^n{a}_j}{b}_{ij}\right)$, where the complete consumption of the i-sector product caused by the unit product is represented by $b_{ij}$. ${\displaystyle \sum _{i=1}^n{a}_j}{b}_{ij}$ is the total indirect energy consumption of all n products caused by the unit product of the j sector. The complete carbon emission coefficient of energy consumption is equal to the sum of direct and indirect carbon emission coefficients, expressed as Equation (1):

  $$c{e}_j=f_j·e_j+f_j·\left({\displaystyle \sum _{i=1}^n{a}_j}{b}_{ij}\right)$$

  (1)

Second: Calculate the embodied carbon emission coefficient in the production process.

First of all, a prerequisite must be met: the i-th sector’s products will produce CO₂ during the production process; then, since the j-th sector consumes the i-th sector’s products, it will cause the j-th sector to produce implicit carbon emissions during the production process, which holds Equation (2):

$$\{{}_{i\ne j,c{e}_j=g_j·b_{ij}}^{i=j,c{e}_j=g_j+g_j·b_{ij}}$$

(2)

In $g_j=\frac{{\omega }_i·Q_i}{X_i}$, ω_i represents the carbon emissions from the industrial production process of the unit physical quantity product in the i sector (tons of CO₂/ton of product), and Q_i represents the product output of the i sector (10,000 tons); X_i represents the total output of the i sector (CNY 10,000). Combining the two equations yields $c{e}_j=g_j·{\mathrm{c}}_{ij}$.

Therefore, Equation (3) is the complete carbon emission coefficient of each sector:

$$c{e}_j(\mathrm{completely})=f_j·\left({\displaystyle \sum _{i=1}^n{e}_i·b_{ij}}\right)+g_j·{\mathrm{c}}_{ij}$$

(3)

On Equation (3), the total carbon emissions in the air can be calculated, as shown in Equation (4):

$$CE={\displaystyle \sum _{j=1}^{n}c{e}_j}·Y_j$$

(4)

(Y_j is the final use of the department (CNY 10,000).)

The CO₂ estimate provided in the IPCC National Greenhouse Gas Inventory Guidelines for energy-based CO₂ is shown in Equation (5):

$$\mathrm{C}{\mathrm{O}}_2={\displaystyle \sum _{i=1}^n\mathrm{C}{\mathrm{O}}_2}={\displaystyle \sum _{i=1}^n{E}_i}\times NC{V}_{\mathrm{i}}\times CE{F}_i\times CO{F}_i\times (44/12)$$

(5)

In Equation (5), CO₂ is the estimated amount of CO₂ emissions; i represents the estimated i-th energy; E_i represents each energy consumption; NCV_i is the average low calorific value of each energy source; CEF_i represents the carbon emission factor per calorific value provided by the IPCC Greenhouse Gas Inventory; COF_i stands for carbon oxidation factor. The molecular coefficient is 44/12 units of CO₂, which represents the amount of CO₂ that 1 unit of carbon element can be converted into [24].

2.4. Temporal and Spatial Characteristics of Carbon Emissions

According to relevant data, the industrial structure, population size, economic development level, opening-up level, carbon emission intensity, etc. are all factors that affect the scale of carbon emission [25]. Carbon emissions have formed a time–space effect along with changes in time series and spatial sequences. When studying carbon emissions, it is necessary to consider the following: 1—spatial connections and changes in different economic regions; and 2—carbon emission prediction requires analysis and research on the spatial characteristics of carbon emission.

2.5. Analysis of Deep Learning Algorithms

(1) Recurrent Neural Network (RNN)

RNN is a neural network with cyclic characteristics. It can perform calculations on the characteristics of carbon emission time series data because it can continuously circulate information and has a short-term information memory function [26]. The most basic RNN network is composed of multiple neuron nodes, and each node has an activation function with time as a variable to enhance adaptability. Meanwhile, all function parameters of the node can be adjusted in real time. The expanded diagram of the RNN network structure is shown in Figure 4.

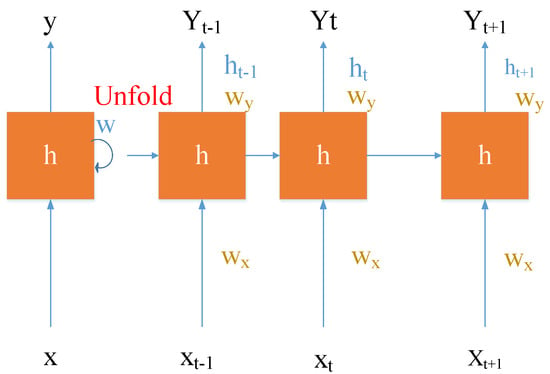
Figure 4. Expanded schematic diagram of an RNN network structure.

In Figure 4, h_t represents the output of the hidden layer node at time t; h_t−1 represents the output at the previous moment; y_t represents the output vector; x_t represents the input vector; h_w, x_w, and y_w all represent the weight vector of the hidden layer neuron node and the next hidden layer neuron node, respectively.

(2) Long Short-Term Memory (LSTM)

LSTM is a classic variant of RNN. LSTM has powerful classification and prediction capabilities and can handle operations with relatively long-time intervals and delays. The important thing is that LSTM can solve the problem of gradient disappearance and gradient explosion during long-sequence training [27].

The LSTM neural network structure uses a gate control unit. The neuron of each cell contains a forget gate, input gate, and output gate to strengthen the network structure, as shown in Figure 5.

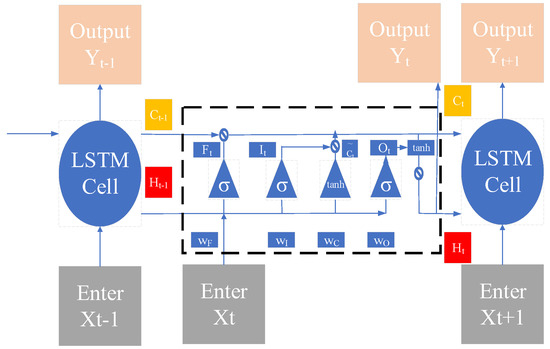
Figure 5. Schematic diagram of an LSTM neural network structure.

In the network structure diagram of LSTM, the cell state similar to the conveyor belt runs on the entire chain. If the cell state undergoes a slight linear operation, the information flows through the entire chain and remains stable. The gate is a weight composed of a sigmoid function, a tanh function, and a point multiplication operation to realize the selection of information.

Demonstrate the operation according to the structure of Figure 5 LSTM.

1.

Forgetting door calculation:

The forgetting door decides whether to leave the information, as shown in Equation (6). In the information entry gate, the information status is read under sigmoid, and the output is a value between 0 and 1—where 1 means complete retention and 0 means complete deletion, as shown in Equation (7):

$$F_t=\sigma \left(w_F\left[h_{t-1},x_t\right]+b_F\right)$$

(6)

$$S(t)=\frac{1}{1+e^{-t}}$$

(7)

2.

Input gate calculation:

The input gate determines how much new information enters, as shown in Equation (8). There are two steps: the first step is to enter the gate to determine the new information that is allowed to enter the cell; the second step is to obtain the candidate information that needs to be remembered at tanh, as shown in Equation (9):

$$I_t=\sigma \left({\mathrm{w}}_I·\left[h_{t-1},x_t\right]+b_I\right)$$

(8)

$${\tilde{C}}_t=\tanh \left({\mathrm{w}}_{\mathrm{c}}·\left[h_{t-1},x_t\right]\right)$$

(9)

3.

Cell status update:

The cell state that C_t−1 is updated to C_t is to multiply the last state value C_t−1 by F_t, discard the unnecessary part, and add the value that allows it to be remembered and multiplied by it. Finally, the information C_t that the update wants to add to the unit state is obtained, as shown in Equation (10):

$${\underset{\_}{C}}_t=F_t\ast C_{t-1}+I_t{}^{\ast }{\tilde{C}}_{\mathrm{t}}\mid$$

(10)

4.

Output gate

The output gate determines the information to be output from the cell state, as shown in Equation (11). By activating the sigmoid function, the cell state information output is determined. The tanh function is used to process the final output information h_t of the cell state at the last current moment, as shown in Equation (12):

$${\underset{\_}{O}}_t=\sigma \left({\mathrm{w}}_O·\left[h_{t-1},x_t\right]+b_O\right)$$

(11)

$$h_t=O_t\ast \tanh \left({\mathrm{C}}_{\mathrm{t}}\right)$$

(12)

In Equations (11) and (12), F_t, I_t, and O_t represent the calculation of the forget gate, input gate, and output gate at time t, respectively; C_t−1 represents the cell state at the previous moment; C_t represents the cell state at time t; x_t represents input information; h_t−1 represents the output at the previous moment; w_F, w_I, and w_O represent the weight vectors of the forget gate, input gate, and output gate, respectively; b_F, b_I, and b_O represent the bias vectors of the forget gate, input gate, and output gate, respectively; σ (•) represents the activation function sigmoid function. The entire forward calculation of the LSTM unit cell is completed through three gates and one cell state.

3. Indicator Creation and Model Design

3.1. Creation of Carbon Emission Information Indicators

After analyzing the industry characteristics of the Yangtze River Economic Belt, the proposed method derives key factors such as industry investment scale and labor output efficiency, which affect carbon emissions in the “economic belt”. Then, the extensible random environmental impact assessment (STIRPAT) model is optimized to determine the information indicators:

(1) ZB1 is used to represent the total carbon emissions in the “Yangtze River Economic Belt” basin, with a unit of 10,000 tons;

(2) ZB2 is used to represent the investment scale of the industry, combined with the research, the sum of fixed assets, and the current assets of enterprises above the designated size used as measurements, with a unit of CNY 100 million;

(3) ZB3 is used to represent industrial economic efficiency, and labor efficiency is used as output as a measure;

(4) ZB4 is used to represent carbon emission intensity, that is, CO₂ emissions per unit of industrial added value;

(5) ZB5 is used to represent the scale of opening up to the outside world, and it is measured by the proportion of the sum of investments from Hong Kong, Macao, and Taiwan in addition to foreign investment in the industrial added value, and the unit is %;

(6) ZB6 is used to represent the intensity of environmental protection, and the investment in environmental pollution control is expressed as the proportion of industrial GDP, for which the unit is % [28].

The expanded model indicator variable list is shown in Table 1.

Table 1. Carbon emission information forecast and expansion model indicators.

Indicator Definition	Representative Symbol	Index Quantification Unit
Total carbon emissions of provinces and cities in the Yangtze River Economic Belt	ZB1	Ten thousand tons
Industry investment scale	ZB2	CNY 100 million
Labor efficiency output	ZB3	CNY 100 million /10,000 people
Carbon intensity	ZB4	10,000 tons/10,000 people
Openness to the outside world	ZB5	%
Environmental protection	ZB6	%

3.2. Carbon Emission Modeling Process

The problem of carbon emission prediction is actually predicting carbon emission information in the future based on the information of carbon emission indicators in the past. Therefore, this study is actually on the relationship between a set of time series containing characteristic data to perform regression prediction on the target value.

Regardless of whether it is for regression algorithms or classification algorithms, data need to be preprocessed before the model is built, especially for practical research on multi-dimensional data. In response to the problem to be dealt with, in the selection of data features, the six indicators in Table 1 are used to predict carbon emission information. Because of the various characteristics of the original data in different dimensions, it needs to perform standardized preprocessing operations on the data.

(1) Data normalization method:

The min–max standardization is also called the maximum value normalization, which is a linear transformation of the original data, and the result value is mapped to between [0,1]. The expression Equation of the normalization method of the data is as in Equation (13):

$$x_{\mathrm{scale}}=\frac{x-x_{\min }}{x_{\max }-x_{\min }}$$

(13)

Maximum normalization is to calculate the maximum and minimum values of each dimension data and then convert the original data. However, maximum normalization has its limitations. If the data change, their maximum and minimum values need to be recalculated. In addition, the maximum normalization is extremely susceptible to extreme values. Therefore, maximum normalization is more suitable for processing boundary data [29].

(2) Normalization of mean variance:

$$x_{\mathrm{scale}}=\frac{x-x_{\mathrm{mean}}}{\sigma }$$

(14)

Mean variance normalization is a common method for preprocessing data. The essence of mean variance normalization is to calculate the mean and standard deviation of the data, so that the original data obey a normal distribution with a mean value of 0 and a standard deviation of 1 [30].

The focus of the evaluation model is to divide the data set that the research has collected. The data can be divided into three sets: training set, validation set, and test set [31]. The training set is passed into the model for model fitting, and the model parameters are optimized on the validation set, and then the model is evaluated. When the model works well, this means that the experiment has found the best model parameters, and then uses the test set for model testing.

Common indicators for evaluating the prediction accuracy of regression models are as follows:

(a)

The MSE is the sum of squares of the difference between the results of the original feature data predicted by the model and the real results, but the sum of squares will continue to accumulate as the number of samples increases. In order to eliminate the influence of the number of samples, the mean value of the square error is calculated, and the MSE is obtained, as shown in Equation (15):

$$MSE=\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left|y_i-y_i^{\prime }\right|}^2}$$

(15)

(b)

The average absolute error (MAE) is the average of the absolute value of the difference between the predicted value and the true value, as shown in Equation (16):

$$MAE=\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left|y_i-y_i^{\prime }\right|}^2}$$

(16)

(c)

RMSE is shown Equation (17):

$$RMSE=\sqrt{MSE}=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left|y_i-y_i^{\prime }\right|}^2}}$$

(17)

(d)

The absolute error of the median, the absolute value of the difference between the predicted value, and the true value are not averaged, but the median is taken, which is MedAE, as shown in Equation (18):

$$MedAE=media{n}_{i=1,\dots ,\mathrm{N}}\left|y_i-y_i^{\prime }\right|$$

(18)

For the median absolute error index, because the expression contains the absolute value, it is necessary to derive the loss function of the model, and the absolute value index usually fails [32].

3.3. Data Source

The data of this experiment were obtained according to the online data query menu system on the official website of the National Bureau of Statistics (https://data.stats.gov.cn) (accessed on 11 December 2021). The database of the National Bureau of Statistics collected data from 2018 to 2020, and the monitoring interval was monthly. The relevant index data obtained are mainly data on the 11 provinces and cities in the Yangtze River Economic Belt. The data collected from the official website of the National Bureau of Statistics were used as the training set and test set of the carbon emission prediction model proposed; the data collected by the official statistical bureaus of local provinces and cities were used as the verification data set for demonstration applications.

Table 2 shows the descriptive data of carbon emissions in the Guizhou and Jiangsu provinces from 2000 to 2020.

Table 2. Carbon emissions in the Jiangsu and Guizhou provinces during the period 2000–2020.

Guizhou Province		Jiangsu Province
Year	Carbon Emissions (×108 t) Year	Year	Carbon Emissions (×108 t)
2000	1.845820987	2000	5.521659376
2001	1.50698462	2001	5.864446639
2002	1.622689431	2002	5.866892432
2003	2.079300127	2003	7.11895019
2004	2.422275528	2004	7.12083157
2005	2.765439067	2005	7.123089224
2006	2.767320446	2006	7.352053055
2007	2.767320446	2007	7.581581299
2008	2.656319082	2008	8.038003857
2009	3.226565072	2009	8.494990828
2010	3.455905178	2010	9.065236819
2011	3.45759842	2011	9.521471238
2012	3.800573821	2012	9.410469874
2013	4.257184516	2013	8.957621937
2014	4.259254033	2014	8.846244297
2015	4.261135412	2015	9.18903156
2016	4.3772165	2016	9.532195099
2017	4.492545036	2017	9.8751705
2018	4.492921311	2018	11.467946
2019	4.608249847	2019	13.51563896
2020	4.950848972	2020	14.54004986

3.4. SVR Machine Model Creation

Support vector machine (SVM) is a powerful machine learning algorithm [33]. SVM can solve classification and regression problems at the same time. In addition, SVM can handle both supervised learning target variables and unsupervised learning without target variables. Additionally, its application scenarios are very rich, which can be used for binary classification problems, multi-classification problems, linear and nonlinear problems, etc.

The problem being studied is essentially to predict the regression problem. The application of SVM to regression is also called support vector regression (SVR) [34]. SVR is achieved by adding an insensitive loss function to SVM. It extends the classification problem to the regression problem, finds an error, and makes all the sample points as far as possible within this error to achieve a prediction of the data.

SVR is an application of SVM in the field of regression. Its principle is to obtain a regression model (Equation (20)) on the known sample set (Equation (19)):

$$\mathrm{D}=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\dots ,\left(x_k,y_k\right),x_i\in R^n,y_i\in R\right\}$$

(19)

$$f(x)={\omega }^{T}x+b$$

(20)

Make f(x) and y as close as possible. Among them, w and b are the parameters to be determined in the model; w is the normal vector of the hyperplane; and b is the displacement term. For general regression problems, only when f(x) and y are exactly equal will the loss of the model be zero. In the SVR model, a certain degree of tolerance deviation ε is given, so that if and only when the absolute value of the difference between f(x) and y is greater than the tolerance deviation ε, it is considered as a loss. At this time, it is equivalent to taking f(x) as the center to construct an isolation band with a width of 2ε, as shown in Figure 6.

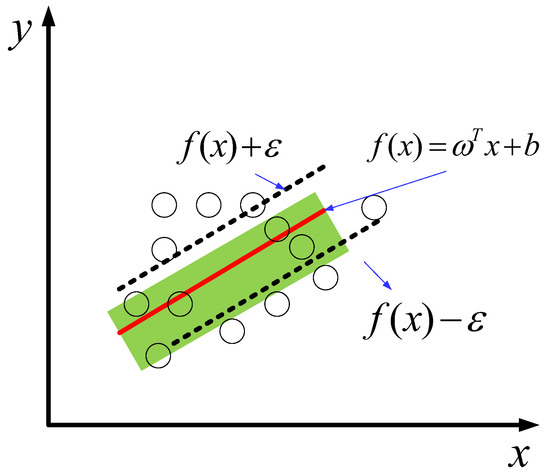
Figure 6. Schematic diagram of SVR.

The problem of the SVR model can be transformed into:

$$\underset{w,b}{\min }\frac{1}{2}\parallel \omega {\parallel }^2+C\sum _{i=1}^m{l}_s\left(f\left(x_i\right)-y_i\right)$$

(21)

$$l_{\epsilon }=\{\begin{array}{cc}0,& \mathrm{if}\left|z\right|\le \epsilon \\ \left|z\right|-\epsilon ,& \mathrm{other}\end{array}$$

(22)

where C is the regularization constant and lε is the ε-insensitive loss function in Figure 6. With the introduction of relaxation factors ${\xi }_i^{\vee }$ and ${\xi }_i^{\wedge }$, Equations (21) and (22) can be rewritten as

$$\text{min}\frac{1}{2}\parallel \omega {\parallel }^2+C\sum _{m-1}^N\left({\xi }_m^v+{\xi }_m^{\wedge }\right)$$

(23)

$$s.t.-\epsilon -{\xi }_i^{\vee }\le y_i-\omega ·\varphi \left(x_i\right)-b\le \epsilon +{\xi }_i^{\wedge }$$

(24)

$$\mathrm{s}.\mathrm{t}.\begin{array}{c}f\left(x_i\right)-y_i\le \epsilon +{\xi }_i^{\vee },\\ y_i-f\left(x_i\right)\le \epsilon +{\xi }_i^{\wedge }\\ {\xi }_i^{\vee }\ge 0,{\xi }_i^{\wedge }\ge 0,i=1,2,\dots ,m\end{array}$$

(25)

SVM aims to solve two-classification problems. The actual problem is often a complex nonlinear problem, and the “dimension increase” is used to deal with the nonlinearity between data [35]. The dimensional data are converted and mapped to a high-dimensional space, and then converted into a low-dimensional space after the high-dimensional space is classified. The purpose of introducing the kernel function can solve this kind of conversion operation. Using the SVR machine to make predictions, different kernel functions are selected for modeling, and the differences between the kernel functions are compared. The kernel function categories and characteristics are shown in Figure 7.

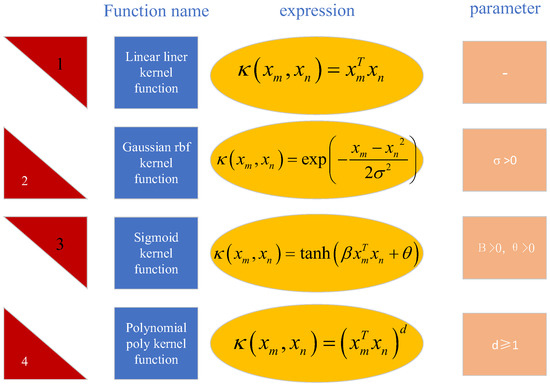
Figure 7. Schematic diagram of kernel function names and characteristic parameters.

Using the duality principle [36] and introducing the kernel function, the SVR model is obtained, as shown in Equation (26):

$$f(x)={\displaystyle \sum _{i=1}^m\left(\widehat{{\alpha }_i}-{\alpha }_i\right)k\left(x_i,x\right)+b}$$

(26)

3.5. LSTM-SVR Hybrid Model Construction

Carbon emission (CO₂) concentration data have the characteristics of time series and non-linearity. The LSTM-SVR hybrid model is proposed to improve the prediction accuracy of CO₂ concentration. Using the LSTM-SVR hybrid model to predict the CO₂ concentration, the specific steps are as follows:

(1) Acquisition of CO₂ concentration data and meteorological factor data;

(2) Preprocessing the acquired data to eliminate errors or abnormal factors in the data;

(3) Use the LSTM model to train and predict the processed data to generate a set of corresponding prediction values $\widetilde{{\mathrm{D}}_{\mathrm{t}}}$;

(4) By making the difference between the processed data Dt and the predicted value $\widetilde{{\mathrm{D}}_{\mathrm{t}}}$, the error value e_t at time t can be obtained;

(5) The SVR model is used to perform regression prediction on the error value e_t at time t, and cross-validation and grid search algorithms are used to find the optimal kernel function parameter g and penalty factor c of the SVR model; the predicted value is obtained, that is, the error value e_t is corrected, and the corrected error value is ${\widehat{e}}_t$;

(6) The corrected error value ${\widehat{e}}_t$ is combined with the predicted value $\widetilde{{\mathrm{D}}_{\mathrm{t}}}$ of LSTM, and finally the predicted value $D_t^{*}$, $D_t^{*}={\widehat{e}}_t+\widetilde{{\mathrm{D}}_{\mathrm{t}}}$ of the mixed model is obtained. The model framework is shown in Figure 8.

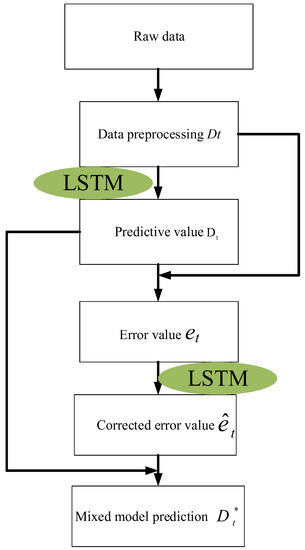
Figure 8. LSTM-SVR hybrid model framework diagram.

4. Experimental Results and Analysis

4.1. SVR Model Fitting Results

The SVR model is used to perform non-linear regression classification and fitting on the carbon emission-related information of all provinces and cities in the “Yangtze River Economic Belt” basin. Under different kernel functions, the fitting results of the model are shown in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.

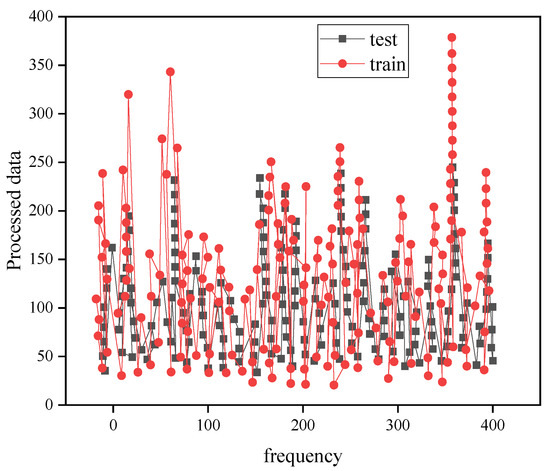
Figure 9. Schematic diagram of linear kernel function fitting results.

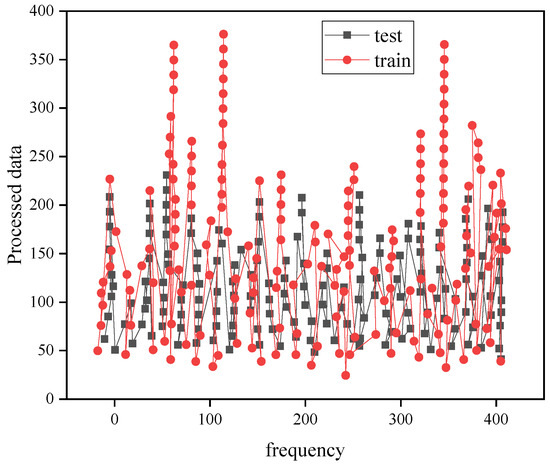
Figure 10. Schematic diagram of the Gaussian kernel function fitting results.

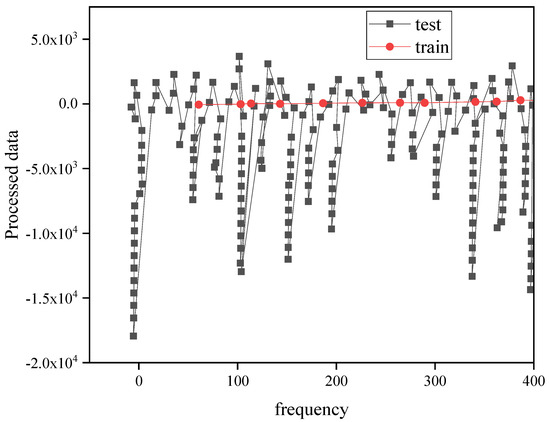
Figure 11. Schematic diagram of the sigmoid kernel function fitting results.

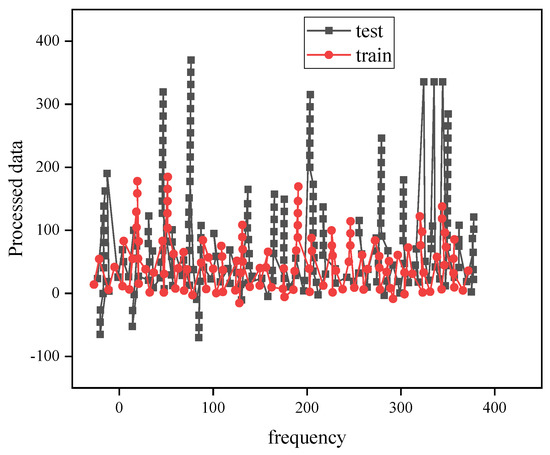
Figure 12. Schematic diagram of the polynomial kernel function fitting results.

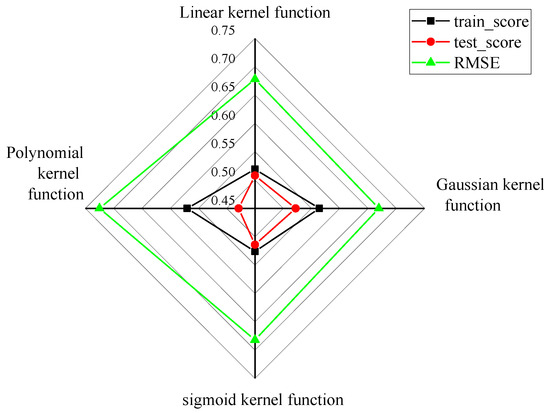
Figure 13. Comparison of the model performance of four types of kernel functions.

The experiment finally obtained the RMSE of the test set to be 0.715. This evaluation index is the result of calculating the normalized data. The fitting result of the Gaussian kernel function is shown in Figure 10.

Figure 11 indicates that the phenomenon of over-fitting is more serious, and the function parameters need to be adjusted. After adjustment, the training set score of the final model is 0.663, the test set score is 0.634, and the RMSE of the test set is 0.682.

Figure 11 reveals that the fitting effect of the sigmoid kernel function is relatively poor, and the scores of the test set and the training set are both negative and relatively low. Meanwhile, the experiment needs to adjust the parameters to achieve a reasonable fitting result.

Figure 12 proves that the performances of the test set and the training set are different, that the training set score is reasonable, and that the test set is low. In all the above figures, the fitting results of the different kernel functions are different, and the specific function fitting score and the RMSE comparison are shown in Figure 13.

Figure 13 visually shows that the training performance scores of the four different kernel functions of the model are relatively small. This is due to the constant use of network search in the process of model training to adjust the parameters of the model.

4.2. Deep Learning Network Model Training Results

This experiment used the LSTM neural network to train the model. After 60 iterations, the loss of the model and its performance on the training and test sets were obtained—these are shown in Figure 14.

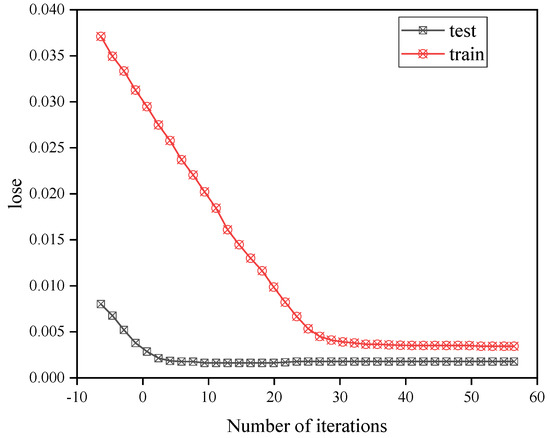
Figure 14. Comparison of the training and testing losses for multiple iterations of LSTM.

Figure 14 shows that the loss gradually stabilizes after multiple iterations. Figure 15 shows the fitting trend graph of the model trained by the LSTM neural network.

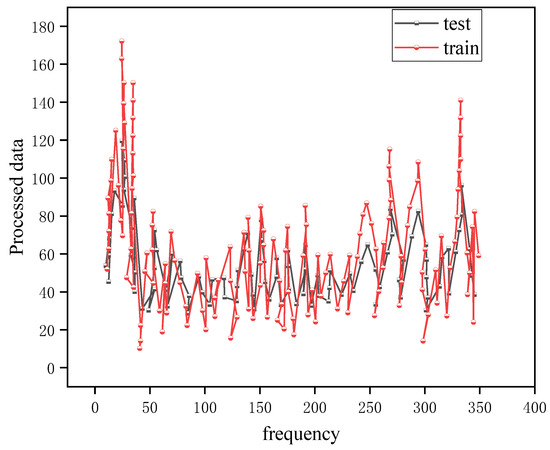
Figure 15. Schematic diagram of the fitting trend results after LSTM training.

4.3. Carbon Emission Forecast Results

According to the SVR model and the LSTM training model, the experimental training on the experimental data set, the comparison between the prediction curve of the carbon emission information-related indicators in the Yangtze River Economic Belt and the real curve is shown in Figure 16, Figure 17 and Figure 18.

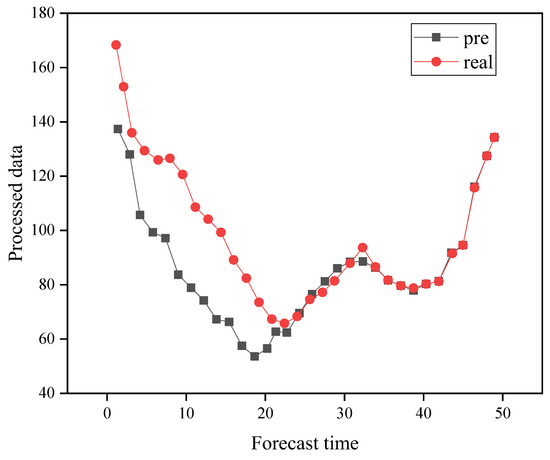
Figure 16. Schematic diagram of the comparison between the industry investment scale information and “Yangtze River Economic Belt” carbon emission information prediction and the actual comparison.

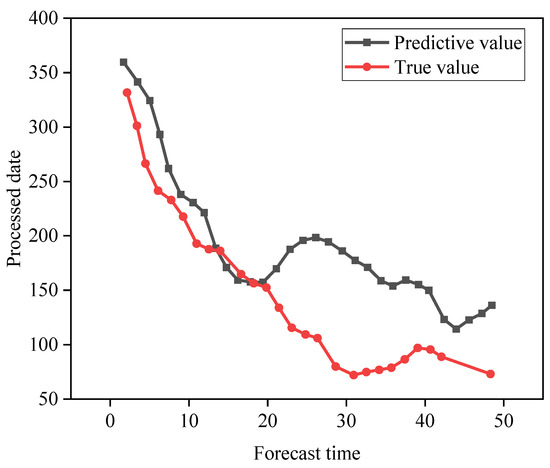
Figure 17. Schematic diagram of the comparison between the labor efficiency output information and carbon emission information prediction and the actual comparison of the “Yangtze River Economic Belt”.

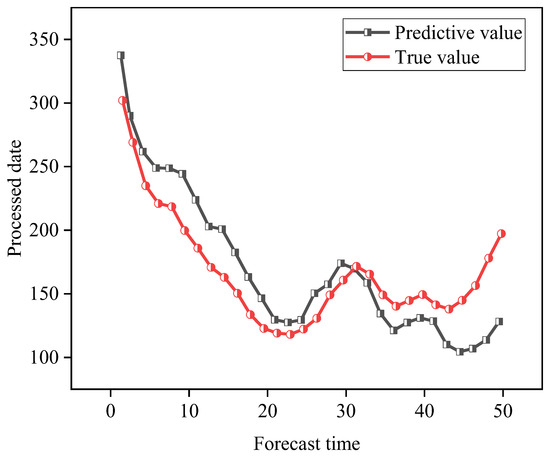
Figure 18. A schematic diagram of the comparison between the scale of carbon emissions information and the carbon emissions information prediction and the actual comparison of the “Yangtze River Economic Belt”.

In Figure 16, the scale of the industry investment is used to predict carbon emissions. There are consistent overall trends. This also reflects the fact that the economic development and growth of the Yangtze River Economic Belt will inevitably increase carbon emissions.

Figure 17 suggests that the labor efficiency output information is not very accurate for the prediction of information on carbon emissions, and that there are certain errors. The reason for this is that the labor efficiency output has spatial lag.

In Figure 18, the information on the scale of carbon emissions is more accurate in predicting the trend of carbon emissions. In summary, in the combination of the SVR model and the LSTM model proposed herein, the relevant index information for predicting carbon emissions in the Yangtze River Economic Zone is relatively accurate. Meanwhile, the ZB1 and ZB2 indicator information play a key role in predicting carbon emissions.

4.4. Policy Recommendations

In response to the proposed factors influencing carbon emissions and the prediction results of the carbon emissions model, the following policy recommendations are proposed as follows, taking account of China’s specific national conditions.

1.

Strengthen carbon market capacity building:

Chinese central state-owned enterprises have the responsibility and obligation to implement and fulfill the state’s requirements in terms of corporate, political, and social responsibility. Chinese central state-owned enterprises should actively implement the national climate change policy requirements. They also should take the lead in promoting research into carbon asset management, low-carbon development strategies and paths, and complete the country’s binding targets for greenhouse gas emissions.

This requires Chinese central state-owned enterprises to interpret carbon emission policies. Meanwhile, they also need to study the extent of their influence on the company’s corporate development strategy selection, production decision making, technological progress, energy conservation, and environmental protection. Furthermore, companies should explore the impact of carbon emission policy structure on the behavior of industrial enterprises, and study the relationship between carbon emission policy and corporate competitiveness. Additionally, companies should also make full use of China’s carbon emission policies to reduce the cost of reducing carbon emissions while creating a green and clean energy company, effectively increasing the value of carbon assets, and preparing for the cultivation of new industries in the future.

2.

Strengthen corporate carbon asset management:

Only three (sub-)sectors are included in the first batch of the unified national carbon market. The pilot carbon emission control companies that were previously included in the pilot areas will also be included (including the Tianjin branch of CNOOC (China) Co., Ltd.).

With the improvement in the carbon market and the increasing pressures of the conditions for implementing a carbon tax, no company will be beyond reducing its carbon emissions. Therefore, it is particularly important to do a good job in terms of corporate carbon asset management in advance. A company’s carbon emissions should be known as soon as possible by utilizing inventory and verification. Companies should make emission reduction or response measures as early as possible following relevant policies and development trends to minimize the impact of carbon emissions on the company. Companies with surplus carbon emission allowances can also strive for additional benefits for these companies.

3.

Properly assess the impact of new projects on carbon emissions:

Carbon emission assessment projects are a new assessment method that has been gradually developed in recent years. Regardless of whether it is the carbon market or the implementation of a carbon tax, for companies with high carbon emissions, it will affect the production and operation of the company to a certain extent. For new or renovated and expanded projects, it is recommended that carbon emission assessment is carried out in the preliminary research stage of the project. The main purposes of the assessment are: 1—predict the carbon emission cost of investment projects and assess the degree of impact of carbon emissions on the economics of the project; and 2—enable a better-informed choice of measures and paths to meet carbon emission requirements through the assessment.

4.

Deploy large-scale carbon emission reduction technologies as early as possible:

CO₂ emission reduction is a long-term and arduous task. Soon, work can be carried out on energy optimization, production energy conservation, and the development and utilization of clean energy by tapping the company’s internal emission reduction potential. However, more CO₂ emission reduction and utilization methods are needed to achieve long-term and effective emission reduction, i.e., “post-processing” technology. Therefore, it is necessary to deploy carbon emission reduction utilization technology research and development as soon as possible, and make full preparations for emission reduction technologies and programs. While fulfilling the goals required by the state, this will also enhance the core competitiveness of the enterprise and promote its low-carbon transformation as well as its sustainable development.

In summary, in the process of carbon emission management, due to the complexity of the factors influencing carbon emission, it is a great challenge to carry out forecasting, and it will also consume a lot of human effort and material resources. The use of deep learning to build a carbon emission prediction model can predict the carbon emissions of the Yangtze River Economic Zone with high accuracy, reduce the human and material investment in carbon emission management, and provide a reference for carbon emission management.

5. Conclusions

According to the model test results, the “Yangtze River Economic Belt” basin and the industry investment scale, the labor efficiency output, carbon emission intensity, and other indicators that affect carbon emissions are relatively accurate in the carbon emission information forecast [37]. Therefore, the proposed method concludes that the SVR model for solving complex nonlinear problems can achieve a relatively excellent prediction effect under the training of LSTM. Due to the complexity of the “carbon sources” of the carbon emissions of the research object, the information affecting carbon emissions has the characteristics of diversity, dynamics, and big data. On the other hand, deep learning algorithms have strong fusion and changeable algorithms. The use of a deep learning network to process the information of the prediction model is complicated, which is main shortcoming of this study [38]. Therefore, the study hereby puts forward expectations that the prediction of carbon emission information is crucial to the country’s mid-to-long-term “carbon peak” strategy. The deep learning network must be used to accurately predict carbon emissions within a specific economic region, and then be promoted nationwide. This process requires the concerted efforts of researchers from related fields to work together.