Abstract
This study quantitatively estimated the precipitation associated with a typhoon in the northwestern Pacific Ocean by using a physical algorithm which included the Weather Research and Forecasting model, Radiative Transfer for TIROS Operational Vertical Sounder model, and data from the Tropical Rainfall Measuring Mission (TRMM)/TRMM Microwave Imager (TMI) and TRMM/Precipitation Radar (PR). First, a prior probability distribution function (PDF) was constructed using over three million rain rate retrievals from the TRMM/PR data for the period 2002–2010 over the northwestern Pacific Ocean. Subsequently, brightness temperatures for 15 typhoons that occurred over the northwestern Pacific Ocean were simulated using a microwave radiative transfer model and a conditional PDF was obtained for these typhoons. The aforementioned physical algorithm involved using a posterior PDF. A posterior PDF was obtained by combining the prior and conditional PDFs. Finally, the rain rate associated with a typhoon was estimated by inputting the observations of the TMI (attenuation indices at 10, 19, 37 GHz) into the posterior PDF (lookup table). Results based on rain rate retrievals indicated that rainband locations with the heaviest rainfall showed qualitatively similar horizontal distributions. The correlation coefficient and root-mean-square error of the rain rate estimation were 0.63 and 4.45 mm·h−1, respectively. Furthermore, the correlation coefficient and root-mean-square error for convective rainfall were 0.78 and 7.25 mm·h−1, respectively, and those for stratiform rainfall were 0.58 and 9.60 mm·h−1, respectively. The main contribution of this study is introducing an approach to quickly and accurately estimate the typhoon precipitation, and remove the need for complex calculations.
1. Introduction
The precipitation of typhoons at the early stages can be estimated by satellites by using visible (VIS) and infrared (IR) channels. VIS channels are used only during daytime. Furthermore, IR channels are affected by cloud layers and, therefore, data for the region below the cloud top cannot be collected. Unlike IR channels, passive microwave channels enable observing precipitation conditions below clouds.
Scientists have established the regression relation between the passive microwave brightness temperature (TB) and the actual rain rate (rain rate, RR); thus, an observed TB can be input into the regression relation to estimate the RR [1,2]. However, the disadvantage of regression relations is that they are restricted to specific periods, areas, and weather systems. Past studies have mentioned various methods in which passive microwave channels are used to estimate the precipitation intensity after 1990 [3,4,5,6,7,8].
Many studies have indicated that a major method for estimating the RR over the ocean involves using multi-satellite passive microwave channels. Satellite passive microwave data can provide estimates of precipitation over the vast ocean, where there is a lack of observed data, and the estimates are unot influenced by cloud layers [9]. In the presence of the emission and scattering effects of raindrops, the relationship between the TB and the RR is non-monotonic [10].
Since 2000, many scholars have used satellite passive microwave channels to estimate the RR. Chen and Li [11] utilized the passive microwave channel of the Tropical Rainfall Measuring Mission (TRMM) along with synchronous satellite data to research precipitation estimation. Kidd et al., [8] developed a precipitation estimation method by combining passive microwave and IR channels, and the time resolution of the method is 30 min. Different microwave channels have different physical features and limitations related to precipitation retrieval. Therefore, some researchers have used multiple channels to estimate the RR and to increase the dynamic range of precipitation retrieval [12,13]. Kummerow et al., [14] presented the Goddard profiling algorithm for passive-microwave-data-based RR estimation.
Although the passive microwave sensor has become the preferred choice for estimating precipitation associated with typhoons over the ocean, an IR sensor is superior for estimating long-period precipitation since the passive microwave sensor has extremely low time resolution [15,16,17]. Clearly, the use of RR estimation algorithms is restricted to the ocean [18,19,20]. Since the ocean has low emissivity (approximately 0.5) and a low (cold) radiation background, regions where precipitation occurs show a high (warm) radiation rate (emissivity close to 1.0). Therefore, precipitation locations over the vast ocean can be easily identified.
Information on the type of land feature, such as whether an area is snow covered, a desert, or semi-arid [18,21,22,23], is necessary when estimating precipitation on land. Thus, it is difficult to conduct a study of land precipitation by using emission data. Studies on land precipitation retrieval typically focus on scattering data [24,25]. High-frequency microwave channels can be used to estimate land precipitation [4,5,18,21,23].
Overall, although satellite precipitation data are quantitative and provide spatiotemporal coverage over the ocean [26], they contain uncertainties and have limitations [27]. Therefore, many studies have evaluated, improved, and used satellite-based rainfall data for different areas [28,29,30]. Moreover, the accuracy of satellite-based rainfall data for different locations, seasons, and weather systems has been evaluated [31,32].
Moreover, a strong relationship exists between the rainfall intensity and water resources management. Water resources management involves the activity of planning, developing, distributing, and managing the optimum use of water resources, such as reservoir operation, rainfall runoff, water supply planning, irrigation system, and so on.
For example, Chau et al., [33] illustrated that the provision of an accurate and timely rainfall forecast is a key factor in reservoir operation. Meanwhile, Wang et al., [34] tried to improve the forecasting accuracy of annual runoff time series using numerical models and empirical models. Although a physical method has shortcomings such as requiring complex computations and being time consuming, regression relations used in a physical method do not change with time and place, similar to statistical methods. The time required to establish a relationship between the RR and attenuation index is longer than the time needed to establish a relationship between the RR and multi channels’ TB. Furthermore, a Bayesian method is a complex and time-consuming physical method in advance. This study simulated the TB of typhoons before their occurrence by using the Weather Research and Forecasting (WRF) and Radiative Transfer for TIROS Operational Vertical Sounder (RTTOV) models. The TB was then transferred to the attenuation index. Finally, a lookup table for the attenuation index and RR was constructed using a Bayesian approach. The following step merely involves transferring the observed TB to the attenuation index and then estimating the RR of typhoons by using the lookup table. Consequently, the use of time-consuming physical methods can be avoided. The main contribution of this study is providing a method that can quickly and accurately estimate the typhoon rain rate.
This paper is organized as follows. In Section 2, we briefly review a theory used in this study; the theory presents the relationship between microwave observations (transferred to the attenuation index) and RR. In Section 3, we detail the basis of our methodology, including the physical algorithm, established rainfall threshold, and Bayesian approach. In Section 4, case validation and the results of this study are discussed. Finally, conclusions are presented in Section 5.
2. Theory
During rainfall, rain droplets over the ocean absorb and emit radiation. Therefore, the TB increases with the RR, implying that the TB can be used for precipitation estimation. The relationship between the TB and RR is shown in Figure 1 [35]. The text in the right side of Figure 1 describes the frequency and polarization of TMI which correspond to each line. For example, TB10V is the 10 GHz vertical polarization. Figure 1 was simulated as the standard atmosphere. For example, the standard atmospheric pressure was 1013.250 hPa.
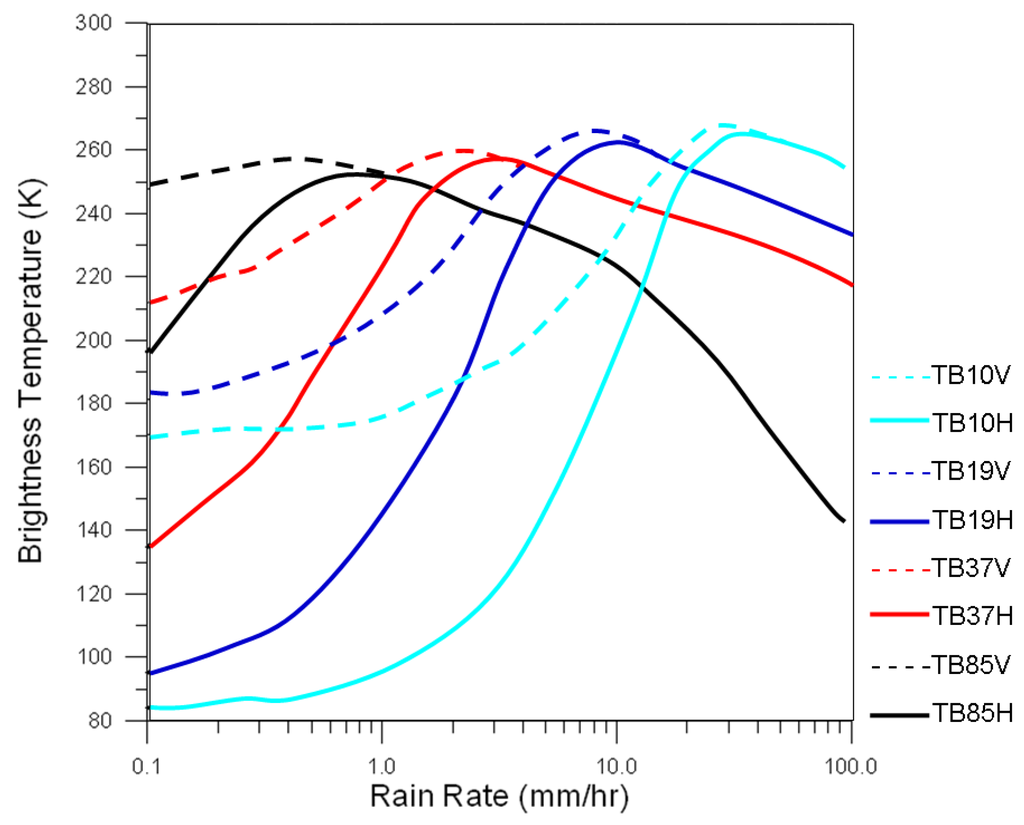
Figure 1.
Ideal plot of brightness temperature (TB) versus rain rate (RR) over the ocean for the Tropical Rainfall Measuring Mission Microwave Imager (TMI) channels [35]. The text in the right side of Figure 1 describes the frequency and polarization of TMI which correspond to each line.
The microwave TB and RR do not have a one-to-one relationship [36]. If an equation relating them is developed directly, it would not be applicable to precipitation estimation. The attenuation index developed by Petty [12] is determined according to the difference between vertical polarization and horizontal polarization, and it is referred to as the P value. It is used to obtain the relationship between the TB and RR. The definition of the P value is as follows:
where and denote the vertical polarization TB and horizontal polarization TB, respectively, and and represent the values of and under identical atmospheric conditions after the removal of the effect of rain clouds. The p value ranges from 0 to 1. The value 1 indicates that clouds and rain are absent from the field of view (FOV) of the satellite, whereas 0 indicates that the optical thickness in the FOV becomes extremely opaque because of clouds and rain [37]. Figure 2 shows the inverse relation between precipitation intensity and the attenuation index [35]. The results of Figure 2 were calculated by Equation (1) using the data of Figure 1. The P10, P19, P37, and P85 in the Figure 2 indicate the attenuation index at 10, 19, 37, and 85 GHz of TMI. Figure 1 was simulated using typhoon cases. Therefore, they are more suitable for estimating the rain rate of the typhoon. In Figure 2, it was found that the attenuation index at 85 GHz approaches zero for RR just above 1 mm/h and, thus, the error of RR estimation from P would be significant at a higher rainfall rate, especially for typhoon cases. Therefore, the 85 GHz data are not used in this study.
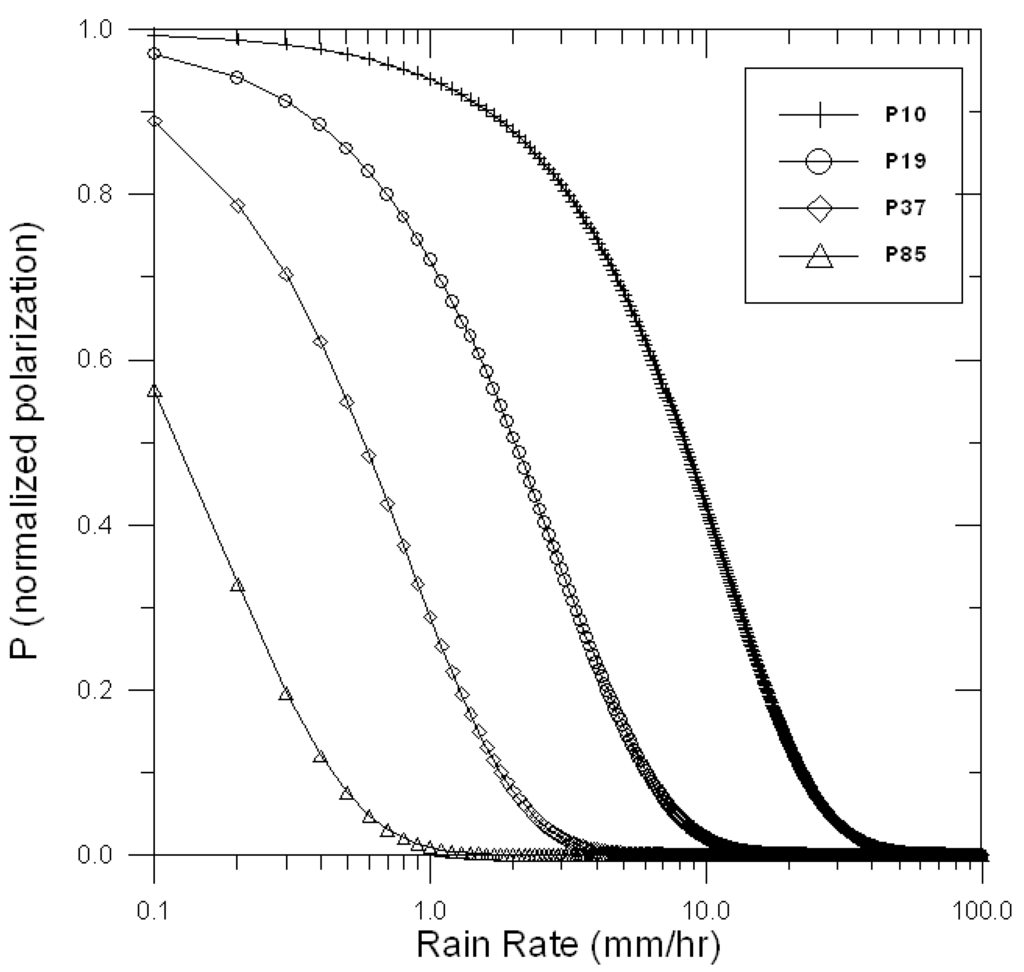
Figure 2.
Relationship between attenuation index and RR for TMI channels [35]. The P10, P19, P37, and P85 in Figure 2 indicate the attenuation index at 10, 19, 37, and 85 GHz of TMI.
3. Methodology
3.1. Physical Algorithm
In the precipitation estimation method proposed in this study, the WRF model is used to simulate the vertical hydrometeor distribution of a typhoon over the western Pacific. The vertical hydrometeor distribution is the standard output products of WRF. The hydrometeor distribution is then inputted into the RTTOV model to simulate the TBs of the TMI channels, and a conditional probability distribution function (PDF) is constructed using the output of the WRF and RTTOV models. Moreover, a prior PDF is constructed using 3,115,544 PR precipitation data over the ocean. Finally, the posterior PDF is obtained on the basis of Bayesian theory. Therefore, a lookup table of the probability of occurrence of various RR corresponding to the attenuation index of TMI channels can be constructed. In other words, a rain rate can be estimated when the satellite observations are converted to the attenuation index.
The complete flowchart for precipitation estimation is shown in Figure 3. The dotted square represents the processing procedure of the model, which includes the WRF and RTTOV models, and the dashed square represents the processing method of the satellite.
3.2. Establishing a Threshold for Rain
To obtain the precipitation threshold of each TMI channel over the northwestern Pacific during summer, TRMM swaths that were within the range of the northwestern Pacific from June to October of 2009 and 2010 were obtained. There were a total of 2242 TRMM swaths, which included observed values of the TMI and PR. Within the 2242 TRMM swaths contains 127,382 PR data points corresponding to the absence of rain. Histograms of the TB for each TMI channel in the absence of rain were drawn (Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8). Samples that were within ±1 of the standard deviation were reanalyzed excluding outlier and possibly noisy data. The average TB values of each channel represented the precipitation threshold (Table 1).
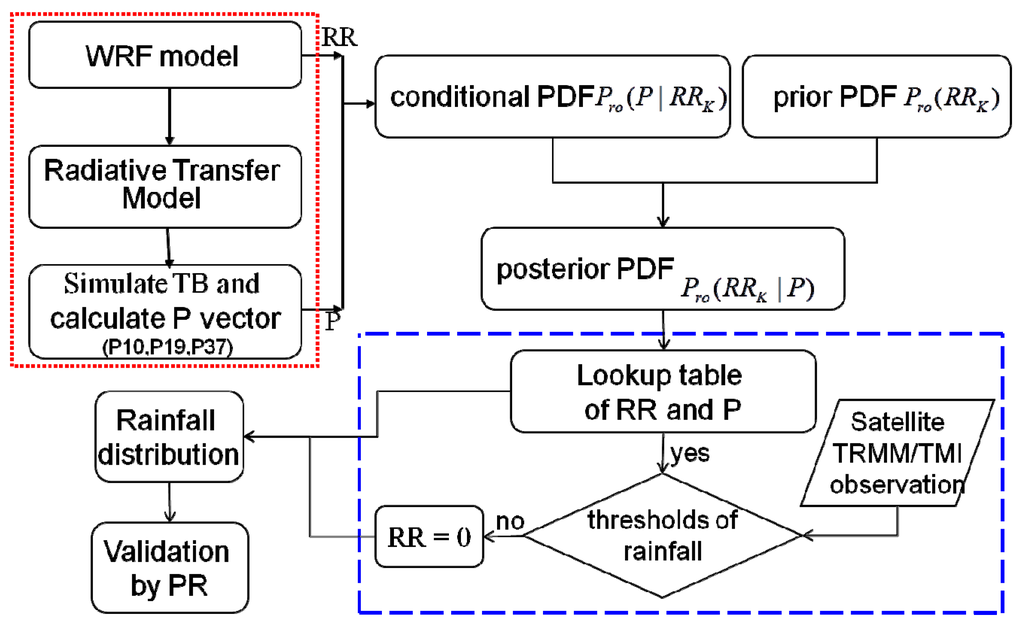
Figure 3.
Flowchart for precipitation estimation proposed in this study.
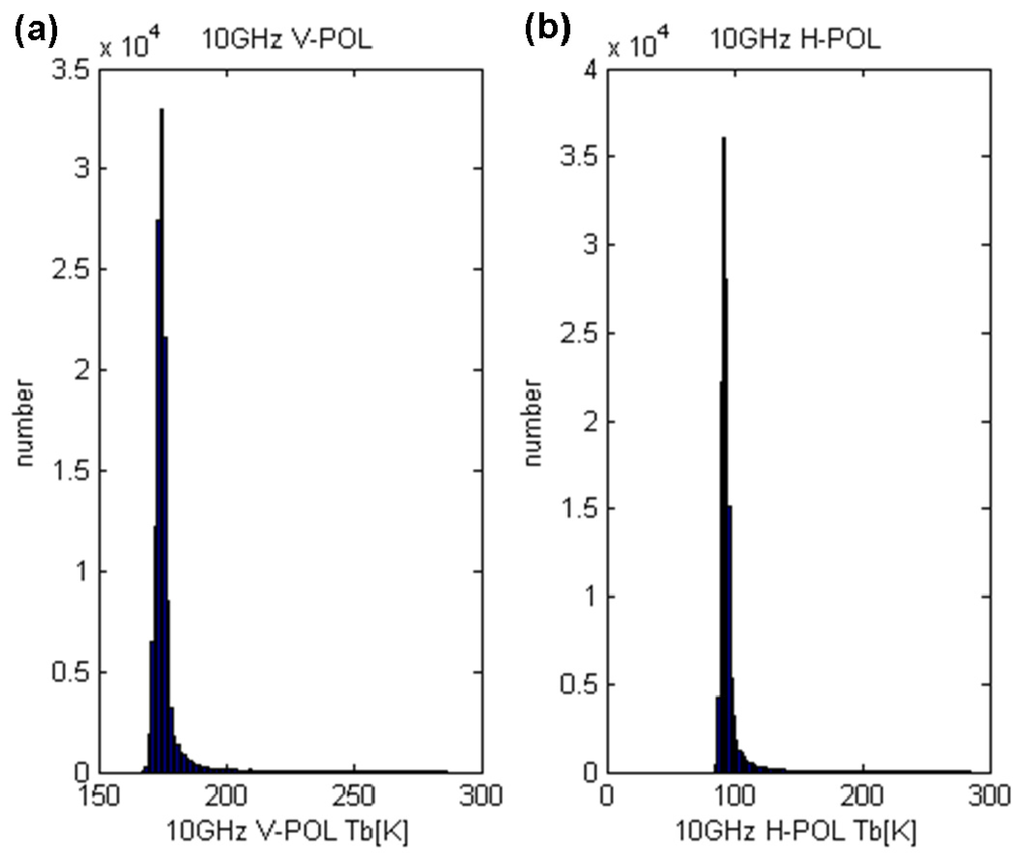
Figure 4.
Histograms of the TB for the TMI in the absence of rain: (a) TB10V and (b) TB10H.
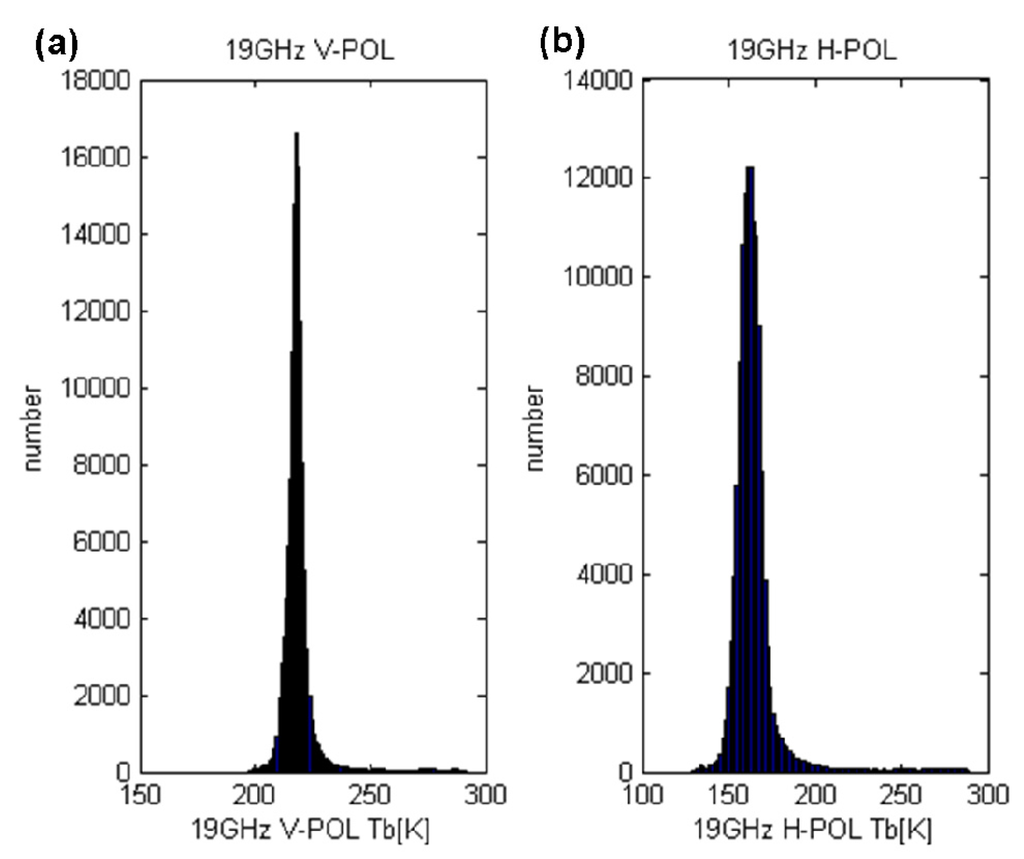
Figure 5.
Histograms of the TB for the TMI in the absence of rain at 19 GHz: (a) TB10V and (b) TB10H.
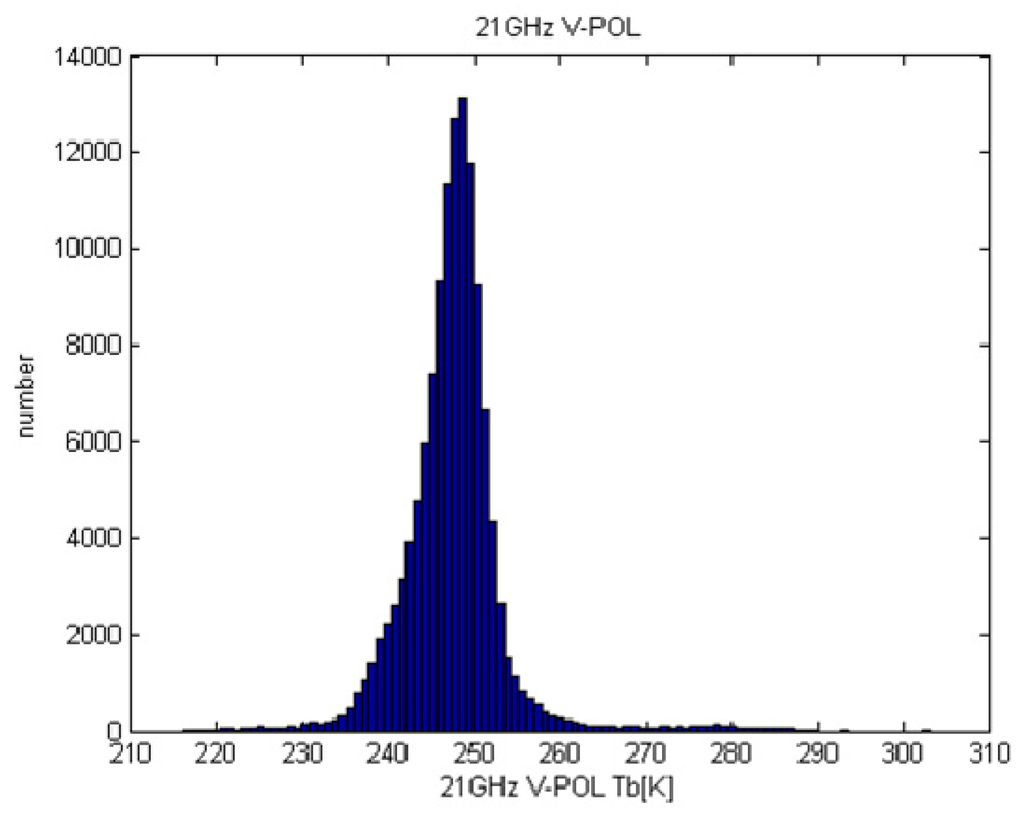
Figure 6.
Histogram of the TB for the TMI in the absence of rain at 21 GHz.
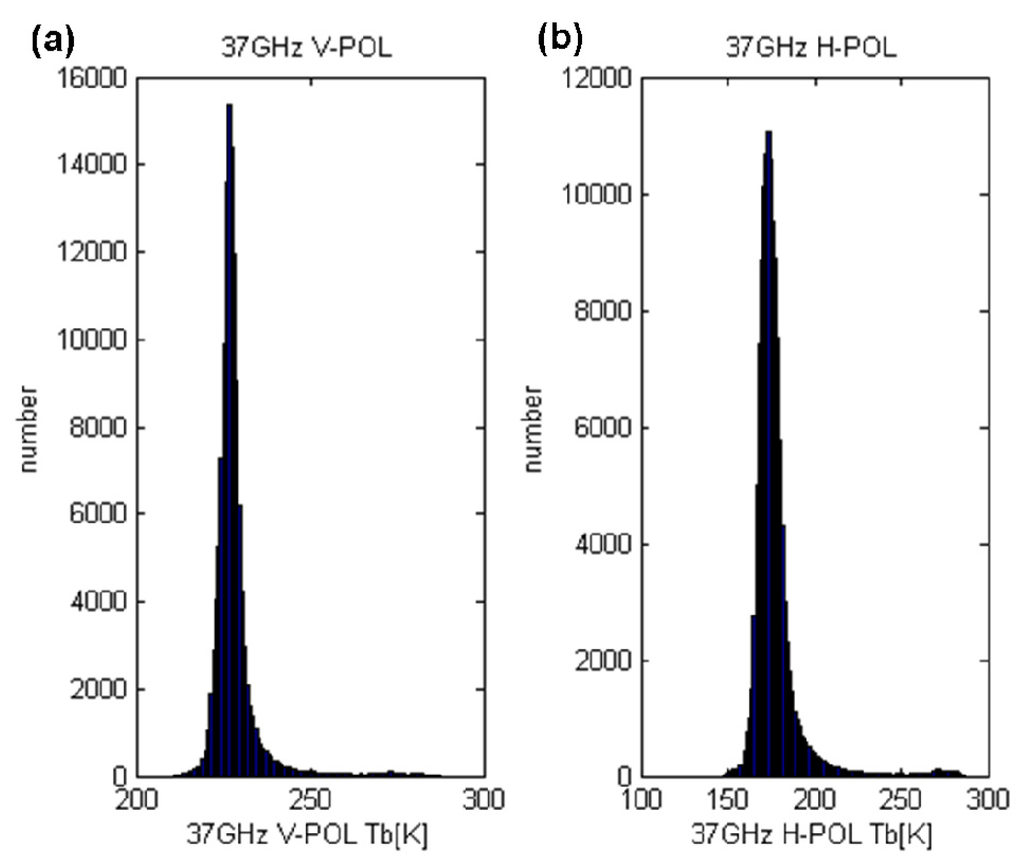
Figure 7.
Histograms of the TB for the TMI in the absence of rain at 37 GHz: (a) TB10V and (b) TB10H.
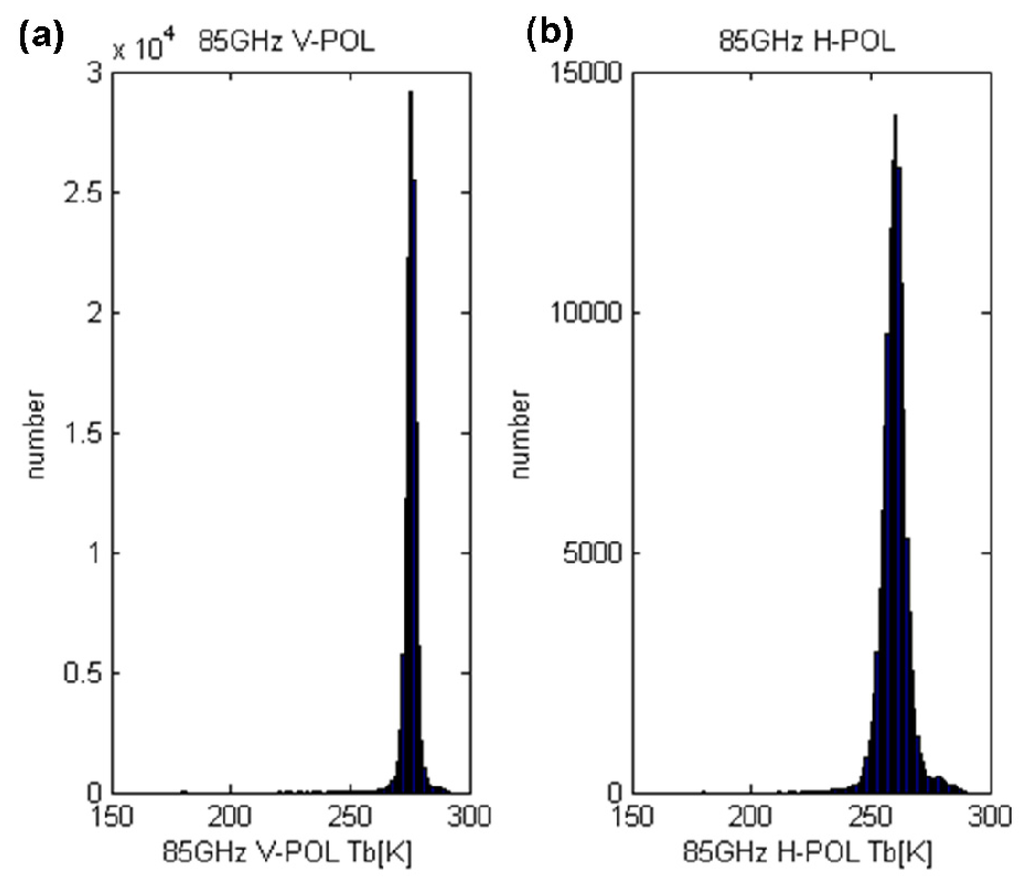
Figure 8.
Histograms of the TB for the TMI in the absence of rain at 85 GHz: (a) TB10V and (b) TB10H.

Table 1.
Precipitation thresholds and standard deviations for TMI channels.
| Frequencies | Threshold (Mean) | Standard Deviation |
|---|---|---|
| 10-V GHz | 175.78 K | 1.27 K |
| 10-H GHz | 93.78 K | 2.39 K |
| 19-V GHz | 218.77 K | 2.73 K |
| 19-H GHz | 163.46 K | 5.05 K |
| 21-V GHz | 248.21 K | 3.41 K |
| 37-V GHz | 228.09 K | 2.39 K |
| 37-H GHz | 175.74 K | 5.05 K |
| 85-V GHz | 276.17 K | 1.63 K |
| 85-H GHz | 260.77 K | 3.76 K |
3.3. Prior PDF
The main difficulties are constructing the prior and conditional PDFs [38] and obtaining numerous and distinct samples to extend the distribution range of the P value and RR. The objective of this study was to estimate the RR associated with typhoons that may impact Taiwan. Therefore, near-surface RR data were collected by using the PR for a nine-year period (2002–2010), from June to November, over the northwestern Pacific and South China Sea regions (longitude 110°–155° E, latitude 5°–35° N), and the data were used to construct the prior PDF.
The minimum measurable echo intensity was 17 dBZ, which is equal to an RR of 0.7 mm·h−1 [39]. A total of 15,480 swaths and over 60 million observation data were obtained over the South China Sea and northwestern Pacific in the nine-year period. The number of RR data used in this study to construct the prior PDF was 3,115,544.
The symbol “+” in Figure 9 is used to represent the RRs near the nadir of the curve. The x coordinate represents the RR, and the y coordinate represents the prior PDF. The solid line represents the probability distribution obtained by fitting a logarithmic normal distribution to the portion of the curve marked by “+” symbols.
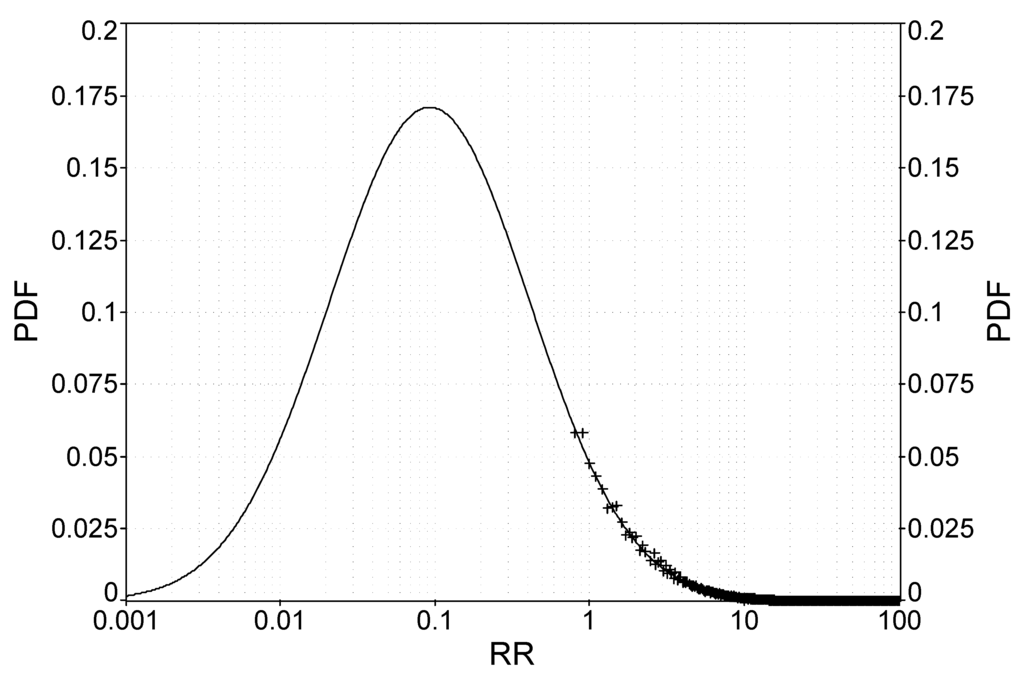
Figure 9.
Rain rate distribution-PR (near nadir). Points marked by “+” represent the RRs near the nadir of the curve, and the solid line denotes the probability distribution.
3.4. Conditional PDF
Calculating the conditional PDF mainly involved calculating the probability distribution of the p value at different RRs. Numerous samples are required to obtain the relevant statistics and increase the dynamic range of the P value and RR. For this purpose, most of the chosen typhoons were moderate or strong when conducting the simulation.
The conditional PDF was calculated by WRF model to simulate various vertical hydrometeor distributions such as rain, snow, hail, and graupel, that is the standard output products of WRF. The results of hydrometeor sensitivity can be found in Yeh et al., [40]. According to Chien et al., [41], an analysis was made on the respective advantages and disadvantages for various combinations of different model parameters. The study used WSM6 (WRF Single-Moment) scheme in the microphysics option, YSU (Yonsei University) scheme in the boundary layer option, and KF (Kain-Fritsch) scheme in the cumulus option. These vertical hydrometeor distributions were inputted into the RTTOV model to obtain the TB of the TMI channels. RTTOV stands for Radiative Transfer for TOVS and is a very fast radiative transfer model for nadir-viewing passive visible, infrared, and microwave satellite radiometers, spectrometers, and interferometers. Fifteen typhoons occurring over the northwestern Pacific (Table 2) were simulated.

Table 2.
Fifteen typhoons considered for constructing the conditional probability density function.
| Number | Typhoon Nane | Typhoon Strength | Simulation Time (UTC) |
|---|---|---|---|
| 1 | BOLAVEN | Strong | 2012/8/25 1800–2012/8/26 1800 |
| 2 | GUCHOL | Strong | 2012/6/17 0600–2012/6/17 0600 |
| 3 | NANMADOL | Strong | 2011/8/25 1800–2011/8/26 1800 |
| 4 | SONGDA | Strong | 2011/5/26 1200–2011/5/27 1200 |
| 5 | SINLAKU | Strong | 2008/9/12 0600–2008/9/13 0600 |
| 6 | PRAPIROON | Medium | 2012/10/11 1800–2012/10/12 1800 |
| 7 | JELAWAT | Medium | 2012/9/28 0000–2012/9/29 0000 |
| 8 | SANBA | Medium | 2012/9/14 1200–2012/9/15 1200 |
| 9 | HAIKUI | Medium | 2012/8/6 0000–2012/8/7 0000 |
| 10 | MUIFA | Medium | 2011/8/3 0600–2011/8/4 0600 |
| 11 | CHABA | Medium | 2010/10/27 1800–2010/10/28 1800 |
| 12 | MEGI | Medium | 2010/10/21 0000–2010/10/22 0000 |
| 13 | FANAPI | Medium | 2010/9/17 1200–2010/9/18 1200 |
| 14 | LUPIT | Medium | 2009/10/18 0000–2009/10/19 0000 |
| 15 | PARMA | Weak | 2009/10/4 0600–2009/10/5 0600 |
3.5. Posterior PDF
Nine years of near-surface RR data were used to construct the prior PDF, and the WRF model was used to simulate the vertical hydrometeor distribution and surface RR for 15 typhoons and to calculate the P value, which was then simulated using the RTTOV model; subsequently, the conditional PDF was constructed. Finally, According to Bayesian theory, the posterior PDF derived from the prior and conditional PDF, and the posterior PDF could be used along with satellite observations to estimate the RR associated with a typhoon. In other words, the rain rate of typhoon was estimated by inputting the vector into the lookup table (posterior PDF). The physical meaning is that the probability distribution of the RR is estimated using a certain known observation vector .
There are two advantages of using the model when the Bayesian approach is used to estimate precipitation. First, the model can simulate a massive amount of data and a wide range of RRs. In the statistical point of view, a large amount of data can improve its reliability. Additionally, a large amount of data can also expand the range of RR estimation and its accuracy. Second, the RR can be estimated instantly without any calculations. The advantage of the Bayesian approach can be found in Chiu and Petty [38]. In addition to the Bayesian approach, the relationship of P and RR, as shown in Figure 2, can also be used to estimate the RR. The result of the RR estimation can be seen in Section 4.2. Meanwhile, additional descriptions have been added to Section 4.2.
4. Validation and Discussion
4.1. Analysis of TB
To clearly understand the differences between the simulated TB and the observed TB, a quantitative analysis of the TB was performed by considering typhoons in only a selected region. The region considered for quantitative analysis and the corresponding number of data for each typhoon are listed in Table 3.

Table 3.
Information on the simulated typhoons.
| No. | Typhoon Name | Scan Time (UTC) | The Range of Quantitative Analysis | Data Number | Correlation Coefficient | ||||
|---|---|---|---|---|---|---|---|---|---|
| North Latitude | East Longitude | ||||||||
| 1 | BOLAVEN | 2012/8/26 | 759 | 23 | 29 | 125 | 133 | 3437 | 0.74 |
| 2 | GUCHOL | 2012/6/17 | 1848 | 19.5 | 24 | 125 | 130 | 1846 | 0.87 |
| 3 | NANMADOL | 2011/8/26 | 842 | 15.5 | 19 | 122 | 126 | 1020 | 0.64 |
| 4 | SONGDA | 2011/5/27 | 609 | 17 | 22.5 | 121.5 | 126 | 1921 | 0.73 |
| 5 | SINLAKU | 2008/9/12 | 1912 | 22 | 26.5 | 121.5 | 125.5 | 1297 | 0.79 |
| 6 | PRAPIROON | 2012/10/12 | 709 | 17 | 23 | 126 | 132 | 3117 | 0.78 |
| 7 | JELAWAT | 2012/9/28 | 1508 | 23 | 28 | 123 | 128 | 1960 | 0.83 |
| 8 | SANBA | 2012/9/15 | 347 | 21.5 | 26 | 126 | 131 | 1840 | 0.8 |
| 9 | HAIKUI | 2012/8/6 | 1820 | 24 | 30 | 121.5 | 128 | 2589 | 0.7 |
| 10 | MUIFA | 2011/8/3 | 1841 | 21.5 | 27 | 128 | 134 | 2682 | 0.77 |
| 11 | CHABA | 2010/10/28 | 1016 | 23 | 28 | 127 | 131 | 1553 | 0.88 |
| 12 | MEGI | 2010/10/21 | 1330 | 21.5 | 27 | 128 | 134 | 2156 | 0.84 |
| 13 | FANAPI | 2010/9/18 | 620 | 21.5 | 25.5 | 123 | 128 | 1575 | 0.84 |
| 14 | LUPIT | 2009/10/18 | 1434 | 15 | 21 | 131 | 137 | 2307 | 0.82 |
| 15 | PARMA | 2009/10/4 | 2232 | 17 | 22 | 117 | 122 | 1691 | 0.72 |
The precipitation lookup table was constructed by using frequencies of 10, 19, and 37 GHz to estimate the precipitation. Therefore, the quantitative analysis involved these three frequencies for the vertical and horizontal polarization. The correlation coefficient of the TB of each channel was calculated, and the average correlation coefficient of six channels was obtained. The average correlation coefficients of the observed TB and simulated TB were obtained. The correlation coefficients of the 15 typhoons are listed in Table 3. The conditional PDF was constructed using the TB and RR of the 15 typhoons, and the average correlation coefficient between the simulation and observation is 0.78.
Validation of TB Simulation
The conditional PDF was constructed by considering the 15 typhoons. The 10 GHz vertical polarization for the typhoons is discussed in this section.
Typhoon Nanmadol occurred on 26 August 2011 at 0842 UTC, and its track number is 78483. Figure 10 shows the satellite IR image at 0830 UTC. Clearly, the center of typhoon Nanmadol was approximately located to the east of the Philippines (latitude 17.5° N, Longitude 123.5° E). The cloud rainband shows a symmetrical and complete structure, indicating that Nanmadol was a strong typhoon.
Figure 11a shows the TB observations of the TMI, Figure 11b shows the TB simulated by the RTTOV model, and Figure 11c shows the histogram of the TB for the region within the dashed square. The blue bar represents TB observations, and the yellow bar denotes the simulated TB.
A qualitative analysis of Figure 11 and Figure 12 shows that the center of the simulation of the typhoon is approximately identical in both figures and the entire simulation pattern is similar to the observed pattern of the typhoon. The TB of the clear sky simulated by the model shows a value that is consistent with the observation. The TB of the simulated typhoon rainband is overestimated.

Figure 10.
Infrared (IR) image recorded at 0830 UTC on 26 August 2011.
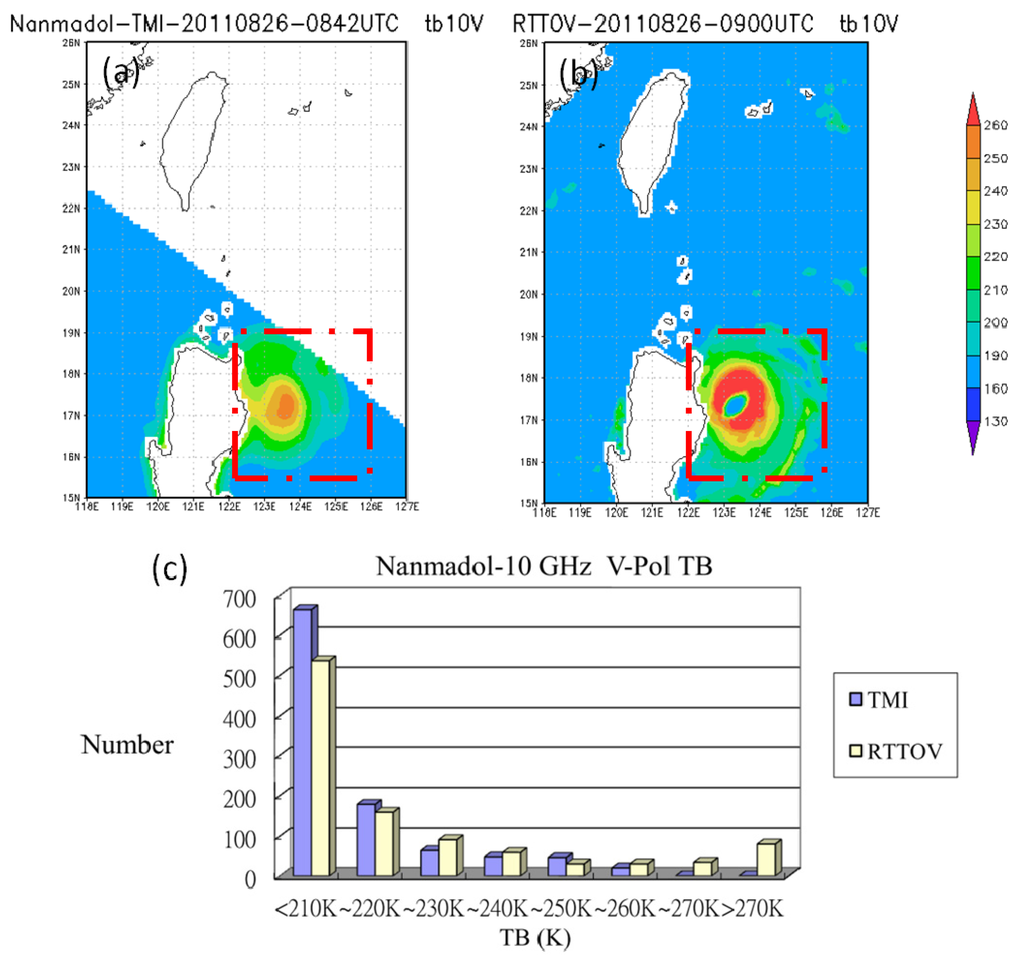
Figure 11.
TB10V of Typhoon Nanmadol: (a) TMI observation; (b) Radiative Transfer for TIROS Operational Vertical Sounder (RTTOV) simulation; and (c) histogram for the region within the dashed square in the preceding panels.
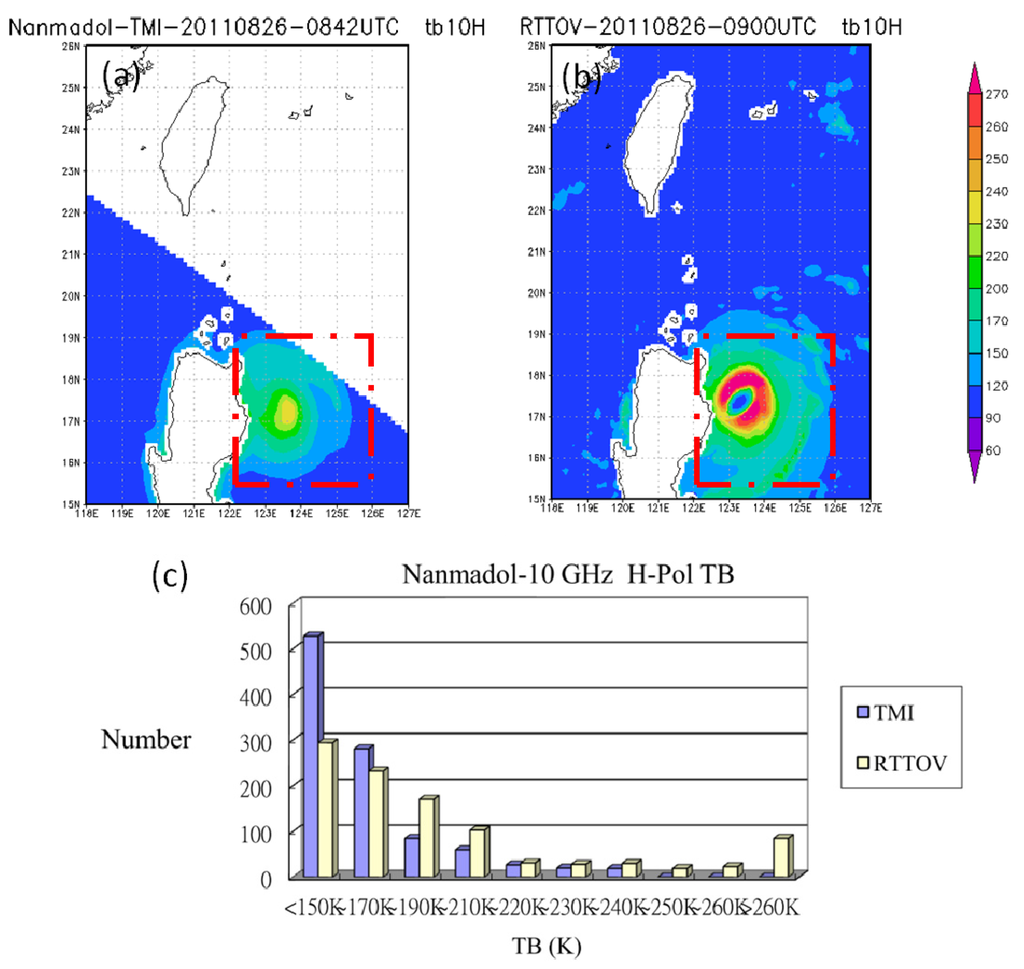
Figure 12.
TB10H of Typhoon Nanmadol: (a) TMI observation; (b) RTTOV simulation; and (c) histogram for the region within the dashed square in the preceding panels.
The TB of the clear sky is identical in the simulation and observation (Figure 11c). The sizes of simulated and observed typhoons are similar. Therefore, the TB values of the clear sky within the dashed squares of the simulated and observed patterns are roughly identical. The highest TB of the rainband in Figure 11a is 230–240 K, and in Figure 11b, it is greater than 270 K. Therefore, the histogram of Figure 11c pertains to simulated TB values above 270 K. Figure 12 shows a similar situation. In other words, the simulation overestimated the TB in the rainband, because the WRF-model simulation of the precipitation associated with the typhoon was overestimated. The simulated RR was overestimated by the WRF model, and emissions dominated the 10 GHz frequency. Therefore, the simulated TB was overestimated because of emissions from raindrops, regardless of whether polarization was vertical or horizontal.
The difference between the simulation time and observation time is 18 min. Overall, the intensity and the structure of the typhoon are similar in the TMI observation and simulation, and only the scale of the typhoon differs slightly between the simulation and the observation. Therefore, the correlation coefficient between the simulation and observation is only 0.64.
4.2. Validation of RR Estimation
In this study, five complete typhoons, including 10 swaths scanned by the TMI in 2011 and 2012, were examined to verify the estimated precipitation. Information on the name, scanning time, and track number of the typhoons is presented in Table 4. Because there were few in situ observations (on islands and buoys), the verification was performed by considering the near-surface RR data recorded by the PR as the true value. RR verification was divided into quantitative analysis and qualitative analysis.
Numbers 1 to 10 in Table 4 represent 10 cases. However, for some typhoons, nadir scanning by the PR did not encompass the full rainband of the typhoons. Therefore, quantitative analysis was not performed for case numbers 1 and 3. The average correlation coefficient for the other eight cases is 0.62, and the average root-mean-square for the other eight cases error is 4.45. The results of the average root-mean-square and RMSE showed that the proposed method can accurately estimate the typhoon rain rate. Overall, the position of the typhoon heavy rainfall could be displayed, but the heaviest rainfall intensity was underestimated. One of the key sources of the error is that this method does not use the high-frequency channel. One case in Table 4 is discussed in this section, and the quantitative analysis results of the other cases are presented in the Table 4.

Table 4.
RR validation cases.
| Number | Typhoon Name | Scan Time (UTC) | Orbital Number | Correlation Coefficient | RMSE |
|---|---|---|---|---|---|
| 1 | MUIFA | 2011/08/03 1307 | 78127 | – | – |
| 2 | MUIFA | 2011/08/03 1940 | 78131 | 0.52 | 3.48 |
| 3 | MUIFA | 2011/08/04 1732 | 78146 | – | – |
| 4 | NANMADOL | 2011/08/29 0025 | 78524 | 0.78 | 2.67 |
| 5 | TEMBIN | 2012/08/23 0943 | 84141 | 0.7 | 4.63 |
| 6 | TEMBIN | 2012/08/26 0832 | 84187 | 0.58 | 4.27 |
| 7 | TEMBIN | 2012/08/27 0736 | 84202 | 0.54 | 2.36 |
| 8 | SANBA | 2012/09/12 0733 | 84451 | 0.44 | 6.05 |
| 9 | SANBA | 2012/09/14 0540 | 84481 | 0.66 | 5.97 |
| 10 | JELAWAT | 2012/09/28 1544 | 84706 | 0.72 | 6.14 |
Case Study
Figure 13 shows the estimated precipitation for typhoon Nanmadol. Figure 13a shows the RR estimated by the PR (hereinafter referred to as PR-RR), Figure 13b shows the RR estimated using the Bayesian method developed in this study (hereinafter referred to as TMI-RR), and Figure 13c shows a scatter plot of both types of estimates. In Figure 13a, typhoon Nanmadol consists of two regions with heavy precipitation. Region A is the southwestern sea area of Taiwan, and region B extends from the Bashi Channel to the southern part of the Taiwan Strait. In Figure 13b, the regions with heavier precipitation are located in regions A′ and B′, which match the locations of regions A and B in Figure 13a. Further analysis of Figure 13a,b regarding the intensity and range of heavy precipitation shows that the maximum PR-RR is higher than the maximum TMI-RR and that the range of the second greatest precipitation (yellow parts, 10–25 mm·h−1) of the TMI-RR is greater than that of the PR-RR.
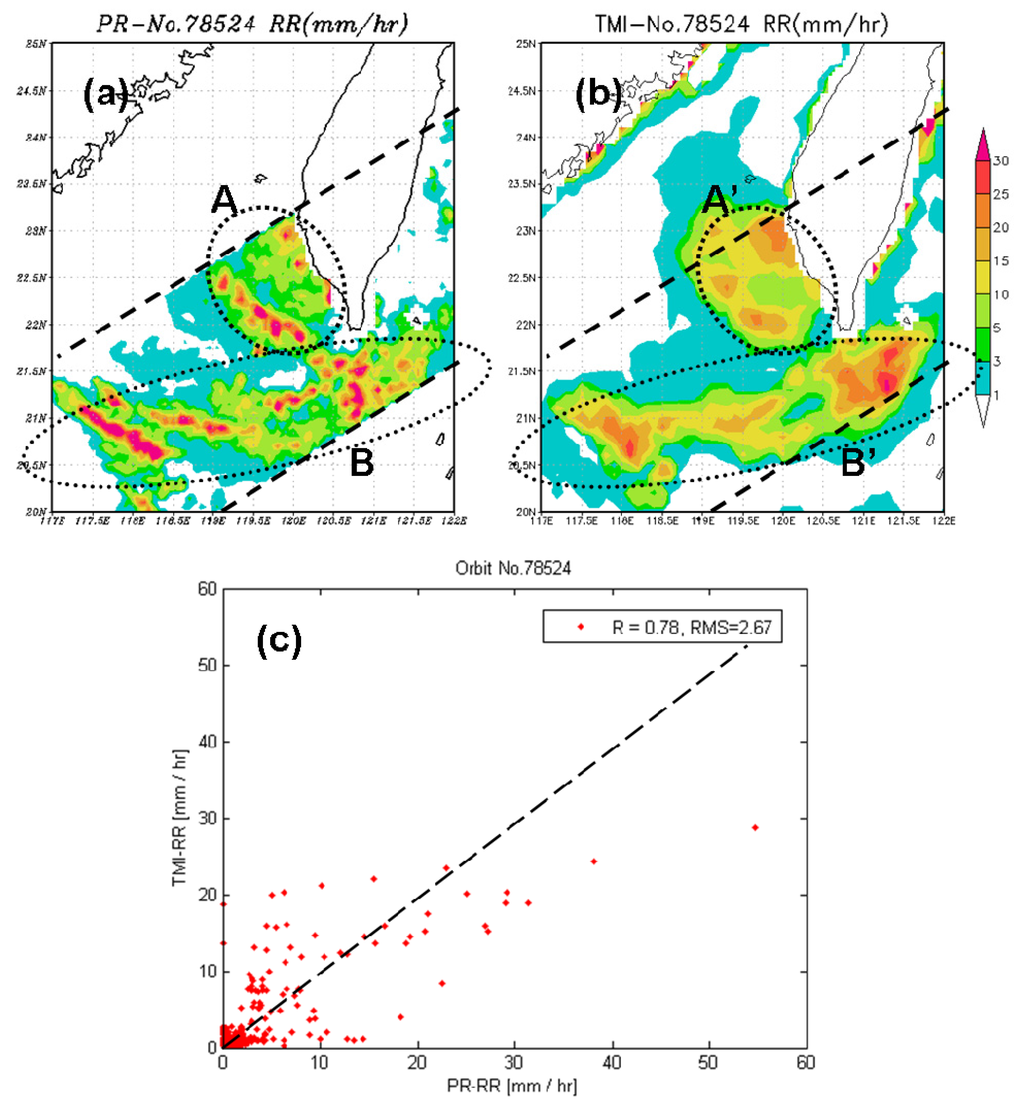
Figure 13.
RR estimation for Typhoon Nanmadol: (a) near-surface RR estimated by the PR (PR-RR); (b) RR estimated using the Bayesian method and the TMI data (TMI-RR); and (c) scatter plot of the PR-RR and TMI-RR.
There is a possible reason for the discrepancy between Figure 13a,b regarding the intensity and range: the space resolution and accuracy of the PR-RR. The horizontal resolution (10 km) of the TMI is twice that of the PR (5 km), and the TMI-RR is the result of averaging smaller RR values and the maximum RR in the FOV. Another possible reason was the physics in models do not reproduce the typhoon environment well. The correlation coefficient between the PR-RR and TMI-RR is 0.78, and the root-mean-square error is 2.67 mm·h−1.
The TMI-RR for this typhoon did not exceed 30 mm·h−1, possibly because the heavy precipitation consists of individual short-range convective cells that average light precipitation in their vicinity. Finally, the maximum RR of the TMI-RR is smaller than that of the PR-RR, and the range of the second largest RR of the TMI-RR is greater than that of the PR-RR.
For the case being discussed, the space resolution of the PR-RR is 5 km, which is suitable for observing a shorter range of convective precipitation. Therefore, a single grid point of RR can show a high precipitation value. By contrast, the space resolution of the TMI-RR is 10 km, and partial heavier precipitation and partial smaller precipitation in the FOV is easier to appear. These factors may cause the maximum RR of the TMI-RR to be smaller than that of the PR-RR, the RR range to be smooth, and the range of the TMI-RR to be greater than that of the PR-RR after averaging the precipitation distribution, as shown in Figure 13a,b. These are the differences in the precipitation features between the PR-RR and the TMI-RR.
Although the space resolution of the PR-RR is superior to that of the TMI-RR, the precipitation estimation of the PR is based on using the radar reflectivity to retrieve the RR. Furthermore, comparing Figure 13a,b reveals that the swath of the TMI-RR is three times that of the PR-RR, and its utilization is superior to that of the PR-RR.
Figure 14 shows the RR estimated by combining RR estimations from the 10, 19, and 37 GHz attenuation indices for Typhoon Nanmadol (hereinafter referred to as P-RR). In Figure 14, Typhoon Nanmadol consists of two regions where the areas that have the heaviest rain. Moreover, the locations of the two regions match the locations of regions A and B in Figure 13a.
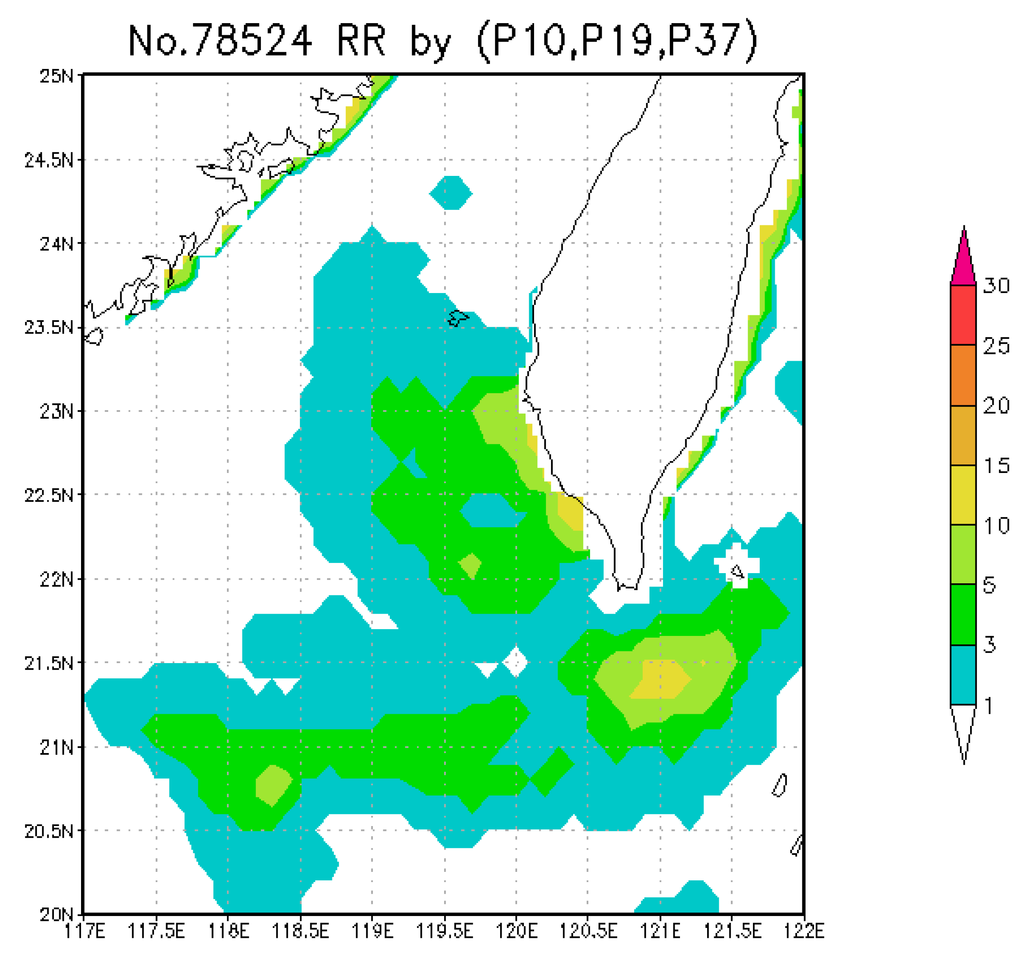
Figure 14.
RR estimated using the 10, 19, and 37 GHz attenuation indice.
Further analysis of Figure 14 regarding the intensity of the heavy precipitation shows that the maximum P-RR is lower than 15 mm·h−1. By comparing the TMI-RR and P-RR, the heavy rainfall locations are similar and match the locations of the PR-RR, and the intensity of P-RR is significantly lower than the PR-RR. The possible season for the low P-RR values less than 15 mm·h−1 at high PR-RR above 25 mm·h−1 is that the Figure 2 is not a production for typhoons near Taiwan. Therefore, the proposed method provides better results than the approach in directly estimating the rain rate from the attenuation index.
4.3. Precipitation Type Analysis
Figure 15 shows all convective and stratiform precipitation of the eight swaths considered in this study and verified using the PR-RR. The type of rain was taken from PR data. The horizontal coordinate represents the PR-RR, and the vertical coordinate denotes the TMI-RR. Figure 15a represents convective precipitation and Figure 15b represents stratiform precipitation. The black dashed line is the straight line x = y. The purpose of classification verification is to determine the performance of different types of precipitation.
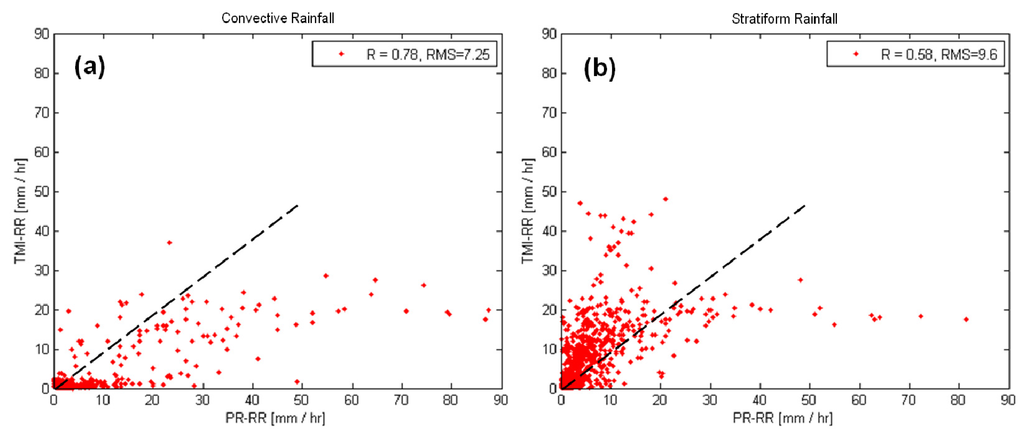
Figure 15.
Scatterplot of TMI-RR and PR-RR for (a) convective rainfall and (b) stratiform rainfall.
An analysis of Figure 15a shows that some rainfall intensity values of the PR are greater than 30 mm·h−1, and the corresponding rainfall of the TMI is less than 10 mm·h−1. The probability of heavy precipitation on a small scale is higher for convective precipitation. Regions A and B in Figure 13a,b are examples. The area which has the maximum RR is smaller than the FOV, and the RR of this area will be averaged. The PR-RR is averaged to the same horizontal resolution as the TMI. The maximum PR-RR can also be obtained by averaging it to the TMI resolution. The correlation coefficient between the TMI-RR and PR-RR is 0.78, and the root-mean-square error is 7.25 mm·h−1.
Compared with Figure 15a,b shows that the points of the TMI-RR are below 5 mm·h−1, but the number of points of the PR-RR that reach 10–50 mm·h−1 is considerably smaller. The TMI-RR data are mostly located on the left side of x = y, whereas the PR-RR values are less than 20 mm·h−1. The right side of x = y contains PR-RR values greater than 30 mm·h−1, implying that the TMI-RR values are overestimating when the PR-RR values are less than 20 mm·h−1. The TMI-RR values are underestimating when the PR-RR values are greater than 30 mm·h−1. Iguchi et al., (2000) [42] showed that there are differences in the coefficients in the reflectivity-rainfall rate relationship between different precipitation types as a result of larger raindrops in convective rain. Thus, an error in classification of convective actual type as stratiform type would lead to lower (by about 40%) estimated rainfall rate PR-RR than the actual value (and 2.5 times higher values for the opposite classification error). A possible reason for the high TMI-RR values above 20 mm·h−1 at low PR-RR less than 10 mm·h−1 values under stratiform rainfall is that they are errors in TRMM precipitation classification as the stratiform type while it is actually the convective type of rain, which leads to lower PR-RR values than actual RR. The correlation coefficient between the TMI-RR and the PR-RR is 0.58, and the root-mean-square error is 9.6 mm·h−1.
Further analysis shows that the distribution of convective precipitation is different from stratiform precipitation. There are two possible reasons for this. First, the reliability of stratiform precipitation reaching 30 mm·h−1 is questionable because such high RR values do not occur in stratiform precipitation. However, if there is a TRMM classification error for these points, the results of the proposed method will underestimate even more significantly if they correspond to classification errors; second, the conditional PDF of Bayesian theory was constructed by considering 15 typhoons (heavy precipitation), and therefore, it is more suitable for heavy precipitation. In theory, high RR values are typical of convective precipitation. The most likely reason of the RR estimation error is that the physics in the models do not reproduce the typhoon environment well.
There are two discussions from Figure 15a,b. First, the convection points are less than the stratiform points and for stratiform retrievals TMI-RR and PR-RR seem to compare better than for convective retrievals. Second, PR-RR greater than 30 mm·h−1 are underestimated by TMI-RR, which could be explained partially by possible rainfall classification errors (actual stratiform rainfall classified as the convective type). The conclusion from Figure 15 is that stratiform rainfall (excluding possible bad classification points) is overestimated by the proposed method and convective rainfall is underestimated (including high convective PR-RR rainfall classified as stratiform from TRMM algorithms in Figure 15b).
5. Conclusions
This study simulated the TB for various atmospheric conditions by using the WRF and RTM models and then compared the simulated TB with the TB observed by the TRMM/TMI. The result showed that the simulated TB was virtually identical to the observed TB at 10 GHz under clear sky conditions, but the rainband was overestimated in the simulation. This discrepancy might originate from the difference between the simulation time and observation time. Another concern was the difference between actual weather conditions and the weather conditions corresponding to the initial data used in the simulation. In other words, the physics in the models do not reproduce the typhoon environment well. For future research, further improvement in the model physics is absolutely needed to better simulate the typhoon environment.
A qualitative comparison of the TB simulated by the RTM, the TB observed by the TMI, and the simulated TB of clear sky showed that the rainband of the typhoons considered and the typhoon patterns were similar to the observed rainband and patterns. A quantitative analysis of 15 typhoons yielded an average correlation coefficient of 0.78. However, a key point is that the conditional PDF was as extensive as possible and could simulate all rainfall intensities and confirm the simulation accuracy. Therefore, the posterior PDF can be used for a variety of rainfall intensities.
The attenuation index can reduce the impact caused by the environment background, and it has the advantage of decreasing with an increase in the RR; both these parameters have a one-to-one relationship. Therefore, the attenuation index is extremely suitable for use in precipitation estimation research. A Bayesian method was used to estimate the RR of 10 satellite swaths, and the estimated values were verified by comparing them with PR-RR. A qualitative analysis of the RR pattern, intensity, and location showed that the TMI-RR was underestimated in short-range heavy precipitation, and the location and range of the TMI-RR were similar to those of the PR-RR. Eight typhoon events were quantitatively analyzed, and the average correlation coefficient between the TMI-RR and the PR-RR is 0.63; the root-mean-square error is 4.45 mm·h−1. Furthermore, the correlation coefficient of the convective RR is 0.78, and the root-mean-square error is 7.25 mm·h−1 with a systematic underestimation of RR compared to PR. The correlation coefficient of the stratiform RR is 0.58, and the root-mean-square error is 9.6 mm·h−1 with a systematic overestimation of RR compared to PR. The results show that the Bayesian method can be effective in estimating the RR associated with typhoons over the ocean.
Acknowledgments
This research was supported by Ministry of Science and Technology of Taiwan under contract MOST 104-2111-M-344-001. In addition the authors would like to thank Wallace Academic Editing and Charlie C.K. Liang for their professionalism in reviewing and editing the English writing.
Author Contributions
Nan-Ching Yeh and and Wann-Jin Chen conceived and designed the study. Nan-Ching Yeh and Chung-Chih Liu collected the data, analyzed the results. Nan-Ching Yeh wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Adler, R.F.; Rodgers, E.B. Satellite-observed latent heat release in tropical cyclones. Mon. Weather Rev. 1997, 105, 956–963. [Google Scholar] [CrossRef]
- Spencer, R.W.; Hinton, B.B.; Olson, W.S. Nimbus-7 37 GHz radiances correlated with radar rain rates over the Gulf of Mexico. J. Climate Appl. Meteorol. 1983, 22, 2095–2099. [Google Scholar] [CrossRef]
- Wilheit, T.T. Algorithm for the retrieval of rainfall from passive microwave measurements. Remote Sens. Rev. 1994, 11, 163–194. [Google Scholar] [CrossRef]
- Barrett, E.C. The first WetNet precipitation intercomparison project (PIP-1): Interpretation of results. Remote Sens. Rev. 1994, 11, 303–373. [Google Scholar] [CrossRef]
- Petty, G.W. The status of satellite-based rainfall estimation over land. Remote Sens. Environ. 1995, 51, 125–137. [Google Scholar] [CrossRef]
- Smith, E.A.; Lamm, J.E.; Adler, R.; Alishouse, J.; Aonashi, K.; Barrett, E.; Bauer, P.; Berg, W.; Chang, A.; Ferraro, R.; et al. Results of WetNet PIP-2 project. J. Atmos. Sci. 1998, 55, 1483–1536. [Google Scholar] [CrossRef]
- Levizzani, V.; Amorati, R.; Meneguzzo, F. A Review of Satellite-based Rainfall Estimation Methods; European Commission Project Music Report: Brussels, Belgium, 2002; pp. 1–66. [Google Scholar]
- Kidd, C.; Kniveton, D.R.; Todd, M.C.; Bellerby, T.J. Satellite Rainfall Estimation Using a Combined Passive Microwave and Infrared Algorithm. J. Hydrometeorol. 2003, 4, 1088–1104. [Google Scholar] [CrossRef]
- Adler, R.F.; Kidd, C.; Petty, G.; Morissey, M.; Goodman, H.M. Intercomparison of global precipitation products: The third precipitation interconparison project (PIP-3). Bull. Am. Meteorol. Soc. 2001, 82, 1377–1396. [Google Scholar] [CrossRef]
- Petty, G.W. Physical Retrievals of Over-Ocean Rain Rate from Multichannel Microwave Imagery. Part I: Theoretical Characteristics of Normalized Polarization and Scattering Indices. Meteorol. Atmos. Phys. 1994, 54, 79–100. [Google Scholar] [CrossRef]
- Chen, W.J.; Li, C.C. Rain Retrievals Using Tropical Rainfall Measuring Mission and Geostationary Meteorological Satellite 5 Data Obtained during the SCSMEX. Int. J. Remote Sens. 2002, 23, 2425–2448. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, C.C.; Kuo, T.H. A Satellite-Derived Objective Potential Index for MCS Development during the Mei-Yu Period. J. Meteorol. Soc. Jpn. 2002, 80, 503–517. [Google Scholar] [CrossRef] [Green Version]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Kummerow, C.; Shin, D.B.; Hong, Y.; Olson, W.S.; Yang, S.; Adler, R.F.; McCollum, J.; Ferraro, R.; Petty, G.; Wilheit, T.T. The Evolution of the Goddard Profiling Algorithm (GPROF) for Rainfall Estimation from Passive Microwave Sensors. J. Appl. Meteorol. 2001, 40, 1801–1820. [Google Scholar] [CrossRef]
- Arkin, P.A.; Meisner, B. The Relationship between Large-Scale Convective Rainfall and Cold Cloud over the Western Hemisphere during 1982–1984. Mon. Weather Rev. 1987, 115, 51–74. [Google Scholar] [CrossRef]
- Chiu, L.S.; North, G.R.; Short, D.A.; McConnell, A. Rain Estimation from Satellites: Effect of Finite Field of View. J. Geophys. Res. 1990, 95, 2177–2185. [Google Scholar] [CrossRef]
- Adler, R.F.; Negri, A.J.; Keehn, P.R.; Hakkarinen, I.M. Estimation of Monthly Rainfall over Japan and Surrounding Waters from a Combination of Low-Orbit Microwave and Geosynchronous IR Data. J. Appl. Meteorol. 1993, 32, 335–356. [Google Scholar] [CrossRef]
- Ferraro, R.R. SSM/I Derived Global Rainfall Estimates for Climatological Applications. J. Geophys. Res. 1997, 102, 16715–16735. [Google Scholar] [CrossRef]
- Wilheit, T.T.; Chang, A.T.C.; Chiu, L.S. Retrieval of Monthly Rainfall Indices from Microwave Radiometric Measurements Using Probability Distribution Functions. J. Atmos. Ocean. Technol. 1991, 8, 118–136. [Google Scholar] [CrossRef]
- Janowiak, J.E. Tropical Rainfall: A Comparison of Satellite-Derived Rainfall Estimates with Model Precipitation Forecasts, Climatologies, and Observations. Mon. Weather Rev. 1992, 120, 448–462. [Google Scholar] [CrossRef]
- Grody, N.C. Classification of Snow Cover and Precipitation Using the Special Sensor Microwave Imager. J. Geophys. Res. 1991, 96, 7423–7435. [Google Scholar] [CrossRef]
- Ferraro, R.R.; Grody, N.C.; Marks, G.F. Effects of Surface Conditions on Rain Identification Using the SSM/I. Remote Sens. Rev. 1994, 11, 195–209. [Google Scholar] [CrossRef]
- Ferraro, R.R.; Weng, F.; Grody, N.C.; Basist, A. An Eight-Year (1987–1994) Time Series of Rainfall, Clouds, Water Vapor, Snow Cover, and Sea Ice Derived from SSM/I Measurements. Bull. Am. Meteorol. Soc. 1996, 77, 891–905. [Google Scholar] [CrossRef]
- Kidder, S.Q.; VonderHaar, T.H. Satellite Meteorology: An Introduction; Academic Press: San Diego, CA, USA, 1995; pp. 1–339. [Google Scholar]
- Wilheit, T.; Kummerow, C.; Ferraro, R. Rainfall Algorithms for AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 204–214. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.T.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104–105, 70–97. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Gourley, J.J.; Kirstette, P.E.; Yong, B.; Tian, Y.; Zhang, Z.; Hardy, J. Similarity and difference of the two successive V6 and V7 TRMM multi-satellite precipitation analysis (TMPA) performance over China. J. Geophys. Res. 2013, 118, 13060–13074. [Google Scholar]
- Chen, S.; Hong, Y.; Gourley, J.J.; Huffman, G.J.; Tian, Y.; Cao, Q.; Kirstetter, P.E.; Hu, J.; Hardy, J.; Xue, X. Evaluation of the successive V6 and V7 TRMM multi-satellite precipitation analysis over the continental United States. Water Resour. Res. 2013, 49, 8174–8186. [Google Scholar] [CrossRef]
- Kirstetter, P.E.; Hong, Y.; Gourley, J.; Schwaller, M.; Petersen, W.; Zhang, J. Comparison of TRMM 2A25 products, version 6 and version 7, with NOAA/NSSL ground radar-based national mosaic QPE. J. Hydrometeorol. 2013, 14, 661–669. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, S.; Cao, Q.; Hong, Y.; Wu, B.; Huang, M.; Qiao, L.; Zhang, Z.; Li, Z.; Li, W.; Yang, X. Evaluation of Version-7 TRMM Multi-Satellite Precipitation Analysis Product during the Beijing Extreme Heavy Rainfall Event of 21 July 2012. Water 2014, 6, 32–44. [Google Scholar] [CrossRef]
- Rana, S.; McGregor, J.; Renwick, J.A. Precipitation seasonality over the Indian Subcontinent: An evaluation of gauge, reanalyses and satellite retrievals. J. Hydrometeorol. 2015, 16, 631–651. [Google Scholar] [CrossRef]
- Chau, K.W.; Wu, C.L. A Hybrid Model Coupled with Singular Spectrum Analysis for Daily Rainfall Prediction. J. Hydroinform. 2010, 12, 458–473. [Google Scholar] [CrossRef]
- Wang, W.C.; Chau, K.W.; Xu, D.M.; Chen, X.Y. Improving forecasting accuracy of annual runoff time series using ARIMA based on EEMD decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
- Hu, J.C.; Chen, W.J.; Chiu, J.C.; Wang, J.L.; Liu, G.R. Quantitative Precipitation Estimation over Ocean Using Bayesian Approach from Microwave Observations during the Typhoon Season. Terr. Atmos. Ocean. Sci. 2009, 20, 817–832. [Google Scholar] [CrossRef]
- Petty, G.W.; Boukabara, S.A.; Snell, N.; Moncet, J.L. Algorithm Theoretical Basis Document (ATBD) for the Conical-Scanning Microwave Imager/Sounder (CMIS) Environmental Data Records (EDRs), Volume 5: Precipitation Type and Rate EDR; Atmospheric and Environmental Research: Lexington, MA, USA, 2001; pp. 1–112. [Google Scholar]
- Chiu, J.C. Bayesian Retrieval of Complete Posterior PDFs of Rain Rate from Satellite Passive Microwave Observations. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2003. [Google Scholar]
- Chiu, J.C.; Petty, G.W. Bayesian Retrieval of Complete Posterior PDFs of Oceanic Rain Rate from Microwave Observations. J. Appl. Meteorol. Climatol. 2006, 45, 1073–1095. [Google Scholar] [CrossRef]
- Okamoto, K. Tropical Rainfall Measuring Mission (TRMM) Precipitation Radar Algorithm Instruction Manual for Version 6. TRMM Precipitation Radar Team. Available online: http://www.eorc.jaxa.jp/TRMM/documents/PR_algorithm_product_information/pr_manual/PR_Instruction_Manual_V7_L1.pdf (accessed on 27 October 2015).
- Yeh, N.C.; Chen, W.J.; Wei, C.H.; Liu, C.Y. The Analysis of Hydrometeor Sensitivity on TRMM/TMI. J. Aeronaut. Astronaut. Aviat. 2014, 46, 203–207. [Google Scholar]
- Chien, F.C.; Hong, J.S.; Chang, W.J.; Jou, J.D.; Lin, P.L.; Lin, T.E.; Liu, S.P.; Miou, H.J.; Chen, C.Y. A Sensitivity Study of the WRF Model Part II: Verification of Quantitative Precipitation Forecasts. Atmos. Sci. 2006, 34, 261–276. (In Chinese) [Google Scholar]
- Iguchi, T.; Kozu, T.; Meneghini, R.; Awaka, J.; Okamoto, K. Rain-profiling algorithm for the TRMM precipitation radar. J. Appl. Meteorol. 2000, 39, 2038–2052. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).