Abstract
Wetting pattern geometry is useful in determining the spacing between emitters and the irrigation time in drip irrigation systems. This research aimed to generate an empirical model to estimate the width and depth of the wetting front in surface drip irrigation based on experimental tests in a cube-shaped container with transparent walls in soils with a sandy clay loam texture, with hydraulic conductivities from 2.316 to 3.945 cm h−1, and organic matter contents from 1.7 to 2.8%, and different irrigation conditions: discharge rates of 1.44, 2.90, 3.00, 3.75, and 4.00 L h−1, initial moisture levels between permanent wilting point and field capacity, and irrigation times from 0.58 to 9.50 h. The experimental conditions and the strategy for measuring the wetting front and soil moisture are detailed so the experiment is verifiable. The proposed model performed better than five other empirical models, with average values of 3 cm for the root mean square error and 0.88 for the Nash and Sutcliffe efficiency coefficient. The generated model is efficient and simple and can be a very useful tool for the design and operation of surface drip irrigation systems in soils with conditions similar to those of this study.
1. Introduction
Due to the high consumption of water available for agriculture, the low efficiency of its use worldwide, and strong competition for this resource by different sectors, agriculture is being called on to optimize food production by using less water without degrading soil and water resources [1]. Drip irrigation technology can help meet this challenge by providing growers greater control over the application of water, fertilizers, and pesticides [2]. Realizing the potential offered by drip irrigation technology requires optimizing its design and operational aspects, such as the frequency and duration of irrigation, emitter spacing, and emitter discharge rates [1].
The drip irrigation application technique is currently used in many parts of the world [3]. With this technique water is conveyed to the plant and delivered in an area-specific manner to the soil with low-pressure emitters, minimizing conduction losses and eliminating surface runoff losses with the potential to minimize losses due to deep percolation and evaporation [4,5]. The objective of this form of irrigation application is to supply water to a limited soil volume in the active root uptake zone, improving nutrient utilization and the effectiveness of pest and disease control [6]. Exploiting the advantages offered by this form of irrigation application requires knowledge and experiences different from those required in other forms of irrigation application that, when not considered, can generate irrigation systems with poor design and operation [7].
In recent years, great strides have been made in the design, technology, and operation of drip irrigation systems, largely due to a better understanding of water movement in the soil [8]. One important aspect to consider in the design and operation of drip irrigation is the geometry of the wetting pattern in the soil [9] since with this information the optimal spacing between emitters to cover the plant’s root system can be determined [10].
With knowledge of the wetting front geometry of the water in the soil, the emitter or emitters can be properly located so that the plant can consume water and nutrients efficiently, with lower costs for cultural work and higher income from increased yield [2,6,11]. Practically, for the design and operation of surface drip irrigation, the geometry of the wetting front can be defined by its width at the soil surface and its depth [12,13].
The water distribution of the wetting pattern generated by an emitter can be obtained by three means: through measurements in in situ experiments, with measurements in physical experimental models in the laboratory, and with the use of mathematical models [10]. Mathematical models can be classified into three main groups: numerical, analytical, and empirical [14,15,16,17]. In all mathematical models, it is essential to evaluate them in order to know their scope and limitations.
The most complex mathematical models are those based on the Richards equation, resulting from the application of the principle of conservation of mass in a partially saturated soil volume [3,14]. The high nonlinearity of this equation prevents its analytical solution, so numerical methods are used instead. Its solution requires the definition of starting conditions, boundary conditions, and detailed meteorological, soil, and crop information, and considerable computational power, which may limit its practical application [2,18,19,20,21]. Analytical models are usually derived from the Richards equation, applying simplifying assumptions such as the Green and Ampt equation [22]; whereas empirical models benefit from their simplicity, having parameters that are more understandable to irrigation technicians and that are usually easy to obtain, making them more convenient to be used in field applications [6,21,23].
In recent decades, several empirical models have been proposed to estimate the geometry of the wetting front (width and depth) of drip-irrigated soil. Most of them were generated from data collected in situ (in the field) with different experimental conditions [6,10,12,13,24]. The effectiveness of these models is reduced when they are used in soils other than those in which they were developed [16], so researchers should specify the conditions of their validity. Another limitation of these models is that they were generated considering a single value or a reduced range of soil moisture prior to irrigation, ignoring that in reality water is applied in different initial moisture conditions since long-duration sowing irrigations are applied where soils are usually dry; later short-duration and frequent irrigations cover the evapotranspiration demand of the crop for short periods seeking high moisture close to field capacity before and after irrigation.
If the proper equipment is not available to avoid digging in the soil at observation sites in field irrigation experiments, there may be some disadvantages: (1) disturbance of soil physical conditions and water dynamics, (2) difficulty in identifying the wetting front if the initial moisture condition is high, and (3) observations are limited to only one irrigation time. Temporal monitoring of the wetted front requires a different sampling site for each observation time since using the excavated site for the first observation time in subsequent temporal observations would risk modifying the dynamics of water movement in the soil because the soil face for observation and measurement would be directly exposed to the environment. These methodological details, for observations of the advance of the wetting front, are not indicated or are not specified in many studies.
Due to the previously mentioned drawbacks and the advancement of soil moisture measurement technologies, some researchers have conducted drip irrigation experiments in controlled environments. They obtained satisfactory results from physical models with transparent walls where they were able to observe the wetting patterns of a point source irrigation system in real time and without physically disturbing the soil during the measurements [8,14,16,25,26]. However, some factors were ignored, such as evaporation from the soil surface and the presence of aggregates greater than 2 mm in diameter in agricultural soils, creating conditions different from those presented in the field, limiting the applicability of the information generated under standard irrigation conditions.
The previously mentioned background of field and laboratory studies shows limitations in their scope since several of them offer few methodological details of the experiments, such as: they only partially describe the characteristics of the soils and in some cases the procedures for their determination are not indicated, the irrigation conditions are not clarified, and the way of measuring the water content in the soil and the wetting front is not precisely explained. In addition, the mathematical models reported by some researchers were generated with information taken from different researchers and studies [6,13,24] without relying on their own information, which can lead to erroneous conclusions due to an incorrect interpretation of their results and the methodologies used to obtain them. For this reason, this research explores the possibility of obtaining a mathematical model that improves the estimates of the soil wetting front in drip irrigation, based on experimental information obtained with a common and careful methodological strategy, in soils with different physical characteristics and subjected to different irrigation conditions.
Therefore, the objective of this research was to generate an improved empirical mathematical model to estimate the horizontal (width) and vertical (depth) dimension of the wetting front in soils under surface drip irrigation by representing field irrigation conditions in a transparent crystal acrylic cube-shaped container and detailing the conditions of the experiment and the measurement strategy of the parameters involved so that the experiment is replicable and verifiable. This study was carried out under the hypothesis that it is possible to improve the existing estimates of the temporal evolution of the geometry of the soil wetting front with an empirical mathematical model that considers the physical properties of the soil and the characteristics of the irrigation, rigorously executing the designed methodology. The performance of the proposed model was evaluated and compared with other empirical models, proving to be more accurate.
2. Materials and Methods
2.1. Experimental Site
The experiments were conducted at the Irrigation and Drainage Laboratory of the Soil Science Department of Chapingo Autonomous University (UACh), located in Texcoco, State of Mexico.
2.2. Characteristics of the Experimental Soils
The soils were obtained from the experimental agricultural fields at UACh’s main campus. Soil samples were air-dried inside a plastic greenhouse and passed through a 6 mm sieve. A sieve with a larger aperture than the one used by Ainechee et al. [8] and Al-Ogaidi et al. [26] was employed in order to achieve conditions similar to those found in the field after lying fallow; in real conditions it is very difficult to find an agricultural soil that does not contain aggregates larger than 2 mm in diameter [27,28].
Table 1 shows the physical properties of the soils used in the experiment. Their texture is sandy clay loam according to the United States Department of Agriculture Soil Conservation Service (US-SCS) classification [29]. The difference in organic matter (OM) content in soils 3 and 4 was generated by the application of corn crop residues in soil 2. Soil bulk density (Pb) was determined with the paraffin-coated clod method, moisture content at field capacity (θCC) was obtained with the pressure cooker method, moisture content at permanent wilting point (θPMP) was obtained with the pressure membrane method, and percent organic matter (OM) was measured with the Walkley and Black method.

Table 1.
Physical properties of the study soils.
The hydraulic parameters of the soils used in this study were obtained according to Cruz-Bautista et al. [10] and Kandelous and Šimůnek [14]. They were estimated with the ROSETTA version 1.2 software package [30]. ROSETTA is based on pedo-transfer functions to estimate soil hydraulic parameters from soil physical properties and van Genuchten [31] and Mualem [32] constitutive relations. With the percentages of sand, silt and clay, bulk density, and soil water contents for suction pressures of 33 and 1500 kPa, the residual and saturation moisture contents (θr, θs), inverse soil air-entry pressure ratio (α), pore size distribution (n), and saturated hydraulic conductivity (Ks) were obtained (Table 2).

Table 2.
Hydraulic parameters of the experimental soils obtained with the ROSETTA version 1.2 software package [30].
2.3. Experimental System
The soil was placed in a 100 cm × 100 cm × 95 cm transparent crystal acrylic cube-shaped container. The water was driven by a horizontal axis centrifugal pump with a 0.5 HP electric motor, and conducted to the emitter through a 38.1 mm nominal diameter PVC main pipe and a 12 mm nominal diameter low-density polyethylene secondary pipe. A return system and a pressure gauge were installed at the pump discharge to maintain the emitter operating pressure (0.703 kg cm−2) (Figure 1).
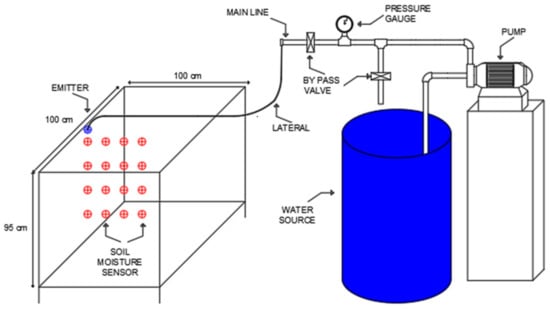
Figure 1.
Experimental system.
The cube-shaped container was filled with soil in 5 cm layers with bulk densities corresponding to the experimental soils shown in Table 1. Holes were drilled in the bottom of the bucket to prevent water stagnation. To prevent preferential flow on the side walls a layer of sand was adhered to them to create a flow surface prior to filling with soil.
The emitter was installed on the soil surface in the center of the cube-shaped container, 10 cm from one of the vertical walls where the evolution of the wetting front geometry was observed (Figure 2). In order to determine soil moisture at the beginning and at the end of irrigation, 16 model S-SMC-M005 moisture sensors (Onset HOBO® corporation), with an error of 3%, were installed under the emitter in a 4 by 4 grid on a vertical plane transversal to the observation wall. With this arrangement, the behavior of half of the wetted front was observed and it was assumed that the same occurred in the other half, approaching it mathematically as an asymmetric axis problem [14]; in effect, the wetting front showed that type of behavior in preliminary tests (Figure 2).

Figure 2.
Observation wall of the wetting front.
Two spacings between soil moisture sensors were used in the installed grid. One of 8 cm horizontal by 8 cm vertical was used to monitor short-duration irrigations and one of 15 cm by 20 cm was used for moderate- and long-duration irrigations (Figure 1).
Before being installed in the experimental module, the soil moisture sensors were individually calibrated with the soils subjected to the experimental trials, following the procedure recommended by the manufacturer and described by Starr and Paltineanu [33]. After filling the cube-shaped container with soil and installing the sensors, the soil was left to settle for at least 24 h before the first irrigation to allow equilibrium in the moisture distribution, applying irrigation when the differences in the volumetric moisture measurements between sensors were less than 0.015 cm3 cm−3.
2.4. Experimental Trials
Two blocks of experiments were carried out based on the magnitude of the irrigation time. Both blocks of the experiment were carried out in a 13-month period. The first experimental block consisted of moderate- and long-duration irrigations (t) with discharge rates (q) of 2.90, 3.75 and 1.44 L per hour (L h−1); the long irrigations were used to try to represent the sowing irrigations in an initially dry soil, with an initial moisture (θi) close to permanent wilting point (0.13 to 0.14), while the moderate-duration irrigations were applied with an initial soil moisture close to field capacity (0.22 to 0.26), representing the supply of the daily evapotranspiration demand (Table 3). The second experimental irrigation block consisted of applying short-duration irrigations with 3.00 and 4.00 L h−1 drippers in soils with an initial moisture content close to the permanent wilting point, simulating the short-period supply of the evapotranspiration demand of crops in early vegetative stages where the root system occupies a reduced volume of soil (Table 4). In both irrigation blocks, a final moisture content between field capacity and saturation was guaranteed, a situation commonly carried out by farmers. In Table 3 and Table 4 the symbol θf represents the average soil moisture content at the end of irrigation.

Table 3.
Characteristics of the moderate- and long-duration irrigations of the first experimental block.

Table 4.
Characteristics of the short-duration irrigations of the second experimental block.
The position of the wetting front was drawn on the observation wall of the cube-shaped container (Figure 3). In the moderate- and long-duration irrigations of the first experimental block, it was performed every 5 min at the beginning of the irrigation, then every 15 min in the intermediate part and finally every 30 min in the final part. In the short-duration irrigations, corresponding to the second block, it was drawn at 5-min intervals. In the irrigations of the first block, the geometry of the wetting front was obtained from the start of irrigation until 12, 36, and 60 h after the end of each irrigation. From these records, the depth and width of the wetting front were determined.

Figure 3.
Marking of the wetting front on the observation wall of the soil container.
2.5. Soil Drying after Irrigations
Nafchi et al. [25] stated that evaporation from the soil surface can be ignored in laboratory experiments. However, to minimize the differences between an enclosed site and those presented in the field in an open site, a heat lamp and a fan were installed in this work to simulate the heat generated by radiation and air currents. The fan and the lamp were turned on 60 h after the end of the moderate- and long-duration irrigations (first experimental block of irrigations). The moisture content at the soil surface was monitored at a depth of 3.8 cm with a Fieldscout TDR 300 soil moisture meter (Spectrum Technologies®, Bridgend, UK), whose error is 3%.
2.6. Proposed Empirical Model
An empirical model was proposed to estimate the vertical (depth) and horizontal (width) dimensions of the wetting front, considering the experiences of Schwartzman and Zur [24], Amin and Ekhmaj [6], Malek and Peters [12], Al-Ogaidi et al. [13] and Cruz-Bautista et al. [10]. Organic matter content was also considered since it has been observed that an increase in it produces a soil with higher water-holding capacity and conductivity, largely as a result of its influence on soil aggregation and associated pore space distribution [34]. The proposed model is composed of the following nonlinear equations:
where d is the horizontal dimension of the wetting front (cm) at the soil surface, z is the vertical dimension of the wetting front (cm), q is the emitter discharge rate (L h−1), Ks is the saturated hydraulic conductivity (cm h−1), t is the irrigation time (h), θi is the initial volumetric moisture content (cm3 cm−3), Pb is the soil bulk density (g cm−3), and OM is the percent organic matter (%).
2.7. Evaluated Models
The model proposed in this research was compared with the models of Schwartzman and Zur [24], Amin and Ekhmaj [6], Malek and Peters [12], Al-Ogaidi et al. [13], and Cruz-Bautista et al. [10].
The Schwartzman and Zur [24] model is a semi-empirical model; the result of a dimensional analysis and experimental observations reported by Bresler [35] for two soil types and two emitter discharge rates. The Amin and Ekhmaj [6] model is an empirical model obtained from four data sets of experimental observations published by Taghavi et al. [36], Angelakis et al. [37], Hammami et al. [9], and Li et al. [38]. The empirical model of Malek and Peters [12] was generated with experimental field data with a single soil type, three emitter discharge rates, and a single initial moisture content. The model of Al-Ogaidi et al. [13] was obtained from five experimental data sets; they corresponded to the four sets used in the generation of the model of Amin and Ekhmaj [6] and the observations of Li et al. [39]. Cruz-Bautista et al. [10] obtained their model with experimental field data in three soil types and three emitter discharge rates, but with a small range of initial moisture values.
The mathematical expressions of the comparison models are as follows.
Schwartzman and Zur (1986) [24]:
Amin and Ekhmaj (2006) [6]:
Malek and Peters (2011) [12]:
Al-Ogaidi et al. (2015) [13]:
Cruz-Bautista et al. (2016) [10]:
where d, z, q, Ks, t, θi, and Pb mean the same as in Equations (1) and (2); V is the total volume of water applied (l); Δθ is the average change in water content due to irrigation (cm3 cm−3) which is obtained as Δθ = θs/2, where θs is the water content at saturation; S is the percentage of sand (%); Si is the percentage of silt (%); C is the percentage of clay (%) and θr is the residual soil moisture content (cm3 cm−3).
Table 5 shows the validity ranges of the evaluated models, according to the limits of the experimental data used for their generation.

Table 5.
Validity ranges of the evaluated models.
2.8. Evaluation of the Models
The evaluation of the predictive capabilities of the models was performed with the mean error (ME), root mean square error (RMSE), and the Nash and Sutcliffe efficiency (NSE) [40,41]:
where N is the total number of data, Pi corresponds to the i-th estimated data, is the i-th observed data, and is the mean of the observed data.
As the ME and RMSE values approach zero, the model becomes better at estimating, with the value of zero being the optimum [40]. To score the models based on the NSE values, the Ritter and Muñoz-Carpena [42] criteria were used: unsatisfactory (NSE < 0.65), acceptable (0.65 ≤ NSE < 0.80), good (0.80 ≤ NSE < 0.90), and very good (NSE > 0.90).
A sensitivity analysis of the proposed models was performed with the aim of identifying the effect of the input parameters on the width and depth of the wetting front. For this, simulations of the model responses were performed with modifications to the input parameter values of −30%, −20%, −10%, +10%, +20%, and +30%, similar to what was performed by Bolaños-Sánchez et al. [43].
3. Results
3.1. Wetting Patterns Geometry
Figure 4 and Figure 5 show the temporal evolution of the wetting front of the irrigations of the first and second irrigation blocks, respectively. The lines labeled A, B, and C of Figure 4 represent the advance front for 12, 36, and 60 h, respectively, after the end of irrigation.
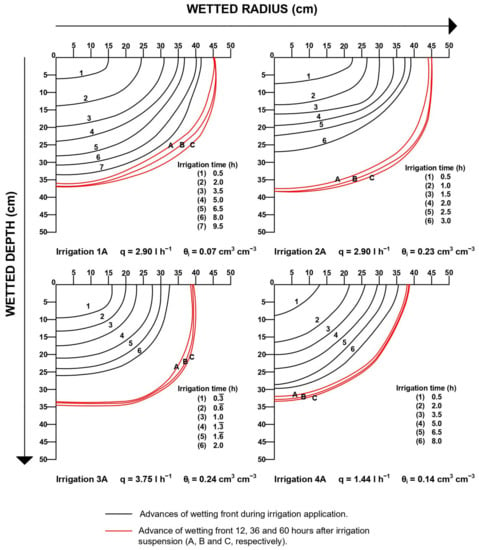
Figure 4.
Geometry of the wetting front as a function of irrigation time in the first irrigation block.
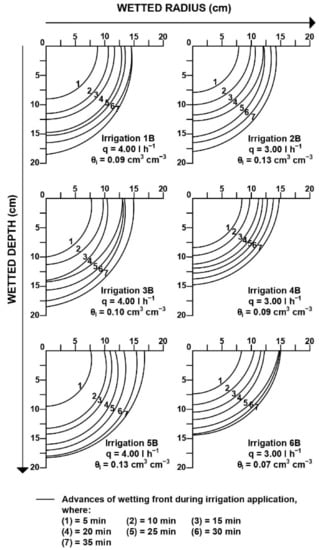
Figure 5.
Geometry of the wetting front as a function of irrigation time in the second irrigation block.
3.2. Model Performance
Table 6, Table 7 and Table 8 show the statistical indicators ME, RMSE, and the efficiency indices (NSE) for the width (d) and depth of the wetting front (z) of the mathematical models evaluated. Figure 6, Figure 7, Figure 8 and Figure 9 show the observed and estimated behaviors of the width and depth of the wetting front of the mathematical models evaluated.

Table 6.
Statistical indicators of the empirical models for the first irrigation block for the width (d) and depth of the wetting front (z).

Table 7.
Statistical indicators of the empirical models for the second irrigation block, with an emitter discharge rate of 4 L h−1, for the width (d) and depth of the wetting front (z).

Table 8.
Statistical indicators of the empirical models for the second irrigation block, with an emitter discharge rate of 3 L h−1, for the width (d) and depth of the wetting front (z).
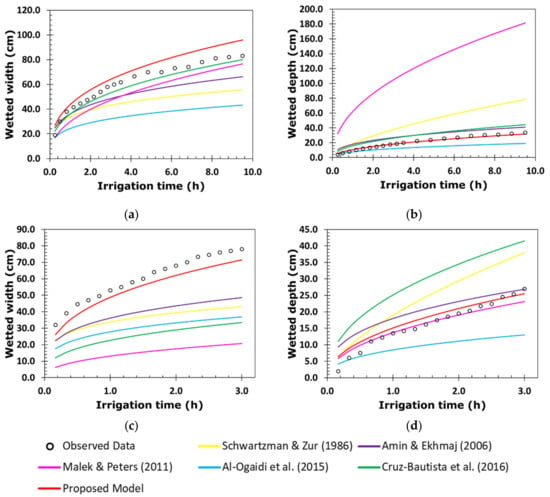
Figure 6.
Temporal evolution of the width and depth of the wetting front of (a,b) irrigation 1A (q = 2.90 L h−1 and θi = 0.07 cm3 cm−3) and (c,d) irrigation 2A (q = 2.90 L h−1 and θi = 0.23 cm3 cm−3) [6,10,12,13,24].
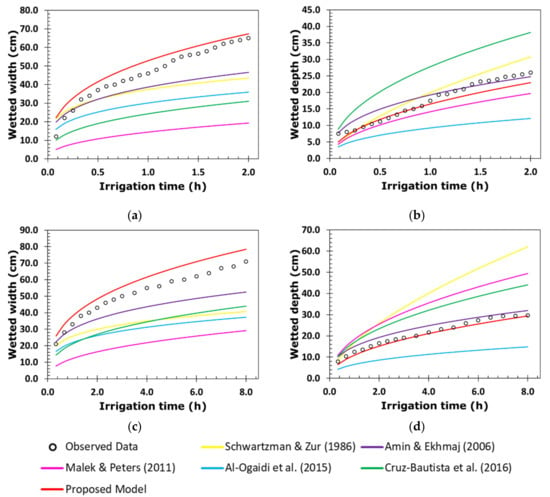
Figure 7.
Temporal evolution of the width and depth of the wetting front of (a,b) irrigation 3A (q = 3.75 L h−1 and θi = 0.24 cm3 cm−3) and (c,d) irrigation 4A (q = 1.44 L h−1 and θi = 0.14 cm3 cm−3) [6,10,12,13,24].
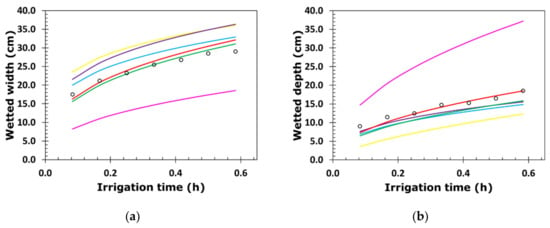
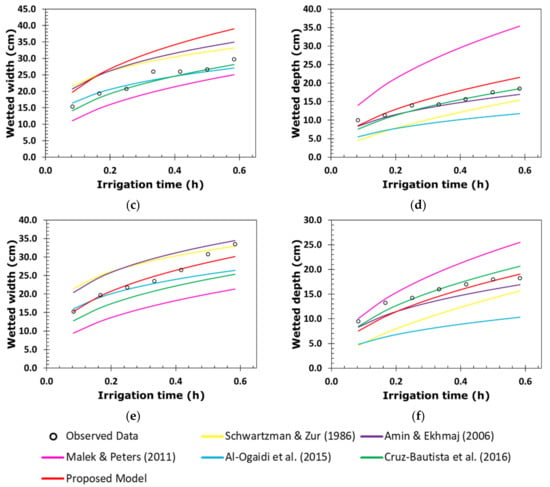
Figure 8.
Temporal evolution of the width and depth of the wetting front of (a,b) irrigation 1B (q = 4.00 L h−1 and θi = 0.09 cm3 cm−3), (c,d) irrigation 3B (q = 4.00 L h−1 and θi = 0.10 cm3 cm−3), and (e,f) irrigation 5B (q = 4.00 L h−1 and θi = 0.13 cm3 cm−3) [6,10,12,13,24].
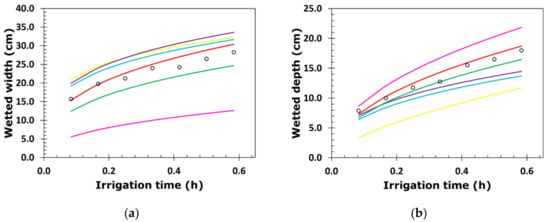
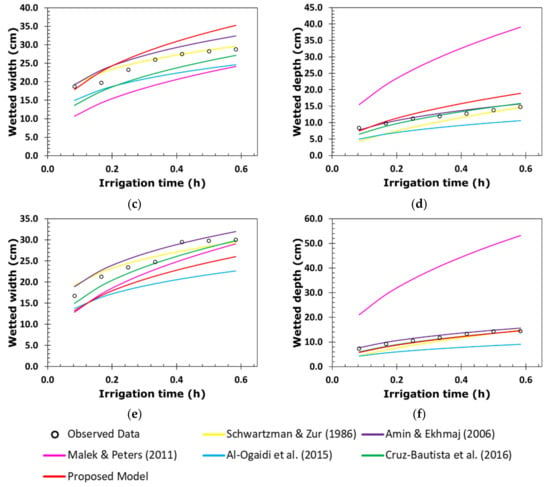
Figure 9.
Temporal evolution of the width and depth of the wetting front of (a,b) irrigation 2B (q = 3.00 L h−1 and θi = 0.13 cm3 cm−3), (c,d) irrigation 4B (q = 3.00 L h−1 and θi = 0.09 cm3 cm−3), and (e,f) irrigation 6B (q = 3.00 L h−1 and θi = 0.07 cm3 cm−3) [6,10,12,13,24].
3.3. Effect of Input Parameters on Model Response
Figure 10 shows the sensitivity of the response of the proposed model to the input parameters.
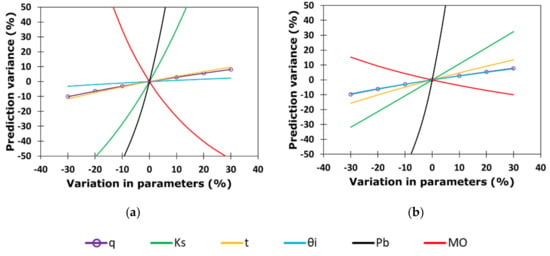
Figure 10.
Effect of input parameters on the response of the proposed models for (a) width and (b) depth of the wetting front.
4. Discussion
4.1. Wetting Patterns Geometry
Figure 4 and Figure 5 show that an increase in the volume of water applied due to an increase in irrigation time or an increase in emitter discharge rate, such as in irrigations 2A and 3A (Figure 4) and irrigations 1B, 2B, and 3B (Figure 5) with similar initial moisture content, generates a greater horizontal and vertical displacement of the wetting front, similar to that obtained by Subbaiah and Mashru [2] and Ainechee et al. [8]. Consequently, it is verified that the volume of water applied influences the movement of water in the soil [10]. In all the applied discharge rates, the wetting front moved faster at the beginning of the irrigations and over time the speed of advance decreased due to the fact that the volume of soil to be wetted increased and thus the water encountered more available empty pore space in its path [9].
In the irrigations with higher discharge rates of the first block (2.90 and 3.75 L h−1), the wetting front had greater horizontal than vertical displacement at the beginning of the irrigation because in those first moments the capillary forces dominated the movement of water in the soil, but as time passed the gravitational forces began to dominate causing an increase in the vertical advance and a decrease in the horizontal advance (irrigations 1A to 3A of Figure 4). In irrigation 4A of the first block (1.44 L h−1) (Figure 4) and in the irrigations of the second block (Figure 5), a similar displacement was observed in all directions of the wetting front.
In irrigations 1A and 2A (Figure 4) of the first block, the effect of initial soil moisture content on the behavior of the wetting front was observed. The higher initial moisture content caused a greater vertical and horizontal advance of the wetting front than in the soil with lower initial moisture content in equal irrigation times, a much greater horizontal advance than vertical advance in the first hours of irrigation was observed. The reason for this behavior is that the higher the initial moisture, the smaller the volume of pores available in the soil [15]; therefore, less water is needed to wet the same volume of soil. Greater spreading of the wetting front in both directions may be undesirable when root zones are shallow, water is scarce, or groundwater contamination is a concern [11]; in such cases, lower volumes of water should be applied to soils with high initial moisture.
In irrigations 2A to 3A (Figure 4) of the first irrigation block, the effect of irrigating with similar initial moisture conditions and different emitter discharge rates can be noted. Irrigation with the highest discharge rate generated a greater vertical advance, causing irrigation 3A to reach vertical dimensions similar to irrigation 2A in less time. This was mainly due to the hydraulic properties of the soil under evaluation and the increase in the discharge rate as indicated by Naglič et al. [15], who suggested that high discharge rates that do not exceed the infiltration capacity of the soil usually generate extended moisture fronts in the vertical direction since there is no ponding that favors horizontal spreading.
The comparison between irrigations 1A and 4A (Figure 4) shows the effect of variations in the emitter discharge rate and initial soil moisture on the behavior of the wetting front. By decreasing the initial moisture and increasing the emitter discharge rate (irrigation 1A) a greater horizontal displacement was generated, a smaller vertical displacement in irrigation 1A than in irrigation 4A in the first hours of irrigation was observed, and similar displacement was observed in long irrigation times. It was expected to obtain a behavior similar to that reported by Skaggs et al. [11], who indicated that increasing the emitter discharge rate generally tends to increase spreading in both directions with greater effect in the vertical direction. This apparent contradiction of the results in the vertical displacement is explained because in irrigation 1A the initial moisture was lower than in irrigation 4A; this condition favored the predominance of capillary forces over gravitational ones in the initial stages, but after time these forces became balanced, resulting in a similar displacement in both directions.
In the first irrigation block, gravitational and capillary forces continued to act significantly 12 h after suspending the application of water in those irrigations where the initial soil moisture was close to field capacity since the wetting front grew horizontally and vertically. After suspending irrigation for 36 and 72 h there was no variation in the wetting front, as can be seen in the red lines (Figure 4).
As in the first irrigation block, the increase in discharge rate favored vertical more than horizontal spreading in the soil with a lower amount of OM (1.7%) in the second irrigation block (irrigation 1B and 3B in Figure 5). More spherical wetting patterns occurred in the soils with a higher amount of OM in the second irrigation block (irrigations 4B, 5B, and 6B in Figure 5) than in the irrigations of the first and second blocks where the OM content is lower.
The increase in the amount of OM favored a homogeneous advance of the wetting front in all directions because it led to an increase in the proportion of macro-aggregates and porosity in the soil and a redistribution of the porous space [44], causing a delay in vertical water movement as observed by Iqbal et al. [16] in soils with high water-holding capacities. Its effects are observed in a decrease in bulk density and an increase in saturated hydraulic conductivity and moisture content at soil saturation (Table 1 and Table 2). The increase in moisture at saturation did not generate an increase in the amount of usable water for the plants, but it caused a greater water-holding capacity [45], which induced similar displacements in the horizontal and vertical directions of the wetting front.
4.2. Model Performance
The proposed model showed the best performance for estimating the vertical and horizontal dimensions of the wetting front since most of the irrigations resulted in the lowest values of the ME and RMSE statistical indicators, and the highest values close to unity of the NSE index (Table 6, Table 7 and Table 8). The ME values for d and z, from the first and second irrigation blocks, ranged from −5.40 to 7.01 cm and from −1.41 to 1.46 cm, and from −3.89 to 6.58 cm and from −1.00 to 1.86 cm, respectively. The RMSE values were between 5.10 and 7.65 cm for d and between 1.18 and 2.01 cm for z in the irrigations of the first block, and between 1.53 and 7.27 cm for d and between 0.76 and 2.56 cm for z in the irrigations of the second block. According to the NSE values and the performance criteria of Ritter and Muñoz-Carpena [42], the model was acceptable to very good in the estimation of d and good to very good in the estimation of z in both irrigation blocks: from 0.85 to 0.91 for d and from 0.91 to 0.98 for z in the first block, and from 0.79 to 0.98 for d and from 0.88 to 0.98 for z in the second block.
Some of the models evaluated were better than the proposed one in some of the irrigations, but only in one of the two directions of the wetting front and in the other direction their estimates were very unfavorable. In some cases, other models performed well in one of the irrigation blocks without outperforming the proposed model, and poorly in the other. These partial favorable results limit their applicability in the various irrigation situations. For example, the statistical indicators obtained with the Cruz-Bautista et al. [10] model in the second irrigation block indicate a good estimation of the depth and width of the wetting front, but a poor representation in the first irrigation block.
According to the irrigation conditions considered (Table 3 and Table 4) and the validity conditions of the models (Table 5), a better prediction would be expected in the models of Al-Ogaidi et al. [13] and Cruz-Bautista et al. [10], but this was not the case since in some irrigations of the first block the models of Schwartzman and Zur [24], Amin and Ekhmaj [6], and Malek and Peters [12] were better even though they did not consider all the parameters of the proposed model or their values were unique or of reduced ranges.
Figure 6, Figure 7, Figure 8 and Figure 9 show the better predictive capacity of the proposed model over the other models. The proposed model, in general, tends to slightly overestimate the horizontal advance of the wetting front in both irrigation blocks, showing a parallelism with the behavior observed during the entire irrigation time. This model tends to slightly underestimate the vertical advance of the wetting front at the end of the irrigations, converging with the behavior observed a little before the halfway point of their duration. The differences between the observed and estimated values in both directions of the advance front are small compared with those of the other models.
The incorporation of soil organic matter content as a variable in the proposed model contributed to improving its estimates. Amin and Ekhmaj [6] and Malek and Peters [12] did not consider organic matter in their models because they considered that it is integrated into the bulk density and hydraulic conductivity at soil saturation; however, in this study the need for its integration was observed since it modifies the porosity and colloidal structure of the soil and consequently its capacity for capillary movement [34,44].
Kandelous and Simunek [14] stated that initial soil water content is an important requirement to properly estimate the behavior of the wetting front with empirical models in drip irrigation. Indeed, a better performance was observed for models that considered initial moisture than those that did not. As an example of this, the deficiency of the estimates of the Schwartzman and Zur [24] model stands out in irrigations 1A and 2A of the first block (Figure 6); where, for the same volume of applied water, the results were the same despite the fact that the initial water contents were very different (one close to PMP and the other to FC).
4.3. Effect of Input Parameters on the Model Response
The sensitivity analysis of the proposed mathematical model shows that soil characteristics were more determinant than initial moisture (Figure 10), as observed by Li et al. [46] and Fan et al. [47]. The resulting values of the input parameters used in the analysis guarantee the range of values contemplated in this study since the reference values on which the variations were made were 2.90 L h−1, 3.24 cm h−1, 0.14 cm3 cm−3, 1.31 g cm−3, 2.4%, and 3.17 h, for discharge rate (q), saturated hydraulic conductivity (Ks), initial moisture content (), bulk density (Pb), percent organic matter (OM), and irrigation time (t), respectively. Pb had a similar impact on the radius and depth of the wetting front, while OM and Ks had a greater impact on radius than on depth. Pb had a direct effect (as its value increases, its effect on the magnitude of the wetting front increases) and Ks and OM had an inverse effect (as its value increases, its effect on the magnitude of the wetting front decreases) in both directions of the wetting front. The q, , and t had a direct and smaller effect than the physical properties of the soils on the displacements in both directions of the wetting front; q and t had practically identical effects on the radius, and q and on the depth. The has the least effect in both directions of the wetting front and attenuates more in depth, so Fan et al. [47] suggested removing it from the modeling; however, in this study the results showed the need for its inclusion as it considerably improved the accuracy of the estimates with respect to those that do not include it. The better predictive capacity of the proposed model to estimate the dimensions of the wetting front was due to the consideration of the parameters involved in water movement, the range of parameter values, and the care taken in the execution of the methodology.
5. Conclusions
A nonlinear empirical mathematical model was generated to estimate the horizontal (width) and vertical (depth) magnitude of the advance front of the wetting front of a sandy clay loam-textured soil as a function of some soil physical characteristics (saturated hydraulic conductivity (Ks), bulk density (Pb), and organic matter content (OM)), initial moisture content (θi), and irrigation operating characteristics (emitter discharge rate q and irrigation time t).
The proposed empirical model had better approximations to the observed values than the empirical models of Schwartzman and Zur [24], Amin and Ekhmaj [6], Malek and Peters [12], Al-Ogaidi et al. [13], and Cruz-Bautista et al. [10]. Its average performance was good (NSE = 0.84) and very good (0.92) to estimate the width and depth of the wetting front, respectively. The average RMSE values for width and depth were 4.50 cm and 1.50 cm, respectively.
As the initial soil moisture increased, the irrigations generated wetting fronts of greater vertical and horizontal magnitude. Increasing the emitter discharge rate had a greater impact on the vertical than on the horizontal advance for the soils studied. Although there is a strong relationship between saturated hydraulic conductivity, bulk density, and soil organic matter content, it was better to consider all three parameters instead of just one or two of them in the predictive model.
The effect of soil characteristics predominates the effect of applied water volume and initial soil moisture content in predicting the horizontal and vertical advance of the wetted front.
The amount of OM in the soil influenced the geometry of the wetting front, favoring a spherical shape, because there is an increase in the proportion of macro-aggregates in the soil and a redistribution of the porous space.
Author Contributions
Conceptualization, J.V.P.-H.; methodology, I.C.-M., J.V.P.-H. and D.C.-M.; software, I.C.-M. and A.M.-R.; validation, I.C.-M., J.V.P.-H. and A.M.-R.; formal analysis, I.C.-M., J.V.P.-H. and D.C.-M.; investigation, I.C.-M., J.V.P.-H., D.C.-A. and F.P.-R.; resources, J.V.P.-H., F.P.-R. and D.C.-A.; writing—original draft preparation, I.C.-M., J.V.P.-H. and D.C.-A.; writing—review and editing, I.C.-M., J.V.P.-H., A.M.-R., F.P.-R., D.C.-A. and D.C.-M.; supervision, I.C.-M. and J.V.P.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by University of Chapingo (UACh).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
UACh’s DGIP is thanked for the economic support provided for the acquisition of the soil container. Soil Physics Laboratory of the Soil Department (University of Chapingo) is thanked for the support provided in soil determinations. The first author thanks to the National Council for Science and Technology (CONACYT) for the scholarship received.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Skaggs, T.H.; Trout, T.J.; Šimůnek, J.; Shouse, P.J. Comparison of HYDRUS-2D Simulations of Drip Irrigation with Experimental Observations. J. Irrig. Drain. Eng. 2004, 130, 304–310. [Google Scholar] [CrossRef]
- Subbauah, R.; Mashru, H.H. Modeling for predicting soil wetting radius under point source surface trickle irrigation. Agric. Eng. Int. CIGR J. 2013, 15, 1–10. [Google Scholar]
- Subbaiah, R. A review of models for predicting soil water dynamics during trickle irrigation. Irrig. Sci. 2013, 31, 225–258. [Google Scholar] [CrossRef]
- Camp, C.R. Subsurface drip irrigation: A review. Trans. ASAE 1998, 41, 1353–1367. [Google Scholar] [CrossRef]
- Ayars, J.E.; Fulton, A.; Taylor, B. Subsurface drip irrigation in California—Here to stay? Agric. Water Manag. 2015, 157, 39–47. [Google Scholar] [CrossRef]
- Amin, M.S.; Ekhmaj, A.I. DIPAC-drip irrigation water distribution pattern calculator. In Proceedings of the 7th International Micro Irrigation Congress, Kuala Lumpur, Malaysia, 13–15 September 2006; Volume 1016. [Google Scholar]
- Waller, P.; Yitayew, M. Introduction. In Irrigation and Drainage Engineering; Waller, P., Yitayew, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–18. ISBN 978-3-319-05699-9. [Google Scholar]
- Ainechee, G.; Boroomand-Nasab, S.; Behzad, M. Simulation of soil wetting pattern under point source trickle irrigation. J. Appl. Sci. 2009, 9, 1170–1174. [Google Scholar] [CrossRef]
- Moncef, H.; Hedi, D.; Jelloul, B.; Mohamed, M. Approach for predicting the wetting front depth beneath a surface point source: Theory and numerical aspect. Irrig. Drain. 2002, 51, 347–360. [Google Scholar] [CrossRef]
- Cruz-Bautista, F.; Zermeño-González, A.; Álvarez-Reyna, V.; Cano-Ríos, P.; Rivera-González, M.; Siller-González, M. Validación de un modelo para estimar la extensión del bulbo de humedecimiento del suelo con riego por goteo. Tecnol. Cienc. Agua 2016, 7, 45–55. [Google Scholar]
- Skaggs, T.H.; Trout, T.J.; Rothfuss, Y. Drip Irrigation Water Distribution Patterns: Effects of Emitter Rate, Pulsing, and Antecedent Water. Soil Sci. Soc. Am. J. 2010, 74, 1886–1896. [Google Scholar] [CrossRef]
- Malek, K.; Peters, R.T. Wetting Pattern Models for Drip Irrigation: New Empirical Model. J. Irrig. Drain. Eng. 2011, 137, 530–536. [Google Scholar] [CrossRef]
- Al-Ogaidi, A.A.M.; Wayayok, A.; Kamal, M.R.; Abdullah, A.F. A modified empirical model for estimating the wetted zone dimensions under drip irrigation. J. Teknol. 2015, 76, 69–73. [Google Scholar] [CrossRef]
- Kandelous, M.M.; Šimůnek, J. Comparison of numerical, analytical, and empirical models to estimate wetting patterns for surface and subsurface drip irrigation. Irrig. Sci. 2010, 28, 435–444. [Google Scholar] [CrossRef]
- Naglič, B.; Kechavarzi, C.; Coulon, F.; Pintar, M. Numerical Investigation of the Influence of Texture, Surface Drip Emitter Discharge Rate and Initial Soil Moisture Condition on Wetting Pattern Size. Irrig. Sci. 2014, 32, 421–436. [Google Scholar] [CrossRef]
- Iqbal, M.; Ghumman, A.R.; Hashmi, H.N. Study of wetting pattern under drip-emitter using sand box model and empirical equations. Pak. J. Agric. Sci. 2017, 54, 699–709. [Google Scholar] [CrossRef]
- Moncef, H.; Khemaies, Z. Optimizing Emitters’ Density and Water Supplies in Trickle Irrigation Systems. Am. J. Water Sci. Eng. 2019, 5, 16. [Google Scholar] [CrossRef]
- Zur, B. Wetted Soil Volume as a Design Objective in Trickle Irrigation. Irrig. Sci. 1996, 16, 101–105. [Google Scholar] [CrossRef]
- Ramírez de Cartagena Bisbe, F.; Sáinz Sánchez, M.A. Modelo de Distribución de Agua En Suelo Regado Por Goteo. Ing. Agua 1997, 4, 57–70. [Google Scholar] [CrossRef][Green Version]
- Dasberg, S.; Or, D. Practical Applications of Drip Irrigation. In Drip Irrigation; Dasberg, S., Or, D., Eds.; Applied Agriculture; Springer: Berlin/Heidelberg, Germany, 1999; pp. 125–138. [Google Scholar] [CrossRef]
- Moncef, H.; Khemaies, Z. An Analytical Approach to Predict the Moistened Bulb Volume beneath a Surface Point Source. Agric. Water Manag. 2016, 166, 123–129. [Google Scholar] [CrossRef]
- Chu, S.-T. Green-Ampt Analysis of Wetting Patterns for Surface Emitters. J. Irrig. Drain. Eng. 1994, 120, 414–421. [Google Scholar] [CrossRef]
- ZhiGang, L.; QinChao, X. Wetting Patterns Estimation in Cultivation Substrates under Drip Irrigation. Desalin. Water Treat. 2018, 112, 319–324. [Google Scholar]
- Schwartzman, M.; Zur, B. Emitter Spacing and Geometry of Wetted Soil Volume. J. Irrig. Drain. Eng. 1986, 112, 242–253. [Google Scholar] [CrossRef]
- Nafchi, R.F.; Mosavi, F.; Parvanak, K. Experimental study of shape and volume of wetted soil in trickle irrigation method. Afr. J. Agric. Res. 2011, 6, 458–466. [Google Scholar] [CrossRef]
- Al-Ogaidi, A.A.M.; Wayayok, A.; Rowshon, M.K.; Abdullah, A.F. Wetting patterns estimation under drip irrigation systems using an enhanced empirical model. Agric. Water Manag. 2016, 176, 203–213. [Google Scholar] [CrossRef]
- Nagaraja, M.S.; Bhardwaj, A.K.; Reddy, G.V.P.; Srinivasamurthy, C.A.; Kumar, S. Estimations of soil fertility in physically degraded agricultural soils through selective accounting of fine earth and gravel fractions. Solid Earth 2016, 7, 897–903. [Google Scholar] [CrossRef]
- Kirkby, C.A.; Kirkegaard, J.A.; Richardson, A.E.; Wilson, B.; Kirkby, C.A.; Kirkegaard, J.A.; Richardson, A.E.; Wilson, B. Gravel-associated organic material is important to quantify soil carbon and nitrogen stocks to depth in an agricultural cropping soil. Soil Res. 2021, 60, 224–233. [Google Scholar] [CrossRef]
- USDA, Soil Survey Staff. Soil Taxonomy: A Basic System of Soil Classification for Making and Interpreting Soil Surveys; Agric. Handbook, 436; US Department of Agriculture: Washington, DC, USA, 1975.
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Starr, J.L.; Paltineanu, I.C. Methods for measurement of soil water content: Capacitance devices. Methods Soil Anal. Part 2002, 4, 114621. [Google Scholar]
- Saxton, K.E.; Rawls, W.J. Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Bresler, E. Analysis of trickle irrigation with application to design problems. Irrig. Sci. 1978, 1, 3–17. [Google Scholar] [CrossRef]
- Taghavi, S.A.; Mariño, M.A.; Rolston, D.E. Infiltration from Trickle Irrigation Source. J. Irrig. Drain. Eng. 1984, 110, 331–341. [Google Scholar] [CrossRef]
- Angelakis, A.N.; Kadir, T.N.; Rolston, D.E. Time-dependent soil-water distribution under a circular trickle source. Water Resour. Manag. 1993, 7, 225–235. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Ren, L. Water and nitrogen distribution as affected by fertigation of ammonium nitrate from a point source. Irrig. Sci. 2003, 22, 19–30. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Rao, M. Wetting patterns and nitrogen distributions as affected by fertigation strategies from a surface point source. Agric. Water Manag. 2004, 67, 89–104. [Google Scholar] [CrossRef]
- Willmott, C.J. Some Comments on the Evaluation of Model Performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Bolaños-Sánchez, C.; Prado-Hernández, J.V.; Silván-Cárdenas, J.L.; Vázquez-Peña, M.A.; Madrigal-Gómez, J.M.; Martínez-Ruíz, A. Estimating Rainfall Interception of Pinus hartwegii and Abies religiosa Using Analytical Models and Point Cloud. Forests 2021, 12, 866. [Google Scholar] [CrossRef]
- Rivera, F.S.; Chaparro, V.O.; Solorio, C.O.; de León González, F. Cambios en las propiedades físicas de dos suelos de una región semiárida debidos al uso agrícola. Agrociencia 2000, 34, 379–386. [Google Scholar]
- Minasny, B.; McBratney, A.B. Limited effect of organic matter on soil available water capacity. Eur. J. Soil Sci. 2018, 69, 39–47. [Google Scholar] [CrossRef]
- Li, Y.-B.; Fan, Y.-W.; Liu, Y.; Ma, X.-Y. Influencing Factors and Simplified Model of Film Hole Irrigation. Water 2017, 9, 543. [Google Scholar] [CrossRef]
- Fan, Y.; Shao, X.; Gong, J.; Wang, Y. An empirical model for estimating soil wetting pattern dimensions during film hole irrigation. Arch. Agron. Soil Sci. 2020, 66, 1765–1779. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).