Abstract
The quantification of driftwood deposition in rivers is important for understanding the total budget of driftwood at the watershed scale; however, it remains unclear how such driftwood storage in rivers contributes to the overall system because of the difficulties in undertaking field measurements. Herein, we perform numerical simulations of driftwood deposition within an idealized river reach with a sand-bed, to describe the role of large-scale bedforms, more specifically, alternate bars, multiple bars, and braiding, in driftwood storage in rivers. The numerical model we propose here is a coupling model involving a Lagrangian-type driftwood model and an Eulerian two-dimensional morphodynamic model for simulating large-scale bedforms (i.e., bars and braiding). The results show that the channel with a braiding pattern provides a wide area with enhanced capacity for deposition of driftwood, characterized by exposed mid-channel or in-channel bars, leading to high driftwood storage. The alternate bar is also a large bedform representing a sediment depositional element in rivers; however, because of the narrow exposed bar area and its downstream-migrating feature during floods, the alternate bars seem to contribute less to driftwood deposition in rivers. This suggests that the role of multiple bars and braiding is critically important for the driftwood deposition in rivers.
1. Introduction
The river acts as a pathway for water in the rainfall-runoff process and also transports many natural (e.g., sediment, carbon, nutrients, etc.) and synthetic materials (e.g., plastic and radionuclides, etc.) from mountainous areas to the ocean. As one such material being transported in rivers, driftwood has recently received considerable attention in various research and engineering studies (e.g., [,]). This is because the large pieces of wood have many roles in river systems; they can provide a large variety of flow and sediment transport fields thereby creating rich habitats for many aquatic species [], have a non-negligible effect on the landscapes [,], and increase flood risks [,,]. A better understanding of wood recruitment, transport, deposition, and remobilization is therefore an important research topic in the fields of environmental and engineering research []. In this study, among the many research questions regarding driftwood in rivers, we focus on how driftwood can be captured in river systems, and how the storage of driftwood caused by large river bedforms can contribute to the total budget of driftwood in rivers.
In small streams, where the river width is close to the typical length of driftwood, there is a high possibility that the wood is trapped by the bed and channel boundaries, so that the deposition rate of the wood in such streams is generally high []. Because the channel becomes wider along the downstream direction, the storage of wood may be decreased in downstream river reach. However, in such river reaches, large-scale bedforms (e.g., sand bars) could be a key element that creates preferential deposition areas for driftwood, since large deposits of wood have been commonly observed on river bedforms after large flood events [].
Figure 1 shows an example of driftwood deposition on the sand bars in an upper reach of the Otofuke River, Japan, after a large flood and subsequent morphological evolution of the bed and channel []. This field observation strongly suggests that the sand bar has a significant role in accumulating driftwood entering the river from its upstream reaches and the floodplain. The deposition of driftwood on the sandbars will contribute to creating a rich ecosystem in the upper reaches of the river, and also reduce the driftwood load in the downstream reaches. Therefore, research on driftwood deposition mechanisms and their contribution to the total wood budget is essential for managing river systems.

Figure 1.
Driftwood deposition observed after large flood event in Otofuke River, Japan. Red color indicates single pieces, and blue denotes formation of logjams following driftwood deposition. (Courtesy of Hokkaisuiko Consultant Corporation).
In this regard, the bed and channel geometries have a significant effect on the wood deposition in rivers because complex bed and channel geometries provide considerable room for wood deposition and high possibility of contact with the riverbed to the driftwood, leading to it being trapped in the river. For instance, in single-thread meandering rivers, the depositional location of the driftwood is mainly the channel-floodplain boundary, such as the edge of the outer bank []. On the other hand, in multi-thread channels, there is a high probability that the driftwood is stranded on the mid-channel bars and island bars, causing higher in-channel wood storage than in single-thread channels [,]. These field observations clearly suggest that the depositional mechanism, pattern, and amount of driftwood are highly dependent on bedform characteristics. However, even though detailed measurements of the transport rate of driftwood during the flood and estimate the total volume of wood deposited after the flood have been conducted in rivers in real-scale [,], it is still challenging to estimate how much driftwood from the upper reaches could be stored in the river reach under study and to understand how different types of bedforms (e.g., alternate bars, multiple bars, braiding, etc.) would contribute to driftwood deposition. This type of depositional mechanism of driftwood has been investigated by detailed flume experiments [] and numerical simulations [] in braiding channel; however, the driftwood depositional mechanisms caused by different types of bedforms; for example, alternate bars have not been quantitatively compared to the case of braiding channel in well-controlled flume experiments or numerical simulations. Therefore, a comprehensive understanding of the role of large-scale bedforms in wood storage remains a challenging and interesting research topic.
In this study, the depositional mechanisms and amount of driftwood deposited on large-scale bedforms were investigated by using a numerical model. More specifically, we discuss the role of different types of bedforms, namely, alternate bars and multiple bars (braided), in driftwood storage in rivers under simple flow and channel conditions. As mentioned earlier, though the importance of sand bars in the mechanism of wood storage in rivers has been confirmed by several field observations, the amount of driftwood from the upper reaches that could be deposited in the river reach under study remains unclear because of the complicated interactions of the flow, changes in the river bed and driftwood behavior, and lack of field data regarding the wood budget. Our attempt to study driftwood storage under a simplified condition will therefore contribute to a better and more straightforward understanding of driftwood storage in the presence of different types of sand bars in river beds.
2. Methods
2.1. Concept of Numerical Model
In this study, we use a Lagrangian–Eulerian coupling approach (e.g., []) to model the driftwood transport and deposition under active bed evolution governed by dynamics of alternate or multiple bars. A Lagrangian-type model was utilized to simulate the motion of individual driftwood, and an Eulerian approach was adopted to model flow, sediment transport, and morphodynamics. The presence of driftwood in the flow and on the bed generally has a non-negligible effect on the overall characteristics of hydrodynamics and morphodynamics (e.g., [,]). To model this feedback mechanism between driftwood presence and flow-sediment transport morphodynamic processes, two-way modeling that includes in the model the effect of driftwood on flow and bed evolution (and vice versa) is essential (e.g., []). However, this modeling approach results in a heavy computational load and additional complexity in the numerical model. Instead of using a two-way approach, we herein use a one-way model that neglects the interaction between driftwood presence and flow-morphodynamic phenomena. Since the experiments of Bertoldi et al. [] that we used for model validation and numerical simulation suggest only a small effect of the driftwood on the overall braided bar pattern, a one-way approach may be an acceptable approximation that is still able to capture the physical processes necessary for elucidating the effect of bar patterns on driftwood storage.
2.2. Flow, Sediment Transort, and Morphodynamics: Eulerian Approach
Herein, we use a two-dimensional morphodynamic model, Nays2DH [], which is a plane two-dimensional morphodynamic model incorporated in the international River Interface Coorperative (iRIC) software package [,] to reproduce the various types of large-scale bedforms including alternate bars and multiple bars (braided channel). This is an unsteady shallow water flow model with a Manning–Strickler type roughness model for the flow field, and an equilibrium-bedload transport model for sediment transport and morphodynamics. Kang et al. [] also applied this model to reproduce the experiments of Bertoldi et al. [], and demonstrated its general applicability in reproducing the braided channel. This type of morphodynamic model has been widely used to reproduce not just the braided channel but different types of large-scale morphodynamic phenomena, i.e., alternate bars [,], multiple bars [], and meandering [,], and its use has been validated as well. These applications suggested that the model can also be applied to model several bar patterns (alternate and multiple bars) in this study. Simulated flow- velocity and bed-elevation change were used to calculate driftwood motion and deposition. This means that we focus on only the planar motion of the driftwood, whereas vertical motion and effect of any three-dimensional flow structure on driftwood motion are neglected. This assumption can be considered reasonable for the cases herein because the water depth is shallow and three-dimensional flow structures (e.g., secondary flows) driven by sand bar morphology are not significant []. On the other hand, this modeling framework will not be applicable to flow fields governed by three-dimensional flow structures and the formation of logjams; in these cases, a three-dimensional flow model is required (e.g., []).
2.3. Driftwood Model: Lagrangian Approach
The behavior of driftwood in rivers is quite complex, and it is challenging to model the transport of individual pieces of driftwood. There are roughly two types of driftwood transport models: (1) Eulerian models which express wood transport using the advection-dispersion equation (e.g., []), and (2) a Lagrangian model which tracks the motion of individual wood pieces (e.g., [,,,,]). The Lagrangian approach is a more straightforward approach for modeling driftwood behavior because of the complex motions that individual wood pieces go through. In this study, we modeled the wood pieces as a cylinder, as shown in Figure 2 [], and calculated the plane motion using the following momentum equations:
t is the time; x and y are the downstream and transverse coordinates, respectively; up and vp are the velocities of the wood piece in the x and y directions, respectively; and u and v are the flow velocities in the x and y directions, respectively, which are obtained from the two-dimensional model, ρ is the density of water, CD is the drag coefficient of the wood piece, and Ax and Ay are the projections of the area of the wood piece in the x and y directions, respectively.
where l and d, are the length and diameter of the wood piece, respectively, and φ is the angle of the wood piece against the x-axis (see Figure 2). m′ is the mass of the wood piece, including the added mass and is given by:
where σ is the density of the wood piece, V is its volume, and Cm is the coefficient of the added mass.
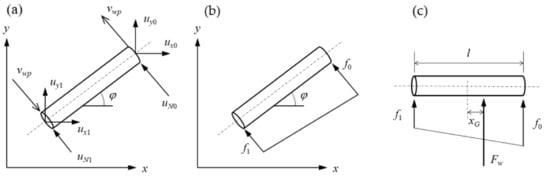

Figure 2.
Definitions of driftwood properties, flow velocity, and forces acting on wood pieces modeled as a cylinder. (a) Flow velocities acting on edge of cylinder, (b) force distribution, and (c) moment balance.
The rotational motion of the wood pieces is calculated using following equation.
where ωp is the rotational speed of the wood piece, and I is its moment of inertia.
m is the total rotational moment acting on the piece of wood. The rotational moment is obtained by considering the balancing forces acting at the edges of the wood piece (i.e., f0 and f1 in Figure 2b). By defining the flow velocities at the edges of the wood piece as ux0, uy0, ux1, uy1 (Figure 2a), we can calculate the flow velocity perpendicular to the longer axis of the wood piece, uN0 and uN1, contributing to the rotational motion, as follows:
The velocity of the wood piece driven by rotational motion (i.e., ωp) can be calculated by:
The forces acting at the edge of the wood piece can then be expressed as
where Cr is the drag coefficient of rotational motion.
The total force acting perpendicular to the wood piece, Fw, is calculated by assuming a linear force distribution along the wood piece, as shown in Figure 2c.
where xg is the distance between the point of action and the point of mass. By substituting M and I into Equation (6), we calculated the rotational motion of the wood pieces.
The Equations (1), (2) and (6) indicate that the driving force for the motion of the wood piece is only the drag force from the hydrodynamic calculation, neglecting the collision of the individual wood pieces and interaction between the wood and bed surface. The former assumption is critical for logjam formation, and the latter might be problematic for wood piece deposition. A detailed modeling of such a process (e.g., []) will be ideal; however, for simplicity, it is assumed that the deposition of the wood pieces occurs when the water depth at the center of gravity is less than the diameter of the wood piece. The deposited wood piece will again be set in motion when the water depth becomes greater than its diameter due to bed erosion.
3. Results
We first apply the proposed model to the experimental study performed by Bertoldi et al. [] to show the model performance in reproducing the morphodynamics of braided channels and the transport and deposition of driftwood. We then perform a numerical simulation to understand the role of large-scale bedforms—that is, alternate bars and multiple bars—in wood storage.
3.1. Model Performance
Case C1 of Bertoldi et al. [] was used in this study to validate our model. The movable bed experiment that includes wood transport and deposition was conducted in a large laboratory flume 11 m long and 1.7 m wide. The initial channel slope was set to 0.013, and the bed was composed of well-sorted sand with a mean grain size of 0.73 mm. For the experimental case, a steady water discharge from the upstream end, at the rate of 1.26 l/s without driftwood supply, was maintained for 20 h to reproduce the braided channel pattern in the flume. Using this channel pattern as an initial bed, the same discharge rate was maintained with wood supply in the channel for 18 h, to understand the behavior of driftwood in the complex channel configuration. The first 6 h of the experiment contributed 10 wood pieces every 10 min, and after that the wood supply rate was decreased to 10 wood pieces every 15 min. The modeled wood piece had a length of 8 cm and a diameter of 3 mm. Some of the supplied wood pieces have a root structure.
In the numerical simulation, the conditions employed were almost identical to those used in the experiment, except for the root of the wood pieces. The Manning’s roughness coefficient was set to 0.0145, and the sediment bed was considered to comprise of a uniform size of sand. The dimension of the computational grid was 3 cm in both the x and y directions. The density of the wood pieces was 670 kg/m3. Some parameters for the driftwood model were determined considering it to be a cylindrical piece; Cd and Cr are approximated as constant, 1 since effect of Reynolds number on drag coefficient is not high for the condition we tested (Table 1) [], and as used by Kang et al. [], added mass coefficient, Cm is set to 0.5.

Table 1.
Computational conditions for numerical simulation.
Figure 3 shows the channel pattern reproduced during the first 20 h of the numerical simulation, and the temporal series showing the bed change and depositional pattern of the wood pieces during simulation. Figure 3a shows a typical braided channel pattern, that is, channel bifurcation and complex bar pattern, which was also observed in the experiment of Bertoldi et al. [], suggesting that the morphodynamic model we used reproduced observed braided channel pattern with reasonable accuracy. The results of the calculation for the latter 18 h show that the supplied wood pieces tend to be deposited at the top of bars and the edge of the channel. As can be seen in Figure 3, the bar and channel patterns are modified in time by the channel shift so that the wood pieces deposited on the previously developed sand bars are remobilized and set in motion by this active channel deformation. The transport, deposition, and remobilization of the wood pieces are consistent with the experimental results of Bertoldi et al. [] and some field observations [,], indicating that the numerical model proposed herein demonstrates a qualitatively good performance with respect to capturing the behavior of driftwood in the braided channel.
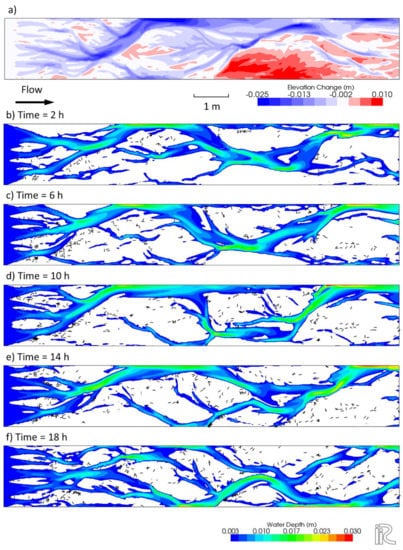
Figure 3.
Numerical simulation of braided channel pattern and depositional pattern of wood pieces for Case C1 of Bertoldi et al. []. (a) bar and channel patterns by first 20 h obtained through morphodynamic calculation; (b–f) temporal changes during the latter 18 h calculated for channel, and depositional patterns of wood piece. Solid-black lines denote wood pieces. The diameter of wood pieces is increased by factor of 5 for visualization.
The deposition of the wood pieces was quantitatively evaluated in terms of the storage of the supplied wood pieces in the modeled braided channel. Figure 4 conveys the number of supplied wood pieces deposited in the computational domain during the experiment and simulation, revealing that the simulation tends to underestimate the wood depositional rate. On the other hand, the overall trend in wood deposition can be captured by the numerical simulation; in particular, the asymptotic equilibrium state of the depositional rate of the wood in the latter part of the run (i.e., after 15 h) seems to be reproduced by the simulation. This behavior is controlled by the balance between the wood deposition onto the bars and the remobilization of the deposited wood by bank erosion and channel shift. The results indicate that the simulation correctly captured this process. The underestimation may have been caused by neglecting the effect of the root in the wood piece in the simulation because the root enhances the probability of deposition of wood onto the sand bars. In addition, neglecting the flow–wood and wood–wood interactions may cause critical underestimation of logjam formation.
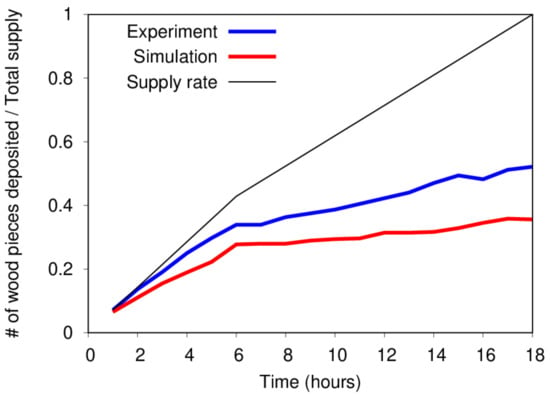
Figure 4.
Comparison between experiment and simulation of rate of deposition of supplied wood pieces onto modeled braided channel.
3.2. Role of Large-Scale Bedforms in Wood Storage
Our simple numerical approach leads to some discrepancy between the results of simulation and experiment; however, the results also prove that the model enables capturing general features of wood deposition in the braided channel. The results of the experiment also indicate that almost 40% of the supplied wood pieces were deposited in this modeled channel reach, indicating the large wood storage capacity of the braided channel. This result motivated us to perform a numerical simulation regarding the role of different types of bedforms in capturing driftwood.
An important controlling parameter in the sand bar regime is the channel width to water depth ratio []. Several criteria have been proposed for the bar regime (e.g., [,,,]). We determined the computational conditions of the numerical simulation using the bar regime criteria derived from a linear stability analysis []. Table 1 shows the detailed computational conditions, and Figure 5 demonstrates how the conditions provided in the table result in the different types of bar characteristics in the context of linear theory (i.e., this criterion is valid for the initial stage of development).
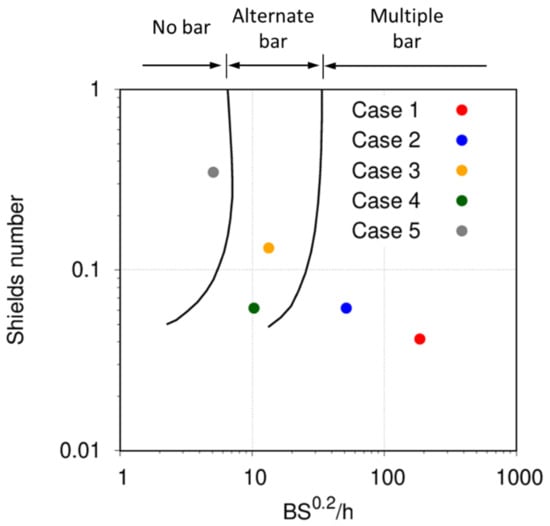
Figure 5.
Dominant bar modes in the numerical simulation predicted by bar regime diagram as proposed by Kuroki and Kishi []. S denotes channel slope.
Here, Case 1 corresponds to case C1 of Bertoldi et al. [], which is the validation case of our study above. The grain size and initial slope were fixed for all the runs while we changed the water discharge and channel width to set the different bar modes for simulation. Cases 2 and 4 have the same Shields number for initial condition, but the dominant bar modes are set to multiple and alternate bars, respectively, to simply observe the effect of bar geometry on wood deposition. Cases 1–2 and cases 3–4 are intended to unveil the effect of Shields number under similar bar characteristics; multiple bars are expected to appear in cases 1–2 and alternate bars in cases 3–4. Case 5 represents the no-bedform condition, where bed configuration is expected to have limited effect on wood deposition. Note that in this study, we do not consider about small-scale bedforms (i.e., dunes [,] and anti-dunes []) since the morphodynamic model we use herein can not reproduce such small-scale bedforms.
It is difficult to set up consistent conditions with regard to the size of the wood pieces when the channel width is changed. The size of the wood pieces indicated in Table 1 was determined by maintaining a constant ratio between channel width and size of the wood pieces. In order to observe the effect of variations in length of the wood piece in this simulation, we also performed a numerical simulation with fixed wood lengths of 3 cm and 5 cm, through cases 1–5.
In this numerical simulation, channel length and width are same as Case 1 through all the runs; however, we used periodic conditions as the upstream and downstream boundary conditions for the morphodynamic calculation in cases 3, 4, and 5 (i.e., alternate bar and no-bar conditions), whereas experiments for cases 1 and 2 were performed under non-periodic boundary conditions. This is because, to reproduce alternate bars during simulation, a longer flume than in the experiment is generally needed since a certain distance is necessary to develop the downstream-migrating alternate bars [,]. This means that the length of the flume in the experiment was not sufficient to obtain alternate bars in the computational domain. However, a longer flume provides a wider depositional area for the wood pieces than the shorter flume, making comparison of wood deposition for the short and long flumes difficult. Under this condition, similar to the validation case (i.e., Case 1), we first performed morphodynamic calculation for 20 h without wood supply; calculation for the next 18 h was then carried out to calculate wood transport and deposition during the morphological evolution of the bed and channel.
Figure 6 and Figure 7 show the temporal changes in the channel pattern and depositional distribution of the wood pieces in cases 2 (multiple-bar dominated) and 4 (alternate-bar dominated). The bed and channel patterns simulated in Case 2 is a braiding, which is a similar pattern to Case 1, although the number of channels seems less, and the exposed bar area is narrower than that in Case 1. In addition, the temporal variations of the bar and channel patterns are more active than for Case 1 because of the higher Shields number. Despite these differences, wood deposition can be observed on top of the bar and the edge of the channel, which is also similar to Case 1. This suggests that braiding or multiple bars provide a wide area for wood deposition, resulting in a high potential for wood storage. On the other hand, in Case 4, in which the dominant bar mode is alternate bars, few wood pieces can be deposited in the limited area on top of the bars, as shown in Figure 7. This is because that the water in this case is relatively deeper than in the multiple-bar dominated condition (i.e., cases 1 and 2), providing less potential area for wood deposition. In addition, the downstream migration of the alternate bars increases the possibility of wood remobilization, and leads to quite small wood deposition. This mechanism is also valid for Case 3 in which the channel width to depth ratio is lower than that of Case 4 (i.e., relatively deeper channel) where alternate bars are more actively migrating downstream, and Case 5, where there are no bedforms, leading to zero wood deposition in these cases. This result indicates that although the alternate bars are features that promote large-scale sediment deposition in the river, and seem to provide a large space for wood deposition, the actual wood storage seems to be not highly effective because of the narrow exposed bar area and its active downstream-migrating feature during floods.
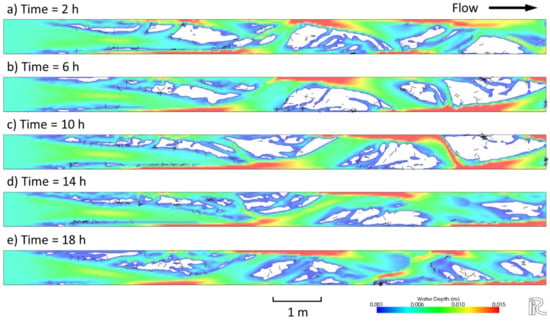
Figure 6.
Calculation results for channel pattern and depositional distribution of wood pieces in Case 2. (a–e) temporal changes during the latter 18 h calculated for channel, and depositional patterns of wood piece. Solid black lines denote wood pieces. The length and diameter of wood pieces are increased by factor of 3 and 5 for visualization, respectively.

Figure 7.
Calculation results for channel pattern and depositional distribution of wood pieces in Case 4 at the end of 18 h. Solid black lines denote wood pieces. The length and diameter of wood pieces are increased by factor of 15 and 20 for visualization, respectively.
Figure 8 describes the temporal changes in wood deposition rate within the computational reach in cases 1, 2, and 4 (the depositional amount in cases 3 and 5 is zero, so these results are not visualized in this figure). The figure indicates that even though multiple bars or braiding patterns are similar between cases 1 and 2, there is a significant difference with respect to the total depositional storage. That is, in Case 2, only 10% of the supplied wood pieces can be retained in the reach, and the depositional amount is likely to decrease toward the end of the computation period. This is because the bar and channel patterns change more actively than in Case 2 because of the higher Shields number, resulting in higher remobilization of wood pieces previously deposited on the bars. This result implies that bank erosion and channel shift are also factors that control wood storage in rivers.
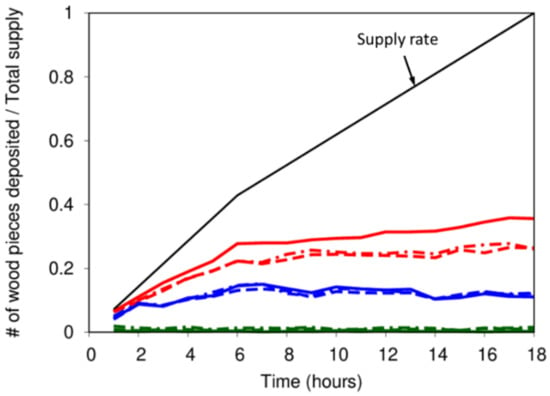
Figure 8.
Temporal change in depositional rate of wood in numerical simulations. Red, blue, and green lines represent the results of cases 1, 2, and 4, respectively. Solid, dash, and dot-dash lines denote depositional rate of wood by different wood length, namely, values shown in Table 1, 3 cm, and 5 cm, respectively.
Figure 8 also demonstrates the effect of the size of the wood pieces on the depositional rate. It demonstrates that smaller size wood pieces results in less depositional rate, but essentially no significant effect of the wood size on wood storage was observed for the cases we tested. This result might be because that the length of the wood used in the simulation was sufficiently less than the typical simulated channel width used in the morphodynamic calculation. The size of the wood is a critical component of the wood depositional mechanisms for narrower channels []; this effect is significant when the length of the wood is close to the width of the channel.
Figure 9 shows the spatial distribution of deposited driftwood observed after the 2016 flood event in the Otofuke River in the braided and alternate bar dominated reaches. This figure clearly indicates that the braiding-dominated reach captured a number of driftwood pieces on top of the bars, whereas the alternate-bar reach has almost no depositional wood. This is at least qualitatively in good agreement with the numerical results mentioned above, suggesting that in natural river systems, braiding is a critical factor affecting driftwood storage brought down from the upstream reaches; however, the alternate bars have a limited role in the deposition of driftwood.

Figure 9.
Spatial distribution of deposited driftwood in (a) braiding dominated, and (b) alternate-bar dominated reaches of Otofuke River, Japan after the 2016 flood event. Red circles denote wood deposition/logjam formation.
4. Discussion
The results presented in this paper show that braiding is a critical element in driftwood storage while the alternate bars have a limited role. This feature has been qualitatively pointed out by field observations [,]. The role of braiding as demonstrated by the simulation seems significant even when computation is performed for a limited channel length. This may suggest that a multiple-bar and braiding dominated channel reach with a sufficiently long length has a critical importance in terms of the overall driftwood budget []. This “cleaning” mechanism of bars in terms of driftwood may reduce the driftwood load in the downstream reaches, contributing to mitigating the driftwood-induced flood risk []. In addition, this also has a positive effect on the river ecosystem [] as this effect might create a unique environment for many species. On the other hand, such an effect due to driftwood storage may not be present in the alternate-bar dominated reach because of its morphodynamic features presented in the numerical simulation. Though the study thus provides a better understanding of the mechanism of driftwood transport and storage, there are some limitations to this study, which are discussed below.
We maintained a steady water discharge from the upstream end; however, it is obvious that in natural streams, the water discharge is unsteady. The hydrograph of the unsteady discharge has a significant effect on the morphodynamics of bar and braiding (e.g., [,]); however, in the context of driftwood transport, the exposure of the bar top (e.g., []) and reduction in bar migration velocity (e.g., []) along the falling limb of the hydrograph is important. This is because reduced water discharge causes exposure of the sand bars developed during high flow, and also reduces bar migration velocity. These exposed bars may play a similar role as the sand bars developed in the braiding reach, providing a large depositional space for driftwood [], with the reduction in migration velocity probably suppressing the remobilization of deposited wood pieces. These effects of discharge variation on depositional features can be found in the case of different floating objects in rivers (e.g., seeds []). Field observations regarding the supply rate of driftwood suggest that most of the driftwood being transported during a flood enters the river in the rising limb of the hydrograph [,,], indicating that the amount of driftwood deposited in the falling limb of the hydrograph might not be significant in terms of the total supply rate. However, it is still worth pursuing the effect of discharge variation on driftwood deposition in several types of bedforms, as the overall wood transport processes remain poorly understood.
In this study, we treat the wood piece as a cylinder and focus only on the floating wood piece, meaning that the density of wood considered is less than that of water. However, the characteristics of wood, namely, structure, density, and size, are also critical parameters for remobilization of the deposited wood and the transport process [,]. In particular, the density of the wood is an important parameter for motion, that is, floating wood will move by the flow velocity at the water surface with less chances of being captured by the bed, whereas the transport process of a heavy wood piece will be controlled by a near-bed flow structure with a high possibility of contact with the bed (e.g., []). Thus, the role of large-scale bedforms presented in this study could be different in the case of heavy wood pieces.
Some model limitations in our simple numerical approach could affect the implications of the study results as well. The most critical limitation may be neglecting the flow-wood and wood-wood interactions. The former is an important physical process in cases where the wood piece is quite large compared to the channel dimension [], and the latter drives logjam formation [,]. As indicated in Figure 1, logjam formation may represent the large amount of driftwood deposition on the sand bars; this effect needs to be included in the numerical model. This simplification may be one of the reasons for the underestimation of the rate of wood deposition in our numerical simulation. The flow–wood and wood–wood interactions are quite complex processes, so modeling this aspect [] will be a challenging task in the future.
5. Summary
This paper presents a numerical simulation of driftwood transport and deposition in modeled alternate-bar-dominated and braiding-dominated channels, to discuss the role of large-scale bedforms in driftwood storage in rivers. We propose a simple physics-based model, which couples a Lagrangian-type driftwood model and an Eulerian two-dimensional morphodynamic model (iRIC-Nays2DH). The model is then validated using a flume experiment by Bertoldi et al. [], focusing on driftwood behavior in the braiding-dominated channel. The results from the model generally show good agreement in terms of the depositional pattern and deposited amount in the modeled braided channel, although the simulation tends to underestimate the amount of supplied wood pieces that are deposited because of approximations adopted in the model (e.g., neglecting flow–wood, wood–wood interactions, and root). We performed an numerical simulation on the morphodynamic and wood transport parameters under different conditions based on which type of bars are dominant, more specifically, under alternate-bar and braiding channel conditions with different Shields numbers. The results show that the braiding channel pattern provides increased depositional capacity with a wide area for the deposition of driftwood characterized by exposed mid-channel or in-channel bars, leading to high driftwood storage. The alternate bar is also a large sediment depositional element in rivers; however, because of the narrow exposed bar area and its downstream-migrating feature during floods, the alternate bars seem to contribute less to driftwood deposition in rivers. This suggests that the role of multiple bars and braiding is critically important for the overall driftwood budget.
Some model approximations and unexplored physical processes (i.e., unsteady hydrographs) need to be revisited to further understand driftwood behavior in river systems. In addition, it will be worth investigating the implications of this study by directly observing the driftwood budget, transport rate, and depositional amount in the field and performing further thorough numerical simulations under different flow, sediment transport, and channel conditions.
Author Contributions
T.I. and T.O. wrote the paper; T.I., Y.S., and T.K. provided research idea; Y.S. developed a numerical model; T.O. performed the numerical simulation and analyzed the result. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JSPS KAKENHI Grant Number JP20K14831.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We thank to Hokkai-suiko Consultant Corporation for providing the depositional pattern of the driftwood in the Otofuke River after 2016 flood event (Figure 1 of this paper).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gurnell, A. Wood and river landscapes. Nat. Geosci. 2012, 5, 93–94. [Google Scholar] [CrossRef]
- Wohl, E.; Iroume, A. Introduction to the wood in world rivers special issue. Earth Surf. Process. Land. 2021. [Google Scholar] [CrossRef]
- Bair, R.T.; Segura, C.; Lorion, C.M. Quantifying the restoration success of wood introductions to increase coho salmon winter habitat. Earth Surf. Dyn. 2019, 7, 841–857. [Google Scholar] [CrossRef]
- Bertoldi, W.; Welber, M.; Gurnell, A.M.; Mao, L.; Comiti, F.; Tal, M. Physical modeling of the combined effect of vegetation and wood on river morphology. Geomorphology 2015, 246, 178–187. [Google Scholar] [CrossRef]
- Bialik, R.; Karpinski, M.; Rajwa, A.; Luks, B.; Rowinski, P.M. Bedform characteristics in natural and regulated channels: A comparative field study on the Wilga River, Poland. Acta Geophys. 2014, 62, 1413–1434. [Google Scholar] [CrossRef]
- Ruiz-Villanueva, V.; Blade Castellet, E.; Diez-Herrero, A.; Bodoque, J.M.; Sanchez-Juny, M. Two-dimensional modelling of large wood transport during flash floods. Earth Surf. Process. Landf. 2014, 39, 438–449. [Google Scholar] [CrossRef]
- Schalko, I.; Lageder, C.; Schmocker, L.; Weitbrecht, V.; Boes, R.M. Laboratory flume experiments on the formation of spanwise large wood accumulations: I. Effect on backwater rise. Water Resour. Res. 2019, 55, 4854–4870. [Google Scholar] [CrossRef]
- Wohl, E.; Scamardo, J.E. The resilience of logjams to floods. Hydrol. Process. 2020, 35, e13970. [Google Scholar] [CrossRef]
- Ruiz-Villanueva, V.; Piegay, H.; Gurnell, A.M.; Marston, R.A.; Stoffel, M. Recent advances quantifying the large wood dynamics in river basins: New methods and remaining challenges. Rev. Geophys. 2016, 54, 611–652. [Google Scholar] [CrossRef]
- Abbe, T.; Montgomery, D.R. Patterns and processes of wood debris accumulation in the Queets River Basin, Washington. Geomorphology 2003, 51, 81–107. [Google Scholar] [CrossRef]
- Gurnel, A.M.; PieGay, H.; Swanson, F.J.; Gregory, S.V. Large wood and fluvial processes. Freshw. Biol. 2002, 47, 601–619. [Google Scholar] [CrossRef]
- Kyuka, T.; Okabe, K.; Shimizu, Y.; Yamaguchi, S.; Hasegawa, K.; Shinjo, K. Dominating factors influencing rapid meander shift and levee breaches caused by a record-breaking flood in the Otofuke River, Japan. J. Hydro Environ. Res. 2020, 31, 76–89. [Google Scholar] [CrossRef]
- Wyzga, B.; Zawiejska, J. Large wood storage in channelized and unmanaged sections of the Czarny Dunajec River, Polish Carpathians: Implications for the restoration of mountain rivers. Folia Geogr. 2010, 41, 5–34. [Google Scholar]
- Van Der Nat, D.; Tockner, K.; Edwards, P.J.; Ward, J.V. Large wood dynamics of complex Alpine river flood-plains. J. N. Am. Benthol. Soc. 2003, 22, 35–50. [Google Scholar] [CrossRef]
- MacVicar, B.; Piegay, H. Implementation and validation of video monitoring for wood budgeting in a wandering piedmont river, the Ain River (France). Earth Surf. Process. Landf. 2021, 37, 1272–1289. [Google Scholar] [CrossRef]
- Bertoldi, W.; Welber, M.; Mao, L.; Zanella, S.; Comiti, F. A flume experiment on wood storage and remobilization in braided river systems. Earth Surf. Process. Landf. 2014, 39, 804–813. [Google Scholar] [CrossRef]
- Kang, T.; Kimura, I.; Shimizu, Y. Numerical simulation of large wood deposition patterns and responses of bed morphology in a braided river using large wood dynamics model. Earth Surf. Process. Landf. 2020, 45, 962–977. [Google Scholar] [CrossRef]
- Persi, E.; Petaccia, G.; Sibillia, S. Large wood transport modelling by a coupled Eulerian-Lagrangian approach. Nat. Hazards 2018, 91, 59–74. [Google Scholar] [CrossRef]
- Kimura, I.; Kitazono, K. Effects of the driftwood Richardson number and applicability of a 3D-2D model to heavy wood jamming around obstacles. Environ. Fluid Mech. 2020, 20, 525–603. [Google Scholar] [CrossRef]
- Shimizu, Y.; Takebayashi, H.; Inoue, T.; Hamaki, M.; Iwasaki, T.; Nabi, M. iRIC-Software: Nays2DH Solver Manual. 2014. Available online: https://i-ric.org/en/ (accessed on 16 March 2021).
- Nelson, J.M.; Shimizu, Y.; Abe, T.; Asahi, K.; Gamou, M.; Inoue, T.; Iwasaki, T.; Kakinuma, T.; Kawamura, S.; Kimura, I.; et al. The international river interface cooperative: Public domain flow and morphodynamics software for education and applications. Adv. Water Resour. 2016, 93, 62–74. [Google Scholar] [CrossRef]
- Shimizu, Y.; Nelson, J.; Arnez, K.F.; Asahi, K.; Giri, S.; Inoue, T.; Iwasaki, T.; Jang, C.L.; Kang, T.; Kimura, I.; et al. Advances in computational morphodynamics using the International River Interface Cooperative (iRIC) software. Earth Surf. Process. Landf. 2019, 45, 11–37. [Google Scholar] [CrossRef]
- Iwasaki, T.; Shimizu, Y.; Kimura, I. Sensitivity of free bar morphology in rivers to secondary flow modeling: Linear stability analysis and numerical simulation. Adv. Water Res. 2016, 92, 57–72. [Google Scholar] [CrossRef]
- Iwasaki, T.; Nelson, J.; Shimizu, Y.; Parker, G. Numerical simulation of large-scale bed load particle tracer advection-dispersion in rivers with free bars. J. Geophys. Res. Earth Surf. 2017, 122, 847–874. [Google Scholar] [CrossRef]
- Asahi, K.; Shimizu, Y.; Nelson, J.; Parker, G. Numerical simulation of river meandering with self-evolving banks. J. Geophys. Res. Earth Surf. 2013, 118, 2208–2229. [Google Scholar] [CrossRef]
- Inoue, T.; Mishra, J.; Kato, K.; Sumner, T.; Shimizu, Y. Supplied sediment tracking for bridge collapse with large-scale channel migration. Water 2020, 12, 1881. [Google Scholar] [CrossRef]
- Harada, D.; Egashira, S. Flood flow characteristics with fine sediment supply and driftwoods—Analysis on the Akatani River flood hazards in July, 2017. J. Jpn. Soc. Civ. Eng. Ser. B1 2018, 74, I_937–I_942. (In Japanese) [Google Scholar]
- Shibuya, H.; Katsuki, S.; Ohsumi, H.; Ishikawa, N.; Mizuyama, T. Trap performance analysis of woody debris capturing structure by distinct element method using cylindrical element. J. Jpn. Soc. Civ. Eng. Ser. A2 2011, 67, 113–132. (In Japanese) [Google Scholar]
- Akahori, R.; Hatta, N.; Shimizu, Y.; Ito, A. Response of woody debris for flows around hydraulic structures. J. Jpn. Soc. Civ. Eng. B1 2014, 70, I_691–I_696. (In Japanese) [Google Scholar]
- Callander, R.A. Instability and river channels. J. Fluid Mech. 1969, 36, 465–480. [Google Scholar] [CrossRef]
- Parker, G. On the cause and characteristic scales of meandering and braiding in rivers. J. Fluid Mech. 1976, 76, 457–480. [Google Scholar] [CrossRef]
- Muramoto, Y.; Fujita, Y. The classification of meso-scale river bed configuration and the criterion of its formation. Proc. JSCE 1978, 22, 275–282. (In Japanese) [Google Scholar]
- Kuroki, M.; Kishi, T. Regime criteria on bars and braids in alluvial straight channels. Proc. JSCE 1984, 342, 87–96. (In Japanese) [Google Scholar] [CrossRef]
- Crosato, A.; Mosselman, E. Simple physics-based predictor for the number of river bars and the transition between meandering and braiding. Water Resour. Res. 2009, 45, W03424. [Google Scholar] [CrossRef]
- Parsons, R.; Best, J.L.; Orfeo, O.; Hardy, R.J.; Kostaschuk, R.; Lane, S.N. Morphology and flow fields of three-dimensional dunes, Río Paraná, Argentina: Results from simultaneous multibeam echo sounding and acoustic Doppler current profiling. J. Geophys. Res. 2005, 110, F04S03. [Google Scholar] [CrossRef]
- Shugar, H.; Kostaschuk, R.; Best, J.L.; Parsons, D.R.; Lane, S.N.; Orfeo, O.; Hardy, R.J. On the relationship between flow and suspended sediment transport over the crest of a sand dune, Río Paraná, Argentina. Sedimentology 2010, 57, 252–272. [Google Scholar] [CrossRef]
- Inoue, T.; Watanabe, Y.; Iwasaki, T.; Otsuka, J. Three-dimensional antidunes coexisting with alternate bars. Earth Surf. Process. Landf. 2020, 45, 2897–2911. [Google Scholar] [CrossRef]
- Federici, B.; Seminara, G. On the convective nature of bar instability. J. Fluid Mech. 2003, 487, 125–145. [Google Scholar] [CrossRef]
- Defina, A. Numerical experiments on bar growth. Water Resour. Res. 2004, 39, 1092. [Google Scholar] [CrossRef]
- Martin, D.J.; Benda, L.E. Patterns of instream wood recruitment and transport at the watershed scale. Trans. Am. Fish. Soc. 2001, 130, 940–958. [Google Scholar] [CrossRef]
- Wohl, E.; Bledsoe, B.P.; Fausch, K.D.; Kramer, N.; Bestgen, K.R.; Gooseff, M.N. Management of large wood in streams: An overview and proposed framework for hazard evaluation. J. Am. Water Resour. Assoc. 2016, 52, 315–335. [Google Scholar] [CrossRef]
- Visconti, F.; Camporeale, C.; Ridolfi, L. Role of discharge variability on pseudomeandering channel morphodynamics: Results from laboratory experiments. J. Geophys. Res. Earth Surf. 2010, 115, F04042. [Google Scholar] [CrossRef]
- Iwasaki, T.; Shimizu, Y.; Kimura, I. Numerical simulation of bar and bank erosion in a vegetated floodplain: A case study in the Otofuke River. Adv. Water Res. 2016, 93, 118–134. [Google Scholar] [CrossRef]
- Masumoto, T.; Watanabe, Y.; Sasaki, A. Experimental study on channel formation at low flow on bars created at high flow. Adv. River Eng. 2009, 15, 225–230. (In Japanese) [Google Scholar]
- Tubino, M. Growth of alternate bars in unsteady flow. Water Resour. Res. 1991, 27, 37–52. [Google Scholar] [CrossRef]
- Sasaki, A.; Watanabe, Y.; Masumoto, T. An experiment on the flow-down of driftwood on riverbeds with sandbars. Adv. River Eng. 2009, 15, 177–182. (In Japanese) [Google Scholar]
- Van Dijk, W.M.; Teske, R.; Van de Lageweg, W.I.; Kleinhans, M.G. Effects of vegetation distribution on experimental river channel dynamics. Water Resour. Res. 2013, 49, 7558–7584. [Google Scholar] [CrossRef]
- Kramer, N.; Wohl, E. Estimating fluvial wood discharge using time-lapse photography with varying sampling intervals. Earth Surf. Process. Landf. 2014, 39, 844–852. [Google Scholar] [CrossRef]
- Ghaffarian, H.; Piegay, H.; Lopez, D.; Riviere, N.; MacVicar, B.; Antonio, A.; Mignot, E. Video-monitoring of wood discharge: First inter-basin comparison and recommendations to install video cameras. Earth Surf. Process. Landf. 2020, 45, 2219–2234. [Google Scholar] [CrossRef]
- Braudrick, C.A.; Grant, G.E. When do logs move in rivers? Water Resour. Res. 2000, 36, 571–583. [Google Scholar] [CrossRef]
- Braudrick, C.A.; Grant, G.E. Transport and deposition of large woody debris in streams: A flume experiment. Geomorphology 2001, 41, 263–283. [Google Scholar] [CrossRef]
- Kato, K.; Sumner, T.; Miura, T.; Kanno, T.; Chiba, K.; Inoue, T.; Shimizu, Y. Numerical analysis on the behavior of driftwood in driftwood capturing facility. J. Jpn. Soc. Civ. Eng. B1 2019, 75, I_1441–I_1446. (In Japanese) [Google Scholar] [CrossRef]
- Davidson, S.L.; MacKenzie, L.G.; Eaton, B.C. Large wood transport and jam formation in a series of flume experiments. Water Resour. Res. 2015, 51, 10065–10077. [Google Scholar] [CrossRef]
- Ader, E.; Wohl, E.; McFadden, S.; Singha, K. Logjams as a driver of transient storage in a mountain stream. Earth Surf. Process. Landf. 2021. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).