Abstract
The vast majority of reservoirs, although built for irrigation and water supply purposes, are also used as regulation tools during floods in river basins. Thus, the selection of the most suitable model when facing the simulation of a flood wave in a combination of river reach and reservoir is not direct and frequently some analysis of the proper system of equations and the number of solved flow velocity components is needed. In this work, a stretch of the Ebro River (Spain), which is the biggest river in Spain, is simulated solving the Shallow Water Equations (SWE). The simulation model covers the area of river between the city of Zaragoza and the Mequinenza dam. The domain encompasses 721.92 km with 221 km of river bed, of which the last 75 km belong to the Mequinenza reservoir. The results obtained from a one-dimensional (1D) model are validated comparing with those provided by a two-dimensional (2D) model based on the same numerical scheme and with measurements. The 1D modelling loses the detail of the floodplain, but nevertheless the computational consumption is much lower compared to the 2D model with a permissible loss of accuracy. Additionally, the particular nature of this reservoir might turn the 1D model into a more suitable option. An alternative technique is applied in order to model the reservoir globally by means of a volume balance (0D) model, coupled to the 1D model of the river (1D-0D model). The results obtained are similar to those provided by the full 1D model with an improvement on computational time. Finally, an automatic regulation is implemented by means of a Proportional-Integral-Derivative (PID) algorithm and tested in both the full 1D model and the 1D-0D model. The results show that the coupled model behaves correctly even when controlled by the automatic algorithm.
1. Introduction
As extreme phenomena, flood events raise concern among governments, institutions and general society. The European Union has been developing plans and directives during the last decades focusing on the control of their impact [1]. River overflows cause the flooding of adjacent lands, urbanised areas and other infrastructures. Additionally, floods can also take human lives, as reported by the UN [2], specially in areas with poor prevention plans and a lack of predictive tools. Frequently, dams and reservoirs are present in river basins as hydraulic elements with different functions. Not only to ensure enough water supply for agricultural activities or energy production, but also as hydraulic structures for discharge adjustment and control during flood events. Basin authorities manage their operation focusing on available space in the reservoir, maximum acceptable downstream discharges, and peak arrival times.
In this context, the development of predictive tools that provide information about the temporal and spatial evolution of water level and discharge along a river during flood events can help to quantify the damage caused and has been widely addressed in last decades [3]. Some works are focused on urban areas coupling their overland models with sewer systems [4,5]. Some others are more oriented to large scale floods quantifying inundated areas in crops and surrounding fields [6,7], including components such as weirs, gates, dams and reservoirs [8,9]. Nowadays, there are even operational tools developed to simulate extremely large domains using massive parallel algorithms [10]. In either case, all models are then used to generate information and data for other models and tools that analyse and classify flood-prone areas [11,12]. Fast and efficient numerical models for the resolution of the equations that govern free surface flows in rivers have been developed and improved in recent years [6,7,10,13,14,15,16,17]. However, including a reservoir in the numerical model of the river reach is an additional difficulty. Even today, it is widely accepted that three dimensional models (3D) are computationally expensive and the phenomenon of a flood in a river at a large scale can be addressed by averaging the equations vertically (2D approximation) [6,7]. However, flood event simulations often involve large domains and long time scales, and practical applications require a compromise between spatial resolution and computational efficiency [18,19]. To achieve the necessary spatial resolution, in many cases quite fine computational grids are needed, so more data storage is required, proportionally increasing the number of operations and reducing the size of the time step allowed for explicit calculations. Therefore, flood risk evaluations are often performed considering the average in the cross section to reduce the phenomenon to a 1D approximation [13]. Finally, depending on terrain morphology, some particular river reaches might transport hydrographs almost immediately, as reservoirs.
On the other hand, reservoirs can be assessed with different approximations depending on the variables of interest. Reservoirs can be solved either as part of the river reach; this is, discretised. Alternatively, they can be considered as a storage volume with a constant level [20,21]. When the detailed phenomena that might occur within a reservoir are of interest, complex numerical models are developed. In [22], a 3D model based on the Reynolds-Averaged Navier-Stokes equations is used to study secondary currents and three dimensional behaviour of the velocity field. When the details of the 3D velocity field are not required but the longitudinal profile of the water surface is of interest, they can be incorporated as part of 1D discretised models [23]. Additionally, when some other additional phenomena must be simulated, such as eutrophization [24] or sediment transport [25], also a spatial discretisation of the reservoir is needed, whether in one or three dimensions. An alternative is an aggregated reservoir routing where only a volume balance is considered [26,27,28]. This may include runoffs, evaporation and some other mass exchanges. In any case, each reservoir must be specifically analysed. Aggregated models may be suitable, due to the representation of the reservoir as a unique volume, providing CPU times in the order of seconds [28], and a discretised model must compute as many operations as grid elements, leading to higher computational times [22]. However, the main disadvantage of these simplified approaches is that they do not represent in detail the flow behaviour of the river and floodplains [29,30,31].
Concerning optimization of the reservoir as a hydraulic structure, several works have focused on their hydropower potential. In [32], for instance, a linear optimization model with three different objective functions was implemented to automatically manage the reservoir in order to maximize total energy.
The aim of the present work is to couple recent research tools based on shallow water numerical models for flood forecasting with an aggregated model for the reservoir, developing a complete efficient simulation tool during flood events.
First, a comparison of the results obtained with a 2D and a 1D model in the middle reach of the Ebro river is carried out for validation purposes. Both, the 2D and the 1D model, are based on a finite volume scheme, which uses terrain data for the 2D mesh and 1D bathymetry creation. The 1D modelling is likely to lose the detail of the floodplain, but nevertheless the computational cost is expected much lower compared to the 2D model. Additionally, the particular nature of this reservoir, which is highly channelised, might turn the 1D discretisation into a more suitable option than the 2D discretisation. Therefore, the quality of the 1D results should be checked and the calculation times of both models should be compared.
Due to the particularity of the simulated section and the Mequinenza reservoir, which transports flood waves almost immediately, an aggregated alternative technique is applied. This approach formulates the reservoir flow globally by means of a volume balance model. Our focus is on checking if the results obtained are similar to those provided by the fully 1D model and comparing the computation times of both simulations. This later option is completed with a PID algorithm for regulation purposes.
2. Study Area
The Ebro River basin is one of the largest drainage areas in the Iberian Peninsula, as seen in Figure 1a,b, where the Ebro River represents the biggest river in Spain. In this work, a stretch of this Ebro River is simulated solving the Shallow Water Equations (SWE). The simulation model, delimited in dashed line in Figure 1c, covers the area between the city of Zaragoza and the Mequinenza dam, encompassing 721.92 km. Between the inlet and outlet locations, there are 221 km of river bed of which the last 75 km belong to the Mequinenza reservoir, where the dynamics of the river changes to be nearly at rest. During the entire stretch, the river descends from 208 m.a.s.l. of the elevation in Zaragoza up to approximately 60 m.a.s.l. at the bottom of the riverbed in the Mequinenza dam, leaving an average slope of 6 per 10,000.
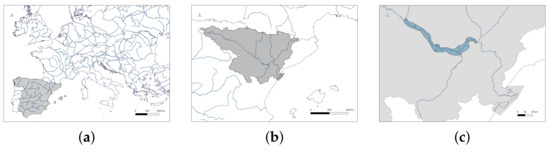
Figure 1.
Location of Spain in Europe (a); location of the Ebro River basin in Spain (b) and location of the computational domain of the study in the basin (c).
The Ebro river is managed by the Ebro River Authority (CHE, www.chebro.es), which controls, rules and prepares the reports of the basin (http://www.chebro.es/contenido.visualizar.do?idContenido=14093&idMenu=3048; accessed on 20 October 2021). CHE monitors the evolution of the flow discharge and water levels at a few control stations along the river course storing data every 15 min. Figure 2 represents the Ebro River reach simulated in this work. In the figure, the most important cities and the CHE gauging stations available for data comparison are marked. The represented domain coincides with the 2D domain used for simulations. The gauging stations in this reach are located in Pina, Villafranca and Gelsa. Additionally, a point of estimation exist near the Mequinenza dam. Each of these stations has an official label that can be seen in the same figure. This region is of special interest due to its agricultural activity, and frequently suffers flooding with important damages. It is a river reach where two different parts can be identified: the first part of the region is characterised by marked meanders and large flooding areas; the second part, around 75 km of the reach, is dominated by the large Mequinenza reservoir provided with vertical walls. The dynamics of the river changes in the reservoir: its velocity is reduced until water is practically at rest and flood waves are transported almost instantly.
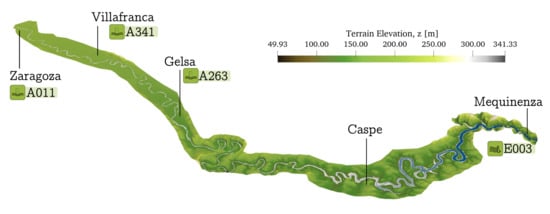
Figure 2.
Representation of the 2D simulation domain of the Ebro River with the most important cities and gauging stations of CHE. The labels correspond to the official names of the gauging stations.
The Mequinenza reservoir, the largest in the entire region, covers a surface area of about 7540 hectares, with a maximum capacity of 1530 hm at a maximum normal surface level of 121 m.a.s.l. The reservoir is exploited for hydroelectric production and irrigation to nearby agricultural areas. At the same time, with its 124 m crest above sea level and its 6 gates, the dam is used to regulate the water storage in order to dump peak discharge during floods and to guarantee hydroelectric generation. At the reservoir, there is only a measurement point for water level that is transformed by CHE into a discharge value through volume estimations. CHE uses two different approaches for discharge estimation, so that the results in the Mequinenza reservoir are compared not with observed but with 2 different estimated data.
Two historical events of the Ebro River, the 2015 and the 2018 floods, have been identified as relevant. Information concerning discharge hydrographs as well as time evolution of the water surface level are available at the gauging stations. Additionally, the European Emergency System (EMS) provides data of flooded area extensions, as seen in Figure 3 (https://emergency.copernicus.eu/; accessed on 20 October 2021). This helped to choose the domain extension setting the boundaries far enough not to interfere the flow.
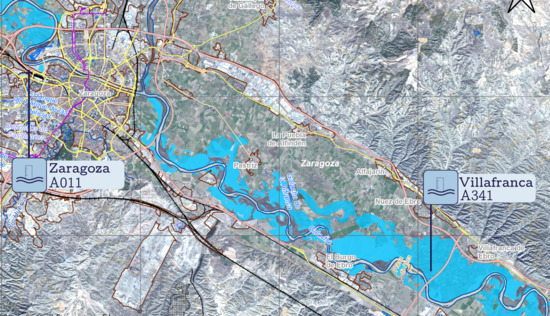
Figure 3.
Zoom view of an ortophoto with measured extension of the flooded area (blue) in 2018 flood event.
3. Methodology
Derived from the Navier-Stokes equations by depth averaging and assuming hydrostatic pressure, the Shallow Water Equations (SWE) can be considered to govern the free surface flow of a river.
3.1. Two Dimensional (2D) Model
The 2D model can be compactly formulated as
with:
in terms of the water depth, h, the depth averaged unit discharges and in the x and y directions respectively. The slopes and are the two components of the bottom surface gradient :
and and represent friction slopes, that are here formulated as:
where n stands for the semiempirical Manning friction coefficient ([33]).
3.2. One Dimensional (1D) Model
When the equations are averaged over the cross sectional area of the flow, a 1D model is obtained, representing changes along the longitudinal direction of the river. The obtained system is analogous to the 2D system, with a mass conservation equation and a linear momentum equation along the river channel:
with:
where Q stands for transversal discharge, A is the cross section wetted area and , are hydrostatic pressure integrals. is the bottom slope along the longitudinal coordinate of the channel:
and is the friction slope, that is also formulated through the Manning law as:
where R is the hydraulic radius, defined as , being A the wetted area and P the wetted perimeter. Finally, the Manning friction coefficient is obtained empirically ([33]).
3.3. Finite Volume Model for the 1D Flow Equations
In this work, an explicit upwind first order finite volume method is used for both systems of equations ([34,35,36]). The systems of Equations (1) and (6), can be generally expressed as:
where in the 2D model, and are given by (2) and (3). Moreover, in the 1D model, with given by (7). When integrating (10) into a control volume or cell, and applying the divergence theorem, the following expression is obtained:
where is the outward unit vector in the normal direction to the volume . From this, the 1D approach is next developed and details for the 2D approach can be found in [7,37]
Due to the hyperbolic character of the 1D equations, the numerical scheme used to solve them is based on the Jacobian matrix of the fluxes:
whose eigenvalues are:
with u and c given by:
being A the cross section and B the free surface width. The celerity c characterizes the speed of the infinitesimal surface deformation waves defining the dimensionless Froude number .
Following [16,35,38], the final updating scheme for a cell i of the domain in the time takes into account the contributions of neighbour cells containing fluxes and source terms as:
being and , respectively, the eigenvalues and eigenvectors of the Jacobian matrix of the flux, , linearised on the cell edge. Additionally, stands for the cell size. The upwind scheme sends the information to the wave propagation direction through the eigenvalues and their sign:
This scheme for the ordinary computational cells must be complemented with proper initial and boundary conditions. The numerical scheme is stabilised by dynamically limiting the time step size, , with the CFL condition:
where [39].
3.4. Reservoir Model
In the context of the 1D shallow water model, the reservoir can be modelled with two different approaches. In both cases, sketched in Figure 4, the upstream river reach is discretised with a 1D finite volume method. However, the two approaches differ in reservoir representation:
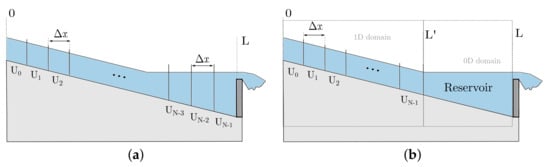
Figure 4.
Representation of the two different approaches for reservoir representation: 1D distributed discretisation as the rest of the domain (a); or coupling the 1D model of the river with an aggregated 0D model of the reservoir (b).
As depicted in Figure 4, the aim of approach (b) is to remove the computational cells needed for the reservoir. Using the sketch as an example, while the fully 1D distributed model encompasses from x = 0 to x = L, the coupled 1D-0D model has a discretised domain only from x = 0 to x = , so that the computational cost is reduced.
In near-rest flows, such as those in a reservoir, the velocity field is negligible so that it is likely that the flow behaviour is properly solved only with volume balance. This represents a 0D approximation. The Modified Puls Method [21] is based on the hypotheses that the flow surface is always horizontal, the stored volume in the reservoir can be formulated as a function of water level () and the outlet discharge can also be expressed as a water level function (). Thus, the volume variation is given by the difference between the reservoir inlet, , and outlet, , as:
When combining this formulation with the 1D model to lead to the 1D-0D model, the water level calculated with expression (19) is set at (Figure 4b). It is important to note, that the resolution of (18) requires knowing and the relation between and volume V at the reservoir. The inflow discharge to the reservoir is directly given by the computation at the last cell of the 1D model. On the other hand, the reservoir outflow discharge depends on the geometry and characteristics of the dam. In the present work the downstream boundary condition, either for pure 1D or for 1D-0D model, is based on a weir/dam law of the form [40]:
where is the water depth above the weir crest. Assuming a trapezoid shape, b is the width of the minor length of the horizontal sides of the weir and the opening angle of the trapezoid. Finally, C is an energy loss coefficient here taken as [9,26].
It is important to note that for both approaches, the full 1D model and the 1D-0D model, the 1D river reach upstream the reservoir must be identically discretised, this is, using the same , so that the analysis can show the differences provoked by the reservoir model.
3.5. PID Regulation
The Mequinenza dam gates can be manually operated at present according to energy, agricultural or safety criteria. In this work, a control Proportional-Integral-Differential (PID) algorithm is implemented to show the possibility to dynamically include in the simulation model the control of the gate opening during a flood. In particular, a specific maximum reservoir surface level is set as target in the automatic algorithm so that the gate opening must change under discharge variations during the flood event.
The PID controller computes the error between the predicted value of the variable water surface level and the stated reference value, and uses it to compute a change on the free parameter, gate opening, using an algorithm based on:
- Proportional term: Expresses a proportionality between the required action and the error.
- Integral term: The required action takes into account the time integral of the error over a given period.
- Derivative term: The controller actuation is formulated from the time derivative of the error.
The equation that describes those PID terms is:
where is the control error (), is the reference value (or setpoint) of water level and is the current water level at time t. K is the proportional coefficient, and are integration and derivative times, respectively.
Equation (21) is discretised as:
where , and , being n the current time step. Parameters , and are the weights given to each of the time steps that are included on the controller operation. Parameter T stands for the sampling period for the input data to the algorithm.
The values for K, , and directly affect the evolution and, thus, have an effect on the speed at which the controlled variable (i.e. water level) reaches the setpoint. Therefore, proper determination of those parameters is essential to optimize and stabilize the algorithm. Otherwise, the controller could lead to extreme gate opening values hence destabilizing the system.
4. Model Application
4.1. Discretisation of the Domain
The Ebro River reach has been first simulated to validate the 1D model comparing with results obtained with the 2D model [7] applied to the same stretch. In both cases the discretisation of the reservoir is included within the computational grid. The aim is to evaluate if the 1D approach provides reliable results improving the efficiency of the 2D model. Once the 1D model is demonstrated to be reliable enough, the coupled 1D-0D model and the control algorithm are evaluated.
The domain discretisation is different depending on the numerical scheme. In the 2D model, the mesh is an unstructured triangulation of the (x, y) domain with piecewise uniform values of terrain elevation and roughness. The triangles can be of variable size and adapt to the terrain topography. The mesh used was generated from a DTM in RASTER format and included 949,445 triangular elements. In the 1D model, the domain is discretised into a set of cells separated by cross sections along the riverbed evenly spaced at a distance .
The 1D mesh was generated from topographic information of the field compound by 433 cross sections. Among them, 100 sections are within the reservoir region (as in example in Figure 5). The lateral span of the sections must capture the shape of the river bed to avoid losing information relevant to the evolution of the variables but avoiding overlapping. It is of vital importance that the sections are always normal to the river in curved regions, as seen in Figure 5. Finally, a 1D mesh of 2000 cells is obtained. Additionally, a uniform roughness coefficient n = 0.032 is chosen ([33]). A steady flow with a discharge value that matches the value at the initial time of the inlet hydrograph is set as initial condition. The upstream boundary condition is a hydrograph, while the downstream boundary condition is a spillway condition, which represents the presence of the Mequinenza dam.
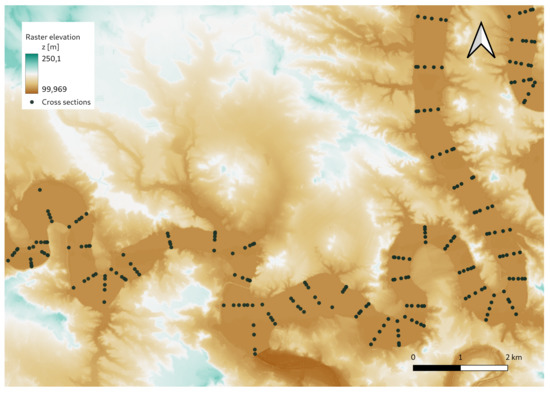
Figure 5.
Top view of several sections over the raster with different river meanders.
4.2. Performance Analysis of the 1D and 2D Models
Two historical events of the Ebro River, the 2015 and the 2018 floods, have been simulated with both the 1D and the 2D models. The 2015 inlet hydrograph, obtained from the Zaragoza gauging station (see Figure 2), is set in Zaragoza as inlet boundary condition and can be seen in Figure 6. The comparison between results obtained with both simulation models and real observation data for this event can be seen in Figure 7 and Figure 8. They show, respectively, the time evolution of discharge and water level at Gelsa (A263) station and Mequinenza dam (E003). It is important to note that the data provided by the CHE gauging station are for water depth (h) and not for water level (), and the actual bed elevation of the station is unknown.
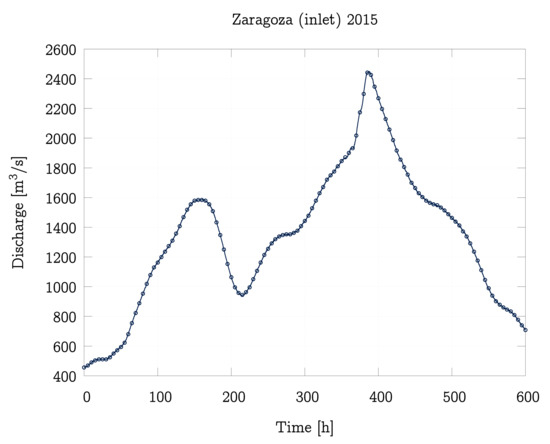
Figure 6.
Inlet hydrograph for the Ebro River flood event in 2015 in Zaragoza (A011).
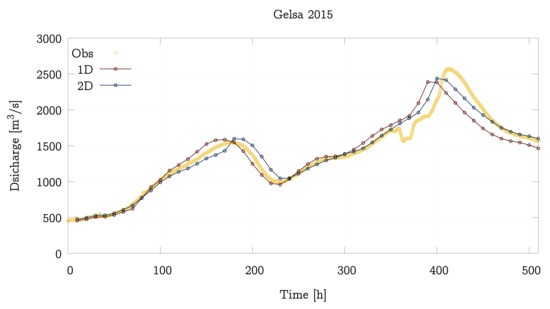
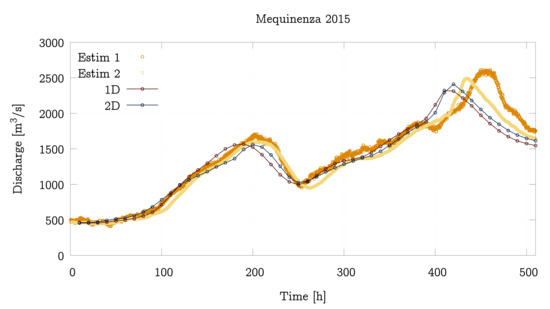
Figure 7.
Discharge temporal evolution comparison between 1D model, 2D model and observation at Gelsa (A263) gauging station (upper) and comparison between models and estimations at Mequinenza dam (E003) (lower) for 2015 event.
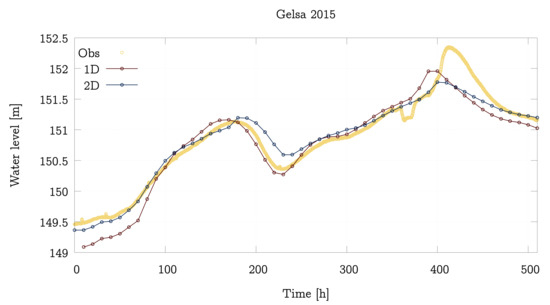
Figure 8.
Water level temporal evolution comparison between 1D model, 2D model and observation data at Gelsa (A263) gauging station for the 2015 event.
It can be seen in Figure 7 and Figure 8 that the 1D and 2D simulations produce remarkably similar data which follow the tendency of the actual data. However, neither of the two models is able to reproduce the detail of the curves at h. This is possibly due to a dynamic change in the terrain such as a levee breach not included in the static terrain representation of the models owing to the lack of available information. It should be noted that, in the first 250 h, it is the 1D model which offers data closer to the reality. This suggests that the flow was more channeled in this period of time and the overflow is estimated by the 2D model too early. From h it is the 2D model which provides a behaviour closer to the real one, possibly due to the fact that, near the peak flow, the floodplains are inundated.
Figure 9 shows the 2018 inlet hydrograph used as upstream boundary condition. Figure 10 displays the discharge time evolution as computed with the 1D and the 2D models together with the observation at Gelsa (A263) gauging station (upper) and Mequinenza dam (E003) (lower) for this event. The time evolution of the surface water level at Villafranca gauging station (the only measured variable) is displayed in Figure 11. The evolution of the water levels predicted by the two models is again quite similar to that of the real data until approximately h. Around this time, the measured data suffer a slight decrease not predicted by the 2D model.
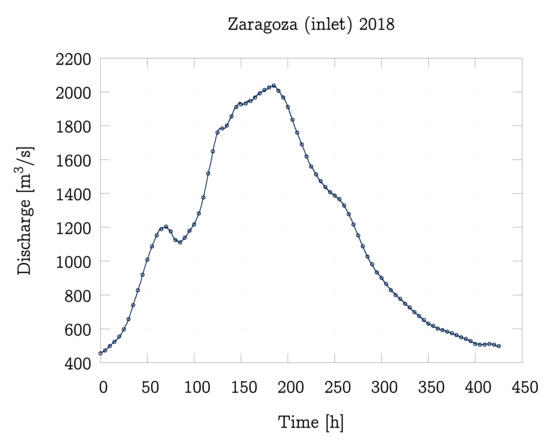
Figure 9.
Inlet hydrographs for the Ebro River flood event in 2018 in Zaragoza (A011).
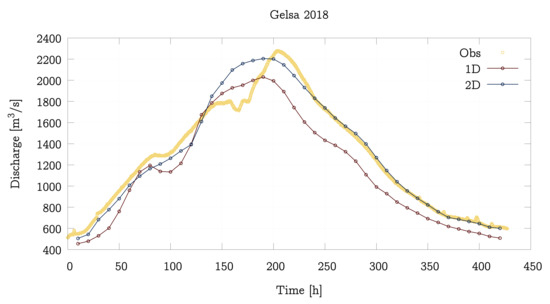
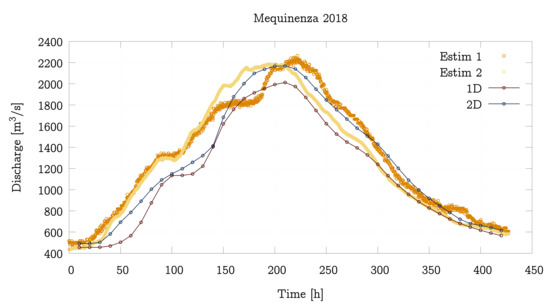
Figure 10.
Discharge temporal evolution comparison between the 1D model, the 2D model and the observation at Gelsa (A263) gauging station (upper) and comparison between models and estimations in Mequinenza dam (E003) (lower) for the 2018 event.
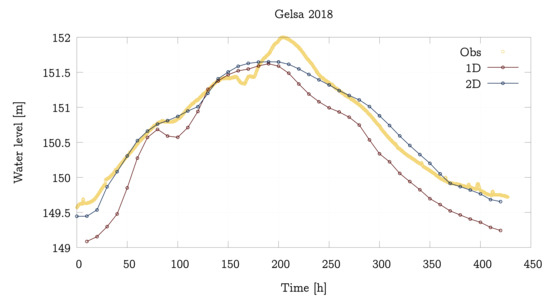
Figure 11.
Water level temporal evolution comparison between the 1D model, the 2D model and the observation in Gelsa (A263) gauging station for the 2018 event.
Regarding computational times, for the 2015 case the 1D model required 511 s to compute the full event, while the 2D model took 47 h, as seen in Table 1. These computations were performed with High Performance Computing (HPC) techniques for the 2D model. In particular, a NVIDIA GeForce GTX 1080 Ti GPU was used to compute the 2D cases, while a simple paralellization into 8 Intel Xeon X5650 CPU’s was necessary for the 1D computations. For the 2018 event, which is a bit shorter, the computational time required by the 1D model was 364 s, while that of the 2D model was 23.8 h.

Table 1.
Comparison of computational times for the two flood events simulated in the Ebro River.
4.3. Performance Analysis of the 1D and 1D-0D Models
The comparison between the full 1D model and the 1D-0D model is next carried out for the 2015 flood event. The discretisation of the full 1D model is the same used in the former subsection, while the 1D-0D model is characterised by a partial discretisation of the domain embedding the reservoir zone within the outlet boundary condition. In this last case, only the first 352 sections and 1511 mesh cells are necessary for the discretised part. This is, following Figure 4, for the river reach from x = 0 to x = L’.
Figure 12 represents the river profile for different times of both the full 1D model (fine and dark lines) and the 1D-0D model (wider and light lines). Bottom elevation, , as well as water level, , profiles are represented for both models. The initial condition can be seen at the upper picture of the figure, with a low water depth profile upstream the reservoir area, where the level remains uniform and the water depth increases. The middle picture corresponds to h, when the discharge is increasing and a higher water depth can be seen. The lower picture coincides with the discharge peak of the inlet hydrograph (see Figure 6), reaching the highest value of water level. In the three cases, the level reached by the last cell of the 1D-0D model is almost the same as the value of the full 1D model, which discretises the whole reservoir. Therefore, it can be said that embedding the reservoir in the outlet boundary condition provides very similar results to those of a full model, without the necessity of such amount of computational cells.
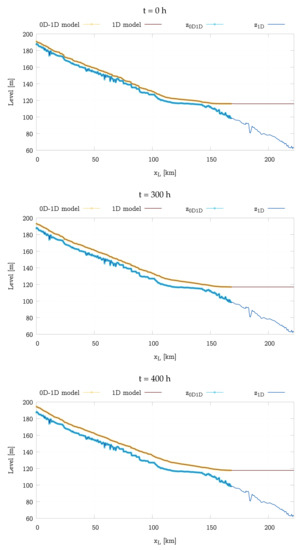
Figure 12.
Longitudinal profile of bottom level, z, and water surface elevation (WSE) at different times computed with the 1D model and the coupled 1D-0D model for the 2015 case.
As illustrated in Figure 12, the section located at x is not exactly the beginning of the reservoir, as the length of the reservoir varies throughout the simulation depending on the level of the water surface. For that reason, this section is chosen displaced forward ensuring that it always belongs to the reservoir. Thus, for high level values, there is part of the reservoir being discretised and also simulated by the 1D numerical scheme.
The temporal evolution of the water level at x can be seen in Figure 13. Although there is a very good agreement, the figure shows that the level of the 1D-0D model is slightly below the value of the full model at that location (x). This is because there is not a uniform level in the entire reservoir and the 1D model represents this behaviour. However, the 0D model assumes a constant level in the reservoir that matches quite exactly the level at the end of the reservoir in the 1D model (x). In addition, the lag previously obtained by the model 1D-0D is no longer present. The reservoir surface area function, , corresponds to the entire reservoir. However, as part of the reservoir is being discretised by the 1D model, the boundary condition of the 1D-0D model causes a slower evolution of the level, as it is considering that there is a larger modeled reservoir than there should be and, therefore, it overestimates the value of .
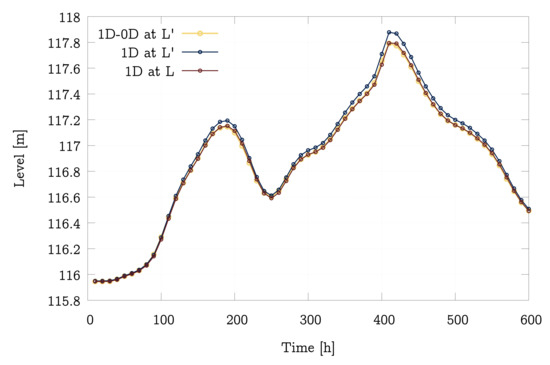
Figure 13.
Comparison of computed water surface elevation (WSE) at x=L’ using 1D model and 1D-0D model and computed WSE at x=L using 1D model.
The computational times of these simulations can be seen in Table 2. It can be seen how the 1D-0D model allows for considerable time reduction due to the due to the absence of the cells representing the reservoir. These results show that the coupled model results accurate enough to predict water levels along the river providing a performance improvement.

Table 2.
Computational times for 2015 flood event simulated in the Ebro River with the 1D-0D model and the pure 1D model.
4.4. Performance Analysis of the 1D and 1D-0D Models Including DAM Regulation
Once the coupled 1D-0D model has been proved to perform properly, a dam regulation algorithm is implemented in both the coupled and the full 1D model. This is, both models include in their outlet boundary condition a PID algorithm that updates the dam crest, , to approach or to maintain a reference water level or setpoint, regardless of the inlet discharge.
For that purpose, both models have been discretised exactly as in the preceding section. The parameters used in the PID controller must be first calculated and validated. In this work, the chosen values are , s, s, s, , and . Those values were obtained following [41]. The dam movement is limited by m per time interval and the water surface level is limited by a maximum and minimum value of 115 m and 105 m respectively. The target water surface level is m. The comparison is done at x (see Figure 4).
It is worth mentioning that variations of dam crest, , are a practical representation of variations in cross section area of spillways. In reality, dams can not change their crest, but the gate opening of their structure. However, the discharge law implemented would be the same and the dam crest results in a very representative parameter of the dam opening.
The Figure 14 shows the temporal variation of water level at x for both models. Besides that, the figure also represents the time evolution of the dam crest throughout the simulation. At the same time, Figure 15 depicts, also for both models, the temporal evolution of outlet discharge. It worth mentioning that this discharge is the flow rate passing through the dam.
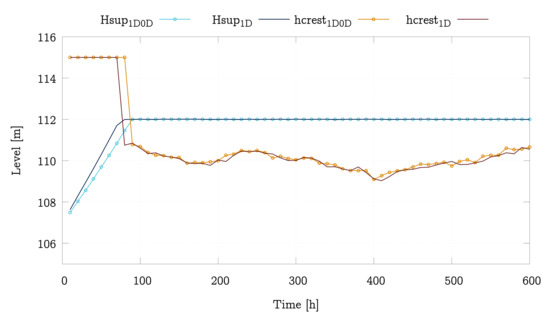
Figure 14.
Temporal evolution of the water level and dam crest computed with the fully 1D model and the coupled 1D-0D model for the 2015 case with the control of a PID algorithm.
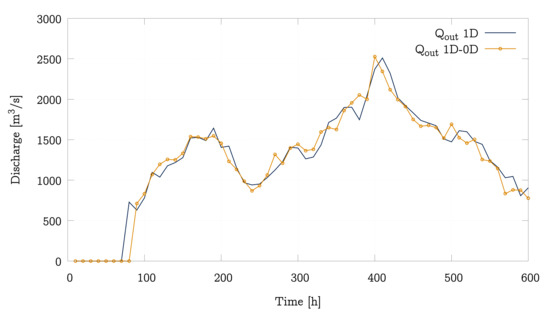
Figure 15.
Temporal evolution of the outlet discharge at Mequinenza dam (E003) computed with the 1D model and the coupled 1D-0D model for the 2015 case with the control of a PID algorithm.
Figure 14 shows that, at the beginning of the simulation, the level of the reservoir is much lower than the setpoint ( m), so the dam crest is at its maximum height preventing the water leaking (see Figure 15) and provoking an increase of water level. Once the reference is reached, the dam crest varies to maintain a constant water level while the inlet flow rate changes. At that time, the outflow hydrograph tends to resemble the inflow rate.
The time evolution of displayed in Figure 14 is rather similar for both models, reaching the target value in a short time. It is worth noting that the 1D model reaches the objective earlier than the 1D-0D model. This is provoked by the lower level obtained with the 1D-0D model at x=L’ (see Figure 4) in comparison with that computed with the 1D model. This causes a delay in the reservoir filling up to the setpoint.
The computational times for the model with the PID algorithm are shown in Table 3. The same trend found for the comparison between the different approaches for the reservoir modellization results into an improvement of the optimization when using the 1D-0D model. Besides that, the PID algorithm does not penalize the computational time, but it makes the model more efficient.

Table 3.
Computational times for 2015 flood event simulated in the Ebro River with the 1D-0D model and the pure 1D model, both with the dam regulated with a PID algorithm.
5. Conclusions
In this work, the performance of several modelling approaches has been compared in order to evaluate their results and computational requirements in a transient river flow event in a reach of the Ebro river (Spain) that includes a reservoir covering a large area. A 2D distributed shallow water model solved over a triangular grid and a 1D shallow water model have been used to discretise the full domain. Additionally, an aggregated volume balance model has been implemented to model the reservoir region in order to allow computational saving. This has led to a coupled 1D-0D model. Finally, a PID control algorithm has been implemented as a regulation technique at the dam location and has been combined with both the 1D model and the 1D-0D model.
From the comparison of the performance of the 2D and 1D models, it can be be concluded that the results of the 1D model for the recent flooding events at the considered Ebro River reach are very similar to those provided by the 2D model. The water level and discharge data predicted by both models follow the same trend. The cross sections used to build the 1D model computational mesh were carefully located to reproduce the river curvature in detail, which is important to obtain a realistic evolution of the hydraulic variables. This effort is justified by the immense computational saving that the use of the 1D model offers, as long as there is no interest in representing the floodplain flow, that the 1D model does not take into account.
The coupling of the 1D model for the river flow at the upstream reach and the 0D model for the reservoir (1D-0D model) offers results very similar to those from the full 1D model. There is some lag due to the instantaneous propagation of the hydrograph in the reservoir assumed by the 0D model but this is acceptable considering the computational savings that the use of this model implies compared to the full 1D model. The computational times observed with the 1D-0D model justifies the use of this combined approach. Therefore, the coupling of a 0D model for the reservoir with the 2D model for the upstream river reach is envisaged as future work since this will lead to high computational savings, something very positive for simulations with 2D models as well as the possibility to simulate the floodplain flow behaviour.
The PID control algorithm has been implemented with the objective to ensure a fixed surface water level at the dam. The results show that this target level value is never reached despite the time variable discharge, which means that the implementation of the control algorithm is a correct security measure to avoid exceeding certain levels in the reservoir. It will be convenient in the future to implement an algorithm that takes into account more realistic and complex objectives.
Author Contributions
Conceptualization, P.G.-N. and I.E.; methodology, P.G.-N. and I.E.; software, I.E.; 2D simulations J.M.; 1D model validation, P.V., I.E. and P.G.-N.; formal analysis, I.E., P.G.-N.; writing original draft preparation, P.V.; writing review and editing, I.E., P.G.-N.; visualization, P.V.; supervision, P.G.-N.; project administration, P.G.-N.; funding acquisition, P.G.-N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the PGC2018-094341-B-I00 research project of the Ministry of Science and Innovation/FEDER. The authors would like to thank also the Confederación Hidrográfica del Ebro staff for their availability and for the supply of the data. Additionally, Isabel Echeverribar was wants to thank to the MINECO for his Research Grant DIN2018-010036.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
River measurements are available at http://www.saihebro.com/saihebro/index.php?url=/datos/mapas/tipoestacion:A; accessed on 20 October 2021.
Acknowledgments
The authors acknowledge the CHE for the data availability and their support. The authors also would like to thank all collaborators for their help performing the 2D simulations: Pilar Brufau and Mario Morales.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- C.o.t.E.U. European Parliament 2007 Directive 2007/60/EC of the European Parliament and of the Council of 23 October 2007 on the Assessment and Management of Flood Risks. EU Directive. 2007. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex:32007L0060 (accessed on 10 October 2021).
- Centre for Research on the Epidemiology of Disasters (CRED). The human cost of weather related disasters (1995–2015); CRED: Brussels, Belgium, 2015; pp. 1–30. [Google Scholar]
- Tanoue, M.; Taguchi, R.; Alifu, H.; Hirabayashi, Y. Residual flood damage under intensive adaptation. Nat. Clim. Chang. 2021, 11, 823–826. [Google Scholar] [CrossRef]
- Leandro, J.; Schumann, A.; Pfister, A. A step towards considering the spatial heterogeneity of urban key features in urban hydrology flood modelling. J. Hydrol. 2016, 535, 356–365. [Google Scholar] [CrossRef]
- GebreEgziabher, M.; Demissie, Y. Modeling Urban Flood Inundation and Recession Impacted by Manholes. Water 2020, 12, 1160. [Google Scholar] [CrossRef]
- Vacondio, R.; Aureli, F.; Ferrari, A.; Mignosa, P.; Palù, A. Simulation of the January 2014 flood on the Secchia River using a fast and high-resolution 2D parallel shallow-water numerical scheme. Nat. Hazards 2016, 80, 1–23. [Google Scholar] [CrossRef]
- Echeverribar, I.; Morales-Hernández, M.; Brufau, P.; García-Navarro, P. 2D numerical simulation of unsteady flows for large scale floods prediction in real time. Adv. Water Resour. 2019, 134, 103444. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Murillo, J.; García-Navarro, P. The formulation of internal boundary conditions in unsteady 2-D shallow water flows: Application to flood regulation. Water Resour. Res. 2013, 49, 471–487. [Google Scholar] [CrossRef]
- Echeverribar, I.; Morales-Hernández, M.; Brufau, P.; García-Navarro, P. Use of internal boundary conditions for levees representation: Application to river flood management. Environ. Fluid Mech. 2019, 19, 1253–1271. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Sharif, M.B.; Kalyanapu, A.; Ghafoor, S.K.; Dullo, T.T.; Gangrade, S.; Kao, S.-C.; Norman, M.R.; Evans, K.J. TRITON: A Multi-GPU open source 2D hydrodynamic flood model. Environ. Model. Softw. 2021, 141, 105034. [Google Scholar] [CrossRef]
- Chen, J.; Hill, A.A.; Urbano, L.D. A GIS-based model for urban flood inundation. J. Hydrol. 2009, 373, 184–192. [Google Scholar] [CrossRef]
- Ghansah, B.; Nyamekye, C.; Owusu, S.; Agyapong, E. Mapping flood prone and Hazards Areas in rural landscape using landsat images and random forest classification: Case study of Nasia watershed in Ghana. Civil Environ. Eng. 2021, 8, 1923384. [Google Scholar]
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 89–99. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P.; Burguete, J.; Brufau, P. The influence of source terms on stability, accuracy and conservation in two-dimensional shallow flow simulation using triangular finite volumes. Int. J. Numer. Methods Fluids 2007, 54, 543–590. [Google Scholar] [CrossRef]
- Kalyanapu, A.J.; Shankar, S.; Pardyjak, E.R.; Judi, D.R.; Burian, S.J. Assessment of GPU computational enhancement to a 2D flood model. Environ. Model. Softw. 2011, 26, 1009–1016. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P. Energy balance numerical schemes for shallow water equations with discontinuous topography. J. Comput. Phys. 2013, 236, 119–142. [Google Scholar] [CrossRef]
- Sampson, C.C.; Smith, A.M.; Bates, P.D.; Neal1, J.C.; Alfieri, L.; Freer, J.E. A high-resolution global flood hazard model. Water Resour. Res. 2015, 51, 7358–7381. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; García-Navarro, P.; Murillo, J. Influence of mesh structure on 2D full shallow water equations and SCS curve number simulation of rainfall/runoff events. J. Hydrol. 2012, 448, 39–59. [Google Scholar] [CrossRef]
- Bomers, A.; Schielen, R.M.J.; Hulscher, S.J.M.H. The influence of grid shape and grid size on hydraulic river modelling performance. Environ. Fluid Mech. 2019, 19, 1273–1294. [Google Scholar] [CrossRef]
- Fread, D.; Hsu, K. Applicability of Two Simplified Flood Routing Methods: Level-Pool and Muskingum-Cunge. In Proceedings of the ASCE National Hydraulic Engineering Conference, San Francisco, CA, USA, 25–30 July 1993; pp. 1564–1568. [Google Scholar]
- Nanía, L.S.; Gómez, M. Ingeniería Hidrológica; Grupo Editorial Universitario: Granada, Spain, 2004. [Google Scholar]
- Haun, S.; Olsen, N.R.B. Three-dimensional numerical modelling of reservoir flushing in a prototype scale. Int. J. River Basin Manag. 2012, 10, 341–349. [Google Scholar] [CrossRef]
- Mohammad, M.E.; Al-Ansari, N.; Issa, I.E.; Knutsson, S. Sediment in Mosul Dam reservoir using the HEC-RAS model. Lakes Reserv. Res. Manag. 2016, 21, 235–244. [Google Scholar] [CrossRef]
- Kawara, O.; Yura, E.; Fujii, S.; Matsumoto, T. A study on the role of hydraulic retention time in eutrophication of the Asahi River Dam reservoir. Water Sci. Technol. 1998, 37, 245–252. [Google Scholar] [CrossRef]
- Bellos, C.; Hrissanthou, V. Numerical simulation of morphological changes in rivers and reservoirs. Comput. Math. Appl. 2003, 45, 453–467. [Google Scholar] [CrossRef][Green Version]
- Henderson, F.M. Open channel flow. In Macmillan Series in Civil Engineering; McGraw-Hill: New York, NY, USA, 1966. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Fiorentini, M.; Orlandini, S. Robust numerical solution of the reservoir routing equation. Adv.Water Resour. 2013, 59, 123–132. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, W.; Wang, X. Development of a SWAT extension module to simulate riparian wetland hydrologic processes at a watershed scale. Hydrol. Process. 2008, 22, 2901–2915. [Google Scholar] [CrossRef]
- Dorchies, D.; Thirel, G.; Jay-Allemand, M.; Chauveau, M.; Dehay, F.; Bourgin, P.-Y.; Perrinb, C.; Joste, C.; Rizzolie, J.L.; Demerliac, S.; et al. Climate change impacts on multi-objective reservoir management: Case study on the Seine River basin, France. Int. J. River Basin Manag. 2014, 12, 265–283. [Google Scholar] [CrossRef][Green Version]
- Cohen Liechti, T.; Matos, J.P.; Ferràs Segura, D.; Boillat, J.-L.; Schleiss, A.J. Hydrological modelling of the Zambezi River Basin taking into account floodplain behaviour by a modified reservoir approach. Int. J. River Basin Manag. 2014, 12, 29–41. [Google Scholar] [CrossRef]
- Ginting, B.M.; Harlan, D.; Taufik, A.; Ginting, H. Optimization of reservoir operation using linear program, case study of Riam Jerawi Reservoir, Indonesia. Int. J. River Basin Manag. 2017, 15, 187–198. [Google Scholar] [CrossRef]
- Arcement, G.; Schneider, V. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; No. 2339. U.S. Geological Survey. Water-Supply Paper. USGS Publications Warehouse; 1984. Available online: https://pubs.er.usgs.gov/publication/wsp2339 (accessed on 10 October 2021).
- Toro, E.F. The Riemann Solver of Roe. In Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Murillo, J.; García-Navarro, P. Weak solutions for partial differential equations with source terms: Application to the shallow water equations. J. Comput. Phys. 2010, 229, 4327–4368. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Petaccia, G.; Brufau, P.; García-Navarro, P. Conservative 1D–2D coupled numerical strategies applied to river flooding: The Tiber (Rome). Appl. Math. Model. 2016, 40, 2087–2105. [Google Scholar] [CrossRef]
- Lacasta, A.; Juez, C.; Murillo, J.; García-Navarro, P. An efficient solution for hazardous geophysical flows simulation using GPUs. Comput. Geosci. 2015, 78, 63–72. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; García-Navarro, P.; Burguete, J.; Brufau, P. A conservative strategy to couple 1D and 2D models for shallow water flow simulation. Comput. Fluids 2013, 81, 26–44. [Google Scholar] [CrossRef]
- Leveque, R. Numerical Methods for Conservation Laws Lectures in Mathematics; ETH Zürich; Birkhuser: Zürich, Switzerland; Basel, Switzerland, 1992. [Google Scholar]
- Sotelo, G. Hidráulica General; Limusa: Johannesburg, South Africa, 2002; Volume 1. [Google Scholar]
- Panda, R.C. Introduction to PID Controllers; IntechOpen: London, UK, 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).