Numerical Modeling of Microfluid Dynamics in Xylem Vessels of Khaya grandifoliola

Abstract

Computational fluid dynamic (CFD) can be used to quantify the internal flow variables of xylem conducting vessels. This study aims to analyze through numerical simulations the xylem water ascent of African mahogany (Khaya grandifoliola) cultivated under different irrigation regimes. We determined a geometric model, defined through the variability of the anatomical structures of the species, observing characteristics of the xylem vessels such as diameter, length, number of pits, and average surface area of the pits. Then we applied numerical simulation through an Eulerian mathematical model with the discretization of volumes via CFD. Compared to other models, we observed that numerical simulation using CFD represented the xylem microstructures in a greater level of detail, contributing to the understanding of the flow of xylem vessels and the interference of its various structures. Analyzing the micrographs, we observed the non-irrigated vessels had a higher number of pits in the secondary wall thickening when compared to the irrigated treatments. This trend influenced the variability of the radial flow of the xylem vessels, causing greater fluid movement in this region and decreasing the influence of the smooth part of the wall, resulting in a lower total resistance of these vessels.

1. Introduction

The water transport and flow characteristics of plant xylem are explored widely through botanical experimentation [1], mainly using two-dimensional mathematical models of the xylem structure [2,3]. Although these analyses help us to understand the partitioning of xylem resistance, they ignore the complex nature of these vessel structures (secondary wall thickening, membranes, and perforations) and the effects of the three-dimensionality of arrangements in conduits and water transport [4]. To better assimilate the interference of these anatomical mechanisms in the microfluidic effects of plant vascular flow, computational fluid dynamics (CFD) can be used to provide a greater level of detail of the phenomena involved, in addition to enabling the simulation of natural conditions and, close to ideal, by using a high level of detail for the physical variables through the governing equations and their flow models [5].

The anatomical structures that make up the xylem vessels play fundamental roles in the resistance of water transport in plants [6,7,8,9,10]. Chen et al. [9], using the numerical model of turbulence for shear stress transport and k–ε to simulate the annular and helical thickening of vessels, verified that the width and inclination angle of the secondary wall thickening had a significant influence on the flow resistance. Schulte et al. [6] analyzed the dynamic effect of flow in the torus region on the conifer pit membrane. They determined that the membrane represented 6% and 18% of the flow resistance for the models exposed to the sun and shade, respectively. Xu et al. [10] found that the resistance of smooth vessels was higher in relation to other structural elements of the xylem, accounting for 66.2% of the total resistance, where the approach used was based on anatomical experiments and numerical simulations.

Characterizing these micro interferences in the vessel water ascent is fundamental, as abiotic factors can influence the vessels during the growth cycle. For example, the water regime influences the formation and development of xylem tissues, phloem, and cambium cell division [11,12,13]. In addition, water deficit can reduce the diameter of the xylem vessels, maintaining their density, hydraulic conductance, and conductive area, and modify the pattern of the secondary wall thickening (number, spatial distribution, and positioning of anatomical structures), influencing the resistances involved in water transport [12,14,15]. The understanding of the xylem’s anatomical variations and its potential interference in water ascent allows researchers to increase water use efficiency, as plants with well-developed vessels that are not collapsed by embolism/cavitation positively influence the transport of water and nutrients. This knowledge enables the study of plant tolerance of climatic stresses and the application of mathematical modeling in water ascent studies [9,14,15].

This study aims to analyze through numerical simulations the water ascent in the xylem vessels of African mahogany (Khaya grandifoliola) cultivated under different irrigation regimes, to define the variability of the anatomical structures of the species.

2. Materials and Methods

2.1. Description of Plant Material and Analysis of Anatomical Samples

Khaya grandifoliola plants were collected from a commercial field in the municipality of Engenheiro Navarro, Minas Gerais, Brazil (17°25′03.5′′ S, 44°04′22.4′′ W, 700 m). The climate of the region is classified by Köppen as A_w [13]. The average annual rainfall is between 950 and 1050 mm, with four to six months of dry season. The mean temperatures in summer range from 24.1 to 25.0 °C and in winter from 21.1 to 22.0 °C [13].

The trees were planted in a 6 m × 5 m plot with spacing in July 2008. Six Khaya grandifoliola plants were randomly selected, with three grown under irrigation and three rainfed. In the irrigated regime, 10 L of water daily per plant was added until the fifth year of planting; in subsequent years, the volume was increased to 50 L per day. In the rainfed plants, the irrigation was used during transplanting to increase the survival rate of seedlings in the field. After this period, there was no water supplementation, with watering dependent on natural rainfall.

Five disc-shaped cross-sections were removed from each plant in different longitudinal locations along the stem at 0%, 25%, 50%, 75%, and 100% of the total height (Figure 1a). From these sections, specimens with dimensions of 1.5 cm (tangential section) × 2.0 cm (radial section) × 3.0 cm (cross-section) were removed [11]. Subsequently, we polished the specimens with sandpapers with a 60-, 120-, 240-, 360-, and 600-grain variation. Samples were submitted to macroscopic analysis under a 25-fold increase to characterize the average diameter of the xylem vessels using the software Image-Pro Plus (Media Cybernetics, Silver Spring, MD, USA).

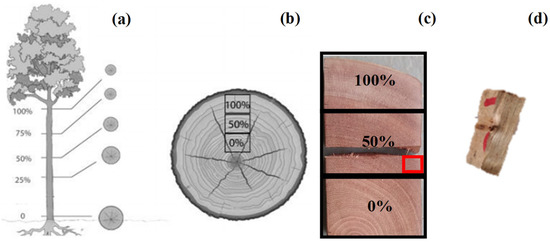
Figure 1. Representation of the sampling points of Khaya grandifoliola. (a) longitudinal positions of the stem, at 0, 25, 50, 75, and 100% of the total height; (b) radial positions of the tree transversals, in the form of disc-shaped; (c) specimen removal point; and (d) fragment used for maceration removed from the specimen. Adapted from Moraes [16].

To measure the length of the xylem vessels, type, and area of interference of the secondary wall, small fragments of the heartwood were removed from the specimens in the radial position of 50%, for maceration, based on the methodology proposed by Trevisan et al. [17] (Figure 1c,d). The samples were then washed in distilled water, stained with 50% (p/v) hydroalcoholic Safranina dye, and kept in a flask until provisional slides were prepared. For a more detailed analysis, we used a scanning electron microscope (SEM) with energy-dispersive X-ray analysis (Jeol JSM-IT300LV; JEOL USA Inc, Peabody, MA, USA) [18]. With these analyses, we determined the vessels’ length, diameter, number of interferences and surface area.

2.2. Determination of the Anatomical Model and Numerical Simulation Parameterization

Three-dimensional calculations and the numerical mesh were elaborated using the software ICEM-CFD (ANSYS Inc., Canonsburg, PA, USA). Unstructured tetrahedrons and hexahedrons were used to discretize the vessel geometry. The control volumes near the walls have been refined enough to keep them within the logarithmic boundary layer. We performed mesh independence tests to ensure that the computed results were independent of refinement. The flux depends on the steady-state conservation equations for mass and momentum in a fluid, which are provided by Equations (1) and (2).

Continuity equation:

$$\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+\frac{\partial \mathrm{v}}{\partial \mathrm{y}}+\frac{\partial \mathrm{w}}{\partial \mathrm{z}}=0,$$

(1)

Momentum equation:

$$\{\begin{array}{c}\rho \left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\right)=-\frac{\partial P}{\partial x}+\mu \left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2}\right)\\ \rho \left(u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}\right)=-\frac{\partial P}{\partial y}+\mu \left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}+\frac{{\partial }^{2}v}{\partial z^2}\right)\\ \rho \left(u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}\right)=-\frac{\partial P}{\partial z}+\mu \left(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2}+\frac{{\partial }^{2}w}{\partial z^2}\right)\end{array}$$

(2)

where u, v, and w are the velocity vector components along the x, y, and z directions, respectively, ρ is the fluid density, P is the fluid pressure, and µ is the dynamic viscosity.

In the model, the fluid domain was considered as water, with an average turbulent intensity of 5%, a temperature of 25 °C, fluid density of 997 kg m⁻³, and fluid viscosity of 0.9 10⁻³ Pa/s. The shear stress transport (SST) model was adopted to obtain a solution for the governing equations. In this model, we used k-ω for the region close to the wall, where the flow is of low velocity and flow is less, and k-ε for the rest of the fluid, where there is a greater influence from the turbulent regime [19]. The number of interactions in each simulation ranged from 50 to 1000, which generated residual errors smaller than 10⁻⁸. The computational mesh used in the study had a total of 1.08 × 10⁷ elements. The simulations were performed on one desktop with the help of a twelve-core AMD Ryzen 9 3900X processor (Advanced Micro Devices, Santa Clara, CA, USA) with 32 GB of RAM. The simulations took around 15 h to complete.

As boundary conditions, we defined zero pressure at the exit of the model and a flow velocity of 0.5 mm s⁻¹ to analyze the resistive effects of anatomical structures on the flow. Xu et al. [10] determined that an extended smooth segment of 25 µm long should be added at the inlet and outlet to avoid backflow effects [20].

To estimate the strengths of the different structures of the components of the vessels, the methodology proposed by Xu et al. [10] was used to obtain data by numerical simulation, resulting in the pressure profile (ΔP) and the average flow (q). The total resistance of the vessels was calculated from the relationship between ΔP and q.

2.3. Statistical Analysis

Data variance analyses were performed using the F distribution test (p < 0.05); the Chi-square test will be applied to assess the distribution of the anatomical characteristics of the vessels, and the Shapiro-Wilk normality test for the frequency of values. The anatomical characteristics of the factorial analysis of variance and differences will be determined by the Tukey test (p < 0.05).

3. Results and Discussion

Figure 2 and Figure 3 show the micrographs of the plants tested in this study. The secondary wall thickening was pitted, with openings throughout the longitudinal section of the xylem vessels (Figure 3).

Figure 2. Detail of secondary wall thickening on light electron microscopy, along the superficial area of the vessels of Khaya grandifoliola.

Figure 3. Field emission scanning electron microscopy of the vessel of Khaya grandifoliola. (a) Full-length xylem vessel; (b,c) details of secondary wall thickening.

Figure 2 and Figure 3 show the micrographs of the plants tested in this study. The secondary wall thickening was pitted, with openings throughout the longitudinal section of the xylem vessels (Figure 3).

Table 1 shows the mean geometric characteristics of the xylem vessels of irrigated and non-irrigated plants. We observed a significant difference in the number of pits and the relationship between the total pit area and the vessel’s surface area. However, the vessel length, diameter, and surface area did not significantly differ.

Table 1. The mean geometric pattern of xylem vessels in the stems of irrigated and non-irrigated Khaya grandifoliola plants.

Treatment	Length (µm)	Diameter (µm)	Reticle Area (µm2)	N. of Pits	RA/SAV 1
Irrigated	359.97 ns	137.01 ns	1.80 ns	4362 b	5.13% b
Non-irrigated	392.65 ns	143.26 ns	1.78 ns	5732 a	5.63% a

¹ RA/SAV is the ratio between the total area of the pit and the vessel’s surface area; ns: non-significant; Means signed by different letters differ statistically by the F test.

Donkor [21] reported diameters ranging from 100 and 275 µm and lengths between 121 and 683 µm in their review. Soranso et al. [22] worked with Khaya ivorensis, a variety of the same species, and has diameters between 41 and 141 µm. Unfortunately, few studies verify the anatomical characteristics of the vessels of Khaya grandifoliola for comparison, but the results mentioned above corroborate the values found in the current study.

With the definition of the geometric characteristics, it was possible to define the geometric model (Figure 4). The secondary wall structures were created using polygons perpendicular to the wall by an extrusion process along the axis of the vessels.

Figure 4. Three-dimensional anatomical model of xylem vessels of Khaya grandifoliola.

The pressure profile in the xylem vessels of irrigated and non-irrigated plants is observed in Figure 5 and Figure 6. In the inner part of the vessel, it was possible to observe a loss of energy of 0.49 Pa in irrigated and 0.47 Pa in the non-irrigated vessels. There is a gradual decrease in pressure between the “inlet” and the “outlet”, along with the entire longitudinal extension. It is possible to observe a non-gradual pressure passage zone with lower pressure than in the surrounding vessel area in the pit. It is still possible to verify that the pressure on the scores that form near the “inlet” is higher than those of the “outlet”.

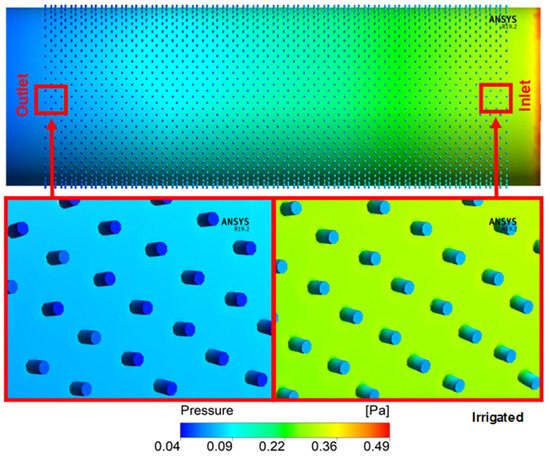
Figure 5. Flow field pressure distribution in section along the axis of irrigated vessels.

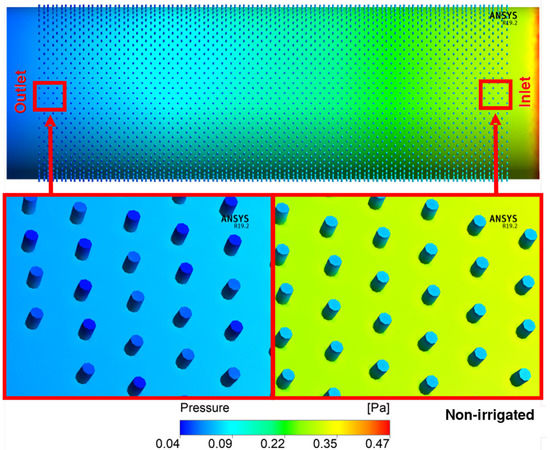
Figure 6. Flow field pressure distribution in section along the axis of non-irrigated vessels.

The numerical predictions of pressure in the transition region between the vessel wall and the pit are shown in Figure 7 and Figure 8. There was a pressure variation in this region and in the entire longitudinal profile in both water regimes. This variation occurs as a function of the determined boundary condition, in which we tried to represent a semipermeable membrane. The radial flow is driven by an osmotic difference in solute concentration between internal and external liquids, representing the forces of cellular absorption. Unlike what was observed by Jensen et al. [20], the axial flow decreases due to the observed radial efflux. Note that the non-irrigated vessel presented higher variability in the pressure profile, due to the higher number of outlets (scores) that were observed anatomically (Table 1).

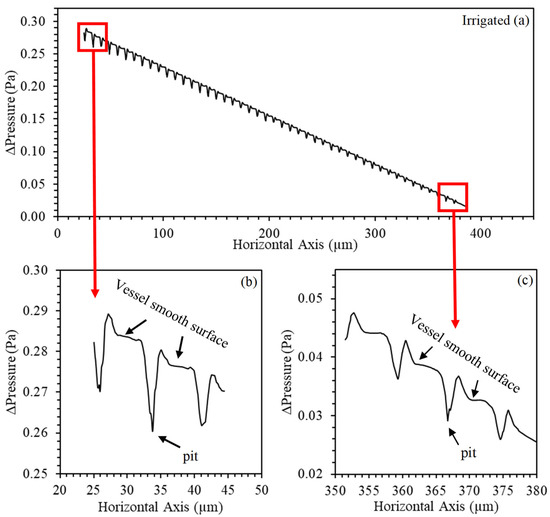
Figure 7. Numerical predictions of the pressure profile (Pa) generated along with the anatomical model in the longitudinal section of the irrigated Khaya grandifoliola xylem vessels. (a) The entire longitudinal axis; (b) input detail; and (c) output detail.

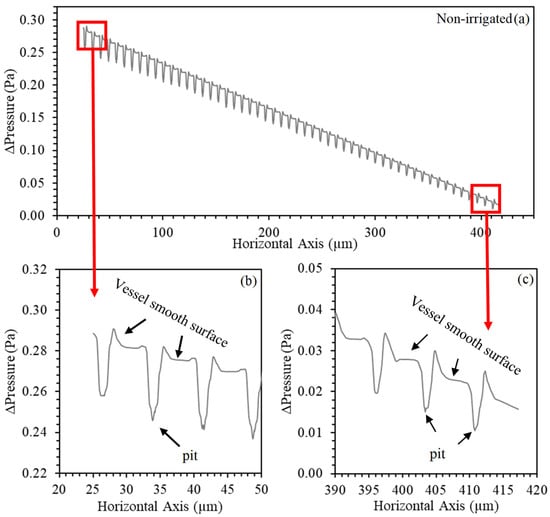
Figure 8. Numerical predictions of the pressure profile (Pa) generated along with the anatomical model in the longitudinal section of the non-irrigated Khaya grandifoliola xylem vessels. (a) The entire longitudinal axis; (b) input detail and (c) output detail.

This pressure drop effect is hydraulically described by Christiansen [23]; the total friction loss equals the sum of the losses between the radial outlets, concentrating on the first outlets that make up 75% of the horizontal axis. Thus, the pressure will be minimal at the distal end and gradually increase towards the initial source. Consequently, the discharge at the end will be minimal, and, as we move towards the beginning, each exit from the pit will, in turn, discharge a little more flow due to the increase in pressure (Figure 7b,c and Figure 8b,c).

The maximum velocity distribution profile presented in Figure 9 highlights a parabolic distribution profile, typical in Newtonian incompressible fluids. In the wall and structure of the secondary wall, the formation of the boundary layer is evident, characterizing an outer flow region in which the velocity varies slowly and a possible tangential zone of velocity increase in the outputs of the scores. In Figure 10, a velocity profile was traced in the longitudinal section of the thickening of the second wall to observe this region and its interaction with the rest of the vessel. In the initial section (25–35 µm) of the non-irrigated vessel, it was possible to observe a variability of the profile of 56.5%, with the irrigated vessel having 19.2%. There was less variability in the vessel’s final section (last 40 µm), around 12.7% and 9.9%, respectively, for non-irrigated and irrigated vessels (Figure 11).

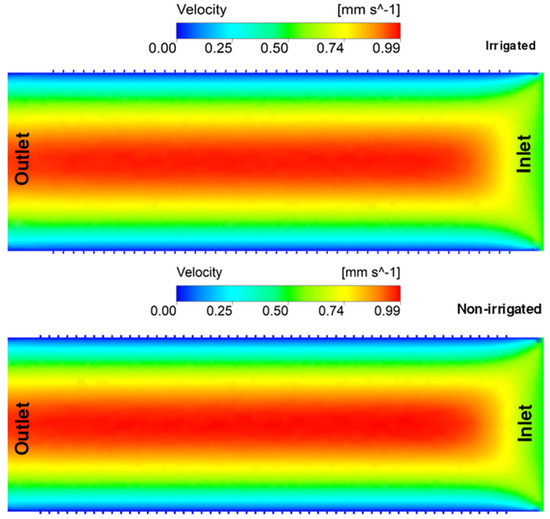
Figure 9. Flow field velocity distribution in section along the axis of irrigated and non-irrigated vessels.

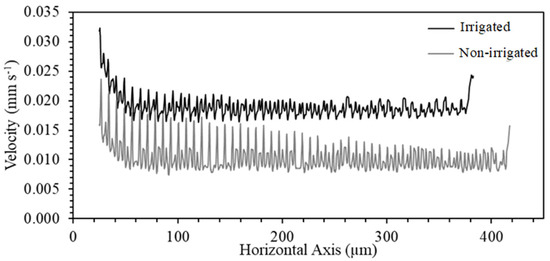
Figure 10. Numerical predictions of flow velocity generated along with the anatomical model in the longitudinal section of irrigated and non-irrigated Khaya grandifoliola xylem vessels.

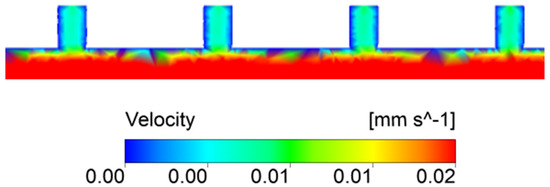
Figure 11. Flow field velocity distribution in the secondary vessel wall structure of the irrigated Khaya grandifoliola xylem.

Comparing the velocity and pressure profiles, it was possible to observe that in the areas with a decrease in pressure due to the existence of pits, there was an increase in the flow velocity, mainly due to the decrease in the fluid movement area, indicating the interference of the secondary wall thickness in the flow. Xu et al. and Schulte et al. [7,24] modeled these flow dynamics in the pit and verified the same behavior, increasing the velocity at the center of the structure and decreasing static pressure at the outlet. These structures presented a significant resistance to flow (Figure 12). Xu et al. [24] further reiterate that in this region, Re is relatively small and the opening of the pit, being a laminar flow without compromising other structures, comprises a direct relationship between the opening diameter of the pit and its resistivity.

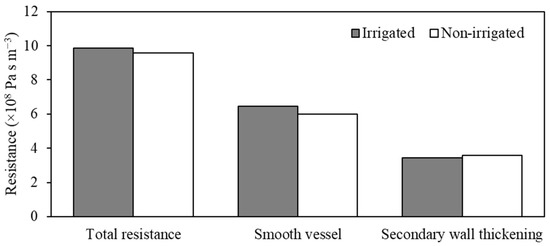
Figure 12. Total and structural component strength of the xylem vessel model in Khaya grandifoliola.

Partitioning the resistances, the smooth wall represented 65.30% and 62.57% of the total resistance, respectively, for irrigated and non-irrigated vessels. The non-irrigated vessel presented a resistance that was 3.04% lower than the irrigated vessel. Water deficit can suppress exchange=cell division and inhibit cell growth caused by turgor [25]. Non-irrigated vessels had a higher number of pits, which increased the resistance of the secondary wall of non-irrigated vessels. Zwieniecki and Secchi [26] relate this change in resistance to adaptation to ensure the hydraulic safety of vessels, as drought can affect anatomical characteristics, such as the structure of the secondary wall, the size of the conduit, and the density of the wood. The literature shows that the anatomical characteristics of the xylem adjust to drought conditions in trees, as drier conditions result in thicker cell walls and a more significant number of lateral structural elements, increasing the efficiency of water transport [26,27].

The secondary wall thickening represented 34.70% and 37.43% of the total resistance, respectively, for irrigated and non-irrigated vessels. Non-irrigated vessels showed higher resistance to the secondary wall thickening due to the higher number of pits, causing a more significant radial movement of fluids in these regions (Figure 8), translating a higher fluid volume to these structures. Thus, the smooth part of the wall had a lower resistance, consequently affecting the total resistance (Figure 10). Zimmermann [28] states that these structures cause a variation in conductivities along the length of the plant, mainly as a function of the vessel diameter and branch junctions, called “hydraulic bottlenecks”. These cellular structures present in the xylem walls influence the radial movement of water inside the plants, resulting from the decrease in diameter along the length of the stem. Therefore, the vessel presents a significant radial flow and exerts forces on the flow resistance [6,28,29,30]. The main challenge of the cohesion-tension theory is to explain how plants, particularly trees, that carry water at negative pressures can avoid cavitation or embolisms that interrupt the flow and result in dry-out [31]. The pit pores add substantial credibility to this theory, as they play essential roles in vessel resistivity [20].

The flow model via CFD in Khaya grandifoliola xylem vessels allowed us to better understand the flow phenomena of different resistances, secondary wall thickening, and smooth vessels. However, when the model is simulated with the universally diffused reading vessels analogous to Ohm’s law, we can see that the resistance has been underestimated at 68.7% and 61.4% for irrigated and non-irrigated vessels, respectively (Table 2). This is because this model uses two-dimensional mathematical models of the xylem structure and simple botanical analyses that neglect the other structural components present in the vessel [2,3]. Three-dimensionalizing and including the use of CFD in these microfluidic analyses is necessary due to the small size, varied structure, and complex internal flow of xylem vessels in plant species, which makes botanical observation tests very complicated, and it is often difficult to obtain accurate results because of the test conditions. Furthermore, other water transmission models are performed by macro-simulation models, which is different from the actual plant water ascent. Therefore, it is difficult to analyze the complex flow pattern and flow mechanism phenomenon within the catheter through experiments alone [9]. Our study and the various other studies cited above [7,8,9,10] contribute to further research into xylem vessel flow and the role of multiple structures in vessels.

Table 2. Comparisons of the mean values of total vessel resistance between those simulated and calculated by Ohm’s law, and analysis of their percentage difference (%Dif).

Total Resistance
Treatments	Simulated	Ohm’s Law	%Diff
Irrigated	9.86 × 108	3.08 × 108	68.72%
Non-irrigated	9.56 × 108	3.68 × 108	61.44%

4. Conclusions

The xylem vessels in Khaya grandifoliola provide a path of low resistance, where the smooth vessels present higher resistance, followed by thickening of the secondary wall. The simulations demonstrated a relationship between the total vessel strength and the total number of scores. Between the irrigated and non-irrigated plants, there was a difference of 2.8% of the total resistance. The non-irrigated vessel had a lower total resistivity but higher resistance to secondary wall thickening. Thus, the total number of crosshairs had a significant influence on radial transmission efficiency. More pits allow the plant to have more xylem vessels connected. Such connectivity will, in the case of an embolism event, allow water to be easily rerouted without drastically reducing the hydraulic conductivity.