Abstract
Determining hydrogeological properties of the rock materials that constitute an aquifer through stress tests or laboratory tests presents inherent complications. An alternative tool that has significant advantages is the study of the groundwater-level response as a result of the pore-pressure variation caused by the internal structure deformation of the aquifer induced by barometric pressure and solid Earth tide. The purpose of this study was to estimate the values of the physical/hydraulic properties of the geological materials that constitute the Guadalupe Valley Aquifer based on the analysis of the groundwater-level response to barometric pressure and solid Earth tide. Representative values of specific storage (1.27 × 10−6 to 2.78 × 10−6 m−1), porosity (14–34%), storage coefficient (3.10 × 10−5 to 10.45 × 10−5), transmissivity (6.67 × 10−7 to 1.29 × 10−4 m2∙s−1), and hydraulic conductivity (2.30 × 10−3 to 2.97 × 10−1 m∙d−1) were estimated. The values obtained are consistent with the type of geological materials identified in the vicinity of the analyzed wells and values reported in previous studies. This analysis represents helpful information that can be considered a framework to design and assess management strategies for groundwater resources in the overexploited Guadalupe Valley Aquifer.
1. Introduction
Water supply for human consumption, agricultural, and industrial activities is a crucial topic for developing the northwest semi-arid zones of Mexico. Particularly, Guadalupe Valley in the Ensenada municipality, BC, Mexico, stands out as the region with the highest wine production in the country. The Guadalupe Valley has had groundwater exploitations as its primary source of water. However, this intense anthropogenic activity has led to a recharge-extraction deficit, resulting in an excessive decrease in groundwater levels, compromising water availability in the region [1,2,3,4].
This situation raises the need to conduct interdisciplinary studies that provide technical and scientific information to design and evaluate new water-resource-management strategies. In 2007, many institutions established an integrated-management plan for the Guadalupe Valley Aquifer [5]. One of the main problems identified was the uncertainty in the knowledge of the aquifer dynamic. Thus, the urgency to establish a hydrogeological-measurement network was pointed out. As part of the hydrogeological-monitoring recommendations, continuous monitoring wells were instrumented by using pressure transducers [6].
Groundwater records are commonly used to study storage evolution, hydraulic gradient, and define the groundwater direction flow [7]. However, it has been observed that the groundwater is sensitive to several natural phenomena (e.g., barometric pressure, earth tides, and seismic activity) [8,9,10,11,12,13,14,15]. Analyzing the groundwater response to barometric pressure and solid Earth tide constitutes an alternative, feasible, and inexpensive tool for hydrogeological parameter estimations. Especially in regions where hydraulic properties’ information is insufficient or null, as a result of that, the sampling density necessary to describes it may be prohibitively expensive (e.g., drilling and testing core, and pumping tests) [7,16]. Therefore, this work aimed to estimate some hydrogeological parameters (specific storage, porosity, storage coefficient, transmissivity, and hydraulic conductivity) related to the geological materials that constitute the Guadalupe Aquifer based on the groundwater response to barometric pressure and solid Earth tide. Results of this analysis represent valuable information that can be considered as a framework to design and assess management strategies for groundwater resources in the overexploited Guadalupe Valley Aquifer.
2. Methods
2.1. Aquifer Response to Earth and Atmospheric Tides
Earth and atmospheric tides are natural phenomena throughout the Earth’s crust, exerting a uniformly distributed surface load that causes a subsurface strain constituted of superimposed signals of various frequencies and amplitudes. Aquifer formations experiment compression and extension at their inner structure as a result of the strain induced. Part of the strain is absorbed by the soil grains, and the rest is transmitted to the water contained in the porous medium modifying the pore pressure, so water level fluctuates, and their amplitude is modulated by geologic materials hydraulic properties that constitute the aquifer [8,10,11,13]. Earth and atmospheric tides utilization is a feasible and inexpensive alternative tool for hydrogeological parameters estimations [14,15,16,17]. The latter was based on the premise that only three variables are required to compute values for some aquifer parameters: (i) computed strain-tensor associated to Earth tides, (ii) measured barometric pressure, and (iii) recorded groundwater heads.
2.2. Groundwater-Level Response to Atmospheric Pressure
Groundwater table (WL) variations show an inverse and proportional correlation to barometric pressure (BP) fluctuations. WL variations are related to BP changes through barometric efficiency (BE), which can be obtained according to Rasmussen and Crawford [18] as follows:
BP fluctuations generate an evenly distributed strain field on the Earth’s surface. This latter causes elastic deformation from the rock materials that constitute the aquifer, and it is also transmitted to the fluid contained into the porous medium [10]. If the aquifer formation presents high transmissivity or specific yield, a drained condition is favored (i.e., mass transfer through flow). Thus, a groundwater response to BP may not be observed [19]. However, it is a common practice to consider the lateral flow negligible as a result of the vast lateral extension of the aquifer formation and the almost uniform effect of atmospheric load on the ground surface [20].
WL variations within the borehole can be conceptualized as aquifer pore-pressure changes, except in wells that are open to the atmosphere, on which the BP also exerts even pressure to the water surface [17]. Thus, a lag in WL response is often produced due to the air contained in the vadose zone. This lag causes pressure differences between the aquifer and borehole, propitiating in- and out-flows, resulting in WL variations [21].
Several methods have been developed for barometric efficiency estimation. Some of them consider independence on the frequency domain of WL–BP and calculated it by using linear regression techniques [18,22,23,24]. In contrast, other methods consider dependency on the frequency domain of WL–BP through transfer functions. There also assesses the simultaneous effect of the solid Earth tide [20,25,26,27].
2.3. Groundwater-Level Response to Solid Earth Tide
Solid Earth tide (SET) corresponds to small periodic variations in the Earth’s shape as a result of expansion and compression forces generated by the gravitational attraction of celestial bodies, mainly the Moon and Sun. These gravitational forces are balanced by pore-pressure changes in an aquifer that generate WL variations within boreholes drilled typically in confined and semi-confined aquifers [10,19]. Pore pressure (PP) is related to the vertical stress (σzz) associated with SET through the tidal efficiency (γe), which is obtained according to Jacob [8] as follows:
Strictly speaking, the fluid contained in the porous medium responds to a three-dimensional strain tensor (εv). Nevertheless, considering the induced deformation associated with SET and tectonic activity, the εv is not well-known as a priori [17,20]. Moreover, the εzz value measured on the terrain surface is approximately equal to the value of a horizontal strain component but with an opposite sign [20]. Therefore, it is more appropriate to analyze the WL response to an areal tidal strain (εA) defined by Rojstaczer and Agnew [13] and calculated as follows:
Because εzz has an opposite sign, εA value is higher than εv. Thus, the WL response may be lower when εv is used rather than εA.
The strain tensor associated with the SET can be estimated from the theoretical gravitational potential, W2 [28]. This differs from the measured gravitational potential due to geological and topographical local discontinuity effects [28,29,30]. Geologic and topo-graphic influence is complicated to define a priori. Thus, in the absence of strain measurements, the use of the theoretical gravitational strain is appropriate [20].
2.4. Aquifer Parameters Estimation
Jacob [8] derived a mathematical expressions that relate BE and γe with the elastic properties of the rock materials that constitute the aquifer, and can be written as follows:
where βk is the rock matrix compressibility, φ corresponds to porosity, and βW is water compressibility. If both expressions are added, the result is unity. Therefore, in calculating any of the previous parameters, it is possible to define the other one (BE = 1 − γe).
In case that the compressibility of the rock materials that constitute the aquifer is not considered, it is possible to estimate values of specific storage and porosity based on the WL response as a result of the SET and BP effects. WL variations produced by aquifer dilatation related to the SET is a function of specific storage (SS) of the rock materials. Bredehoeft [10] indicated that SS could be calculated from the water-table fluctuations record (dh), and assuming a characteristic value of Poisson’s ratio (ν) in undrained conditions. Van der Kamp and Gale [11] derived an expression to estimate SS as follows:
where KU is the rock matrix compressibility under undrained conditions, h = 0.6031 and l = 0.0839 are the Love numbers [31]; Er corresponds to the Earth’s radius, and g indicates gravity acceleration.
The relationship between W2 and dh is equivalent to the relation among the amplitude of the dominant harmonic components of W2 denoted as (A2 (τ, θ)), and the amplitude of the dh (Adh (τ)) at the same period (τ). Merrit [14] proposed that the derivatives (dW2 and dh) can be approximated by a finite differential scheme; thus, Equation (6) can be written as follows:
where A2(τ, θ) is calculated as follows:
The general lunar coefficient (Km), the particular amplitude factor (b) for each harmonic component with a period (τ), and the latitude function (f (θ)) values were determined by Merrit [14].
The classic method to study W2 is to represent it through a finite set of harmonic functions, sinus, and cosines. Each k-tidal harmonic component has a particular frequency (fTk), amplitude (ATk), and phase angle (ΦTk) [32]. Amplitude (Adhk) and phase-angle (Φdhk) estimations from the WL variations at the exact frequencies of the harmonic components of W2 are calculated from the regression coefficients (adhk and bdhk) obtained as follows [17]:
Similarly, ATk and ΦTk are computed from the theoretical strain-tensor associated to Earth tides, using Equations (9) and (10). Thus, areal strain sensitivity (ASK) is calculated based on Adhk and ATk according to Rojstaczer and Agnew [13]:
In case the rock materials that constitute the aquifer are incompressible, the volume aquifer changes as a result of the deformation induced by SET could be approximated as a variation on the porosity [33]. This assumption is appropriate for most of the aquifers studied in hydrogeology; the exceptions are aquifers related to low-porosity rocks [10]. Thus, the porosity can be estimated according to Merrit [14] as follows:
where ρ is the fluid density, and it is a function of its temperature.
Cooper et al. [9] demonstrated that the WL harmonic response depends on transmissivity (T), storage coefficient (Sc), periodicity of disturbance (τ), radius of the well casing (RWC), and radius of the well screened (RWS). A set of dimensionless parameters that relate these hydraulic rock properties and borehole characteristics was derived by Hsieh et al. [34]:
Graphs of the amplitude ratio and phase shift as a function of Equation (13) for selected values of the parameters in Equation (14) were prepared by Hsieh et al. Figures 2 and 3 [34].
Values of T can be estimated if the phase shift and an order of magnitude estimate of storage coefficient are known [34]. The phase shift of the kth-tidal harmonic component (ηk) is determined by Hsieh et al. [34] as follows:
3. Study Area and Database
3.1. Study Area
The Guadalupe Valley (GV) is located in the Guadalupe River basin (GRB), northwest region of Baja California, Mexico. The runoff in the basin originates in the Sierra Juarez and flows in a NE–SW direction trough the Ojos Negros-Real del Castillo, Guadalupe, and La Mision Valleys up to its discharge in the Pacific Ocean (Figure 1).
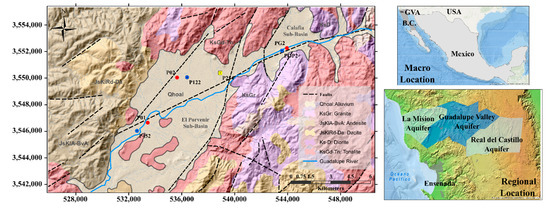
Figure 1.
Macro and regional location of the Guadalupe Valley Aquifer. Monitoring wells (P452, P122, and POP2) instrumented are shown. Reference wells (P01, P02, and PG02) included as a part of the study (lithology column availability) are shown. The location of the barometer (P254) is also shown. Geological features are illustrated and described at inset legend [35,36].
The region’s climate is characterized by a moderate semi-arid Mediterranean climate, according to the Kopen classification [37]. Mean monthly temperatures vary from 0.6 to 30 °C [38]. Rainfall events are generally intense, and mean annual precipitation may range from 12 to over 750 mm [39]. As a result, streamflow is highly seasonal, with most of the winter precipitation deriving streamflow from December through February and corresponds to the major source of recharge of the Guadalupe aquifer [40].
From a geological perspective, in GV, several tectonic processes originated two sub-basins: Calafia and El Porvenir (Figure 1). These are aligned to a NE–SW direction and eventually were filled with unconsolidated material from erosion, transport, and sedimentation processes. Intrusive and extrusive igneous rocks delimit the valley and constitute the hydraulic basement of the aquifer. Granodiorite, Tonalite, and Granite rocks from the Upper Cretaceous dominate in the north, east, and south regions. Meanwhile, Riodacite and Andesite rocks from the Upper Jurassic prevail in the west zone. Quaternary unconsolidated alluvial deposits constitute the Guadalupe Valley Aquifer (GVA) [3].
In a hydrogeological setting, the GVA is considered as a heterogeneous, unconfined aquifer formation made of three principal hydrogeological units of variable thickness: (i) highly permeable unit (alluvium, gravel, sand, and silt); (ii) semi-permeable unit (gravel, sand, and clay); and (iii) low permeability unit (igneous basement). These hydrogeological units are present in both sub-basins and constitute the main groundwater reservoir in the GVA (Figure 2a). The El Porvenir sub-basin (EPSB) prevails in the southern region of the GV and varies in depth from 70 to 100 m. The Calafia sub-basin (CSB) dominates the northeastern zone of the GV, and its depth varies from 300 to 350 m. The aquifer recharge is based on two dominant processes: (i) horizontal recharge, as a result of superficial and subterranean Guadalupe River flows; and (ii) vertical recharge, associated to percolation of precipitation and agricultural-irrigation excess [2,4,5,6].
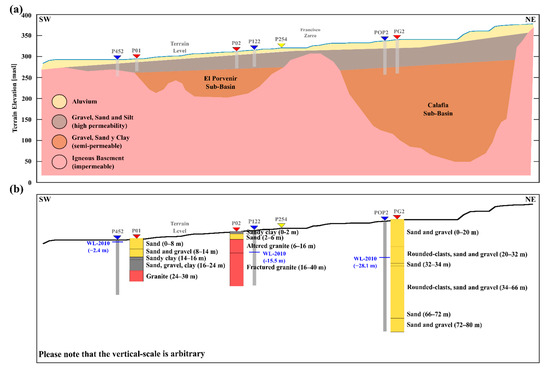
Figure 2.
(a) Schematic hydrogeological conceptualization of the Guadalupe Valley Aquifer, after Reference [5]. The approximate location of the monitoring wells included as a part of this study is shown. (b) Simplified stratigraphic columns of the rock units drilled by the reference wells (P01, P02, and PG2) [2]. The water level measured in 2010 is indicated.
The available information regarding the hydraulic properties of the rock materials that constitute the GVA is limited. Only two studies based on pumping tests have been carried out to estimate hydrogeological properties in the GVA. Andrade-Borbolla [1] determined that, the transmissivity values vary from 0.34 × 10−3 to 52.40 × 10−3 m2∙s−1, prevailing higher values of 1.00 × 10−3 m2∙s−1. CNA [4] estimated transmissivity values ranging from 0.04 × 10−3 to 60.00 × 10−3 m2∙s−1, hydraulic conductivity values between 0.05 to 64.80 m∙d−1; and mean values of storage coefficient of 0.00005 and specific yield of 0.065.
Some previous studies have aimed at determining the spatial distribution of the groundwater-table elevation, for which, hydrogeological properties values have been proposed to control the adjusting between field measurements and modeled water-table elevations. Campos-Gaytan and Kretzschmar [41] developed a groundwater-flow regional model based on historical water-level measurements for GVA. Moreover, hydraulic conductivity values for the rock materials that filled the sub-basins were estimated based on the misfit of the measurement and modeled water-table elevation. A typical value of hydraulic conductivity for EPSB and CSB was calculated as 5.47 m∙d−1. The exception to this was the southwestern region of EPSB, where the characteristic value determined was 68.49 m∙d−1. Hydraulic conductivity and storage coefficient values ranging from 2.00 to 8.00 m∙d−1, and 0.10 to 0.28, respectively; were used to simulate the groundwater-table response to extraordinary rainfall events within GV by [3].
On the other hand, Del Toro-Guerrero et al. [40] conducted the water-balance estimation in El Mogor sub-basin that derives in GV. As a part of the characterization activities, 48 soil samples from the vadose zone were analyzed to define its grain size. As a result, porosity values ranging from 26 to 38%, and hydraulic conductivity values ranging from 0.50 to 31.85 m∙d−1 were calculated by using the Vukovic–Soro and Kozeny–Carman empirical equations proposed by [42]. Molina-Navarro et al. [38] and Montecelos-Zamora [43] modeled the Global warming hydrogeological impact on the northern zone of the Guadalupe River, using a SWAT model. As a result of the simulation, typical values of hydraulic conductivity, ranging from 2.14 to 2.71 m∙d−1, were calculated.
3.2. Data
Vázquez-González et al. [6] established a groundwater monitoring network in the GVA. The monitoring wells were instrumented by using ten pressure-transducers of semi-continuous records (Solinst Levelogger and Solinst Barologger). González-Ramírez and Vázquez-González [3] reported that the monitoring network consisted of up to 17 observation wells, but the pressure-transducers were installed on the monitoring wells during different periods. In 2012, the monitoring network only had eight instrumented wells, five of them located in the CSB, and three in the EPSB. For this study, as a result of the database continuity inspection, only a relatively short period (1 June 2010 to 31 January 2011) of simultaneous record on three monitoring-wells was identified. The instrumented wells were POP2 (SW region of CSB), P122 (N region of EPSB), and P452 (SW region of EPSB). Additionally, during the same period, well P254 (NE region of EPSB) was instrumented to record barometric pressure. The location of the monitoring wells is illustrated in Figure 1. Groundwater-table level and barometric-pressure time-series recorded in each previously mentioned monitoring wells are shown in Figure 3a. Some design characteristics of the monitoring-wells considered in this study are presented in Table 1. The three monitoring wells were drilled into Quaternary alluvial deposits. Unfortunately, there is no information regarding the drilled lithological column. Nevertheless, establishing a correlation with near wells described by Campos-Gaytan [2] is feasible (Figure 2b and Table 2).
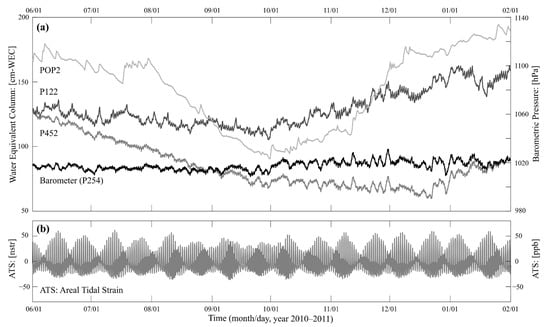
Figure 3.
(a) Records of water level (P452, P122, and POP2) and barometric pressure (P254) in terms of centimeters of Water Equivalent Column (cm-WEC) and hectopascals. (b) Calculated tidal strain (P254) expressed as nanostrain (1 nstr = 1 ppb).

Table 1.
Summary of the characteristics of the three monitoring wells studied. Nomenclature: well head elevation (WHE, meters above sea level (masl)), borehole depth (BD), water-table elevation (WTE), radius well-casing (RWC), radius well-screened (RWS), and saturated thickness (B).

Table 2.
Summary of the characteristics of the reference wells included as a part of this study.
3.3. Data Processing
The theoretical gravitational potential (W2) and its strain tensor (εA) were calculated at each well location, using the SPOTL package ver. 3.3.0.2 [44,45]. The geologic–topographic discontinuities and oceanic tide influence were not considered. The WL, BP, and εA time-series were processed and analyzed by using a set of MatLab codes written particularly for this study. The recorded time-series were detrended by using polynomial functions to represent it in a stationary fashion. A third-degree polynomial better reproduces the influence of annual and semi-annual cycles. Using the characteristic polynomial equation, the very low frequency effect was calculated and removed from the measured time-series. From the detrended data, BE was calculated with the method proposed by Rahi [24]. This technique estimates BE only considering BP perturbations and filtering the areal strain effect.
The periodic fluctuations in the time-series were identified utilizing the Discrete Fourier-Transform technique. The WL response to areal strain was analyzed from the discrete amplitude spectra. The high-frequency WL variations (>3.00 cycles per day, cpd) were removed by using a low-pass filter (Chebyshev-I, frequency-cut = 3.00 cpd). Then the low-frequency WL fluctuations (<0.50 cpd) were eliminated applying a high-pass filter (Chebyshev-I, frequency-cut = 0.50 cpd).
Amplitudes (Adhk) and phase angle (Φdhk) values were determined at the exact frequencies of the tidal harmonic components, using the t-tide code [46], and applying Equations (9) and (10). Similarly, ATk and ΦTk were calculated. Areal strain sensitivity was calculated based on Adhk and ATk, using Equation (11). Moreover, the phase shift was estimated based on Φdhk and ΦTk, using Equation (15). Therefore, the transmissivity magnitude order was estimated by utilizing Equation (13) and considering the values of RWC and RWS reported in Table 1.
Based on the ASK estimates, the specific storage was calculated by using Equation (7). For this, gravitational acceleration at a GV representative latitude was calculated as g = 9.795 [m∙s−2]. Moreover, the Earth’s radius of 6,371,000 m and Poisson’s ratio equal to 0.25 [47] were assumed. Using estimations of BE and SS, porosity values were calculated applying Equation (12). For this βW = 4.40 × 10−10 [Pa−1] and ρ = 998.20 [kg∙m−3] were used.
The saturated thickness (B) was determined relating the well head elevation (WHE), borehole depth (BD), and water-table elevation (WTE) reported in Table 1. From B, approximation of the storage coefficient was conducted based on the relation (SC = SS∙B). Similarly, the hydraulic conductivity magnitude-order was estimated from the relation (K = T∙B−1).
4. Results and Discussion
This study synthesized methods for estimating hydraulic aquifer properties from water-level fluctuations measured in a set of monitoring wells at Guadalupe Valley, Mexico. While this analysis was limited to the response of the well-aquifer system to deformation induced by Earth and atmospheric tides, similar methods are available to study water-level fluctuations due to other naturally occurring stresses, such as seismic events (e.g., see Reference [9]). The major simplifying assumption is that solids grains are incompressible. In addition, the primary uncertain source was the use of the tidal strain derived from the theoretical tidal potential. Nonetheless, the methods described in this work showed to be capable of providing reasonable aquifer properties estimates.
An example of the theoretical areal tidal strain calculated at well P254 reported in nanostrain units (1 nstr = 1 ppb) is shown in Figure 3b. The discrete amplitude spectra calculated for WL variations observed in wells P452, P122, and POP2 are shown in Figure 4a. Moreover, the spectra associated with the recorded BP and theoretical areal strain calculated in well P254, are shown in Figure 4b,c, respectively. The dominant harmonic components in the εA were five, two of them are diurnal (O1, Lunar; K1, Lunar-Solar) and three are semi-diurnal (N2, Lunar; M2, Solar; and S2, Lunar). Its period and nomenclature also are indicated in inset Figure 4c. The amplitude of the tidal harmonic components calculated in the three monitoring wells was comparable. On the reference well P254, amplitudes estimated were O1 = 5.3, K1 = 7.1, N2 = 1.7, M2 = 8.2, S2 = 4.2 nstr. These last harmonic components are responsible for 95% of tidal potential and play an essential role in hydrogeological studies [10,48].
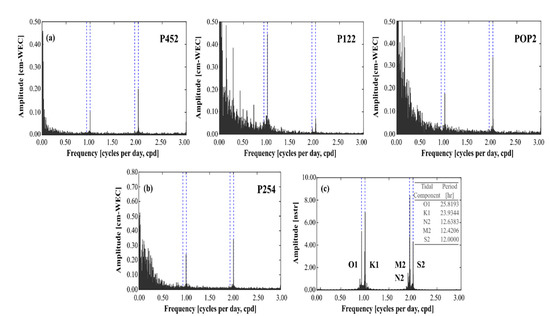
Figure 4.
Discrete amplitude spectra for water levels in wells P452, P122, and POP2 (a); barometric pressure expressed as centimeters of Water Equivalent Column (cm-WEC) (b); and the calculated areal tidal strain (c). The dominant Earth tides’ frequencies are indicated in the spectra.
BP periodic fluctuations in well P254 were diurnal and semi-diurnal. Its values were K1 = 2.6 and S2 = 3.4 mm-WEC (mm of Water Equivalent Column). These fluctuations are generally associated with the warming and cooling processes of the air column as a result of solar radiation. Moreover, diurnal and semi-diurnal periodic fluctuations in the WL spectra were identified. Semi-diurnal variations were dominant in wells P452 and POP2 (S2 = 2.0 and S2 = 3.3 mm-WEC, respectively), while diurnal fluctuations were dominant in well P122 (K1 = 4.4 mm-WEC).
The tidal harmonic components (K1 and S2) were also identified in the BP spectra. Therefore, the WL response analysis at these specific frequencies is challenging since both phenomena simultaneously influence the well-aquifer system. Moreover, the WL amplitude in the N2 frequency component is typically smaller compared with the other dominant components. As a result, the signal ratio is low and is often discarded since it becomes a relevant error source in the analysis [17]. Based on the above, K1, S2, and N2 harmonic components have been ignored in the WL response analysis. Consequently, only O1 and M2 harmonic components were used to estimate hydrogeological properties of the rock material in the vicinity of the studied monitoring wells.
The highest amplitude in the WL spectra for the O1 and M2 harmonic components was identified in well P122 (0.6 and 0.3 mm-WEC, respectively). While in wells P452 and POP2, amplitudes were lower than 0.1 mm-WEC. Bredehoeft [10] and Weeks [19] mentioned that it is unusual to identify the O1 and M2 harmonic components in the WL variations from wells drilled on unconfined aquifers, which is the typical conceptualization of the GVA. However, Rahi and Halihan [21] indicated that if O1 and M2 signatures are present in the WL spectra, it may be related to a lag of fluctuations K1 and S2 as a result of passing through the vadose zone, suggesting conditions of a semi-confined aquifer.
Estimation of Adhk and Φdhk at the specific frequencies of the O1 and M2 harmonic components was carried out from the regression coefficients adhk and bdhk, using Equations (9) and (10). The highest amplitudes were determined in well P122 (O1 = 1.06 mm-WEC and M2 = 0.59 mm-WEC). These last values were approximately two times the observed value on the amplitude spectra. The amplitudes determined from wells P452 and POP2 were minor relative to well P122 and are shown in Table 3. Similarly, values of ATk and ΦTk at the exact frequencies of O1 and M2 were calculated. The amplitude value for O1 was 10.67 nstr and 19.88 nstr for M2. These last two values are nearly two times the observed value on the amplitude spectra. The underestimated amplitude from the frequency spectra may be related to digital filtering and Discrete Fourier-Transform inherent problems, for example, the aliasing.

Table 3.
Summary of results of the regression analysis, areal strain sensitivity, and barometric efficiency.
Areal strain sensitivity values were calculated from the amplitudes and phase angles determined of the WL variations and the theoretical areal strain (Table 3). Likewise, the phase shift values were also calculated and reported (Table 3). The highest value of ASK was calculated in well P122 for the harmonic component O1 = 9.90 × 10−2 mm∙nstr−1; this value was approximately three times the value determined for M2. Added to this, a negative phase shift was determined in well P122 (ηk-O1 = −34°, and ηk-M2 = −83°). These last results indicate that the WL variations are produced as a result of the areal tidal strain effect. In wells, P452 and POP2 values of areal strain sensitivities ranging between 1.13 × 10−2 to 2.13 × 10−2 mm∙nstr−1 of ASK were calculated. WL variations as a result of the areal tidal strain effect were determined in wells P452 (M2, harmonic component) and POP2 (O1 harmonic component). In contrast, a positive phase shift was determined for the O1 harmonic component in well P452 and for the M2 component in well POP2. In previous studies, the positive phase shift has been related to the borehole storage effect and water diffusion processes [18,25,26,49].
Barometric efficiency values were calculated and reported for each monitoring well (Table 3). In wells P452 and P122 located on the EPSB, the estimated BE values were similar, 41.46% and 48.32%, respectively. In contrast, for well POP2 located on the CSB, the value calculated was 79.79%, this value is higher in relation to those calculated for the monitoring-wells on EPSB. BE is related to the rock materials that constitute the aquifer and is also an indicator of the confinement conditions. The BE represents the fraction of induced stress held by the rock materials; the remaining fraction is transmitted to the fluid [50]. Typically, a BE value of zero implies that the pressure perturbation is entirely held by the fluid contained in the porous media. While a unit BE value signifies that the pressure perturbation is held by the grains of the rock materials. Based on the above, the rock materials (gravel, sand, clay, and altered/fractured granite) that characterize the EPSB hold up 40–50% of the pressure perturbation related to BP fluctuations. While the sand/gravel alternating layers of the CSB support almost 80% of the stress related to BP fluctuations, this last hydraulic behavior may be explained if the presence of clays (high compressibility) on the EPSB is considered. It is contrasting with the relatively low compressibility of the sand and gravel that constitutes the CSB.
Added to this, in an ideal unconfined aquifer with shallow water table, the BE value should be zero. Instead, when the water table is relatively deep or the rock material generates confinement conditions, the BE value increases. Based on this, the BE values determined could suggest that in the vicinity of the analyzed wells, the aquifer is semi-confined. Moreover, the observed O1 and M2 harmonic components in the WL spectra support that locally the GVA is a semiconfined formation. This result is surprising and contrasts with the typical conceptualization of the GVA [2,6,51]. Nonetheless, the characteristics of rock materials that constitute the aquifer and the water-table relative depth may justify the local semi-confined hydraulic behavior of the GVA. Despite this latter, regionally the GVA is a unique unconfined aquifer formation.
Estimations of SS in the GVA has not been obtained because previously conducted studies have considered an unconfined aquifer, where the specific yield is much higher than SS. Nevertheless, the results of this study suggest local semi-confined behavior in the GVA. The determined SS values ranged from 1.27 × 10−6 to 2.78 × 10−6 m−1 (Table 4). The lowest value was calculated for well P122, while the highest value was estimated for well P452. The comparison between the SS estimations and the expected values as a function of the rock-materials type is shown in Figure 5. In general, the SS estimations were two orders of magnitude lower than the expected values related to the rock materials that dominate the lithologic column of wells P01, P02, and PG2 reported by Campos-Gaytán [2]. However, these stratigraphic columns also showed the presence of clay lens (P01 and P02), granite (P01), and altered/fractured granite (P02). Based on these last rock materials, the calculated SS values for wells P452 and P122 are slightly in agreement with the expected SS values (Figure 5). SS estimations for well POP2 showed relevant discrepancies concerning the expected SS values as a function of the rock materials observed in the lithologic column of well PG2 (sand and gravel). Nonetheless, shallow clay layers have been interpreted on recent electromagnetic surveys (TEMs) conducted in the CSB [52]. This last geological feature may explain the calculated SS values in well POP2 and support the GVA local semi-confined hydraulic behavior deduced.

Table 4.
Summary of estimations of hydrogeological parameters for the rock materials that constitute the Guadalupe Valley Aquifer.
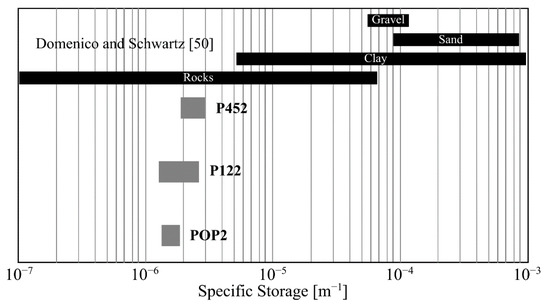
Figure 5.
Comparison between the estimated specific storage values (P452, P122, and POP2) and the expected values as a function of the rock-material type.
Porosity values were calculated based on estimations of SS and BE. The estimated porosity values ranged from 14 to 34% (Table 4). The lowest value was calculated for well P122, located in the EPSB in which a shallow hydraulic basement has been reported. The highest porosity value was estimated for well POP2 situated in the CSB and is consistent with the expected value associated with the rock materials that constitute the PG2 reference stratigraphic column. Furthermore, calculated porosity values are comparable with the porosity values (26–38%) determined in El Mogor, GVA’s tributary sub-basin [40]. Additionally, estimated porosity values are consistent with the expected porosity values reported in the classic hydrogeological literature [50,53]. For practical purposes and in the absence of local determinations, a representative porosity value for the rock materials in the CSB is 30%, 20% for EPSB, and 25% for the GVA.
Storage coefficient values were calculated based on the estimations of SS and B. The estimated SC values ranging from 3.10 × 10−5 to 10.45 × 10−5 (Table 4). The lowest SC value was calculated for well P122, and the highest SC value was in well P452; both wells are in the EPSB. The SC value estimated for well POP2 situated in the CSB was lower than the calculated value for well P452. The estimated SC values were up to four orders of magnitude lower in comparison to those used in the water-table simulations by González-Ramírez and Vázquez-González [3]. Nevertheless, estimated SC values are similar in the order of magnitude (10−5) with those determined through pumping tests by CNA [4].
Transmissivity values were calculated based on estimations of ηk, the order of magnitude of SC, and Figure 2 from Hsieh et al. [34]. The estimated T-values were ranging from 6.67 × 10−7 to 1.29 × 10−4 m2∙s−1 (Table 4). The lowest T-value was calculated for well P122, and the highest T-value in well P452, both wells are in the EPSB. Estimated T-values are comparable with those (3.40 × 10−4 to 52.40 × 10−3 m2∙s−1) determined by Andrade-Borbolla [1], and to those (4.00 × 10−5 a 60.00 × 10−3 m2∙s−1) calculated by CNA [4]. Finally, hydraulic conductivity values were calculated from estimations of T and B. The estimated K-values ranged between 2.30 × 10−3 to 2.97 × 10−1 m∙d−1 (Table 4). The highest K-value was calculated for well P452 located at the SW of EPSB; a similar hydraulic behavior was described by Campos-Gaytán and Kretzschmar [41]. The lowest K-value was calculated for well POP2 located on the CSB. In general, the estimated K-values were up to two or four orders of magnitude lower in comparison (Figure 6) to those determined from water-table elevation modeling [3,38,41,43]. In contrast, the estimated K-values are comparable with those reported in the classic hydrogeological literature [50,53]. Moreover, the estimated K-values are pretty similar to those determined from the soil grain-size analysis by Del Toro-Guerrero et al. [40] and with those calculated from pumping tests in wells of the GVA by CNA [4].
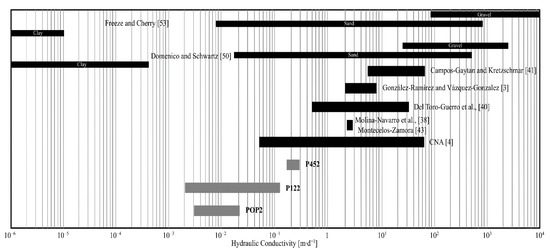
Figure 6.
Comparison between the estimated hydraulic-conductivity values (P452, P122, and POP2) and the expected values as a function of the rock-material type, and determined values from previous studies.
5. Conclusions
Based on the analysis of the groundwater response in three monitoring wells to barometric pressure and solid Earth tide, we determined crucial information about the hydrogeological properties of the rock materials that constitute the Guadalupe Valley Aquifer. In particular, representative values of specific storage (1.27 × 10−6 to 2.78 × 10−6 m−1), porosity (14–34%), storage coefficient (3.10 × 10−5 to 10.45 × 10−5), transmissivity (6.67 × 10−7 to 1.29 × 10−4 m2∙s−1), and hydraulic conductivity (2.30 × 10−3 to 2.97 × 10−1 m∙d−1) were calculated. These results were consistent with previous determinations. Moreover, based on our literature review, the calculated specific storage values correspond to the first estimations reported in the Guadalupe Valley Aquifer.
About the hydraulic behavior of the rock materials as a result of the induced stress tensor related to perturbation of barometric pressure and areal tidal strain, the results suggested local semi-confined conditions of the aquifer formation. This behavior differed from the typical conceptualization of the Guadalupe Valley Aquifer. Nevertheless, the observed clay-lens in lithologic columns, the interpreted electrical-resistivity models, and the storage coefficient values determined from pumping tests, corroborated the local conditions of semi-confinement identified in this study.
The main sources of uncertainty of the estimations correspond to using the theoretical areal strain and the assumed saturated thickness. Nonetheless, the estimated hydrogeological values showed consistency with those expected for the rock-materials types reported in the classic literature. In addition, a notable similarity was defined between the estimated values and those calculated directly from aquifer stress tests. In the absence of hydrogeological information, the estimated parameters of this study may be considered as a benchmark and used to design and assess management strategies for the groundwater in the Guadalupe Valley Aquifer.
Future research should be focused on integrating water-level records from a broader set of monitoring wells to extend the hydrogeological characterization of the Guadalupe Valley Aquifer. Moreover, the investigation should explore hydrogeologic–poroelastic relationships to determine geomechanical properties associated with the rock materials that constitute the Guadalupe Valley Aquifer.
Author Contributions
Conceptualization, M.A.F.-A., J.R.-H. and R.V.-G.; methodology, M.A.F.-A. and J.R.-H.; software, M.A.F.-A.; validation, M.A.F.-A. and J.R.-H.; formal analysis, M.A.F.-A. and J.R.-H.; investigation, M.A.F.-A., R.V.-G. and A.D.-F.; resources, M.A.F.-A., R.V.-G., D.N. and J.G.-R.; data curation, M.A.F.-A., A.D.-F. and J.G.-R.; writing—original draft preparation, M.A.F.-A., J.R.-H., R.V.-G. and J.G.-R.; writing—review and editing, M.A.F.-A., J.R.-H. and D.N.; visualization, M.A.F.-A.; funding acquisition, R.V.-G. All authors have read and agreed to the summited version of the manuscript.
Funding
This research received no external funding. The APC was partially funded by the Guadalajara University Project 258044 (Programa de Difusión de los Resultados de Investigación del Centro Universitario de la Costa de la Universidad de Guadalajara, Proyecto 258044).
Data Availability Statement
The groundwater-level and barometric data may be available for collaborative research projects by specific agreements. For information, contact marioafar@gmail.com.
Acknowledgments
The authors express their gratitude to the staff of the Comité Técnico de Aguas Subterráneas del Valle de Guadalupe for providing the water-level and barometric-pressure recorded data of the wells analyzed in this study. The authors gratefully acknowledge Geraldine Castillo-Martínez for her valuable English language edition. Thanks are extended to the reviewers and Editor for useful comments that improved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Andrade-Borbolla, M. Actualización hidrogeológica del Valle de Guadalupe, Municipio de Ensenada, Baja California; Grupo Agroindustrial Valle de Guadalupe: Ensenada, Mexico, 1997; p. 66. (In Spanish) [Google Scholar]
- Campos-Gaytán, J.R. Simulación Del Flujo de Agua Subterránea en El Acuífero Del Valle de Guadalupe. Ph.D. Thesis, Centro de Investigación Científica y de Educación Superior de Ensenada, Ensenada, Mexico, 2008; 240p. (In Spanish). Available online: https://biblioteca.cicese.mx/catalogo/tesis/ficha.php?id=17841 (accessed on 14 May 2021).
- Gonzalez-Ramirez, J.; González, R.V. Modeling of the water table level response due to extraordinary precipitation events: The case of the guadalupe valley aquifer. Int. J. Geosci. 2013, 4, 950–958. [Google Scholar] [CrossRef][Green Version]
- CNA; Comisión Nacional del Agua. Actualización de la Disponibilidad Media Anual de Agua en El Acuífero Guadalupe (0207); Comisión Nacional del Agua: Mexico, Mexico, 2018; 28p, (In Spanish). Available online: https://sigagis.conagua.gob.mx/gas1/Edos_Acuiferos_18/BajaCalifornia/DR_0207.pdf (accessed on 14 May 2021).
- Ramírez-Hernández, J.; Carreón, C.D.; Campbell, R.H.; Palacios, B.R.; Leyva, C.O.; Ruíz, M.L.; Vázquez, G.R.; Rousseau, F.P.; Campos, G.R.; Mendoza, E.L.; et al. Informe Final. Plan de Manejo Integrado de las Aguas Subterráneas en el Acuífero de Guadalupe, Estado de Baja California. Tomo I. Reporte Interno. Elaborado por la; Convenio: SGT-OCPBC-BC-07-GAS-001; Universidad Autónoma de Baja California para la Comisión Nacional del Agua, Organismo de Cuenca Península de Baja California, Dirección Técnica: Ensenada, Mexico, 2007. (In Spanish) [Google Scholar]
- Vázquez-González, R.; Romo-Jones, J.M.; Kretzschmar, T. Estudio Técnico Para El Manejo Integral Del Agua en El Valle de Guadalupe; División de Ciencias de la Tierra, Centro de Investigación Científica y de Educación Superior de Ensenada: Baja California, Mexico, 2007; p. 53. (In Spanish) [Google Scholar]
- Fuentes-Arreazola, M.A. Estimación de Parámetros Geohidrológicos, Poroelásticos Y Geomecánicos Con Base en El análisis de Las Variaciones Del Nivel Del Agua Subterránea en Pozos de Monitoreo en El Valle de Mexicali. Ph.D. Thesis, Centro de Investigación Científica y de Educación Superior de Ensenada, Baja California, Mexico, 2018; p. 127. (In Spanish). Available online: https://biblioteca.cicese.mx/catalogo/tesis/ficha.php?id=25077 (accessed on 14 May 2021).
- Jacob, C.E. Flow of groundwater. In Engineering Hydraulic; Rouse, H., Ed.; John Wiley & Son, Inc.: New York, NY, USA, 1950; pp. 321–386. [Google Scholar]
- Cooper, H.H.; Bredehoeft, J.D.; Papadopulos, I.S.; Bennett, R.R. The response of well-aquifer systems to seismic waves. J. Geophys. Res. Space Phys. 1965, 70, 3915–3926. [Google Scholar] [CrossRef]
- Bredehoeft, J.D. Response of well-aquifer systems to Earth tides. J. Geophys. Res. Space Phys. 1967, 72, 3075–3087. [Google Scholar] [CrossRef]
- Van Der Kamp, G.; Gale, J.E. Theory of earth tide and barometric effects in porous formations with compressible grains. Water Resour. Res. 1983, 19, 538–544. [Google Scholar] [CrossRef]
- Roeloffs, E.A. Hydrologic precursors to earthquakes: A review. Pure Appl. Geophys. 1988, 126, 177–209. [Google Scholar] [CrossRef]
- Rojstaczer, S.; Agnew, D. The influence of formation material properties on the response of water levels in wells to Earth tides and atmospheric loading. J. Geophys. Res. Space Phys. 1989, 94, 12403–12411. [Google Scholar] [CrossRef]
- Merritt, M.L. Estimating Hydraulic Properties of the Floridan Aquifer System by Analysis of Earth-Tide, Ocean-Tide, And Barometric Effects, Collier and Hendry Counties, Florida; US Geological Survey: Reston, VA, USA, 2004; p. 80.
- Fuentes-Arreazola, M.A.; Vázquez-González, R. Estimation of some geohydrological properties in a set of monitoring wells in Mexicali Valley, B.C., México. Revista Ingeniería del Agua 2016, 20, 87. [Google Scholar] [CrossRef]
- Fuentes-Arreazola, M.A.; Ramírez-Hernández, J.; Vázquez-González, R. Hydrogeological properties estimation from groundwater level natural fluctuations analysis as a low-cost tool for the Mexicali Valley aquifer. Water 2018, 10, 586. [Google Scholar] [CrossRef]
- Cutillo, P.A.; Bredehoeft, J.D. Estimating aquifer properties from the water level response to earth tides. Ground Water 2010, 49, 600–610. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, T.; Crawford, L.A. Identifying and removing barometric pressure effects in confined and unconfined aquifers. Ground Water 1997, 35, 502–511. [Google Scholar] [CrossRef]
- Weeks, P.E. Barometric fluctuations in wells tapping deep unconfined aquifers. Water Resour. Res. 1979, 15, 1167–1176. [Google Scholar] [CrossRef]
- Galloway, D.; Rojstaczer, S. Analysis of the frequency response of water levels in wells to earth tides and atmospheric loading. In Proceedings of the Fourth Canadian/American Conference in Hydrogeology; Canada National Ground Water Association: Banff, AB, Canada, 1988; pp. 100–113. [Google Scholar]
- Rahi, K.A.; Halihan, T. Identifying aquifer type in fractured rock aquifers using harmonic analysis. Ground Water 2013, 51, 76–82. [Google Scholar] [CrossRef]
- Clark, W.E. Computing the barometric efficiency of a well. J. Hydraul. Div. 1967, 93, 93–98. [Google Scholar] [CrossRef]
- Toll, N.J.; Rasmussen, T. Removal of barometric pressure effects and earth tides from observed water levels. Ground Water 2007, 45, 101–105. [Google Scholar] [CrossRef] [PubMed]
- Rahi, K.A. Estimating the Hydraulic Parameters of the Arbuckle-Simpson Aquifer by Analysis of Naturally-Induced Stresses. Ph.D. Dissertation, Oklahoma State University, Oklahoma, OK, USA, 2010; p. 168. Available online: https://core.ac.uk/download/pdf/215232243.pdf (accessed on 14 May 2021).
- Rojstaczer, S. Intermediate period response of water levels in wells to crustal strain: Sensitivity and noise level. J. Geophys. Res. Space Phys. 1988, 93, 13619–13634. [Google Scholar] [CrossRef]
- Rojstaczer, S. Determination of fluid flow properties from the response of water levels in wells to atmospheric loading. Water Resour. Res. 1988, 24, 1927–1938. [Google Scholar] [CrossRef]
- Lai, G.; Ge, H.; Wang, W. Transfer functions of the well-aquifer systems response to atmospheric loading and Earth tide from low to high-frequency band. J. Geophys. Res. Solid Earth 2013, 118, 1904–1924. [Google Scholar] [CrossRef]
- Harrison, J.C. New Computer Programs for the Calculation of Earth Tides; Cooperative Institute for Research in Environmental Sciences: Colorado, CO, USA, 1971; p. 30. [Google Scholar]
- Berger, J.; Beaumont, C. An analysis of tidal strain observation from the United States of America II: The inhomoge-neous tide. Bull. Seismol. Soc. Am. 1976, 66, 1821–1846. [Google Scholar]
- Harrison, J.C. Cavity and topographic effects in tilt and strain measurement. J. Geophys. Res. Space Phys. 1976, 81, 319–328. [Google Scholar] [CrossRef]
- Agnew, D.C. Earth tides. In Treatise on Geophysics and Geodesy; Herring, T.A., Ed.; Elsevier: New York, NY, USA, 2007; pp. 163–195. [Google Scholar]
- Doodson, A.T.; Warburg, H.D. Admiralty Manual of Tides; Her Majesty´s Stationary Office: London, UK, 1941; p. 270. [Google Scholar]
- Jacob, C.E. On the flow of water in an elastic artesian aquifer. Trans. Am. Geophys. Union 1940, 21, 574–586. [Google Scholar] [CrossRef]
- Hsieh, P.A.; Bredehoeft, J.D.; Farr, J.M. Determination of aquifer transmissivity from Earth tide analysis. Water Resour. Res. 1987, 23, 1824–1832. [Google Scholar] [CrossRef]
- INEGI. Datos de geología del Instituto Nacional de Estadística y Geografía. 2018. Available online: http://gaia.inegi.org.mx/mdm6/ (accessed on 14 May 2021).
- SGM. Sistema GEOINFOMEX del Servicio Geológico Mexicano. 2018. Available online: https://www.sgm.gob.mx/GeoInfoMexGobMx (accessed on 14 May 2021).
- García, E. Modificaciones Al Sistema de Clasificación Climática de Köpen Para Adaptarlo a Las Condiciones de la República Mexicana; Instituto de Geografía, Universidad Nacional Autónoma de México: Ciudad Universitaria, Mexico, 1981; p. 97, (In Spanish). Available online: http://www.publicaciones.igg.unam.mx/index.php/ig/catalog/view/83/82/251-1 (accessed on 14 May 2021).
- Molina-Navarro, E.; Hallack-Alegría, M.; Martínez-Pérez, S.; Ramírez-Hernández, J.; Moctezuma, A.M.; Sastre-Merlín, A. Hydrological modeling and climate change impacts in an agricultural semiarid region. Case study: Guadalupe River basin, Mexico. Agric. Water Manag. 2016, 175, 29–42. [Google Scholar] [CrossRef]
- Hallack-Alegría, M.; Ramírez-Hernández, J.; Watkins, D.W. ENSO-conditioned rainfall drought frequency analysis in northwest Baja California, Mexico. Int. J. Clim. 2011, 32, 831–842. [Google Scholar] [CrossRef]
- Del Toro-Guerrero, F.J.; Kretzschmar, T.; Hinojosa-Corona, A. Estimación del balance hídrico en una Cuenca semiárida, El Mogor, Baja California, México. Technol. Cienc. Agua 2014, 5, 69–81. [Google Scholar]
- Campos-Gaytán, J.R.; Kretzschmar, T. Numerical understanding of regional scale water table behavior in the Guada-lupe Valley aquifer, Baja California, Mexico. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 707–730. [Google Scholar] [CrossRef]
- Odong, J. Evaluation of empirical formulae for determination of hydraulic conductivity based on grain-size analysis. J. Am. Sci. 2007, 3, 54–60. [Google Scholar]
- Montecelos-Zamora, Y. Modelación Del Efecto de la Variación Climática en El Balance Hídrico en Dos Cuencas (México Y Cuba) Bajo Un Escenario de Cambio Climático. Ph.D. Thesis, Centro de Investigación Científica y de Educación Superior de Ensenada: Baja California, Mexico, 2018; p. 100. (In Spanish). Available online: https://biblioteca.cicese.mx/catalogo/tesis/ficha.php?id=25188 (accessed on 14 May 2021).
- Berger, J.; Farrell, W.; Harrison, J.C.; Levine, J.; Agnew, D.C. ERTID 1: A Program for Calculation of Solid Earth Tides; Technical Report; Scripps Institution of Oceanography: La Jolla, CA, USA, 1987; p. 20. [Google Scholar]
- Agnew, D.C. SPOTL: Some Programs for Ocean-Tides Loading; Technical Report; Scripps Institution of Oceanography: La Jolla, CA, USA, 2012; p. 30. Available online: https://igppweb.ucsd.edu/~agnew/Spotl/spotlmain.html (accessed on 14 May 2021).
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Gercek, H. Poisson’s ratio values for rocks. Int. J. Rock Mech. Min. Sci. 2007, 44, 1–13. [Google Scholar] [CrossRef]
- Melchior, P. Earth tides. In Research in Geophysics; Odishaw, H., Ed.; Massachusetts Institute of Technology Press: Cambridge, MA, USA, 1964; pp. 183–193. [Google Scholar]
- Rojstaczer, S.; Riley, F.S. Response of the water level in a well to Earth tides and atmospheric loading under unconfined conditions. Water Resour. Res. 1990, 26, 1803–1817. [Google Scholar] [CrossRef]
- Domenico, P.A.; Schwartz, F.W. Groundwater movement, hydraulic conductivity and permeability of geological material. In Physical and Chemical Hydrogeology, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1997; pp. 33–54. [Google Scholar]
- Hernández-Rosas, M.; Mejía-Vázquez, R. Relación de las Aguas Superficiales y Subterráneas del Acuífero BC-07; Gerencia Regional de la Península de Baja California, Subgerencia Regional Técnica, Technical Report; Comisión Nacional del Agua: Valle de Guadalupe, Mexico, 2003; p. 13. (In Spanish) [Google Scholar]
- Monge-Cerda, F.E. Detección Del Nivel Freático Con Métodos Geoeléctricos: El Caso Del Valle de Guadalupe. Master’s Thesis, Centro de Investigación Científica y de Educación Superior de Ensenada, B.C. Baja California, Mexico, 2020; p. 97. (In Spanish). Available online: https://biblioteca.cicese.mx/catalogo/tesis/ficha.php?id=25639 (accessed on 14 May 2021).
- Freeze, R.A.; Cherry, J.A. Physical properties and principles. In Groundwater; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1979; pp. 14–79. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).