An Effective Kalman Filter-Based Method for Groundwater Pollution Source Identification and Plume Morphology Characterization
Abstract
1. Introduction
2. Methodology
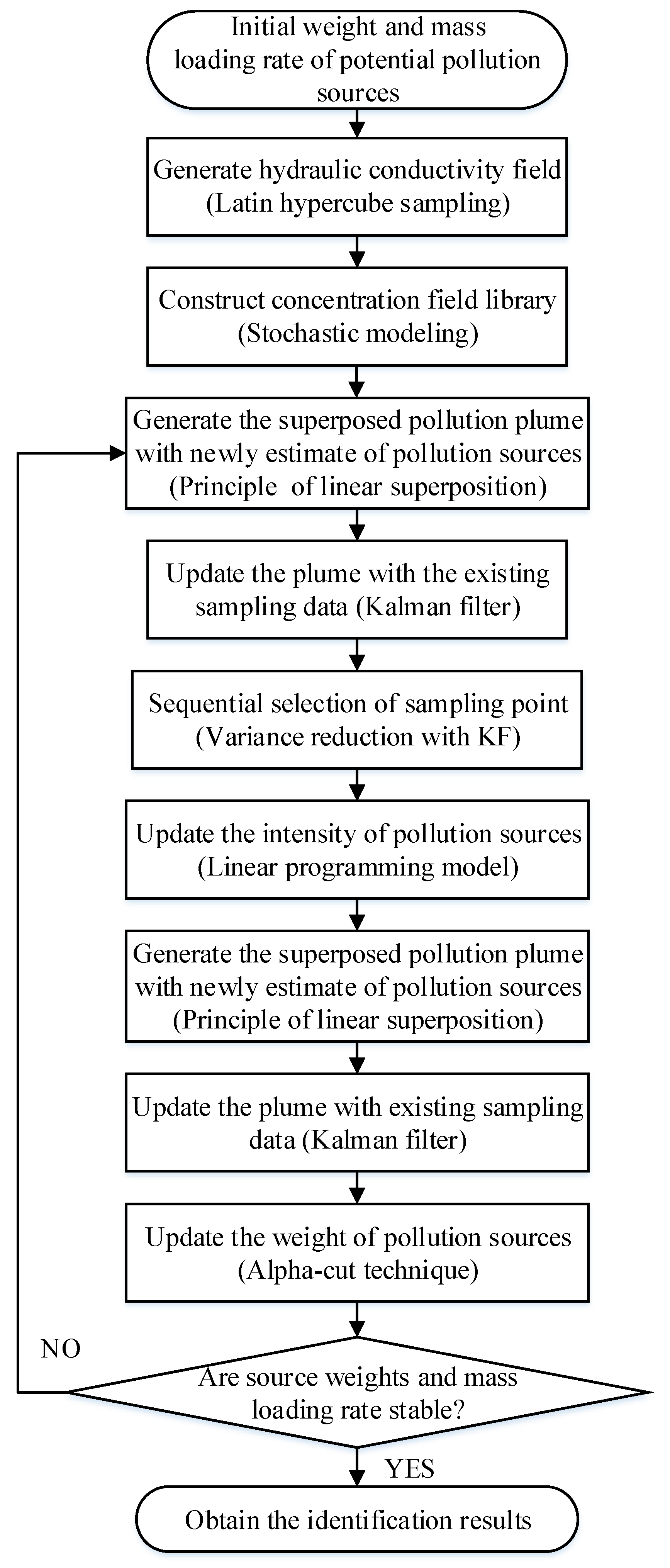
2.1. Framework of the Proposed Method
- Step 1: On the basis of the site investigation, the location of possible pollution sources is preliminarily determined and the initial weight and mass-loading rate for each potential pollution source are given based on expert opinion.
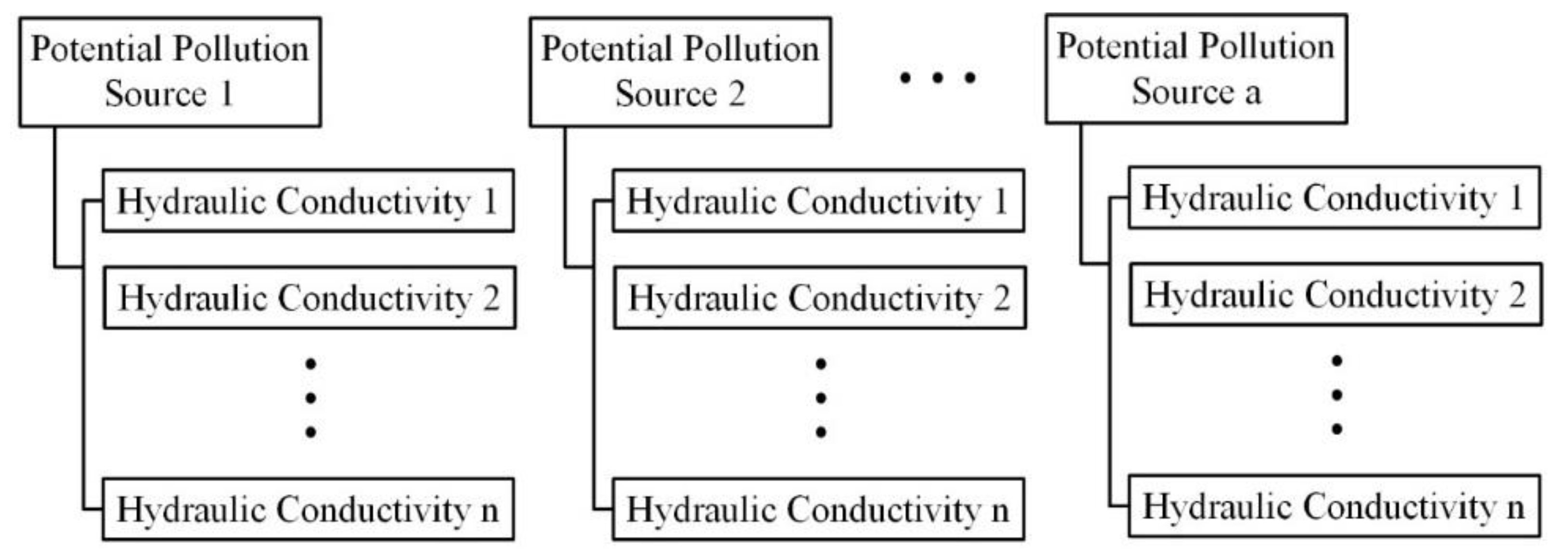
- Step 2: Considering the uncertainty of site information, the random hydraulic conductivity field is generated by the LHS (Latin hypercube sampling) technique assuming hydraulic conductivity in a random process.
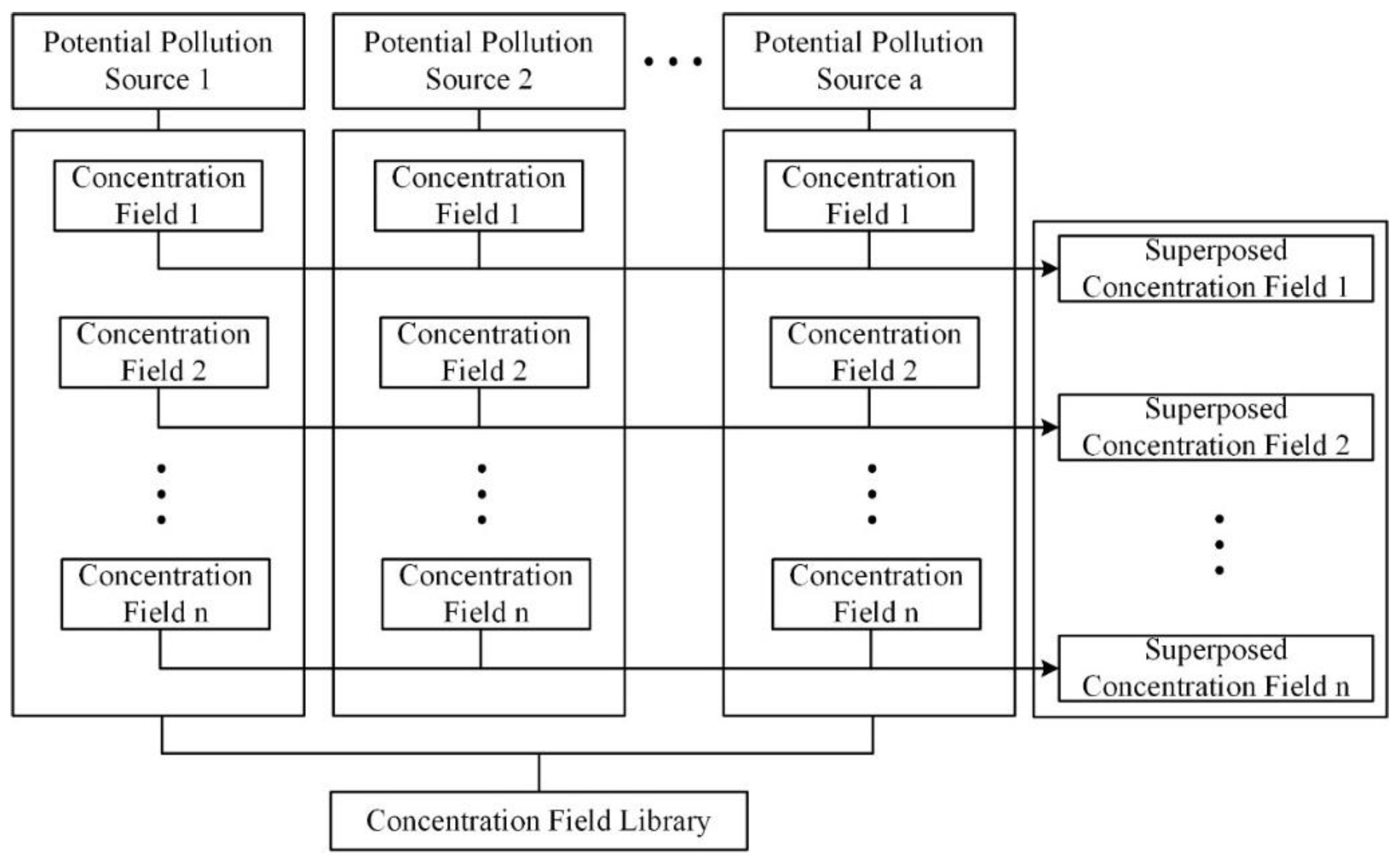
- Step 3: Groundwater flow and the transport model are constructed and the concentration field library is obtained by Monte Carlo simulation. In the Monte Carlo simulation, each potential pollution source with unit mass-loading rate is calculated at each hydraulic conductivity realization.
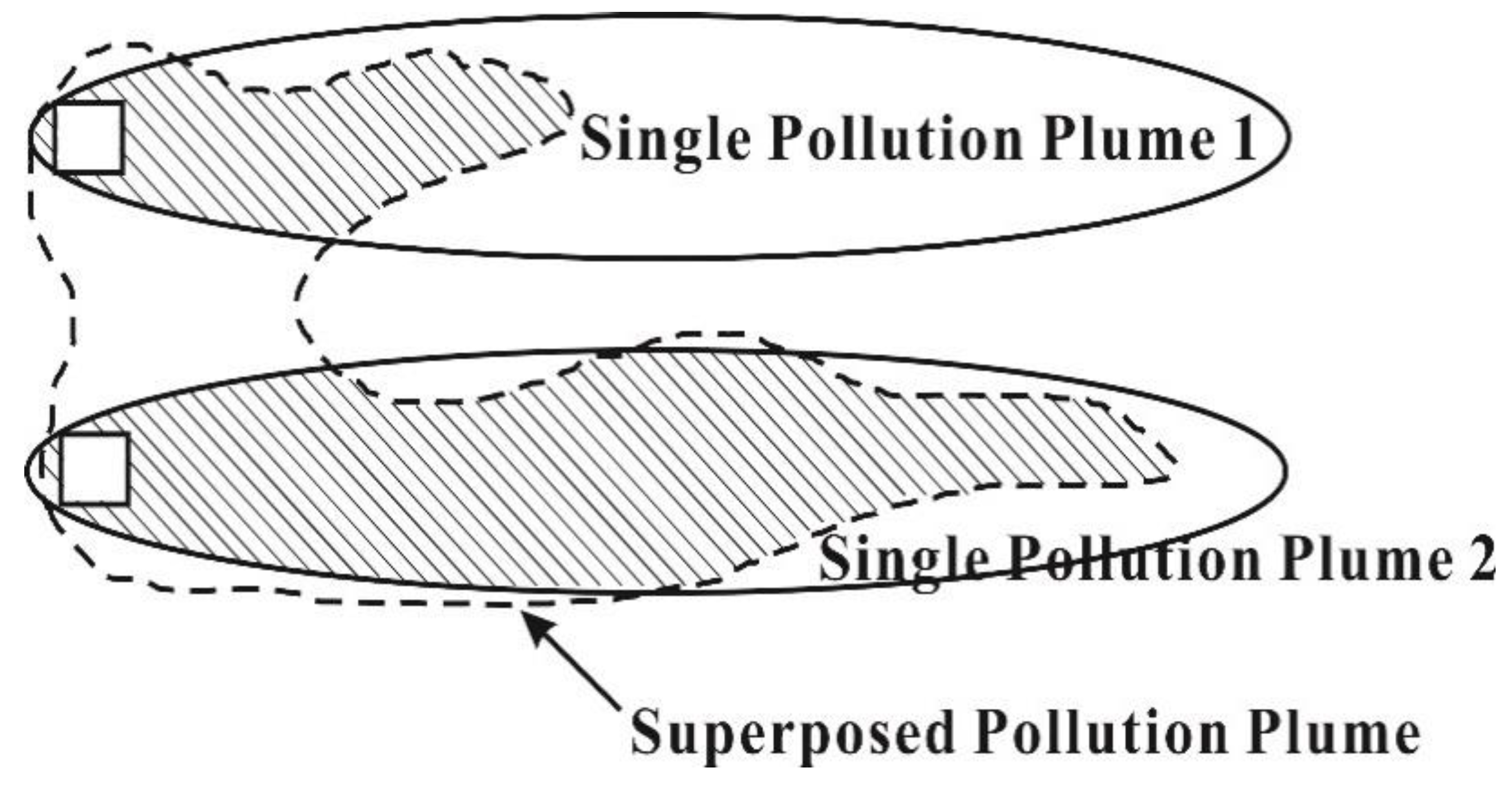
- Step 4: According to the weight of the pollution source, the concentration field is randomly selected from the concentration field library and the superposed pollution plume and covariance matrix are generated in combination with the mass-loading rate of the pollution source.
- Step 5: Combined with the existing sampling data, the Kalman filter method is used to update the superposed pollution plume and the covariance matrix.
- Step 6: According to the reduction in the overall uncertainty, new sampling data are selected sequentially using variance reduction with the Kalman filter method.
- Step 7: Without adjusting the weight value of the pollution source, a linear programming model is adopted to identify the source mass-loading rate by using the existing sampling data.
- Step 8: The superposed pollution plume is generated from the concentration field library based on the weight and mass-loading rate values prior to this step.
- Step 9: Combined with the sampling data obtained prior to this step, the Kalman filter method is used to update the superposed pollution plume.
- Step 10: Based on the morphological comparison of pollution plume, the weight value of the pollution source is updated by using the alpha-cut technique.
2.2. Groundwater Contaminant Transport Simulation
2.3. Stochastic Simulation
2.4. Concentration Field Library
2.5. Kalman Filter Approach
2.6. Alpha-Cut Technique of a Fuzzy Set
2.7. Linear Optimization Model
3. Application of the Proposed Method
3.1. Aquifer Site
3.2. Pollution Source Identification Problem
3.3. Erroneous Monitoring Data
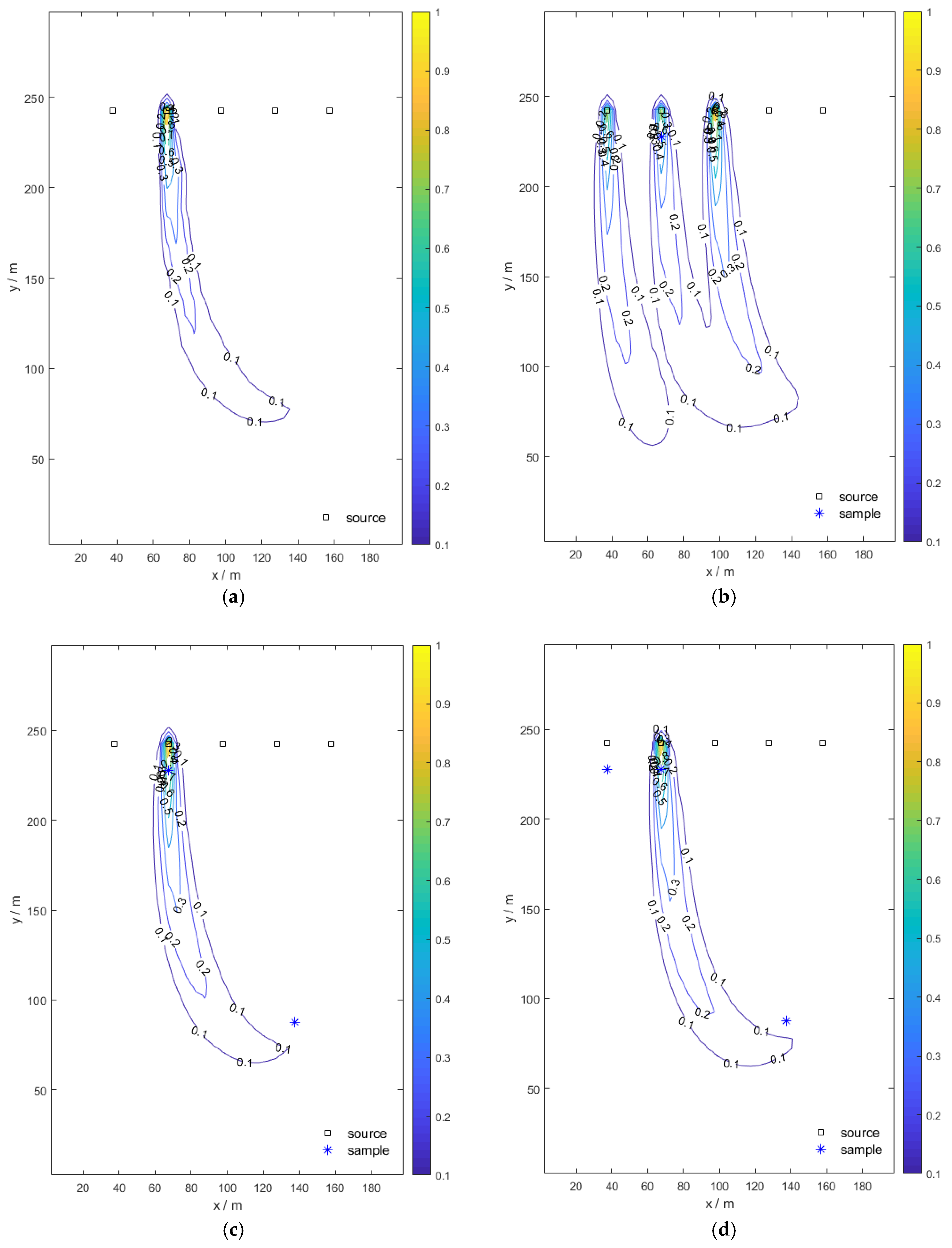
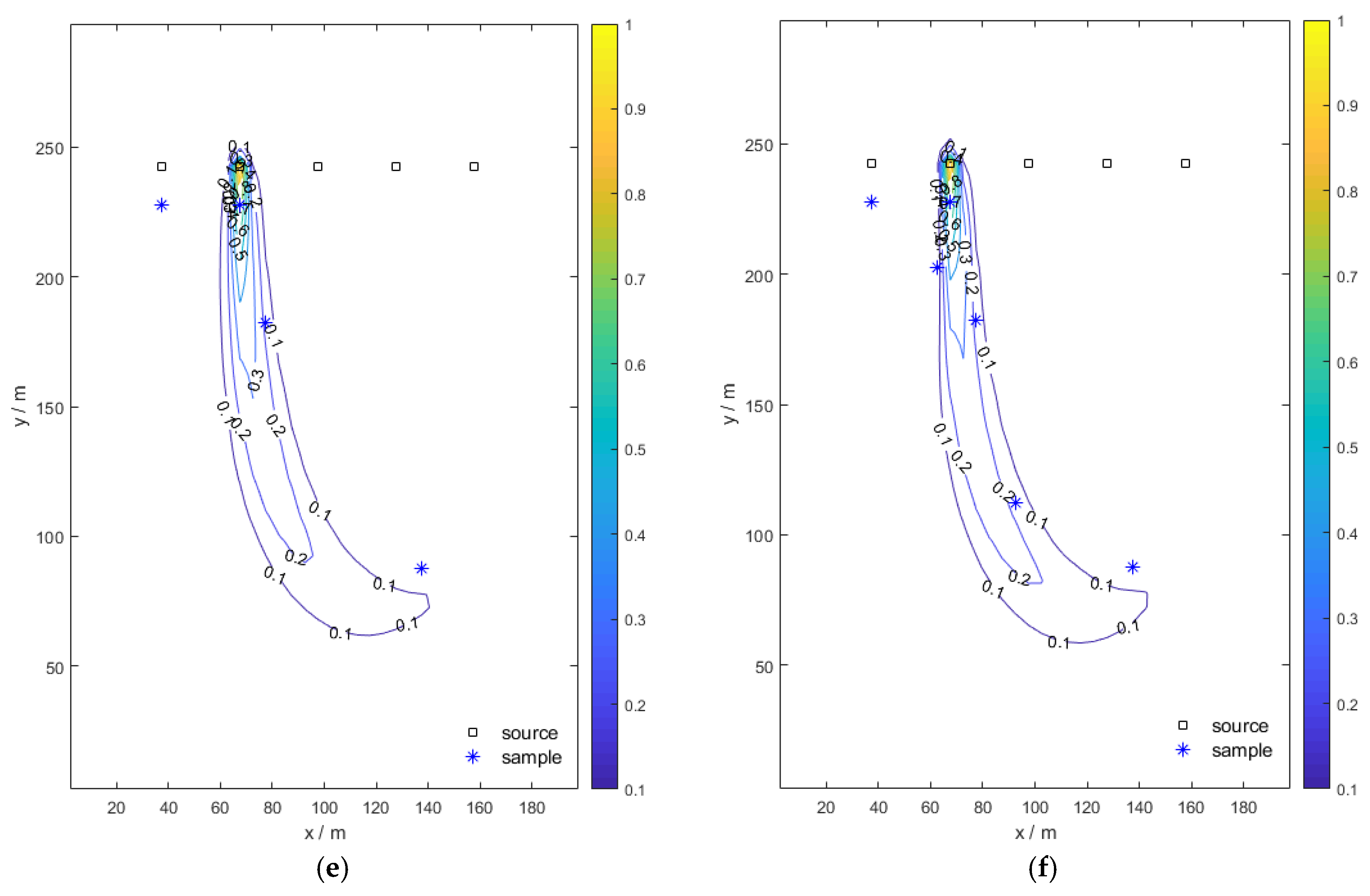
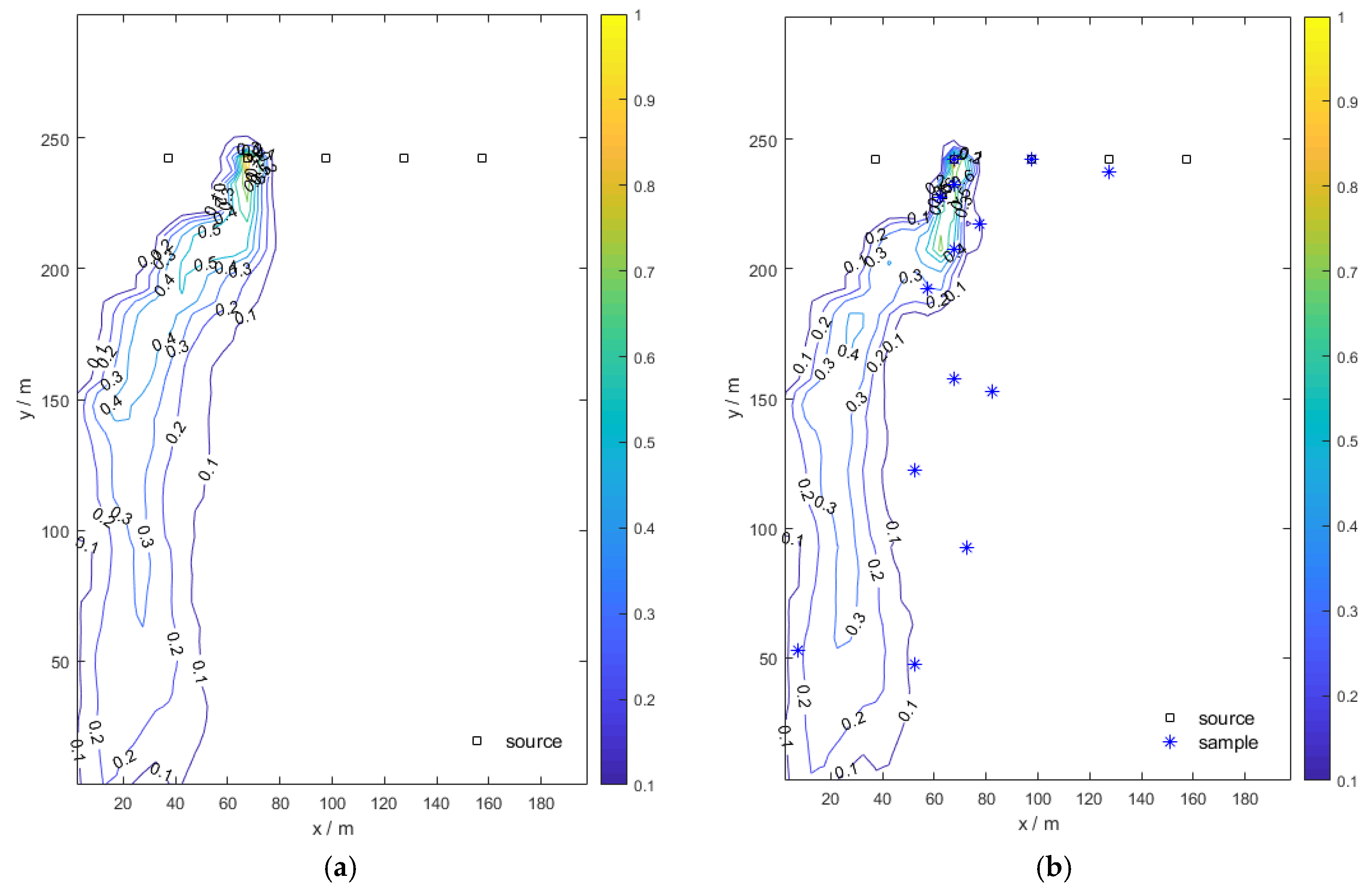
4. Results and Discussion
4.1. Stochastic Modeling Analysis
4.2. Pollution Source Identification
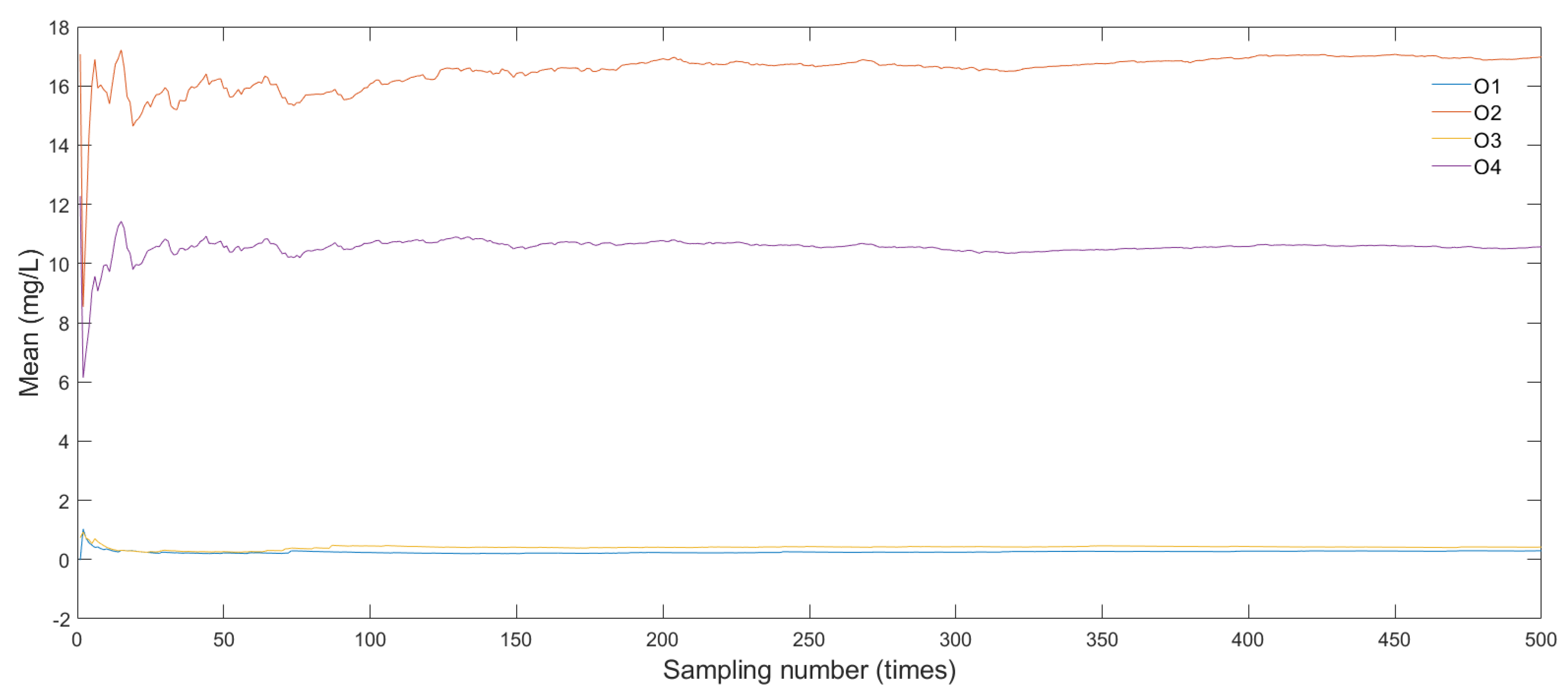
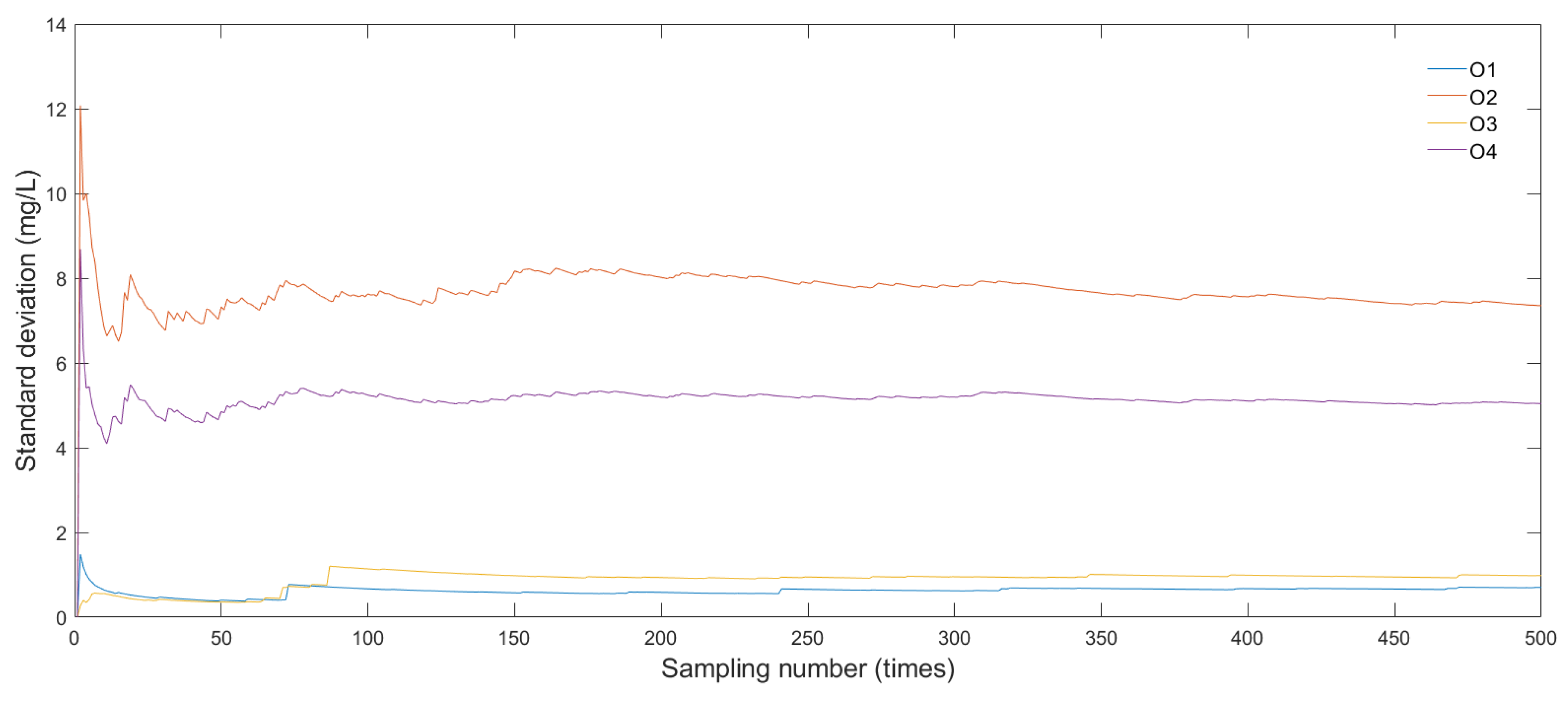
4.3. Sensitivity Analysis
5. Summary and Conclusions
- (1)
- The purpose of the proposed method is to facilitate the remediation strategy of the contaminated sites in an attempt to realize the cost of the pollution source identification and the plume characterization (optimal monitoring network design).
- (2)
- The proposed Kalman filter-based method incorporates multiple techniques such as the concentration field library, the covariance reduction with the Kalman filter, the alpha-cut technique of the fuzzy set, and the linear programming model, which are demonstrated for the pollution source identification and plume characterization.
- (3)
- The performance of this methodology is evaluated on an illustrative groundwater pollution source identification problem and the identified results indicate that the proposed Kalman filter-based optimization model can give satisfactory estimations even when the random hydraulic conductivity field, erroneous monitoring data, prior information shortage of potential pollution sources, and unexpected unknown pumping well are considered.
- (4)
- The results of the sensitivity analysis investigate the effect of various algorithm parameters on convergence. It is concluded that the most important parameter is the setting of α-cuts used at the plume comparison step. The identification results are less sensitive to the setting of initial weights and is not sensitive to the setting of the initial mass-loading rate.
- (5)
- The results from the sensitivity analysis on heterogeneity of hydraulic conductivity field proves that our proposed method would be effective in identifying the true source location and characterizing the pollution plume even under a moderate heterogeneity condition, but the performance may be less satisfied. Additionally, our proposed method is completely ineffective in a highly heterogeneous field (variance = 16.0). It indicates that the proposed method can provide relatively satisfied results for a homogeneous domain or domain with small and moderate heterogeneity, but it cannot validate the transport in the relatively high heterogeneous field.
- (6)
- In this work, our proposed method is designed and assembled for two-dimensional problems and it should be modified to be integrated into three-dimensional problems. In the two-dimensional field, new sampling points are selected to minimize the overall uncertainty of the concentration field. However, for the three-dimensional field, sampling points may exist in different layers and, therefore, exhibit different uncertainties. Whether layered processing is more effective requires further study by comparing it with overall processing. The extension of the alpha-cut technique for comparison of plume in a three-dimensional field is another aspect worthy of further study.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abriola, L.M. Guest editorial: Contaminant source zones: Remediation or perpetual stewardship? Environ. Health Perspect. 2005, 113, A438–A439. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Mahar, P.S.; Datta, B. Optimal monitoring network and ground-water–pollution source identification. J. Water Res. Plan. Man. 1997, 123, 199–207. [Google Scholar] [CrossRef]
- McGrath, W.A.; Pinder, G.F. Search strategy for groundwater contaminant plume delineation: Search strategy for contaminant plume. Water Resour. Res. 2003, 39, 3163–3170. [Google Scholar] [CrossRef]
- Nunes, L.M.; Paralta, E.; Cunha, M.C.; Ribeiro, L. Groundwater nitrate monitoring network optimization with missing data: Groundwater nitrate monitoring optimization. Water Resour. Res. 2004, 40, 935–945. [Google Scholar] [CrossRef]
- Ayvaz, M.T. A hybrid simulation–optimization approach for solving the areal groundwater pollution source identification problems. J. Hydrol. 2016, 538, 161–176. [Google Scholar] [CrossRef]
- Datta, B.; Chakrabarty, D.; Dhar, A. Optimal dynamic monitoring network design and identification of unknown groundwater pollution sources. Water Resour. Manag. 2009, 23, 2031–2049. [Google Scholar] [CrossRef]
- Dhar, A.; Datta, B. Multiobjective design of dynamic monitoring networks for detection of groundwater pollution. J. Water Res. Plan. Man. 2007, 133, 329–338. [Google Scholar] [CrossRef]
- Jha, M.K.; Datta, B. Linked simulation-optimization based dedicated monitoring network design for unknown pollutant source identification using dynamic time warping distance. Water Resour. Manag. 2014, 28, 4161–4182. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, Y.; Wang, P.; Zheng, M. An almost-parameter-free harmony search algorithm for groundwater pollution source identification. Water Sci. Technol. 2013, 68, 2359–2366. [Google Scholar] [CrossRef] [PubMed]
- Prakash, O.; Datta, B. Sequential optimal monitoring network design and iterative spatial estimation of pollutant concentration for identification of unknown groundwater pollution source locations. Environ. Monit. Assess. 2013, 185, 5611–5626. [Google Scholar] [CrossRef] [PubMed]
- Atmadja, J.; Bagtzoglou, A.C. Pollution source identification in heterogeneous porous media. Water Resour. Res. 2001, 37, 2113–2125. [Google Scholar] [CrossRef]
- Michalak, A.M.; Kitanidis, P.K. Estimation of historical groundwater contaminant distribution using the adjoint state method applied to geostatistical inverse modeling. Water Resour. Res. 2004, 40, W08302. [Google Scholar] [CrossRef]
- Sun, A.Y.; Painter, S.L.; Wittmeyer, G.W. A constrained robust least squares approach for contaminant release history identification. Water Resour. Res. 2006, 42, W04414. [Google Scholar] [CrossRef]
- Cupola, F.; Tanda, M.G.; Zanini, A. Laboratory sandbox validation of pollutant source location methods. Stoch. Environ. Res. Risk A 2015, 29, 169–182. [Google Scholar] [CrossRef]
- Ayvaz, M.T. A linked simulation–optimization model for solving the unknown groundwater pollution source identification problems. J. Contam. Hydrol. 2010, 117, 46–59. [Google Scholar] [CrossRef] [PubMed]
- Dokou, Z.; Pinder, G.F. Optimal search strategy for the definition of a dnapl source. J. Hydrol. 2009, 376, 542–556. [Google Scholar] [CrossRef]
- Herrera, G.S.; Pinder, G.F. Space-time optimization of groundwater quality sampling networks: Groundwater quality sampling networks. Water Resour. Res. 2005, 41, W12047. [Google Scholar] [CrossRef]
- Ross, J.L.; Andersen, P.F. The ensemble kalman filter for groundwater plume characterization: A case study: The ensemble kalman filter for groundwater plume characterization: A case study. Groundwater 2018. [Google Scholar] [CrossRef]
- Zhang, Y.; Pinder, G.F.; Herrera, G.S. Least cost design of groundwater quality monitoring networks: Design of groundwater monitoring network. Water Resour. Res. 2005, 41, 553–559. [Google Scholar] [CrossRef]
- Man, J.; Li, W.; Zeng, L.; Wu, L. Data assimilation for unsaturated flow models with restart adaptive probabilistic collocation based Kalman filter. Adv. Water Resour. 2016, 92, 258–270. [Google Scholar] [CrossRef]
- Xu, T.; Gómez-Hernández, J.J. Joint identification of contaminant source location, initial release time, and initial solute concentration in an aquifer via ensemble Kalman filtering. Water Resour. Res. 2016, 52, 6587–6595. [Google Scholar] [CrossRef]
- Xu, T.; Gómez-Hernández, J.J. Simultaneous identification of a contaminant source and hydraulic conductivity via the restart normal-score ensemble Kalman filter. Adv. Water Resour. 2018, 112, 106–123. [Google Scholar] [CrossRef]
- Xue, L. Application of the Multimodel Ensemble Kalman Filter Method in Groundwater System. Water 2015, 7, 528–545. [Google Scholar] [CrossRef]
- Chang, L.F.; Sun, N.Z.; Yeh, W.G. Optimal observation network design for parameter structure identification in groundwater modeling. Water Resour. Res. 2005, 41, 69–80. [Google Scholar] [CrossRef]
- Kollat, J.B.; Reed, P. A framework for visually interactive decision-making and design using evolutionary multi-objective optimization (video). Environ. Model. Softw. 2007, 22, 1691–1704. [Google Scholar] [CrossRef]
- Marsily, G.D.; Delhomme, J.P.; Coudrain-Ribstein, A.; Lavenue, A.M. Four decades of inverse problem in hydrogeology. Spec. Pap. Geol. Soc. Am. 2000, 348, 1–17. [Google Scholar] [CrossRef]
- Amirabdollahian, M.; Datta, B. Identification of contaminant source characteristics and monitoring network design in groundwater aquifers: An overview. J. Environ. Prot. 2013, 04, 26–41. [Google Scholar] [CrossRef]
- Kollat, J.B.; Reed, P.M. Comparing state-of-the-art evolutionary multi-objective algorithms for long-term groundwater monitoring design. Adv. Water Resour. 2006, 29, 792–807. [Google Scholar] [CrossRef]
- Loaiciga, H.A. An optimization approach for groundwater quality monitoring network design. Water Resour. Res. 1989, 25, 1771–1782. [Google Scholar] [CrossRef]
- Wu, J.; Zheng, C.; Chien, C.C.; Zheng, L. A comparative study of Monte Carlo simple genetic algorithm and noisy genetic algorithm for cost-effective sampling network design under uncertainty. Adv. Water Resour. 2006, 29, 899–911. [Google Scholar] [CrossRef]
- Cieniawski, S.E.; Eheart, J.W.; Ranjithan, S. Using genetic algorithms to solve a multiobjective groundwater monitoring problem. Water Resour. Res. 1995, 31, 399–409. [Google Scholar] [CrossRef]
- Reed, P.M.; Minsker, B.S. Striking the balance: Long-term groundwater monitoring design for conflicting objectives. J. Water Res. Plan. Man. 2004, 130, 140–149. [Google Scholar] [CrossRef]
- Zeng, X.; Ye, M.; Burkardt, J.; Wu, J.; Wang, D.; Zhu, X. Evaluating two sparse grid surrogates and two adaptation criteria for groundwater Bayesian uncertainty quantification. J. Hydrol. 2016, 535, 120–134. [Google Scholar] [CrossRef]
- Singh, A.; Mishra, S.; Ruskauff, G. Model Averaging Techniques for Quantifying Conceptual Model Uncertainty. Ground Water 2010, 48, 701–715. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Pinder, G. Latin hypercube lattice sample selection strategy for correlated random hydraulic conductivity fields. Water Resour. Res. 2003, 39, 472–477. [Google Scholar] [CrossRef]
- Gorelick, S.M.; Evans, B.; Remson, I. Identifying sources of groundwater pollution: An optimization approach. Water Resour. Res. 1983, 19, 779–790. [Google Scholar] [CrossRef]
- Butera, I.; Tanda, M.G.; Zanini, A. Simultaneous identification of the pollutant release history and the source location in groundwater by means of a geostatistical approach. Stoch. Environ. Res. Risk A 2013, 27, 1269–1280. [Google Scholar] [CrossRef]
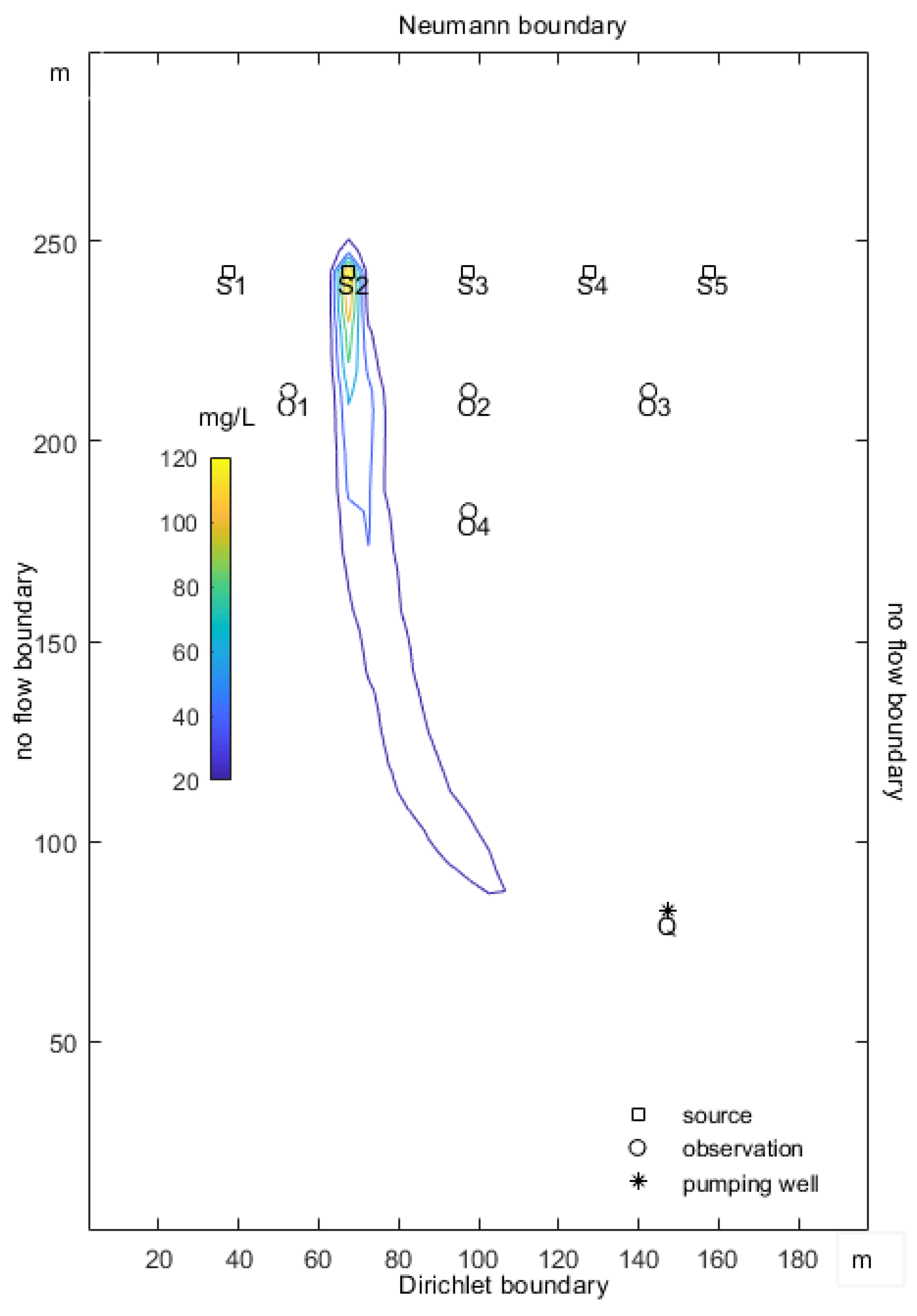
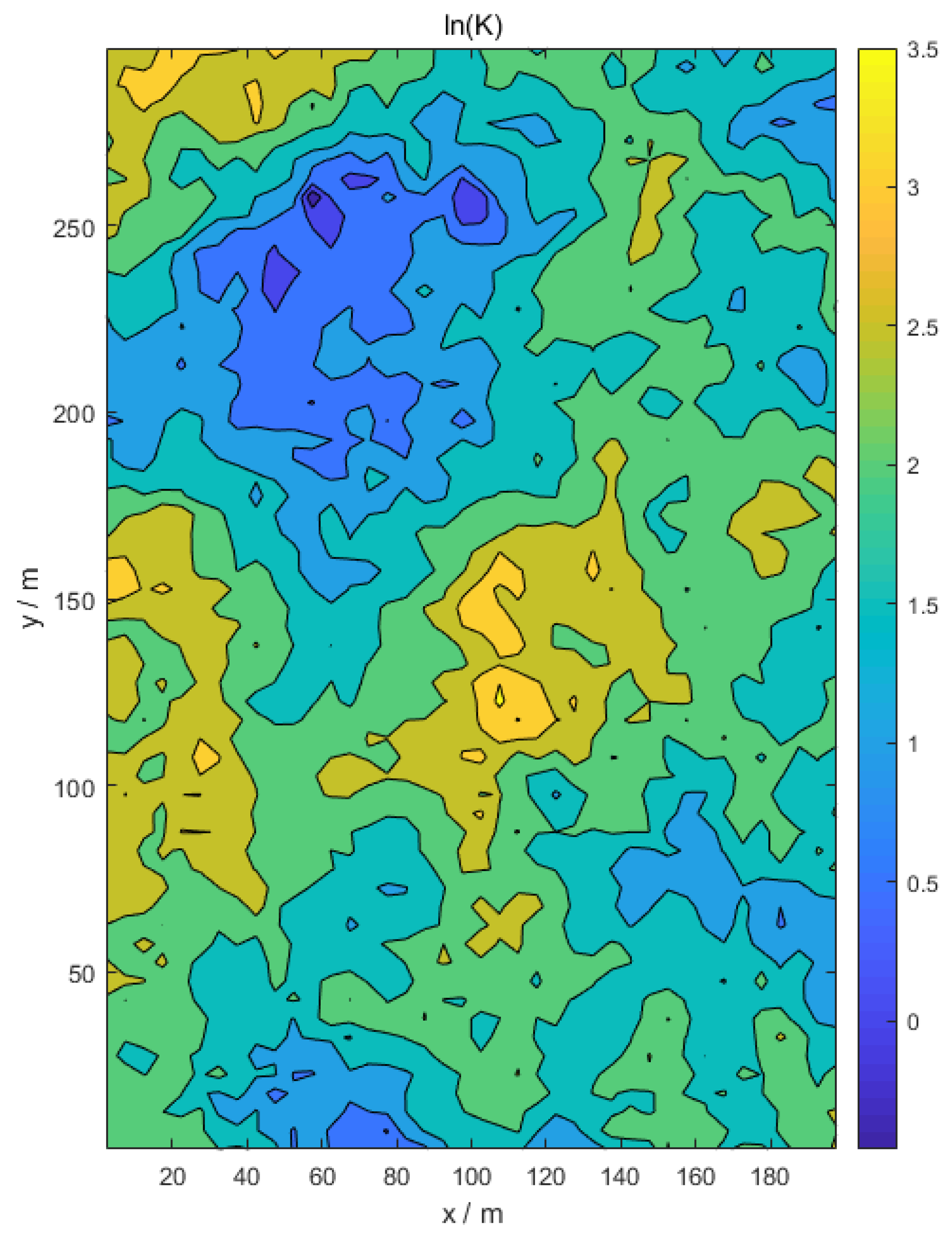
| Parameters | Unit | Value |
|---|---|---|
| Grid spacing in x direction | m | 5 |
| Grid spacing in y direction | m | 5 |
| Saturated thickness | m | 10 |
| Top elevation of aquifer | m | 20 |
| Bottom elevation of aquifer | m | 10 |
| Effective porosity | dimensionless | 0.30 |
| Longitudinal dispersivity | m | 4 |
| Transverse dispersivity | m | 1.2 |
| Effective diffusion coefficient | m2/day | 1.75 × 10−4 |
| Sampling Number | Source 1 | Source 2 | Source 3 | Source 4 | Source 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | |
| 0 | 200 | 0.7 | 200 | 0.8 | 200 | 0.9 | 200 | 0.6 | 200 | 0.8 |
| 1 | 1000 | 0.48 | 868.4 | 0.39 | 1000 | 1.0 | 0.01 | 0 | 0.01 | 0 |
| 2 | 0.01 | 0 | 1000 | 1 | 60.2 | 0 | 0.01 | 0 | 0.01 | 1 |
| 3 | 0.01 | 0 | 694.72 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 1 |
| 4 | 0.01 | 0 | 578.52 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 1 |
| 5 | 0.01 | 0 | 530.64 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 1 |
| 6 | 0.01 | 0 | 530.64 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 |
| α-Cuts Setting | Sampling Points Needed | Source 1 | Source 2 | Source 3 | Source 4 | Source 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | ||
| (0.2 0.4 0.6 0.8) | 6 | 0.01 | 0 | 530.64 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 |
| (0.2 0.4 0.6) | 13 | 0.01 | 0 | 578.26 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 |
| (0.3 0.6 0.78 0.9) | 10 | 0.01 | 0 | 542.36 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 |
| Initial Weight | Sampling Points | Source 1 | Source 2 | Source 3 | Source 4 | Source 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | ||
| (0.7 0.8 0.9 0.6 0.8) | 6 | 0.01 | 0 | 530.64 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 |
| (0.7 0.1 0.9 0.6 0.8) | 11 | 0.01 | 0 | 543.28 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 |
| (0.1 0.1 0.1 0.1 1.0) | 11 | 0.01 | 0 | 551.73 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 |
| Initial Mass-Loading Rate | Sampling Points | Source 1 | Source 2 | Source 3 | Source 4 | Source 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | ||
| (200 200 200 200 200) | 6 | 0.01 | 0 | 530.64 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 |
| (200 20 200 200 200) | 6 | 0.01 | 0 | 530.64 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 |
| (195 16 85 16 171) | 6 | 0.01 | 0 | 530.64 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 |
| Heterogeneity | Sampling Points | Source 1 | Source 2 | Source 3 | Source 4 | Source 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | Mass-Loading Rate (g/day) | Weight | ||
| small | 6 | 0.01 | 0 | 530.64 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 |
| moderate | 14 | 0.01 | 0 | 422.32 | 1 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, S.; Fan, J.; Xia, X.; Li, X.; Zhang, R. An Effective Kalman Filter-Based Method for Groundwater Pollution Source Identification and Plume Morphology Characterization. Water 2018, 10, 1063. https://doi.org/10.3390/w10081063
Jiang S, Fan J, Xia X, Li X, Zhang R. An Effective Kalman Filter-Based Method for Groundwater Pollution Source Identification and Plume Morphology Characterization. Water. 2018; 10(8):1063. https://doi.org/10.3390/w10081063
Chicago/Turabian StyleJiang, Simin, Jinhong Fan, Xuemin Xia, Xianwen Li, and Ruicheng Zhang. 2018. "An Effective Kalman Filter-Based Method for Groundwater Pollution Source Identification and Plume Morphology Characterization" Water 10, no. 8: 1063. https://doi.org/10.3390/w10081063
APA StyleJiang, S., Fan, J., Xia, X., Li, X., & Zhang, R. (2018). An Effective Kalman Filter-Based Method for Groundwater Pollution Source Identification and Plume Morphology Characterization. Water, 10(8), 1063. https://doi.org/10.3390/w10081063





