Abstract
This study proposes a flow field modeling analysis of kitchen environments with air-conditioning range hoods. The substructure approach is applied to resolve the challenges of low computational efficiency and convergence difficulties associated with the simultaneous consideration of the range hood and the cooling air-conditioning fan impeller rotation models. The presented approach effectively enhances computational efficiency while ensuring accuracy. A flow field analysis of the air-conditioning substructure was performed in Fluent to obtain the velocity contour plot at the air-conditioning outlet monitoring surface. The data were then mapped to the full kitchen hood model to enable a comprehensive flow field analysis of the kitchen setup. The results show that the proposed substructure-based method to analyze the flow field in kitchens with air-conditioning hoods is computationally efficient, achieving an alignment accuracy above 95% across four measurement points. These findings establish a strong foundation for future comfort assessments and the optimization of kitchens with air-conditioning hoods.
1. Introduction
Research into the effects of air quality and thermal environments on health, comfort, and productivity [1], along with growing awareness of the unsatisfactory physical conditions in Chinese residential kitchens (CRKs) [2], has led to steadily increasing environmental standards for CRKs [3,4,5]. Currently, cooker hoods are widely used to expel heat and pollutants generated during cooking, thereby improving the thermal environment and indoor air quality in CRKs [2]. The effects of indoor air quality and thermal conditions in residential kitchens on occupant health and comfort are significant, particularly in high-density urban areas, where cooking-related pollutants and heat contribute to poor indoor environmental quality. Understanding how kitchen ventilation systems, including those with air-conditioning features, can be optimized is crucial for enhancing indoor air quality and thermal comfort.
Although cooker hoods are designed with cooling in mind, their actual cooling effectiveness is limited, highlighting the need for research on hoods equipped with air-conditioning features. The air-conditioning hood includes not only the hood fan impeller but also a chiller air-conditioning fan impeller, among other components. Therefore, studying the impact of multiple fan impellers on the kitchen flow field is essential.
However, the existing models for analyzing kitchen flow fields often overlook the combined effects of the air-conditioning and hood fan impellers, which limit both the accuracy and practicality of simulations. Zhang et al. [6] used CFD simulations to calculate the key parameters influencing the exhaust air volume and supply air temperature of a commercial kitchen ventilation and air-conditioning (VAC) system, which included exhaust, supplementary air, and air conditioning. They proposed that personalized regulation of supply air can significantly reduce the energy consumption of the VAC system. Wang et al. [7] examined an air-conditioning system that combined rear and ceiling air conditioning and found it to be effective in enhancing the thermal environment in commercial kitchens. Xu et al. [8] conducted an experimental study to evaluate the effect of exhaust airflow on the residential kitchen environment, measuring the thermal and humidity conditions, air quality, and noise levels of cooker hoods with varying exhaust airflows.
Guo et al. [9] studied the performance of cooker hoods across different cooking scenarios using orthogonal experiments and CFD simulations and designed various auxiliary ventilation systems to improve particle concentration capture efficiency in the breathing zone. Bartolozzi et al. [10] developed the SMACK (SM Art Energy Efficient Kitchen) system in the field of architectural design to promote energy efficiency and sustainability, minimizing the need for separate heating and cooling equipment in kitchens and, thereby, reducing overall energy consumption. These studies demonstrate that multifunctional systems have extensive applications in kitchen design.
Currently, flow field analyses of kitchen air-conditioning hoods primarily focus on examining the impact of parameters such as the exhaust rate of the hood, the intensity of the heat source, and the velocity of the air curtain [11,12,13,14,15] or the refrigerant flow rate and the air supply temperature of the air conditioner [16,17,18,19] on the outcomes. However, research on kitchen systems integrating both air conditioning and hoods remains scarce, with most studies analyzing calculations from a single perspective [20].
Existing research on centrifugal fan design has primarily focused on optimizing the geometry of components such as blades and volutes and the spacing between the blade and the volute tongue to improve aerodynamic performance. For instance, Li et al. [21] demonstrated that larger impellers increase the total pressure but reduce efficiency, while Younsi et al. [22] analyzed the effects of irregular blade spacing and the radial distance between the impeller’s perimeter and the volute tongue. These studies have significantly contributed to the structural optimization of centrifugal fans, particularly by improving performance through modifications to the internal flow characteristics.
However, when simulating the aerodynamic behavior of multi-impeller systems, traditional computational fluid dynamics (CFD) methods face substantial challenges. Direct simulation of multiple impellers requires separate modeling of each impeller’s rotating domain, leading to high computational demands and poor convergence, especially in complex systems with multiple rotating fans. These methods are computationally expensive and time-consuming, rendering them impractical for real-time simulations or large-scale applications.
In this study, we adapt the substructure function-mapping technique, originally developed in solid mechanics, to fluid dynamics. This technique decomposes complex systems into smaller substructures, improving computational efficiency. By modeling only the impeller’s rotating domain within a substructure model and mapping the resulting data to the full system model, this approach eliminates redundant calculations for each rotating domain. As a result, the substructure method significantly reduces computational complexity and improves convergence while maintaining high simulation accuracy.
For example, traditional CFD methods require extensive computation and significant time to simulate each impeller’s rotational effects, leading to inefficiencies. In contrast, by applying the substructure method, the number of rotational models is reduced, thereby preserving computational efficiency and achieving comparable or even better accuracy in flow field predictions. This is particularly evident when modeling multi-impeller systems, where the substructure approach provides a more efficient and scalable solution compared to conventional CFD methods.
This study employs the computational fluid dynamics (CFD) method to construct a comprehensive model of a kitchen with an air-conditioning hood and performs a calibration analysis of the simulation model using empirical test data. To enhance the efficiency and accuracy of the simulation, this study utilizes the solid mechanics substructure method [23,24], addressing the challenge of convergence in the calculations involving the rotating models of the hood and air-conditioning fan impellers by incorporating them into the complete model, thereby significantly improving computational efficiency and accuracy. This approach proposes a robust method for studying and analyzing the flow field in kitchen environments with air-conditioning hoods.
The paper begins with a brief theoretical background and the governing equations. It then explains the CFD-modeling approach used to simulate the kitchen environment with the integrated air-conditioning hood, which includes the hood fan impeller, the chiller air-conditioning fan impeller, and the cooling fan impeller. The application of the substructure method to handle the rotating fan impellers is discussed in detail, followed by a presentation of the simulation results. Finally, the study discusses the significance of the findings, the limitations, and the potential directions for future research.
2. Theoretical Analysis
2.1. Basic Equations
This study employs ANSYS Fluent 2021 software for CFD simulations, modeling the flow field within the kitchen environment as a steady and incompressible turbulent flow. To ensure the applicability of the governing equations under the incompressible flow assumption, the density was considered constant, which is a valid simplification for the low Mach number flows typically encountered in kitchen environments. To streamline the model without compromising the required accuracy, energy losses due to viscous interactions between gas molecules are neglected.
The governing Equations (2)–(4) are presented in their general form and are applicable to both compressible and incompressible flows. These fundamental conservation equations of mass, momentum, and energy provide the foundation for fluid dynamics analysis. Under the incompressible flow assumption, which is appropriate for low Mach number ventilation scenarios in kitchen environments, density is treated as constant [25,26]. Consequently, the continuity equation simplifies to the divergence-free condition:
while the momentum equation retains its general form but is solved under the incompressible assumption. The energy equation is not explicitly solved in this study, as the primary focus is on airflow distribution rather than temperature-driven density variations. The incompressible flow assumption is a well-established simplification in computational fluid dynamics (CFD), particularly for low Mach number flows where density variations are negligible. This assumption has been widely adopted in ventilation system modeling and indoor airflow studies, ensuring computational efficiency while maintaining accuracy [25,26,27,28].
The relevant governing equations, including the continuity equation and Navier–Stokes equations, represent the fundamental physical principles governing fluid motion.
The continuity equation is:
The conservation of momentum equation (Navier–Stokes equation) is:
The energy conservation equation is:
where is the spatial coordinate, is the magnitude of the velocity, is the partial velocity in the Cartesian coordinate system, , is time, is the fluid density, is the pressure on the fluid element, is the dynamic viscosity coefficient, is the instantaneous temperature, is specific heat capacity at constant pressure, and is the heat transfer coefficient.
2.2. Sub-Model Function-Mapping Technique
In the numerical simulation of complex hydrodynamic systems, direct simulation of the entire system often requires extensive computational resources and poses significant convergence challenges. To enhance simulation efficiency and accuracy, modular modeling approaches are widely adopted. Among these, the sub-model function-mapping (SFM) technique provides an effective method for transferring flow field information and mapping boundary conditions between sub-models and the full system model. This technique, originally developed for solid mechanics, has been widely applied in various studies to improve computational efficiency and reduce time consumption [29,30].
2.2.1. Theoretical Basis of Sub-Model Function-Mapping
The sub-model function-mapping technique relies on the continuum medium assumption in fluid dynamics and the principle of boundary condition transfer. By mapping flow field data from the local sub-model onto the corresponding boundary of the overall model, an integrated coupling between the local and global flow fields can be achieved. This approach effectively reduces the need for redundant modeling and the computation of complex components, ensuring the simulation’s accuracy and efficiency.
The substructure method was originally developed and widely applied in solid mechanics to analyze the strength and vibrational characteristics of complex systems. This method involves dividing large-scale models into smaller, more manageable substructures, which significantly reduces computational time and complexity. In this study, we have innovatively extended the application of the substructure method from solid mechanics to fluid dynamics [29,30]. Specifically, we applied this technique to model the multi-fan impeller system in a kitchen air-conditioning range hood. By leveraging this approach, we addressed significant challenges in simulating complex fluid flows, such as the low computational efficiency and poor convergence typically encountered when modeling multiple rotating fan impellers. This innovative application not only enhances the accuracy and efficiency of the simulation but also provides a robust solution for the specific modeling needs of kitchen ventilation systems.
2.2.2. Technical Implementation Steps
(1) Sub-model Calculation and Data Export
In ANSYS Fluent 2021, this study simulates the rotation of the fan impeller in the air-conditioning substructure model to obtain the velocity distribution on the air-conditioning outlet surface. The velocity vector data for this surface is exported as a .prof file, which records the coordinates of the outlet nodes and their corresponding velocity components, forming a function that describes the surface’s velocity field.
(2) Mapping and Boundary Condition Setting for Sub-model Functions
The boundary surfaces in the full model that correspond to the air-conditioning outlet are identified. By using Fluent’s “Import Profile” function, the previously exported .prof file is imported into the full system model. This file is then assigned as a velocity boundary condition to the relevant boundary surface, enabling the transfer of the sub-model’s velocity field data to the full model. At this point, the air-conditioning sub-model’s flow field characteristics are accurately incorporated into the full model, eliminating the need to re-model and recalculate the air-conditioning fan impeller.
(3) Simulation and Verification of the Full Model
In the full model, only the hood fan impeller is simulated using a rotational domain, which reduces the complexity of the model. CFD simulations of the full model are then performed using the mapped sub-model functions. To verify the effectiveness of the sub-model function mapping, this study compares the flow field distribution near the air-conditioning outlet in the full model with the corresponding sub-model calculations, ensuring accurate data transfer.
This study innovatively applies the sub-model function-mapping technique to the CFD simulation of a combined kitchen air-conditioning and hood system, achieving effective coupling between the local sub-model and the full model. This approach addresses challenges in computational efficiency and accuracy associated with simulating multi-fan impeller systems, providing an efficient and reliable methodology for the modular simulation of complex hydrodynamic systems with broad application potential.
3. CFD Modeling of a Kitchen with an Air-Conditioning Hood
3.1. Model Description
Figure 1 shows the geometric model of the test kitchen developed in this study, with dimensions of 3760 mm (length) × 3000 mm (width) × 2850 mm (height). The air-conditioning outlet in the air-conditioning hood is positioned below the hood. Additionally, a human body model with a height of 1.6 m was incorporated to consider the kitchen environment’s impact on the human body.
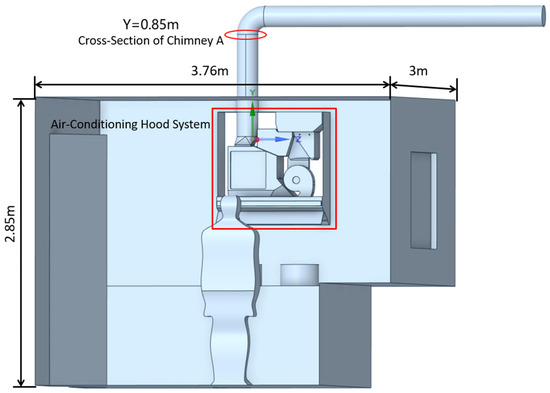
Figure 1.
Geometric model of the kitchen environment.
The air-conditioning hood system contains three rotating fan impellers (Figure 2): the hood fan impeller, the chiller air-conditioning fan impeller, and the cooling fan impeller. The hood fan impeller is equipped with a volute and is primarily used to extract fumes, which are discharged to the outside through a top exhaust pipe. The air-conditioning fan impeller is a critical component of the air-conditioning system and is responsible for supplying cool air. The cooling unit fan impeller aids in fume extraction and air filtration, enhancing air circulation within the kitchen and maintaining air quality.
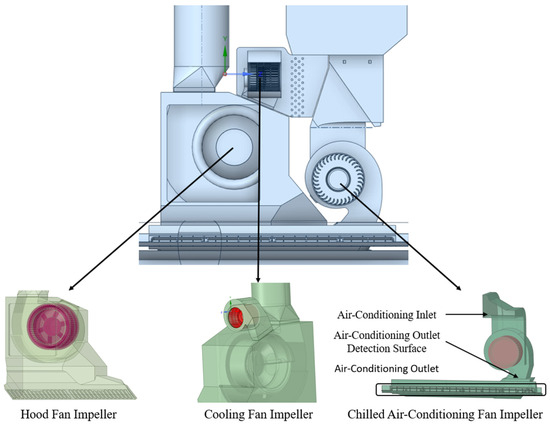
Figure 2.
Diagram of the three fan impellers in the air-conditioning hood.
To enhance the efficiency of the kitchen flow field simulation and account for the complex internal structure of the air-conditioning hood, this study adopts a modular and simplified modeling approach. In the simulation process, only the rotational model of the hood fan impeller is used to simulate its impact on the overall flow field, while the other fan impellers are simulated by setting flow control boundary conditions.
In this study, we employ an integrated air-conditioning hood system that combines both air-conditioning and fume extraction functions into a single unit. While this type of integrated system, which we refer to as SMACK, is not the traditional setup in Chinese kitchens, it is gaining traction, especially in modern kitchen designs where space optimization is a key factor. The main benefits of this arrangement include:
1. Space optimization: the combined system reduces the need for multiple separate units, which is particularly useful for compact kitchen spaces;
2. Reduction in ductwork: this integration reduces the complexity of the installation by minimizing the number of ducts required;
3. Improved indoor air quality: by simultaneously addressing cooling and air filtration, the system maintains better temperature and air quality control.
However, this approach also presents some challenges:
1. Increased design complexity: the integration of both systems requires careful design to ensure they do not interfere with each other, especially regarding thermal performance;
2. Thermal interference: the coexistence of cooling and fume extraction processes can result in thermal conflicts, potentially affecting overall system efficiency;
3. Higher installation cost: the initial setup of such integrated systems may be more costly compared to conventional separate systems.
This innovative design is becoming more common in urban kitchens, where space and efficiency are paramount. We believe that future studies could further explore the feasibility and potential optimization of such integrated kitchen systems.
3.2. Mesh Generation and Independence Analysis
An unstructured mesh is applied to mesh the air-conditioning hood model, with a minimum mesh size of 1 mm in critical regions and a maximum mesh size of 100 mm in less dynamically sensitive areas. To ensure sufficient resolution in regions with significant flow development, mesh refinement is specifically implemented in high-velocity gradient areas, including the pan surface, the rotational domain of the hood, and the air-conditioning outlet region, as shown in Figure 3.
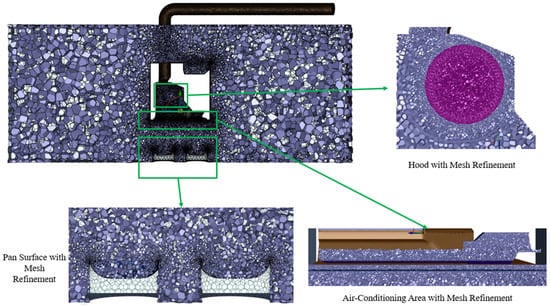
Figure 3.
Mesh refinement in critical areas of the model.
Steady-state flow field analyses of the kitchen with an air-conditioning hood during the cooking process are conducted. Mesh sizes of 2.02 million, 2.40 million, and 2.85 million cells were selected to perform a systematic mesh independence study. The cross-section of chimney A in Figure 1 was chosen as the monitoring surface. Simulated flow calculations were carried out for each of the three mesh models, and the results were compared with the test flow data.
As shown in Table 1, the simulated and tested flow rates at the chimney A cross-section exhibit minimal differences when using mesh sizes of 2.4 million and 2.85 million cells, with the errors maintained within 5% of the experimental results. Considering a balance between computational efficiency and accuracy, this study selected the 2.4 million mesh size for further calculations. The results indicate that the adopted mesh resolution is sufficient to capture key flow features without unnecessary computational expense.

Table 1.
Comparison of flow rates at the monitoring surface for different mesh sizes.
3.3. Simulation Methods and Boundary Condition Settings
Table 2 presents the models and computational boundary conditions used in this study, while Table 3 provides the boundary condition settings for the three types of fan impellers.

Table 2.
Boundary condition parameters for the CFD model.

Table 3.
Control boundary conditions for fan impellers in the base model.
In this study, oil fumes were modeled as water vapor using a simple species transport model. Since the focus of this research is on airflow and temperature–humidity distribution in the kitchen environment rather than oil fume particle dynamics, no multiphase flow model was employed. Additionally, neither the discrete phase model (DPM) nor the volume of fluid (VOF) model was used, as the transport of oil droplets was not explicitly simulated.
Since this study focuses on the overall airflow characteristics in the kitchen environment rather than detailed near-wall flow effects, boundary layer meshes (prism layers) were not generated, and y+ values were not explicitly computed [25,26]. The mesh resolution is designed to ensure an accurate representation of the overall velocity and temperature distributions while maintaining computational efficiency. This approach is consistent with previous studies on airflow modeling in indoor environments, where near-wall effects are not the primary concern [27,28].
3.4. Experimental Validation and Comparison Analysis
The accuracy of the simulation model in this study is validated using flow field test results from the air-conditioned hood test kitchen during the cooking process. Figure 4 shows the locations of the four test points positioned above and at an angle to the pan surface (test point 1) and at the air-conditioning outlets (test points 2 to 4). These points monitored the airflow velocity at the pan surface and air-conditioning outlets with the air conditioner running during cooking. Table 4 shows the specific test control conditions, and the field test setup is shown in Figure 5.
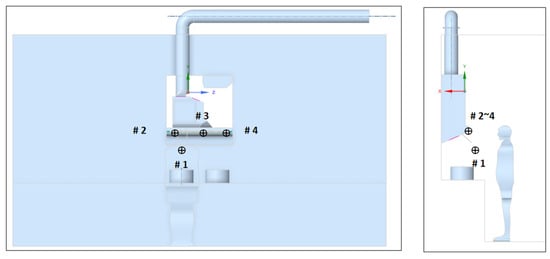
Figure 4.
Measurement points in the kitchen model (#1–4 indicate test points 1–4).

Table 4.
Experimental control conditions for the test setup.

Figure 5.
Field test setup in the test kitchen.
During the field test, a mixture of oil and water was added to a frying pan to simulate real-life cooking conditions. Personnel movement was restricted during the test phase to prevent airflow from affecting the cooking-related airflow diffusion. To accurately measure airflow velocity, data were recorded using a test instrument once the airflow stabilized, capturing measurements every second for a total of 120 s. Figure 6 illustrates the test data curves over 120 s for different measurement positions, with the corresponding average velocities for each position. These average values are directly labeled in the figure to provide a more intuitive presentation of the results.
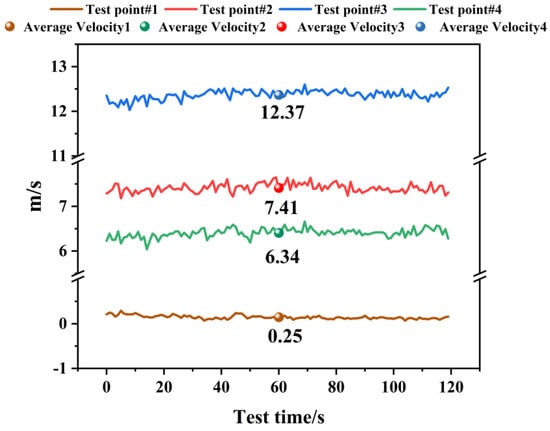
Figure 6.
Airflow velocity data at different test points.
Figure 7 and Figure 8 show the velocity cloud map results for the center cross-section of the human body model and the air-conditioning outlet in the kitchen model. Table 5 compares the simulated velocity at each measurement point with the test results. The results show that measurement points 1 to 3 demonstrate relatively high accuracy, while measurement point 4 shows a larger error. This discrepancy arises because the cold air-conditioning fan impeller in Table 3 does not use a rotational model, and a uniform flow assumption was applied at the outlet.
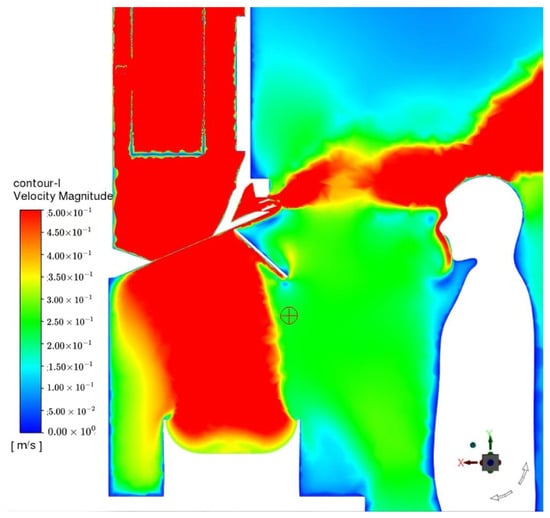
Figure 7.
Velocity cloud map of the center cross-section in the kitchen model.
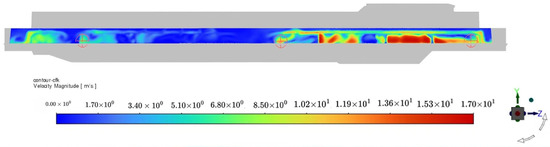
Figure 8.
Velocity cloud map of the air-conditioning outlet in the kitchen model.

Table 5.
Comparison of simulated and test velocities at measurement points.
To address this issue, four scenarios were designed, as shown in Table 6.

Table 6.
Four scenarios designed to optimize the original model and improve simulation accuracy.
Scenario A is where all three fan impellers in the model are simulated with rotational models. However, this approach increases the mesh size from 2.4 million to 5.21 million, significantly reducing computational efficiency and leading to convergence challenges.
Scenario B is where, since the cooling fan impeller has a relatively minor effect on the airflow at the air-conditioning outlet, only the hood and chilled air-conditioning fan impellers use rotational models. Although mesh size is reduced, convergence remains challenging due to the presence of two rotational models.
For Scenario C, this scenario builds on Scenario B by simulating the air-conditioning outlet detection surface with a uniform flow assumption, using only the hood impeller’s rotational model. However, the uniform flow assumption introduces significant error.
For Scenario D, in this improved scenario, the chilled air-conditioning fan impeller is modularized. A substructure model simulates the impeller’s rotational characteristics, mapping the resulting flow data from the substructure model to the corresponding location in the kitchen hood model. This approach reduces the number of rotational models, eliminating errors from the uniform flow assumption and improving both the model accuracy and the efficiency.
4. CFD Modeling with the Air-Conditioning Substructure
In solid mechanics, the substructure method is commonly used to analyze the strength and vibration characteristics of complex systems by dividing large finite-element models into substructures, thereby reducing computation time [30].
4.1. Air-Conditioning Substructure Model and Boundary Condition Settings
The control boundary conditions for the fan impeller in the air-conditioning substructure model are set according to Scenario D from Table 6. Figure 9 presents the air-conditioning substructure model, which is meshed using an unstructured mesh to calculate the flow distribution at the air-conditioning outlet detection surface.
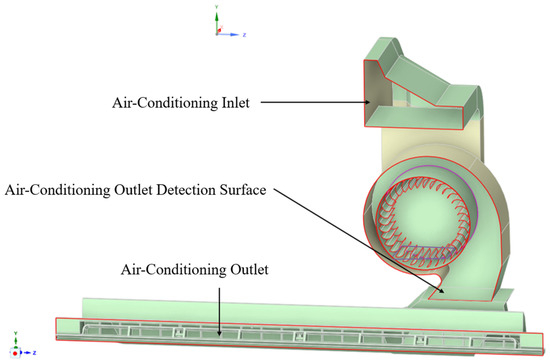
Figure 9.
Air-conditioning substructure model (for clarity, the front impeller baffle has been hidden).
4.2. Analysis of the Air-Conditioning Substructure Model
The air-conditioning substructure model is analyzed using the same simulation approach as the full kitchen model. Figure 10 shows the velocity distribution on the air-conditioning outlet detection surface of the substructure model. As indicated in the figure, due to the rotation of the air-conditioning impeller, the velocity distribution at the outlet detection surface is non-uniform, with higher flow rates observed in the outer-edge regions of the impeller’s rotation.
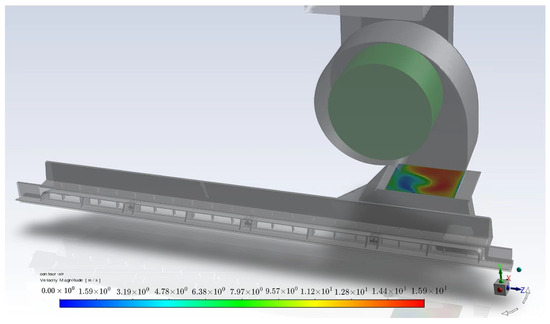
Figure 10.
Velocity cloud map at the air-conditioning outlet detection surface in the substructure model.
4.3. Sub-Model Function Mapping
After completing the calculations for the air-conditioning substructure model, the velocity data on the air-conditioning outlet detection surface are exported as a Fluent .prof file. This file is then imported into the full kitchen model, allowing the flow data from the air-conditioning outlet detection surface in the substructure model to be mapped onto the corresponding location in the kitchen hood model.
Figure 11 shows the velocity cloud map of the air-conditioning outlet detection surface in the full kitchen model under the uniform flow assumption, while Figure 12 shows the velocity cloud map at the air-conditioning outlet detection surface after mapping the flow data from the substructure model. In the sub-model function-mapping (SFM) process, the comparison between Figure 11 and Figure 12 clearly highlights the improvements achieved by using the substructure model for mapping flow data at the air-conditioning outlet. Figure 11 displays the velocity cloud map at the air-conditioning outlet detection surface in the full kitchen model, assuming a uniform flow distribution. As shown, the velocity distribution appears relatively uniform across the outlet, which fails to capture the detailed variations in the actual flow behavior at the outlet.
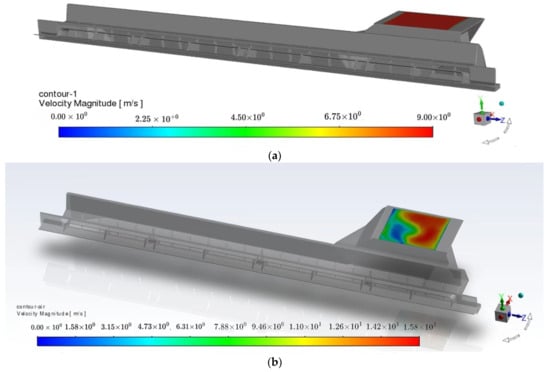
Figure 11.
(a) Velocity cloud map at the air-conditioning outlet detection surface in the full kitchen model under the uniform flow assumption. (b) Velocity cloud map at the air-conditioning outlet detection surface in the full kitchen model after mapping the substructure model data.

Figure 12.
Comparison of velocity cloud maps at the air-conditioning outlet with and without the substructure model.
In contrast, Figure 12 illustrates the velocity cloud map after applying the substructure model, which offers a more accurate representation of the actual airflow. This map captures the true variability in the airflow at the air-conditioning outlet, particularly in regions with higher velocity gradients. Such improvements are significant because the substructure-mapping technique better simulates the effects of the rotating impellers, highlighting the localized variations in velocity due to the impellers’ influence.
The advantage of using the substructure function-mapping approach is evident in the enhanced resolution and more realistic representation of the airflow dynamics. This approach is particularly critical for understanding the detailed airflow behavior, which is crucial for optimizing kitchen ventilation systems and ensuring an accurate simulation of complex fluid flow phenomena.
4.4. Comparison and Analysis
After applying the air-conditioning substructure model, the simulated velocities at the measurement points and their comparisons with the test velocities are shown in Table 7. The comparison of velocity cloud maps at the measurement point locations is presented in Figure 12 The results indicate that, in the original model, the velocity at the air-conditioning outlet is primarily concentrated on the right side. However, after applying the substructure model, the velocity distribution becomes more uniform and realistic.

Table 7.
Comparison of simulated and test velocities at measurement points after applying the air-conditioning substructure model.
A comparison of the simulation results with the test data indicates that the velocity error at measurement point 4 is reduced by 10.4%, with the errors at all four measurement points within 5%. The airflow velocity at the air-conditioning outlet shows a trend of higher flow rates in the center and lower flow rates on both sides, which aligns with the trend observed in the test results. This confirms that the air-conditioning substructure model significantly improves the simulation accuracy and effectively resolves the issue of there being a larger error at measurement point 4 in the original model.
5. Discussion
5.1. Significance of Results
This study introduces an innovative application of the substructure method, originally developed in solid mechanics, to fluid dynamics for kitchen airflow simulations. By modularizing the air-conditioning fan impeller and mapping its flow characteristics to the overall system, the proposed method achieved exceptional computational efficiency and accuracy. Specifically, it resolved the convergence challenges associated with dual-fan models and improved the accuracy at critical measurement points to within a 5% error margin. These results highlight the potential of this method for optimizing air-conditioning hood designs and managing airflow in kitchen environments. Its demonstrated precision and computational efficiency make it a valuable tool for addressing practical engineering challenges, such as improving thermal comfort, minimizing pollutant dispersion, and enhancing energy efficiency in kitchens.
Furthermore, the findings underscore the versatility of the substructure method for broader applications in complex multi-subsystem simulations. The potential applications include HVAC system designs and internal engine flow analyses. By significantly reducing computational demands while maintaining high accuracy, this study lays the groundwork for real-time simulations and large-scale industrial implementations.
5.2. Limitations of the Study
Despite its promising results, this study has certain limitations.
First, the simulation assumes steady-state flow conditions, which may not fully capture transient effects, such as variations in cooking intensity or environmental disturbances like opening windows. While steady-state simulations are computationally efficient, they do not account for time-dependent dynamics, such as the varying behavior of rotating impellers or changes in flow patterns due to fluctuating cooking conditions. Future research could address this limitation by incorporating unsteady-state simulations, which would better represent real-world dynamics and provide more detailed insights into the unsteady behavior of the system. This would allow for a more comprehensive understanding of the transient effects, which is particularly important for capturing the time-varying behavior of kitchen airflow under different operating conditions.
Second, the boundary conditions applied in the model are idealized. Real kitchen environments, with their multiple heat sources and human movement, introduce complexities that were not fully considered in this study. Accurate calibration and validation of boundary conditions across diverse scenarios will be critical to improving the reliability of the model.
Lastly, this study focuses on a single kitchen configuration, which limits the generalizability of the results. Variations in kitchen layouts, equipment placement, and ventilation systems may require additional modifications to the model. Expanding the validation process to include different kitchen setups would enhance the robustness and applicability of the proposed method.
5.3. Future Research Directions
Building on the findings of this study, future research could explore the following directions:
(1) Developing unsteady-state models to capture dynamic changes in airflow caused by cooking activities or environmental fluctuations;
(2) Integrating more realistic boundary conditions to better reflect diverse kitchen environments and improve model applicability;
(3) Extending the application of the substructure method to other complex fluid dynamic systems, such as multi-zone HVAC systems or industrial ventilation setups;
(4) Further optimizing the substructure method to enhance computational efficiency, enabling real-time simulation capabilities;
(5) Conducting experimental validation of the method in various kitchen configurations to establish its universality and adaptability;
6. Conclusions
This study focuses on analyzing the flow field in a kitchen equipped with an air-conditioning hood and introduces a new method for kitchen flow field analysis. By combining simulation with experimental data, the following main conclusions are drawn:
- (1)
- Application of the substructure method: This study effectively applies the substructure method from solid mechanics to flow field analysis in fluid mechanics. Dividing the complex system into multiple substructures simplifies the calculations, reduces computational complexity, and enhances simulation accuracy;
- (2)
- Development of a flow field analysis method: A kitchen flow field analysis method based on the substructure approach is introduced. In this method, the fan impeller rotation model is first considered in the cooling air-conditioning substructure model. The corresponding results are then mapped to the overall model, which includes the hood fan impeller rotation model. This approach addresses the computational inefficiency and convergence issues typically associated with considering both fan rotation models within a single system;
- (3)
- Enhanced modularity and scalability through sub-model function mapping: This study enhances the modularity and scalability of the model using sub-model function mapping. This technique not only improves computational efficiency and accuracy but also makes the proposed method versatile, enabling its application in other CFD simulation scenarios with complex multi-subsystems, such as HVAC systems and the internal flow field analysis of engines;
- (4)
- Improved simulation accuracy at the air-conditioning outlet: A comparison between simulated and test airflow velocities at the air-conditioning outlet shows that the velocity error at measurement point 4 is reduced by 4.8%, from an initial error of 15.4% to a final error within 5%, after applying the substructure method. This result validates the substructure method’s effectiveness in flow field analysis, demonstrating significant improvements in simulation accuracy and efficiency.
In summary, this study applies the sub-model function-mapping technique to the CFD simulation of a combined kitchen air-conditioning and range hood system, achieving effective coupling between the local sub-model and the overall model. By enhancing computational efficiency, ensuring simulation accuracy, and improving model modularity and scalability, this method provides an efficient and reliable approach for simulating complex fluid dynamic systems. The close integration of theory and practical engineering demonstrates the method’s substantial potential and broad applicability in real-world applications, offering a valuable reference for future research in related fields.
Author Contributions
X.H.: Conceptualization, Writing—original draft, Formal analysis, Supervision, Software. Z.S.: Data curation, Visualization, Writing—review and editing. S.Z.: Conceptualization, Data curation, Supervision, Writing—review and editing. Y.T.: Data curation, Methodology. A.L.: Investigation, Validation, Visualization. B.Y.: Methodology, Visualization. Y.J.: Software, Supervision. L.P.: Project administration, Visualization. Z.C.: Funding acquisition, Resources, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding, and the APC was funded by Zhenlei Chen.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available upon request from the corresponding author, Zhenlei Chen, upon reasonable request.
Acknowledgments
We would like to thank the Zhejiang Province Public Welfare Technology Application Research Project (LGG22E080020), the Healthy & Intelligent Kitchen Engineering Research Center of Zhejiang Province (ZFGGJ2021-389), digital simulation design for high-end equipment manufacturing of Shijiazhuang (248790037A) and the National “111” Centre on Safety and Intelligent.
Conflicts of Interest
Authors Ang Li, Bingsong Yu and Yi Jiang were employed by the company Fotile Group Ningbo Fotile Kitchenware Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CRKs | Chinese Residential Kitchens |
| CFD | Computational Fluid Dynamics |
| VAC | Ventilation and Air Conditioning |
| SMACK | SM Art Energy Efficient Kitchen |
| SFM | Sub-model Function Mapping |
| DPM | Discrete Phase Model |
| VOF | Volume of Fluid |
| HVAC | Heating Ventilation Air Conditioning |
References
- Zhao, Y.; Li, A.; Gao, R.; Tao, P.; Shen, J. Measurement of Temperature, Relative Humidity and Concentrations of CO, CO2 and TVOC during Cooking Typical Chinese Dishes. Energy Build. 2014, 69, 544–561. [Google Scholar] [CrossRef]
- Liu, S.; Dong, J.; Cao, Q.; Zhou, X.; Li, J.; Lin, X.; Qing, K.; Zhang, W.; Chen, Q. Indoor Thermal Environment and Air Quality in Chinese-Style Residential Kitchens. Indoor Air 2020, 30, 198–212. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Li, C.; Dong, J.; Meng, C.; Hu, K. Improving Kitchen Environment Comfort and Health: A Comprehensive Evaluation Method Based on Objective and Subjective Factors. Energy Build. 2023, 301, 113700. [Google Scholar] [CrossRef]
- Lai, C. Assessment of Side Exhaust Systems for Residential Kitchens in Taiwan. Build. Serv. Eng. Res. Technol. 2005, 26, 157–166. [Google Scholar] [CrossRef]
- Wei, P.; Zhou, B.; Tan, M.; Li, F.; Lu, J.; Dong, Z.; Xu, M.; Wang, G.; Xiao, Y. Study on Thermal Comfort under Non-Uniform Thermal Environment Condition in Domestic Kitchen. In Proceedings of the 10th International Symposium on Heating, Ventilation and Air Conditioning, ISHVAC 2017, Jinan, China, 19–22 October 2017; Volume 205, pp. 2041–2048. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, F.; Liu, H.; Xia, Y.; He, L.; Yu, Y.; Zeng, L.; Cao, C.; Gao, J. Energy Savings of Commercial Kitchen Ventilation and Air Conditioning Systems Based on Cooking Oil Control and Thermal Comfort. Energy Build. 2024, 315, 114317. [Google Scholar] [CrossRef]
- Wang; Jiang, Y.L.; Shi, H.; Wang, Y. Numerical Analysis of Indoor Thermal Comfort in Large Commercial Kitchen. World Sci-Tech. R D 2014, 36, 236–240. [Google Scholar]
- Xu, X.; Li, C.; Liu, Y.; Dong, J.; Meng, C. Optimizing the Range Hood Airflow Rate to Improve the Kitchen Environment and Reduce Energy Consumption. Sustain. Energy Technol. Assess. 2024, 69, 103915. [Google Scholar] [CrossRef]
- Guo, Z.; Li, H.; Feng, G.; Huang, K.; Yu, T. Analysis and Research on Inherent Angle Ventilation Control of Residential Kitchen Range Hoods. Energy Built Environ. 2025, 6, 432–447. [Google Scholar] [CrossRef]
- Bartolozzi, G.; Palma, G.; Rizzo, A. Energy Saving Starts in the Kitchen. Energy Build. 2024, 322, 114726. [Google Scholar] [CrossRef]
- Lv, L.; Zeng, L.; Wu, Y.; Gao, J.; Xie, W.; Cao, C.; Zhang, J. The Application of an Air Curtain Range Hood in Reducing Human Exposure to Cooking Pollutants. Build. Environ. 2021, 205, 108204. [Google Scholar] [CrossRef]
- Lv, L.; Gao, J.; Zeng, L.; Cao, C.; Zhang, J.; He, L. Performance Assessment of Air Curtain Range Hood Using Contaminant Removal Efficiency: An Experimental and Numerical Study. Build. Environ. 2021, 188, 107456. [Google Scholar] [CrossRef]
- Shi, L.; Liu, Z.; Wen, W.; Son, J.H.; Li, L.; Wang, L.; Chen, J. Spatial Distributions of Particle Number Size Distributions Generated during Cooking Processes and the Impacts of Range Hoods. Sci. Total Environ. 2023, 881, 163243. [Google Scholar] [CrossRef]
- Benchikh Le Hocine, A.E.; Poncet, S.; Fellouah, H. CFD Modeling of the CO2 Capture by Range Hood in a Full-Scale Kitchen. Build. Environ. 2020, 183, 107168. [Google Scholar] [CrossRef]
- Han, O.; Li, A.; Kosonen, R. Hood Performance and Capture Efficiency of Kitchens: A Review. Build. Environ. 2019, 161, 106221. [Google Scholar] [CrossRef]
- Cho, W.; Heo, J.; Park, M.H.; Seo, H.J.; Lee, K.; Lee, D.G.; Kim, Y. Energy Performance and Thermal Comfort of Integrated Energy Recovery Ventilator System with Air-Conditioner for Passive Buildings. Energy Build. 2023, 295, 113302. [Google Scholar] [CrossRef]
- Bojic, M.; Lee, M.; Yik, F. Influence of a Depth of a Recessed Space to Flow Due to Air-Conditioner Heat Rejection. Energy Build. 2002, 34, 33–43. [Google Scholar] [CrossRef]
- Yu, B.F.; Hu, Z.B.; Liu, M.; Yang, H.L.; Kong, Q.X.; Liu, Y.H. Review of Research on Air-Conditioning Systems and Indoor Air Quality Control for Human Health. Int. J. Refrig. 2009, 32, 3–20. [Google Scholar] [CrossRef]
- Reddy, T.A.; Claridge, D.E. Effect of Air-Conditioner Oversizing and Control on Electric-Peak Loads in a Residence. Energy 1993, 18, 1139–1152. [Google Scholar] [CrossRef]
- Zhang, S.; Huang, X.; Li, A.; Yu, B.; Jiang, Y.; Peng, L.; Chen, Z. Improving Kitchen Thermal Comfort in Summer Based on Optimization of Airflow Distribution. J. Build. Eng. 2024, 96, 110614. [Google Scholar] [CrossRef]
- Chunxi, L.; Ling, W.S.; Yakui, J. The Performance of a Centrifugal Fan with Enlarged Impeller. Energy Convers. Manag. 2011, 52, 2902–2910. [Google Scholar] [CrossRef]
- Younsi, M.; Bakir, F.; Kouidri, S.; Rey, R. Influence of Impeller Geometry on the Unsteady Flow in a Centrifugal Fan: Numerical and Experimental Analyses. Int. J. Rotating Mach. 2007, 2007, 034901. [Google Scholar] [CrossRef]
- Bui, T.A.; Park, J.; Kim, J.-S. A Reduced-Order Model for Geometrically Nonlinear Curved Beam Structures with Substructuring Techniques. Int. J. Non-Linear Mech. 2024, 162, 104724. [Google Scholar] [CrossRef]
- Iroz, I.; Carvajal, S.; Hanss, M.; Eberhard, P. Inverse Fuzzy Arithmetic for the Quality Assessment of Substructured Models. Procedia IUTAM 2015, 13, 34–42. [Google Scholar] [CrossRef][Green Version]
- Pope, S.B. Turbulent Flows; Higher Education from Cambridge; Cambridge University Press: Cambridge, UK, 2000; Available online: https://www.cambridge.org/highereducation/books/turbulent-flows/C58EFF59AF9B81AE6CFAC9ED16486B3A (accessed on 4 February 2025).
- Batchelor, G.K. (Ed.) An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000; Available online: https://www.cambridge.org/core/books/an-introduction-to-fluid-dynamics/18AA1576B9C579CE25621E80F9266993/listing (accessed on 4 February 2025).
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Wiley: New York, NY, USA; Longman Scientific & Technical: Harlow, UK, 1995; ISBN 978-0-470-23515-7. [Google Scholar]
- Srinivasacharya, D.; Reddy, K.S. (Eds.) Numerical Heat Transfer and Fluid Flow: Select Proceedings of NHTFF 2018; Springer: Singapore, 2018; Available online: https://link.springer.com/book/10.1007/978-981-13-1903-7 (accessed on 4 February 2025).
- Narvydas, E.; Puodziuniene, N.; Thorappa, A.K. Application of Finite Element Sub-Modeling Techniques in Structural Mechanics. Mechanics 2021, 27, 459–464. Available online: https://www.semanticscholar.org/paper/Application-of-Finite-Element-Sub-modeling-in-Narvydas-Puodziuniene/f483d7750f2773eccf837e022d7050512f52b0b1 (accessed on 4 February 2025). [CrossRef]
- Ramsay, A.C.A.; Maunder, E.A.W. Sub-Modelling and Boundary Conditions with p-Type Hybrid-Equilibrium Plate-Membrane Elements. Finite Elem. Anal. Des. 2006, 43, 155–167. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).