Reconstruction of Daily Courses of SO42−, NO3−, NH4+ Concentrations in Precipitation from Cumulative Samples
Abstract
:Highlights
- Long-term precipitation chemistry data from professional Czech Hydrometeorological Institute stations were analysed.
- We examined the behaviour of SO42−, NO3− and NH4+ concentrations from wet-only samples.
- Daily concentrations were reconstructed from cumulative samples of different exposure time length.
- Useful for study of systematic annual and seasonal changes and other analyses.
- We integrated Nested Laplace Approximation, a useful, novel tool for exploiting complicated large-scale data.
Abstract
1. Introduction
2. Methods
2.1. Measuring Sites
2.2. Precipitation Sampling and Chemical Analysis
2.3. Statistical Modelling
- t is the time in daily resolution indexed from the beginning of the data available from the station modelled.
- is a function that extracts the year from a given time position t.
- is a function that extracts the position of the day within a year from a given time position t.
- is the natural logarithm of the ion concentration.
- is the overall mean (unknown constant to be estimated from data).
- is the annual component. That is, a (potentially nonlinear) concentration trend in years. It is an unknown smooth function of no pre-assumed functional form (to be estimated from data). It is implemented non-parametrically as the random walk of second order; i.e., for an integer j, we assume , where .
- is the seasonal component. That is, an unknown smooth function of no pre-assumed functional form (to be estimated from data) describing a smooth within-year concentration pattern common for all years with available data. In order to be physically realistic, this component is periodic (the 31 December value has to smoothly match the 1 January value). It is implemented non-parametrically, as the first-order cyclic random walk.
- is the component describing the potential interaction between the annual and seasonal parts. It is this term that allows for smooth deformation of the seasonal part over the years. The presence of this term generalises the overly restrictive standard annual plus seasonal decomposition. This is necessary, as it is clear both from previous knowledge and from even a crude look at the data that the seasonal concentration profile can change quite profoundly over the years (standard decomposition would insist that it does not change systematically, hence it would provide a potentially highly distorted picture of the reality). The term is, in fact, an unknown function of two variables (to be estimated from the data) assumed to be smooth. Beyond that, no particular functional form is assumed. Formally, this is a parsimonious interaction term (not a full, saturated interaction as in standard ANOVA models [46]). It is implemented non-parametrically, as a smooth Gaussian random field [47] with Matérn covariance structure (with smoothness parameter ). This allows for a rather flexible modelling of departures from the fixed annual plus seasonality model.
- is the systematic part of the model (linear predictor).
- is the measurement error (assuming ).
- is the nx1 vector of available observations (where n is the number of measurements available).
- is the nx1 vector of measurement errors.
- is the nxT matrix specifying the time aggregation invoked by the non-trivial collection lengths. In our application, it is a matrix of zeros and ones (generally, it can contain zeros and non-negative weights when considering decays). Its i-th row has ones at column positions corresponding to days over which the i-th sample was collected, and zeros otherwise.
- is the Tx1 vector of linear predictors from model (1) for the T days covering the time interval of interest between the start of the first (I = 1) sample and end of the last (I = n) sample available in the data. arises as a sum of overall mean vector (). is an annual component (Tx1 vector of from model (1) evaluated at T days’ stretch of interval of interest), is a seasonal component (Tx1 vector of from model (1) evaluated at T days of interval of interest) and is an interaction component (Tx1 vector of from model (1) evaluated at T days of interval of interest).
3. Results
4. Discussion
4.1. Specific Comments on the Observed Patterns
4.2. Problems in Long-Term Assessment Arising from Changes in Monitoring with Respect to Sampling Period Length
4.3. Overall Evaluation
5. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics; John Wiley: New York, NY, USA, 1998; p. 1326. [Google Scholar]
- Pacyna, J.M. Atmospheric Deposition. In Encyclopedia of Ecology; Academic Press: Cambridge, MA, USA, 2008; pp. 275–285. Available online: https://www.sciencedirect.com/science/article/pii/B9780080454054002585 (accessed on 10 April 2022).
- Galloway, J.N.; Cowling, E.B. The Effects of Precipitation on Aquatic and Terrestrial Ecosystems: A Proposed Precipitation Chemistry Network. J. Air Pollut. Control Assoc. 1978, 28, 229–235. [Google Scholar] [CrossRef] [Green Version]
- Sirois, A.; Vet, R.; Lamb, D.A. Comparison of the Precipitation Chemistry Measurements Obtained by the CAPMoN and NADP/NTN Networks. Environ. Monit. Assess. 2000, 62, 273–303. [Google Scholar] [CrossRef]
- Wetherbee, G.A.; Shaw, M.J.; Latysh, N.E.; Lehmann, C.M.B.; Rothert, J.E. Comparison of precipitation chemistry measurements obtained by the Canadian Air and Precipitation Monitoring Network and National Atmospheric Deposition Program for the period 1995–2004. Environ. Monit. Assess. 2010, 164, 111–132. [Google Scholar] [CrossRef] [PubMed]
- Tørseth, K.; Aas, W.; Breivik, K.; Fjæraa, A.M.; Fiebig, M.; Hjellbrekke, A.G.; Lund, M.C.; Solberg, S.; Yttri, K.E. Introduction to the European Monitoring and Evaluation Programme (EMEP) and observed atmospheric composition change during 1972–2009. Atmos. Chem. Phys. 2012, 12, 5447–5481. [Google Scholar] [CrossRef] [Green Version]
- Amodio, M.; Catino, S.; Dambruoso, P.R.; de Gennaro, G.; di Gilio, A.; Giungato, P.; Laiola, E.; Marzocca, A.; Mazzone, A.; Sardaro, A.; et al. Atmospheric Deposition: Sampling Procedures, Analytical Methods, and Main Recent Findings from the Scientific Literature. Adv. Meteorol. 2014, 2014, 161730. [Google Scholar] [CrossRef]
- Vet, R.; Artz, R.S.; Carou, S.; Shaw, M.; Ro, C.-U.; Aas, W.; Baker, A.; Bowersox, V.C.; Dentener, F.; Galy-Lacaux, C.; et al. A global assessment of precipitation chemistry and deposition of sulphur, nitrogen, sea salt, base cations, organic acids, acidity and pH, and phosphorus. Atmos. Environ. 2014, 93, 3–10. [Google Scholar] [CrossRef]
- Seinfeld, J.H. Air Pollution: A Half Century of Progress. AIChE J. 2004, 50, 1096–1108. [Google Scholar] [CrossRef]
- Erisman, J.W.; Draaijers, G.P.J. Atmospheric Deposition: In Relation to Acidification and Eutrophication; Studies in Environmental Science 63; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Forsius, M.; Posch, M.; Holmberg, M.; Vuorenmaa, J.; Kleemola, S.; Augustaitis, A.; Beudert, B.; Bochenek, W.; Clarke, N.; de Wit, H.A.; et al. Assessing critical load exceedances and ecosystem impacts of anthropogenic nitrogen and sulphur deposition at unmanaged forested catchments in Europe. Sci. Total Environ. 2021, 753, 141791. [Google Scholar] [CrossRef]
- Lovett, G.M.; Burns, D.A.; Driscoll, C.T.; Jenkins, J.C.; Mitchell, M.J.; Rustad, L.; Shanley, J.B.; Likens, G.E.; Haeuber, R. Who needs environmental monitoring? Front. Ecol. Environ. 2007, 5, 253–260. [Google Scholar] [CrossRef]
- Likens, G.E.; Butler, T.J.; Claybrooke, R.; Vermeylen, F.; Larson, R. Long-term monitoring of precipitation chemistry in the U.S.: Insights into changes and condition. Atmos. Environ. 2021, 245, 118031. [Google Scholar] [CrossRef]
- Weatherhead, E.C.; Reinsel, G.C.; Tiao, G.C.; Meng, X.-L.; Choi, D.; Cheang, W.-K.; Keller, T.; DeLuisi, J.; Wuebbles, D.J.; Kerr, J.B.; et al. Factors affecting the detection of trends: Statistical considerations and applications to environmental data. J. Geophys. Res. 1998, 103, 17149–17161. [Google Scholar] [CrossRef]
- Farmer, G.; Barthelmie, R.; Davies, T.; Brimblecombe, P.; Kelly, P.M. Relationships between concentration and deposition of nitrate and sulphate in precipitation. Nature 1987, 328, 787–789. [Google Scholar] [CrossRef]
- Lehmann, C.M.B.; Bowersox, V.C.; Larson, S.M. Spatial and temporal trends of precipitation chemistry in the United States, 1985–2002. Environ. Pollut. 2005, 135, 347–361. [Google Scholar] [CrossRef]
- Staelens, J.; Wuyts, K.; Adriaenssens, S.; Van Avermaet, P.; Buysse, H.; Van den Bril, B.; Roekens, E.; Ottoy, J.-P.; Verheyen, K.; Thas, O.; et al. Trends in atmospheric nitrogen and sulphur deposition in northern Belgium. Atmos. Environ. 2012, 49, 186–196. [Google Scholar] [CrossRef]
- Waldner, P.; Marchetto, A.; Thimonier, A.; Schmitt, M.; Rogora, M.; Granke, O.; Mues, V.; Hansen, K.; Karlsson, G.P.; Žlindra, D.; et al. Detection of temporal trends in atmospheric deposition of inorganic nitrate and sulphate to forests in Europe. Atmos. Environ. 2014, 95, 363–374. [Google Scholar] [CrossRef] [Green Version]
- Fanta, J. Rehabilitating degraded forests in Central Europe into self-sustaining forest ecosystems. Ecol. Eng. 1997, 8, 289–297. [Google Scholar] [CrossRef]
- Moldan, B.; Hak, T. Environment in the Czech Republic: A Positive and Rapid Change. Environ. Sci. Technol. 2007, 41, 358–362. [Google Scholar] [CrossRef] [Green Version]
- EEA. Air Quality in Europe—2020 Report; European Environmental Agency, No 09/2020; EEA: Copenhagen, Denmark, 2020. [Google Scholar]
- Keresztesi, A.; Birsan, M.-V.; Nita, I.-A.; Bodor, Z.; Szep, R. Assessing the neutralisation, wet deposition and source contributions of the precipitation chemistry over Europe during 2000–2017. Environ. Sci. Eur. 2019, 31, 50. [Google Scholar] [CrossRef] [Green Version]
- Bruce, A.; Bray, D.; Hopkin, K.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Essential Cell Biology, 4th ed.; Garland Science, Taylor & Francis Group, LLC: New York, NY, USA, 2014. [Google Scholar]
- Likens, G.E.; Bormann, F.H.; Johnson, N.M. Interactions between major biogeochemical cycles in terrestrial ecosystems. In Some Perspectives of the Major Biogeochemical Cycles; Likens, G.E., Ed.; SCOPE: Chichester, UK, 1981; pp. 93–112. [Google Scholar]
- Galloway, J.N.; Dentener, F.J.; Capone, D.G.; Boyer, E.W.; Howarth, R.W.; Seitzinger, S.P.; Asner, G.P.; Cleveland, C.C.; Green, P.A.; Holland, E.A.; et al. Nitrogen cycles: Past, present, and future. Biogeochemistry 2004, 70, 153–226. [Google Scholar] [CrossRef]
- Galloway, J.N.; Townsend, A.R.; Erisman, J.W.; Bekunda, M.; Cai, Z.; Freney, J.R.; Martinelli, L.A.; Seitzinger, S.P.; Sutton, M.A. Transformation of the nitrogen cycle: Recent trends, questions and potential solutions. Science 2008, 320, 889–892. [Google Scholar] [CrossRef] [Green Version]
- Fowler, D.; Pyle, J.A.; Raven, J.A.; Sutton, M.A. The global nitrogen cycle in the twenty-first century: Introduction. Philos. Trans. R. Soc. B Biol. Sci. 2013, 368, 20130165. [Google Scholar] [CrossRef] [PubMed]
- Bridges, K.S.; Jickells, T.D.; Davies, T.D.; Zeman, Z.; Hůnová, I. Aerosol, precipitation and cloud water observations on the Czech Krusne Hory plateau adjacent to a heavily industrialised valley. Atmos. Environ. 2002, 36, 353–360. [Google Scholar] [CrossRef]
- Bridgman, H.A.; Davies, T.D.; Jickells, T.; Hůnová, I.; Tovey, K.; Bridges, K.; Surapipith, V. Air pollution in the Krusne hory region, Czech Republic during the 1990s. Atmos. Environ. 2002, 36, 3375–3389. [Google Scholar] [CrossRef]
- Hůnová, I. Ambient Air Quality in the Czech Republic: Past and Present. Atmosphere 2020, 11, 214. [Google Scholar] [CrossRef] [Green Version]
- Hůnová, I. Ambient air quality for the territory of the Czech Republic in 1996–1999 expressed by three essential factors. Sci. Total Environ. 2003, 303, 245–251. [Google Scholar] [CrossRef]
- Hůnová, I.; Kurfürst, P.; Maznová, J.; Coňková, M. The contribution of occult precipitation to sulphur deposition in the Czech Republic. Erdkunde 2011, 65, 247–259. [Google Scholar] [CrossRef]
- Hůnová, I.; Kurfürst, P.; Baláková, L. Areas under high ozone and nitrogen loads are spatially disjunct in Czech forests. Sci. Total Environ. 2019, 656, 567–575. [Google Scholar] [CrossRef]
- Hůnová, I.; Brabec, M.; Malý, M.; Valeriánová, A. Long-term trends in fog occurrence in the modern-day Czech Republic, Central Europe. Sci. Total Environ. 2020, 711, 135018. [Google Scholar] [CrossRef]
- CHMI. Air pollution in the Czech Republic in 2019; Czech Hydrometeorological Institute: Prague, Czech Republic, 2020. [Google Scholar]
- Hůnová, I.; Šantroch, J.; Ostatnická, J. Ambient air quality and deposition trends at rural stations in the Czech Republic during 1993–2001. Atmos. Environ. 2004, 38, 887–898. [Google Scholar] [CrossRef]
- Hůnová, I.; Maznová, J.; Kurfürst, P. Trends in atmospheric deposition fluxes of sulphur and nitrogen in Czech forests. Environ. Pollut. 2014, 184, 668–675. [Google Scholar] [CrossRef]
- Hůnová, I.; Kurfürst, P.; Stráník, V.; Modlík, M. Nitrogen deposition to forest ecosystems with focus on its different forms. Sci. Total Environ. 2017, 575, 791–798. [Google Scholar] [CrossRef] [PubMed]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian Inference for Latent Gaussian Models Using Integrated Nested Laplace Approximations (with discussion). J. R. Stat. Soc. Series B 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Sanyal, S.; Rochereau, T.; Maesano, C.N.; Com-Ruelle, L.; Annesi-Maesano, I. Long-Term Effect of Outdoor Air Pollution on Mortality and Morbidity: A 12-Year Follow-Up Study for Metropolitan France. Int. J. Environ. Res. Public Health 2018, 15, 2487. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shaddick, G.; Thomas, M.L.; Amini, H.; Broday, D.; Cohen, A.; Frostad, J.; Green, A.; Gumy, S.; Liu, Y.; Martin, R.V.; et al. Data Integration for the Assessment of Population Exposure to Ambient Air Pollution for Global Burden of Disease Assessment. Environ. Sci. Technol. 2018, 52, 9069–9078. [Google Scholar] [CrossRef]
- Limpert, E.; Stahel, W.; Abbt, M. Lognormal distributions across the sciences: Keys and clues. BioScience 2001, 51, 341–352. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications: With R Examples, 4th ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Hastie, T.; Tibshirani, R. Generalized Additive Models; Chapman & Hall/CRC: Boca Raton, FL, USA, 1990. [Google Scholar]
- Wood, S.N. Generalized Additive Models: An Introduction with R, 2nd ed.; Chapman & Hall/CRC: New York, NY, USA, 2017. [Google Scholar]
- Rawlings, J.O.; Pantula, S.G.; Dickey, D.A. Applied Regression Analysis; Springer: New York, NY, USA, 1998. [Google Scholar]
- Rue, H.; Held, L. Gaussian Markov Random Fields: Theory and Applications; Monographs on Statistics and Applied Probability; Chapman & Hall: London, UK, 2005; Volume 104. [Google Scholar]
- Simpson, D.P.; Rue, H.; Riebler, A.; Martins, T.G.; Sørbye, S.H. Penalising model component complexity: A principled, practical approach to constructing priors (with discussion). Stat. Sci. 2017, 32, 1–28. [Google Scholar] [CrossRef]
- Bakka, H.; Rue, H.; Fuglstad, G.; Riebler, A.; Bolin, D.; Illian, J.; Krainski, E.; Simpson, D.; Lindgren, F. Spatial modelling with R-INLA: A review. WIRE Comput. Stat. 2018, 10, e1443. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: www.R-project.org (accessed on 14 May 2022).
- Lindgren, F.; Rue, H.; Lindström, J. An explicit link between Gaussian fields and Gaussian Markov random fields: The SPDE approach (with discussion). J. R. Stat. Soc. Series B 2011, 73, 423–498. [Google Scholar] [CrossRef] [Green Version]
- EC. Directive 2008/50/EC of the European Parliament and of the Council of 21 May 2008 on Ambient Air Quality and Cleaner Air for Europe; EC: New York, NY, USA, 2008. [Google Scholar]
- Sutton, M.A.; Reis, S.; Baker, S.M. (Eds.) Atmospheric Ammonia; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Fagerli, H.; Aas, W. Trends in nitrogen in air and precipitation: Model results and observations at EMEP sites in Europe, 1980–2003. Environ. Pollut. 2008, 154, 448–461. [Google Scholar]
- Du, E.; de Vries, W.; Galloway, J.N.; Hu, X.; Fang, J. Changes in wet nitrogen deposition in the United States between 1985 and 2012. Environ. Res. Lett. 2014, 9, 095004. [Google Scholar] [CrossRef]
- Li, X.; Shi, H.; Xu, W.; Liu, W.; Wang, X.; Hou, L.; Feng, F.; Yuan, W.; Li, L.; Xu, H. Seasonal and spatial variations of bulk nitrogen deposition and the impacts on the carbon cycle in the arid/semiarid grassland of Inner Mongolia, China. PLoS ONE 2015, 10, e0144689. [Google Scholar] [CrossRef] [PubMed]
- Boxman, A.W.; Peters, R.C.J.H.; Roelofs, J.G.M. Long-term changes in atmospheric N and S throughfall deposition and effects on soil solution chemistry in a Scots pine forest in the Netherlands. Atmos. Environ. 2008, 156, 1252–1259. [Google Scholar] [CrossRef] [PubMed]
- Verstraeten, A.; Neirynck, J.; Genouw, G.; Cools, N.; Roskams, P.; Hens, M. Impact of declining atmospheric deposition on forest soil solution chemistry in Flanders, Belgium. Atmos. Environ. 2012, 62, 50–63. [Google Scholar] [CrossRef]
- Pascaud, A.; Sauvage, S.; Coddeville, P.; Nicolas, M.; Croisé, L.; Mezdour, A.; Probst, A. Contrasted spatial and long-term trends in precipitation chemistry and deposition fluxes at rural stations in France. Atmos. Environ. 2016, 146, 28–43. [Google Scholar] [CrossRef] [Green Version]
- Fuhrer, J. Study of Acid Deposition in Switzerland: Temporal Variation in the Ionic Composition of Wet Precipitation at Rural Sites during 1983-1984. Environ. Pollut. 1986, 12, 111–129. [Google Scholar] [CrossRef]
- Irwin, J.G.; Williams, M.L. Acid Rain: Chemistry and Transport. Environ. Pollut. 1988, 50, 29–59. [Google Scholar] [CrossRef]
- Lovarelli, D.; Conti, C.; Finzi, A.; Bacenetti, J.; Guarino, M. Describing the trend of ammonia, particulate matter and nitrogen oxides: The role of livestock activities in northern Italy during COVID-19 quarantine. Environ. Res. 2020, 191, 110048. [Google Scholar] [CrossRef]
- Menut, L.; Bessagnet, B.; Siour, G.; Mailler, S.; Pennel, R.; Cholakian, A. Impact of lockdown measures to combat COVID-19 on air quality over western Europe. Sci. Total Environ. 2020, 741, 140426. [Google Scholar] [CrossRef]
- Naethe, P.; Delaney, M.; Julitta, T. Changes of NOx in urban air detected with monitoring VIS-NIR field spectrometer during the coronavirus pandemic: A case study in Germany. Sci. Total Environ. 2020, 748, 141286. [Google Scholar]
- Vichova, K.; Veselik, P.; Heinzova, R.; Dvoracek, R. Road Transport and Its Impact on Air Pollution during the COVID-19 Pandemic. Sustainability 2021, 13, 11803. [Google Scholar] [CrossRef]
- CHMI. Air Pollution in the Czech Republic in 2020; Czech Hydrometeorological Institute: Prague, Czech Republic, 2021. [Google Scholar]
- Galloway, J.N.; Likens, G.E. The collection of precipitation for chemical analysis. Tellus 1978, 30, 71–82. [Google Scholar] [CrossRef] [Green Version]
- Krupa, S. Sampling and physico-chemical analysis of precipitation: A review. Environ. Pollut. 2002, 120, 565–594. [Google Scholar] [CrossRef]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Schafer, J.L. Analysis of Incomplete Multivariate Data; Monographs on Statistics and Applied Probability; Chapman & Hall: London, UK, 1997; Volume 72. [Google Scholar]
- Sirois, A.; Vet, R. The Precision of Precipitation Chemistry Measurements in the Canadian Air and Precipitation Monitoring Network (CAPMoN). Environ. Monit. Assess. 1999, 57, 301–329. [Google Scholar] [CrossRef]
- Schwab, J.J.; Casson, P.; Brandt, R.; Husain, L.; Dutkewicz, V.; Wolfe, D.; Demerjian, K.L.; Civerolo, K.L.; Rattigan, O.V.; Felton, H.D.; et al. Atmospheric Chemistry Measurements at Whiteface Mountain, NY: Cloud Water Chemistry, Precipitation Chemistry, and Particulate Matter. Aerosol Air Qual. Res. 2016, 16, 841–854. [Google Scholar] [CrossRef] [Green Version]
- Itahashi, S.; Yumimoto, K.; Uno, I.; Hayami, H.; Fujita, S.-I.; Pan, Y.; Wang, Y. A 15-year record (2001–2015) of the ratio of nitrate to non-sea-salt sulfate in precipitation over East Asia. Atmos. Chem. Phys. 2018, 18, 2835–2852. [Google Scholar] [CrossRef] [Green Version]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Jacob, D.J.; Winner, D.A. Effect of climate change on air quality. Atmos. Environ. 2009, 43, 51–63. [Google Scholar] [CrossRef] [Green Version]
- Jones, J.M.; Davies, T.D. The influence of climate on air and precipitation chemistry over Europe and downscaling applications to future acidic deposition. Clim. Res. 2000, 14, 7–24. [Google Scholar] [CrossRef] [Green Version]
- von Schneidemesser, E.; Monks, P.S.; Allan, J.D.; Bruhwiler, L.; Forster, P. Chemistry and the Linkages between Air Quality and Climate Change. Chem. Rev. 2015, 115, 3856–3897. [Google Scholar] [CrossRef]

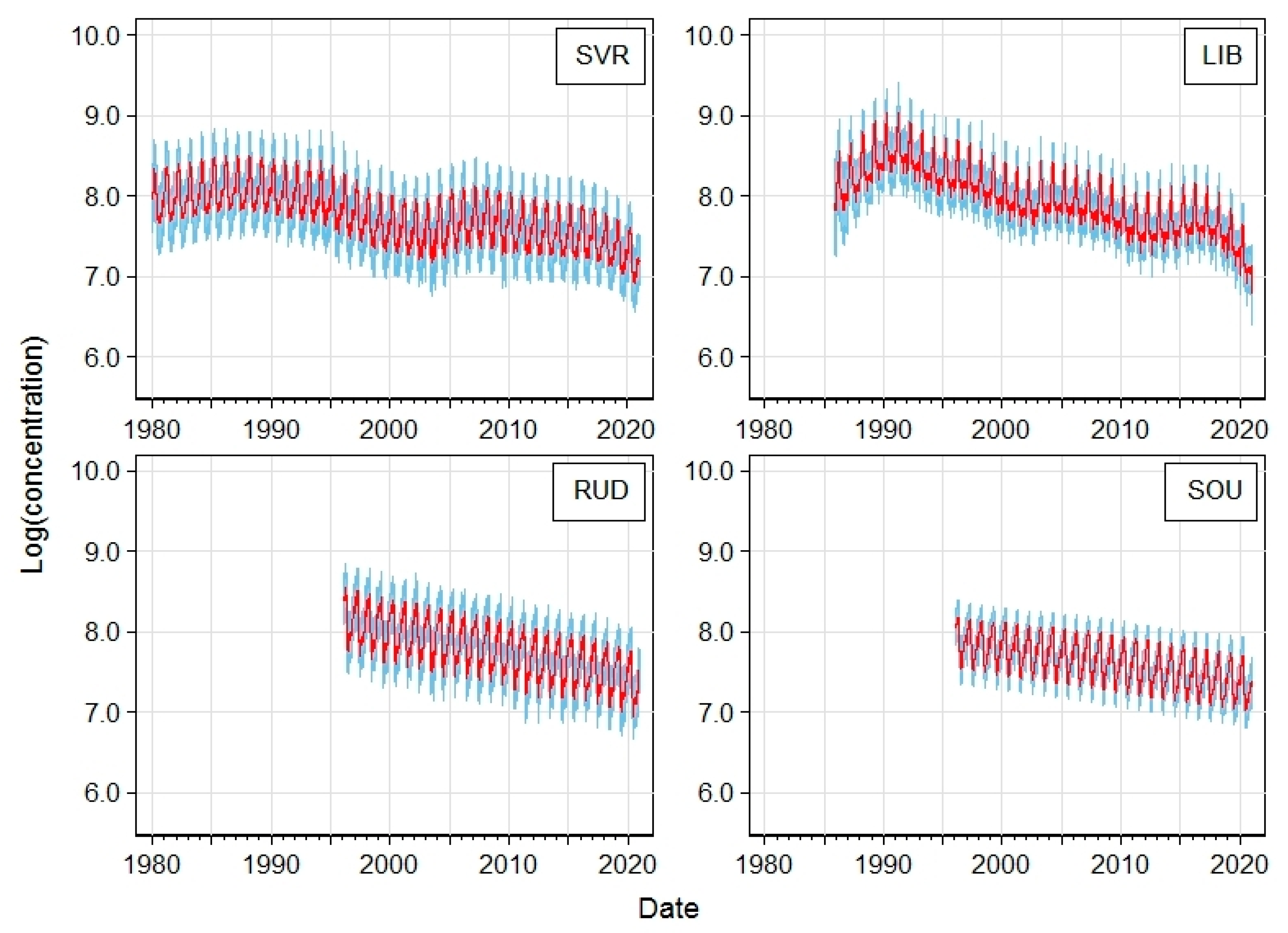
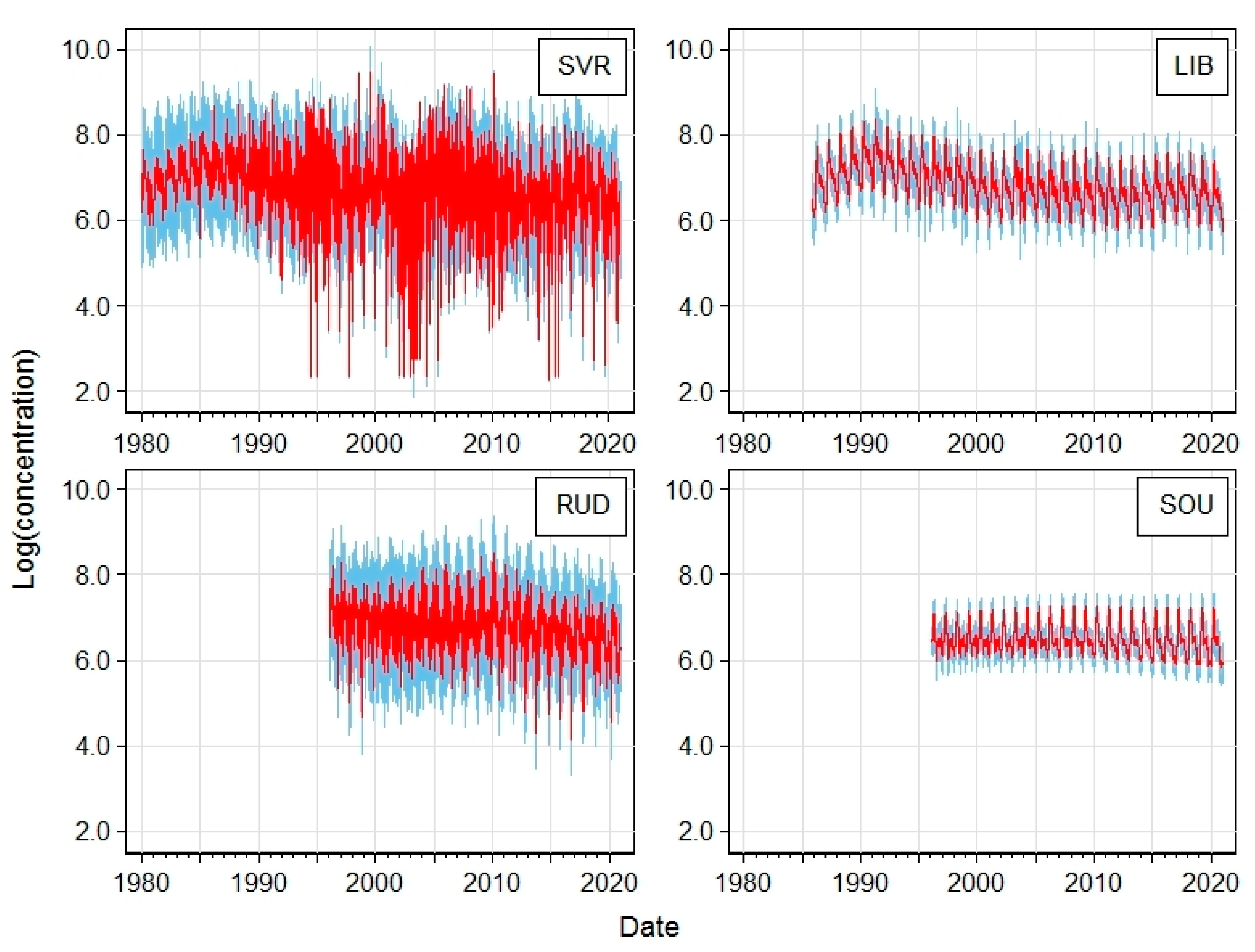

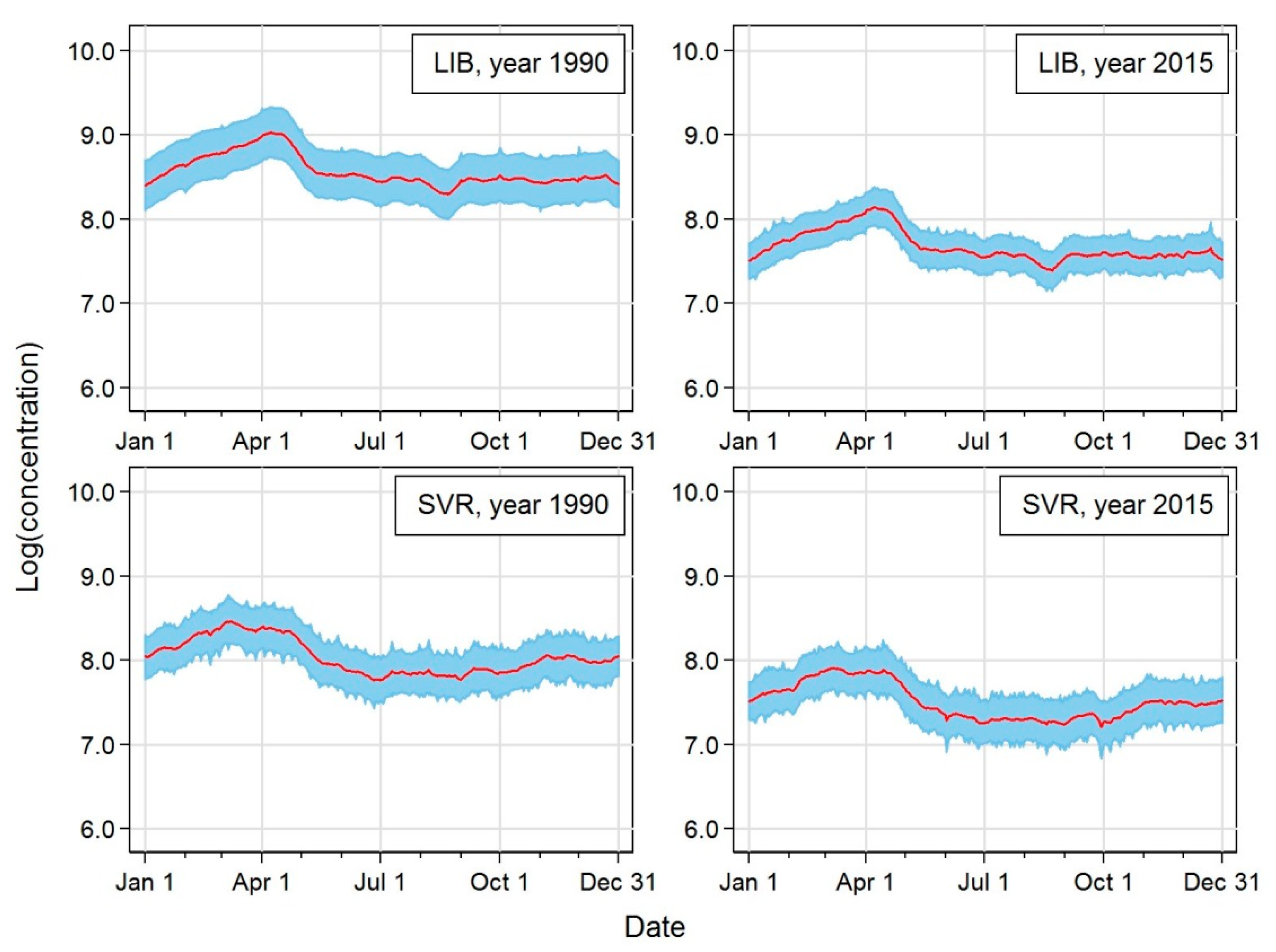
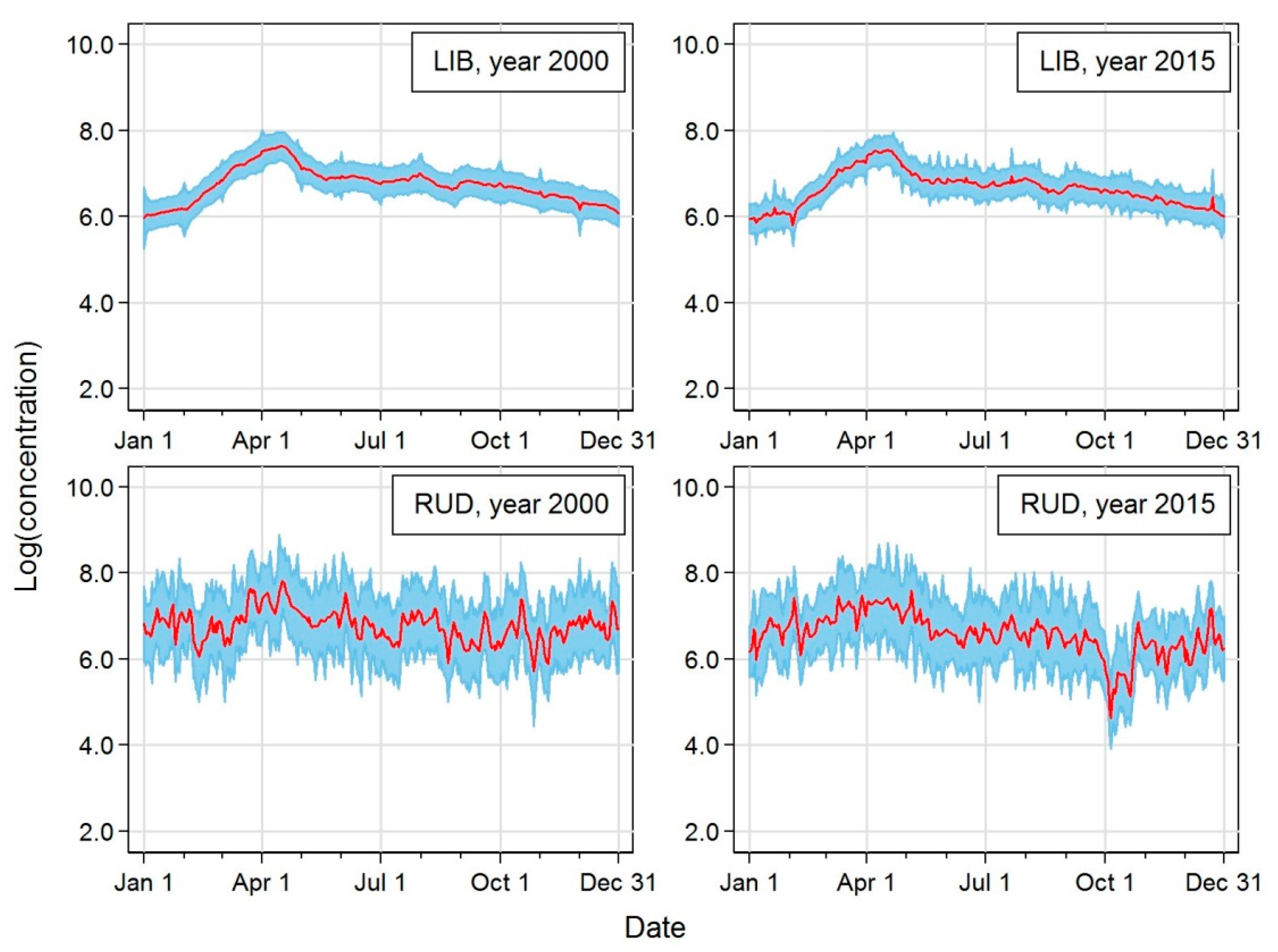
| Station | Acronym | Latitude | Longitude | Altitude [m a.s.l.] | Region | EoI Classification |
|---|---|---|---|---|---|---|
| Praha4-Libuš | LIB | 14°26′49.401″ N | 50°0′28.400″ E | 301 | Capital Prague | B/S/R-NCI |
| Svratouch | SVR | 49°44′6.304″ N | 16°2′3.109″ E | 735 | top of the hill | B/R/NA-REG |
| Souš | SOU | 50°47′22.726″ N | 15°19′10.859″ E | 771 | Jizerské hory Mountains | B/R/N-REG |
| Rudolice v Horách | RUD | 50°34′47.402″ N | 13°25′10.222″ E | 840 | Krušné hory Mountains | B/R/N-REG |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hůnová, I.; Brabec, M.; Malý, M.; Škáchová, H. Reconstruction of Daily Courses of SO42−, NO3−, NH4+ Concentrations in Precipitation from Cumulative Samples. Atmosphere 2022, 13, 1049. https://doi.org/10.3390/atmos13071049
Hůnová I, Brabec M, Malý M, Škáchová H. Reconstruction of Daily Courses of SO42−, NO3−, NH4+ Concentrations in Precipitation from Cumulative Samples. Atmosphere. 2022; 13(7):1049. https://doi.org/10.3390/atmos13071049
Chicago/Turabian StyleHůnová, Iva, Marek Brabec, Marek Malý, and Hana Škáchová. 2022. "Reconstruction of Daily Courses of SO42−, NO3−, NH4+ Concentrations in Precipitation from Cumulative Samples" Atmosphere 13, no. 7: 1049. https://doi.org/10.3390/atmos13071049
APA StyleHůnová, I., Brabec, M., Malý, M., & Škáchová, H. (2022). Reconstruction of Daily Courses of SO42−, NO3−, NH4+ Concentrations in Precipitation from Cumulative Samples. Atmosphere, 13(7), 1049. https://doi.org/10.3390/atmos13071049







