Abstract
Fluctuation spectroscopy measurements of quasi-two-dimensional organic charge-transfer salts (BEDT-TTF)X are reviewed. In the past decade, the method has served as a new approach for studying the low-frequency dynamics of strongly correlated charge carriers in these materials. We review some basic aspects of electronic fluctuations in solids, and give an overview of selected problems where the analysis of -type fluctuations and the corresponding slow dynamics provide a better understanding of the underlying physics. These examples are related to (1) an inhomogeneous current distribution due to phase separation and/or a percolative transition; (2) slow dynamics due to a glassy freezing either of structural degrees of freedom coupling to the electronic properties or (3) of the electrons themselves, e.g., when residing on a highly-frustrated crystal lattice, where slow and heterogeneous dynamics are key experimental properties for the vitrification process of a supercooled charge-liquid. Another example is (4), the near divergence and critical slowing down of charge carrier fluctuations at the finite-temperature critical endpoint of the Mott metal-insulator transition. Here also indications for a glassy freezing and temporal and spatial correlated dynamics are found. Mapping out the region of ergodicity breaking and understanding the influence of disorder on the temporal and spatial correlated fluctuations will be an important realm of future studies, as well as the fluctuation properties deep in the Mott or charge-ordered insulating states providing a connection to relaxor or ordered ferroelectric states studied by dielectric spectroscopy.
1. Introduction
The quasi-two-dimensional organic charge-transfer salts (BEDT-TTF)X (where BEDT-TTF stands for bis-ethylenedithio-tetrathiafulvalene, representing CS[CH], often abbreviated as ET, and X is a monovalent anion) in the last few decades have been viewed as model systems for investigating the physics of strongly correlated electrons in reduced dimensions [1,2,3,4]. The model character becomes manifest in (i) the rich phase diagrams sustaining a wealth of interesting ground states; and (ii) the possibility of fine-tuning the materials’ properties using subtle physical or chemical means. Therefore, these materials are a test ground for studying the fundamental properties of novel electronic ground states that emerge from the mutual interaction of electron charges or spins in reduced dimensions, and the interaction of electrons with the underlying crystal lattice.
In the -phase materials with polymeric anions, two ET molecules form a dimer, which results in an effectively half-filled conduction band, and charge carriers reside on a more or less frustrated triangular lattice, giving rise to a possible spin-liquid ground state in systems with a high degree of frustration. Further prominent research topics in the past several years have been the nature of superconductivity and the unconventional normal conducting metallic phase displaying a pseudogap behavior, as well as the Mott metal-insulator transition where a charge gap opens due to electron–electron interactions, and its universal critical properties. Finally, the intra-dimer degrees of freedom recently have been considered to play an important role for ferroelectric ordering and relaxation phenomena, and charge-order driven formation of electric dipoles that exhibit ferroelectricity, thereby enabling magnetic order has been suggested [5].
A second example of substantial recent research activities, which will be addressed in this review, are quarter-filled -phase systems with large, discrete anion structures that are unstable against a charge-ordering metal-insulator transition. This transition from a charge-liquid to an ordered charge-crystal state sometimes can be kinetically avoided, depending on the degree of geometric frustration of the underlying crystal lattice, and a new charge-glass state occurs without long-range order of the localized charges on the triangular lattice. Non-volatile switching operation between the charge-order and charge-glass states has been demonstrated and the vitrification and crystallization of electrons currently are being intensively investigated.
These two examples have been chosen because both the critical properties of the Mott transition and the glassy freezing of charge carriers on a frustrated lattice involve slow dynamics of charge carriers, and it is therefore important and desirable to study the dynamics of the electrons not only with optical techniques but also at very low frequencies.
Dynamical properties of the correlated charge carriers in organic charge-transfer salts have been extensively and successfully studied, e.g., by optical conductivity measurements and dielectric spectroscopy. The former method utilizes the interaction of matter with light covering a wide range of energies in order to study not only basic electronic but also magnetic and vibrational excitations as well as fundamental interaction effects (see, e.g., [6]). The accessible frequencies in microwave to infrared spectroscopy are in the GHz–10 Hz regime.
The ultrafast dynamics in photoinduced phase transitions can be studied with fs light pulses (see, e.g., [7]). Insulating (low-conductance) samples of organic charge-transfer salts have been investigated by dielectric spectroscopy covering the Hz–MHz regime, which allows for addressing numerous physical phenomena, as, e.g., dielectric relaxation, charge transport of localized carriers (through hopping of electrons) and ferroelectricity [8].
The aim of our complementary approach of investigating the time-dependent fluctuations of a sample’s resistance or conductance (i.e., the measured “noise”) over a certain time interval is to spectroscopically access the charge carrier dynamics without injecting additional electrons into the system at relatively low frequencies covering the mHz–kHz regime. We will give an overview of physical phenomena—specific for the present materials—causing such slow excitations. The time scale involved in excitations of clusters of electronic systems usually increases with increasing volume of the fluctuation object. Therefore, the method proves beneficial when nano- or microscopic objects are subject to fluctuations, as, e.g., for electronic phase separation caused by competing order parameters or interactions, a scenario frequently found in low-dimensional molecular metals. Likewise, the charge carrier dynamics strongly slow down at a critical point or line of a phase transition, as, e.g., the Mott metal-insulator transition, and localization of charge carriers can be investigated here. The particular scaling behavior at critical points involving power-law divergence of relaxation time and length results in temporal and spatial correlations (a dynamic phase separation), which can lead to very slow fluctuations of large magnitude. Another origin of slow dynamics, even of individual fluctuating objects, is a sufficiently high energy barrier that must be overcome in a thermally-activated trapping or tunneling excitation process, e.g., of electrons in hopping transport or molecules changing their relative orientation. Finally, both percolative phase transitions and a collective glassy freezing of either structural or electronic degrees of freedom result in strong low-frequency fluctuations.
This review is organized as follows. In Section 2, first we will give a brief description of the electronic and structural peculiarities of the investigated materials and discuss the phase diagram of the -(BEDT-TTF)X salts with polymeric anions. Second, we will discuss the basics of fluctuation spectroscopy and fundamental models to understand -type electronic noise, which is ubiquitous in condensed matter systems. In Section 3, we will review a collection of specific problems, where fluctuation spectroscopy in recent years has provided new information and has helped to better understand the underlying physics. Finally, we will give an outlook to possible future fields of applications.
Noise experiments and the theoretical treatment of fluctuation processes is a wide field of research and spans from the need to understand the fluctuations in order to be able to optimize the performance of sensors and devices by increasing their signal-to-noise ratio to the quest for regarding the noise as the signal in order to gain information on the dynamics of charge carriers and the kinetics of their fluctuations. After we have introduced the method as a new approach for studying the charge carrier dynamics in low-dimensional molecular metals about a decade ago, we have reviewed the technique and first results [9]. Since then, the spectrum of applications of the technique and the physical problems to be studied have considerably broadened, and the method has developed into a powerful tool now applied by various experimental groups.
2. Materials and Methods
2.1. Organic Charge-Transfer Salts—Quasi Two-Dimensional Molecular Metals
In contrast to ordinary metals like sodium, potassium or aluminum, where the basic units are nearly point-like atoms, the building blocks of organic charge-transfer salts consist of extended molecules, and the materials’ unit cells contain a few hundred atoms. This leads not only to challenges in determining the electronic band structure, being addressed by the molecular orbital approximation, but also to multiple excitations, as e.g., a large spectrum of vibrational degrees of freedom due to intra-molecular excitations, i.e., the displacement of atoms within the molecules, in addition to inter-molecular motions and rotations. By combining two sorts of molecules, one with a high electron affinity and the other with a low ionization energy, a charge-transfer process takes place, where charge is transferred from the donor D to the acceptor molecule X with a charge-transfer ratio [2]. This oxidation process results in a molecular compound DX, where m and n quantify the stoichiometry, with partially-filled molecular orbitals on the donor (cation) site and a closed-shell configuration on the acceptor (anion) site. When the donor molecules are stacked rather densely, the orbitals of adjacent molecules overlap and an electronic band structure forms, allowing the generated charge carriers to delocalize along the stacking axis. As the acceptor molecules often adopt a closed-shell configuration, they do not contribute to the conduction process. For theoretical calculations, the relevant molecular orbitals are either the highest occupied molecular orbitals (HOMO) or the lowest unoccupied molecular orbitals (LUMO) of the -electrons, which can be further used for a tight-binding approach to calculate the electronic band structure [1,2,10,11].
The existence of complex building-blocks leads to a large structural variety, where, for instance, the shape and coordination of the cation and anion decide about the system’s dimensionality. For the BEDT-TTF molecules, specific steric effects prevent an infinite face-to-face stacking and a relatively strong side-by-side overlap of the -orbitals of adjacent molecules results in a quasi-two-dimensional electronic structure of the ET salts. A linear combination of the atomic s- and p-orbitals leads to - and -orbitals, which have a perpendicular and parallel orientation to the bonding axis, respectively. Due to the lower binding energy of the -electrons, they can easily delocalize, so that the free charge carriers have mainly -hole character. Besides this, different spatial arrangements of the donor molecules, the so-called packing motifs, result in variations of the physical properties due to changes in the molecular overlap and hence the transfer integrals. These packing types are labeled with Greek letters, such as -, -, -, - and -phases, and characterize the ET molecules’ relative orientation, often visualized when viewed along the long axis of the donor molecules (see Figure 1b).
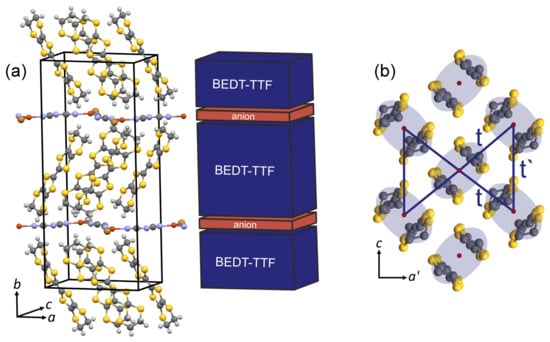
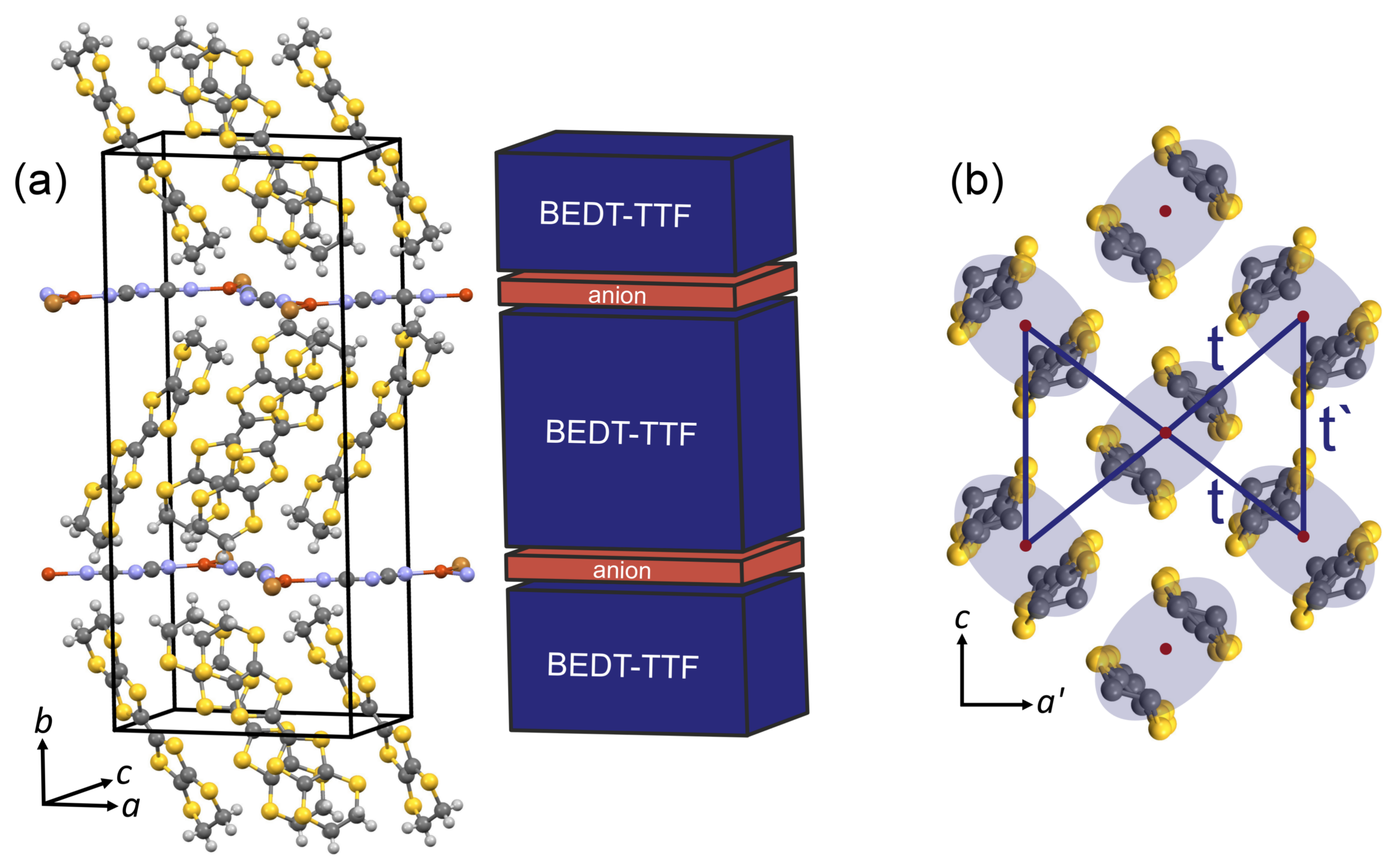
Figure 1.
(a) crystal structure (left) of -(BEDT-TTF)Cu[N(CN)]Z with Z = Br, Cl, which can be simply viewed as alternating blocks (right) of conducting and insulating layers with the donor ET and polymeric chain-forming acceptor Cu[N(CN)]Z molecules, respectively. The box represents the unit cell hosting four formular units; (b) spatial arrangement of the ET molecules in the -phase viewed along the long axis of the molecules. Two ET molecules form a dimer (shaded ellipse), whereas two dimers are arranged almost orthogonal to each other. Considering the dimers as the basic structural units, the conduction band is effectively half-filled and the charger carriers reside on a triangular lattice with two transfer integrals t and t′.
The crystal structure of the most intensively studied quasi-two-dimensional -(BEDT-TTF)X salts can be simply considered as alternating thick conducting layers with the ET molecules (blue color) and thin insulating layers with the anions X (red color), as shown in Figure 1a, for polymeric anions X = Cu[N(CN)]Z with Z = Cl, Br, where the direction perpendicular to the conducting plane is along the crystallographic b-axis. Characteristic for the -phase packing motif is a strong structural dimerization indicated by the shaded ellipses in Figure 1b, which—despite the 2:1 stoichiometry—results in the opening of a dimerization gap in the nominally three-quarter-filled band structure leading to an effectively half-filled conduction band [2]. The charge carriers then reside on the ET dimers, which form a triangular lattice, as shown in Figure 1b, with the relevant transfer integrals t and in a minimal model [10,12]. The degree of frustration depends on and varies with the structure of the anion X [11]. This effective dimer model, however, recently has been challenged, since the intra-dimer electronic degrees of freedom seem to play an important role in understanding dielectric relaxation and ordering phenomena. For instance, in [5], it is argued that the localization (charge-order) of holes on one of the molecules within the dimers results in the formation and subsequent ferroelectric ordering of electric dipoles in -(ET)Cu[N(CN)]Cl, thereby lifting the frustration and enabling antiferromagnetic order of the localized spins [5,13].
Compared to ordinary inorganic metals, the organic compounds are characterized by low charge carrier densities of order , since the volume of the molecules providing the free charge carriers is considerably large. This, in combination with the relatively narrow bandwidth (due to the weak overlap of neighboring molecular orbitals) and the reduced dimensionality of the electronic system resulting in a reduced screening of the charge carriers, leads to strong electron–electron correlations quantified by a ratio of bandwidth eV to on-site Coulomb repulsion eV, which is close to unity. Experimentally, this results in enhanced effective masses seen in experiments of quantum oscillations [14,15] and specific heat [16], where . Importantly, however, part of the mass renormalization is due to the strong electron–phonon coupling involving both high-frequency intra- and low-frequency intermolecular vibrations.
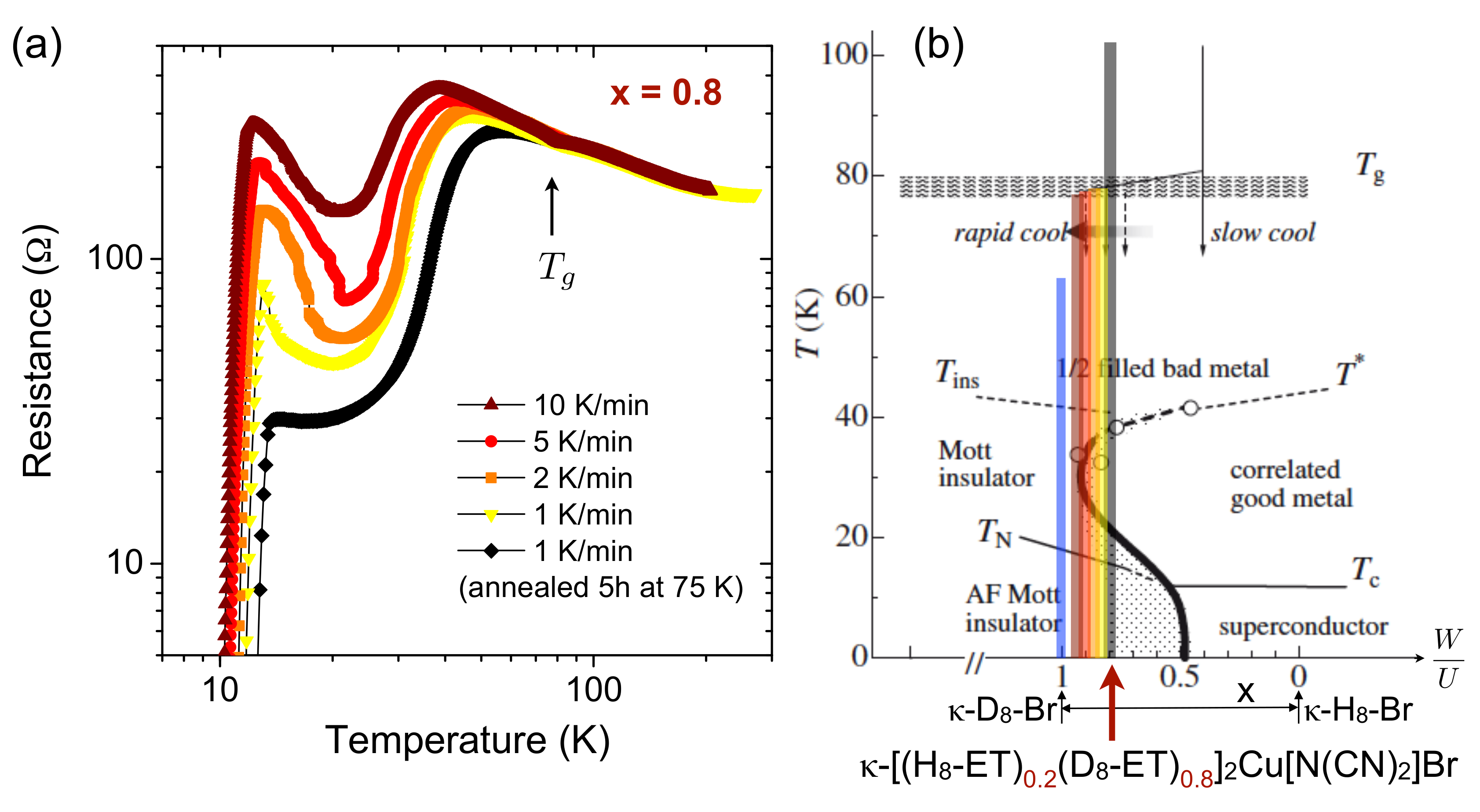
Due to relatively weak bonding energies, the materials’ properties can be easily affected by changing external parameters like temperature, pressure, chemical substitution, cooling rate, etc. Thus, the temperature–pressure phase diagram of the -(BEDT-TTF)X salts, depicted in Figure 2, displays a variety of different ground states and transition lines [17,18,19,20,21]. Whereas the system with X = Cu[N(CN)]Cl (in short -Cl) has an insulating ground state with antiferromagnetic and ferroelectric ordering at , the compound X = Cu[N(CN)]Br (in short -Br) with the slightly larger Br atom in the anion complex is located on the metallic side of the phase diagram with a superconducting transition at . Thus, the salts -Cl and -Br at ambient pressure are located on opposite sides of the first-order Mott metal-insulator transition (red line in Figure 2). The universality of the phase diagram (see also Figures 5a and 10b below) is seen by the fact that applying a moderate hydrostatic pressure of only 300 bar shifts -Cl to the metallic side and a superconducting ground state with . Since hydrostatic pressure increases the molecular overlap of adjacent molecules, the pressure axis can be mapped to the ratio of bandwidth to on-site Coulomb repulsion [17], i.e., the Mott transition is a bandwidth-controlled transition not affecting the bandfilling. Another possible tuning mechanism is the substitution of atoms, mostly in the ET donors by different isotopes. Most effective and controllable is either the successive replacement of one to eight of the hydrogen atoms in the ET molecules’ terminal ethylene groups [CH] by deuterium atoms or the successive replacement of the conventional hydrogenated ET molecules H-ET in the crystal structure by the fully-deuterated analogue D-ET, which in both cases results in a chemically-induced shift (negative pressure) from the metallic towards the Mott insulating state [22]. Thus, the partial substitution with deuterated molecules in systems -[(H-ET)(D-ET)]Cu[N(CN)]Br (in short: -H/D-Br) allows for tuning the ambient-pressure position in the phase diagram in fine steps across the metal-insulator transition and critical region of the phase diagram. These systems are ideal to study the critical properties of the Mott transition at ambient pressure.
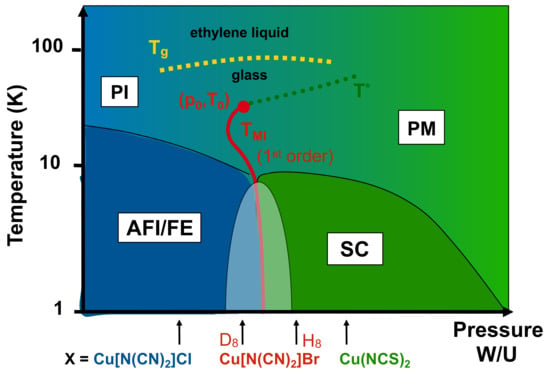
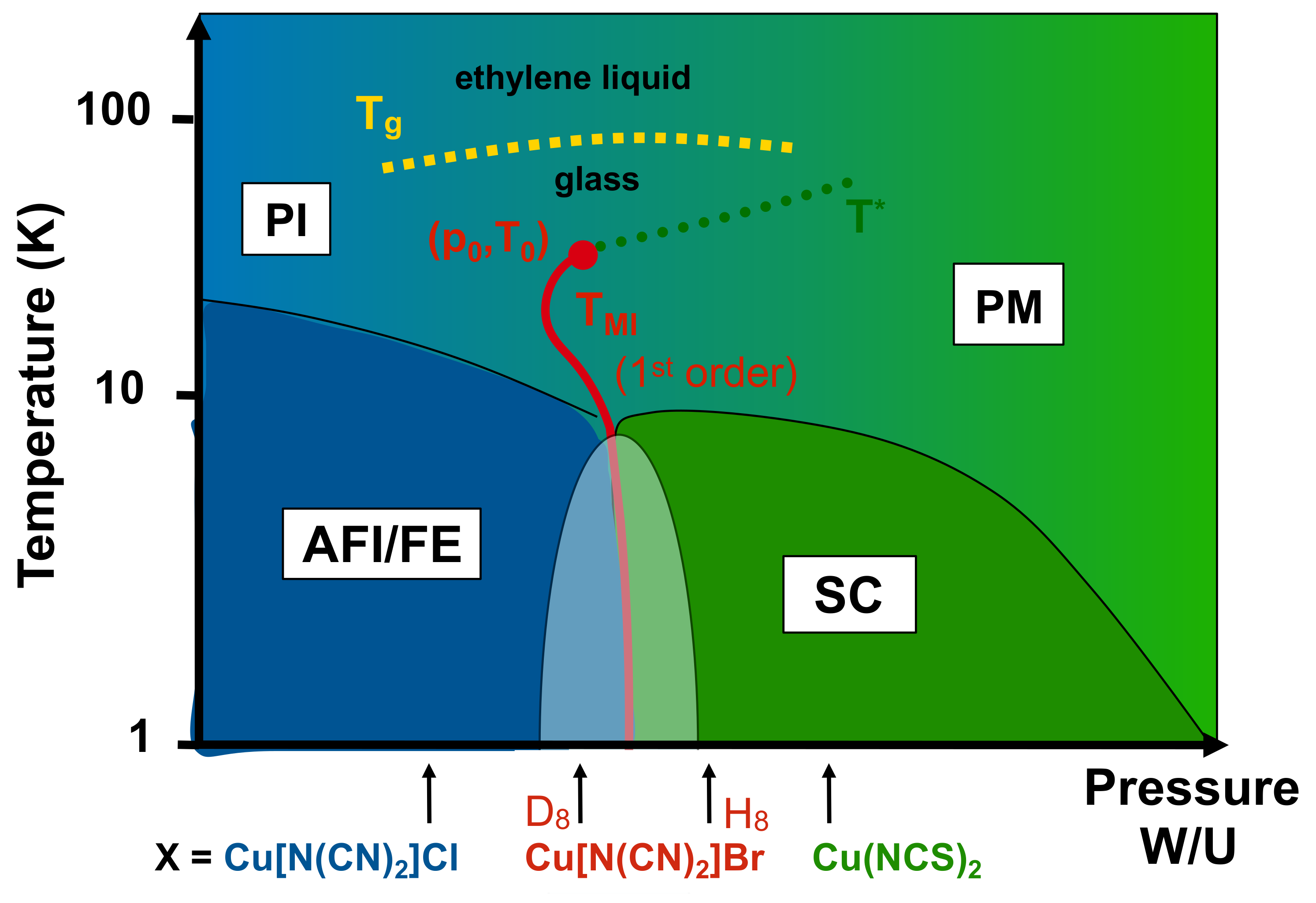
Figure 2.
Schematic temperature–pressure phase diagram of the -(BEDT-TTF)X salts with polymeric anions, after Refs. [17,18,19,20,21]. Indicated is the position of systems with different anions X at ambient pressure. Hydrostatic pressure can be mapped on an increasing ratio of (see text). PI, PM, AFI, FE and SC stand for the paramagnetic insulating, paramagnetic metallic, antiferromagnetic insulating, ferroelectric and superconducting phase, respectively. The red line marks the first-order Mott metal-insulator transition, which terminates in a finite-temperature critical point. At elevated temperatures, a structural glass-like transition of the ET molecules’ ethylene endgroup rotational degrees of freedom occurs (dashed yellow line). The green dotted line marks the crossover to an anomalous metallic (’bad metal’) phase above the Fermi liquid.
As is schematically shown in Figures 2, 5a and 10b, at a critical ratio , the first-order Mott metal-insulator transition occurs, illustrated as a red line in Figure 2, which terminates in a finite-temperature second-order critical endpoint at (230–250 bar, 36–40 K). At lower temperatures, an inhomogeneous region (blue/green shaded area in Figure 2), where the antiferromagnetic insulating and superconducting grounds states coexist, is found close to the transition line [18].
After the charge-transfer is completed in the crystallization process of (ET)X, the ET molecules are essentially planar, except the ethylene endgroups (EEG in short), which are the most deformable parts of the molecule and for which the relative orientation of the outer C−C bonds can be either parallel (eclipsed, E) or canted (staggered, S). At high temperatures, the EEG are disordered due to strong thermal vibrations, and, upon cooling to low temperatures, the EEG adopt one of the two possible conformations (E in the case of -Cl and -Br) depending on the anion and crystal structure [1]. For kinetic reasons (see Section 3.2), however, an ordered state cannot be achieved in some compounds -(ET)X and the EEG freeze in a glassy fashion at temperatures of , below which thermal equilibrium cannot be reached such that a part of the EEG remains locked (frozen) in the energetically unfavorable non-equilibrium configuration [19]. Hence, the glass-like transition temperature depends on the cooling rate , which therefore determines the degree of intrinsic structural disorder that becomes frozen [23]. Since the latter degree of non-equilibrium occupation determines [24], a varying cooling rate can be used as yet another powerful tuning parameter in the phase diagram [25], such that more rapid cooling decreases and shifts the systems towards the insulating side of the phase diagram.
2.2. Fluctuation (’Noise’) Spectroscopy
2.2.1. Definitions and Basic Relations
In a usual electronic transport measurement, in order to increase the sensitivity or signal-to-noise ratio, the mean value of an otherwise more-or-less randomly fluctuating quantity (voltage or current) is used to calculate the sample’s resistance or conductance. This is achieved by averaging over a certain time interval, e.g., determined by the frequency-bandwidth (time-constant) of a lock-in amplifier in an AC-measurement.
Naturally, large fluctuations about the mean value are unwanted and therefore are sought to be suppressed or largely eliminated. Fluctuation spectroscopy is a time-resolved electronic transport measurement, either of a sample’s resistance (preferred for conducting metallic samples) or its conductance (preferred for semiconducting/insulating samples), where the fluctuations are amplified instead by a suitable measurement system and analyzed in the time and frequency domain by means of simple Fourier analysis, i.e., here “the noise is the signal” [26,27]. The basics of noise and fluctuations are described in many textbooks on (non-equilibrium) statistical physics and time-dependent statistical mechanics, as well as in review articles on noise in condensed matter systems (see e.g., [9,28,29,30,31,32,33,34] and references therein). Therefore, in the following, we will only give a brief account of the important definitions, relevant relations and simple models.
In order to gain information from the fluctuations in a quantity , it is useful to ask how much power is associated with different parts of the frequency spectrum of the random signal. Mathematically, this means calculating the noise power spectral density (PSD) of the signal, , by considering the modulus square of the Fourier-transformed noisy signal and taking an average over a suitable time interval. If the fluctuating part of the signal is , where is the time-averaged mean value that may be considered equal to zero [35], and the noise PSD is given by:
This is the standard engineering definition, where the variance of the random signal is normalized by:
Next, we ask for a connection relating the power spectrum to some time-like property of the statistically varying function (which equals for without loss of generality). This time-like behavior is given by the autocorrelation function
which, for statistically stationary processes, is only a function of (and t is unimportant) and is symmetric in [36].
The Wiener–Khintchine theorem states that
Equation (4) is the most informative way to express the time dependence of a random variable and, specifically, kinetic processes of electrons in condensed matter. The fluctuations of a system are determined by the temporal (and sometimes also spatial) correlations, which are quantified by a suitable correlation function, where the variable x is either the measured voltage V or current I. It describes the ’memory’ of the system, i.e., what remains of a fluctuation at a later time. Whereas is of course random, the correlation function is a non-random characteristic of the kinetics of these random fluctuations, describing how the fluctuations evolve in time on average [33].
The Wiener–Khintchine theorem describes the equivalence of the standard engineering definition of noise, Equation (1), and the definition of noise as the Fourier transform of the autocorrelation function (Equation (3)). A third definition, which is essentially realized by calculating noise spectra in the experiment, i.e., either by a software or by using a spectrum analyzer, involves passing the time signal through a ’realizable filter’ of finite bandwidth, squaring it, and averaging it over some large finite time. For the bandwidth approaching zero, e.g., by realizing a sufficiently sharp filter in an R-L-C-circuit with a large quality factor, the result will (aside from a normalization factor) approach the ideal value of the two preceding definitions [37].
In general, the time dependence of the fluctuations’ correlation function (or, equivalently, the frequency dependence of the power spectral density) and the response of the system to external perturbations are governed by the same kinetic processes. In thermal equilibrium, there is an exact relation between and the dissipative part of the system’s linear response to an external perturbation, which is described by the fluctuation–dissipation theorem (FDT), which in the quasi-classical limit reads:
where . Here, is the imaginary part of the complex susceptibility and the real function is the response function of the system [38].
Obviously, the autocorrelation function (Equation (3)) without a temporal delay () equals the statistical variance:
If the correlation time of a fluctuation is very short, and decays to zero very fast (and therefore before, in an experiment, the next data point is taken), the system appears totally random (and, in fact, infinitely ’choppy’), and the corresponding PSD is frequency independent (sometimes referred to as ’white’ noise). An example is thermal noise (first measured by Johnson for a variety of materials as a function of their resistance [39]) of a resistor, where the noise PSD of the fluctuating voltage drop across the resistor in thermal equilibrium is given by:
Equation (7) is known as Nyquist theorem [40] expressing a special formulation of the FDT in Equation (5), which describes the spontaneous voltage fluctuations arising from an ideal passive resistance, i.e., the electrical Brownian Movement [28,41]. Integrating Equation (7) reveals that the variance of thermal (white) noise (see Equation (2)) converges at low frequencies but diverges at high frequencies, i.e., the mean value converges as one averages over longer and longer time intervals, but the instantaneous value of the signal is undefined.
The mathematical counterpart extreme of such a totally random signal is a random walk noise, which is an integral of white noise resulting in a PSD , where the integration brings in a factor in the Fourier transform, which becomes a factor in its square, the power spectrum. Opposite to white noise, the random walk noise contains an infinite power at low frequencies, but the spectrum is convergent when integrated in frequency from some constant to infinity. Thus, a random walk has a well-defined value at each point, whereas the divergence of the spectrum when integrating down to zero frequency means that this noise has no well-defined mean value over long times [42,43].
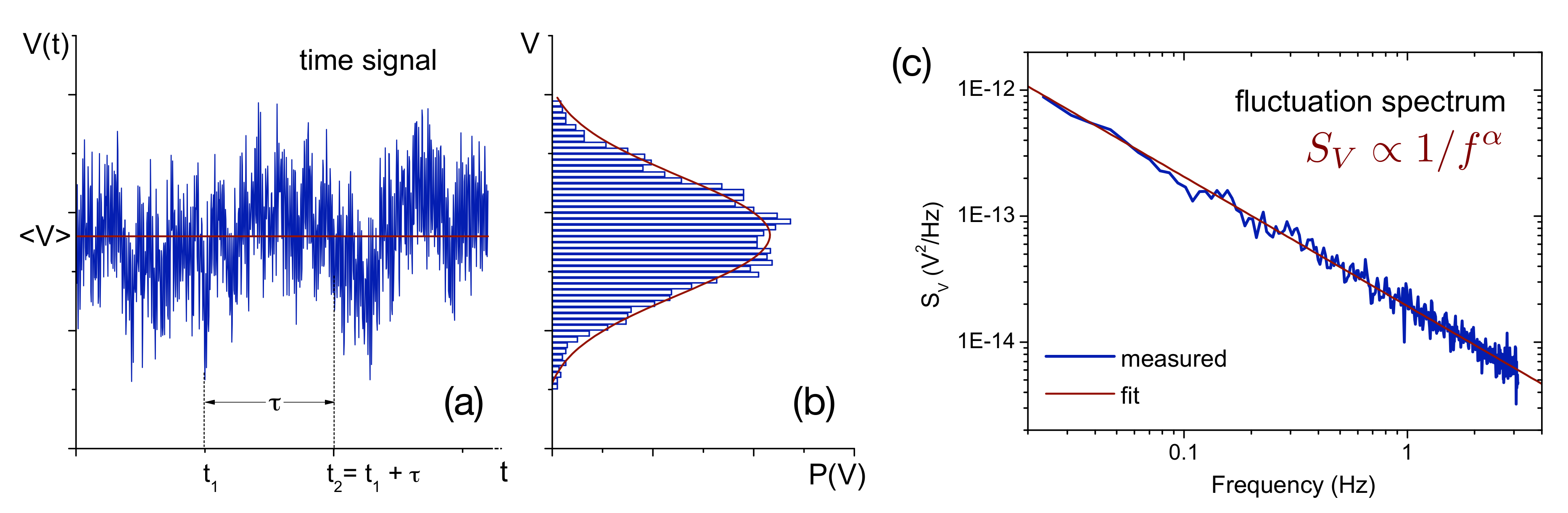
In between thermal noise (PSD ) and random walk noise (PSD ) is -noise, which is the most interesting noise being ubiquitous in nature and abundant in condensed matter physics. It may be described as the accumulative effect of ’something happening sometimes’ on all time scales. Figure 3a shows the time train of a voltage (i.e., resistance) measurement typical for many condensed matter systems, which neither appears totally random nor fully correlated (from time step to time step) or—to put it the other way around—it shows both rapid fluctuations down to the resolution limit of the instrument (e.g., a lock-in amplifier with a wide bandpass filter of time constant ms) as well as general long-term up and down trends, resulting in clearly visible maxima and minima. The noise is Gaussian and the spectrum varies as (see the histogram Figure 3b and the power spectral density (c), respectively, which is half way between white and random walk noise). Perfect -noise is self similar, i.e., scale invariant, since (each logarithmic frequency interval contributes the same power) and diverges both at the high and low frequency end, i.e., there is neither a well-defined value at a single point, nor a well-defined long-term mean. The divergence on both ends, however, is only logarithmic, i.e., so slow that even absurdly high and low values for frequency cutoffs hardly change the noise at all [9]. Experimentally, the high-frequency cutoff often naturally is given by the frequency, where the -type noise drops below the thermal noise, which is always present, and the low-frequency cutoff is determined by the experimentalist’s patience [44].
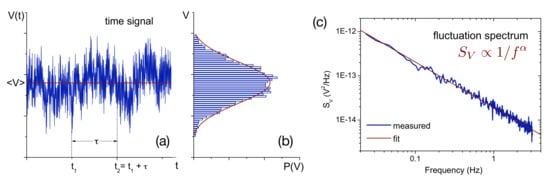
Figure 3.
Schematics of a voltage (resistance) noise measurement. (a) time-train of the voltage signal and (b) histogram of the voltage distribution fitted by a Gaussian function; (c) noise power spectral density (PSD) of the signal in (a) fitted by a power law with frequency exponent . Reprinted with permission from [9]. Copyright (2011) John Wiley and Sons.
A simple model to understand -noise in solids is the superposition of many independent two-level fluctuators with a characteristic distribution of time constants/energies. We assume for simplicity a symmetric double-well potential with a thermally activated characteristic time-constant for overcoming the energy barrier as sketched in Figure 6 below. This may be viewed as an idealized model to describe the emission of an electron from a donor state in the band gap of a semiconductor into the conduction band (detrapping), thereby contributing to the total conductance of the system, and subsequent capture by the donor (trapping). Considering only this one electron, the conductance (or resistance) will switch randomly between two distinct states leading to so-called random telegraph noise (generation–recombination noise). The current–current correlation function of this process decays exponentially as has been calculated by S. Machlup [45]:
Employing the Wiener–Khintchine theorem (Equation (4)), one finds for the current noise PSD (the equations for the voltage autocorrelation function and voltage noise PSD are analogous):
i.e., a Lorentzian spectrum. It has been recognized [29,30,46] that a superposition of Lorentzians
results in -noise for a certain distribution of relaxation times [47] in the experimentally accessible range between and :
Likewise, writing the integration in Equation (10) can be carried out over energy E resulting in for a distribution of activation energies in an energy interval for with and an attempt frequency .
A constant distribution of activation energies, however, is a strong constraint that is usually not fulfilled, which results in deviations from ‘perfect’ -noise, i.e., with [34]. A model where the energy distribution captures the often observed changes of the frequency exponent with temperature is described in Section 3.2 (see Equations (15) and (16) below).
Finally, we like to mention that for a random process the so-called second spectrum accesses the higher-order correlation function and describes the power spectrum of the fluctuations of with time, i.e., the Fourier transform of the autocorrelation function of the time series of . In the experiment, an additional frequency related to the time over which fluctuates is thereby introduced. The second spectrum probes a fourth-order noise statistics and therefore deviations from Gaussian behavior [33,48]: it is independent of the frequency if the fluctuations are uncorrelated, e.g., caused by independent two-level systems. However, a distinct frequency dependence, often with , is observed for correlated (interacting) fluctuators. A frequency-dependent second noise spectrum is important in spin glass physics [49] and is often observed accompanying the sudden slowing down of the charge carrier dynamics at a metal-insulator transition and is interpreted as glass-like freezing of the electrons undergoing correlated transitions over a large number of metastable states [50,51,52,53].
2.2.2. Measuring Resistance Fluctuations and Hooge’s Law for Organic Charge-Transfer Salts
What is fascinating about -noise is that it is ubiquitous in nature and can be found for example in melody and loudness fluctuations of classical music [54], fluctuations of a traffic current on expressways [55], the light emission of astronomical objects [42], or the dynamics of human heart rate [56,57,58] to give only very few examples. This has raised the question of whether a universal theory for -type fluctuations exists. However, considering such different complex systems, it is fair to say that commonalities likely result from mathematical coincidence rather than a fundamental underlying principle. The same is possibly true for condensed matter, where -noise is found in such different systems as semiconductors and devices, metals and insulators, granular systems, magnetic thin films and sensors, tunnel junctions, spin glasses, superconductors, colossal magnetoresistance materials, etc., where it is assumed that resistance fluctuations are the intrinsic cause of the -noise, which upon application of a driving current I lead to a fluctuating voltage drop . Likewise, the intrinsic conductance fluctuations result in a fluctuating current, when a source voltage is applied across the sample . In other words, in a resistance measurement, say, the applied current merely probes the fluctuations and facilitates the detection of -type voltage fluctuations rather than causing them. This intrinsic nature of -noise was experimentally demonstrated in [59], where fluctuations in the mean-square Johnson–Nyquist-noise exhibit -type spectra.
As mentioned above, the fluctuations are measured by employing the definition of the noise spectrum using realizable filters [37], where the fluctuating signal is processed either by a software or a spectrum analyzer consisting of a bandpass filter with adjustable frequency and a narrow bandwidth around a central frequency, and an output detector that responds to the mean square of the signal [33] (see [9,60] for a more detailed description of the five-terminal bridge setup and AC frequency-shift method [61] mainly used for obtaining the noise spectra presented in this review).
An important test regarding the intrinsic nature of the measured -noise in a four-terminal configuration, which to a large part eliminates the contribution of the electric contacts, or five-terminal bridge, which in addition makes the setup insensitive to fluctuations of the source current/voltage or the bath temperature, is the scaling and the observation of a flat (’white’) spectrum in the limit of vanishing current . For AC lock-in measurements, often a voltage-divider circuit is used. Another stringent test, discussed, e.g., in [60], of the intrinsic nature of the observed -noise is the independence of the scaling of the limiting resistor in the circuit determining the sample current. For metallic samples, a five-terminal AC setup [61] with a driving current is preferred, where the sample is placed in a Wheatstone bridge in order to suppress the DC offset. The resistance fluctuations are pre-amplified and modulate the sinusoidally excited carriers to produce noise sidebands, which can be demodulated by a phase-sensitive detector in a lock-in amplifier. The advantage of an AC current is that the pre-amplifier, the internal semiconductor components of which often contribute a large spurious (extrinsic) -noise, can be operated close to its optimal frequency, ideally in the eye of its noise figure [61]. Then, the background noise merely consists of the thermal noise of the resistive components of the experimental setup and all spurious -noise is eliminated. Suitable impedance matching and choice of therefore allows for measurements from down to Hz. The output signal of the lock-in amplifier is then processed by the spectrum analyzer. As elegantly formulated in [33], this spectrum analyzer, which also includes an amplifier, plays the role of a magnifying glass, which enables us to visualize the microscopic motion and transition of particles.
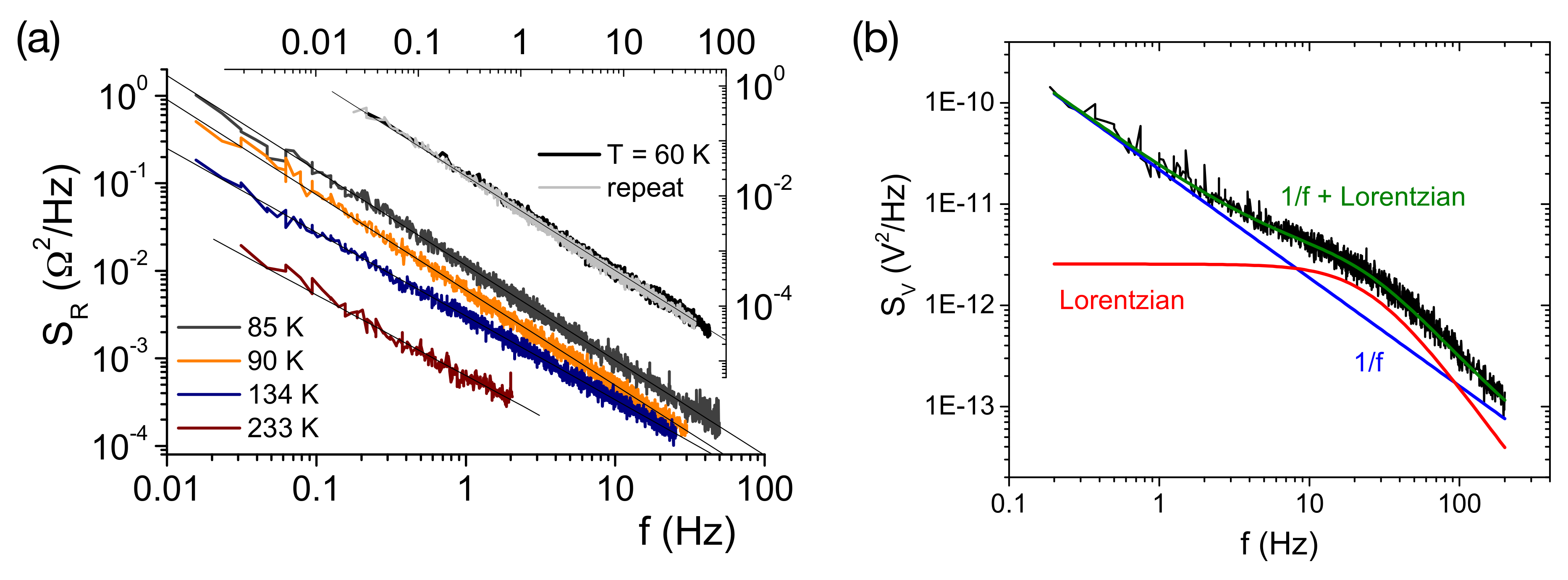
Figure 4a shows typical -type noise spectra representative for organic charge-transfer salts (taken from [60]), and (b) a typical spectrum where a Lorentzian contribution is superimposed on the background. The latter spectrum can be well described by these two separate contributions, which allows for determining both the magnitude of the -noise level and the magnitude and characteristic frequency of the Lorentzian two-level switching, cf. Equation (14) below. The meaning of the fluctuating resistance (or voltage) as a statistically stationary variable is nicely visualized by the reproducibility of the -spectra taken at K (see Figure 4a), showing that, while the noise is random, its PSD is not. The black spectrum has been taken during cool-down of the sample in discrete steps and the light-gray colored spectrum several days later during warm-up. At all temperatures, very clean -spectra with around 1 are observed. One then evaluates the temperature dependence of the slope, (see Section 3.2 below), and the temperature dependence of the noise magnitude where often the value at 1 Hz, conveniently is considered or the spectral weight in some finite frequency interval is calculated.
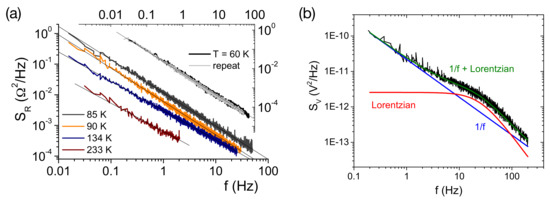
Figure 4.
Typical noise spectra. (a) representative resistance noise PSD of an organic charge transfer salt measured at different temperatures. Lines are fits to . Reprinted with permission from [60]. Copyright (2009) by the American Physical Society; (b) voltage noise PSD with a Lorentzian contribution superimposed in the -type background.
Empirically, for a large variety of semiconductors, it was found by F. N. Hooge (1969) that the normalized noise magnitudes are identical for x representing current I, voltage V or conductance G and resistance R, i.e., . (The amplitude was originally thought to be a constant that could be theoretically justified, which, however, failed.) Therefore, the measured voltage noise power spectral density , and for ohmic behavior one has . From the comparison of various semiconducting samples, a normalization with respect to the number of free charge carriers in the system, , was suggested [62]:
with the charge carrier density n, the sample’s ’noisy volume’ and therefore , and the Hooge parameter , which for clean and homogeneous semiconductors often is found to be . (Note that only for pure -noise, i.e., for frequency exponents , is a dimensionless quantity.) The assumption that -noise is composed of independent fluctuation processes of individual mobile charge carriers is of course in many cases a crude oversimplification [63]. However, as already mentioned, is useful to compare the relative noise level of different compounds or different samples of the same compound and Equation (12) may serve as a guide to optimize the shape of a metallic sample for noise measurements [64].
Early -noise measurements on organic charge-transfer salts have been reported for conducting Langmuir–Blodgett thin films based on the molecules CH-TCNQ and CH-DMTTF as well as prototypical TTF-TCNQ single crystals [65]. It was found that the room-temperature Hooge parameter of the thin films is enhanced about three orders of magnitude as compared to the values of clean semiconductors and even seven to eight orders of magnitude for the TTF-TCNQ crystals. This is worth mentioning, since a simple geometrical model has been proposed related to the quasi-one-dimensional nature of these systems, where crystal imperfections force the charge carriers to hop from stack to stack in the process of propagation along the molecular stacking axis and a fluctuating number of charge propagation paths is suggested to account for the strongly enhanced -noise [65].
Indeed, also the quasi-two-dimensional organic charge-transfer salts (BEDT-TTF)X discussed in this review exhibit very large Hooge parameters of order [66], which is certainly on the higher end of the range of values of found for different classes of materials [33,34], whereas in many systems strongly varies with temperature. In the picture of Hooge’s model—despite being empirical and oversimplified—the large values of for organic charge-transfer salts may result from an overestimation of the noisy volume , e.g., due to inhomogeneous current paths in the sample related to the specific conduction mechanism, in particular when measured perpendicular to the highly conductive layers.
3. Results
In the following, we review selected problems related to the rich physics of quasi-two-dimensional organic charge-transfer salts (BEDT-TTF)X, which have been addressed and better understood by fluctuation spectroscopy measurements. These physical phenomena resulting in characteristic fluctuation properties are related to (1) spatial electronic inhomogeneities, i.e., electronic phase separation and percolation in the coexisting region of competing ground states; (2) glass-like structural excitations, involving the coupling of molecular degrees of freedom to the electronic transport; (3) charge crystallization and vitrification leading to heterogeneous slow dynamics; and (4) charge carrier dynamics at the Mott metal-insulator transition leading to critical slowing down of the charge fluctuations and ergodicity breaking.
In an outlook, we will briefly mention future efforts to investigate the low-frequency charge carrier dynamics deep in the insulating phase of dimer Mott systems exhibiting interesting dielectric relaxation or ferroelectricity.
3.1. Example (1): Superconducting Percolation in Phase Coexistence Regions
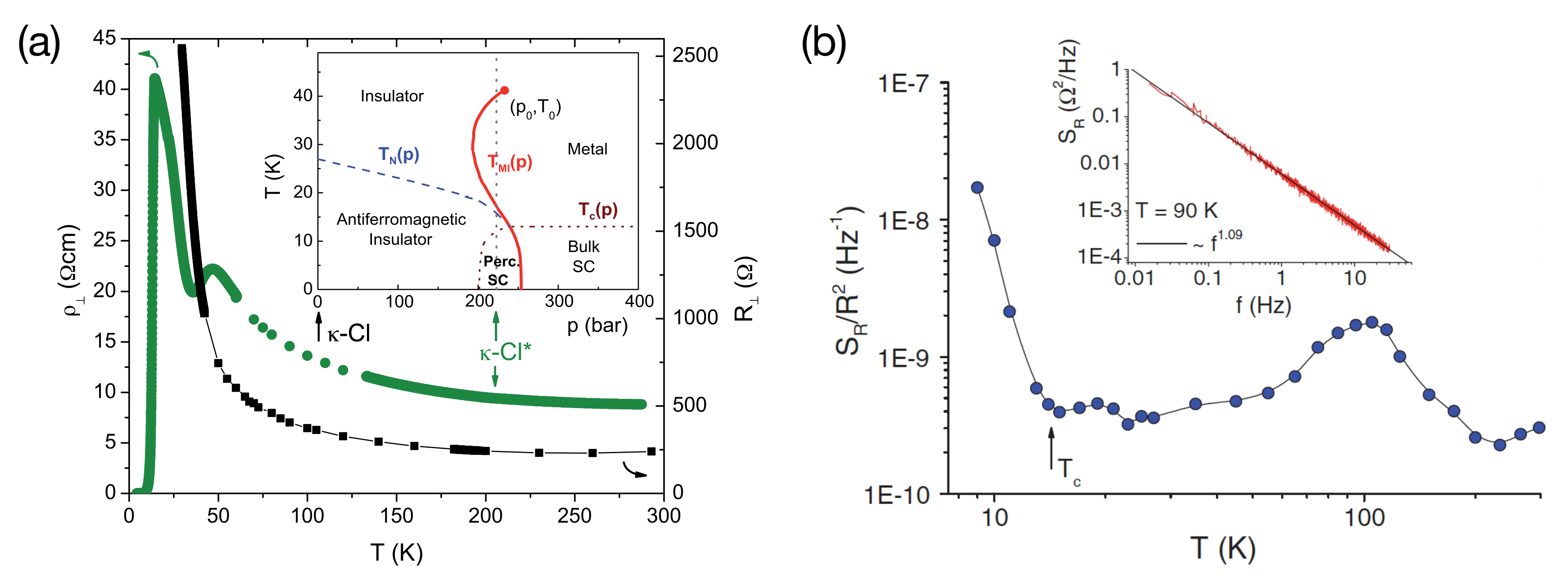
The first example deals with the fluctuation properties of an inhomogeneous state caused by the close vicinity of two phases with competing order parameters. In the phase diagram of -(BEDT-TTF)X, Figure 2, the phase boundary of the first-order Mott MIT separates an antiferromagnetic insulating/ferroelectric ground state (for low pressure, small , X = Cu[N(CN)]Cl) from a superconducting one (for high pressure, large , X = Cu[N(CN)]Br). Tuning an insulating sample -Cl by physical or chemical-induced pressure to a position close to the phase boundary results in a region of inhomogeneous phase coexistence [18], where superconductivity was believed to be percolative [67]. From resistance measurements alone, however, conclusive evidence for percolation and information on the mechanism of percolation have not been drawn. In [68], we report on measurements of the intrinsic -noise, namely , in the superconducting percolation regime of pressurized -(ET)Cu[N(CN)]Cl (in short: -Cl), an ambient pressure Mott insulator exhibiting antiferromagnetic and ferroelectric ordering being shifted to the inhomogeneous coexistence region in the phase diagram. This is seen by comparing the resistance curves shown in Figure 5a. At ambient pressure, of -Cl shows the familiar semiconducting behavior with a strong increase below about 50 K (black curve), where the charge gap opens due to the localization of the charge carriers on the (ET) dimers [69]. In contrast, pressurized -Cl shows the typical dip in the resistance upon cooling when entering the metallic phase and re-entering the insulating Mott phase due to crossing the S-shaped MIT line twice. A sudden drop of the resistivity at K indicates superconductivity. Surprisingly, for the so-prepared material, we observe a strong increase of the resistance noise PSD, , for K, i.e., upon entering the superconducting phase (see Figure 5b). A similar behavior has been observed for strongly disordered high- cuprates [70,71,72]. Whereas for homogeneous superconductors both the resistance and the -type resistance fluctuations are expected to vanish in the superconducting phase, basic percolation theory of a random resistor network (RRN), with a portion of resistor elements in the lattice being short-circuited, predicts a power-law growth of the relative resistance fluctuations , with the percolation threshold , as the portion of the superconductor increases and approaches the critical value at which an infinite superconductive cluster appears, see [33] and references therein.
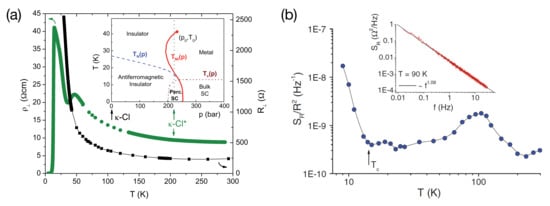
Figure 5.
Noise at the percolative superconducting transition. (a) resistance of two samples of -(ET)Cu[N(CN)]Cl. Inset shows a schematic phase diagram, cf. Figures 2 and 10b. Arrows indicate the positions of the samples measured at ambient conditions (-Cl) and at a finite pressure (-Cl); (b) normalized resistance noise PSD of -Cl. Arrow indicates the superconducting transition (onset of ). Inset: PSD of the resistance noise at 90 K in a log-log plot revealing a clean spectrum with . Reprinted with permission from [68]. Copyright (2009) by the American Physical Society.
The strong increase of the low-frequency fluctuations observed when entering the superconducting phase and approaching the superconductor-insulator transition can therefore be explained by the decrease of the number of effective current paths such that the fluctuations of R in this disordered conductor are determined only by a small volume in the sample. This—in agreement with the simple Hooge-model (Equation (12))—leads to a high noise level, whereas, far from the superconductor-insulator transition, the large number of effective current paths in the RRN results in a cancellation of the fluctuations of R along the different uncorrelated paths and a lower total noise level [33]. Under the simplifying assumption of uncorrelated resistance fluctuations in an RRN, the resistance noise is given by:
where is the local current passing through the resistance divided by the total current I, that passes through the sample [33,73,74]. The function describes the mechanism of fluctuations in the local resistances , which usually is of type with . Hence, in a simple percolative phase separation scenario, the magnitude of the noise varies depending on the fourth moment of the current distribution, whereas the frequency exponent in first approximation remains unchanged [75].
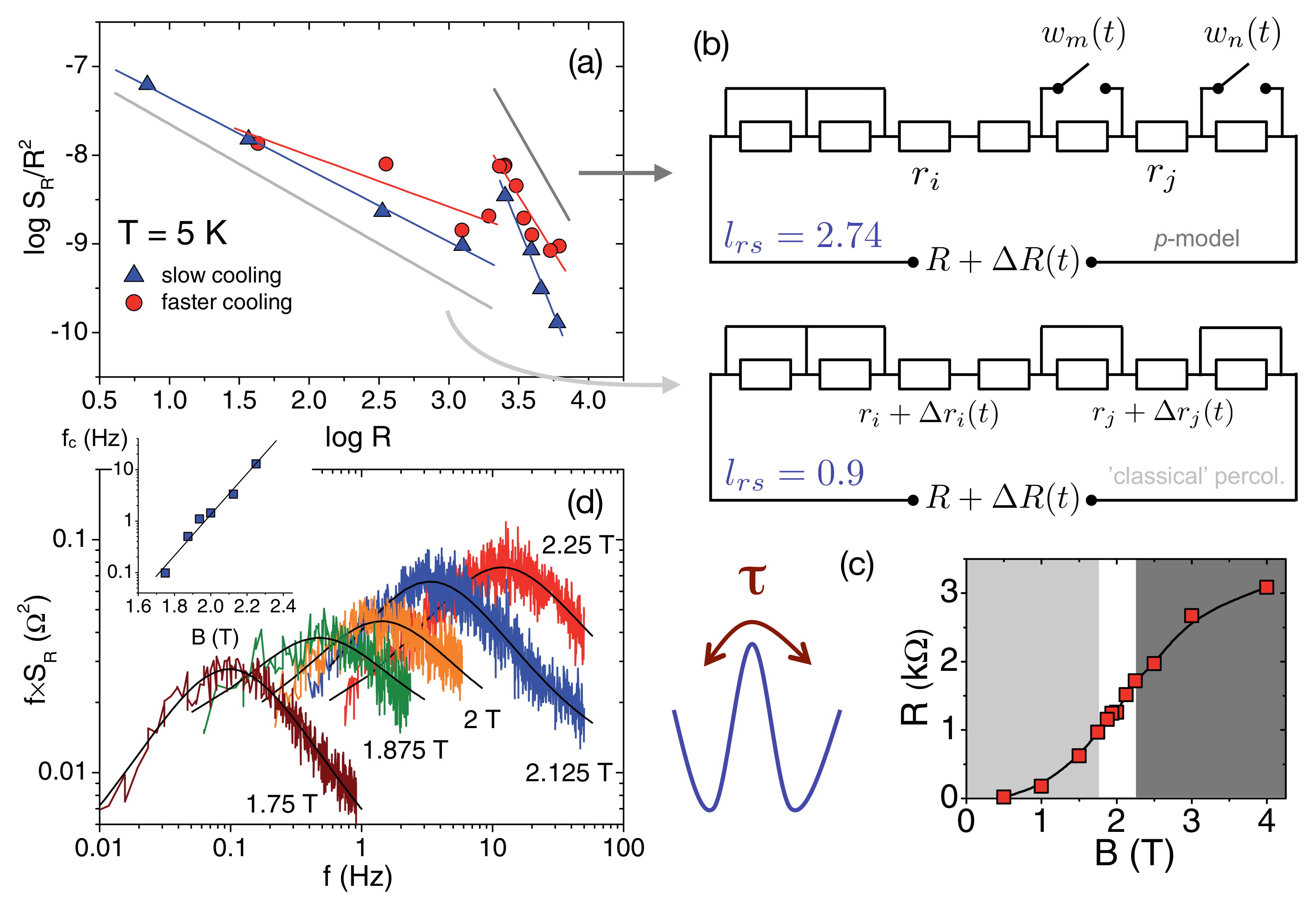
In general, since in percolation problems the measure of the vicinity to the percolation threshold is a microscopic quantity that usually is experimentally accessible only in rather specially-constructed cases [76], it is convenient to evaluate the variation of the resistance noise with respect to the actual resistance value for which a scaling behavior is predicted, resulting in [77,78]. The scaling exponent then can be compared to the predictions of theoretical calculations in order to clarify the mechanism of the underlying percolation process. Figure 6a shows a scaling plot of vs. of the pressurized -Cl sample shown in Figure 5 at a fixed temperature of K, where the magnetic field is the implicit parameter driving the system from the superconducting to the normal conducting state as shown in Figure 6c. From the slope of the data in Figure 6a yielding the scaling exponent of the resistor–superconductor network [79], we infer a change of the percolation mechanism occurring just below the midpoint of the superconducting transition. A small exponent at low fields (see that the light gray region in Figure 6c is in agreement with a ’classical’ percolation model [78]), where the -noise is generated by fluctuating resistor elements that may be identified with the portion of p resistive junctions. For larger fields, i.e., when approaching the normal conducting state, the scaling exponent becomes significantly larger and is close to the value of that is found for the so-called p-model of percolation, first discussed for disordered high- cuprate superconductors [78,80]. The difference between these two mechanisms of percolation is schematically sketched in Figure 6b, where p-noise leads to a new class of scaling exponents and describes a random on/off switching of superconducting links in the resistor network resulting in spontaneous fluctuations . These may be identified with dynamic perturbations of the Josephson coupling energy between superconducting clusters, resulting in a stronger power-law increase of the macroscopic resistance fluctuations.
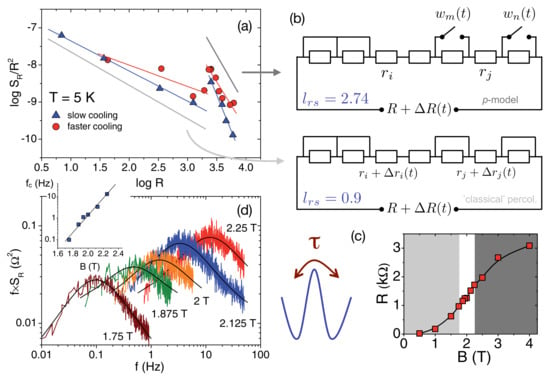
Figure 6.
Percolation models in superconductors. (a) scaling of the normalized noise of -Cl in a representation vs. , where the slope reveals the power-law exponent , for data taken at K and different magnetic fields up to 4 T as an implicite tuning parameter of the sample resistance (see (c)); (b) schematics of classical (bottom) and novel (top) percolation noise. In the former case (), the noise originates from the resistor elements, where the short-circuits represent superconducting subvolumes. The latter case of p-noise () originates from switching elements controlled by random processes representing subvolumes with unstable superconductivity, after [72]. Reprinted with permission from [9]. Copyright (2011) John Wiley and Sons; (c) magnetoresistance at K. Light and dark gray areas denote different percolation regimes characterized by the scaling exponent . In the white area, Lorentzian spectra are superimposed on the background noise (see (d)), where the inset shows the shift of the corner frequency . (a,d) reprinted with permission from [68]. Copyright (2009) by the American Physical Society.
Besides these insights in the microscopic dynamics of the inhomogeneous state in the coexistence region of the generalized phase diagram, noise measurements provide information on the characteristic length scales of phase separation. This becomes possible through a dominating two-level process in a narrow field range around the crossover from ’classical’ to p-type percolation (see the white region in Figure 6c). In this particular noise window, the action of a single fluctuator is enhanced and Lorentzian spectra, the characteristic energies of which depend on the applied magnetic field, can be resolved superimposed on the underlying -type noise. Figure 6d shows such spectra in a representation vs. f, where the ’background’ is nearly a constant for . Clearly, the additional contribution of the observed spectra can be fitted by a single two-level process with a characteristic time constant , cf. Equation (9):
In the time domain, Equation (14) corresponds to a random telegraph signal, i.e., a switching between a high- and low resistance state that may be caused by a cluster that switches between the superconducting and normal conducting state. The observed shift of the corner frequency [81] with magnetic field shown in the inset of Figure 6d and assuming , where is an attempt frequency typically related to the characteristic phonon frequencies and the energy barrier for the switching process at , allow to determine the energy . Considering the fluctuating entity as a cluster that switches between the superconducting and normal conducting state, and comparing this energy to the condensation energy , where is the thermodynamic critical field and the free space permeability, allows for a rough estimate of the fluctuating sample volume yielding [68], therefore providing evidence for a nano-scale phase separation. We note that for the high- cuprates vortex dynamics is discussed as a source of p-fluctuations [72,80], in which case we may compare to the pinning energy , where n is the number of flux lines per unit area and the energy per unit length of a vortex ( is the flux quantum and the lower critical field) leading to a volume of the same order. In order to distinguish between both scenarios, direct measurements of the magnetic flux noise are desirable.
To summarize, the intrinsic -noise in the superconducting state revealed microscopic information on (i) the mechanism of percolation and (ii) the size of the fluctuating entities and thus the characteristic scale of phase separation in the inhomogeneous coexistence region of the phase diagram. It is interesting to note that real-space imaging by means of scanning micro-region infrared spectroscopy of partially-deuterated -(ET)Cu[N(CN)]Br revealed a static phase separation and coexisting metallic and insulating domains also on a larger length scale of 50–100 and at all temperatures along the first-order Mott MIT line below the critical endpoint K [21,82]. This suggests volume fractionalization on a wide range of length scales, which, in turn, results in fluctuations with a hierarchy of corresponding time scales, a prerequisite of the widely observed enhanced -type noise in the critical region of the phase diagram (see Section 3.4 below).
3.2. Example (2): Glass-Like Structural Ordering
In this section, we exemplarily discuss the coupling of the charge fluctuations to slow structural dynamics in -(ET)X with polymeric anions X = Cu[N(CN)]Cl, Cu[N(CN)]Br, or Cu(SCN). From thermodynamic measurements, a glass-like freezing of the ET molecules’ terminal ethylene groups (EEG) was identified [19,83,84,85,86]. The dynamical properties at low frequencies—a characteristic fingerprint of all glass transitions, however—had not been studied due to the lack of dielectric spectroscopy, which cannot be applied in the relevant temperature range around 100 K, where the conductivity—even of the Mott insulating samples—is still too high. An understanding of the slow dynamics, however, is of paramount importance in these materials, since the degree of frozen EEG entities depends on the cooling rate and affects the electronic ground state properties through (i) the degree of quenched disorder and (ii) the lattice contraction occurring upon cooling through K, which strongly influences the bandwidth W and on-site Coulomb repulsion U, and therefore the sample’s position in the phase diagram (see e.g., [21,22,23,24,25,87,88,89,90,91]). In this context, fluctuation spectroscopy served as a method complementary to dielectric spectroscopy allowing for a comprehensive study of the low-frequency glassy dynamics and a systematic understanding of the glassy properties. These findings (i) revealed the phenomenology of the glassy transition in these materials [60,92,93]; (ii) allowed for controlling the glassy freezing in the critical region of the phase diagram by varying the cooling rate or applying heat pulses, thereby enabling non-volatile switching functions between metallic and Mott insulating phases and establishing a protocol for fine-tuning through the phase diagram with unprecedented precision [23,25]; and (iii)—in combination with ab initio quantum chemical calculations—now allow to predict whether a certain crystal structure favors a glassy freezing of the EEG orientational degrees of freedom or not [93]. Based on this, the specifics of the glass-like transition in the system -(ET)Hg(SCN)Cl have been correctly predicted [94].
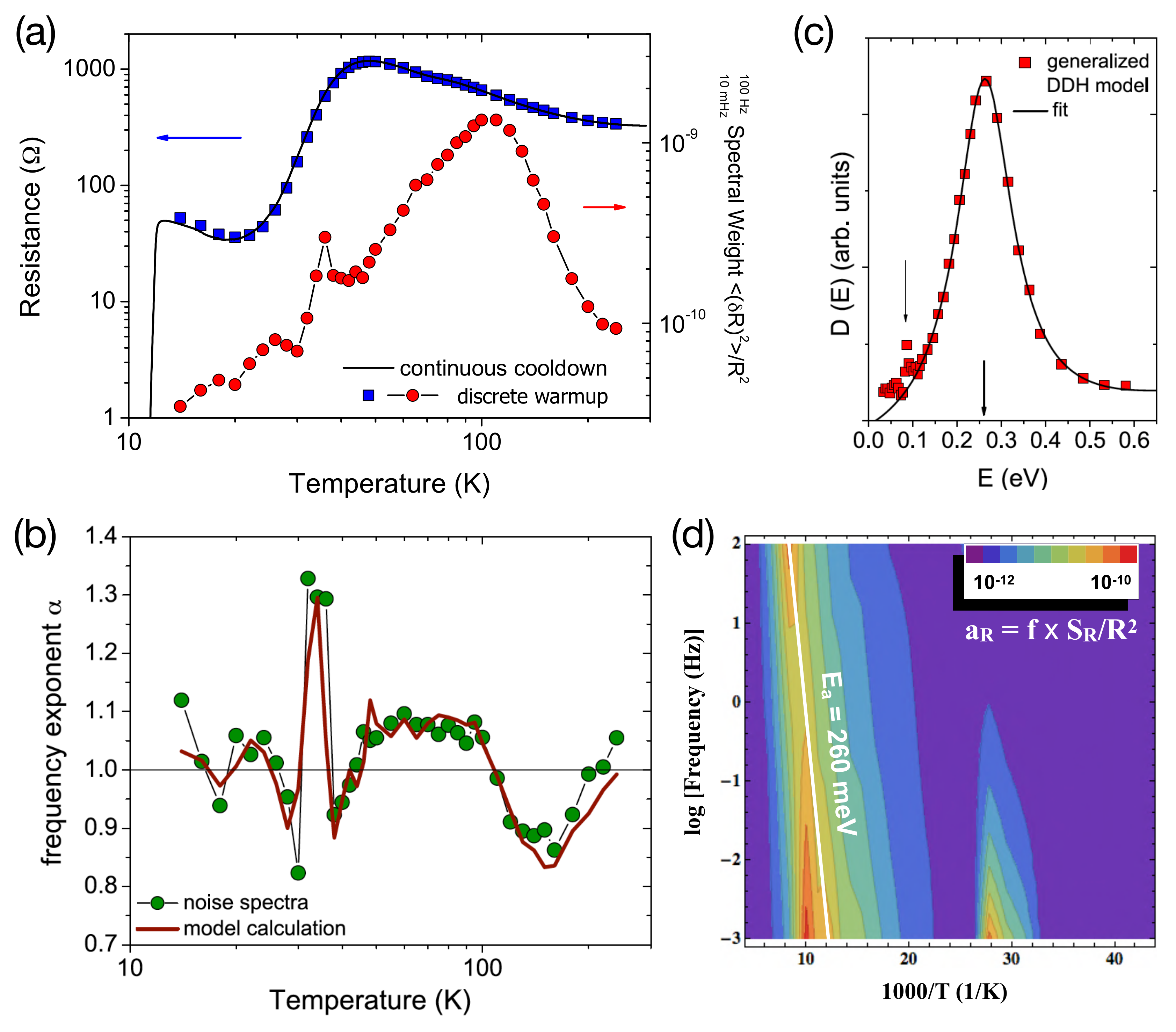
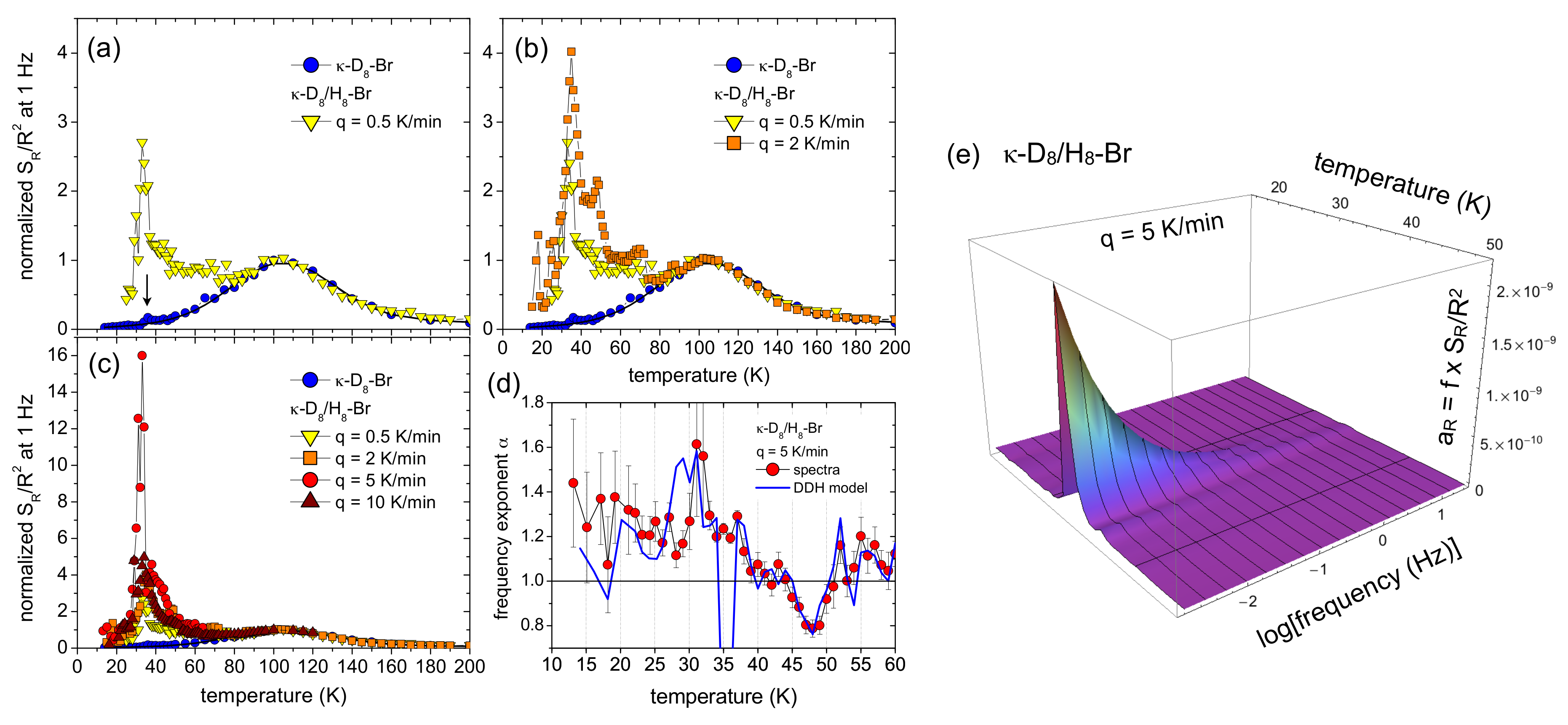
Figure 7a shows the temperature dependence of the resistance and the resistance fluctuations for deuterated -(D-ET)Cu[N(CN)]Br, which—regarding the structural glassy properties discussed here—is representative for the -(ET)X family with polymeric anions [93]. After the sample’s resistance has been measured during continuous cool down (black line), resistance values (blue squares) and noise spectra (red circles) have been taken in discrete steps while warming up the sample. The resistance shows the typical behavior for samples located close to the critical region of the phase diagram but still away from the critical point at , cf. Figure 10b below [95]. The observed noise was of generic -type at all temperatures, i.e., , and the data in Figure 7a represent the spectral weight calculated as , which represents the variance of the fluctuating resistance in the measured frequency range. Strikingly, the resistance fluctuations behave markedly different than the resistance (i.e., the mean value): a pronounced broad maximum of the normalized resistance noise at about 100 K has almost no corresponding feature in , and so does the sharp peak in the noise at about 35–36 K. The latter feature marks a sudden slowing down of the charge carrier dynamics, see the strong increase of the relative noise level —a dimensionless quantity characterizing the strength of the fluctuations—at low frequencies shown in the contour plot Figure 7d, due to the near vicinity of the critical endpoint of the Mott transition and this will be discussed in detail in Section 3.4 below.
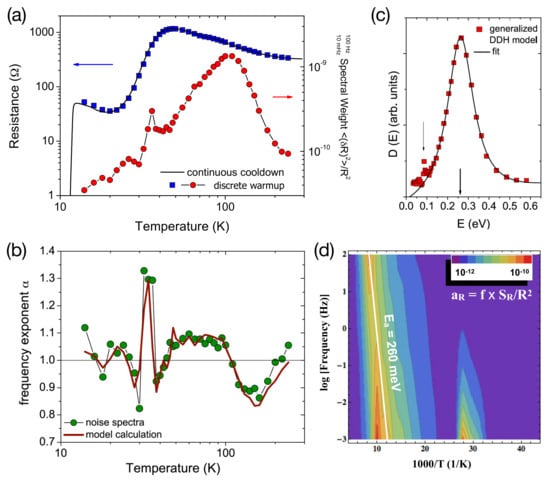
Figure 7.
Noise spectroscopy and DDH analysis (see text) on fully-deuterated -(D-ET)Cu[N(CN)]Br. (a) resistance (blue squares) and integrated noise PSD (red circles) of a fully-deuterated sample -(D-ET)Cu[N(CN)]Br; (b) corresponding frequency exponent (green circles) and model calculation within the generalized DDH model (Equation (16)) (red line); (c) distribution of activation energies at Hz calculated using Equation (18). Arrows indicate the two strongest maxima at 260 meV and 90 meV; (d) contour plot of the relative noise level vs. frequency f and temperature T in an Arrhenius representation. The slope of the white line corresponds to an activation energy of meV, corresponding to the maximum in in (c) as extracted from the DDH model. Reproduced from [92,93]. Copyright IOP Publishing.
In order to understand the origin of the -noise, we apply the phenomenological model of Dutta, Dimon and Horn (DDH) [31,96], which describes non-exponential kinetics [97] caused by a superposition of individual, thermally activated fluctuators—not specified a priori—with characteristic relaxation times , where – s corresponding to typical inverse phonon frequencies. The individual fluctuators are presumed to be independent (Gaussian) and linearly coupled to the resistance (or conductance) of the sample. Although these assumptions are quite general, the strength of the model is that a distribution (or weighting function) of activation energies determines both the temperature dependence of the noise (i.e., its deviations from a linear-in-T behavior) [98]
and the deviations of its frequency dependence from a pure law (i.e., deviations from ) via the connection
The logarithmic factor in ensures that at the temperatures and frequencies, where -noise is usually observed, the characteristic energies eV are of the same order as ordinary activation energies in solids [33]. The frequency exponent calculated with Equation (16) can then be compared to the measured slope of the spectra
If this consistency check proves successful, then the assumptions of the DDH model [99] are fulfilled, and the distribution function can be determined from the relation
Introducing the function in Equations (15) and (16) is a generalization of the original DDH model [100,101,102]. The function accounts for an explicit temperature dependence of the distribution of activation energies. The physical meaning is that the coupling constant between the random processes and the resistance, and hence the total noise magnitude, may not be independent of temperature. As described in detail in [93], we have assumed the simplest case of a power law , where b describes a constant vertical shift of as compared to the measured . For the measurements in Figure 7b, the best description of the data is found for for (no offset) and for resulting in a vertical offset. As for the physical meaning of the function , a temperature dependence of the number and/or coupling strength of the fluctuators is discussed [102,103]. Figure 7b shows that, for the deuterated -D-Br system, an excellent agreement is observed between the calculated and measured frequency exponent, where nearly every feature of the non-monotonic temperature dependence is quantitatively reproduced. This justifies the conversion of the temperature axis using and determining from Equation (18) shown in Figure 7c. The broad noise peak at about 100 K in Figure 7a therefore corresponds to a peak in centered around meV ( K). (Note that the contour plot Figure 7d of the relative noise level in an Arrhenius plot consistently reveals a slope of the noise maximum corresponding to the same energy.) Energy of this order is well known in -(ET)X as the activation energy of structural, orientational degrees of freedom of the ET molecules’ EEG undergoing a glass-like freezing at K and has been determined, e.g., in NMR [104,105], and thermal expansion and specific heat measurements [19,84] for the thermodynamic glass transition (see also [2]). Therefore, the fluctuators causing the enhanced noise at elevated temperatures can be assigned a posteriori to the thermal motion of the EEG, emphasizing the strong coupling of lattice vibrations to the electronic system.
Here, the non-monotonic behavior of shown in Figure 7b reflects the shape of the distribution of the activation energies, i.e., and corresponds to and , respectively. The corresponding shift of spectral weight to lower frequencies is related to the expected slowing down of molecular dynamics when approaching the glass transition. In [93], we argue that the observed charge carrier dynamics is caused by the slow, so-called -process of the glass-forming EEG rotations embedded in the anion structure forming a ‘cage’ environment through short C−H⋯anion contacts [106]. In dielectric spectroscopy, the -relaxation peak of the frequency-dependent dielectric loss shifts with decreasing temperature to lower frequencies in a similar way [107], which is expected from the fluctuation–dissipation theorem connecting with the imaginary part of the dynamic susceptibility, cf. Equation (5).
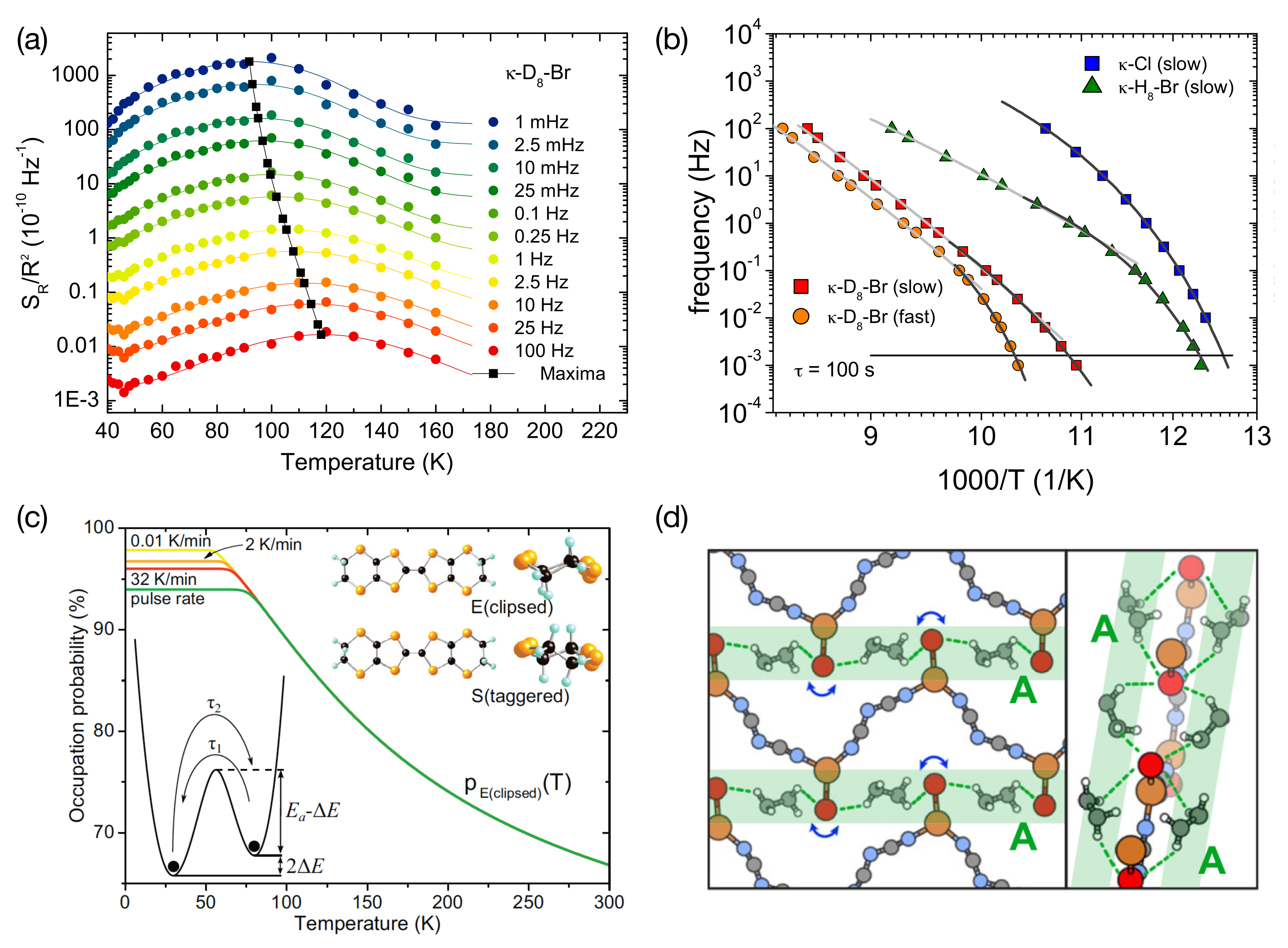
This a posteriori assignment provides a spectroscopic tool to investigate the slow dynamics of the EEG, which undergo a glassy freezing at a characteristic temperature . Figure 8a,b show the position of the peak in of the same sample -D-Br discussed in Figure 7a–c for different frequencies in our measurement window of 1 mHz–100 Hz. (Note that in Figure 7a the spectral weight over the full frequency range is shown.) As seen in Figure 8b for -D-Br, the data at higher frequencies show an Arrhenius behavior, where the slope corresponds to an activation energy of 260 meV corresponding to the maximum in shown in Figure 7c. At lower frequencies towards the glassy freezing transition (which may be defined by a characteristic relaxation time of s), however, the slowing down of the molecular motions coupled to the resistance fluctuations is much stronger, resulting in a curvature that can be described by the empirical Vogel–Fulcher–Tammann law
where D is a strength parameter and the Vogel–Fulcher–Tammann temperature. The observed slowing down of the structural units’ motion stronger than given by an Arrhenius law may be interpreted as an increase of the effective energy barrier for decreasing temperatures approaching . A possible origin is an increasingly cooperative character of the molecular motions, i.e., a larger number of correlated molecules and an increase in correlation length [108]. The strength parameter D describes the deviations from a thermally activated behavior, whereas the glass-forming system is characterized as ‘fragile’ for small values of D (typically ) with large deviations from an Arrhenius behavior and as ‘strong’ for following an Arrhenius law more closely. Many properties of glass-forming materials are correlated with their strength (fragility). For the different systems, we consistently find that the present charge-transfer salts are rather fragile glasses, which may be explained by a growing number of correlated molecules moving cooperatively, which leads to an increase of the apparent activation energy for decreasing temperatures.
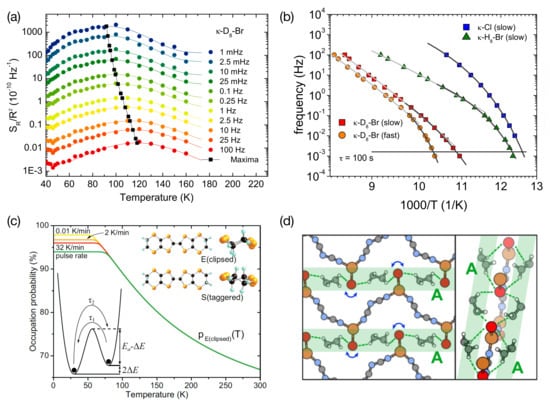
Figure 8.
Glass-like structural EEG ordering in -(ET)X. (a) normalized resistance noise PSD of -D-Br for different frequencies. Lines are fits to a Gaussian function. Black circles connect the maxima at each frequency; (b) Arrhenius plot of the noise peak frequency for selected systems of -(ET)X (see legend). Light grey lines are fits of thermally activated (Arrhenius) behavior to the high-frequency data, whereas dark grey lines are Vogel-Fulcher-Tammann (VFT) fits after Equation (19) to the low-frequency data. The horizontal line equals s and may be used to define the dynamic glass-transition temperature; (c) occupation probability of the eclipsed (E) ground state conformation (see right inset) calculated from a simple two-level model (left inset) for various cooling rates. ’Pulse rate’ refers to cooling after a heat pulse is applied resulting in cooling rates of order 1000 K/min. Reprinted with permission from [23]. Copyright (2014) by the American Physical Society; (d) preferred conformations of the EEGs for -Br in relation to the nearby anion layer. Dashed lines indicate close EEG⋯Br contacts, while blue arrows indicate soft vibrational degrees of freedom of the terminal Br ligands suggested to couple to the EEG rotation. In -Br, all EEGs are crystallographically equivalent. (a,b,d) reproduced from [93]. Copyright IOP Publishing.
Finally, we note that the cooling-rate dependence of the VFT behavior, observed for -D-Br shown in Figure 8b, is unusual since, for classical glass-forming systems, the curves for different q should coincide for . Rather than being a purely dynamical effect, we have speculated that, for the present glass-like materials, different cooling rates produce different glass-forming molecular environments formed by the anion structure through short C−H⋯anion contacts, resulting in a varying fragility and therefore different values of .
Ab initio quantum chemical calculations provide an explanation for the origin and phenomenology of the glassy dynamics in different systems in terms of a simple two-level model (see Figure 8c) where the relevant energy scales are determined by the coupling of the EEG to the anions [93]. For -Br, the EEGs are all crystallographically equivalent and were computationally found to prefer the E conformation by 520 K per ET molecule, which is of the same order although somewhat larger than the value of 210 K estimated from the temperature dependence of the relative E/S occupancy of -Br for fixed cooling rate [23]. The computed K, however, lies well within the range of values found in various experiments of 1900–3100 K as determined e.g., by NMR, specific heat, thermal expansion, resistivity measurements and noise spectroscopy [19,84,104,105]. Strikingly, more than half of the computed energy difference results from strong van der Waals coupling between the EEG and anion layers, which is dominated by close Br H (or D) contacts between each EEG and two terminal ligands in adjacent anionic chains (see Figure 8d). The coupling of the terminal ligands’ thermal motion with the EEG rotation in nearby ET molecules provides a possible mechanism for the cooperative behavior implied by the observed deviations from the Arrhenius law in Figure 8b, i.e., it is the collective motion of EEG and anions that freezes out at instead of being simply a property of the vibrational degrees of freedom of the EEG within each individual, separated ET layer [93,94].
It is interesting to consider the suggestion [109,110] that the arrangement of the ET molecules and conformational preferences in -(ET)X salts with polymeric anions result from a particular pattern of empty spaces in the anion layers, allowing the donor molecules to fit in between, thus minimizing the van der Waals interactions. From this perspective, glassy freezing of the EEG rotation requires that the EEG–anion interaction is relatively ineffective at distinguishing the E and S states, allowing for similar energies of both states, and thus metastability. Indeed, in our simple model of Figure 8c, it can be shown that the degree of frozen-in disorder is determined by the ratio of (at fixed ), with increasing occupancy of the minor conformation below with increasing ratio. We have suggested an empirical threshold of for the occurrence of a glass transition in (BEDT-TTF)X. Recently, this has led to the successful prediction of glass-like EEG freezing in the salt -(ET)Hg(SCN)Cl, where—as opposed to -Cl and -Br—a peculiar EEG ordering occurs, in which only one of the two crystallographically inequivalent EEG is subject to glass-like ordering [94].
3.3. Example (3): Charge-Cluster Glass
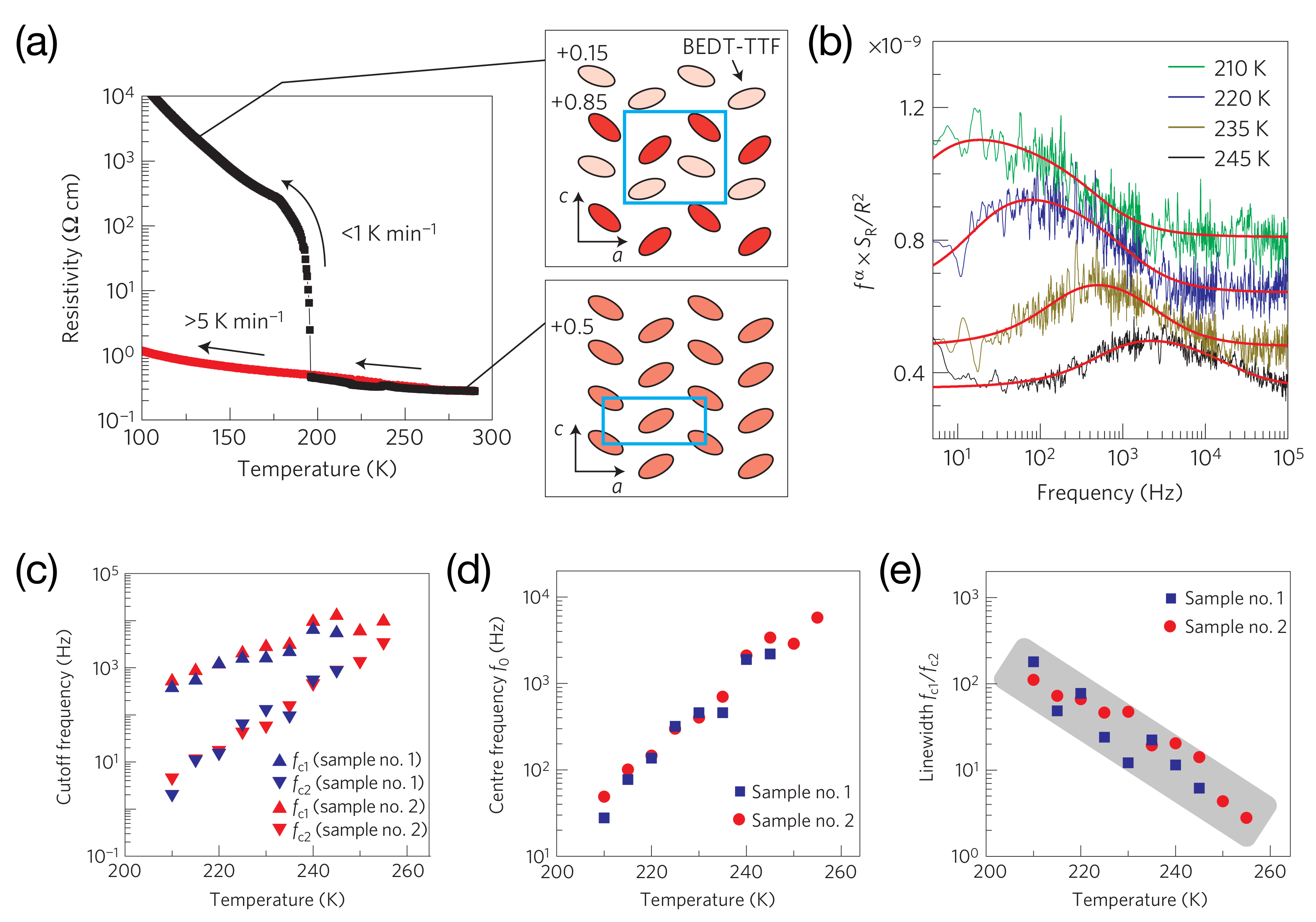
In the previous section, we have shown exemplarily for the -phase (ET)X salts with polymeric anions that noise measurements allow for a spectroscopic study of glassy structural phenomena, where dielectric spectroscopy fails due to the high conductivity of the samples. Naturally, fluctuation spectroscopy is not only sensitive to electronic fluctuations coupled to a structural dynamic glass transition, but also to glassy phenomena of the electronic system itself. Here, the systems -(ET)MM(SCN) with M = Tl, Rb, Cs and M = Co, Zn recently have attracted considerable attention [111,112]. In these materials, the BEDT-TTF molecules form a triangular lattice and the charge transfer leads to a quasi-two-dimensional quarter-filled hole band system (that is, one hole per two BEDT-TTF molecules), in which the inter-site Coulomb repulsions give rise to an instability towards charge ordering (CO). The system -(ET)RbZn(SCN) undergoes a CO transition at 190 K, where the charge carriers are localized periodically with a horizontal stripe pattern (see Figure 9a), which is regarded as a ’charge-crystal’ state in contrast to the ’charge-liquid’ state above the CO transition temperature, where the charge of per one BEDT-TTF molecule is distributed uniformly in space. Geometrical frustration leads to an unconventional electronic ’charge-glass’ state without long-range order, when the system is cooled faster than a critical rate , which depends on the degree of geometric frustration. As first discussed in [113], a combination of noise measurements and X-ray diffraction reveals that the charge-liquid phase hosts two-dimensional charge clusters that fluctuate extremely slowly and heterogeneously. On further cooling, the cluster dynamics freezes, and a charge-cluster glass is formed.
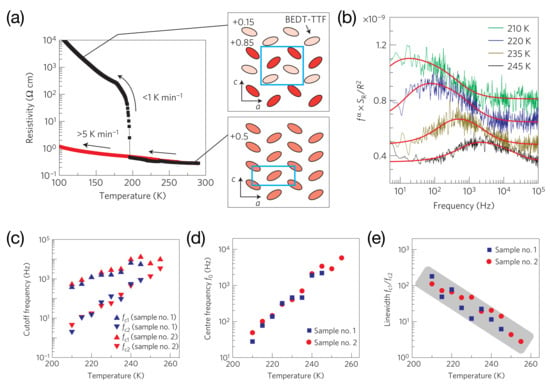
Figure 9.
Charge-cluster glass in -(ET)RbZn(SCN). (a) temperature dependence of the resistivity during cooling for different sweeping rates . Insets indicate the crystal structures and charge distribution of the high-temperature (charge-liquid) phase (lower inset) and the slowly cooled low-temperature (charge-ordered) phase (upper inset); (b) resistance noise PSD for various temperatures as vs. f with fits (red lines) to the distributed Lorentzian model (see text); (c) temperature profiles of the fitting parameters and ; (d) slowing of the centre frequency and (e) concomitant growth of the dynamic heterogeneity, respectively. Reprinted with permission from [113]. Copyright (2013) Springer Nature.
Since slow dynamics accompanied by dynamic heterogeneities are known to be key experimental properties for the vitrification process in supercooled conventional liquids, resistance noise spectroscopy has been applied in order to detect the expected slow charge carrier dynamics in these materials upon approaching the glassy freezing of the electrons [111,113,114,115]. Figure 9b shows the resistance noise PSD in a representation vs. f [113], which highlights the superposition of two-level fluctuations on top of a background noise, cf. Figure 6b above. The important point here is that the two-level switching cannot be described by a single Lorentzian contribution but rather is modeled by a superposition of continuously distributed Lorentzians with high-frequency () and low-frequency () cutoffs. Thereby, the authors of [113] assume a density of states (distribution of relaxation times) in between the related cutoff lifetimes in Equation (10) with and . The integration in Equation (11) then yields curves of the spectral form shown in Figure 9b, which fit the data very well. In this scheme, the extracted values for and (see Figure 9c) reflect the fastest and slowest fluctuators, respectively, from which a centre frequency and a linewidth can be defined (see Figure 9d,e, respectively). The temperature profiles of these quantities show a slowing down of the center frequency by several orders of magnitude (see Figure 9d), before, at approximately 200 K a frustration-relaxing structural transition occurs. A strong increase of the ratio for decreasing temperature (see Figure 9e) indicates a more heterogeneous dynamics [113]. Thus, the key experimental properties for the vitrification process in conventional supercooled liquids, namely slow and heterogeneous dynamics, are observed for the freezing of electric charges on a frustrated lattice.
This notion of an unconventional electronic state without long-range order as inferred from the observed heterogeneous slow dynamics is corroborated by X-ray diffusive scattering revealing that the charge-liquid phase above 200 K is transforming into a charge-cluster glass. This glass transition of the charge clusters formed in the charge-frustrated triangular lattice is expected to occur only if the frustration-relaxing transition at 200 K is kinetically avoided by rapid cooling and occurs at 160–170 K.
Further detailed resistance noise, time-dependent resistance and X-ray diffusive scattering experiments have been performed on the related system -(ET)CsZn(SCN), which does not exhibit long-range charge order at usual laboratory time scales but always shows a charge-glass state, i.e., the critical cooling rate is very slow due to the higher degree of geometrical frustration [114]. Again, cooling-rate dependent charge vitrification and nonequilibrium aging behavior are successfully demonstrated. The temperature evolution of the relaxation time is found to obey an Arrhenius law , indicating that the glass-forming charge liquid can be classified as a ’strong’ liquid in the scheme of canonical structural-glass formers (see Section 3.2 above). The activation energy meV is ascribed to the energy related to the rearrangement of the charge configurations, which may be accompanied by a distortion of the local lattice/molecules [114]. Finally, the characteristics of the charge-glass are summarized as follows (see [116] and references therein): (i) the valence of BEDT-TTF appears to be spatially inhomogeneous; (ii) short-range order or charge clusters, with distinct symmetry from that of the charge-ordered state, develops as the temperature decreases, where below the charge-glass transition temperature, the characteristic size of the charge clusters saturates (iii) the time scale of charge fluctuations is slower than the laboratory time scale; and (iv) aging behavior is observed in resistivity, analogous to the dielectric aging in structural glasses.
Finally, in a recent work on monoclinic -(ET)TlZn(SCN)—a material where the electron-lattice coupling and lattice distortion are weak and which is believed to approximate a system where the observed effects are purely electronic in nature—similar noise measurements as discussed above reveal an Arrhenius law of the Lorentzians’ corner frequencies and confirm the emergence of slow dynamics accompanied by increasing dynamic heterogeneity upon approaching the charge-glass transition [111]. Here, it is important to note that the charge vitrification in the present case is distinctly different from the drastic slowing down of charge carrier dynamics and onset of non-Gaussian fluctuations observed in noise measurements as a precursor of metal-insulator transitions (MITs) [50,51,52,53] (see the discussion in the following Section 3.4). The electronic glassiness in MIT systems seemingly only becomes stabilized by disorder in the presence of strong electronic correlations and may not be observed for ’clean’ samples.
3.4. Example (4): Mott Metal-Insulator Transition
In pressure-tuned -(BEDT-TTF)Cu[N(CN)]Cl, unconventional critical exponents at the finite-temperature second-order critical endpoint of the Mott metal-insulator transition have been reported from DC electronic transport measurements [20]: the power-law exponents of the measured conductance upon approaching the critical point on the temperature and pressure axes seem to be inconsistent with any known universality classes (mean-field, 3D XY, Heisenberg and Ising). Since then, the critical properties have been a matter of controversial debate [117,118,119,120]. Recently, in [121], a breakdown of Hooke’s law of elasticity has been observed at the critical endpoint of the Mott transition. These nonlinear strain-stress relations are assigned to an intimate, nonperturbative coupling of the critical electronic system to the lattice degrees of freedom. The authors point out that their results are fully consistent with mean-field criticality, predicted for electrons in a compressible lattice with finite shear moduli and argue that the Mott transition for all systems that are amenable to pressure tuning shows the universal properties of an isostructural solid-solid transition [121]. In contrast to these static properties of the Mott critical endpoint, dynamical critical phenomena are related to the existence of very long time scales known as critical slowing down of the order parameter relaxation rate, where the length and time scales that measure the correlations of the order parameter become infinite upon approaching a second-order phase transition. Therefore, the kinetics of the order parameter near a critical point causes a slow dynamics of correlated regions in a macroscopic system, and diverging resistance or conductance fluctuations are expected. However, this critical slowing down of the order-parameter fluctuations had not been observed for the Mott transition before.
In Section 3.2, we have mentioned that the cooling-rate dependence of the glass-like EEG ordering can be used to fine-tune systems through the critical region of the Mott transition. The effect originates in an anisotropic change of the in-plane lattice parameters at [19,86], which changes the relevant transfer integrals such that more rapid cooling leads to slightly smaller bandwidth (and ratio) (see discussion in [21,23]). In particular, in [24], it has been shown that the molecular conformations of the EEG are intimately connected to the electronic structure and significantly influence not only the transfer integrals and therefore W but also the Hubbard repulsion parameter U. These results place -(BEDT-TTF)Cu[N(CN)]Br in eclipsed (E) and staggered (S) configurations on opposite sides of the metal-insulator transition [24].
For our study of the dynamic criticality, we therefore have chosen a partially-deuterated system -[(H-ET)(D-ET)]Cu[N(CN)]Br (in short: -H/D-Br), where the partial substitution of the ET molecules with their deuterated analogues places the sample on the high-pressure (metallic) side of the phase diagram very close to the critical pressure of the MIT [21]. Figure 10a shows the sample resistance for different cooling rates q representing different positions of the sample in the generalized phase diagram, schematically indicated in Figure 10b [53]. Clearly, the slowly cooled (annealed) sample is located on the metallic/superconducting side of the phase diagram, whereas increasing q shifts the sample to the left (low pressure, small ) towards the insulating side, where the typical re-entrant behavior, when crossing the first-order Mott transition line twice, is observed. We assume that the critical point is crossed by one of the curves taken in between the slowest and fastest cooling rate (colors from black to dark red). Blue color denotes the position of the fully-deuterated sample shown in Figure 7 above. The superconducting transition observed at low temperatures for all cooling rates is of inhomogeneous, percolating type due to the coexistence of metallic (superconducting) and insulating (antiferromagnetic) phases as discussed in Section 3.1 above. We note that the fine-tuning of the electronic bandwidth by controlling the cooling rate is reversible; i.e., upon warming above 75–80 K, the frozen EEG glass melts and the lattice relaxes and the pristine state and position in the phase diagram is recovered.
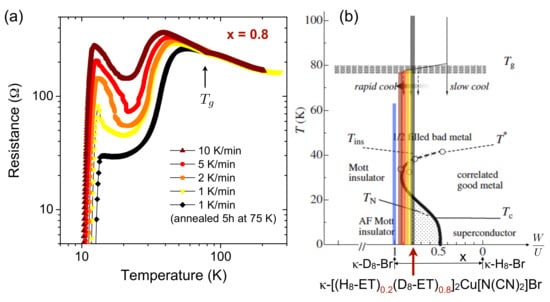
Figure 10.
Tuning a partially-deuterated sample -[(H-ET)(D-ET)]Cu[N(CN)]Br with through the Mott transition. (a) resistance measurements for various cooling rates q; (b) generic phase diagram after [21]. Open circles indicate values taken from the literature of the second-order critical end point of the first-order Mott MIT (thick solid curve). The arrow indicates the position of the slowly cooled, pristine sample in the generic phase diagram. The change of the sample position with q is schematically indicated by the colored lines. For comparison, the blue color represents fully-deuterated -D-Br shown in Figure 7. Reprinted with permission from [53]. Copyright (2015) by the American Physical Society.
The comparison of -D-Br (same sample as shown in Figure 7a, blue curve) with slowly-cooled -H/D-Br (yellow) is displayed in Figure 11a, where the normalized resistance noise PSD, , taken at 1 Hz is shown. Measurements have been performed in a five-point AC bridge setup perpendicular to the conductive planes, i.e., along the crystallographic b-axis. In order to highlight the drastic changes of the fluctuation properties originating from different positions in the phase diagram tuned by the cooling rate q, i.e., the effects of electronic origin, the data are normalized to the broad maximum at around 100 K, which we have shown in Section 3.2 to be of structural origin. Strikingly, the two samples behave similarly for temperatures above the glass-like transition , where the resistance fluctuations are dominated by the EEG structural excitations. However, the -H/D-Br sample exhibits a considerably higher noise level below , which may be caused by the higher degree of structural disorder due to the random distribution of H and D molecules, resulting in a tendency for the charge carriers to localize and/or electronic phase separation. Most strikingly, however, is the sharp peak in the noise at K, which we attribute to the near vicinity of the critical endpoint of the Mott transition. Note that an increase of the noise accompanied by a shift of spectral weight to low frequencies is seen also for -D-Br (see the arrow in Figure 11a as well as Figure 7a,d). This sudden slowing down of the charge carrier dynamics due to critical fluctuations, however, for this sample remains a small effect as compared to the effect of the structural EEG fluctuations. This is not the case for -H/D-Br, where upon increasing q, the peak in the noise initially increases (Figure 11b, orange squares) and becomes very pronounced and sharp (note the rescaled axis) for K/min, red circles in Figure 11c, before it starts decreasing again for a larger cooling rate (dark red triangles). We therefore assume the sample’s state at K/min as being closest to the critical point [122] and now evaluate the fluctuations in the whole accessible frequency range. The frequency exponent , shown in Figure 11d, exhibits a monotonic increase from about (at K) to a very large value of about (at K) upon approaching the critical region from high temperatures. This corresponds to a drastic shift of spectral weight to low frequencies. This behavior is highlighted in Figure 11d, where the relative noise level is shown, a dimensionless quantity characterizing the strength of fluctuations. We interpret the incipient power-law divergence of at very low (approaching mHz) frequencies in a narrow temperature interval as critical slowing down of doublon density (two electrons sitting on the same atomic orbitals) fluctuations [118,123,124], since the measured resistance (conductance) noise PSD is proportional to the Fourier transform of the voltage (current) autocorrelation function (Section 2.2), which couples to the kinetics of the order parameter of the Mott MIT [20,125]. Near a critical point, the latter is dominated by slow dynamics of correlated regions in a macroscopic system.
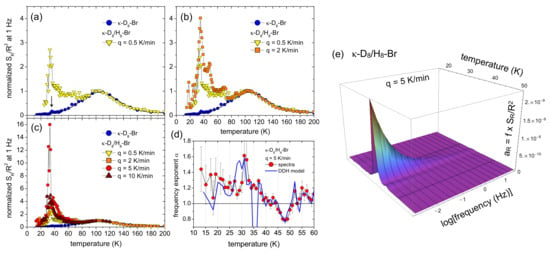
Figure 11.
Critical slowing down of charge fluctuations. (a) resistance noise PSD of slowly-cooled -H/D-Br (yellow triangles) in comparison to the data of -D-Br (blue circles) normalized to the value of the local maximum around 100 K. The black arrow indicates a peak in the noise level, cf. data of the same sample shown in Figure 7a. (b,c) measurements for increasing cooling rates q. Note the rescaling of the ordinate in (c); (d) frequency exponent for K/min, where the noise level shown in (c) is largest. The line represents the DDH model calculation; (e) relative noise level vs. f vs. T for the same cooling rate. Reprinted with permission from [53]. Copyright (2015) by the American Physical Society.
Whereas the strong increase of slow fluctuations in -H/D-Br is observed at a finite-temperature critical point, a similar behavior has been reported for metal-insulator transitions occurring only in the zero temperature limit, namely a disorder-driven Anderson transition in P-doped Si [52] and electron-density driven MIT in Si inversion layers (Si-MOSFET) [50,51,126]. It is interesting to consider if there is a connection to the notion of the quantum-critical nature of the Mott instability [125]. In both cases, the onset of non-Gaussian fluctuations resulting in a frequency-dependent second spectrum (see Section 2.2.1) have been reported. If , the statistics of the system is fully determined by the first spectrum and the fluctuations are Gaussian. Slow dynamics and deviations from a ’white’ second spectrum, i.e., are an indication for correlated (interacting) fluctuators [48,49] and have been observed for the abovementioned P-doped Si and the Si inversion layers systematically as a precursor of the MIT. A possible interpretation is a glassy freezing of the electrons preceding their localization, and it is suggested that such correlated dynamics may be a universal feature of MITs, irrespective of the systems’ dimensionality [52]. In the present case of a finite-temperature critical endpoint, the deviations of the measured frequency exponent from calculated within the DDH model (assuming independent fluctuators) shown in Figure 11d for K/min and a frequency-dependent second spectrum with for K/min indicate a finite region in the phase diagram, where the fluctuations are correlated and deviate from Gaussian behavior.
Here, a residual structural disorder potential and/or the inherent frustration of the triangular lattice geometry of the ET molecules forming dimers could result in a large number of metastable states, which the strongly interacting electrons have to overcome. General models for such correlated dynamics applied to spin glasses are often invoked also for the charge degrees of freedom [51,126]. In a model of interacting droplets or clusters, should be a decreasing function of f for constant [49]. For the present system, however, we observe a scale invariance in f pointing to a hierarchical picture, where the system wanders collectively between metastable states related by a kinetic hierarchy. The large exponent of found in our experiment for the sample cooled with K/min indicates that only few such states are visited during the time of measurement. From the theoretical point of view, a Coulomb glass behavior in the vicinity of the Mott transition remains controversial. For example, a self-generated glass transition caused by the frustrated nature of the interactions (and not related to the presence of quenched disorder) is predicted in doped Mott insulators [127]. In [128], however, the metallic glassy phase is suggested to be suppressed for Mott localization and to become stabilized only for increasing disorder, in apparent agreement with experimental results on Si inversion layers with different degrees of disorder.
A systematic mapping of the region of ergodicity breaking for samples at different positions in the phase diagram (i.e., varying distance to the critical endpoint) and with different degrees of quenched disorder (random lattice potential) may help to answer these fundamental questions and will be an elaborate but worthwhile future effort.
Sample Dependences
Instead of using different cooling rates, an alternative way to tune through the phase diagram in even finer, in principle arbitrarily small steps is to apply different thermal relaxation protocols in the vicinity of the transition temperature for glass-like EEG ordering [25]. Again, we choose a partially-deuterated compound, which is located very close to the Mott transition, -[(H-ET)(D-ET)]Cu[N(CN)]Br with a deuteration degree of . Depending on the initial more or less rapid cooling, a certain amount of the EEGs energetically unfavored staggered (S) conformation is frozen, which results in a reduced ratio of bandwidth to on-site Coulomb repulsion [24] and thus in a state further on the insulating side of the phase diagram than the pristine, slowly-cooled condition. The so-prepared initial state, which is referred to as warming cycle 1, is characterized by a resistance showing the typical re-entrance behavior (see the red curve in Figure 12a, where the Mott transition line is crossed twice).
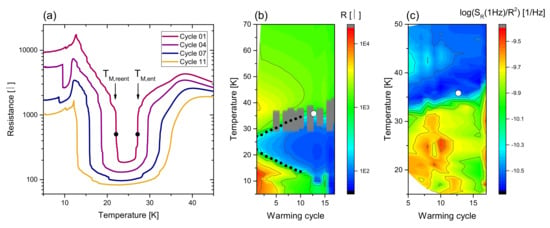
Figure 12.
Resistance and noise measurements at the Mott transition in partially-deuterated -[(H-ET)(D-ET)]Cu[N(CN)]Br with . (a) resistance measurements of some selected warming cycles generated by using different thermal relaxation protocols described in the text. The black points mark the temperatures of the entrance and re-entrance half-maximum resistance jump, indicating the crossing of the Mott transition line; (b) contour plot of the resistance vs. temperature and warming cycle. The grey area marks the region where the DDH model shows strong deviations; the white circle indicates the critical point; (c) contour plot of the normalized resistance noise PSD taken at in dependence of temperature and warming cycle (note different scales).
After the initial cool down with a rate of , the sample is warmed up to a temperature close to the glass transition at about . After a specific waiting time on the order of a few minutes, which relaxes the EEG occupation to the energetically favored eclipsed orientation, and thus the structural distortion, the sample is slowly cooled down again while measuring the resistance yielding a new state with a larger ratio of , and therefore located further on the metallic side of the phase diagram. By repeating this relaxation protocol several times (and by adjusting the relaxation time), the sample can be tuned—in principle in arbitrarily small steps—through the Mott critical endpoint. Some selected resistance measurements of the generated states (warming cycles 1–17) are shown in Figure 12a, where the higher warming cycles are characterized by a lower resistance value and—due to the S shape of the transition line—a broader region in the metallic phase. From the temperature values of the entrance and re-entrance half-maximum resistance jump, and , respectively, marked by black points in the resistance measurements, it is possible to reproduce the Mott transition line in dependence of the warming cycle. A contour plot of the resistance as a function of temperature and warming cycle is shown in Figure 12b where the blue color corresponds to a low-resistance metallic state and the red color to the high-resistance insulating state. Hence, at the warming cycle for which the corresponding resistance curve turns into a continuous course without clear discontinuities, the critical endpoint is expected and is visualized as a white circle at in Figure 12b,c.
In order to analyze the charge carrier dynamics at the Mott transition in comparison to the sample with a deuteration degree of discussed above, we employ fluctuation spectroscopy in a four-terminal AC configuration, where the resistance fluctuations are again measured out-of-plane, i.e., along the crystallographic b-axis. For each warming cycle, the resistance noise PSD was measured during cooling down the sample (in discrete temperatures steps ) starting at sufficiently far below the glass-like transition so that the EEG configuration is frozen. The results of the normalized resistance noise PSD taken at for different warming cycles are shown in Figure 12c as a contour plot vs. temperature vs. warming cycle. Similar as for the sample shown in Figure 10 and Figure 11, the noise level increases when approaching the Mott MIT. However, instead of a large peak indicating diverging low-frequency fluctuations in the vicinity of the critical point, for the present sample m, we observe a one-order-of-magnitude, step-like increase of the normalized resistance noise PSD when crossing the Mott transition line, which shifts to higher temperatures for higher warming cycles coinciding with the development of the metallic phase. Even for warming cycles beyond the critical point (the white circle in Figure 12b,c), this behavior is observed at the crossover from the ’bad metal’ to the Fermi liquid region. One possible explanation for the higher noise level in the metallic phase is electronic phase separation into insulating and metallic domains due to the competing interactions in the vicinity of the Mott transition [21,82,129]. Since electronic inhomogeneities are accompanied by a smaller noisy volume, the formation of domains on the micrometer to nanometer scale close to the Mott transition might cause a larger noise PSD in the metallic region.
In addition to the absolute noise level at the frequency exponent gives information about the distribution of activation energies within the DDH model and is shown in Figure 13 for selected warming cycles to be compared with Figure 7b for -D-Br () and Figure 11d for -H/D-Br (). Whereas for higher temperatures below 50 K a weak temperature dependence with slightly larger than 1 is observed, for all warming cycles, a peak in is found with values of 1.2–1.4 occurs around the temperature of the Mott MIT. Although this shift of spectral weight to low frequencies is not as pronounced and the noise does not peak as is observed for the sample, there is a consistent slowing down of the charge carrier dynamics at the transition. Strikingly, there is also a distinct region around the Mott MIT, where the DDH model fails to describe the low-frequency fluctuations. The black line in Figure 13 shows the values obtained from the DDH model (Equation (16)), where a power-law function has been used in order to take an explicit temperature dependence of the resistance fluctuations into account, with different exponents for the low and high temperature regions indicating a change in the fluctuating properties, their number or their coupling to the resistance and/or the electronic transport mechanism. Strikingly, outside the transition region the DDH model agrees very well with the experimental , i.e., the energy distribution of independent fluctuators can be determined rather accurately (not shown) [130]. However, in the transition region—marked by the gray shaded area in Figure 12 and Figure 13—there is a strong deviation of the measured and the DDH calculation implying that the assumption of independent fluctuating entities loses its validity in the region close the Mott transition and non-Gaussian, possibly spatially-correlated fluctuations are dominating. This again is similar to the sample discussed above, where this phenomenon was also observed and confirmed by measurements of the second spectrum , which revealed a frequency dependence for the curve with K/min resulting in a state close but on the insulating side beyond the critical point [53]. The measurements on the present sample, although not showing a divergent increase of the noise around the critical endpoint, exhibit a rather wide region of non-Gaussian noise and possibly ergodicity breaking around the Mott MIT. Besides these similarities, the differences demonstrate strong sample dependences of the investigated compounds, which in part may be related to different degrees of disorder. Measurements of different samples with nominally the same degree of deuteration are desirable. In addition, a systematic investigation of the interplay of disorder and strong electron–electron correlations is possible. To that end, samples with different degrees of deuteration and therefore pristine starting position in the phase diagram could be tuned through the phase diagram by applying warming cycles. This would result in a varying degree of intrinsic frozen EEG disorder at the critical endpoint of the Mott transition allowing for studying the influence of a random lattice portential on the critical slowing down of the charge carrier dynamics.
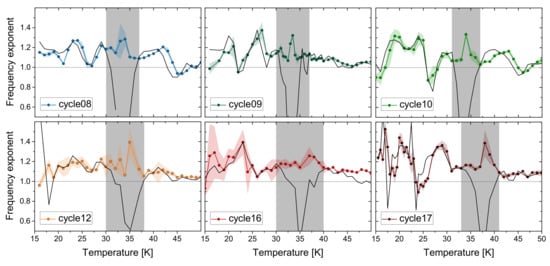
Figure 13.
Temperature dependent frequency exponent for some selected warming cycles. The black line corresponds to the values determined with the DDH model; the grey shaded area emphasizes the temperature region where the DDH model deviates from the experimental data.
4. Conclusions
To summarize, the fascinating electronic, magnetic and structural properties of quasi-two-dimensional strongly-correlated molecular metals (BEDT-TTF)X have been introduced and the need for studying the charge carrier dynamics at low frequencies—complementary to optical and dielectric spectroscopy—has been motivated. We have given an overview of the definitions and basic relations of the statistical properties of physical quantities with the focus on time-resolved electronic transport measurements. At the heart of noise spectroscopy measuring the resistance (or conductance) noise power spectral density () is a time-like property, namely the voltage (or current) autocorrelation function which is a non-random characteristic of the microscopic kinetics of the charge fluctuations. The fluctuation spectrum and the autocorrelation function are related via the Wiener–Khintchine theorem. The fluctuation–dissipation theorem makes an exact connection between the autocorrelation function and the imaginary part of the frequency-dependent response function associated with dissipation in thermal equilibrium.
The examples selected for this review demonstrate where studying low-frequency charge carrier dynamics via the electronic noise provides information on the underlying physics that cannot be easily (or at all) gained otherwise. In general, noise is a sensitive probe, when the electronic transport (the current distribution in a sample) is inhomogeneous, which is the case for electronic phase separation and at percolative transitions (1). Another important example, where slow dynamics dominates the physics of the system, is a glassy freezing either of structural degrees of freedom coupling to the electronic properties (2) or of the electrons themselves, either when residing on a highly-frustrated crystal lattice (3) or due to correlated transitions of electrons over a large number of metastable states, leading to glassy relaxation as a precursor of a metal-insulator transition (4). Indications for such an emerging behavior, like diverging low-frequency fluctuations and critical slowing down of the order parameter fluctuations, for the first time have been observed at the finite-temperature critical endpoint of the Mott transition. Here, mapping out the region of ergodicity breaking and understanding the influence of disorder on the temporal and spatial correlated fluctuations will be an important realm of future studies.
Combining different experimental techniques from four-point and five-point AC or DC resistance fluctuation measurements to two-terminal DC conductance noise measurements, an impressive span of sample impedances from – can be covered. This allows for extending the applications of noise studies to samples, also non-ET-based compounds [131,132], deep in the Mott or charge-ordered insulating phase, where spin-liquid behavior is observed and the intra-dimer degrees of freedom often cause intriguing dielectric relaxation phenomena or ferroelectric ordering. First measurements of such insulating samples, e.g., of the dimer-Mott insulators -(ET)Cu(CN) and -(ET)ICl, are underway. They will focus on the origin of relaxor ferroelectricity and make a connection between the concepts of conductance fluctuation spectroscopy and dielectric spectroscopy.
Acknowledgments
This work was financially supported by the Deutsche Forschungsgemeinschaft (DFG) within the collaborative research center SFB/TR 49 “Condensed Matter Systems with Variable Many-Body Interactions”. We are particularly grateful to John A. Schlueter from Argonne National Laboratory and NSF, USA and Takahiko Sasaki from the Institute for Materials Research (IMR) at Tohoku University, Sendai, Japan for the fruitful and rewarding collaboration in the past years and for kindly providing many excellent samples. J.M. acknowledges pleasantly working with many students from Goethe-University Frankfurt on noise properties of organic charge-transfer salts, namely Jens Brandenburg, Robert Rommel, Benedikt Hartmann, David Zielke, Jana Polzin, Yannick Herrmann, Yassine Agarmani, Marvin Kopp and Martin Lonsky.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CO | charge ordering |
| DDH model | model by Dutta, Dimon and Horn for -type noise in metals |
| EEG | ethylene endgroups |
| ET | BEDT-TTF (bis-ethylenedithio-tetrathiafulvalene) |
| FDT | fluctuation-dissipation theorem |
| -Br | -(BEDT-TTF)Cu[N(CN)]Br |
| -Cl | -(BEDT-TTF)Cu[N(CN)]Cl |
| MIT | metal-insulator transition |
| NMR | nuclear magnetic resonance |
| PSD | power spectral density |
| RRN | random resistor network |
| VFT | Vogel-Fulcher-Tammann |
References and Notes
- Ishiguro, T.; Yamaji, K.; Saito, G. Organic Superconductors; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Toyota, N.; Lang, M.; Müller, J. Low-Dimensional Molecular Metals; Solid State Science, Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Lebed, A. The Physics of Organic Superconductors and Conductors; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Powell, B.J.; McKenzie, R.H. Quantum frustration in organic Mott insulators: From spin liquids to unconventional superconductors. Rep. Prog. Phys. 2011, 74, 056501. [Google Scholar] [CrossRef]
- Lunkenheimer, P.; Müller, J.; Krohns, S.; Schrettle, F.; Loidl, A.; Hartmann, B.; Rommel, R.; de Souza, M.; Hotta, C.; Schlueter, J.A.; et al. Multiferroicity in an organic charge-transfer salt that is suggestive of electric-dipole-driven magnetism. Nat. Mater. 2012, 11, 755–758. [Google Scholar] [CrossRef] [PubMed]
- Dressel, M.; Drichko, N. Optical Properties of Two-Dimensional Organic Conductors: Signatures of Charge Ordering and Correlation Effects. Chem. Rev. 2004, 104, 5689–5716. [Google Scholar] [CrossRef] [PubMed]
- Iwai, S. Photoinduced Phase Transitions in α-, θ-, and κ-type ET Salts: Ultrafast Melting of the Electronic Ordering. Crystals 2012, 2, 590–617. [Google Scholar] [CrossRef]
- Lunkenheimer, P.; Loidl, A. Dielectric spectroscopy on organic charge-transfer salts. J. Phys. Condens. Matter 2015, 27, 373001. [Google Scholar] [CrossRef] [PubMed]
- Müller, J. Fluctuation Spectroscopy: A New Approach for Studying Low-Dimensional Molecular Metals. ChemPhysChem 2011, 12, 1222–1245. [Google Scholar] [CrossRef] [PubMed]
- Powell, B.J.; McKenzie, R.H. Strong electronic correlations in superconducting organic charge transfer salts. J. Phys. Condens. Matter 2006, 18, R827. [Google Scholar] [CrossRef]
- Kandpal, H.C.; Opahle, I.; Zhang, Y.Z.; Jeschke, H.O.; Valentí, R. Revision of Model Parameters for κ-Type Charge Transfer Salts: An Ab Initio Study. Phys. Rev. Lett. 2009, 103, 067004. [Google Scholar] [CrossRef] [PubMed]
- Seo, H.; Hotta, C.; Fukuyama, H. Toward Systematic Understanding of Diversity of Electronic Properties in Low-Dimensional Molecular Solids. Chem. Rev. 2004, 104, 5005–5036. [Google Scholar] [CrossRef] [PubMed]
- Lang, M.; Lunkenheimer, P.; Müller, J.; Loidl, A.; Hartmann, B.; Hoang, N.H.; Gati, E.; Schubert, H.; Schlueter, J.A. Multiferroicity in the Mott Insulating Charge-Transfer Salt κ-(BEDT-TTF)2Cu[N(CN)2]Cl. IEEE Trans. Magn. 2014, 50, 2700107. [Google Scholar]
- Wosnitza, J. Fermi Surfaces of Low-Dimensional Organic Metals and Superconductors; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Singleton, J. Studies of quasi-two-dimensional organic conductors based on BEDT-TTF using high magnetic fields. Rep. Prog. Phys. 2000, 63, 1111–1207. [Google Scholar] [CrossRef]
- Elsinger, H.; Wosnitza, J.; Wanka, S.; Hagel, J.; Schweitzer, D.; Strunz, W. κ-(BEDT-TTF)2Cu[N(CN)2]Br: A Fully Gapped Strong-Coupling Superconductor. Phys. Rev. Lett. 2000, 84, 6098–6101. [Google Scholar] [CrossRef] [PubMed]
- Kanoda, K. Electron correlation, metal-insulator transition and superconductivity in quasi-2D organic systems (ET)2X. Phys. C Superconduct. 1997, 282–287, 299–302. [Google Scholar] [CrossRef]
- Lefebvre, S.; Wzietek, P.; Brown, S.; Bourbonnais, C.; Jérome, D.; Mézière, C.; Fourmigué, M.; Batail, P. Mott Transition, Antiferromagnetism, and Unconventional Superconductivity in Layered Organic Superconductors. Phys. Rev. Lett. 2000, 85, 5420–5423. [Google Scholar] [CrossRef] [PubMed]
- Müller, J.; Lang, M.; Steglich, F.; Schlueter, J.A.; Kini, A.M.; Sasaki, T. Evidence for structural and electronic instabilities at intermediate temperatures in κ-(BEDT-TTF)2X for X=Cu[N(CN)2]Cl, Cu[N(CN)2]Br and Cu(NCS)2: Implications for the phase diagram of these quasi-two-dimensional organic superconductors. Phys. Rev. B 2002, 65, 144521. [Google Scholar] [CrossRef]
- Kagawa, F.; Miyagawa, K.; Kanoda, K. Unconventional critical behaviour in a quasi-two-dimensional organic conductor. Nature 2005, 436, 534–537. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, T.; Yoneyama, N.; Suzuki, A.; Kobayashi, N.; Ikemoto, Y.; Kimura, H. Real Space Imaging of the Metal—Insulator Phase Separation in the Band Width Controlled Organic Mott System κ-(BEDT-TTF)2Cu[N(CN)2]Br. J. Phys. Soc. Jpn. 2005, 74, 2351–2360. [Google Scholar] [CrossRef]
- Kawamoto, A.; Miyagawa, K.; Kanoda, K. Deuterated κ-(BEDT-TTF)2Cu[N(CN)2]Br: A system on the border of the superconductor-magnetic-insulator transition. Phys. Rev. B 1997, 55, 14140–14143. [Google Scholar] [CrossRef]
- Hartmann, B.; Müller, J.; Sasaki, T. Mott metal-insulator transition induced by utilizing a glasslike structural ordering in low-dimensional molecular conductors. Phys. Rev. B 2014, 90, 195150. [Google Scholar] [CrossRef]
- Guterding, D.; Valentí, R.; Jeschke, H.O. Influence of molecular conformations on the electronic structure of organic charge transfer salts. Phys. Rev. B 2015, 92, 081109. [Google Scholar] [CrossRef]
- Müller, J.; Hartmann, B.; Sasaki, T. Fine-tuning the Mott metal–insulator transition and critical charge carrier dynamics in molecular conductors. Philos. Mag. 2017, 97, 3477–3494. [Google Scholar] [CrossRef]
- Landauer, R. Condensed-matter physics: The noise is the signal. Nature 1998, 392, 658–659. [Google Scholar] [CrossRef]
- Beenakker, C.; Schönenberger, C. Quantum shot noise. Phys. Today 2003, 56, 37–42. [Google Scholar] [CrossRef]
- MacDonald, D.K.C. Noise and Fluctuations: An Introduction; John Wiley & Sons: New York, NY, USA, 1962. [Google Scholar]
- Van der Ziel, A. Flicker noise in electron devices. Adv. Electron. Electron Phys. 1979, 49, 225–297. [Google Scholar]
- Hooge, F.N.; Kleinpenning, T.G.M.; Vandamme, L.K.J. Experimental studies on 1/f noise. Rep. Prog. Phys. 1981, 44, 479–532. [Google Scholar] [CrossRef]
- Dutta, P.; Horn, P.M. Low-frequency fluctuations in solids: 1/f noise. Rev. Modern Phys. 1981, 53, 497–516. [Google Scholar] [CrossRef]
- Weissman, M.B. 1/f noise and other slow, nonexponential kinetics in condensed matter. Rev. Modern Phys. 1988, 60, 537–571. [Google Scholar] [CrossRef]
- Kogan, S. Electronic Noise and Fluctuations in Solids; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Raquet, B. Electronic Noise in Magnetic Materials and Devices. In Spin Electronics; Springer: Berlin/Heidelberg, Germany, 2000; Chapter 11; pp. 232–273. [Google Scholar]
- Indeed, this “DC-offset” is sought to be suppressed in a five-terminal experimental setup [9,61], so that only the fluctuating part can be amplified and analyzed. If not suppressed, a finite mean value contributes a δ-function to Sx(f) at zero frequency.
- The ergodicity theorem states that the time-average for a single system in statistical equilibrium may be replaced by an average over an equilibrium ensemble. The autocorrelation function (Equation (3)) is to be evaluated at a fixed time t over a sufficiently large ensemble in thermal equilibrium or through averaging the same system over a sufficiently large number of different times t. In each case, the result is independent of t (and only depends on τ) for a statistically stationary variable.
- Lax, M.; Wei, C.; Min, X. Random Processes in Physics and Finance; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- The function is defined by the response of the quantity x to an external (generalized) force via
with (causality). With the Fourier transform , the convolution theorem gives . In the complex dynamic susceptibility , the real part is the elastic (in-phase) part and the imaginary part the dissipative (out-of-phase) part of the response. The FDTdescribes the direct connection between the autocorrelation function of the fluctuations and the imaginary part of the response function associated with dissipation and becomes Equation (5) in the quasi-classical limit .
- Johnson, J.B. Thermal Agitation of Electricity in Conductors. Phys. Rev. 1928, 32, 97–109. [Google Scholar] [CrossRef]
- Nyquist, H. Thermal Agitation of Electric Charge in Conductors. Phys. Rev. 1928, 32, 110–113. [Google Scholar] [CrossRef]
- Note that for thermal noise as the limiting factor, the signal-to-noise ratio of a voltage measurement, defined as , with bandwidth , can be enhanced by increasing the current I. This is not the case, if -noise limits the accuracy of a physical measurement! As can be seen for example when calculating the using Equation (12) below, -noise represents a big obstacle for miniaturization (e.g., of nanoscale devices).
- Press, W.H. Flicker Noise in Astronomy and Elsewhere. Comments Astrophys. Space Phys. 1978, 7, 103–119. [Google Scholar]
- Note that the (biased) random walk plays an important role in finance, i.e., in modern risk management and for the pricing of derivates.
- Of course, there should be theoretical limits also. At high frequencies, there can be no fluctuations faster than the fastest electronic processes possible in the system. At low frequencies, however, a cutoff has not been observed down to the Hz regime for -noise in Ge semiconductor devices [133]. How to explain correlations (’memory’) over averaging times of several weeks remains a fascinating intellectual problem.
- Machlup, S. Noise in Semiconductors: Spectrum of a Two-Parameter Random Signal. J. Appl. Phys. 1954, 25, 341–343. [Google Scholar] [CrossRef]
- McWhorter, A.L. 1/f Noise and Germanium Surface Properties. In Semiconductor Surface Physics; Pennsylvania University Press: Philadelphia, PA, USA, 1957; pp. 207–228. [Google Scholar]
- A distribution is the basis of the famous McWhorter model (1957) [46] describing -noise e.g., in Si-MOSFETs, where the fluctuations are caused by tunneling processes between the conducting channel and traps in the dielectric SiO layer. A spatially homogeneous trap distribution (tunneling distances) leads to the required distribution of time constants.
- Weissman, M.B. What is a spin glass? A glimpse via mesoscopic noise. Rev. Modern Phys. 1993, 65, 829–839. [Google Scholar] [CrossRef]
- Weissman, M.B.; Israeloff, N.E.; Alers, G.B. Spin-glass fluctuation statistics: mesoscopic experiments in Mn. J. Magn. Magn. Mater. 1992, 114, 87–130. [Google Scholar] [CrossRef]
- Bogdanovich, S.; Popović, D. Onset of Glassy Dynamics in a Two-Dimensional Electron System in Silicon. Phys. Rev. Lett. 2002, 88, 236401. [Google Scholar] [CrossRef] [PubMed]
- Jaroszyński, J.; Popović, D.; Klapwijk, T.M. Universal Behavior of the Resistance Noise across the Metal-Insulator Transition in Silicon Inversion Layers. Phys. Rev. Lett. 2002, 89, 276401. [Google Scholar] [CrossRef] [PubMed]
- Kar, S.; Raychaudhuri, A.K.; Ghosh, A.; Löhneysen, H.v.; Weiss, G. Observation of Non-Gaussian Conductance Fluctuations at Low Temperatures in Si:P(B) at the Metal-Insulator Transition. Phys. Rev. Lett. 2003, 91, 216603. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, B.; Zielke, D.; Polzin, J.; Sasaki, T.; Müller, J. Critical Slowing Down of the Charge Carrier Dynamics at the Mott Metal-Insulator Transition. Phys. Rev. Lett. 2015, 114, 216403. [Google Scholar] [CrossRef] [PubMed]
- Voss, R.F.; Clarke, J. 1/f-noise in music and speech. Nature 1975, 258, 317–318. [Google Scholar] [CrossRef]
- Musha, T.; Higuchi, H. The 1/f fluctuation of a traffic current on an expressway. Jpn. J. Appl. Phys. 1976, 15, 1271–1275. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Rigney, D.R.; Mietus, J.; Antman, E.M.; Greenwald, S. Nonlinear dynamics in sudden cardiac death syndrome: Heartrate oscillations and bifurcations. Experientia 1988, 44, 983–987. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, D.T.; Talajic, M. Dynamics of heart rate. Chaos Interdiscip. J. Nonlinear Sci. 1991, 1, 251–256. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.K.; Mietus, J.; Hausdorff, J.M.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 1993, 70, 1343–1346. [Google Scholar] [CrossRef] [PubMed]
- Beck, H.G.E.; Spruit, W.P. 1/f Noise in the variance of Johnson noise. J. Appl. Phys. 1978, 49, 3384–3386. [Google Scholar] [CrossRef]
- Müller, J.; Brandenburg, J.; Schlueter, J.A. 1/f noise in the quasi-two-dimensional organic conductor κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Phys. Rev. B 2009, 79, 214521. [Google Scholar] [CrossRef]
- Scofield, J.H. AC method for measuring low-frequency resistance fluctuation spectra. Rev. Sci. Instrum. 1987, 58, 985–993. [Google Scholar] [CrossRef]
- Hooge, F.N. 1/f noise is no surface effect. Phys. Lett. A 1969, 29, 139–140. [Google Scholar] [CrossRef]
- An argument is that any fluctuations tied to individual free charge carriers cannot persist for times longer than the carrier transit time in the sample. Since the latter and typical diffusion times are of order microseconds to milliseconds, a resulting -spectrum would be required to flatten out below characteristic frequencies within this range [32].
- It is important to mention that already for the simple Drude model of transport one expects that both carrier number (or density) fluctuations and mobility fluctuations contribute to the observed -noise: . Their particular role for the resistance fluctuations in semiconductors and metals is still a matter of controversial debate [34].
- Galchenkov, L.A.; Ivanov, S.N.; Pyataikin, I.I.; Chernov, V.P.; Monceau, P. 1/f noise in conducting Langmuir-Blodgett films. Phys. Rev. B 1998, 57, 13220–13226. [Google Scholar] [CrossRef]
- Brandenburg, J.; Müller, J.; Wirth, S.; Schlueter, J.A.; Schweitzer, D. Strongly enhanced 1/f-noise level in κ-(BEDT-TTF)2X salts. Phys. B 2010, 405, 141–143. [Google Scholar] [CrossRef]
- Kagawa, F.; Itou, T.; Miyagawa, K.; Kanoda, K. Transport criticality of the first-order Mott transition in the quasi-two-dimensional organic conductor κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Phys. Rev. B 2004, 69, 064511. [Google Scholar] [CrossRef]
- Müller, J.; Brandenburg, J.; Schlueter, J.A. Magnetic-Field Induced Crossover of Superconducting Percolation Regimes in the Layered Organic Mott System κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Phys. Rev. Lett. 2009, 102, 047004. [Google Scholar] [CrossRef] [PubMed]
- Kornelsen, K.; Eldridge, J.; Wang, H.H.; Charlier, H.A.; Williams, J.M. Infrared study of the metal-insulator transition in the organic conductor κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Solid State Commun. 1992, 81, 343–349. [Google Scholar] [CrossRef]
- Testa, J.A.; Song, Y.; Chen, X.D.; Golben, J.; Lee, S.I.; Patton, B.R.; Gaines, J.R. 1/f-noise-power measurements of copper oxide superconductors in the normal and superconducting states. Phys. Rev. B Condens. Matter 1988, 38, 2922–2925. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, S.C.; Khim, Z.G. Noise measurement near the transition region in YBa2Cu3O7−x thin-film superconductors. Phys. Rev. B 1989, 40, 6806–6809. [Google Scholar] [CrossRef]
- Kiss, L.B.; Svedlindh, P. Noise in high-Tc superconductors. IEEE Trans. Electron. Devices 1994, 41, 2112–2122. [Google Scholar] [CrossRef]
- Rammal, R.; Tannous, C.; Breton, P.; Tremblay, A.M.S. Flicker () Noise in Percolation Networks: A New Hierarchy of Exponents. Phys. Rev. Lett. 1985, 54, 1718–1721. [Google Scholar] [CrossRef] [PubMed]
- Rammal, R.; Tannous, C.; Tremblay, A.M.S. 1/f noise in random resistor networks: Fractals and percolating systems. Phys. Rev. A 1985, 31, 2662–2671. [Google Scholar] [CrossRef]
- We note that in this simple model of a one-component RRN the local microgeometry of the current distribution leads to so-called weakly nonlinear transport [134], since the most significant contribution to R and comes from ‘bottlenecks’ or ‘hot spots’ in the RRN, in which the local electric field and current density are much greater than the average values. The contribution of such a region to R is proportional to the local electric field squared [33]. and the local current distribution in Equation (13) is then proportional to the third-harmonic component in an AC transport (voltage) measurement with a driving current through the sample. This connection of -noise and nonlinear transport is widely observed in percolation problems (see e.g., [135] and references therein). For the organic charge-transfer salts -(ET)X, there is also a relation between enhanced -noise due to electronic correlations and a third-harmonic contribution in AC resistance measurements, but the phenomenology appears to be rather complex [129].
- Dubson, M.A.; Hui, Y.C.; Weissman, M.B.; Garland, J.C. Measurement of the fourth moment of the current distribution in two-dimensional random resistor networks. Phys. Rev. B Condens. Matter 1989, 39, 6807–6815. [Google Scholar] [CrossRef]
- Yagil, Y.; Deutscher, G. Third-harmonic generation in semicontinuous metal films. hys. Rev. B Condens. Matter 1992, 46, 16115–16121. [Google Scholar] [CrossRef]
- Kiss, L.B.; Svedlindh, P. New noise exponents in random conductor-superconductor and conductor-insulator mixtures. Phys. Rev. Lett. 1993, 71, 2817–2820. [Google Scholar] [CrossRef] [PubMed]
- We consider the coexistence region close to the MIT as a mixture of superconducting and non-superconducting (normal or insulating) phases, i.e., a lattice of resistors with a temperature- and magnetic field-dependent fraction p that is short-circuited, simulating the superconducting links. For instance, one can think of a network of p Josephson-coupled junctions formed by connections between superconducting grains or clusters. A wide distribution of junction critical currents means that at a given macroscopic current I, the local currents i can be either larger or smaller than which determines if the junction is superconducting or resistive [68].
- Kiss, L.B.; Larsson, T.; Svedlindh, P.; Lundgren, L.; Ohlsén, H.; Ottosson, M.; Hudner, J.; Stolt, L. Conductance noise and percolation in YBa2Cu3O7 thin films. Phys. C Superconduct. 1993, 207, 318–332. [Google Scholar] [CrossRef]
- In Figure 6, a symmetric double-well potential is sketched. As has been pointed out in [136], the time constants and can be determined individually from the noise spectra only if the two lifetimes are either roughly the same or if one of them is much greater than the other. In the former case , both fit coefficients of Equation (14), namely and , are proportional to and the slopes in an Arrhenius plot should give a similar value [137].
- Sasaki, T.; Yoneyama, N.; Kobayashi, N.; Ikemoto, Y.; Kimura, H. Imaging Phase Separation near the Mott Boundary of the Correlated Organic Superconductors κ-(BEDT-TTF)2X. Phys. Rev. Lett. 2004, 92, 227001. [Google Scholar] [CrossRef] [PubMed]
- Saito, K.; Akutsu, H.; Sorai, M. Glass transition in the organic superconductor with the highest Tc under ambient pressure, κ-(ET)2Cu[N(CN)2]Br. Solid State Commun. 1999, 111, 471–475. [Google Scholar] [CrossRef]
- Akutsu, H.; Saito, K.; Sorai, M. Phase behavior of the organic superconductors κ-(BEDT-TTF)2Cu[N(CN)2]X (X = Br and Cl) studied by ac calorimetry. Phys. Rev. B 2000, 61, 4346–4352. [Google Scholar] [CrossRef]
- Sato, A.; Akutsu, H.; Saito, K.; Soraj, M. Glass transition in κ-(BEDT-TTF)2Cu[N(CN)2]X (X = Br and Cl). Synth. Met. 2001, 120, 1035–1036. [Google Scholar] [CrossRef]
- Müller, J.; Lang, M.; Steglich, F.; Schlueter, J.A. Glass-like transition in κ-(ET)2Cu[N(CN)2]Br at Tg ∼ 75 K: implications for the superconducting ground-state properties. J. Phys. IV Fr. 2004, 114, 341–342. [Google Scholar] [CrossRef]
- Su, X.; Zuo, F.; Schlueter, J.A.; Kelly, M.E.; Williams, J.M. Structural disorder and its effect on the superconducting transition temperature in the organic superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. Phys. Rev. B 1998, 57, R14056–R14059. [Google Scholar] [CrossRef]
- Su, X.; Zuo, F.; Schlueter, J.A.; Kelly, M.E.; Williams, J.M. Dynamic disorders and its relaxation in organic superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. Solid State Commun. 1998, 107, 731–734. [Google Scholar] [CrossRef]
- Tanatar, M.; Ishiguro, T.; Kondo, T.; Saito, G. Nonmetal to metal crossover and ethylene ordering in the organic superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. Phys. Rev. B 1999, 59, 3841–3844. [Google Scholar] [CrossRef]
- Taniguchi, H.; Kanoda, K.; Kawamoto, A. Field switching of superconductor-insulator bistability in artificially tuned organics. Phys. Rev. B 2003, 67, 014510. [Google Scholar] [CrossRef]
- Taylor, O.J.; Carrington, A.; Schlueter, J.A. Superconductor-insulator phase separation induced by rapid cooling of κ-(BEDT-TTF)2Cu[N(CN)2]Br. Phys. Rev. B 2008, 77, 060503. [Google Scholar] [CrossRef]
- Brandenburg, J.; Müller, J.; Schlueter, J.A. Sudden slowing down of charge carrier dynamics at the Mott metal-insulator transition in κ-(D8-BEDT-TTF)2Cu[N(CN)2]Br. N. J. Phys. 2012, 14, 023033. [Google Scholar] [CrossRef]
- Müller, J.; Hartmann, B.; Rommel, R.; Brandenburg, J.; Winter, S.M.; Schlueter, J.A. Origin of the glass-like dynamics in molecular metals κ-(BEDT-TTF)2X: implications from fluctuation spectroscopy and ab initio calculations. N. J. Phys. 2015, 17, 083057. [Google Scholar] [CrossRef]
- Gati, E.; Winter, S.M.; Schlueter, J.A.; Schubert, H.; Müller, J.; Lang, M. Insights from experiment and ab initio calculations into the glasslike transition in the molecular conductor κ-(BEDT-TTF)2Hg(SCN)2Cl. Phys. Rev. B 2018, 97, 075115. [Google Scholar] [CrossRef]
- As shown in [93], the systems -(ET)X with X = Cu[N(CN)]Cl,Cu[N(CN)]Br, or Cu(SCN) show a similar behavior in above about 50 K (see also Figure 11a–c below), which will be explained in this section. In contrast, for K the temperature characteristics of the noise PSD strongly depends on the position in the phase diagram and is strongly enhanced for systems with stronger electron–electron correlations being located closer to the Mott transition [138].
- Dutta, P.; Dimon, P.; Horn, P.M. Energy Scales for Noise Processes in Metals. Phys. Rev. Lett. 1979, 43, 646–649. [Google Scholar] [CrossRef]
- In the simple case of a two-level fluctuation with a single relaxation time , the correlation function (Equation (8)) is purely exponential. If the kinetics of the fluctuating quantity is a superposition of many relaxation times, the correlation function falls off with time not exponentially and the PSD equals Equation (10) [33].
- The function of activation energy E in Equation (15) constitutes a narrow peak of width with the maximum at [33].
- Besides independent thermally activated fluctuators and linear coupling, the width of the weighting function must be far greater than . As stated above, this is the case when is small in comparison to the relevant activation energy in solids.
- Black, R.D.; Restle, P.J.; Weissman, M.B. Hall effect, anisotropy, and temperature-dependence measurements of 1/f noise in silicon on sapphire. Phys. Rev. B 1983, 28, 1935–1943. [Google Scholar] [CrossRef]
- Fleetwood, D.M.; Postel, T.; Giordano, N. Temperature dependence of the 1/f noise of carbon resistors. J. Appl. Phys. 1984, 56, 3256–3260. [Google Scholar] [CrossRef]
- Raquet, B.; Coey, J.M.D.; Wirth, S.; von Molnár, S. 1/f noise in the half-metallic oxides CrO2, Fe3O4, and La2/3Sr1/3MnO3. Phys. Rev. B 1999, 59, 12435–12443. [Google Scholar] [CrossRef]
- Sometimes, a related scattering mechanism is found in the resistivity, i.e., a contribution , which may be linked to the function via the number and/or strength of the fluctuators, as has been argued for the contribution of spin fluctuations in certain manganites [102]. See [93] for details.
- Miyagawa, K.; Kawamoto, A.; Nakazawa, Y.; Kanoda, K. Antiferromagnetic Ordering and Spin Structure in the Organic Conductor κ-(BEDT-TTF2Cu[N(CN)2]Cl. Phys. Rev. Lett. 1995, 75, 1174. [Google Scholar] [CrossRef] [PubMed]
- Wzietek, P.; Mayaffre, H.; Jérome, D.; Brazovskii, S. NMR in the 2D Organic Superconductors. J. Phys. I Fr. 1996, 6, 2011–2041. [Google Scholar] [CrossRef]
- Geiser, U.; Schults, A.J.; Wang, H.H.; Watkins, D.M.; Stupka, D.L.; Williams, J.M.; Schirber, J.; Overmyer, D.; Jung, D.; Novoa, J.; et al. Strain index, lattice softness and superconductivity of organic donor-molecule salts: Crystal and electronic structures of three isostructural salts k-(BEDT- TTF)2Cu[N(CN)2]X (X = Cl, Br, I). Phys. C Superconduct. 1991, 174, 475–486. [Google Scholar] [CrossRef]
- Lunkenheimer, P.; Schneider, U.; Brand, R.; Loid, A. Glassy dynamics. Contemp. Phys. 2000, 41, 15–36. [Google Scholar] [CrossRef]
- Bauer, T.; Lunkenheimer, P.; Loidl, A. Cooperativity and the Freezing of Molecular Motion at the Glass Transition. Phys. Rev. Lett. 2013, 111, 225702. [Google Scholar] [CrossRef] [PubMed]
- Hiramatsu, T.; Yoshida, Y.; Saito, G.; Otsuka, A.; Yamochi, H.; Maesato, M.; Shimizu, Y.; Ito, H.; Kishida, H. Quantum spin liquid: Design of a quantum spin liquid next to a superconducting state based on a dimer-type ET Mott insulator. J. Mater. Chem. C 2015, 3, 1378–1388. [Google Scholar] [CrossRef]
- Yamochi, H.; Komatsu, T.; Matsukawa, N.; Saito, G.; Mori, T.; Kusunoki, M.; Sakaguchi, K. Structural aspects of the ambient-pressure BEDT-TTF superconductors. J. Am. Chem. Soc. 1993, 115, 11319–11327. [Google Scholar] [CrossRef]
- Sasaki, S.; Hashimoto, K.; Kobayashi, R.; Itoh, K.; Iguchi, S.; Nishio, Y.; Ikemoto, Y.; Moriwaki, T.; Yoneyama, N.; Watanabe, M.; et al. Crystallization and vitrification of electrons in a glass-forming charge liquid. Science 2017, 357, 1381–1385. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Miyagawa, K.; Kanoda, K. Electronic crystal growth. Science 2017, 357, 1378–1381. [Google Scholar] [CrossRef] [PubMed]
- Kagawa, F.; Sato, T.; Miyagawa, K.; Kanoda, K.; Tokura, Y.; Kobayashi, K.; Kumai, R.; Murakami, Y. Charge-cluster glass in an organic conductor. Nat. Phys. 2013, 9, 419–422. [Google Scholar] [CrossRef]
- Sato, T.; Kagawa, F.; Kobayashi, K.; Miyagawa, K.; Kanoda, K.; Kumai, R.; Murakami, Y.; Tokura, Y. Emergence of nonequilibrium charge dynamics in a charge-cluster glass. Phys. Rev. B 2014, 89, 121102. [Google Scholar] [CrossRef]
- Sato, T.; Miyagawa, K.; Kanoda, K. Fluctuation Spectroscopy Analysis Based on the Dutta–Dimon–Horn Model for the Charge-Glass System θ-(BEDT-TTF)2CsZn(SCN)4. J. Phys. Soc. Jpn. 2016, 85, 123702. [Google Scholar] [CrossRef]
- Kagawa, F.; Oike, H. Quenching of Charge and Spin Degrees of Freedom in Condensed Matter. Adv. Mater. 2017, 29, 1601979. [Google Scholar] [CrossRef] [PubMed]
- Papanikolaou, S. Universality of liquid-gas Mott transitions at finite temperatures. Phys. Rev. Lett. 2008, 100, 026408. [Google Scholar] [CrossRef] [PubMed]
- Kagawa, F.; Miyagawa, K.; Kanoda, K. Magnetic Mott criticality in a κ-type organic salt probed by NMR. Nat. Phys. 2009, 5, 880–884. [Google Scholar] [CrossRef]
- Bartosch, L.; de Souza, M.; Lang, M. Scaling Theory of the Mott Transition and Breakdown of the Grüneisen Scaling Near a Finite-Temperature Critical End Point. Phys. Rev. Lett. 2010, 104, 245701. [Google Scholar] [CrossRef] [PubMed]
- Zacharias, M.; Bartosch, L.; Garst, M. Mott Metal-Insulator Transition on Compressible Lattices. Phys. Rev. Lett. 2012, 109, 176401. [Google Scholar] [CrossRef] [PubMed]
- Gati, E.; Garst, M.; Manna, R.S.; Tutsch, U.; Wolf, B.; Bartosch, L.; Schubert, H.; Sasaki, T.; Schlueter, J.A.; Lang, M. Breakdown of Hooke’s law of elasticity at the Mott critical endpoint in an organic conductor. Sci. Adv. 2016, 2, e1601646. [Google Scholar] [CrossRef] [PubMed]
- We find that for even larger cooling rates K/min to 32 K/min, the noise level starts to increase again [25]. This is because increasing q not only reduces but at the same time increases the degree of quenched EEG disorder [23] resulting in a stronger random lattice potential for the correlated charger carriers at the verge of Mott localization. The effect of disorder in this scenario is strong and qualitatively different from the situation for simple Anderson localization (see e.g., [139,140,141,142,143,144]). Since the change in induced by varying q is quite drastic, covering several tens of bars on the pressure axis, further noise studies starting at different pristine positions in the phase diagram and with smaller increments of q are required in order to understand the intricate interplay of randomness and strong electron correlations in -(ET)X salts and the consequences for the low-frequency dynamics of the carriers.
- Kotliar, G.; Lange, E.; Rozenberg, M.J. Landau theory of the finite temperature Mott transition. Phys. Rev. Lett. 2000, 84, 5180–5183. [Google Scholar] [CrossRef] [PubMed]
- Imada, M. Universality classes of metal-insulator transitions in strongly correlated electron systems and mechanism of high-temperature superconductivity. Phys. Rev. B 2005, 72, 075113. [Google Scholar] [CrossRef]
- Furukawa, T.; Miyagawa, K.; Taniguchi, H.; Kato, R.; Kanoda, K. Quantum criticality of Mott transition in organic materials. Nat. Phys. 2015, 11, 221–224. [Google Scholar] [CrossRef]
- Jaroszyński, J.; Popović, D.; Klapwijk, T.M. Magnetic-Field Dependence of the Anomalous Noise Behavior in a Two-Dimensional Electron System in Silicon. Phys. Rev. Lett. 2004, 92, 226403. [Google Scholar] [CrossRef] [PubMed]
- Schmalian, J.; Wolynes, P.G. Stripe Glasses: Self-Generated Randomness in a Uniformly Frustrated System. Phys. Rev. Lett. 2000, 85, 836–839. [Google Scholar] [CrossRef] [PubMed]
- Dobrosavljević, V.; Tanasković, D.; Pastor, A.A. Glassy Behavior of Electrons Near Metal-Insulator Transitions. Phys. Rev. Lett. 2003, 90, 016402. [Google Scholar] [CrossRef] [PubMed]
- Rommel, R.; Hartmann, B.; Brandenburg, J.; Schlueter, J.A.; Müller, J. Nonlinear electronic transport in the anomalous metallic state of quasi-2D organic superconductors κ-(BEDT-TTF)2X. Phys. Status Solidi B 2013, 250, 568–574. [Google Scholar] [CrossRef]
- Thomas, T. Charge Carrier Dynamics at the Mott Transition in κ-(BEDT-TTF)2Cu[N(CN)2]Br. Master’s Thesis, Goethe-University Frankfurt, Frankfurt, Germany, 2017. [Google Scholar]
- Kanoda, K.; Kato, R. Mott Physics in Organic Conductors with Triangular Lattices. Annu. Rev. Condens. Matter Phys. 2011, 2, 167–188. [Google Scholar] [CrossRef]
- Kato, R. Development of π-Electron Systems Based on [M(dmit)2] (M = Ni and Pd; dmit: 1,3-dithiole- 2-thione-4,5-dithiolate) Anion Radicals. Bull. Chem. Soc. Jpn. 2014, 87, 355–374. [Google Scholar] [CrossRef]
- Caloyannides, M.A. Microcycle spectral estimates of 1/f noise in semiconductors. J. Appl. Phys. 1974, 45, 307–316. [Google Scholar] [CrossRef]
- Bergman, D.J. Nonlinear behavior and 1/f noise near a conductivity threshold: Effects of local microgeometry. Phys. Rev. B 1989, 39, 4598–4609. [Google Scholar] [CrossRef]
- Das, P.; Amyan, A.; Brandenburg, J.; Müller, J.; Xiong, P.; von Molnár, S.; Fisk, Z. Magnetically driven electronic phase separation in the semimetallic ferromagnet EuB6. Phys. Rev. B 2012, 86, 184425. [Google Scholar] [CrossRef]
- Kirtley, J.R.; Theis, T.N.; Mooney, P.M.; Wright, S.L. Noise spectroscopy of deep level (DX) centers in GaAs-AlxGa1−x as heterostructures. J. Appl. Phys. 1988, 63, 1541–1548. [Google Scholar] [CrossRef]
- Müller, J.; von Molnár, S.; Ohno, Y.; Ohno, H. Decomposition of 1/f Noise in AlxGa1−xAs/GaAs Hall Devices. Phys. Rev. Lett. 2006, 96, 186601. [Google Scholar] [CrossRef] [PubMed]
- Müller, J.; Brandenburg, J.; Schweitzer, D.; Schlueter, J.A. Different electronic transport regimes in the quasi-two-dimensional organic conductors κ-(BEDT-TTF)2X. Phys. Status Solidi B 2012, 249, 957–961. [Google Scholar] [CrossRef]
- Sano, K.; Sasaki, T.; Yoneyama, N.; Kobayashi, N. Electron Localization near the Mott Transition in the Organic Superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. Phys. Rev. Lett. 2010, 104, 217003. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, T. Mott-Anderson Transition in Molecular Conductors: Influence of Randomness on Strongly Correlated Electrons in the κ-(BEDT-TTF)2X System. Crystals 2012, 2, 374–392. [Google Scholar] [CrossRef]
- Taniguchi, H.; Kawamoto, A.; Kanoda, K. Superconductor-insulator phase transformation of partially deuterated κ-(BEDT-TTF)2Cu[N(CN)2]Br by control of the cooling rate. Phys. Rev. B 1999, 59, 8424–8427. [Google Scholar] [CrossRef]
- Shinaoka, H.; Imada, M. Soft Hubbard Gaps in Disordered Itinerant Models with Short-Range Interaction. Phys. Rev. Lett. 2009, 102, 016404. [Google Scholar] [CrossRef] [PubMed]
- Shinaoka, H.; Imada, M. Single-Particle Excitations under Coexisting Electron Correlation and Disorder: A Numerical Study of the Anderson—Hubbard Model. J. Phys. Soc. Jpn. 2009, 78, 094708. [Google Scholar] [CrossRef]
- Diehl, S.; Methfessel, T.; Tutsch, U.; Müller, J.; Lang, M.; Huth, M.; Jourdan, M.; Elmers, H.J. Disorder-induced gap in the normal density of states of the organic superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. J. Phys. Condens. Matter 2015, 27, 265601. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).