2. Energy of Ground State Exciton in Nanosystems
Consider the model of quasi-zero-nanosystems: Semiconductor spherical QD with a radius, which contains in its volume semiconductor (dielectric) material with permittivity ε2, surrounded by a dielectric matrix with ε1 permittivity. In the QD volume h hole moves with the effective mass mh, and e electron with the effective mass mе(1) is situated in the matrix (rе and rh—the distance of electron and hole from the QD center). Let us assume that in QD the valence band has a parabolic form. We also assume that on the spherical surface boundary of QD/matrix infinite high potential barrier exists. Therefore, in the studied model h hole cannot go out from the QD volume, and e electron can not penetrate into the QD volume.
The energy of polarization interaction of the electron and hole
with spherical surface boundary of QD/matrix in the case of relative
permittivity can be represented as the algebraic sum of the hole and electron interaction energies with their
,
and “foreign”
,
images, respectively [
5]:
where
Here the parameter of the nanosystem (ε2 − ε1)/(ε2 + ε1).
For the simplicity, without losing the generality, we will assume that the hole
h with the effective mass
mh, is located in the center of the QD (wherein
rh = 0), and the
e electron with an effective mass
mе(1) is localized in the matrix of the spherical surface QD (
rе =
r—the distance of
e electron from the QD center). Such assumption is justified, as the ratio of the effective masses of electrons and holes in nanosystem
. In the observed quasi-zero nanosystems model, in the frame of the above mentioned approximations, as well as in the effective mass approximation and the center of mass of nanosystem, the Hamiltonian of exciton (from spatially separated hole, moving in QD volume, and the electron situated in the dielectric matrix) takes the form:
where the first member is the operator of exciton’s kinetic energy, (
µ0 = mе(1)mh/(mе(1) +
mh)—the reduced mass of the exciton from spatially separated electrons and holes), the second describes the centrifugal energy of the exciton
(
,
l = 0, 1, 2,—orbital quantum number of the electron),
—width of semiconductor bandgap with
ε2 permitivity. In the Hamiltonian (6), the energy of the Coulomb interaction between the electron and hole is described by the equation [
5]:
Polarization interaction energy (2), (4), (5) of electron and hole with spherical surface boundary of QD/matrix, when
rh = 0, takes the form:
Then taking into account (3), (9), (10) and (11), the energy of polarization interaction (3), may be written in the following form:
Consideration of interaction energy of hole with its (9) and “foreign” (10) images, as well as the electron with the “foreign” (11) image, leads to the increase of the polarization interaction energy (9) by , which decreases with the increase of QD radius.
In the nanosystem the Hamiltonian
(6) of the exciton from spatially separated electron and hole considering the formulas (7), (8) and (12) takes the following form:
where effective potential energy of the exciton
with the increase of the QD radius (so that
а >>
аех, where
аех = (ε
2 ћ2/
µ е2)—exciton Bohr radius,
µ = mе(2) mh/(mе(2) +
mh) is the reduced exciton mass and
mе(2)—the effective mass of electron in the semiconductor with permittivity ε
2), the spherical surface between boundary of two media goes into the flat boundary surface. Wherein the exciton from the spatially separated electrons and holes (the hole moves in the semiconductor, and the electron is situated in the matrix) becomes two-dimensional. In the Hamiltonian (6) potential energy, describing the motion of the exciton in the nanosystem, containing QD with large radius (
а >>
аех) the main contribution is the energy of the Coulomb interaction
(8) between electron and hole. Interaction energy between electron and hole with their (9), (11) and “foreign” (11), (10) images gives a much smaller contribution to the potential energy (14) of the Hamiltonian (6). By the first approximation this contribution may be neglected. In the potential energy (14) of the Hamiltonian (6) remains only the energy of the Coulomb interaction (8) between electron and hole. The Schrodinger equation with this Hamiltonian describes a two-dimensional exciton (2D exciton) from spatially separated electron and hole energy spectrum, which takes the form [
14]:
where
n = 0,1,2 ...—the principal quantum number of exciton,
Ry0 = 13.606 eV—the Rydberg constant. Bohr radius of such 2D exciton is described by the following equation:
and the binding energy of the ground state of 2D exciton, according to (15), is given by:
If
l ≠ 0, the contribution of the centrifugal energy into the effective potential energy
(14) creates a positive potential barrier, the maximum value of which is the following
for QD with large radius
S 1 (
—the dimensionless radius of QD). The formation of such barrier means that along with the stationary states
the exciton (from spatially separated electrons and holes)), over the spherical surface of the QD, can occur quasi-stationary states of the exciton with energy
. With the increase of radius
S of QD, starting from the value of
S greater than a certain critical radius of
(1,
l), i.e., at
first quasi-stationary states should be appeared. At bigger radii of QD
they need to pass into stationary states. When
stationary states passes into two-dimensional exciton state with energy
(
a) = (
) (14), localized on flat surface between two media [
5,
6], i.e., the energy spectrum
(
S) of the stationary states of the exciton energy is bounded from below (
(14). The existence of the critical radius
(1,
l) shows that for QD with determined radius
S the energy spectrum
(
S) of the exciton is bounded above by the maximum value
, forming a band of surface states, localized on the surface spherical boundary of (QD/matrix), part of which has a quasi-stationary character. Such band of surface states contains a finite number of levels (1,
l), and this band is finished by
level. Radius
(1,
l) corresponds to the highest acceptable value of energy
of ground state at fixed
l. This maximum value of the energy coincides with the
(15).
Let us define the energy of the ground (
n = 1) state of the exciton Hamiltonian (10) for arbitrary values of
S and
l by means of variational method. By making a standard replacement of the radial wave function
the variational function
will be given as:
where
—variational parameter. Choosing the wave function
in the form (21) provides its passage to the limit when
in the wave function of electrons localized on the plane surface between two media [
15,
16]. We write the mean value of the exciton Hamiltonian (10) on the wave functions (18) in the following form:
The results of the variational calculation of energy
(
a) (22) of the ground state of the exciton in nanosystems containing aluminum oxide QD with average
а radius not exceeding 20 nm, are obtained for the nanosystem containing aluminum oxide QD (with permittivity
= 10 and the effective mass of hole (
mh/
m0) = 6.2; the value of the effective mass of the electron in the matrix (
mе(1)/m0) = 0.537 [
17], situated in the matrix (vacuum oil), which was studied in experimental studies [
2,
3,
4] (see
Figure 1).
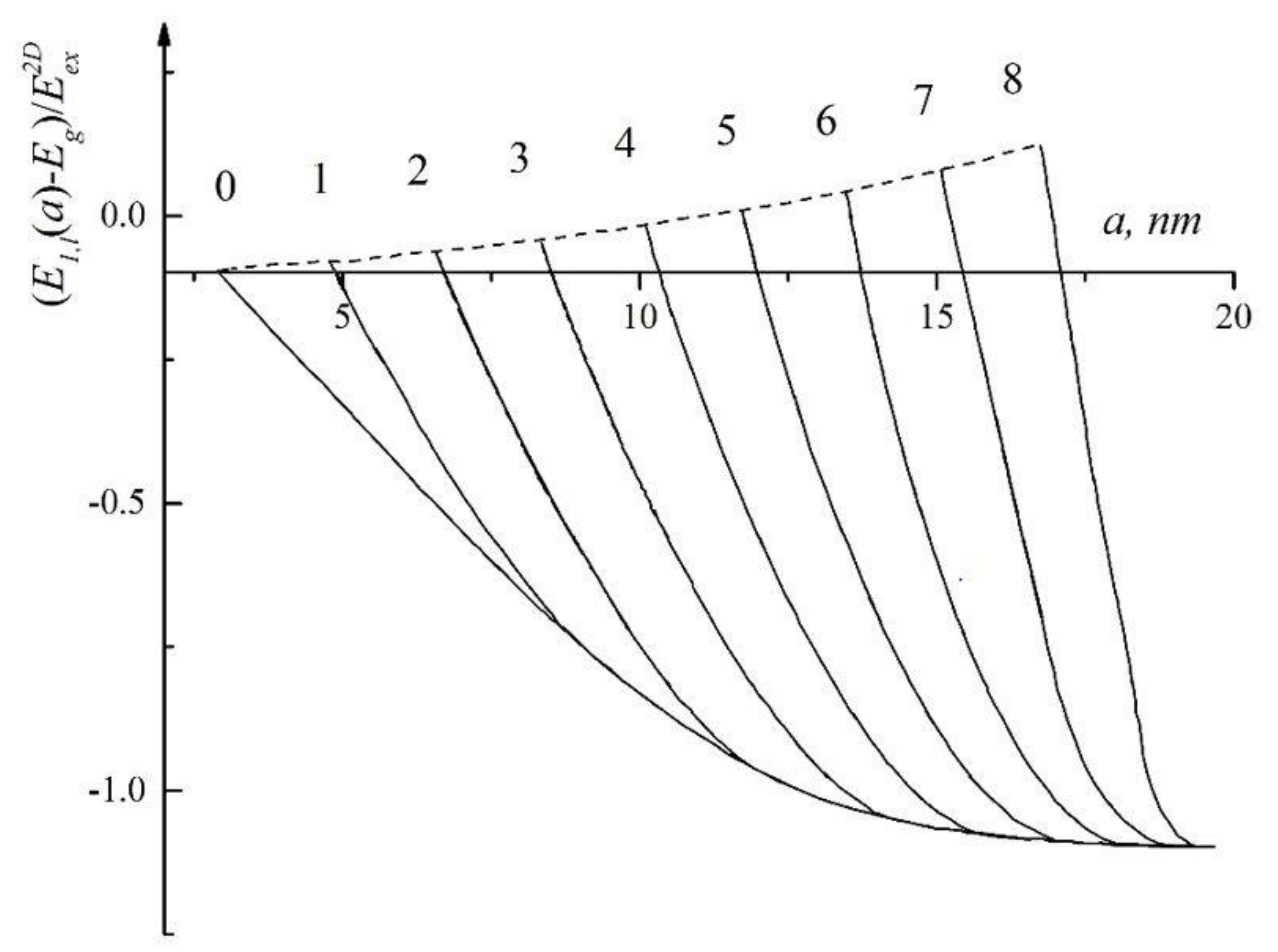
Figure 1 shows the dependence of
(
a) (19) for the states with
l = 0, 1, 2, 3, 4, 5, 6, 7, 8 with quasi-stationary states spectrum border
. The obtained results (see
Figure 1) clearly illustrate the abovementioned qualitative features of considered dependences
(
a) (22). The critical radii of QD for
have are respectively values:
In nanosystems with the increase of radius
а of QD, starting from the value not exceeding a certain critical radius of QD
at
quasi-stationary states of the exciton firstly appear (see
Figure 1). For instance, the smallest radius
of QD in which case quasi-stationary states of the exciton appear (in the state (1,
= 1)) according to (20) is equaled to
, whereas the largest radius of QD
, at which the quasi-stationary state exciton occurs (in the state (1,
l = 8) is equaled to
).
In the range of values of QD radii
(at
quasi-stationary states (1,
l) of the exciton goes into the two-dimensional exciton state (12) localized on a flat surface bounding two media [
5,
6]), and the quasi-stationary state goes into the exciton stationary states (see
Figure 1). The smallest radius of QD
at which the exciton stationary states appear (in the state (1,
l = 0), according to (20) is equaled to
[
5,
6], wherein the largest radius of QD
(in exciton state (1,
l = 8))
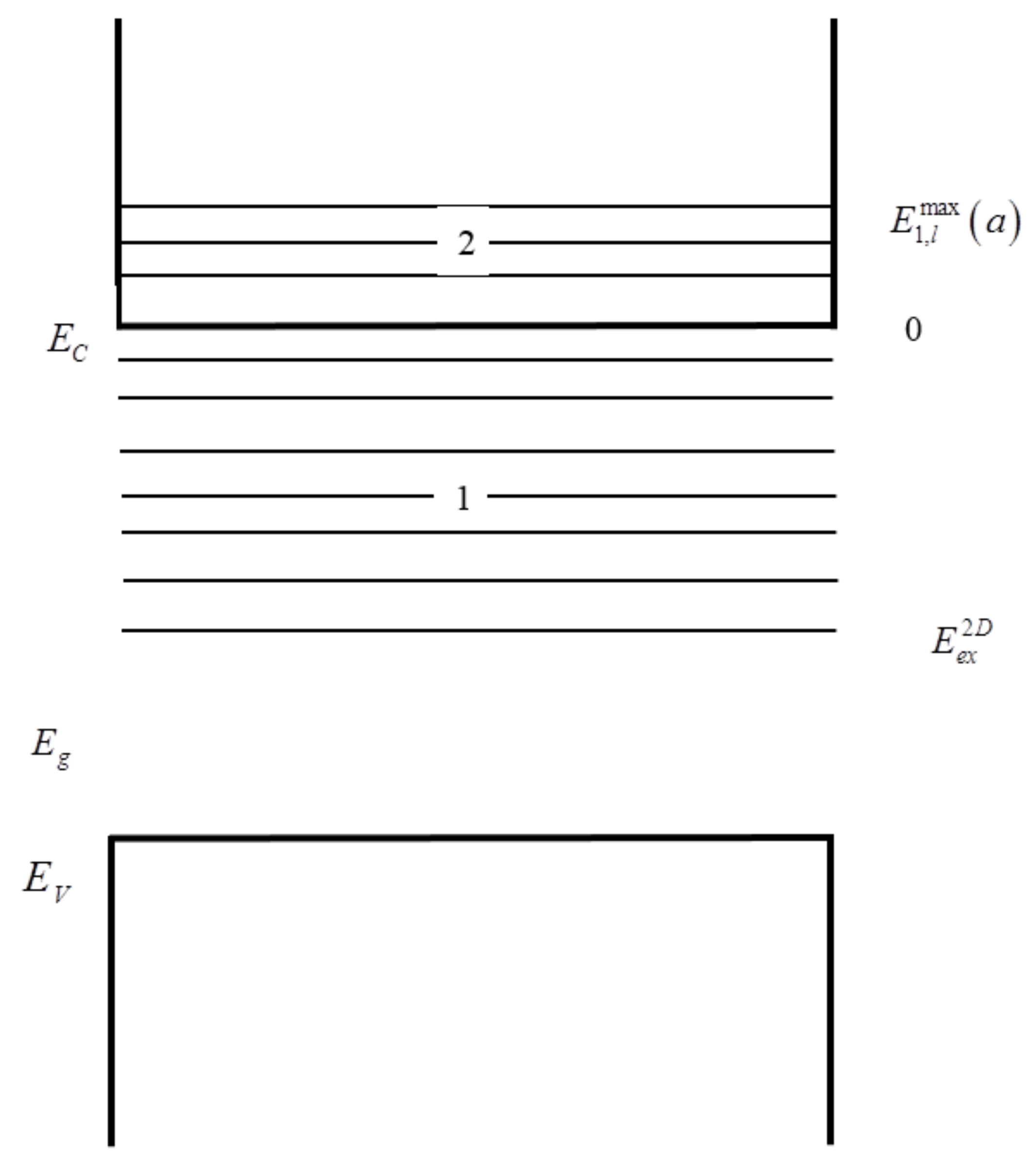
. In nanosystem the stationary states of the exciton (from spatially separated electrons and holes) are located in the bandgap of aluminum oxide QD (below the bottom of the conduction band
of aluminum oxide QD (see
Figure 2, area 1)). They are limited below by level
(14), which is equal to the binding energy of the ground state of two-dimensional exciton (from spatially separated electrons and holes). Quasi-stationary states of the exciton are in the conduction band
(above the bottom of the conduction band
of aluminum oxide QD (see
Figure 2, area 2). They are limited to the top by the border of the spectrum
of quasi-stationary states. The magnitude of
takes a maximum value in the state (1,
l = 8), wherein the
(see
Figure 1). In the nanosystem hole moves in the valence band
of QD, and the electron is in the quasi-stationary and stationary states (in areas 1 and 2 of the conduction band and the band gap of QD, see
Figure 2).
Such high quasi-stationary states could be significant in the processes of scattering of electrons on the QD with sufficient large radius and may lead to strong suppression of the electron mobility in dielectric matrices. The electron trapping on the quasi-stationary states, herewith it is possible also without changing the total energy.
Thus, for aluminum oxide QD, which radius is in the interval (25), the energy spectrum (a) of the exciton is limited above by the maximum value of the orbital quantum number , forming surface states band. Such band of the surface states of the exciton (from spatially separated electron and hole) consists of stationary and quasi-stationary states and has a finite number of levels (1, l), is equal to nine.
Obtained results allow us to follow the transition from the exciton states localized on the surface of a spherical QD, to the states of the exciton localized on the boundary plane surface. For QD with large radius
S (in the limit of
S ∞) not only arbitrary values of
l, but also
, which within
define the finite quasimomentum
of free movement of the electron parallel to the boundary surface, become permitted. As a result, the expression
(
a) (22) proceeds into the spectrum of exciton states localized on the boundary plane surface, which in the dimensional units has a following form
Thus, all surface states become stationary, as in the case of specified passage to the limit potential barrier (14) becomes infinitely wide, and its height (18) 0 (in the dimensional units) defines the kinetic energy of the “free” motion of the electron along the plane of the media boundary.
The more elementary method to detect and study of observed exciton states in nanosystems consisting of aluminum oxide with an average radius of
a (25) placed in the matrix(vacuum oil) [
2,
3,
4], can be investigated the interband, which is formed by the electron transitions in the surface exciton states band between the quasi-stationary states, located in the conductivity band
of QD and stationary states, being in the band gap of the QD (see
Figure 2)) and intraband (which is caused by the electron transitions between the stationary states) of light absorption. Such transitions with a change in the orbital quantum number
per unit are allowed by the selection rules. The photon energy for such transitions
(where
l is takes values from 0 to 8).
Consider the qualitative picture of the appearance of transition states in nanosystem (see
Figure 1 and
Figure 2 and
Table 1). Starting from the radius of aluminum oxide QD
in the range of QD radii:
interband transition occurs between states of (1, 1) and (1, 0) photons with energies in the range of
With the increase of the radius
a of QD in the range of radii
a
there are two interband transitions: The transition between the states (1, 1) and (1, 0) with photon energies in the range of
and transition between states (1, 2) and (1, 1) in the range of QD radii
with the energy of the quantum
and in the range of QD radii
such transition is intraband with energies of the quantum in the range of
in the range of QD radii
interband transition between (1, 3) and (1, 2) is added to two transitions which occur in the range of QD
a radii (30), which range in radii of QD
will be interband with photon energy
in the range of QD radii
such transition is intraband with photons energies
In the range of
a radii of QD (36) intraband transition between states (1, 2) and (1, 1) will be observed with photon energies in the range of
Intraband transitions between the states (1, 1) and (1, 0) disappears when .
In the range of radii of QD
three transitions exist: intraband transitions between the states (1, 2) and (1, 1), which, with energy not exceeding (188 meV), disappears when
, and intraband transitions between the states (1, 3) and (1, 2) with photon energies
Arising new transition between (1, 4) and (1, 3) states in the range of
a radii of QD
is interband with a photon energy
in the range of radii
such transition will be intraband with photons energies
In the range of
a
two transitions that occur in the range of
a radii of QD (42) is added to the transition between (1, 5) and (1, 4) states, which range is in the range of QD radii
will be interband, with photon energy
in the range of radii
such transition is intraband with photons energies
In the same range of QD radii (47) intraband transitions between the states (1, 3) and (1, 2) occurs with the photon energies
and intraband transitions between the states (1, 4) and (1, 3) is observed with photon energies
In the range
of QD
there are three transitions: intraband transitions between the states of (1, 4) and (1, 3), and between (1, 5) and (1, 4) with photon energies which are in the following ranges respectively:
transitions between (1, 6) and (1, 5) in the range of QD radii
will be intraband with the photon energy
and in the range of QD radii
Such transition is intraband with photon energies
In the range of QD
a radii
there are three transitions: two intraband between states (1, 5) and (1, 4), and also between the states of (1, 6) and (1, 5) with photon energies which lie in the ranges, respectively
Transition between (1, 7) and (1, 6) states in the range of QD radii
in intraband with the photon energy
in the range of
a
this transition will be intraband with photon energies with the range of
In the range of
a
there are three transitions: two intraband between states (1, 6) and (1, 5), and between the states (1, 7)
(1, 6) with photon energies lying in the ranges respectively:
transition between (1, 8) and (1, 7) states in the range of QD
will be intraband with photons energies
In the range of
a
there are three intraband transitions: the transition between the states (1, 6) and (1, 5) with photons energies in the interval
transition between (1, 7) and (1, 6) states with photon energies
and transition between (1, 8) and (1, 7) states with photon energies
Thus, in the nanosystem in which average values of aluminum oxide QD radii vary in the range of:
interband and intraband transitions create energy bands, lying in the QD bandgap. Energy of photons
(26) of such interband and intraband transitions reach high values comparable to the binding energy
(17) of the ground state of two-dimensional exciton (see
Figure 1 and
Table 1). Energies of the interband transitions
(26) are significantly exceed the energies corresponding to the intraband transitions for given average radius of QD
a (in the interval (77)). Spectra of emission, absorption and transmittance of light, which are located in the visible and infrared wavelengths, are formed from such energy bands. Such spectra were observed in experimental works [
2,
3,
4].
It should be noted that in the nanosystems, in which average
a radii of aluminum oxide QD vary in the interval (77) at
T temperature satisfying
(where
—Boltzmann constant), the observation of nanosystems is possible in the processes of absorption and emission on the transitions with frequencies
, depending on the values of the average radius of the QD (in the interval (77)), lying in the range from the infrared to the visible spectrum. Such processes do not occur on QD with small radii
. New transition states
, starting from
at
to (1, 8) state at
(see
Table 1), will give a contribution to the absorption (and also emission) at large values of QD radii
. Therefore, for instance, it is possible specroscopically control the nucleation of QD in the dielectric matrix, fixing the formation stage of the QD, starting from the radii
, i.e., the emergence of a new phase in the nanosystem. The dependence of the energy spectrum of
(22) of the exciton on the
a radius of QD and its threshold feature enable opportunity to make selection by laser spectroscopy methods in nanosystems, determining the degree of dispersion of nanosystems (see
Figure 1).
It should be noted that in the energy of the ground state of the exciton (22) (of spatially separated electrons and holes) in nanosystems containing aluminum oxide QD with a radii (25), the main contribution is the average value of the energy of the Coulomb interaction between the electron and hole. Wherein the average value of the energy interaction between electron and hole with her and “foreign” images gives much smaller contribution to the energy of the ground state of the exciton (22) (the ratio of which to the contribution of the average value of the Coulomb interaction energy does not exceed 8%). The latter circumstance is due to the fact that the values of the average energies of the interaction of holes and electrons with their images, as well as the values of average interaction energies of the hole and electron with “foreign” images makes contribution to the (22) with different signs, which are largely compensate each other.
Thus, the energy of the ground state of the exciton (22) (of spatially separated electrons and holes) is due to the renormalization of the Coulomb interaction energy (8) between the electron with a hole, as well as the polarization interaction energy (5) of electron and hole with spherical surface of boundary QD/matrix associated with the spatial restriction of the area of the volume quantization volume of QD.
One can see from the
Figure 1, which shows the dependence of the total energy
Е1,l(а) (22) of the ground state of exciton (of spatially separated electrons and holes) in nanosystem containing aluminum oxide QD with average radius
a from the interval (25), it follows that with the increase of QD radius
Е1,l(а) (19) total energy of the ground state of the exciton increases. Herewith, the energy (22) of the ground state of the exciton significantly exceeds (3–49 times) the value of the binding energy of the exciton
51.16 meV) in aluminum oxide single crystal. Starting from the radius
, the value of the total energy (22) of the ground state of the exciton asymptotically tends to the, accordingly, values of
2.5038 eV) (17) (characterizing the binding energy of the ground state of the two-dimensional exciton (from spatially separated electrons and holes)) (see
Figure 1).