Abstract
Hybrid ion-pair crystals involving hexadentate [Fe(III)(3-OMesal2-trien)]+ spin-crossover (SCO) cationic complexes and anionic gold complexes [Au(dmit)2]− (1) (dmit = 4,5-dithiolato-1,3-dithiole-2-thione) and [Au(dddt)2]− (2) (dddt = 5,6-dihydro-1,4-dithiin-2,3-dithiolate) were synthesized and studied by single-crystal X-ray diffraction, P-XRD, and SQUID magnetometry. Our study shows that both complexes have similar 1:1 stoichiometry but different symmetry and crystal packing. Complex 1 has a rigid structure in which the SCO cations are engaged in strong π-interplay with molecular surrounding and does not show SCO transition while 2 demonstrates a reversible transition at Tsco = 118 K in a much “softer”, hydrogen-bonded structure. A new structural indicator of spin state in [Fe(sal2-trien)]+ complexes based on conformational analysis has been proposed. Aging and thermocycling ruined the SCO transition increasing the residual HS fraction from 14 to 41%. Magnetic response of 1 is explained by the AFM coupled dimers S = 5/2 with J1 = −0.18 cm−1. Residual high-spin fraction of 2, apart from a contribution of the weak dimers with J12 = J34 = −0.29 cm−1, is characterized by a stronger interdimer coupling of J23 = −1.69 cm−1, which is discussed in terms of possible involvement of neutral radicals [Au(dddt)2].
1. Introduction
Octahedral complexes with d4-d7 metal ions can demonstrate spin-crossover (SCO) transition under external factors such as temperature, pressure, and electromagnetic radiation [1,2,3]. As soon as the bistability between a high-spin (HS) and low-spin (LS) states of the metal ion embraces not only magnetic response but also the electronic structure of the entire complex, various endeavors have been undertaken to use the SCO compounds in magnetic memory or display devices, as well as multi-modal sensors [4,5,6]. Moreover, polyfunctional compounds combining the conductivity and the spin-crossover transition have been highlighted in connection with spin-dependent transport and single molecular switching [7,8,9]. Spin-lattice relaxation in the low-dimensional conducting networks of centrosymmetrical molecules is strongly suppressed. The hybrid structures implementing efficient exchange interaction between the SCO and conducting subsystems would facilitate the development of new molecular spintronic devices where the spin transport is controlled by spin-crossover complexes.
Metal bis-1,2-dithiolene complexes, as organic donors and acceptors, possess a delocalized electron system as a planar central core M(C2S2)2 and present different formal oxidation states. This type of complex has been intensively studied as a component of molecular conductors [10,11,12]. In addition, metal dithiolene complexes have a rich variety of physical properties, such as Peierls instability of the low-dimensional systems and the quantum fluctuations [10,13]. Thus, both SCO and metal dithiolene complexes could undergo phase transition, and combining two components in one crystal structure might give rise to a novel molecular material with exotic phenomena.
The interplay between spin-crossover and conductivity was already observed in some of such materials [14,15,16]. The majority of conducting SCO compounds are represented by the Fe(III) cation complexes with [M(dmit)2]δ− anions [17,18,19]. As a first step in this way, Faulmann et al. have published a simple salt [Fe(sal2-trien)][Ni(dmit)2] showing a cooperative spin transition behavior with a wide hysteresis loop (30 K) [19]. These results convinced us that metal bis(dithiolene) anionic [M(dmit)2] and [M(dddt)2] complexes [12] might be promising candidates for enhancing cooperativity in SCO of cations based on mononuclear Fe(III) complexes with hexadentate Schiff base ligands. To achieve systems with molecular shape flexibility and rich in hydrogen bonding [20], we prepared the 3-methoxy derivative (3-OMesal2-trien)2− and used it as a ligand (Figure 1).
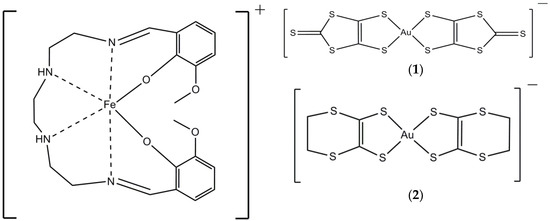
Figure 1.
Scheme of the cation [Fe(3-OMesal2-trien)]+ and anions [Au(dmit)2]− (1), [Au(dddt)2]− (2).
In this paper, we report synthesis, crystal structure, and magnetic properties of [Fe3+(3-OMesal2-trien)][Au3+(dmit)2] (1) and the analogous compound [Fe3+(3-OMesal2-trien)][Au3+(dddt)2]·CH3CN (2) involving a nonmagnetic gold bis(dithiole) anions (Figure 1). The incomplete SCO conversion was observed in 2 and was not in the compounds 1, where 100% of Fe(III) ions remained in HS state. Furthermore, while 1 exhibited weak antiferromagnetic (AFM) interactions between adjacent cations, the remnant HS fraction in 2 revealed an order of magnitude stronger AFM exchange coupling. We discuss a degradation of SCO phenomenon and a character of the exchange interactions in terms of aging and thermo cycling. Despite the degradation with aging, the structures and physical properties of fresh crystals from independent syntheses were consistent. We believe that the method of slow diffusion solution provides a reliable processability for other systems of that type.
2. Results and Discussion
2.1. Synthesis
Commercial solvents were used without further purification unless otherwise specified. Reactants commercially obtained: 3-methoxysalicylaldehyde (o-vanillin), 1,8-diamino-3,6,-diazaoctane (trien-oil), iron nitrate nonahydrate [Fe(NO3)3·9H2O] and sodium methoxide (NaOCH3) from Sigma-Aldrich (Saint Louis, MO, USA). Complexes [(Et)4N][Au(dmit)2], [(Et)4N][Au(dddt)2] and [Fe(3-OMe-sal2-trien)]·NO3·H2O were prepared according to the literature [21,22,23].
2.1.1. [Fe(3-OMesal2-trien)][Au(dmit)2] (1)
To the stirred solution of [(Et)4N][Au(dmit)2] (84 mg, 0.15 mmol) in acetonitrile (15 mL) was added dropwise a solution of [Fe(3-OMesal2-trien)]·NO3·H2O (82 mg, 0.15 mmol)) in acetonitrile (5 mL). The reaction mixture was heated up to 60 °C for 10 min, and then cooled to −18 °C. The precipitate was filtered, washed with cooled acetonitrile, and dried in vacuo at room temperature. [Fe(3-OMesal2-trien)][Au(dmit)2] (1) was obtained as black polycrystalline powder with a total yield 78.14%. Elemental Anal. Found: C, 31.84; H, 2.73; N, 5.36%. Calcd for (Mw = 1057) C28H28FeN4AuO4S10: C, 31.79; H, 2.65; N, 5.30%. For the results of thermogravimetric analysis see Figure S1.
By means the method of slow diffusion solution of [(Et)4N][Au(dmit)2] (6 mg, 0.01 mmol) in acetone (4 mL) into solution of [Fe(3-OMesal2-trien)]·NO3·H2O (5.5 mg, 0.01 mmol) in acetonitrile (1 mL), after one week the black plate-like crystals of 1 suitable for X-ray diffraction was filtered and dried at ambient temperature. The electron-probe X-ray microanalysis (EPMA) information on the elements proportion in 1 is Fe:Au:S = 1:1:10. Powder diffractogram (P-XDR) of the samples taken for magnetic measurements is presented in Figure S2.
2.1.2. [Fe(3-OMesal2-trien)][Au(dddt)2]·CH3CN (2)
To the stirred solution of [(n-Bu)4N][Au(dddt)2] (120 mg, 0.15 mmol) in acetonitrile (10 mL) was added dropwise a solution of [Fe(3-OMe-sal2-trien)]·NO3·H2O (82 mg, 0.15 mmol)) in acetonitrile (10 mL). The reaction mixture was heated up to 50 °C for 10 min, and then cooled to −18 °C. The precipitate was filtered, twice washed with ether, and dried at room temperature in air. [Fe(3-OMesal2-trien)][Au(dddt)2]·CH3CN (2) was obtained as black polycrystalline powder with a total yield 76.13%. Elemental Anal. Found: C, 36.21; H, 3.73; N, 6.58%. Calcd for (Mw = 1066) C32H39FeN5AuO4S8: C, 36.02; H, 3.66; N, 6.57%.
A weight loss of 3% was observed in the temperature range 145–200 °C which is assigned to the loose of one molecule of CH3CN (3.85% by theory) from 2. For the results of thermogravimetric analysis see Figure S3. The plot shows that weight loss occurs in two stages. A weight decrease of 3% corresponding to the loss of 0.8 solvate molecules is observed in the 145–200 °C range. The results indicate a relatively good agreement with the formulation deduced from elemental analysis and X-ray crystal structure determinations (see below). Decomposition of 2 begins above 225 °C. Although X-ray analysis before and after magnetic measurements did not show changes it seems likely that desolvation reveals itself at time exposures of months.
By means of slow diffusion method in U-shaped sell the solution of [(n-Bu)4N][Au(dddt)2] (8.0 mg, 0.01 mmol) in acetone (2 mL) was added into solution of [Fe(3-OMesal2-trien)]·NO3·H2O (5.5 mg, 0.01 mmol) in acetonitrile (2 mL). Black shinny plate-like crystals of 2 with up to 3 mm length were obtained after one week. Crystals were filtered, washed with ether, and dried at ambient temperature. Suitable single crystals were chosen for X-ray diffraction. The EPMA information on the elements proportion in 2 is Fe:Au:S=1:1:8. Figure S4 displays the P-XDR of 2 in the 2θ range from 1.95° to 30°.
The purity of the complexes and their solvation state was verified by determining the carbon, hydrogen and nitrogen content, at the Vario MICRO Cube (Elementar GmbH, Langenselbold, Germany) Analysis Service. Microphotos of single crystals of 1, 2 are shown in Figure S5 left and right panels, respectively. Polycrystalline sample taken for magnetic measurements are shown in Figure S6.
2.2. Crystal Structures
2.2.1. [Fe(III)(3-OMesal2-trien)] [Au(dmit)2] (1)
Complex 1 crystallizes in the triclinic space group P with one formula unit in the asymmetric volume (Figure 2). The refinement of the structure at 120 and 293 K (Table 1) showed identity of the structural characteristics at both temperatures. Below the details of the 120 K structure are described.
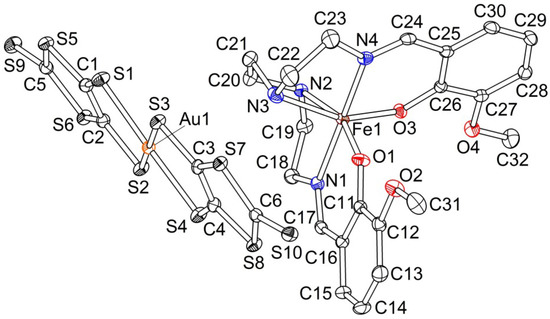
Figure 2.
Asymmetric unit in 1 (120 K, ORTEP drawing with 50% probability ellipsoids).

Table 1.
Crystal structure and refinement data.
In the crystal structure the layers of [Au(dmit)2]− anions alternate with the layers of [Fe(3-OMesal2-trien)]+ cations along the c-axis (Figure 3). The anion layer (Figure 4) consists of {[Au(dmit)2]2}2− dimers with the intradimer interplane distance of 3.56(3) Å and ring-over-atom overlap mode. Adjacent dimers are strongly shifted from each other along the long molecular axis and interdimer overlapping is absent (Figure 4b). Shortened S…S contacts are observed both inside the dimers [the S…S distances of 3.643(1) Å] and between them [3.218(1), 3.442(1), 3.508(1), 3.579(1) Å] and link the dimers into infinite ribbons along the [1 −1 0] direction. All the S…S distances between the anions from the neighbor ribbons exceed the sum of van-der Waals radii of 3.7 Å. Charge state of dmit in the [Au(III)(dmit)2]ˉ anion is 2−. It is confirmed by short lengths of double C=C bonds in dmit which are sensitive to the charge: the average value of C=C bond lengths in 1 is 1.348(2) Å.

Figure 3.
View of the structure 1 along b.

Figure 4.
(a) The ab layer of Au(dmit)2. The S…S contacts < 3.7 Å are shown by dashed lines. (b) Overlap mode inside and between the centrosymmetric [Au(dmit)2]2 dimers.
The magnetic layer consists of the chains of [Fe(3-OMesal2-trien)]+ cations, running along a (Figure 5). The cations within the chain are paired by π-stacking. The distance between centroids of two interacting phenyl cycles in the pair is 3.467(2) Å; there is several intermolecular C…C contacts in the range of 3.386(2)–3.507(3) Å which are shown by dashed lines in Figure 5. The Fe(III) ion in [Fe(3-OMesal2-trien)]+ is octahedrally coordinated by two O and four N atoms of the ligand. At 120 K Fe(III) is in a high-spin state, that is testified by lengthened Fe-N and Fe-O bonds (Table 2) as well as noticeable distortion of the octahedron: the O–Fe–N angles are 155.30(5) and 160.07(5)°. The other indicator of HS state is obtuse dihedral angle α between two salicylidene groups of 3-OMesal2-trien ligand of 94.22(3)°. Very similar geometry of the cation, characteristic for the high-spin Fe(III) ion, is retained in the complex 1 at room temperature (Table 2).
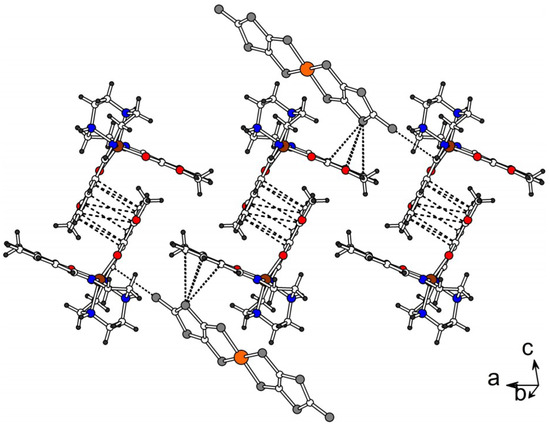
Figure 5.
Ribbons of [Fe(3-OMesal2-trien)]+ in the ab plane. The shortened C…C contacts < 3.6 Å in π-stacked pairs are shown by dashed lines. The anion…cation S…C contacts are shown by dotted lines.

Table 2.
Selected bond lengths (Å) and angles (°) in [Fe(3-OMesal2-trien)]+.
The cation and anion layers interact through hydrogen contacts of N−H...S (H…S of 2.62 Å) and C−H...S types (H…S of 2.81–2.98 Å). Besides, the S…π interaction between the S(8) atom of [Au(dmit)2]− and π-system of the C(11)-C(16) cycle of [Fe(3-OMesal2-trien)]+ is observed (Figure 2 and Figure 5). The distance S(8)…centroid C(11)-C(16) is 3.226(1) Å, the six S…C contacts are in the range of 3.473(2)–3.566(2) Å (dotted lines in Figure 5). One more S…C contact of 3.500(2) Å links terminal S(10) atom of the anion to the cation from the next cation pair in the ribbon. Figure 5 clearly demonstrates that both salicylidene arms of the [Fe(3-OMesal2-trien)] cation have very strong π-interactions with surrounding molecules: one arm is π-stacked to the similar arm of another cation in the pair and linked to the terminal S atom of the anion, while the another arm has strong π…S connection to the anion. Thus, one can conclude that very strong cooperation (or interplay) of the [Fe(3-OMesal2-trien)] cation with molecular environment should prevent its conformational switching needed for thermo-induced spin-crossover and in this reason the complex 1 retains the HS state at cooling.
2.2.2. [Fe(3-OMesal2-trien)][Au(dddt)2]·CH3CN (2)
Complex 2 crystallizes in the monoclinic space group I2/c. Asymmetric unit includes a half of the [Au(dddt)2]− anion with Au at an inversion center, a half of the [Fe(3-OMesal2-trien)]+ cation with Fe on a two-fold axis (Figure 6) and an acetonitrile molecule in a half-occupied general position near a two-fold axis. The structure of 2 was investigated at 120 and 293 K. Symmetry of the crystal is the same at both temperatures; however, some important structural changes are observed.
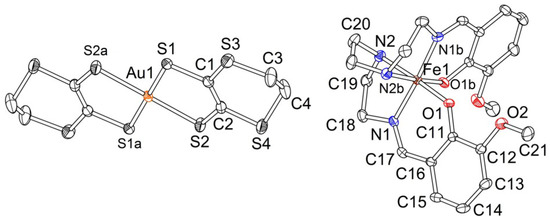
Figure 6.
Independent molecules in 2 (120K, ORTEP drawing with 50% probability ellipsoids). Symmetry codes: a (1 − x, −y, −z), b (−x, y, 0.5 − z).
In the structure of 2 the layers of the [Au(dddt)2]− anions alternate with the layers of the [Fe(3-OMesal2-trien)]+ cations along c (Figure 7a). The anion layer is shown in Figure 7b. Solvent molecules are sited in the cation layer (Figure 7c). The length of the double C=C bond in dddt is equal to 1.339(2) Å, i.e., the charge of the dddt part in the [Au(III)(dddt)2]− anion is 2−. There are no stacks in the anion layer because the anions are located near orthogonally to each other.
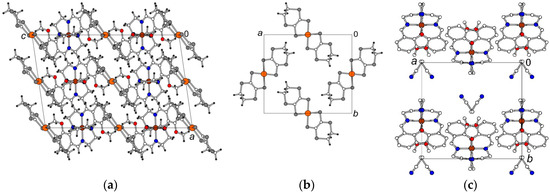
Figure 7.
(a) Structure 2 (120 K) projected along b. Solvent molecules located in the cation layer are omitted for clarity. (b) View of the anion layer along c. (c) View of the cation layer along c (H-atoms are omitted).
In the cation layer (Figure 7c), π-stacking between the [Fe(3-OMesal2-trien)]+ cations is not observed. The disordered acetonitrile molecules are in the zigzag cavity of the layer, their –CH3 groups being in between the salicylidene moieties of one cation and N atoms being near the middle ethylene group of the trien fragment of the next cation along b. The structure is supported by hydrogen bonding of cation…cation type [C–H…O contacts with H…O distance of 2.49 Å) and cation…anion type [N–H…S, H…S 2.58 Å; C–H…S, H…S 2.81, 2.88 Å]. In the complex 2 the Fe(III) ions in [Fe(3-OMesal2-trien)]+ are in a low-spin state at 120 K. The LS geometry of central FeO2N4 octahedron is very different from the HS one found in 1 (Table 2): all Fe–Nim, Fe–Nam and Fe–O bonds are noticeably shorter in LS whereas distortion of the octahedron decreases in comparison to the HS state, the O–Fe–N angle is 174.82(5)°. The dihedral angle α between two salicylidene groups of (3-OMesal2-trien) ligand is 88.94(1)°, i.e., α < 90° that is a feature of LS complexes (Figure 7, middle). At room temperature the HS characteristics of Fe(III) coordinated octahedron similar to the complex 1 are found: extended coordination bonds Fe-O/Fe-N by 0.02/0.15 Å, decreased O–Fe–N angle by 12° and grown α angle by about 5° up to 93.75(3)° (Figure 8, right).
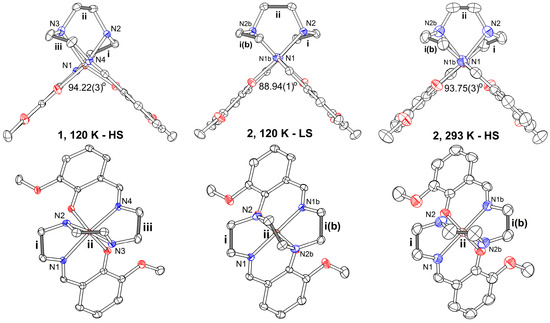
Figure 8.
Molecular conformation of the [Fe(III)(3-OMesal2-trien)]+ cation in 1 at 120 K (left), in 2 at 120 K (middle) and 293 K (right), side (upper row) and top (bottom row) view. Symmetry code: b (−x, y, 0.5 − z). The values of α angles between the salicylidene groups are given in the figure. The angles between C–C lines of ethylene groups i, ii and iii are listed in Table 2.
We believe that it is important to also analyze a conformation of the ethylene groups –CH2–CH2– in the trien fragment of the cation. The ethylene groups i, ii and iii are denoted by grey-colored bonds in Figure 8. We found that the orientation of central ethylene group changes upon the spin-crossover whereas the orientations of ethylene groups in side cycles do not change significantly. In both 1 and 2 complexes central –CH2–CH2– bond ii is near normal to the side bonds i and iii in the HS state (Figure 8, left and right in bottom row). In the LS state the central ethylene group ii switches its conformation to be near parallel to the side bonds (Figure 8, middle in bottom row). The angles between lines i, ii and iii are given in Table 2. We have shown that different orientations of ethylene groups are energetically favorable for HS and LS complexes and therefore can be used as indicator of spin state of [Fe(III)(sal2trien)]+ cations along with usual characteristics such as bond lengths and valent angles in the FeO2N4 octahedron and α angle between salicylidene moieties [24,25]. The paper with detailed conformational analysis and density functional theory (DFT) calculations in the spin-crossover [Fe(III)(sal2trien)]+ complexes will be published soon [26].
2.3. Conductivity.
Electrical conductivity for 1 and 2 was measured in the conducting plane of single crystals at room temperature by a conventional four-probe method. Platinum wire contact (d = 10µm) was glued to the crystal using the DOTITE XC-12 graphite paste. Both compounds were insulators with σ1(300 K) = 3 × 10−9 Ω−1 cm−1 (1) and σ2(300 K) = 1 × 10−9 Ω−1 cm−1 (2). This is consistent with small transfer integrals between the anions compared to the known ones for the conducting salts of metal bis-dithiolene anion complexes family [7].
2.4. Magnetic Properties
Magnetic measurements were performed by using a Quantum Design MPMS-5-XL SQUID magnetometer. Static magnetic susceptibility χ(T) was measured on polycrystalline samples at the magnetic field H = 100 Oe, while warming (↑) and cooling (↓) regimes. The temperature range of measurements was 2–300 K. The magnetization curves M(H) were obtained during several loops over the field range +50 kOe to −50 kOe. Preliminary, the samples had been cooled down to 2.0 K in zero magnetic field and virgin curves were recorded.
Temperature dependences of the product χT↓ for complexes 1 and 2 are depicted in Figure 9. The measurements were performed on fresh crystals while cooling in the range of 300→2 K, H = 100 Oe. The χT↓ value of 1 starts at 4.26 cm3 K/mol, remains unchanged till 50 K, undergoes the inflection at Ti1 = 46 K, and then decreases continuously down to 2.79 cm3 K/mol. Polycrystalline powder of 2 demonstrate a sharp SCO transition at Tsco = 118 K, during which the χT↓ value changes from 4.25 cm3 K/mol at 300 K (HS) down to 1.07 cm3 K/mol at the plateau in the vicinity of 60 K (LS). The shape of the transition curve was reproduced in several same-day subsequent measurements. Evolution at longer time exposures is discussed below. Hysteresis behavior was not observed between χT↓ and χT↑ curves in the transition range. In the vicinity of Ti2 = 55 K there was also a slightly pronounced inflection below which χT decreases down to 0.51 cm3 K/mol. The χT values at 300 K of both compounds are consistent with the theoretical spin-only value of 4.375 cm3 K/mol corresponding to 100% amount of HS Fe(III) ions, S = 5/2, g = 2.0. This is also in agreement with the assertion that both anions Au(dmit2)− and Au(dddt2)− do not have magnetic moment.
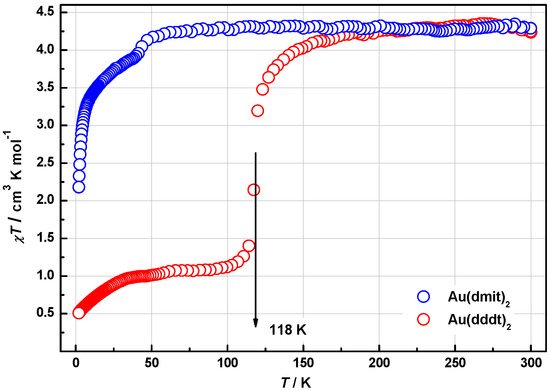
Figure 9.
Temperature dependences of χT↓ for 1 (○) and 2 (○).
Magnetic properties of both compounds changed with aging and thermal history, revealing an irreversible behavior of χT while cooling and warming regimes. An uncomplicated behavior for 1 is shown in Figure 10. Irreversibility is observed below the inflection point, Ti1 = 46 K, in a form of a hysteresis loop, while above it the curves follow the same Curie-Weiss trend with C = 4.3 cm3 K/mol (S = 5/2) and Θ = −0.5 K (see Figure 10, inset). This shape was reproduced in several cycles and it did not depend on the age of the sample. System 2 was found unstable. Both aging at ambient conditions and thermocycling led to a degradation of the SCO transition. The curves in Figure 11 present this evolution: the initial curve (black color, ↑↓ regimes) was recorded on the crystals aged over a period of several months; the other data sets depicted in blue and purple colors show a character of SCO degradation after several subsequent cooling-warming cycles. A solid red line indicating the transition in freshly synthesized sample (see Figure 9) is given for reference. With aging the HS state was reached in a more gradual manner, so that the χT value only got 3.8 cm3K/mol at 300 K. The value χT on the plateau below Tsco corresponds to γLS = 78% of S = 1/2 and γHS = 22% of S = 5/2, where γLS and γHS are molar LS and HS fractions. We took 0.375 cm3K/mol and 4.375 cm3K/mol for 100 % of LS and HS fractions, respectively. The ratio γLS/γHS did not change with time exposure, and varied from 3.6 (fresh) to 6.1 from sample to sample. However, thermocycling of seasoned crystals led to a quick spreading of the transition and to an irreversible growth of the residual HS fraction. In subsequent warming-cooling cycles γHS changed from 14% to 32% and 41% respectively.
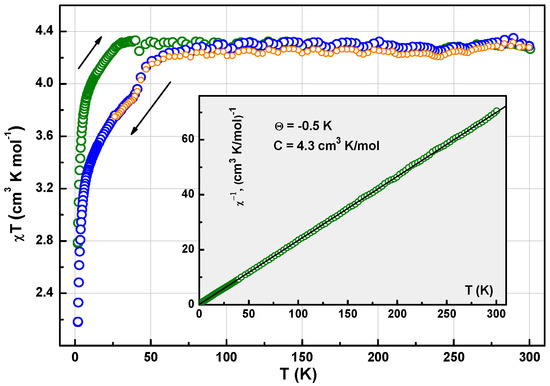
Figure 10.
Temperature evolution of χT in warming (○) and cooling (○, ○) regimes. Inset: Plot χ−1(T)↑ vs. T in 1. Solid line is Curie-Weiss fit with C = 4.3 cm3 K/mol and Θ = −0.5 K.
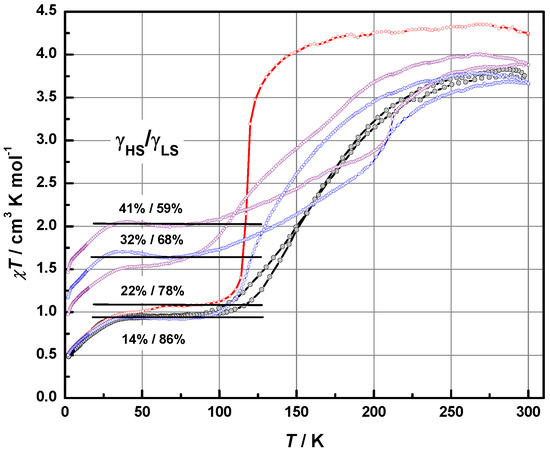
Figure 11.
Temperature evolution of χT for aged crystals 2: initial curves χ(T)↑↓ (○), γHS = 14%, first warming-cooling cycle (○), γHS = 32%, second cycle (○), γHS = 41%. Solid red line is a reference curve for fresh crystals from Figure 1.
Magnetization curves, M(H), are presented in Figure 12 and Figure 13 for 1 and 2, respectively. The data points in Figure 12 reveal a weak hysteresis with the coercive force Hc = 13 Oe and the remnant magnetization value Mr = 4 × 10−3 μB. Saturation at highest fields was not observed. However, a combination of the Brillouin function for S = 5/2 with a magnitude factor 0.9 (black line), Ms = 4.7 μB, and linear function with the factor k = 0.04 μB/kOe gave a perfect fitting. Linear contribution is conceivable in terms of AFM interaction between HS Fe(III) cations. Magnetization curves for the AFM coupled spin system, including dimers, often show Brillouin dependences and a gradual growth proportional to the field strength when |J1| << kT, T = 2 K [27]. The magnetization curve of 2 depicted in Figure 13 also reveals hysteresis, Hc = 50 Oe and Mr = 3 × 10−3 μB. The value M at 50 kOe reaches 1.14 μB. Field dependence was perfectly fitted by Brillouin function for S = 1/2 and magnitude factor 1.23 (solid line). The data points could not be fitted by a combination of Brillouin functions for S = 1/2 and S = 5/2 regardless the weight factors. A surplus contribution of 0.23 μB remains unclear. Whereas the absence of contribution from HS Fe(III) cations could be explained by stronger AFM coupling, |J2| >> kT. Brillouin shape indicates that the local moments of LS Fe(III) ions remain non-interacting.
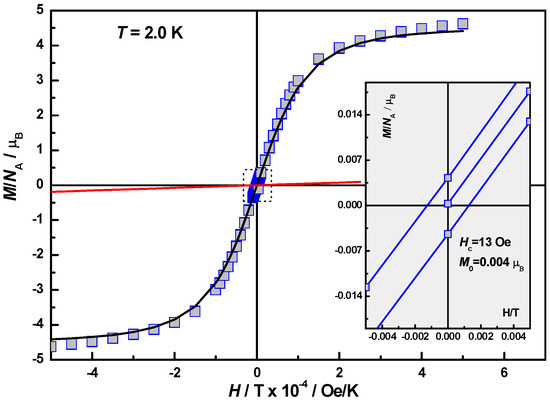
Figure 12.
Field dependence of the magnetization, M(H), in 1 at T = 2.0 K. Solid black line is a Brillouin function for S = 5/2 and magnitude factor 0.9. Solid red line fits the difference between experimental curve and Brillouin fitting. Inset: Near zero-field segment of the hysteresis loop with Hc = 13 Oe and Mr = 4 × 10−3 μB.
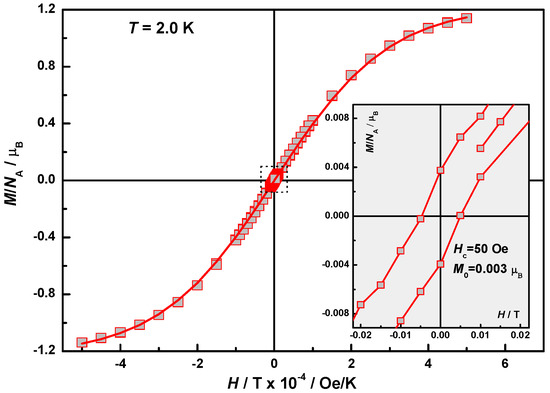
Figure 13.
Field dependence of the magnetization, M(H), in 2 at T = 2.0 K. Solid line is a Brillouin function for S = 1/2 and magnitude factor 1.23. Inset: Near zero-field segment of the hysteresis loop with Hc = 50 Oe and Mr = 3 × 10−3 μB.
A comparison of the χT evolution in 1 and 2 with their structural characteristics gives rise to several essential notions:
Results of our magnetic measurements agree well with the structural features of the compounds. Complex 1 has a rigid structure which is characterized by extensive π-interactions of both salicylidene moieties of the SCO cation with nearest neighbors, one with the cation and another with the anion. This makes changing conformation of [Fe(3-OMesal2-trien)]+ unit at the SCO impossible and explains absence of the latter in 1. Similar situation was discussed for one of the polymorphic phases of [Fe(sal2-trien)][Ni(dmit)2] which also does not show SCO at cooling [28]. In complex 2, the cation layer includes solvent molecules, π-stacking is absent and crystal packing is controlled mainly by weak hydrogen bonding allowing conformation freedom necessary for SCO. We believe this view is also consistent with the results of [28,29,30].
Although a significant loss of acetonitrile molecules was observed in the 145–200 °C range (Figure S3), the desolvation was evidently taking place at ambient conditions. These small changes significantly affect the configuration of the ligand and therefore the spin transition [25,31,32,33]. We believe, solvent vacancies in the seasoned crystals 2, as well as the defects, provoke stabilization of the HS configuration in their vicinity. Thermocycling stimulates growth of the HS fraction by promoting a diffusion of the solvent molecules out of the bulk because the sample is placed in the chamber with helium atmosphere. In several cycles the remnant HS fraction in aged crystals 2 rose from 14% to 40% (Figure 11). It is worth noting that up to 20% HS fraction was found in the original fresh samples (depending on batch). This either relates to a presence of the HS conformers [26] or is likely deals with disproportion between [Fe(3-OMesal2-trien)] and [Au(dddt)2], when the metal dithiolene complex might become a neutral radical [Au(dddt)2]•. The former was not confirmed by our structural data. Presence of neutral radical is possible since the dddt ligand can carry a various charge form [11]. The interaction of the local magnetic moment of the SCO complex with the radical in the anion counterpart was observed recently [14]. The additional spin contribution from the radicals (~7%) could hardly be distinguished on the top of the total magnetic response in SQUID measurements. However, a spin density on the dithiolene ligand may substantially enhance the superexchange coupling (J2). This assumption will be verified in forthcoming electron paramagnetic resonance (EPR) experiments.
In both compounds the χT curves revealed a characteristic inflection. Below the inflection points Ti1 = 46 K (1) and Ti2 = 55 K (2) χT continuously declined. We fitted experimental data by using julX software [34]. The AFM coupled HS Fe(III) dimers were considered as a model system. The best fit parameters for 1 were gi1 = gi2 = 2.0, Di1 = Di2 = 0, J1 = −0.18 cm−1 (0.26 K). It is worth noting that even a very small ZFS factor such as for example Di = −0.1 cm−1 strongly distort the calculated M(H) curve. We did not observe significant deviation from the Brillouin shape in Figure 12. Therefore, we took Di = 0 in our fitting. The other interesting feature of the fitting was a magnitude factor of 0.9. This might mean that only ~90% of HS Fe(III) moments was effectively enough for the description of the χT↓ curve below the inflection point. A noticeable portion of the moments Fe(III) ions “disappeared” out of the total magnetic response. This is a signature of weak AFM interactions.
The value |J1| = 0.26 K for 1 is indeed lower than 2 K, at which the magnetization curves were measured. It is not surprising then that the calculated M(H) line fits the Brillouin-like behavior in the experiment (Figure 12) and, at the same time, calculated χ(T) describes the decline of χT↓ in experiment. Figure 14 shows a low temperature part of the experimental data set of 1 and two fitting lines: fitting by a Curie-Weiss law with Θ1 = −1.7 K and C = 4.0 cm3 K/mol, and quantum calculations in the model of AFM coupled dimers with S = 5/2 and J = J1. In cases when every magnetic ion has the same number and the same kinds of interactions, the Weiss temperature can be expressed via pair exchange constants Ji,j in the usual form found in the literature:
where zij is the number of j neighbors of the ith atom. For 1 Θ and Jij = J1 match at Z ≈ 1.1, which is close to the dimer case and may speak in favor of AFM interaction between the adjacent SCO complexes linked by the π–π bonding of their aromatic groups.
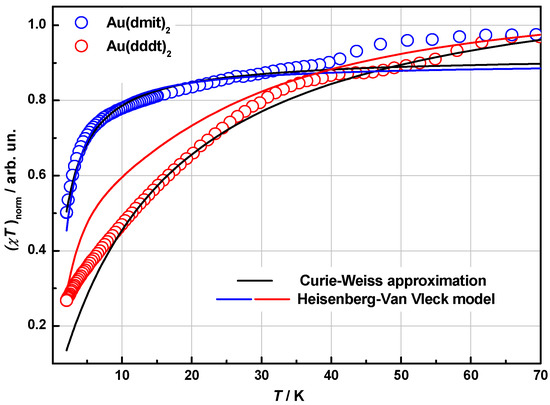
Figure 14.
Temperature dependences of normalized χT for HS fractions in 1 (○) and 2 (○). Solid lines are the best fit curves for the two models: Curie-Weiss law (black line) and Heisenberg-Van Vleck model (blue and red lines, see details in the text).
For the fresh crystals of 2 we estimated ~20% of the residual HS fraction. This contribution was extracted from the low temperature plateau (T < 70 K) of the experimental data set χT↓ on Figure 9. Then we recovered its value to the virtual 100% HS phase, attributing a low temperature decline to the AFM coupling in this HS fraction. The data after the treatment are shown in Figure 14. The best fit curve by Curie-Weiss law, Θ2 = −16 K, is shown as the solid black line. Attempts of describing it within the uniform quantum model of AFM coupled moments failed. A satisfactory agreement was reached by using a model of two linked dimers and two coupling constants, J. A solid red line shows the best fit curve for |J23| = 2.46 K and |J12| = |J34| = 0.43 K (gi = 2.0, Di = 0). Although there are no structural dimers in 2, the magnetic dimer is a reasonable approximation of the short-range coupling. As soon as we do not have an idea about the morphology of the HS fraction this model might seem to a certain extent speculative. Nevertheless, it brings an understanding that the much stronger exchange interaction came to the stage. Therefore, in 2 additionally to a routine weak coupling between the adjacent iron complexes there comes a stronger coupling which apparently involves the gold dithiolene complexes as well. In other words, structural defects and, possibly, solvent vacancies may serve not only as a source of the residual HS fraction, but also as a promoter of stronger exchange interactions between respective HS complexes. If the defects cause a charge disproportionation, then the appearance of neutral radicals [Au(dddt)2]• would facilitate stronger exchange coupling via the anion sublattice. This also suggests an additional spin contribution from Au(dddt)2, ~10% of S = 1/2 (χT ≈ 0.04 cm3 K/mol). Evidently, the inflections points Ti1 = 46 K and Ti2 = 55 K also reflect changes in metal dithiolene subsystem. A comparison of two above approaches by using (1) gives:
which matches at Z = 0.9. This means that one pair of stronger coupled S = 5/2 moments (J23) and two linked pairs of weaker coupled ones (J12, J34) is enough to describe the decrease of χT below the SCO transition in 2. It is worth noting that anion driven modulation [11,33,35] may modify the intermolecular interactions but it cannot facilitate the exchange coupling via a network of hydrogen bonds.
Of course, a model of two strongly coupled dimers plays a merely symbolic role linking together a weak coupling of the same nature as in 1, and stronger coupling that is, in our understanding, a quantitative characteristic of the involvement of the electronic states of dithiolene into superexchange interactions between HS Fe(III) magnetic moments.
3. Conclusions
We have found that a structure organization of 1 with strong intermolecular π-interactions between aromatic rings of [Fe(III)(3-OMesal2-trien)]+ and molecular environment suppresses SCO. Such π-bonding is absent in 2 and the reversible SCO transition was observed at Tsco = 118 K. The conformational changes in [Fe(III)(3-OMesal2-trien)]+ at SCO were analyzed and it was shown at first time that reorientation of the central ethylene group of the trien occurs at the transition: it is near perpendicular to two side ethylene groups of the trien in the HS state and becomes near parallel to them in the LS state. This can be used as a very fast and visible indicator of the spin state in saltrien complexes [26]. It was also found that aging and subsequent thermocycling of the complex 2 led to a degradation of the spin-crossover transition. As a result, the residual HS fraction in our experiments increased to 41%, which was apparently associated with the release of acetonitrile out of the crystal bulk.
Total magnetic response of 1 indicates that 100% of magnetic moments in the system are the local magnetic moments of HS Fe(III) ions, S = 5/2. These moments form the AFM dimers with exchange constant J1 = −0.18 cm−1, which conceivably arise due to the strong π–π bonding between terminal aromatic groups of adjacent iron complexes. Though there is no π–π bonding in crystals 2, they demonstrate surprisingly stronger AFM coupling, J23 = −1.69 cm−1, within the residual HS fraction. A satisfactory agreement between experimental χT vs. T plot and model calculations was reached in the framework of two exchange coupled dimers, |J12| = |J34| = 0.29 cm−1, linked via a stronger superexchange bridge |J23| >> |J12|, |J34|. We assume that such a bridge suggests involvement of the molecular orbitals of the [Au(dddt)2] complexes, so that the distortions in the dithiolene sublattice not only stabilize the high-spin state of the iron complexes, but also facilitate the exchange interaction between them. If so, EPR experiments would shed the light on that. Such work is in progress.
Supplementary Materials
The following are available online at http://www.mdpi.com/2073-4352/8/10/382/s1, Figure S1: Thermogravimetric analysis of [Fe(3-OMe-sal2-trien)][Au(dmit)2] (1), Figure S2: Powder X-ray diffractogram for [Fe(3-OMe-sal2-trien)][Au(dmit)2]: experimental (line) and simulation (dots), Figure S3: The thermogravimetric analysis of [Fe(3-OMe-sal2-trien)][Au(dddt)2]·CH3CN (2), Figure S4: Powder X-ray diffractogram for [Fe(3-OMe-sal2-trien)][Au(dddt)2]·CH3CN: experimental (line) and simulation (dots), Figure S5: Single crystals of [Fe(3-OMesal2-trien)][Au(dmit)2] (left) and [Fe(3-OMesal2-trien)][Au(dddt)2] (right), Figure S6: Polycrystalline sample of [Fe(3-OMe-Sal2-trien)][Au(dddt)2] CH3CN.
Author Contributions
N.G.S., M.A.B., E.B.Y.—synthesis, chem. analyses; L.V.Z., S.V.S.—structure resolution; Y.N.S., D.V.S., E.L., A.A.K.—magnetic part.
Acknowledgments
This work was done on the topic of the State task (No. 0089-2014-0026) with using of the Computational and Analytical Center for Collective Use of the IPCP RAS tool base and was partially supported by the Program of Russian Academy of Sciences topic “Spin” №AAAA-A18-118020290104-2. The authors would like to thank L.I. Buravov for conductivity measurements.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Gutlich, P.; Goodwin, A.H. Spin Crossover in Transition Metal Compounds III; Springerlink: Berlin, Germany, 2004; Volume 235, p. 1. [Google Scholar]
- Brooker, S. Spin-crossover with thermal hysteresis: Practicalities and lessons learnt. Chem. Soc. Rev. 2015, 44, 2880–2892. [Google Scholar] [CrossRef] [PubMed]
- Gutlich, P. Spin Crossover—Quo Vadis? Eur. J. Inorg. Chem. 2013, 5–6, 581–591. [Google Scholar] [CrossRef]
- Okai, M.; Takahashi, K.; Sakurai, T.; Ohta, H.; Yamamoto, T.; Einagad, Y. Novel Fe(II) spin crossover complexes involving a chalcogen-bond and π-stacking interactions with a paramagnetic and nonmagnetic M(dmit)2 anion (M = Ni, Au; dmit = 4,5-dithiolato-1,3-dithiole-2-thione). J. Mater. Chem. C 2015, 3, 7858–7864. [Google Scholar] [CrossRef]
- Bousseksou, A.; Molnár, G.; Salmon, L.; Nicolazzi, W. Molecular spin crossover phenomenon: Recent achievements and prospects. Chem. Soc. Rev. 2011, 40, 3313–3335. [Google Scholar] [CrossRef] [PubMed]
- Gentili, D.; Demitri, N.; Schäfer, B.; Liscio, F.; Bergenti, I.; Ruani, G.; Ruben, M.; Cavallini, M. Multi-modal sensing in spin crossover compounds. J. Mater. Chem. C 2015, 3, 7836–7844. [Google Scholar] [CrossRef]
- Sato, O.; Li, Z.-Y.; Yao, Z.-S.; Kang, S.; Kanegawa, S. Multifunctional materials combining spin-crossover with conductivity and magnetic ordering. In Spin-Crossover Materials: Properties and Applications; Halcrow, M., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 303–319. [Google Scholar]
- Valade, L.; Malfant, I.; Faulmann, C. Toward bifunctional materials with conducting, photochromic, and spin crossover properties. In Multifunctional Molecular Materials; Ouahab, L., Ed.; Pan Stanford Publishing: Singapore, 2013; p. 149. [Google Scholar]
- Huang, J.; Xie, R.; Wang, W.; Li, Q.; Yang, J. Coherent transport through spin-crossover magnet Fe2 complexes. Nanoscale 2016, 8, 609–616. [Google Scholar] [CrossRef] [PubMed]
- Kato, R. Conducting metal dithiolene complexes: Structural and electronic properties. Chem. Rev. 2004, 104, 5319–5346. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.H.; Fox, S.B.; Yagubskii, E.B.; Kushch, L.A.; Kotov, A.I.; Whangbo, M.-H. Direct observation of the electron-donating property of the 5,6-dihydro-1,4-dithiin-2,3-dithiolate (dddt) ligands in square planar M(dddt)2 complexes (M = Ni, Pd, Pt, and Au). J. Am. Chem. Soc. 1997, 119, 7601–7602. [Google Scholar] [CrossRef]
- Yagubski, E.B. Molecular conductors based on M(dddt)2 bisdithiolene cation complexes. J. Solid State Chem. 2002, 168, 464–469. [Google Scholar] [CrossRef]
- Fujiyama, S.; Kato, R. Algebraic charge dynamics of the quantum spin liquid β-EtMe3Sb[Pd(dmit)2]2. Phys. Rev. B 2018, 97, 035131. [Google Scholar] [CrossRef]
- Shvachko, Y.N.; Starichenko, D.V.; Korolyov, A.V.; Kotov, A.I.; Buravov, L.I.; Zverev, V.N.; Simonov, S.V.; Zorina, L.V.; Yagubskii, E.B. The highly conducting spin-crossover compound combining Fe(III) cation complex with TCNQ in a fractional reduction state. Synthesis, structure, electric and magnetic properties. Magnetochemistry 2017, 3, 9. [Google Scholar] [CrossRef]
- Shvachko, Y.N.; Starichenko, D.V.; Korolyov, A.V.; Yagubskii, E.B.; Kotov, A.I.; Buravov, L.I.; Lyssenko, K.A.; Zverev, V.N.; Simonov, S.V.; Zorina, L.V.; et al. The conducting spin-crossover compound combining Fe(II) cation complex with TCNQ in a fractional reduction state. Inorg. Chem. 2016, 55, 9121–9130. [Google Scholar] [CrossRef] [PubMed]
- Phan, H.; Benjamin, S.M.; Steven, E.; Brooks, J.S.; Shatruk, M. Photomagnetic response in highly conductive iron(II) spin-crossover complexes with TCNQ radicals. Angew. Chem. Int. Ed. 2015, 127, 837–841. [Google Scholar] [CrossRef]
- Takahashi, K.; Cui, H.-B.; Okano, Y.; Kobayashi, H.; Einaga, Y.; Sato, O. Electrical conductivity modulation coupled to a high-spin–low-spin conversion in the molecular system [FeIII(qsal)2][Ni(dmit)2]3 CH3CN H2O. Inorg. Chem. 2006, 45, 5739–5741. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Cui, H.-B.; Okano, Y.; Kobayashi, H.; Mori, H.; Tajima, H.; Einaga, Y.; Sato, O. Evidence of the chemical uniaxial strain effect on electrical conductivity in the spin-crossover conducting molecular system: [FeIII(qnal)2][Pd(dmit)2]5 acetone. J. Amer. Chem. Soc. 2008, 130, 6688–6689. [Google Scholar] [CrossRef] [PubMed]
- Dorbes, S.; Valade, L.; Real, J.A.; Faulmann, C. [Fe(sal2-trien)][Ni(dmit)2]: Towards switchable spin crossover molecular conductors. Chem. Commun. 2005, 1, 69–71. [Google Scholar] [CrossRef] [PubMed]
- Coronado, E.; Gimenez-Lopez, M.C.; Gimenez-Saiz, C.; Romero, F.M. Spin crossover complexes as building units of hydrogen-bonded nanoporous structures. CrystEngComm 2009, 11, 2198–2203. [Google Scholar] [CrossRef]
- Steimecke, G.; Sieler, H.-J.; Kirmse, R.; Houer, E. 1.3-dithiol-2-thion-4.5 ditholat aus schwefelkohlenstoff und alkalimetall. Phosphorus Sulfur Silicon Relat. Elem. 1979, 7, 49–55. [Google Scholar] [CrossRef]
- Kirmse, R.; Stach, J.; Dietzsch, W.; Steimecke, G.; Hoyer, E. Single-crystal EPR studies on nickel(III), palladium(III), and platinum(III) dithiolene chelates containing the ligands isotrithionedithiolate, o-xylenedithiolate, and maleonitriledithiolate. Inorg. Chem. 1980, 19, 2679–2685. [Google Scholar] [CrossRef]
- Nweedle, M.F.; Wilson, L.J. Variable spin iron(III) chelates with hexadentate ligands derived from triethylenetetramine and various salicylaldehydes. Synthesis, characterization, and solution state studies of a new 2T-6A spin equilibrium system. J. Am. Chem. Soc. 1976, 98, 4824–4834. [Google Scholar]
- Halcrow, M.A. Structure: Functional relationship in molecular spin-crossover complexes. Chem. Soc. Rev. 2011, 40, 4119–4142. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, R.; Barrett, S.A.; Kilner, C.A.; Halcrow, M.A. The influence of ligand conformation on the thermal spin transitions in iron(III) saltrien complexes. Dalton Trans. 2008, 3159–3168. [Google Scholar] [CrossRef] [PubMed]
- Blagov, M.A.; Krapivin, V.B.; Simonov, S.V.; Spitsyna, N.G. Insights into the influence of ethylene groups orientation on iron (III) spin state in the spin crossover complex [FeIII(Sal2-trien)]+. Dalton Trans. 2018. submitted. [Google Scholar]
- Benelli, C.; Gatteschi, D. Introduction to Molecular Magnetism: From Transition Metals to Lanthanides; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany, 2015. [Google Scholar]
- Faulmann, C.; Szilágyi, P.; Jacob, K.; Shahene, J.; Valade, L. Polymorphism and its effects on the magnetic behaviour of the [Fe(sal2-trien)][Ni(dmit)2] spin-crossover complex. New J. Chem. 2009, 33, 1268–1276. [Google Scholar] [CrossRef]
- Faulmann, C.; Dorbes, S.; Real, J.; Valade, L. Electrical conductivity and spin crossover: Towards the first achievement with a metal bis dithiolene complex. J. Low Temp. Phys. 2006, 142, 265–270. [Google Scholar]
- Faulmann, C.; Jacob, K.; Dorbes, S.; Lampert, S.; Malfant, I.; Doublet, M.-L.; Valade, L.; Real, J. Electrical conductivity and spin crossover: A new achievement with a metal bis dithiolene complex. Inorg. Chem. 2007, 46, 8548–8559. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Liu, M.-J.; Liu, C.-M.; Kou, H.-Z. Iron(III) complexes of 2-methyl-6-(pyrimidin-2-yl-hydrazonomethyl)-phenol as spin-crossover molecular materials. Dalton Trans. 2017, 46, 16562–16569. [Google Scholar] [CrossRef] [PubMed]
- Milin, E.; Benaicha, B.; El Hajj, F.; Patinec, V.; Triki, S.; Marchivie, M.; Gómez-García, C.J.; Pillet, S. Magnetic bistability in macrocycle-based FeII spin-crossover complexes: Counter ion and solvent effects. Eur. J. Inorg. Chem. 2016, 34, 5305–5314. [Google Scholar] [CrossRef]
- Vieira, B.J.C.; Dias, J.C.; Santos, I.C.; Pereira, L.C.J.; Vasco, D.G.; Waerenborgh, J.C. Thermal hysteresis in a spin-crossover FeIII quinolylsalicylaldimine complex, FeIII(5-Br-qsal)2Ni(dmit)2·solv: Solvent effects. Inorg. Chem. 2014, 54, 1354–1362. [Google Scholar] [CrossRef] [PubMed]
- Bill, E. JULX 1.4.1 Simulation of Molecular Magnetic Data Software; Matrix Diagonalization Was Realized with the Routine ‘zheev’ from the LAPACK Numerical Package; Max-Planck Institute for Bioinorganic Chemistry: Mulheim/Ruhr, Germany, May 2008. [Google Scholar]
- Nemec, I.; Herchel, R.; Ruben, I.M.; Linert, W. Anion driven modulation of magnetic intermolecular interactions and spin crossover properties in an isomorphous series of mononuclear iron(III) complexes with a hexadentate Schiff baseligand. CrystEngComm 2012, 14, 7015–7024. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).