Na4Yb(CO3)3F: A New UV Nonlinear Optical Material with a Large Second Harmonic Generation Response
Abstract
1. Introduction
2. Materials and Methods
2.1. Reagents
2.2. Syntheses of Na4Yb(CO3)3F
2.3. Single Crystal X-ray Diffraction
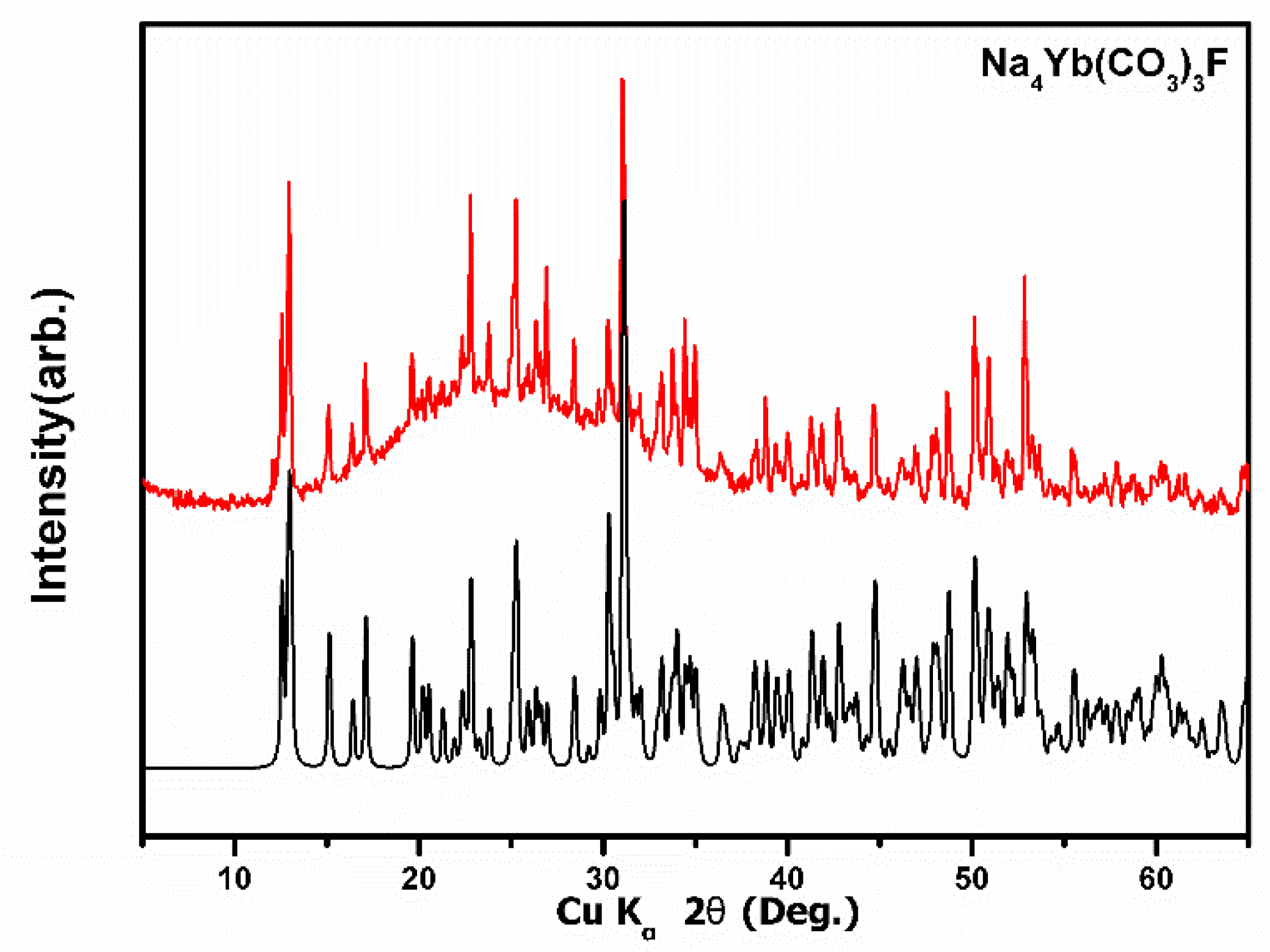
2.4. Powder X-ray Diffraction
2.5. Thermal Analysis
2.6. UV-Vis Diffuse Reflectance Spectroscopy
2.7. Second-Harmonic Generation
2.8. Computational Methods
3. Results and Discussion
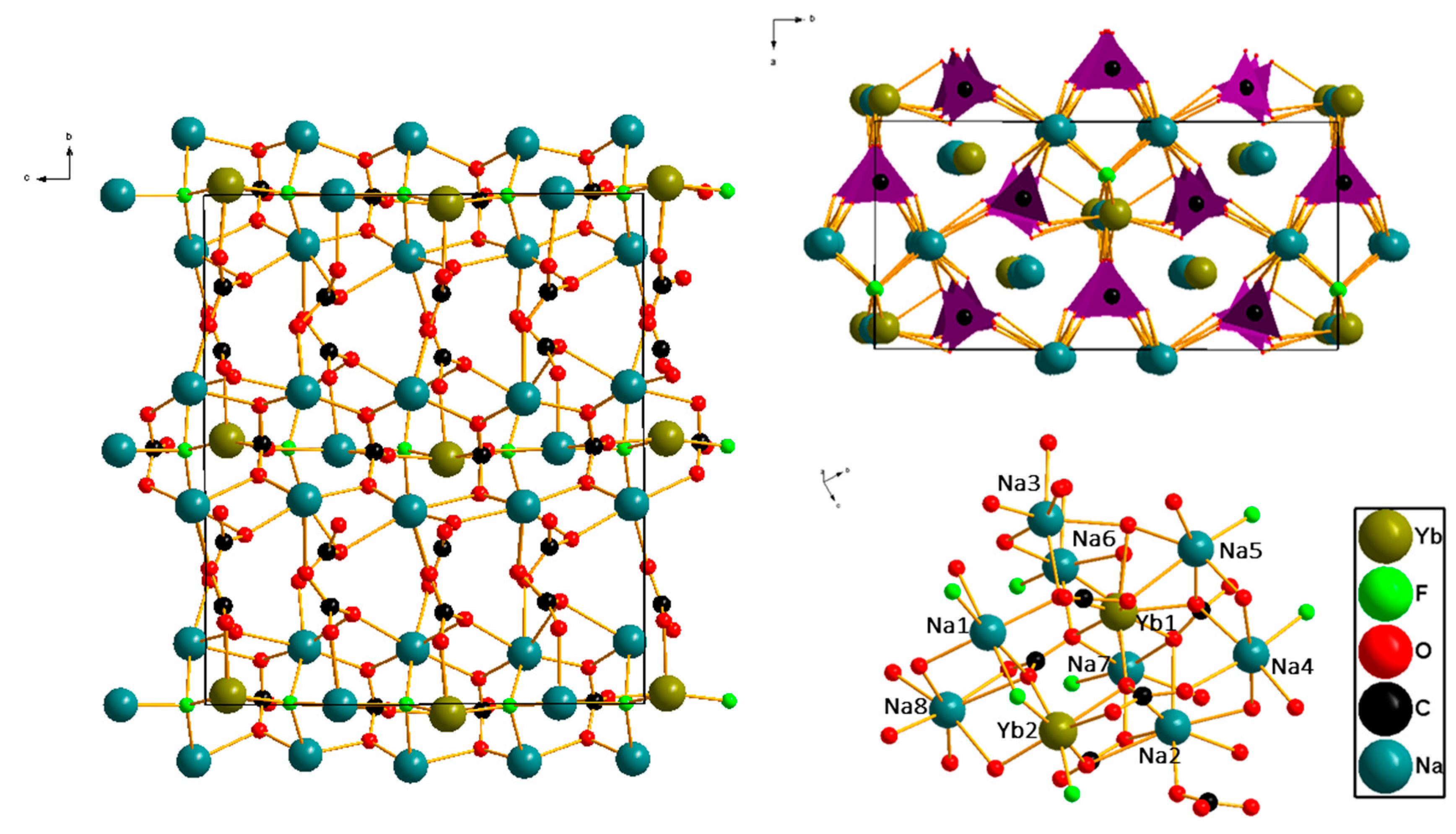
3.1. Crystal Structure
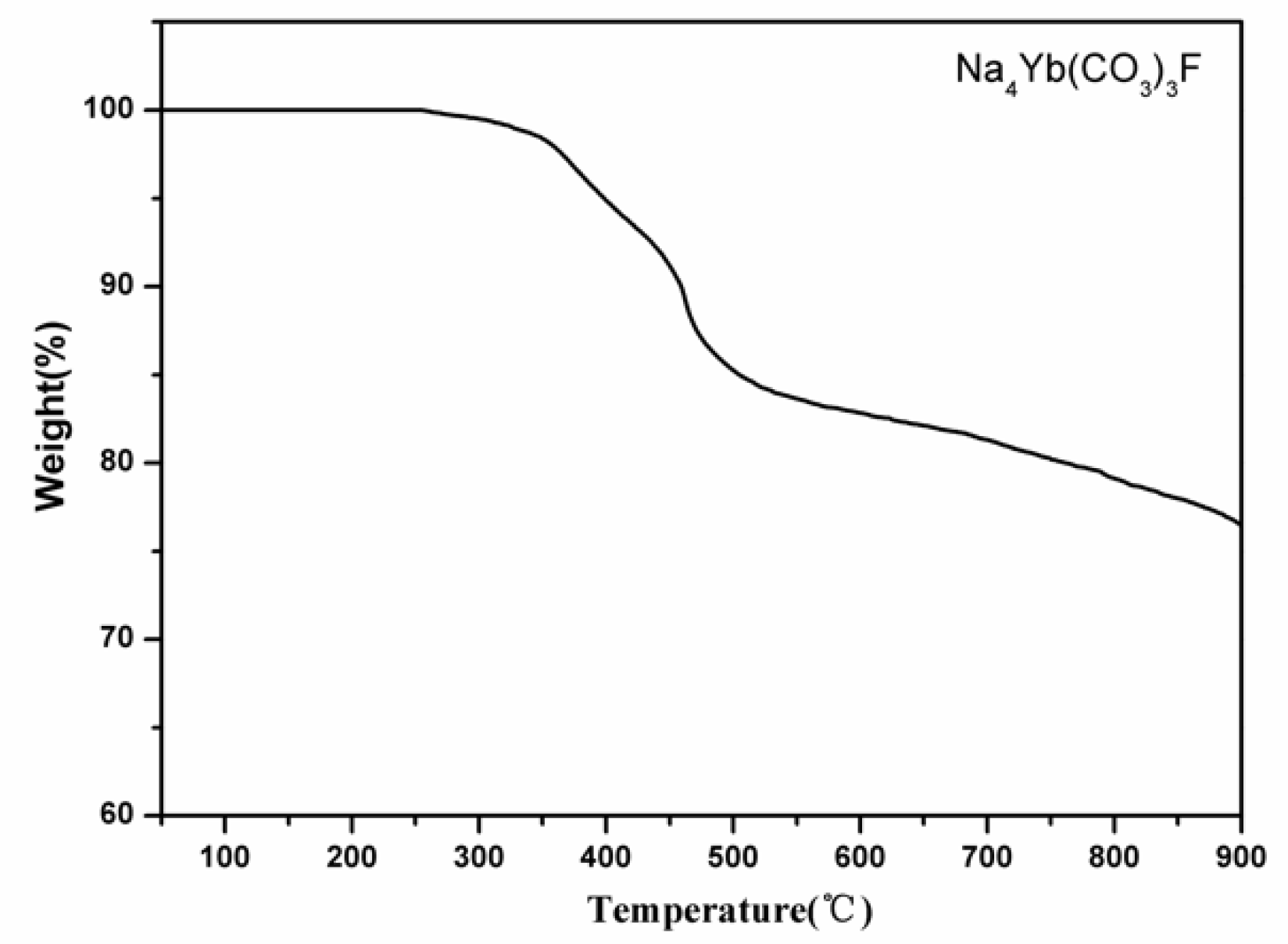
3.2. Thermal Analysis
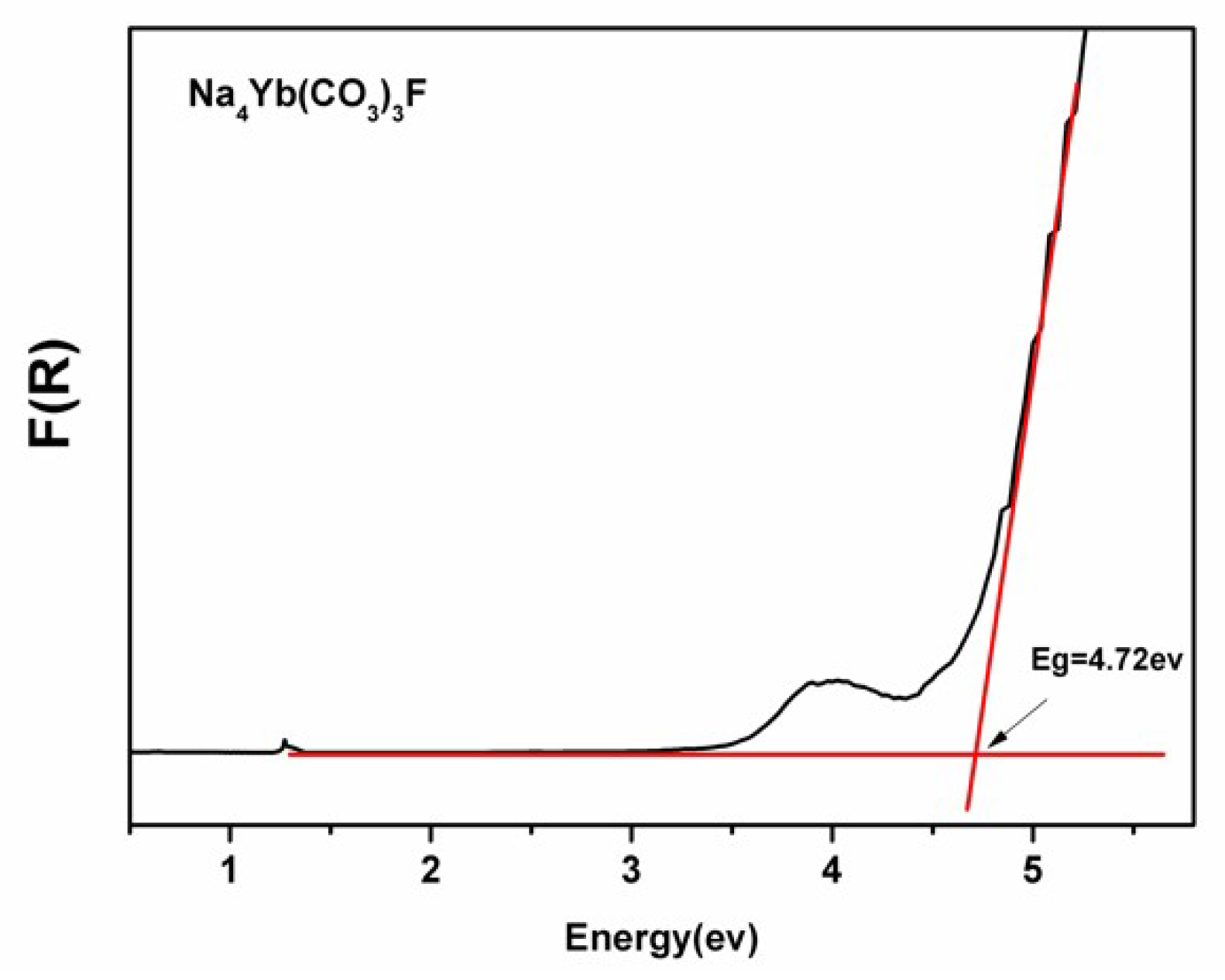
3.3. Diffuse-Reflectance Spectroscopy
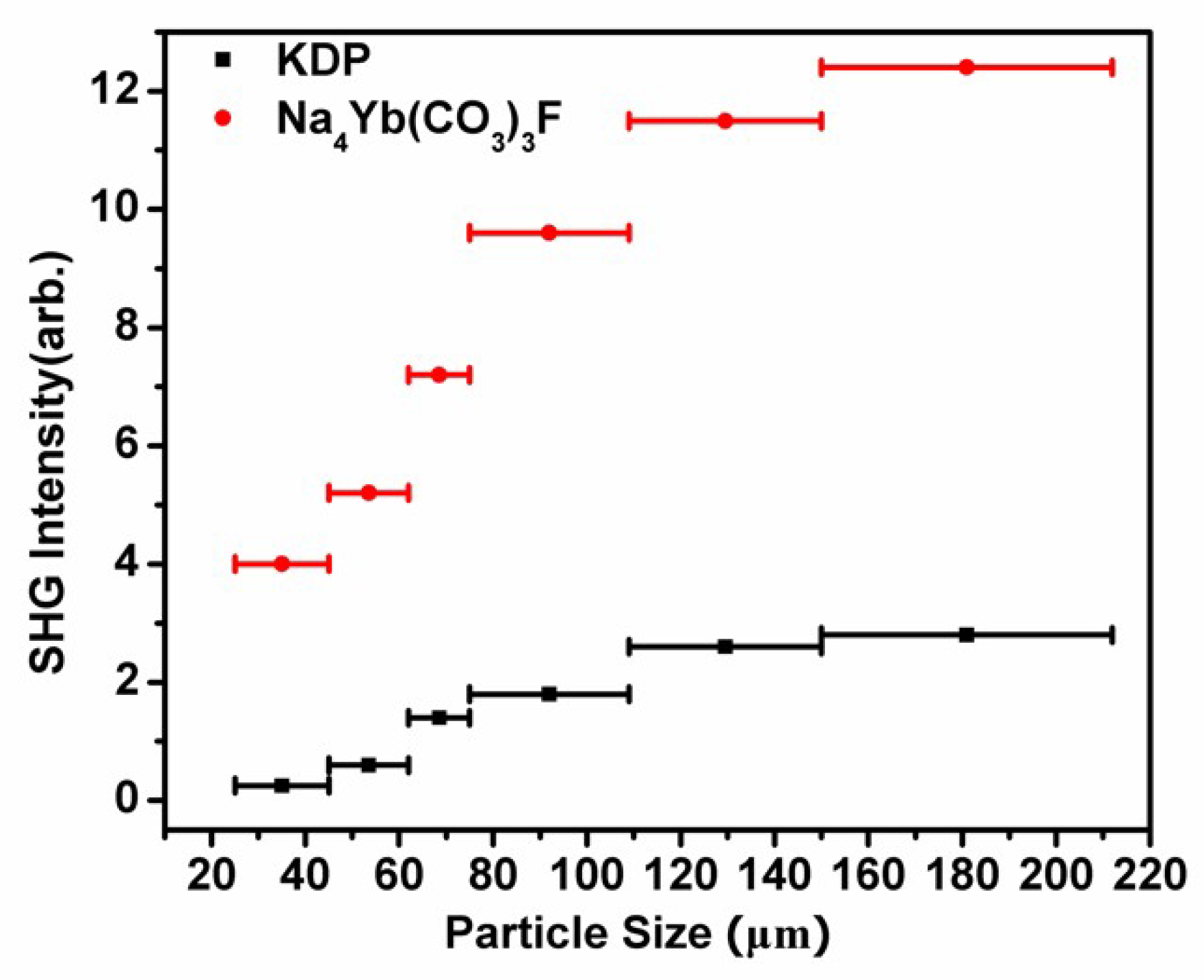
3.4. NLO Properties
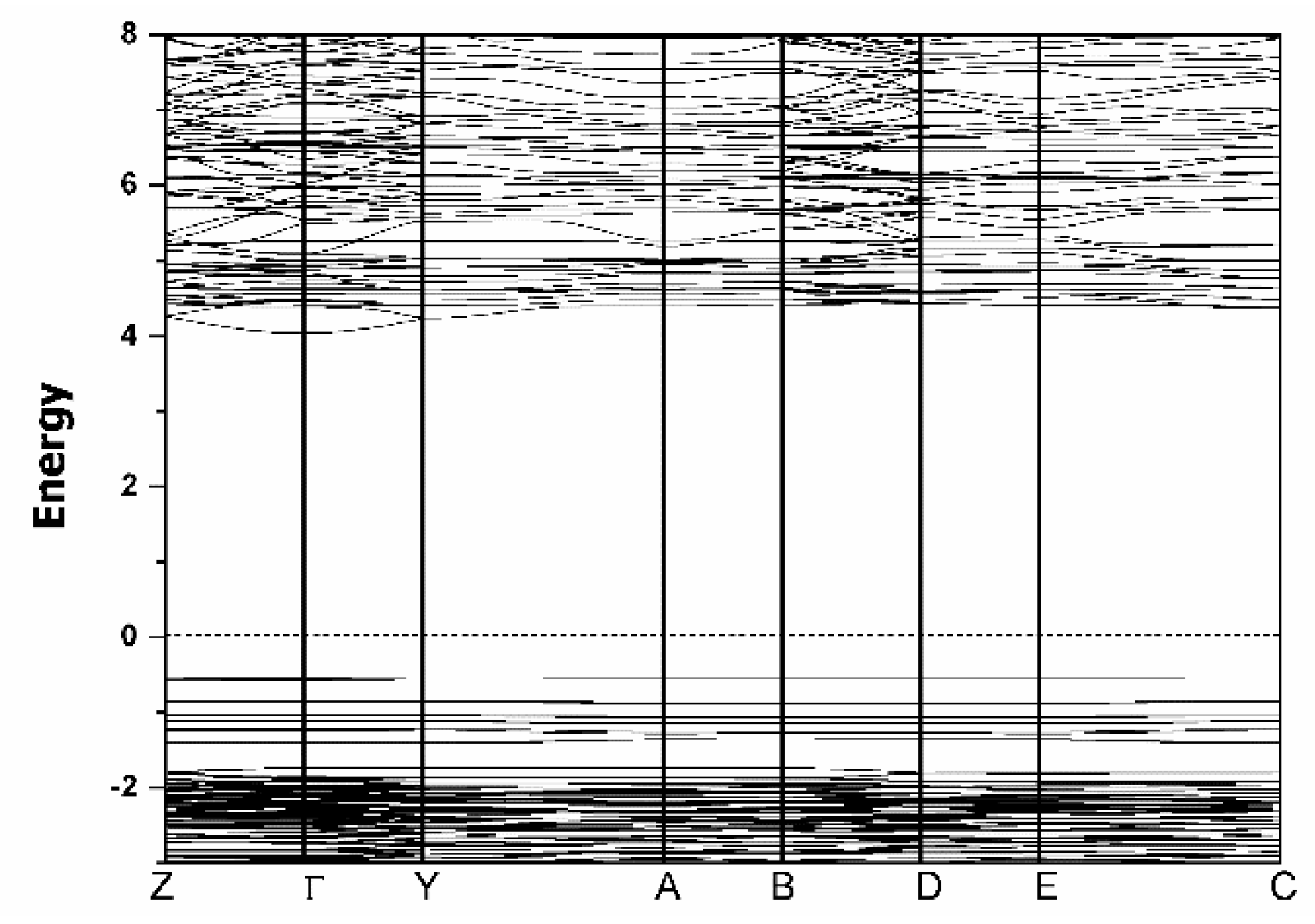
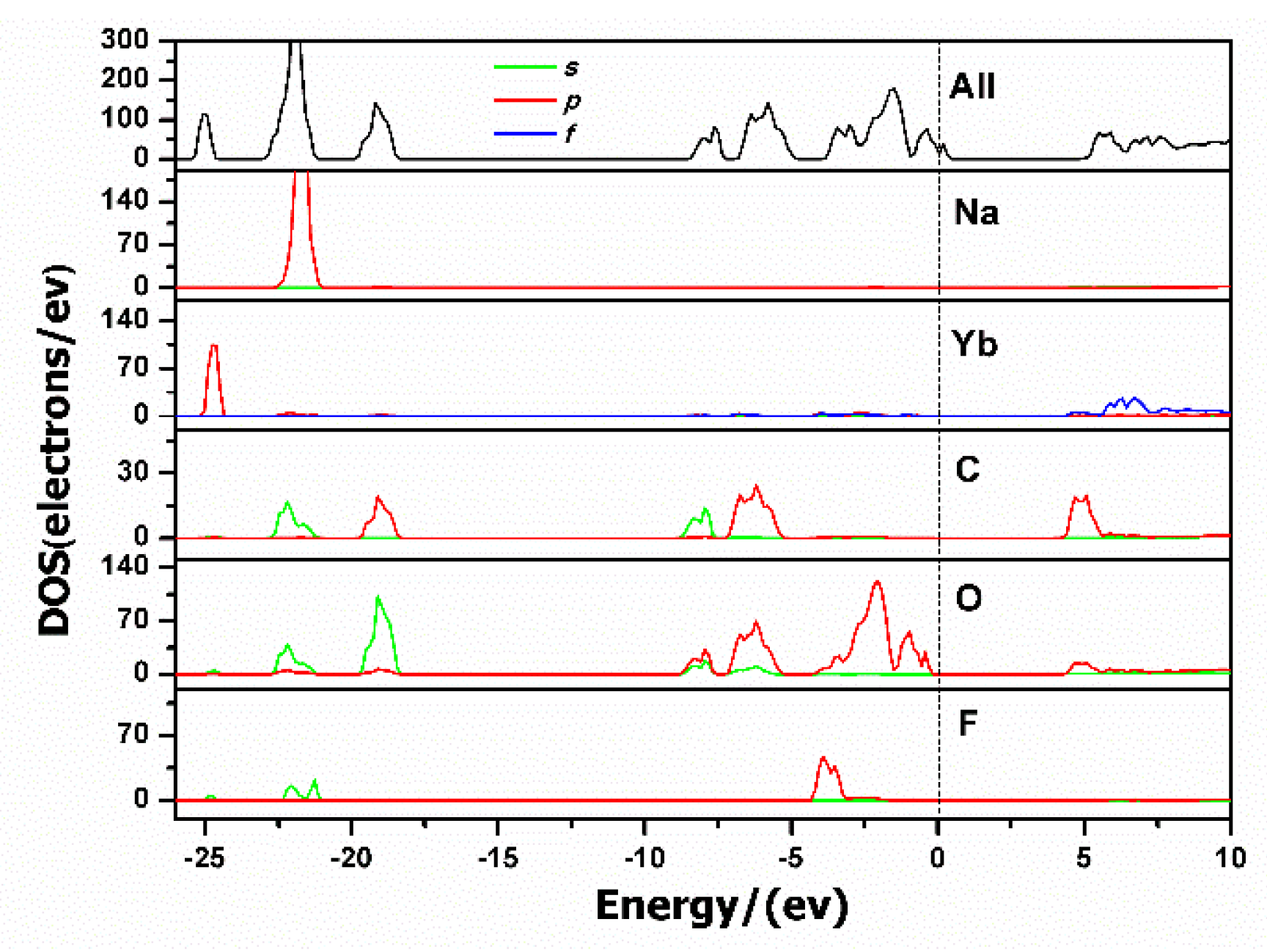
3.5. Theoretical Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Luo, M.; Song, Y.; Liang, F.; Ye, N.; Lin, Z. Pb2BO3Br: A novel nonlinear optical lead borate bromine with a kbbf-type structure exhibiting strong nonlinear optical response. Inorg. Chem. Front. 2018, 5, 916–921. [Google Scholar] [CrossRef]
- Zou, G.; Lin, C.; Jo, H.; Nam, G.; You, T.-S.; Ok, K.M. Pb2BO3Cl: A tailor-made polar lead borate chloride with very strong second harmonic generation. Angew. Chem. Int. Ed. 2016, 55, 12078–12082. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.T.; Koocher, N.Z.; Rondinelli, J.M.; Halasyamani, P.S. Beryllium-free β-Rb2Al2B2O7 as a possible deep-ultraviolet nonlinear optical material replacement for KBe2BO3F2. Angew. Chem. Int. Ed. 2017, 56, 2969–2973. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Luo, M.; Liang, F.; Lin, C.; Ye, N.; Yan, G.; Lin, Z. Experimental and ab initio studies of Cd5(BO3)3Cl: The first cadmium borate chlorine nlo material with isolated BO3 groups. Dalton Trans. 2017, 46, 15228–15234. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Kang, L.; Shen, Y.; Wang, X.; Asghar, M.A.; Lin, Z.; Xu, Y.; Zeng, S.; Hong, M.; Luo, J. Designing a beryllium-free deep-ultraviolet nonlinear optical material without a structural instability problem. J. Am. Chem. Soc. 2016, 138, 2961–2964. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Wang, S.C.; Ye, N.; Liang, F.; Lin, Z.S.; Luo, M.; Poeppelmeier, K.R. A deep-ultraviolet nonlinear optical crystal: A strontium beryllium borate fluoride with planar Be(O/F)3 groups. Chem. Mater. 2016, 28, 4563–4571. [Google Scholar] [CrossRef]
- Guo, S.; Jiang, X.; Liu, L.; Xia, M.; Fang, Z.; Wang, X.; Lin, Z.; Chen, C. BaBe2BO3F3: A kbbf-type deep-ultraviolet nonlinear optical material with reinforced [Be2BO3F2]∞ layers and short phase-matching wavelength. Chem. Mater. 2016, 28, 8871–8875. [Google Scholar] [CrossRef]
- Young, J.; Lalkiya, P.; Rondinelli, J.M. Design of noncentrosymmetric perovskites from centric and acentric basic building units. J. Mater. Chem. C 2016, 4, 4016–4027. [Google Scholar] [CrossRef]
- Cammarata, A.; Zhang, W.; Halasyamani, P.S.; Rondinelli, J.M. Microscopic origins of optical second harmonic generation in noncentrosymmetric–nonpolar materials. Chem. Mater. 2014, 26, 5773–5781. [Google Scholar] [CrossRef]
- Cammarata, A.; Rondinelli, J.M. Contributions of correlated acentric atomic displacements to the nonlinear second harmonic generation and response. ACS Photonics 2014, 1, 96–100. [Google Scholar] [CrossRef]
- Chen, C.; Wu, Y.; Li, R. The anionic group theory of the non-linear optical effect and its applications in the development of new high-quality nlo crystals in the borate series. Int. Rev. Phys. Chem. 1989, 8, 65–91. [Google Scholar] [CrossRef]
- Chen, C.T.; Liu, G.Z. Recent advances in nonlinear optical and electro-optical materials. Annu. Rev. Mater. Res. 1986, 16, 203–243. [Google Scholar] [CrossRef]
- Mei, L.; Huang, X.; Wang, Y.; Wu, Q.; Wu, B.; Chen, C. Crystal-structure of KBe2BO3F2. Z. Kristallogr. 1995, 210, 93–95. [Google Scholar] [CrossRef]
- Hu, Z.G.; Yoshimura, M.; Muramatsu, K.; Mori, Y.; Sasaki, T. A new nonlinear optical crystal-BaAlBO3F2 (BABF). Jpn. J. Appl. Phys. 2002, 41, L1131. [Google Scholar] [CrossRef]
- Chen, C.T.; Wang, Y.B.; Wu, B.C.; Wu, K.C.; Zeng, W.L.; Yu, L.H. Design and synthesis of an ultraviolet-transparent nonlinear-optical crystal Sr2Be2B2O7. Nature 1995, 373, 322–324. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Zhang, B.; Zhang, F.; Yang, Z.; Pan, S. CsB4O6F: A congruent-melting deep-ultraviolet nonlinear optical material by combining superior functional units. Angew. Chem. Int. Ed. 2017, 129, 14307–14311. [Google Scholar] [CrossRef]
- Shi, G.; Wang, Y.; Zhang, F.; Zhang, B.; Yang, Z.; Hou, X.; Pan, S.; Poeppelmeier, K.R. Finding the next deep-ultraviolet nonlinear optical material: NH4B4O6F. J. Am. Chem. Soc. 2017, 139, 10645–10648. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, Y.; Zhang, B.; Yang, Z.; Pan, S. Polar fluorooxoborate, nab4o6f: A promising material for ionic conduction and nonlinear optics. Angew. Chem. Int. Ed. 2018, 130, 6687–6691. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, B.; Yang, Z.; Pan, S. Cation-tuned synthesis of fluorooxoborates: Towards optimal deep-ultraviolet nonlinear optical materials. Angew. Chem. Int. Ed. 2018, 57, 2150–2154. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Liang, F.; Song, Y.; Zhao, D.; Xu, F.; Ye, N.; Lin, Z. M2B10O14F6 (M = Ca, Sr): Two noncentrosymmetric alkaline earth fluorooxoborates as promising next-generation deep-ultraviolet nonlinear optical materials. J. Am. Chem. Soc. 2018, 140, 3884–3887. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Liang, F.; Song, Y.; Zhao, D.; Ye, N.; Lin, Z. Rational design of the first lead/tin fluorooxoborates MB2O3F2 (M = Pb, Sn), containing flexible two-dimensional [B6O12F6]∞ single layers with widely divergent second harmonic generation effects. J. Am. Chem. Soc. 2018, 140, 6814–6817. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Lin, C.; Zou, G.; Ye, N.; Cheng, W. Sodium–rare earth carbonates with shorite structure and large second harmonic generation response. CrystEngComm 2014, 16, 4414–4421. [Google Scholar] [CrossRef]
- Zou, G.; Ma, Z.; Wu, K.; Ye, N. Cadmium-rare earth oxyborates Cd4ReO(BO3)3 (Re = Y, Gd, Lu): Congruently melting compounds with large shg responses. J. Mater. Chem. 2012, 22, 19911–19918. [Google Scholar] [CrossRef]
- Aka, G.; Kahn-Harari, A.; Mougel, F.; Vivien, D.; Salin, F.; Coquelin, P.; Colin, P.; Pelenc, D.; Damelet, J.P. Linear and nonlinear-optical properties of a new gadolinium calcium oxo-borate crystal, Ca4GdO(BO3)3. J. Opt. Soc. Am. B 1997, 14, 2238–2247. [Google Scholar] [CrossRef]
- Mercier, N.; Leblanc, M.; Durand, J. New frequency doubling compounds K4Ln2(CO3)3F4 (Ln = Pr, Nd, Sm, Gd, Eu); crystal structure and Characterization. Eur. J. Solid State Inorg. Chem. 1997, 34, 241–249. [Google Scholar] [CrossRef]
- Zou, G.; Ye, N.; Huang, L.; Lin, X. Alkaline-alkaline earth fluoride carbonate crystals ABCO3F (A = K, Rb, Cs; b = Ca, Sr, Ba) as nonlinear optical materials. J. Am. Chem. Soc. 2011, 133, 20001–20007. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Ye, N.; Zou, G.; Lin, C.; Cheng, W. Na8Lu2(CO3)6F2 and Na3Lu(CO3)2F2: Rare earth fluoride carbonates as deep-uv nonlinear optical materials. Chem. Mater. 2013, 25, 3147–3153. [Google Scholar] [CrossRef]
- Tran, T.T.; Halasyamani, P.S. New fluoride carbonates: Centrosymmetric KPb2(CO3)2F and noncentrosymmetric K2.70Pb5.15(CO3)5F3. Inorg. Chem. 2013, 52, 2466–2473. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.T.; Halasyamani, P.S.; Rondinelli, J.M. Role of acentric displacements on the crystal structure and second- harmonic generating properties of RbPbCO3F and CsPbCO3F. Inorg. Chem. 2014, 53, 6241–6251. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Halasyamani, P.S. Crystal growth and optical properties of a UV nonlinear optical material KSrCO3F. Crystengcomm 2017, 19, 4742–4748. [Google Scholar] [CrossRef]
- Sheldrick, G. A short history of shelx. Acta Crystallogr. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Spek, A.L. Single-crystal structure validation with the program platon. J. Appl. Crystallogr. 2003, 36, 7. [Google Scholar] [CrossRef]
- Kubelka, P.; Munk, F. Ein beitrag zur optik der farbanstriche. Z. Tech. Phys. 1931, 12, 593–601. [Google Scholar]
- Tauc, J. Absorption edge and internal electric fields in amorphous semiconductors. Mater. Res. Bull. 1970, 5, 721–729. [Google Scholar] [CrossRef]
- Kurtz, S.K.; Perry, T.T. Powder technique for the evaluation of nonlinear optical materials. J. Appl. Phys. 1968, 39, 3798–3813. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. Cryst. Mater. 2005, 220, 567. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Ghahramani, E.; Moss, D.J.; Sipe, J.E. Full-band-structure calculation of second-harmonic generation in odd-period strained (si)n(ge)n/si superlattices. Phys. Rev. B 1991, 43, 8990–9002. [Google Scholar] [CrossRef]
- Ye, N.; Chen, Q.X.; Wu, B.C.; Chen, C.T. Searching for new nonlinear optical materials on the basis of the anionic group theory. J. Appl. Phys. 1998, 84, 555. [Google Scholar] [CrossRef]

| Formula | Na4Yb(CO3)3F |
|---|---|
| Formula Mass (amu) | 464.03 |
| Crystal System | Monoclinic |
| Space Group | Cc |
| a (Å) | 8.018(3) |
| b (Å) | 15.929(5) |
| c (Å) | 13.950(5) |
| β (°) | 101.425(6) |
| V (Å3) | 1746.4(11) |
| Z | 8 |
| ρ (calcd) (g/cm3) | 3.530 |
| Temperature (K) | 293(2) |
| λ (Å) | 0.71073 |
| F (000) | 1647 |
| Μ (mm−1) | 11.602 |
| R/wR (I > 2σ (I)) | 0.0171/0.0347 |
| R/wR (all data) | 0.0177/0.0350 |
| GOF on F2 | 1.077 |
| Absolute Structure Parameter | 0.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Luo, M.; Lin, C. Na4Yb(CO3)3F: A New UV Nonlinear Optical Material with a Large Second Harmonic Generation Response. Crystals 2018, 8, 381. https://doi.org/10.3390/cryst8100381
Chen Q, Luo M, Lin C. Na4Yb(CO3)3F: A New UV Nonlinear Optical Material with a Large Second Harmonic Generation Response. Crystals. 2018; 8(10):381. https://doi.org/10.3390/cryst8100381
Chicago/Turabian StyleChen, Qiaoling, Min Luo, and Chensheng Lin. 2018. "Na4Yb(CO3)3F: A New UV Nonlinear Optical Material with a Large Second Harmonic Generation Response" Crystals 8, no. 10: 381. https://doi.org/10.3390/cryst8100381
APA StyleChen, Q., Luo, M., & Lin, C. (2018). Na4Yb(CO3)3F: A New UV Nonlinear Optical Material with a Large Second Harmonic Generation Response. Crystals, 8(10), 381. https://doi.org/10.3390/cryst8100381





