Abstract
The detection and extraction of weak signals are crucial in various engineering and scientific fields, yet current acoustic sensing technologies are restricted by fundamental pressure detection methods. This paper proposes gradient-equivalent medium-coupled metamaterials (GEMCMs) utilizing strong wave compression and an equivalent medium mechanism to capture weak signals in complex environments and enhance target acoustic signals. Overcoming shape and impedance mismatch limitations of traditional gradient structures, GEMCMs significantly improve control performance. Experimental and numerical simulations indicate that GEMCMs can effectively enhance specific frequency components in acoustic signals, outperforming traditional gradient structures. This enhancement of specific frequency components relies on the resonance effect of the unit cell structure. By introducing acoustic resonance within a spatially wound acoustic channel, a significant amplification of weak acoustic signals is achieved. This provides a new research direction for acoustic wave manipulation and enhancement, and holds significant importance in fields such as mechanical fault diagnosis and medical diagnostics.
1. Introduction
Weak signal enhancement technologies have emerged as critical tools across diverse domains, including structural health monitoring [,], underwater acoustic communication [,,,], and biomedical applications [,]. In recent years, notable advancements have been achieved in improving signal-to-noise ratio (SNR) through electrical sensor systems. For instance, based on the research by Chen et al. [], a noise reduction method utilizing Principal Component Analysis (PCA) and a Variable Step Size Normalized Least Mean Squares (VSS-NLMS) algorithm was proposed. This approach successfully improved the Signal-to-Noise Ratio (SNR) of the vibration signals in a Φ-OTDR (Phase-sensitive Optical Time-Domain Reflectometry) system by 17.40 dB, which significantly enhanced the detection capability for weak signals. Nevertheless, certain vital acoustic features—such as harmonic components indicative of structural damage [,]—often remain undetected due to their amplitudes falling below the sensitivity threshold of conventional sensors or being masked by strong background noise. This leads to the loss of critical diagnostic or environmental information []. To overcome these limitations, there is an urgent need to design acoustic transmission systems capable of perceiving and amplifying weak sound signals. Such systems would significantly improve the identification and detection accuracy of faint signals, ensuring the reliable capture and analysis of essential information critical for diagnostics and environmental monitoring.
Over the past two decades, acoustic metamaterials have garnered significant attention due to their extraordinary physical properties. [] By exploiting features such as negative mass density and negative bulk modulus [,,,], researchers have engineered metamaterials with tailored acoustic microstructures, enabling precise manipulation of sound wave propagation. These advances have led to the realization of remarkable physical phenomena, including efficient sound absorption [,], acoustic focusing [,], directional sound transmission [,,], and acoustic rainbow trapping effects [,]. Compared with conventional periodic metamaterials, metamaterials or media with gradient refractive index profiles offer superior flexibility for acoustic wave manipulation. In a pioneering study, Chen et al. [] introduced gradient acoustic metamaterials (GAMs), which achieve selective sound wave capture and amplitude enhancement across multiple frequency bands through spatial variations in geometric parameters. Subsequently, in 2020, Huang’s group [] advanced this concept by developing improved gradient structures (AMMs) with gradient curves, thicknesses, and gap widths, demonstrating over an order of magnitude acoustic gain in underwater experiments. In 2023, Hao et al. [] designed a novel nonlinear gradient curled metamaterial (NGCM) that demonstrated high sensitivity to weak signals in complex environments. Recent research by Chen [] showed that adding subwavelength curled structures to the gaps in the gradient structure enhanced the sensitivity of the gradient structure to weak acoustic signals. However, in the aforementioned structure, the construction of serrated structures formed by convoluted channels makes it difficult to match the overall gradient growth trend, leading to significant impedance discontinuities between adjacent slits. Since traditional gradient structures typically adopt fixed geometric shapes (e.g., right angles, circular arcs), this design results in discontinuous connections between adjacent units, thereby deviating from the ideal gradient sequence growth pattern. This inherent structural discontinuity leads to acoustic impedance mismatch. When sound waves travel from a low acoustic impedance medium into a high acoustic impedance medium, strong reflections occur at the interface, causing significant loss of acoustic energy. This impedance mismatch effect severely reduces the transmission efficiency and energy focusing effect of the sound waves, ultimately limiting the overall performance of the structure. To address this issue, Han’s research group [,] developed a tunable Z-shaped channel gradient metamaterial that effectively broadened the operating bandwidth while maintaining the pressure amplification effect. Despite these advancements, most existing studies rely heavily on specific gradient shape designs to achieve impedance matching, a requirement that significantly restricts the general applicability and scalability of these metamaterial structures.
To achieve broadband acoustic signal enhancement sensing and effectively regulate strong wave compression effects and acoustic dispersion characteristics, this paper designs a structure that gradient-equivalent medium-coupled metamaterials (GEMCMs). In a single closed grid structure of equal length, the impedance difference between air and solid materials is utilized. By introducing a convoluted channel resembling a maze structure, the equivalent refractive index of each gap is effectively controlled, achieving a gradient increase in refractive index along the gap direction. Numerical simulations reveal that, in comparison to conventional Gradient Acoustic Metamaterials (GAMs), the proposed GEMCMs achieve superior miniaturization and exhibit a more uniform frequency response, all while preserving desirable acoustic dispersion properties. Furthermore, experimental validation demonstrates that GEMCMs significantly enhance acoustic signal detection performance. In particular, within the target frequency range, an acoustic pressure gain exceeding 18 is achieved, underscoring the structure’s exceptional broadband response and sensitivity. This acoustic metamaterial design, which concurrently delivers compactness and broadband functionality, presents a promising and efficient solution for the detection of weak acoustic signals in complex or noisy environments.
The structure of this paper is arranged as follows. Section 2 presents the design of the GEMCMs structure and derives its fundamental characteristics through numerical modeling and theoretical analysis. Section 3 details finite element simulations carried out to evaluate the acoustic enhancement capabilities of the proposed structure and to examine its effective operating frequency range. Section 4 describes the experimental setup and procedures, in which the acoustic response of the GEMCMs structure is tested using a predefined acoustic signal source. Section 5 concludes the paper by summarizing the key findings and outlining potential implications for future research.
2. Materials and Methods
2.1. Numerical Analysis
Based on the above characteristics of constructing GEMCMs, this paper establishes a numerical model to perform a quantitative analysis of its performance. Generally, sound waves in uniform media are controlled by their scalar wave equation []:
In this equation, p represents sound pressure. The speed of sound is explicitly given by . Li et al. [] used equivalent medium theory to derive the mechanism of acoustic amplification lenses, and the effective mass density and bulk modulus can be expressed as follows:
Among them, is the filling rate of the parallel plates. In Section 2, the constructed GEMCMs model was made of photosensitive resin, with a density of and a bulk modulus of . The density of air is , and the bulk modulus is . Based on transformed acoustics, the curled structure between the two plates is calculated using the following equation []:
The computational derivation yields the mass density , bulk modulus , and effective refractive index for the i-th gap, where is the compression ratio of the curled structure. By altering the spatial dimensions w and c of the curled structure, we can modify the compression ratio , resulting in a linear increase in the equivalent refractive index for different gaps. The constructed GEMCMs model can be approximated as an infinite number of uniform metamaterial cross-sections, and the effective refractive index of the metamaterial can be obtained as follows:
Based on the solution of the effective refractive index in the above equation, the relationship between the sound pressure along the x-axis and the input frequency can be derived as follows:
2.2. Model Structure Design
The GEMCMs structure proposed in this study is illustrated in Figure 1a. The entire configuration is fabricated from a photosensitive resin with an elastic modulus of 2.65 GPa and a density of 1130 kg/m3, utilizing high-resolution 3D printing to ensure precision and reproducibility. The structure comprises ten curled-type unit cells, each exhibiting a continuous gradient characteristic. Notably, the first unit lacks the rectangular tooth-like features, while the remaining units incorporate an increasing number of such features—characterized by the geometric parameter w—to achieve a linear modulation of the equivalent refractive index along the propagation direction. Figure 1b presents a planar schematic of two representative gap units along with their key geometric parameters. A comprehensive list of all design specifications is provided in Table 1. During the parameter selection process, the fabrication resolution of the 3D printing system, material suitability, and experimental feasibility were thoroughly considered to ensure that all structural dimensions fall within the realizable manufacturing range and exhibit high consistency and repeatability across experimental trials. In the acoustic excitation setup, a plane wave is introduced along the positive x-axis of the structure, serving as the incident source. By precisely tailoring the geometric features of each gradient unit, the design establishes a spatially continuous distribution of the effective refractive index, enabling gradual modulation and compression of the acoustic wave propagation path. This provides the physical foundation for subsequent broadband acoustic energy convergence and localized field enhancement [,,].
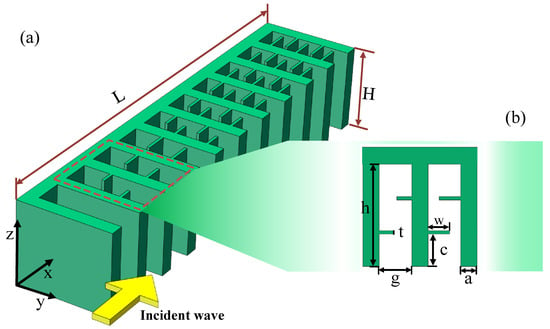
Figure 1.
(a) Three-dimensional view of the structure of GEMCMs; (b) Amplified two-dimensional view of the coiling cell.

Table 1.
Summary of Characteristic Parameters.
The aforementioned theory utilizing equivalent media demonstrates that GEMCMs can effectively amplify acoustic signals. Incident sound waves of different wavelengths are captured and amplified at distinct positions. From a microscopic perspective, due to the subwavelength curled structures between the two plates of the gradient structure, different gaps capture acoustic signals of corresponding frequencies. Simultaneously, since the propagation speed of sound in air exhibits isotropic properties, the increased propagation distance within the convoluted structures reduces the equivalent sound velocity between slits. This enhances the structure’s effective refractive index, thereby amplifying the amplitude of the acoustic waves.
As shown in Figure 2, it can be observed that as the frequency increases, the working gap shifts forward, and the nGEMCMs gradually decrease. At a given frequency, the larger the gap position, the greater the reflected nGEMCMs. In this paper, the position of maximum refractive index (cutoff frequency) is regarded as the operating frequency. Through the above derivation, the acoustic rainbow effect becomes clearly observable: different gaps respond to different frequencies, thereby enhancing the detection of broadband signals.
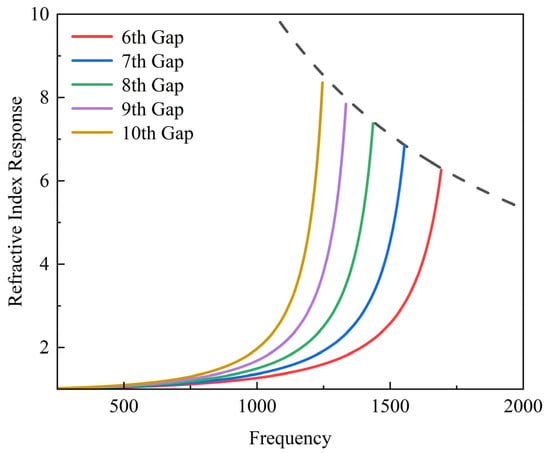
Figure 2.
Refractive index response obtained from GEMCM calculations with different air gap values.
3. Simulation Analysis
To evaluate the acoustic performance of GEMCMs structures, this study used COMSOL Multiphysics 6.1 Multiphysics to perform finite element analysis and established a two-dimensional numerical model, as shown in Figure 3. Based on the theoretical two-dimensional characteristics of the structure, the model simultaneously considered the pressure acoustics and thermoviscous acoustics physical fields. The gray regions within the model represent air as the acoustic medium, with rigid boundary conditions (Rigid Boundary, RB) applied to simulate reflective surfaces. A plane wave with an amplitude of 1 Pa was introduced as the excitation source, incident perpendicularly from the left side of the model. To mitigate boundary reflections and ensure computational accuracy, Perfectly Matched Layers (PMLs) were implemented at both lateral sides of the incident boundary and on the opposite side, as indicated by the blue borders in Figure 3. The orange boundary lines denote thermoviscous acoustic boundaries, which are employed to simulate thermal and viscous losses that occur during acoustic wave propagation. For quantitative assessment of acoustic enhancement, pressure monitoring points were placed in the sixth to tenth air gaps of the structure (highlighted in red). The pressure gain (PG), a key performance metric, is defined as PG = PM⁄PF, where PM denotes the acoustic pressure amplitude within the metamaterial structure and PF refers to the corresponding amplitude in a free-field environment. This modeling approach effectively replicates realistic acoustic conditions and provides a robust theoretical foundation for subsequent comparative performance evaluations.
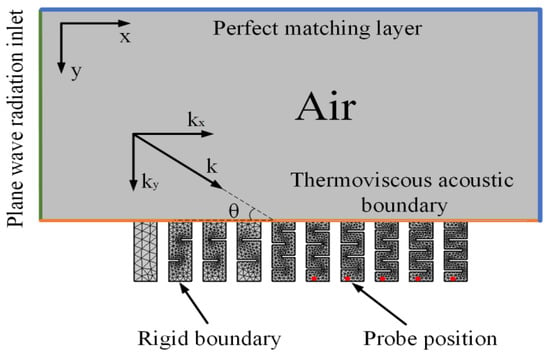
Figure 3.
Simulation of the two-dimensional structure of GEMCMs.
To systematically investigate the impact of gradient-equivalent media on acoustic wave control, a comparative structural analysis framework was established under identical simulation boundary conditions and physical parameters. A traditional gradient acoustic metamaterial (GAMs) structure, composed of the same material as the GEMCMs, was designed for this purpose. In the GAMs configuration, the physical length of each gradient gap was configured to match the equivalent propagation length of the corresponding curled unit in the GEMCMs structure, thereby ensuring functional equivalence and enabling a fair and meaningful comparison. Building on this foundation, this paper employs frequency-domain analysis methods to conduct systematic numerical simulation studies on the acoustic performance of these two structures, with a focus on investigating the mechanism by which the introduction of gradient-equivalent media affects the sound wave enhancement effect.
Numerical simulation results reveal that the center frequencies corresponding to sound pressure enhancement at the 6th to 10th air gap positions of the GEMCMs structure are 1605 Hz, 1520 Hz, 1450 Hz, 1350 Hz, and 1250 Hz, respectively. Figure 4a–e illustrate the spatial distributions of the sound pressure fields at each air gap under their respective center frequencies. For comparative purposes, Figure 4f–j display the corresponding sound pressure field distributions for the GAMs structure at the same spatial positions. The comparison results clearly demonstrate that the GEMCMs structure generates a significant sound compression effect during sound wave propagation, manifested as the selective localized aggregation of sound wave energy at specific air gap regions across different frequencies. Compared to GAMs structures, GEMCMs can achieve multi-band acoustic wave spatial focusing and manipulation without increasing the overall structural size. This demonstrates superior performance in guiding and locally enhancing acoustic energy, with significantly reduced inter-channel coupling. The continuous gradient in the equivalent refractive index introduced on the left side of the GEMCMs enables better impedance matching between adjacent units, thereby suppressing the crosstalk effect between channels. In contrast, the abrupt change in the geometry of the GAM’s slits on the right end creates a distinct impedance mismatch, which enhances inter-channel coupling and weakens the local resonance characteristics. Therefore, GEMCMs can achieve clearer frequency-spatial correspondence and stronger localized sound field focusing.
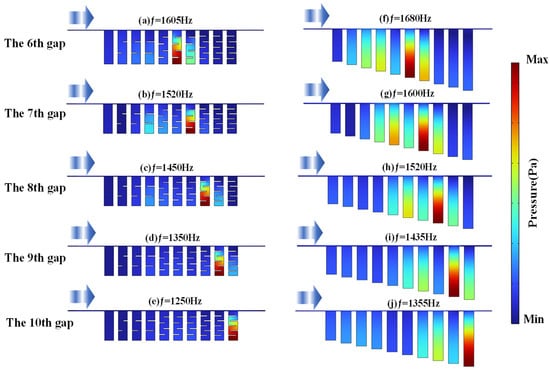
Figure 4.
Simulation results of sound pressure distribution for two structures at different frequencies: (a) GEMCMs structure at f = 1605 Hz; (b) GEMCMs structure at f = 1520 Hz; (c) GEMCMs structure at f = 1450 Hz; (d) GEMCMs structure at f = 1350 Hz; (e) GEMCMs structure at f = 1250 Hz; (f) GAMs structure at f = 1680 Hz; (g) GAMs structure at f = 1600 Hz; (h) GAMs structure at f = 1520 Hz; (i) GAMs structure at f = 1435 Hz; (j) GAMs structure at f = 1355 Hz.
Compared to traditional GAMs structures, the GEMCMs design achieves a downward shift in the acoustic wave capture frequency of approximately 80 Hz. This performance improvement carries notable engineering significance. In conventional gradient metamaterial designs, effective capture of low-frequency acoustic signals typically requires a substantial increase in structural volume—often by 30% to 50%. In contrast, the GEMCMs structure enhances low-frequency detection by optimizing the spatial configuration of the curled units, while retaining only 85% of the volume of the reference GAMs structure. This breakthrough provides compelling validation for the effectiveness of gradient structural design based on equivalent medium theory in low-frequency acoustic regulation.
As illustrated in Figure 5, the simulation results comparing the absolute sound pressure gain versus frequency for the GEMCMs and traditional GAMs structures at various air gap positions (6th to 10th gaps) are presented. Figure 5a,b correspond to the measured data for the GEMCMs and GAMs structures, respectively. The experimental data clearly demonstrate that the GEMCMs structure consistently outperforms the GAMs structure across all evaluated positions in terms of sound pressure gain. Taking the characteristic frequency of 1350 Hz as an example, the sound pressure gain at the 9th air gap reaches approximately 18.3 times in the GEMCMs structure, while the GAMs structure achieves only approximately 4.2 times at the same frequency, demonstrating a performance improvement of nearly 4 times. To ensure a fair comparison, we extracted the maximum sound pressure gain and the corresponding resonance frequency for both the GEMCMs and GAM from their ninth channels. The results show that the GEMCMs achieved a maximum sound pressure gain of approximately 18.3 times at a resonance frequency of f = 1350 Hz. In contrast, the GAM’s maximum sound pressure gain was only about 10.2 times at its resonance peak, which occurred at approximately f = 1435 Hz. This demonstrates that even under their respective optimal operating conditions, the GEMCMs’s performance in localized sound energy enhancement significantly surpasses that of the GAM. This finding further validates the advantages of a design based on the equivalent medium gradient approach. The GEMCMs structure enhances the multiple reflections and phase accumulation effects of sound waves within the structure by introducing internal labyrinth-like curled channels and an equivalent refractive index gradient design, thereby effectively improving the local efficiency of sound energy.
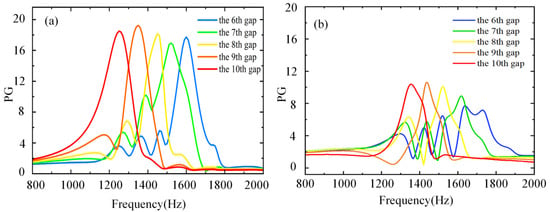
Figure 5.
Absolute sound pressure gain between different structures and different air gaps (a) Absolute sound pressure gain of GEMCMs structure (b) Absolute sound pressure gain of GAMs structure.
Further comparative analysis indicates that the GEMCMs structure exhibits multiple local sound pressure gain peaks within the approximately 1000–1500 Hz frequency band at multiple test air gap positions, with a maximum gain exceeding 18, and multiple air gaps exhibiting peak values above 15, demonstrating significant frequency domain energy enhancement characteristics. In contrast, the traditional GAMs structure only exhibits peak enhancements within a relatively narrow frequency band of approximately 1000–1400 Hz, with a maximum gain of approximately 10.2, significantly lower than that of the GEMCMs structure. The above results indicate that the GEMCMs structure, through the introduction of a gradient equivalent medium design, effectively broadens the frequency range available for sound energy capture, enhancing its performance advantages in broadband acoustic response.
In addition to the substantial improvements in sound pressure gain, the GEMCMs structure demonstrates significantly enhanced capabilities in capturing and manipulating low-frequency acoustic signals. As shown in Figure 4a, the resonance frequency at the 10th air gap is observed to be as low as approximately 1200 Hz, which is notably lower than the corresponding resonance frequency in the conventional GAMs structure. This downward shift highlights the superior low-frequency acoustic control performance of the GEMCMs configuration. Traditional gradient acoustic metamaterials typically require increased structural dimensions to effectively manipulate low-frequency acoustic energy. In contrast, the proposed curled-type GEMCMs structure, grounded in the theory of gradient equivalent media, achieves efficient acoustic energy localization and amplification at reduced physical scales by enhancing coupling efficiency with low-frequency waves while maintaining a compact form factor. Moreover, compared to GAMs structures, the GEMCMs exhibit sharper resonance peaks and narrower bandwidths at each gradient air gap, indicating significantly improved frequency-domain selectivity. This pronounced frequency-domain focusing behavior enables high-resolution, frequency-selective acoustic responses, offering a promising technical route for the deployment of gradient-based acoustic metamaterials in practical applications such as precision acoustic sensing, low-frequency noise suppression, and localized acoustic field manipulation.
4. Experimental Validations
To experimentally validate the acoustic performance of the GEMCMs structure, a dedicated testing system was established, as depicted in Figure 6. In this configuration, a loudspeaker was employed as the acoustic source and positioned at a fixed distance of D = 0.7 m from the structural reference plane to generate a stable incident sound field. The GEMCMs structure was aligned along the propagation path to modulate the acoustic field distribution. The acoustic response was measured using a high-precision MEMS microphone (model: S15OT421-005), featuring a sensitivity of −42 dB and an amplification gain of 66. The sensor was precisely positioned at the edge of the terminal gradient air gap to ensure accurate detection of local sound pressure variations and enable quantitative assessment of the localized enhancement effect. In the absence of active acoustic excitation, the microphone’s no-load output voltage stabilized at approximately 1.5 V, which served as the system’s static reference level. This experimental setup ensured high sensitivity and low noise throughout the measurement process, providing a robust and reliable data foundation for subsequent analysis of sound pressure gain and frequency-domain response characteristics.
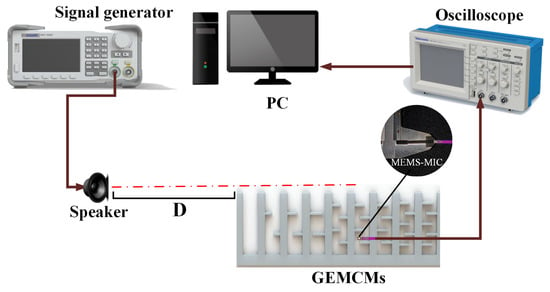
Figure 6.
Test system based on GEMCMs.
To verify the accuracy of the numerical simulation results presented in Section 2 and Section 3, systematic experimental measurements were conducted. A frequency scanning method was employed, wherein the excitation signal was swept in 30 Hz increments over the range of 250 Hz to 1200 Hz. During the experiments, a high-precision MEMS microphone was sequentially positioned at the 3rd through 10th air gaps of the GEMCMs structure to acquire the acoustic field response at each location under different excitation frequencies. Based on the collected data, the center frequencies corresponding to the respective air gaps were determined to be 1790Hz, 1685 Hz, 1610 Hz, 1590 Hz, 1505 Hz, 1435 Hz, 1320 Hz, and 1237 Hz. As shown in Figure 7 and Figure 8, the experimental results clearly demonstrate the frequency-selective enhancement effect of the GEMCMs structure at each test air gap, where the sound pressure gain exhibits significant amplification within a specific frequency range. The sound pressure gains at the 3rd to 10th air gaps are 17, 17.5, 17.2, 17.3, 16, 17.6, 18 and 17.9, respectively, as shown in Table 2. Compared with numerical calculations and simulation analyses, the gain capability of actual tests has decreased to a certain extent. This is because in the actual test environment, the edges of the materials printed with photosensitive resin are somewhat rough, resulting in acoustic–thermal viscous losses in the test environment.
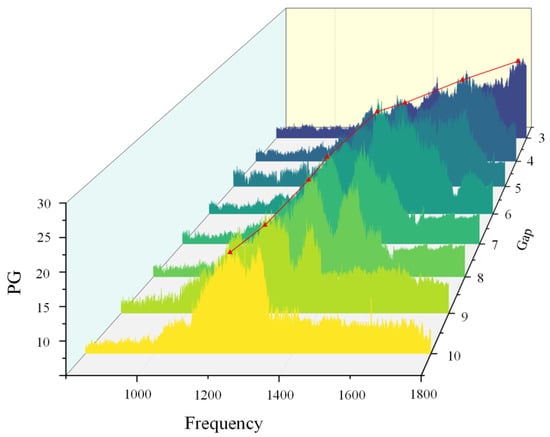
Figure 7.
Maximum spectral amplitude of target frequency corresponding to different gaps.
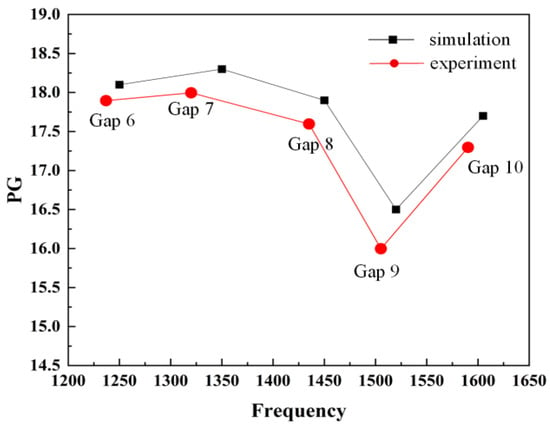
Figure 8.
Comparison of simulation and experimental gains.

Table 2.
Center frequency and sound pressure gain for different gaps.
Through a comparative analysis of the finite element simulation and experimental results, it is evident that the experimental data further validate the enhanced frequency selectivity of the GEMCMs structure. Across the entire tested frequency range, each air gap position exhibits a pronounced sound pressure amplification only in the vicinity of its corresponding target frequency, while showing minimal response and negligible gain in non-resonant frequency bands.
This behavior clearly corroborates the frequency-domain response trend predicted by numerical simulations and provides direct experimental evidence for the spatially resolved, frequency-specific acoustic energy localization mechanism inherent to the GEMCMs design. These findings not only demonstrate the structure’s high-efficiency capability for acoustic energy focusing at specific frequencies, but also confirm the effectiveness and practical feasibility of the proposed gradient-equivalent medium design for achieving precise frequency-domain acoustic wave manipulation.
5. Conclusions
This study presents an acoustic metamaterial based on GEMCMs, which effectively enhances the amplitude of weak acoustic signals within the target frequency band by coupling strong acoustic compression effects with a gradient-index control mechanism. Compared to conventional gradient acoustic metamaterials (GAMs), the GEMCMs exhibit significantly superior acoustic performance while maintaining comparable operational bandwidths across all slit units. Experimental results demonstrate that the average sound pressure gain of GEMCMs within the critical operating frequency range is approximately 40% higher than that of GAMs, clearly underscoring their enhanced performance. This substantial improvement is primarily attributed to the gradient-optimized distribution of the equivalent refractive index along the direction of acoustic wave propagation, which improves local acoustic impedance matching and significantly enhances both wave–structure coupling efficiency and localized energy focusing. Overall, the proposed GEMCMs structure validates the effectiveness of the equivalent medium–based design strategy and offers a robust theoretical foundation and practical pathway for its application in acoustic sensing and noise suppression under complex acoustic environments.
Author Contributions
Conceptualization, Formal analysis, Software; Writing—original draft preparation, Y.R.; Data curation, Validation, Writing—review and editing, G.H.; Investigation; Methodology, X.Z.; Supervision, Resources, Writing—review and editing, Project administration, Funding acquisition, J.H. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by Shanxi Scholarship Council of China (2023-127), Natural Science Foundation of Shanxi Province (202103021224201) and The National Natural Science Foundation of China (61671414).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had role in the writing of the manuscript and in the decision to publish the results.
References
- Danawe, H.; Okudan, G.; Ozevin, D.; Tol, S. Conformal Gradient-Index Phononic Crystal Lens for Ultrasonic Wave Focusing in Pipe-Like Structures. Appl. Phys. Lett. 2020, 117, 021906. [Google Scholar] [CrossRef]
- Ochôa, P.A.; Groves, R.M.; Benedictus, R. Effects of High-Amplitude Low-Frequency Structural Vibrations and Machinery Sound Waves on Ultrasonic Guided Wave Propagation for Health Monitoring of Composite Aircraft Primary Structures. J. Sound Vib. 2020, 475, 115289. [Google Scholar] [CrossRef]
- Bu, F.; Luo, H.; Ma, S.; Li, X.; Ruby, R.; Han, G. Auv-Aided Optical-Acoustic Hybrid Data Collection Based on Deep Reinforcement Learning. Sensors 2023, 23, 578. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Shi, Y.; Sun, X.C.; Jia, H.; Jin, Z.K.; Deng, K.; Yang, J. Underwater Acoustic Multiplexing Communication by Pentamode Metasurface. J. Phys. D-Appl. Phys. 2021, 54, 205303. [Google Scholar] [CrossRef]
- Yongdong, S.; Junxian, S.; Yonggang, L. Early Weak Fault Signal Enhancement and Recognition Method of Rudder Paddle Bearings Based on Parameter Adaptive Stochastic Resonance. IEEE Access 2024, 12, 9458–9467. [Google Scholar] [CrossRef]
- Wang, Y.; Zang, C.; Yu, B.; Zhao, W.; Wang, X.; Xu, C.; Cui, G. Wte-Cgan Based Signal Enhancement for Weak Target Detection. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Zhao, X.S.; Han, J.N.; Yang, P.; Zhao, R.R. Research on High-Efficiency Transmission Characteristics of Multi-Channel Breast Ultrasound Signals Based on Graphene Structure. Crystals 2021, 11, 507. [Google Scholar] [CrossRef]
- Nakamura, T.; Takata, M.; Michimoto, I.; Koyama, D.; Matsukawa, M. Site Dependence of Ultrasonically Induced Electrical Potentials in Bone. JASA Express Lett. 2021, 1, 012002. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Yu, H.; Xu, J.; Gao, F. An SNR Enhancement Method for Φ-OTDR Vibration Signals Based on the Pca-Vss-Nlms Algorithm. Sensors 2024, 24, 4340. [Google Scholar] [CrossRef] [PubMed]
- Bovsunovsky, A.; Nosal, O. Highly Sensitive Methods for Vibration Diagnostics of Fatigue Damage in Structural Elements of Aircraft Gas Turbine Engines. Procedia Struct. Integr. 2022, 35, 74–81. [Google Scholar] [CrossRef]
- Yin, T.; Ng, C.-T.; Kotousov, A. Damage Detection of Ultra-High-Performance Fibre-Reinforced Concrete Using a Harmonic Wave Modulation Technique. Constr. Build. Mater. 2021, 313, 125306. [Google Scholar] [CrossRef]
- Tan, J.; Cheer, J.; Daley, S. Realisation of Nonreciprocal Transmission and Absorption Using Wave-Based Active Noise Control. JASA Express Lett. 2022, 2, 054801. [Google Scholar] [CrossRef]
- Chen, T.; Yu, D. A Novel Method for Enhanced Demodulation of Bearing Fault Signals Based on Acoustic Metamaterials. IEEE Trans. Ind. Inform. 2022, 18, 6857–6864. [Google Scholar] [CrossRef]
- Zhang, T.; Bok, E.; Tomoda, M.; Matsuda, O.; Guo, J.; Liu, X.; Wright, O.B. Compact Acoustic Metamaterial Based on the 3D Mie Resonance of a Maze Ball with an Octahedral Structure. Appl. Phys. Lett. 2022, 120, 161701. [Google Scholar] [CrossRef]
- Zhai, S.; Chen, H.; Ding, C.; Zhao, X. Double-Negative Acoustic Metamaterial Based on Meta-Molecule. J. Phys. D Appl. Phys. 2013, 46, 475105. [Google Scholar] [CrossRef]
- Sheng, P.; Zhang, X.X.; Liu, Z.; Chan, C.T. Locally Resonant Sonic Materials. Phys. B Condens. Matter 2003, 338, 201–205. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, Z.; Qiu, C.; Shi, J. Metamaterial with Simultaneously Negative Bulk Modulus and Mass Density. Phys. Rev. Lett. 2007, 99, 093904. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Xie, L.-X.; Huang, W.; Zhang, X.J.; Lu, M.-H.; Chen, Y.-F. Broadband Acoustic Absorbing Metamaterial Via Deep Learning approach. Appl. Phys. Lett. 2022, 120, 251701. [Google Scholar] [CrossRef]
- Comandini, G.; Khodr, C.; Ting, V.P.; Azarpeyvand, M.; Scarpa, F. Sound Absorption in Hilbert Fractal and Coiled Acoustic Metamaterials. Appl. Phys. Lett. 2022, 120, 061902. [Google Scholar] [CrossRef]
- Chen, D.-C.; Zhu, X.-F.; Wei, Q.; Wu, D.-J. Bidirectional Asymmetric Acoustic Focusing with Two Flat Acoustic Metasurfaces. Chin. Phys. B 2018, 27, 124302. [Google Scholar] [CrossRef]
- Chen, D.-C.; Zhu, X.-F.; Wei, Q.; Yao, J.; Wu, D.-J. Broadband Tunable Focusing Lenses by Acoustic Coding Metasurfaces. J. Phys. D Appl. Phys. 2020, 53, 255501. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Fleury, R. Acoustic Analogues of High-Index Optical Waveguide Devices. Sci. Rep. 2018, 8, 10401. [Google Scholar] [CrossRef]
- Sun, J.-H.; Wu, T.-T. Propagation of Surface Acoustic Waves Through Sharply Bent Two-Dimensional Phononic Crystal Waveguides Using a Finite-Difference Time-Domain Method. Phys. Rev. B 2006, 74, 174305. [Google Scholar] [CrossRef]
- Dai, H.; Liu, T.; Xia, B.; Yu, D. Quasilossless Acoustic Transmission in an Arbitrary Pathway of a Network. Phys. Rev. B 2017, 95, 054109. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, Y.; Zhu, X.; Garcia-Vidal, F.J.; Yin, X.; Zhang, W.; Zhang, X. Acoustic Rainbow Trapping. Sci. Rep. 2013, 3, 1728. [Google Scholar] [CrossRef]
- Arjunan, A.; Baroutaji, A.; Robinson, J.; Vance, A.; Arafat, A. Acoustic Metamaterials for Sound Absorption and Insulation in Buildings. Build. Environ. 2024, 251, 111250. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, H.; Reilly, M.; Bae, H.; Yu, M. Enhanced Acoustic Sensing Through Wave Compression and Pressure Amplification in Anisotropic Metamaterials. Nat. Commun. 2014, 5, 5247. [Google Scholar] [CrossRef]
- Xinjing, H.; Yutian, Y.; Jinyu, M.; Jian, L.; Xiaobo, R. An Acoustic Metamaterial-Based Sensor Capable of Multiband Filtering and Amplification. IEEE Sens. J. 2020, 20, 4413–4419. [Google Scholar] [CrossRef]
- Hao, G.; Zhao, X.; Han, J. A Nonlinear Gradient-Coiling Metamaterial for Enhanced Acoustic Signal Sensing. Crystals 2023, 13, 1291. [Google Scholar] [CrossRef]
- Chen, T.; Jiao, J.; Yu, D. Enhanced Broadband Acoustic Sensing in Gradient Coiled Metamaterials. J. Phys. D Appl. Phys. 2021, 54, 085501. [Google Scholar] [CrossRef]
- Ren, Y.; Hao, G.; Zhao, X.; Han, J. A Tunable Z-Shaped Channel Gradient Metamaterial for Enhanced Detection of Weak Acoustic Signals. Crystals 2025, 15, 216. [Google Scholar] [CrossRef]
- Zhao, X.; Hao, G.; Shang, Y.; Han, J. Three-Dimensional Gradient Metamaterial Devices Coupled with Phononic Crystals for Acoustic Enhancement Sensing. Crystals 2023, 13, 1191. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling Sound with Acoustic Metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Li, J.; Fok, L.; Yin, X.; Bartal, G.; Zhang, X. Experimental Demonstration of an Acoustic Magnifying Hyperlens. Nat. Mater. 2009, 8, 931–934. [Google Scholar] [CrossRef]
- Zhu, X.; Liang, B.; Kan, W.; Peng, Y.-G.; Cheng, J. Deep-Subwavelength-Scale Directional Sensing Based on Highly Localized Dipolar Mie Resonances. Phys. Rev. Appl. 2016, 5, 054015. [Google Scholar] [CrossRef]
- Yang, Z.; Mei, J.; Yang, M.; Chan, N.H.; Sheng, P. Membrane-Type Acoustic Metamaterial with Negative Dynamic Mass. Phys. Rev. Lett. 2008, 101, 204301. [Google Scholar] [CrossRef]
- Cingolani, M.; Fusaro, G.; Fratoni, G.; Garai, M. Influence of Thermal Deformations on Sound Absorption of Three-Dimensional Printed Metamaterials. J. Acoust. Soc. Am. 2022, 151, 3770–3779. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Guo, Q.; Hu, G.; Yang, J. Ultrathin Low-Frequency Sound Absorbing Panels Based on Coplanar Spiral Tubes or Coplanar Helmholtz Resonators. Appl. Phys. Lett. 2014, 105, 121901. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).