Abstract
A bainite dual-phase (FB) steel containing polygonal ferrite and granular bainite is thermo-mechanically rolled, followed by an accelerated cooling. Two different cooling rates are applied to obtain two different materials. The aim of the study is to explore the reasons for the differences in the mechanical response experimentally observed for these two materials which are modeled by means of high-resolution crystal plasticity simulations with a phenomenological constitutive description. First, the CP parameters of the individual constituents are determined. Second, different three-dimensional (3D) representative volume elements (RVEs)—one of which includes the substructure of bainite—are used to study the mechanical properties of both FB microstructures. It is shown that, in contrast to the macroscopic response, the microscopic response differs among the RVEs. Third, a comparison of both materials is performed by analyzing their stress–strain response. The onset of plasticity in granular bainite is found to be different for both materials in addition to the strain partitioning, although they both obeyed the iso-work assumption. Finally, a parameter study is carried out in order to investigate the correlation between different microstructures and damage initiation that can be seen experimentally in this steel. It is shown that the difference in ultimate elongation may depend on whether the first voids appear within polygonal ferrite or at the phase boundary.
1. Introduction
Heavy plate manufacturers worldwide are researching and developing high-strength line pipe grades suitable for oil and gas transmission exposed to sour environments [1,2,3]. One of the main routes for producing these pipeline steels is the thermomechanical control process (TMCP), which consists of controlled rolling combined with a suitable subsequent accelerated cooling [4]. The cooling rate during TMCP is a controllable factor that can significantly alter the properties of the final product [5]. The typical microstructure that can be accomplished by TMCP for a high-strength pipeline steels consists of ferrite and bainite phases with relatively small amounts of martensite and/or retained austenite [6]. Past research has consistently demonstrated that the combination of polygonal ferrite and granular bainite in FB steels results in a favorable balance between strength and ductility [7,8]. These rapidly cooled, control-rolled steels that mainly contain ferrite and bainite are usually referred to as bainite dual-phase, ferritic–bainitic, ferrite–bainite, or FB steels.
The number of works dedicated to the mechanical properties of FB is significant. Akbarpour and Ekrami [9] studied the effect of the ferrite volume fraction on the work hardening. Ishikawa et al. [10] experimentally examined microscopic deformation using a micro-grid method and accompanied their investigation with a simulation study. Tang et al. [11] also combined experiments and simulations in order to investigate the micromechanical behavior and the experimentally observed failure mechanism of these FB steels. Tu et al. [12] studied the differences between layered and network microstructures based on experiments and simulations. The most recent and relevant contribution to the field was the characterization of the tensile deformation behavior of these steels by Tu et al. [13,14].
Modeling is a promising route in order to facilitate the development of FB steels with enhanced properties. However, to the knowledge of the authors, no model considering the hierarchical substructure of the bainite has been used for such investigations. In this study, the substructure is considered based on the crystal plasticity (CP) method which is a well-established approach to predict the mechanical responses of crystalline materials [15]. This method takes into account crystallographic anisotropy and captures the underlying physics at the crystal level [16]. Furthermore, CP models are able to predict not just the relationship between stress and strain, but also the texture evolution, micro-mechanical field distributions, regions of strain localization, etc. [17,18,19]. For instance, Tasan et al. [20,21] introduced a novel experimental–numerical methodology to strengthen the integrated understanding of the microstructure and mechanical properties of a martensite–ferrite dual-phase steel.
The goals of the mechanical model developed in this study are twofold: to investigate the reasons for the differences in the mechanical responses experimentally observed for two materials that are produced by applying two different cooling rates to a FB steel and to analyze other aspects of these steels which may be of interest. The study is structured as follows. First, the CP modeling framework is described in Section 2. Second, the experimental results obtained are described in Section 3. The simulation setup is described in Section 4. Here, the methodology for determining the CP parameters is introduced and the creation and use of representative volume elements (RVEs) with the hierarchical microstructure of the bainite substructure is explained in detail. In Section 5, the simulation results are presented. The final conclusions are given in Section 6.
2. Modeling Framework
DAMASK [22] was used as the CP modeling framework. The phenomenological power law implemented therein was used as the constitutive law for the simulations. Assuming that the dislocation slip is the only plastic deformation process, the plastic velocity gradient, , is given by
where the vectors and are unit vectors describing the slip direction and the normal to the slip plane of the slip system , respectively, N is the number of (active) slip systems, and is the shear rate on that same system. In this study, the CP model is an adoption of the phenomenological description of Hutchinson [23] (for details see [15]). The kinetic law on a slip system follows
where is the reference shear rate, , and n is the stress exponent. The microstructure is parametrized in terms of the slip resistance, , on the twelve <1 1 1>{1 1 0} slip systems, the twelve <1 1 1>{1 1 2} slip systems, and the twenty-four <1 1 1>{1 2 3} slip systems, indexed by . These resistances evolve asymptotically from towards with shear according to the relationship:
where , a, and are hardening parameters and are the components of the slip–slip interaction matrix, which describes the interaction between the different slip systems.
3. Materials and Methods
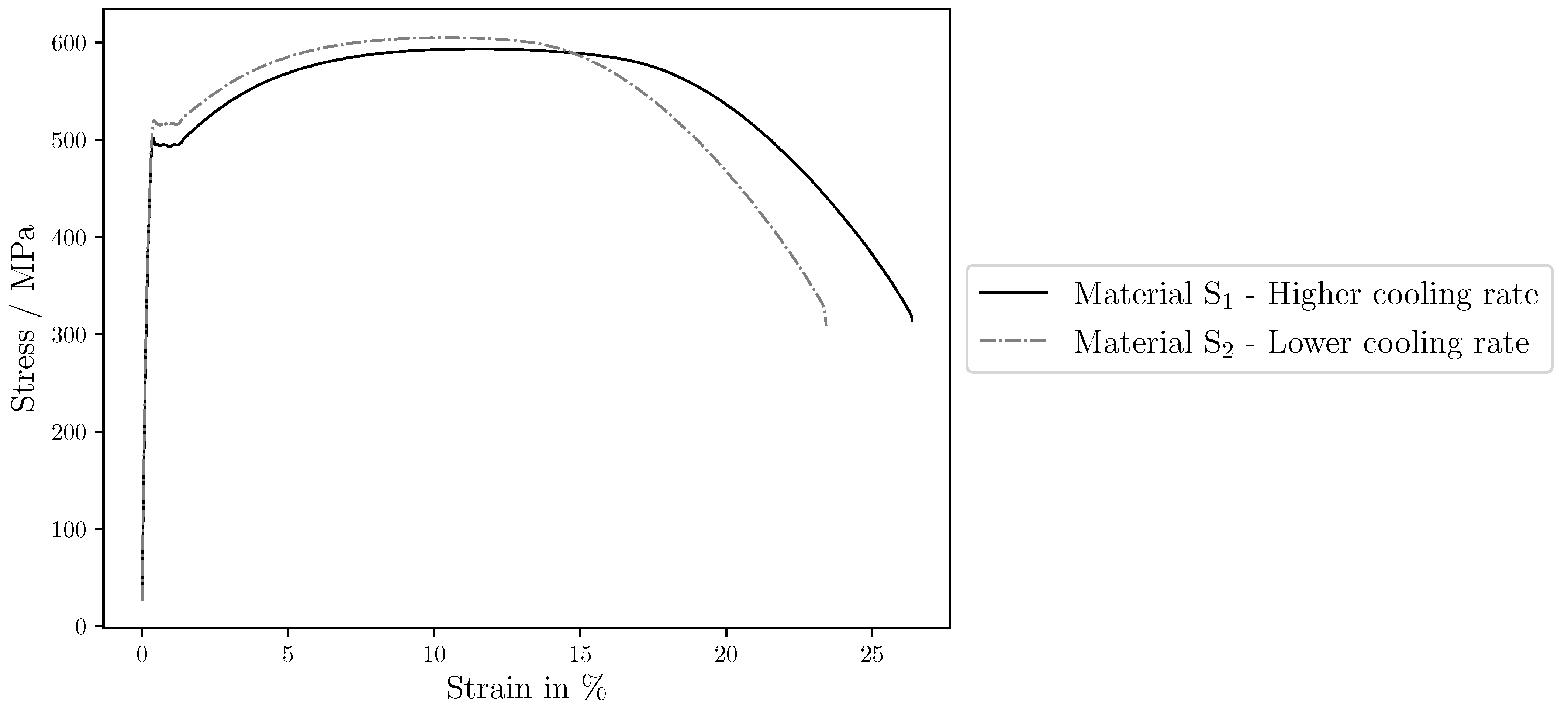
A high-strength, low-alloy steel with the chemical composition (Fe-0.04C-0.32Si-1.45Mn () and additions of Cu, Ni, Nb, and Ti) was thermo-mechanically rolled, followed by an accelerated cooling. Two different cooling rates were applied to obtain material (higher rate) and material (lower rate). The macroscopic behavior of these materials was assessed by carrying out tensile tests transverse to the rolling direction (RD) that are shown in Figure 1. The 0.5% extension under load yield strength (), the ultimate tensile strength (UTS), and the ultimate elongation (UE) of both materials are presented in Table 1.
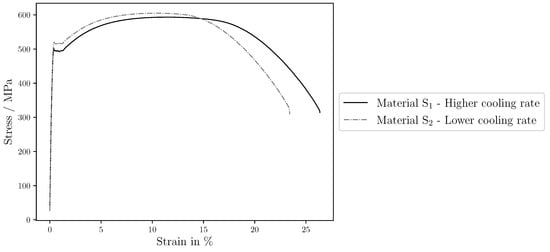
Figure 1.
Experimental macroscopic tensile stress–strain curves in the rolling direction (RD) for the materials obtained from applying different cooling rates to a high-strength, low-alloy steel.

Table 1.
Summary of experimental results for materials and from [24].
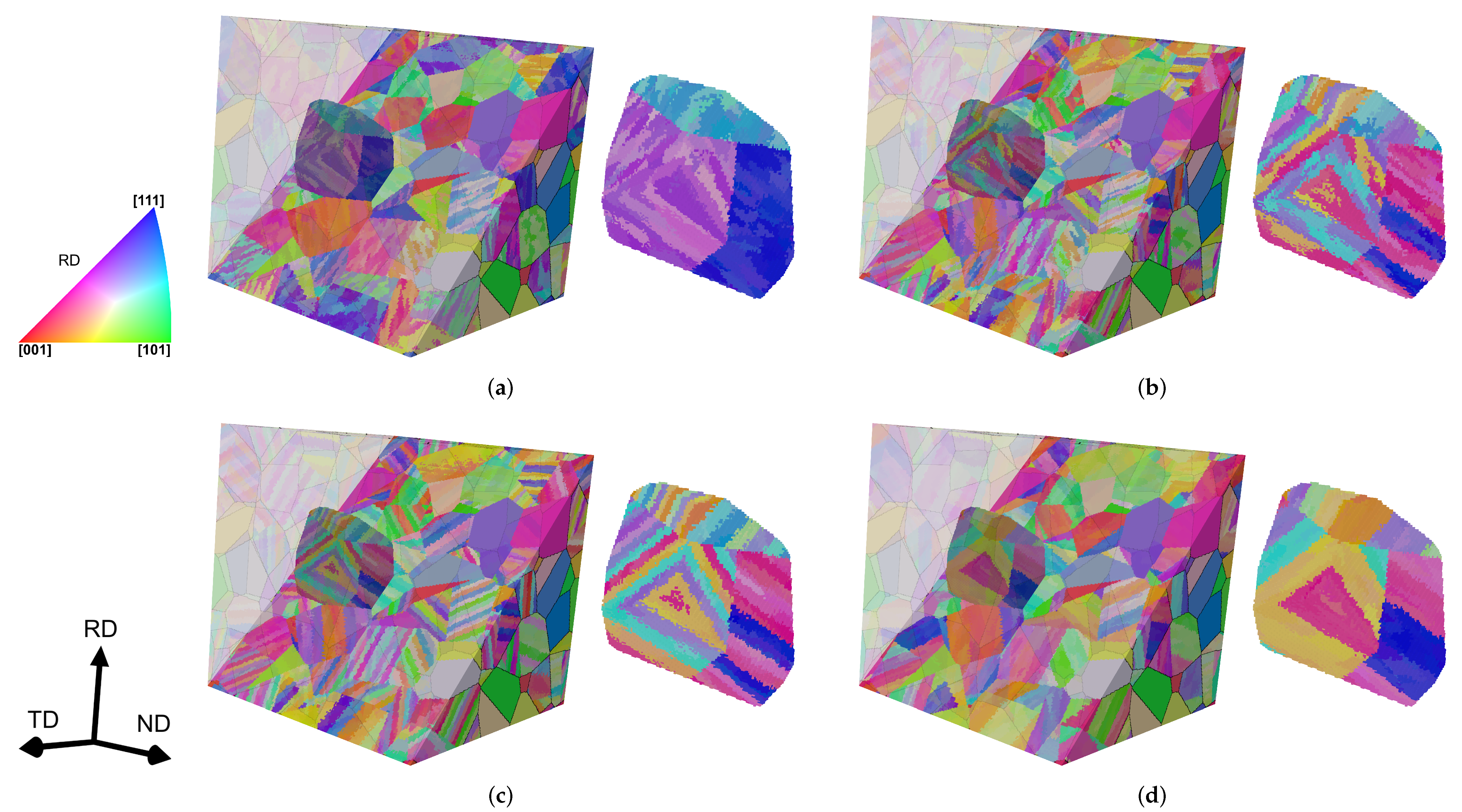
The quantification of the phase fractions of granular bainite (GB) and polygonal ferrite (PF) based on electron backscatter diffraction (EBSD) scans was performed using the automated classification tool described in work by Jentner et al. [25], since other methods have been proven to be ineffective for these microstructures [26]. For each material, a representative scan of 80 m × 80 m (RD × ND) was measured with an EDAX system and a step size of 50 . These scans are shown in Figure 2b,d, colored by their inverse pole figure (IPF) representation. The separation of both phases first requires the determination of grain boundaries. For the calculation of the grains, a grain tolerance angle of 5° was used. Then, the kernel average misorientation (KAM) angle was calculated for each pixel ignoring misorientation angles larger than 4.9° and considering up to -degree neighbors (equivalent to a kernel size of 350 ). Grains with at least one pixel with a KAM bigger than 3° were classified as GB, and the rest were classified as PF. The results of this classification are shown in Figure 2a,c, where PF and GB are colored in blue and orange, respectively. According to this method; material is made of 75% GB and 25% PF and material is made of 59% GB and 41% PF. Two more scans, one per material, were performed at different locations on the same surface and following the same procedure. The phase fractions calculated using these two scans were identical to those calculated previously, confirming the consistency of the methodology.
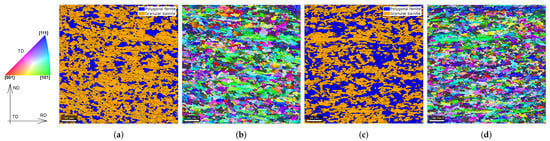
Figure 2.
An EBSD scan and a phase map are shown in (a,b) for material S and in (c,d) for material S. EBSD scans are colored by their IPF. Phase maps, showing polygonal ferrite and granular bainite phases, were calculated from the EBSD scans with the classification tool described in work by Jentner et al. [25]. The grain boundaries are colored in black.
The grain size was calculated from the experimental EBSD scans and is presented in Table 1. The orientation distribution function (ODF) for each phase in each material was also calculated from the EBSD scans with the MTEX toolbox [27]. Based on this, pole figures were computed and are displayed in Figure 3. From the intensity in the pole figures, where a maximum of 2 “multiples of random density” (mrd) are observed, a weak, almost random crystallographic texture can be concluded for all four phases. The texture index of the ODF () is presented in Table 1.

Figure 3.
Pole figures for each phase in materials (a,b) and (c,d). Contour lines are plotted in blue for polygonal ferrite (a,c) and in orange for granular bainite (b,d). The white-to-black scale bar indicates the “multiples of random density”.
Micro-compression tests are carried out to calculate the critical resolved shear stresses (CRSSs) for each slip plane family as described in [24,28]. The average value and the standard error per phase and per material are shown in Table 2.

Table 2.
Micropillar compression test results grouped by slip plane families for materials and S.
The dislocation density () was also calculated using electron channeling contrast imaging and is given in Table 1, where all the experimental differences between materials S and S are presented. A more detailed description of the characterization of these two steels can be found in work by Jentner et al. [24].
Finally, nanoindentation tests on a regular grid followed by a topographical characterization of the post-mortem indents were carried out as described in work by Gallardo-Basile et al. [28]. In this case, an extra step of using the phase classification tool was introduced to determine the indented phase.
4. Simulation Setup
In the following, the setup of the simulations is explained in detail. The first set of simulations aims to determine the CP parameters of PF and GB. The second set of simulations using these parameters is used to reveal the different mechanical properties obtained by using different RVEs. The third set of simulations targets understanding the difference in the mechanical behavior between both materials. The last set of simulations is used for finding a correlation between damage initiation and the bainitic microstructure and for interpreting the difference in the ultimate elongation between both materials. In all cases, the boundary conditions imposed mimic the tensile tests in Figure 1 up to the ultimate yield stress to obtain a macroscopic stress–strain curve. The part after necking is ignored in the modeling since damage propagation is not considered.
4.1. Fitting of CP Parameters
The CP parameters (see Section 2) of GB were determined following the inverse modeling procedure described by Gallardo-Basile et al. [28]. The method is based on measuring a post mortem nanoindentation imprint by atomic force microscopy and comparing it to a simulated one.
The CP parameters of PF were determined by fitting the output of an RVE simulation. To this end, an RVE, labeled “3D-RVE”, with a regular grid of 256 × 256 × 256 = 16,777,216 material points and around 10,000 grains was created for each material. The microstructure with a grain size distribution matching the experimental results was created with DREAM.3D [29]. The phase of the grains was randomly assigned and shuffled until the experimental phase fraction was achieved. The orientation of the grains was selected by randomly sampling the orientations of the experimental EBSD scan. The IPF representation and the phase map of the “3D-RVE” for material are shown in Figure 4a. Note that there is no substructure of bainite in this RVE. The “3D-RVE” for material is comparable.

Figure 4.
3D-RVE (a), 3D-RVE no-substructure (b), 3D-RVE gb-substructure (c), and 2D-RVE measured (d) for material . IPFs along the RD (horizontal direction in the 2D-RVE) are displayed in the left. Phase maps are shown in the right, where blue corresponds to polygonal ferrite and orange corresponds to granular bainite.
For the calculation of the CP parameters, the CRSSs determined from micropillar compression experiments (see Table 2) were used to estimate an upper bound of the initial resistance of the slip plane families and the ratio between them. This procedure is part of the inverse modeling described in [28] and therefore it was used for the calculation of the GB parameters. In addition, here it was also used for fitting the PF parameters.
The results from the fitting are presented and discussed in Section 5.1. The determined CP parameters are used for all further simulations in this work.
4.2. Representative Volume Element—RVE
An RVE is a key idea in continuum mechanics. It plays the role of a mathematical point of a continuum field that approximates the material microstructure. This volume contains a set of micro-scale elements (e.g., grains) that posses statistically homogeneous and ergodic properties (e.g., elasto-plastic response) [30]. In praxis, the selection of the RVEs size and complexity is a compromise between correctly representing the microstructure by using a large enough and complex enough volume and the computational expense regarding its creation and later use of it (e.g., time of simulation, time for analyzing the results, etc.).
In this work, different RVEs are compared with respect to their mechanical properties. The RVEs (see Figure 4 for their IPF representation and phase map) used in this section are the following:
- “3D-RVE”: described in Section 4.1.
- “3D-RVE no-substructure”: similar to “3D-RVE” but the implementation of the experimental grain size distribution is substituted by a Voronoi tesellation of 80 random seeds. The main difference with “3D-RVE” is the lower accuracy in the statistical representation of the texture, i.e., 80 grains compared to 10,000 grains.
- “3D-RVE gb-substructure”: based on “3D-RVE no-substructure”. PF grains are kept unchanged. GB grains of “3D-RVE no-substructure” are used as prior austenite grains which is the input required in the microstructure generation tool of Gallardo-Basile et al. [31]. This tool is used to generate a lath-martensite substructure for the GB (justification for this at the end of this section). The following values for the input parameters of the tool are used: = 647 A.U. (arbitrary units of volume), A.U. (arbitrary units of length), = 9:3:1, and = 3°.
- “2D-RVE measured”: a direct 2D takeover of the measured crystallographic orientation of each pixel of the EBSD scan in Figure 4d. The phase is assigned according to the classification tool. Cleaning is performed with OIM software [32] for assigning a phase and an orientation to non-indexed pixels and the ones indexed as austenite (most of them are measuring errors).
Different RVEs are needed in order to evaluate which aspects are decisive for predicting the mechanical properties. The “3D-RVE” allows a good statistical representation of the texture and grain size distribution but the resolution is not sufficient to represent the bainitic substructure. On the other hand, the “3D-RVE gb-substructure” does allow the substructure to be represented, with the downside of using a lower amount of grains. For a direct comparison of RVEs with and without the bainitic microstructure, “3D-RVE no-substructure” is considered. Finally, “2D-RVE measured” was created to capture the correct grain and phase representation but only in 2D.
The results from simulations using these RVEs for material are shown in Section 5.2.
Great care is taken when using a lath-martensite substructure for the GB. Martensite and bainite are both microstructural phases that can form in steel during cooling from the austenite phase field. Martensite has high hardness and strength but low ductility [33], while bainite has mechanical properties between those of ferrite and martensite [34]. Besides formation and mechanical properties, there exists differences in terms of their microstructures, which is a key aspect for building “3D-RVE gb-substructure”.
In ferrous martensite, the martensite is the most common and exists in two major types: plate martensite and lath martensite [35]. Lath martensite has a unique complex hierarchical morphology. At the smallest scale, elongated domains with the same crystallographic orientations are named laths [36,37]. A group of laths with similar crystallographic orientation form a block. Multiple blocks with the same habit plane form a packet [38,39,40]. Regarding the orientation relationship to the parent austenite, three main models have been proposed: Nishiyama–Wassermann (NS [41,42]), Kurdjumov–Sachs (KS [43]), and Greninger–Troiano (GT [44]). When considering the KS model, laths with similar crystallographic orientation are called variants. A group of laths from a single variant form a sub-block. These sub-blocks appear in pairs that form low-angle misorientation boundaries. Each pair of sub-blocks is named a block [31,38].
Granular bainite was discovered after microstructural observations on an optical scale had an insufficient resolution to establish that the “coarse ferrite plates” were in fact made of sub-units with very thin regions of austenite between them [5,45]. De-Castro et al. [46] showed that in a low carbon micro-alloyed steel “no significant differences were observed between bainitic ferrite matrix in granular and lath-like bainite at high magnifications using TEM and that both possessed the same crystallographic hierarchy”. Granular bainite, such as upper and lower bainite, consists of aggregates of platelets or laths of ferrite (“sub-units”) that can be separated by regions of residual phases. The aggregates of bainitic platelets are called sheaves [47]. Clusters of platelets within which the traces of the habit planes of bainite are parallel are sometimes called “packets of bainite”, analogously to the lath martensite case [48]. The orientation relationship between bainitic ferrite and its parent austenite is always close to GT (between KS and NW) and always lies within the Bain region [34,49]. When the sub-units of bainitic ferrite are in the form of laths, these can be idealized as parallelepipeds of dimensions l, w, and t, with . The growth direction and longest direction (l) of each lath are aligned with the close-packed direction of the ferrite [ ], which is parallel to the corresponding close-packed direction of the parent austenite [ ] [50], analogous to lath martensite. The surface is in the plane (1 0 1), as it is in martensite. The habit plane () of bainitic lath has been measured to be close to (2 3 2) ≈ ( ) [51], which deviates from the one in lath martensite (1 1 1).
Considering the many similarities and few differences in the morphology and crystallography between them, the granular bainite in “3D-RVE gb-substructure” was modeled using an approach that was originally developed for martensite [31].
One must note that the parent austenite reconstruction performed by Gallardo-Basile et al. [31] cannot be directly replicated. While the PF grains in FB steels that nucleate at austenite grain boundaries (allotriomorphic ferrite) obey KS, GT, or NW orientation relationships (depending on the chemistry and the cooling conditions), their growth may extend to adjacent austenite grains with a random orientation [52]. Additionally, they exhibit a lower number of variants than lath structures. These two factors make the reconstruction of the prior austenitic grains challenging when the PF volume fraction is high [53]. Therefore, a random texture is assumed for the prior austenite grains in the “3D-RVE gb-substructure” RVEs.
4.3. Mechanical Behavior of Materials S1 and S2
The mechanical behavior of both materials was analyzed using the “3D-RVE gb-substructure” within the modeling framework. The following simulation results are presented for both materials: the stress–strain curves, the average stress and plastic strain per phase, the activation of the different slip systems, and the strain partitioning. Regarding the latter, the validity of different laws of mixtures (explained below) is investigated. The results are shown in Section 5.3 and are discussed with a comparison to the experimental behavior from Section 3.
The mechanical law of mixture is a principle that describes how the mechanical properties of a composite material are related to the properties of its individual constituents and their relative proportions.
A generalized law of mixture was proposed by I. Tamura [54]. Assuming that there are only two constituents, a and b, the equation for a point in the stress–strain curve () is given by:
The greater the value of , the more close the situation is to the iso-strain assumption [55]. Conversely, the iso-stress condition [56] is given by .
A variation of the mechanical law of mixture is the iso-work rule of mixture that asserts that the work done by both constituents is equal. It was proposed by Bouaziz and Buessler [57] and is given by:
4.4. Microstructural Study of Ferritic Bainite
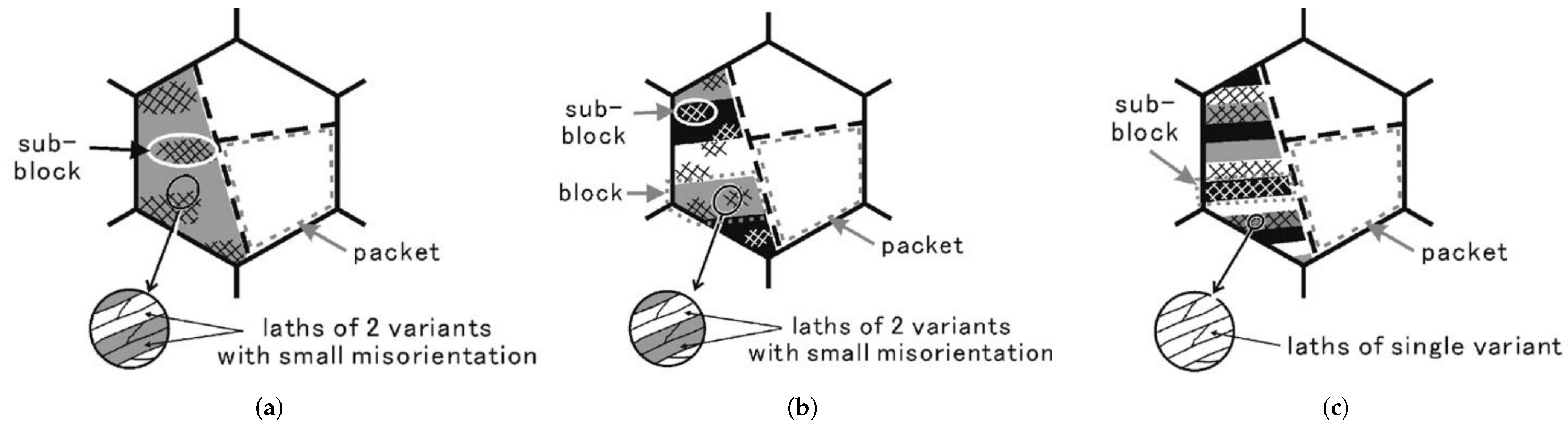
The “3D-RVE gb-substructure” of Section 4.2 was built using the approach of Gallardo-Basile et al. [31] which is based on lath martensite. However, bainite can exhibit microstructural variations that differ from the lath-like substructure. Furuhara et al. [58] described three different types of bainitic packets (see Figure 5).
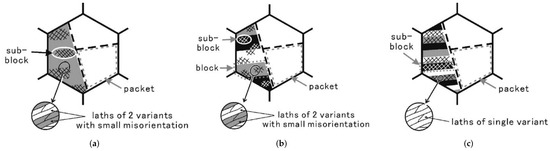
Figure 5.
Bainitic packets of type-A (a), type-B (b), and type-C (c) in Fe-9Ni-C alloys. Taken from Furuhara et al. [58]. In (c), the originally labeled “block” is renamed to “sub-block”.
The RVEs presented in this section were constructed to represent the different bainitic packets labelled type A, B, and C shown in Figure 5. The microstructure hierarchy in type C is identical to the one presented by Gallardo-Basile et al. [31]. To achieve the microstructure of type B, a type C microstructure is first generated and then the orientations of the laths within a block are randomly shuffled. To achieve the microstructure of type A, a microstructure of type B is generated with a very big block size so that a packet is filled with a single block. The default values for the “3D-RVE gb-substructure”, which are mentioned in Section 4.2, were used. In the case of type B, it is understood that . The microstructure of type A is translated to “type B sb ”. In addition, in order to systematically investigate the influence of the sub-block size, RVEs with different values for this parameter were built (, and 15 A.U.). Some of these RVEs for material are shown in Figure 6.
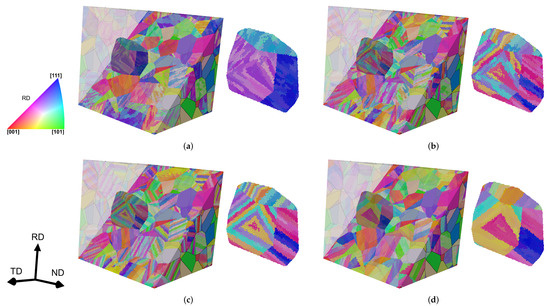
Figure 6.
IPF representations of type-B sb (a), type-B sb = 5 (b), type-C sb = 5 (c), and type-C sb = 15 (d) RVEs of material S. The RVEs are clipped with a plane on the left to show the same single grain extracted which is magnified on the right.
The random features (the rotation of the packet geometry, the sequence of variants within a sub-block, the sequence of pairs within a block, and the misorientaton distribution of the laths within the same sub-block) were kept unchanged among all RVEs in order to minimize statistical differences from random parameters. Still, some features were randomly created and to diminish the influence of the random choices, a larger RVE would be required.
The RVEs in this section are used to study the macroscopic response. Additionally, the damage initiation behavior is analyzed. To this end, the equivalent plastic strain (), which is commonly used to assess the extent of damage in materials subjected to plastic deformation [59], is used as a ductile damage indicator. The damage behavior of this steel is outlined in what follows.
For a FB steel, three types of micro-voids are present, depending on the location of the nucleation:
- Type-I voids at the PF–GB boundary.
- Type-II voids at the PF–PF boundary or in the PF grain.
- Type-III voids at the GB–GB boundary.
According to the literature, type-I voids appear first during deformation [10,11,13], and type-II and type-III voids may appear later [11,14]. When the steel fractures, type-I and type-II micro-voids can develop into large dimples located in PF which are caused by the growing and tearing within the PF grains. It has been experimentally determined that highly strained regions at the PF–GB boundary expand toward the inner region of the PF grains, forming micro-cracks [10]. Type-III voids develop into small dimples caused by the coalescence of voids in GB without tearing [11]. Type-III voids can use type-II voids for propagation and micro-crack formation [13]. These two modes of strain propagation along different paths to form micro-cracks was also shown by Tu et al. [13].
All of the above is in agreement with the fact that type-I voids appear first. However, Tu et al. [12] showed that the above behavior was only seen in a layered-type microstructure, where the strain concentration was preferentially generated at the PF–GB boundaries. Micro-voids of type-I then combined with the ones in GB (type-III) to form micro-cracks through bainite, leading to final fracture. In this case, the plastic capacity of PF was not fully utilized. In contrast, in a steel with a network-type microstructure, the strain was preferentially located at the PF phase, increasing the required strain for micro-voids to sprout, while those in GB did not expand rapidly, as determined by Tu et al. [12]. In this case, type-II voids were formed early on and the plastic capacity of PF was fully utilized.
The results for this section are shown in Section 5.4 where the interpretation of these results applied to the materials S and S is given at the end.
5. Results and Discussion
5.1. Fitting of CP Parameters
The CP parameters determined for the GB and PF phases for both materials are displayed in Table 3. Note that the GB parameters are determined through the described inverse method approach [28], while the PF parameters are determined through fitting the macroscopic stress–strain curves of the tensile tests. In both cases, the CRSSs from micropillar compression tests (see Table 2) were used as upper bounds and to determine the ratio between the slip plane families, which is estimated to be approximately 1:1:1. The initial resistances (), the saturation resistances (), and the strain hardening exponent (a) were determined. The initial hardening rate () was also fitted, in contrast to work by Gallardo-Basile et al. [28], where it was fixed. The elastic constants (, , and ), the stress exponent (n), and the reference shear rate () taken from work by Gallardo-Basile et al. [28] were assumed to be fixed and the same for both phases in both materials.

Table 3.
Determined crystal plasticity parameters.
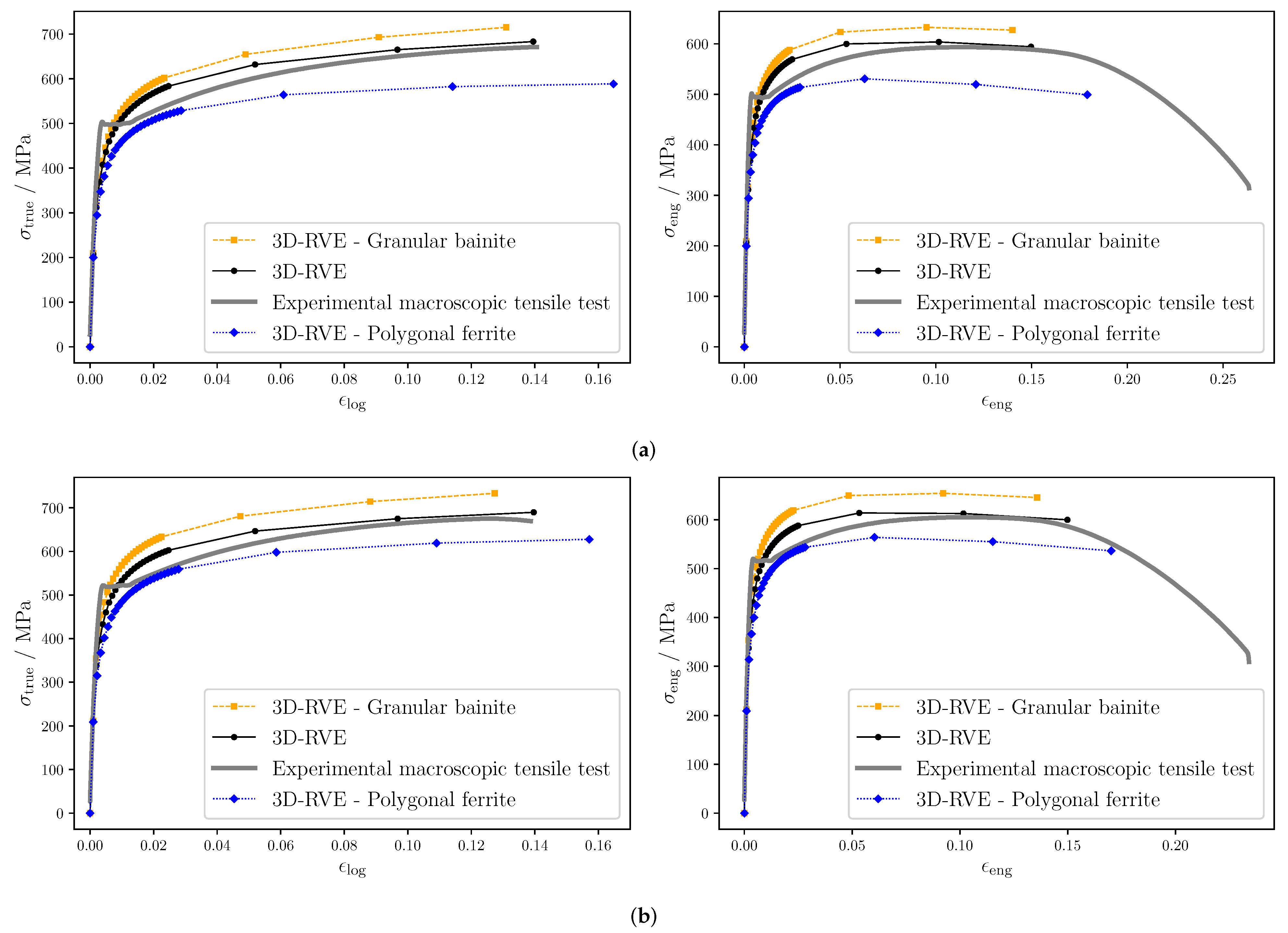
The simulated true and engineering stress–strain curves determined from the fitted CP parameters are plotted in Figure 7. The average simulation material response is colored in black and the experimental macroscopic tensile test in gray. The individual phase response of each phase is plotted in blue and in orange for PF and GB, respectively. Note that the fitting considers only the true stress–strain curves up to the ultimate yield stress. The experimental engineering stress–strain curves are displayed including the part after necking. The experimental tensile test exhibits the Lüders Bands phenomenon. This discontinuity when transitioning from elastic to plastic deformation is not included in the CP model and therefore the fitting is expected to deviate more in that zone.
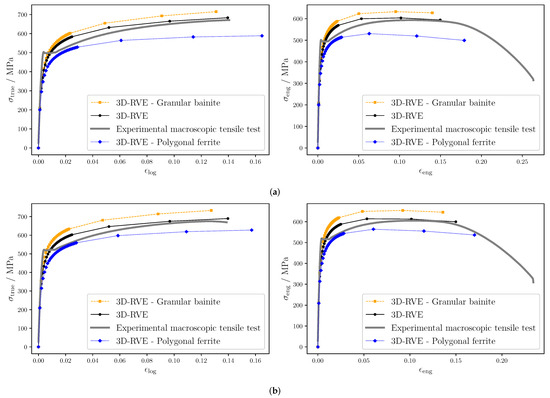
Figure 7.
True (left) and engineering (right) stress–strain curves for materials (a) and (b). The simulation results were obtained using a 3D-RVE with the fitted CP parameters of each individual phase.
5.2. Representative Volume Element—RVE
The average response of the material and of each individual phase is displayed in Figure 8 for the different RVEs used in this work.
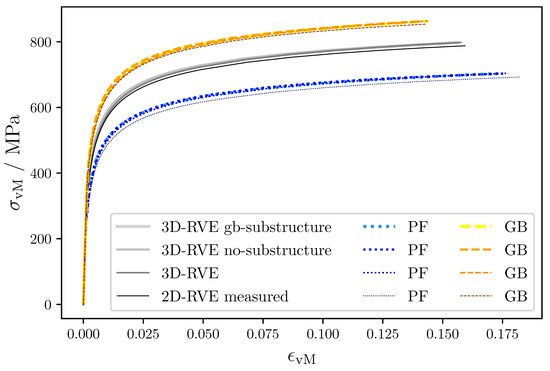
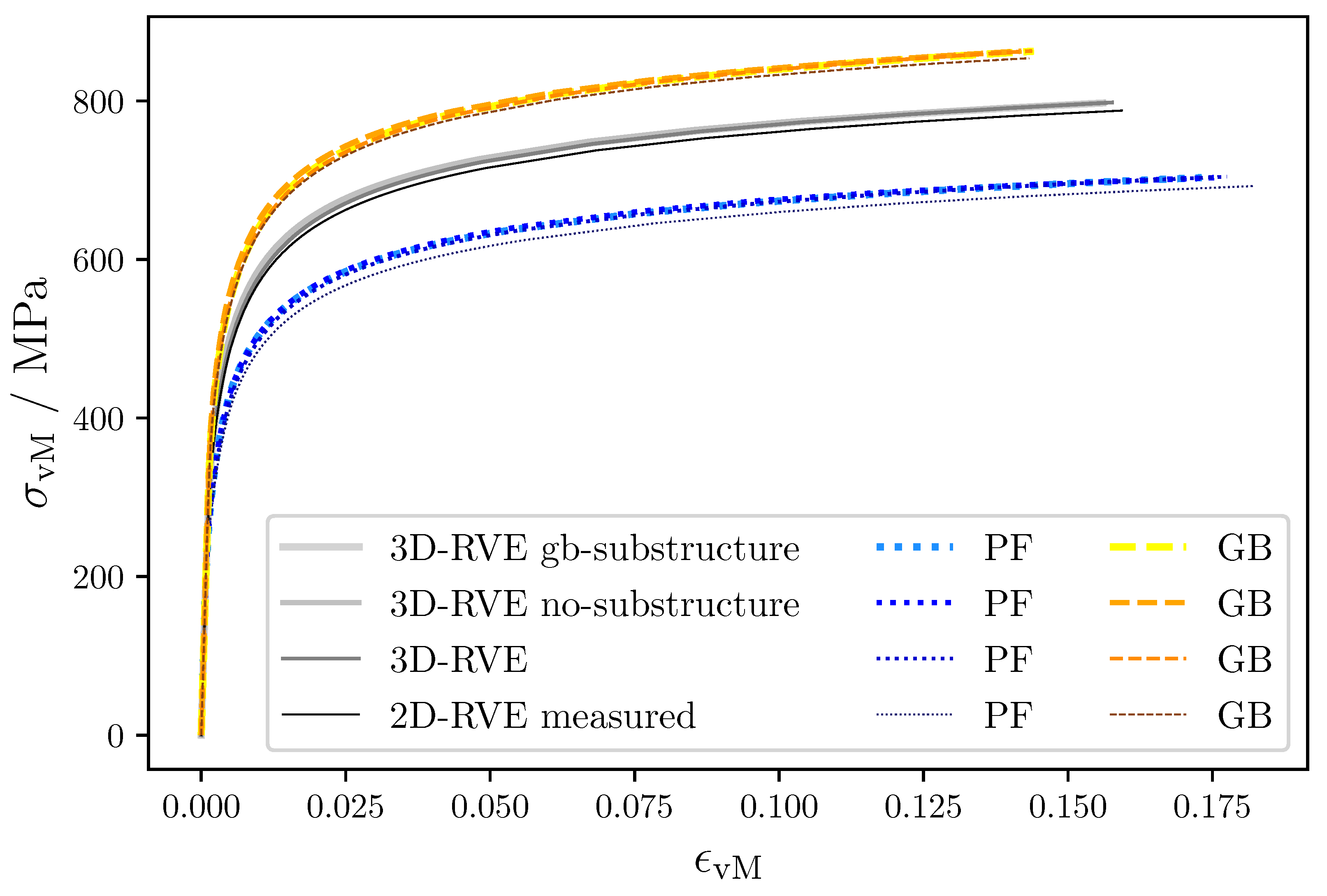
Figure 8.
Macroscopic stress–strain curves for the different RVEs used in this work. Polygonal ferrite is shown in blue and granular bainite is shown in in orange.
The von Mises stress–strain curves in Figure 8 show no significant differences among the RVEs. Only the output from the “2D-RVE measured” RVE deviates by exhibiting a softer behavior in each phase and in the whole material. This is expected, since the soft grains penetrate through thickness in the 2D case. The small differences among the other RVEs imply that the macroscopic results are not significantly affected by:
- Using a 2D- or a 3D-RVE. The 2D vs. 3D transition shows the biggest differences among all RVEs, but still the deviation is not significant. A small difference in the macroscopic results achieved from a 2D-RVE vs. a 3D-RVE has already been reported by Gallardo-Basile et al. [31]. There, a comparison was made between a 2D-RVE based on a direct measurement and a 3D-RVE with lath-like microstructure (similar to “2D-RVE measured” and “3D-RVE gb-substructure” in this manuscript). Additionally, a 2D-RVE with lath-like microstructure is created by cutting a slice of the 3D-RVE. In all the cases, the stress–strain curves showed small deviations from each other.
- Using the experimental grain size distribution or the one created from Voronoi tesellation of random seeds. Similar results were obtained from the “3D-RVE”, where the experimental grain size distribution was used and the “3D-RVE no-substructure”, where Voronoi tesellation is used. This is expected since the constitutive law used is not size dependent.
- Representing the experimental texture (low texture index) with 80 or 10 k grains. Similar results were obtained from “3D-RVE” and “3D-RVE no-substructure”.
- Including the substructure modeling of bainitic ferrite or not. Similar results were obtained from “3D-RVE no-substructure” and “3D-RVE gb-substructure”.
All these results also suggest that, for the utilized CP model, the main inputs required to predict the macroscopic behavior are the phase fraction and the CP parameters of each phase.
To investigate if the microscopic results are consistent among the different RVEs, the von Mises stress distributions were calculated for the final applied strain and are plotted in Figure 9.
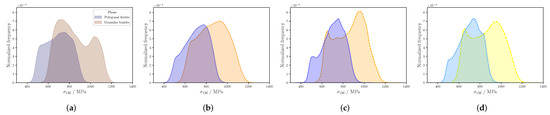
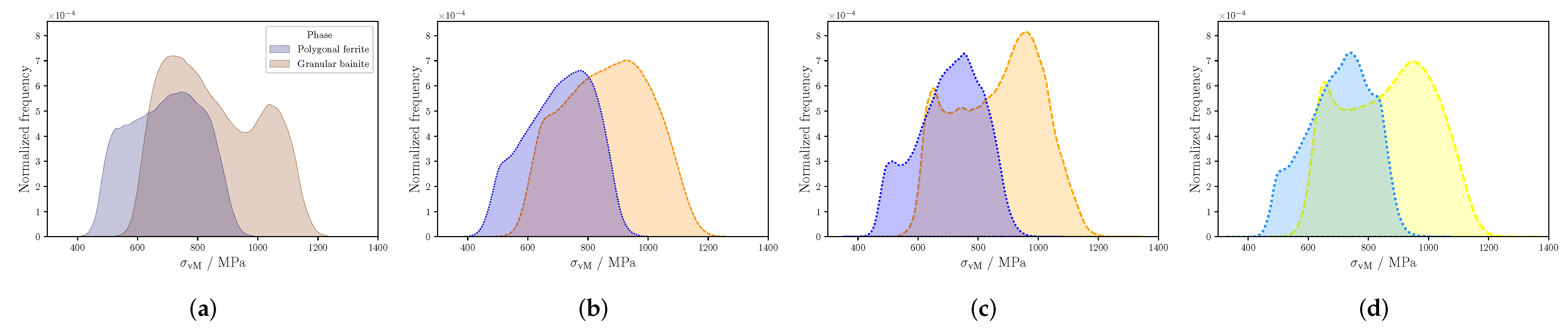
Figure 9.
Stress distributions at the final applied strain for 2D-RVE measured (a), 3D-RVE (b), 3D-RVE no-substructure(c), and 3D-RVE gb-substructure (d) RVEs. Polygonal ferrite is colored in blue tones and granular bainite in orange tones.
From Figure 9, it can be seen that the stress distributions of PF resemble a bi-modal distribution with two peaks, one around 500 and the other around 800 . For the 2D-RVE, both peaks have similar frequencies and it appears more like a uni-modal distribution, while for the 3D-RVEs, both peaks are much more clearly differentiated and the second one is around double the frequency of the first one. Regarding the GB, all four RVEs exhibit a different stress distribution. The 2D-RVE shows a bi-modal distribution with peaks at 800 and 1100 MPa, the first peak having a higher frequency. The “3D-RVE” shows an almost uni-modal distribution around 1000 . The “3D-RVE no-substructure” shows a bi-modal distribution with peaks at 600 and 1000 , with the second peak having a higher frequency, while for the “3D-RVE gb-substructure”, both peaks have approximately the same frequency.
From the results in Figure 9 it becomes clear that, in contrast to the macroscopic response, the microscopic response is significantly different for the different RVEs. Therefore, if the interest is on a microscopic level, an accurate description of the microstructure is needed.
5.3. Mechanical Behavior S1 and S2
The stress–strain curves for the “3D-RVE gb-substructure” (almost identical to those shown in Figure 7) were used to calculate the simulated and the simulated flow stress at a point close to the final deformation (). These values and the experimental ones are compared in Table 4. The simulated values are 82 and 63 less than the experimental ones for materials and S, respectively. Two facts potentially contributed to this discrepancy. First, the CP parameters of GB were determined using a method with reported inaccuracy in calculating the initial resistances () [28], which is directly related to . Secondly, the fitting of the CP parameters of PF was complicated by the Lüders Bands phenomenon; the zone where is measured and where the simulation and the experimental stress–strain curves deviate significantly. However, the simulation results in Table 4 show that material has a lower than , which is in agreement with the experiments. The flow stresses close to the final deformation are very similar to the experimental ones and also show a higher value for S compared to S. For both materials, the stress values for the individual phase GB are higher than those for PF. This is expected, since GB shows greater strength in micropillar compression and a higher dislocation density than PF (see Table 1).

Table 4.
Results from the stress–strain curves for materials S and S.
To further investigate the differences in the mechanical behavior of both materials, the average stress and the plastic strain (see Figure 10) were analyzed for each phase of both materials. The plastic strain indicator () was calculated in terms of the cumulative plastic shear of all slip systems. In Figure 10a, the average stress responses of both phases of are weaker than the ones of S. PF and GB have a higher yield point in compared to S, in accordance with the higher initial resistances shown in Table 3. In Figure 10b, the plastic strains of PF and GB are slightly higher in S. A zoom-in on the initial part shows that the onset of the plastic deformation of PF is almost the same for both materials and that the GB plasticity is delayed for S. This last result agrees with the one of Ishikawa et al. [10], where it was shown that a lower bainitic fraction was associated with a delay in the onset of the plasticity of GB.
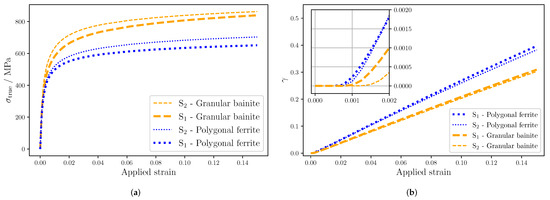
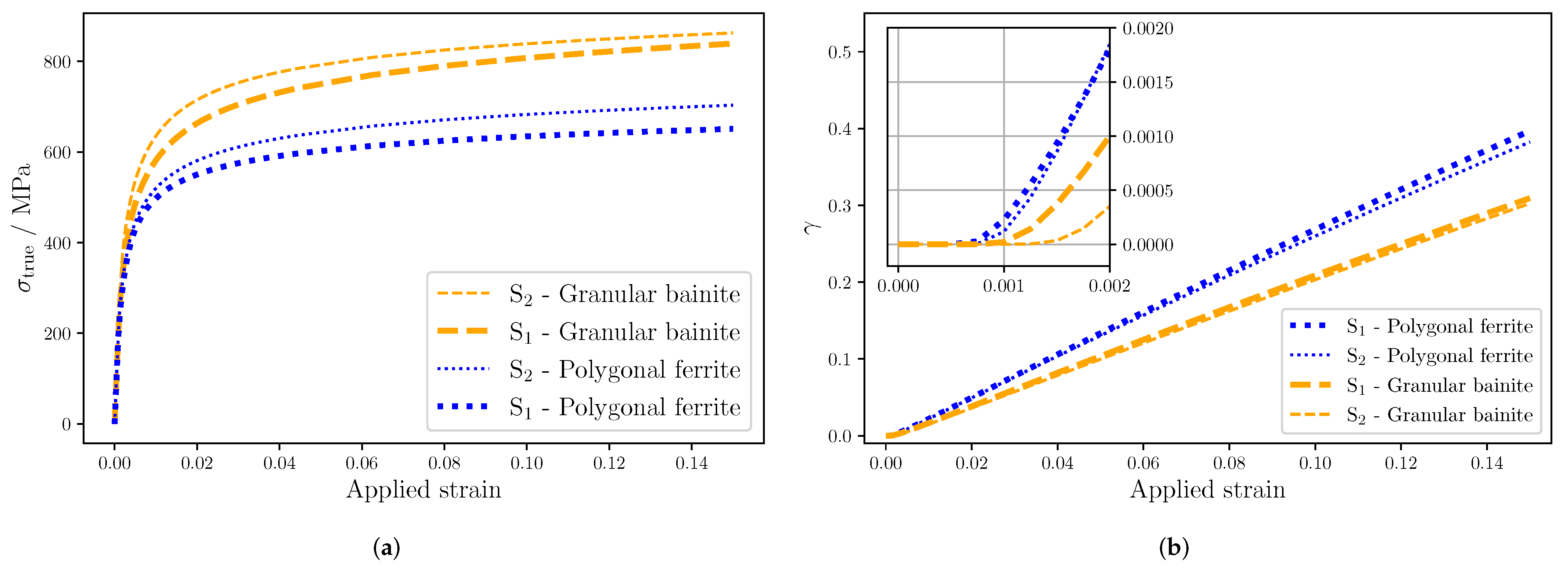
Figure 10.
Average stress per phase (a) and plastic strain per phase (b) in materials and S.
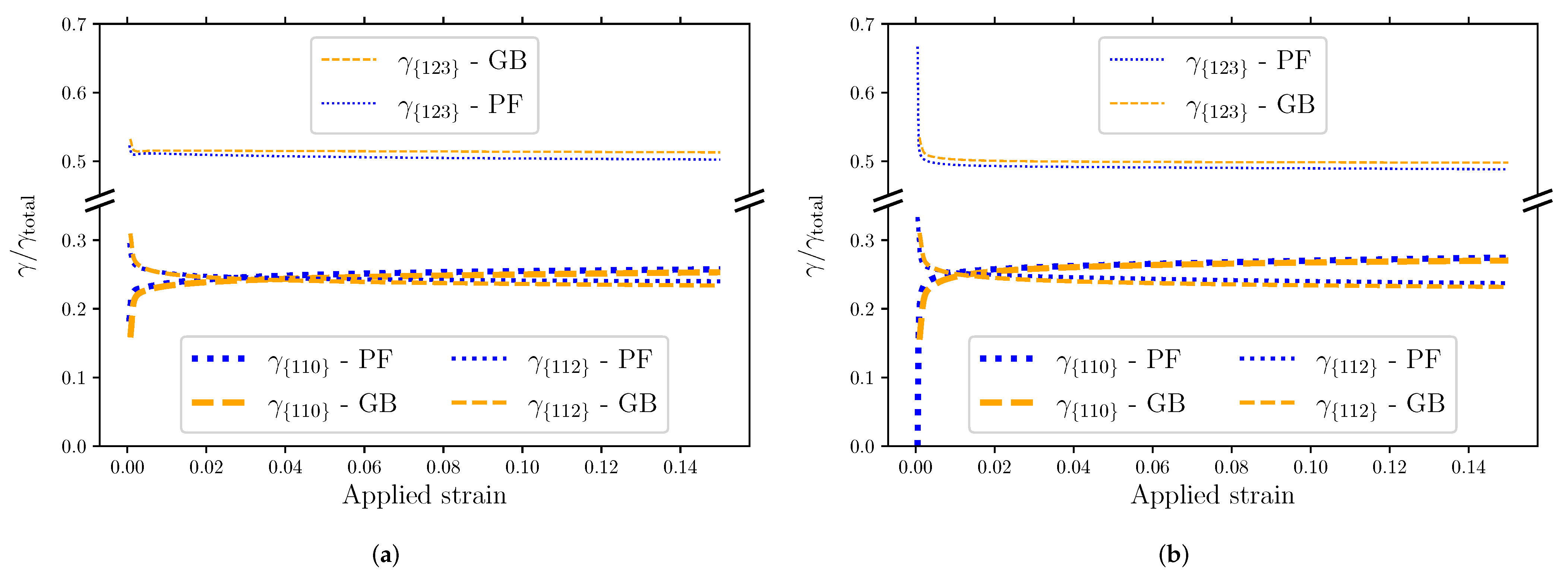
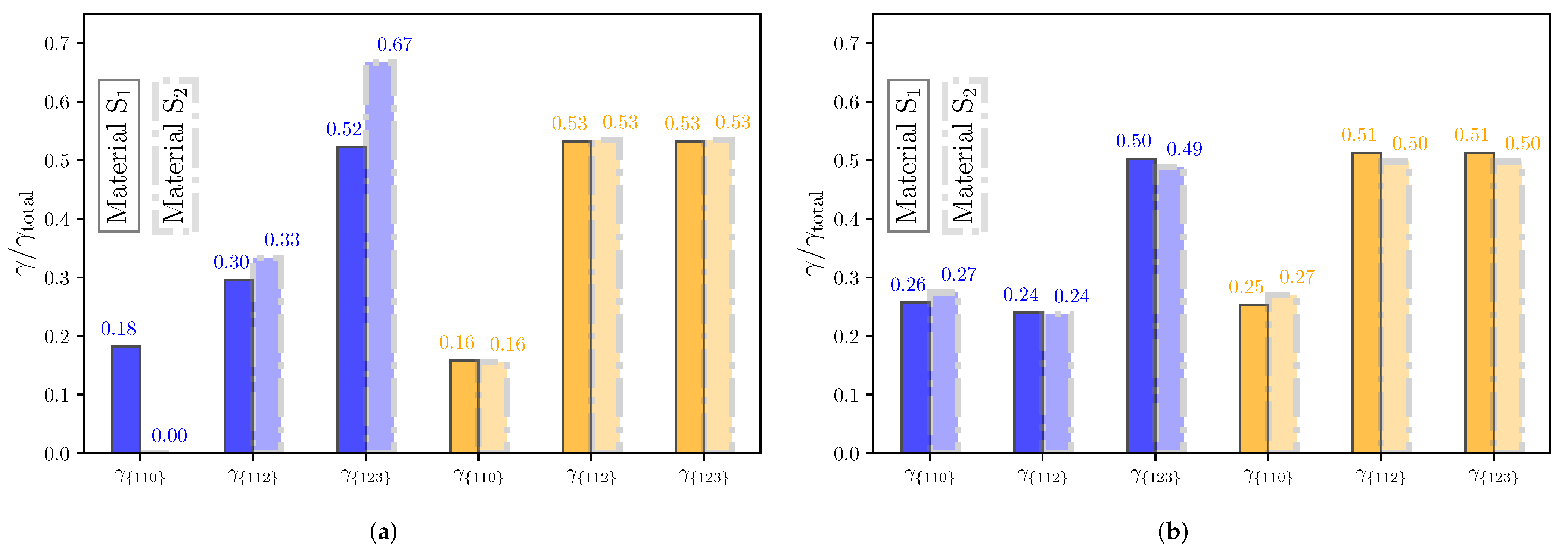
The cumulative plastic shear per slip system is presented in Figure 11. Both materials exhibit a similar behavior. The plastic shear is initially mainly in the {1 2 3} slip planes, with some contribution from the {1 1 2} family, while the {1 1 0} is contributing less (S) or not at all (S). The contribution of the {1 2 3} slip system saturates quite quickly and is stable throughout the whole deformation process. Note that the contribution of the {1 1 0} slip system catches up with the one of {1 1 2} at applied strains of approximately 0.03 and 0.01 for materials S and S, respectively. The contributions of both are around 25%, with the {1 1 0} slip system contributing slightly more in the end than {1 1 2}. These results are similar to those experimentally measured by Tu et al. [14] (51.7%, 15.0%, and 33.3% for {1 2 3}, {1 1 2}, and {1 1 0}, respectively). The contributions at the beginning and at the end of the applied strain are plotted in Figure 12. The main difference can be seen for PF at the initial deformation (see Figure 12a). For material S, the partitioning of is between {1 2 3} and {1 1 2}, while for material S, {1 1 0} contributes 0.18% from the start.
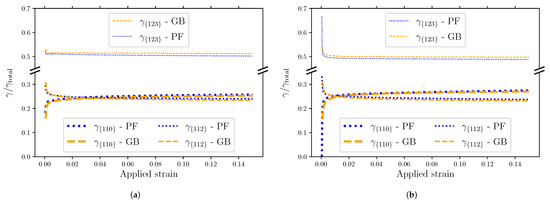
Figure 11.
Contributions per slip plane family to the total cumulative plastic shear in materials (a) and (b). Polygonal ferrite is shown in blue and granular bainite is shown in orange.
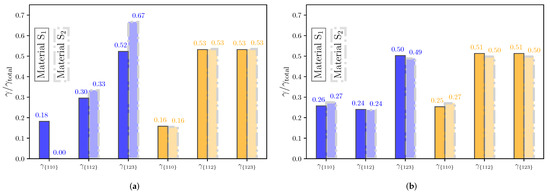
Figure 12.
Contributions per slip plane family to the total cumulative plastic shear at the initial (a) and final (b) deformation. Polygonal ferrite is shown in blue and granular bainite is shown in orange.
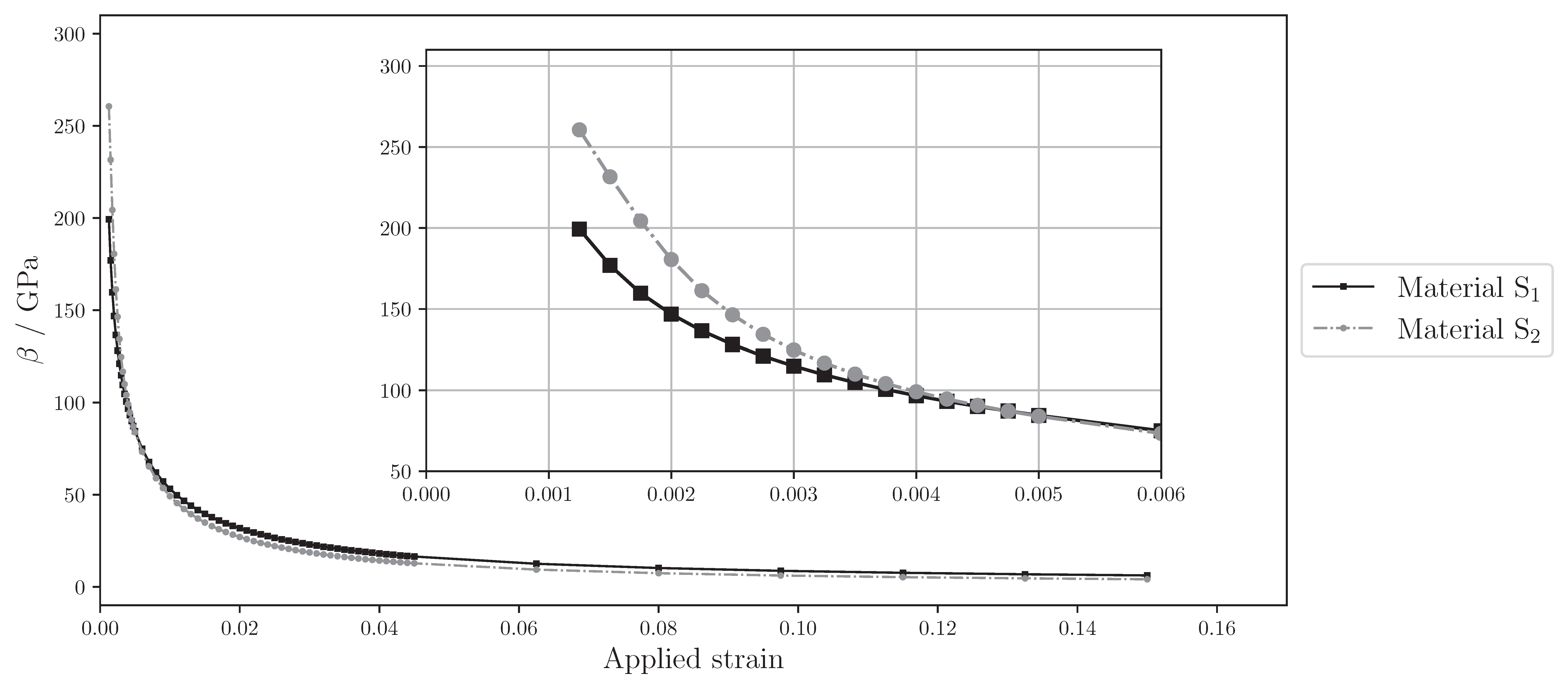
To investigate the strain partioning in the two materials, the parameter β described in Section 4.3 was calculated in dependency of the applied strain and shown in Figure 13. A zoom-in on the initial part reveals the differences in the early stage of deformation. It can be seen that the strain partitioning has a peak at the beginning for both materials. Initially, β of S2 is higher than that of S1, i.e., S2 is closer to the iso-strain behavior while S1 is closer to the iso-stress behavior. The faster decay of β for S2 leads to the same value of β ≈ 100 GPa at a strain of approximately 0.004. Beyond an applied strain of approximately 0.005 up to the final deformation, S2 has a slightly lower β.
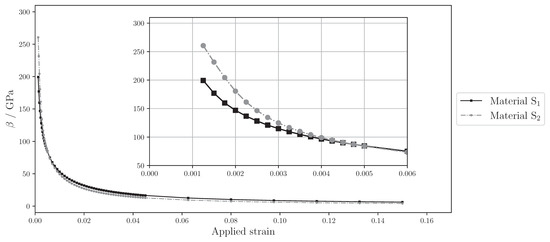
Figure 13.
Strain partioning parameter against the applied strain.
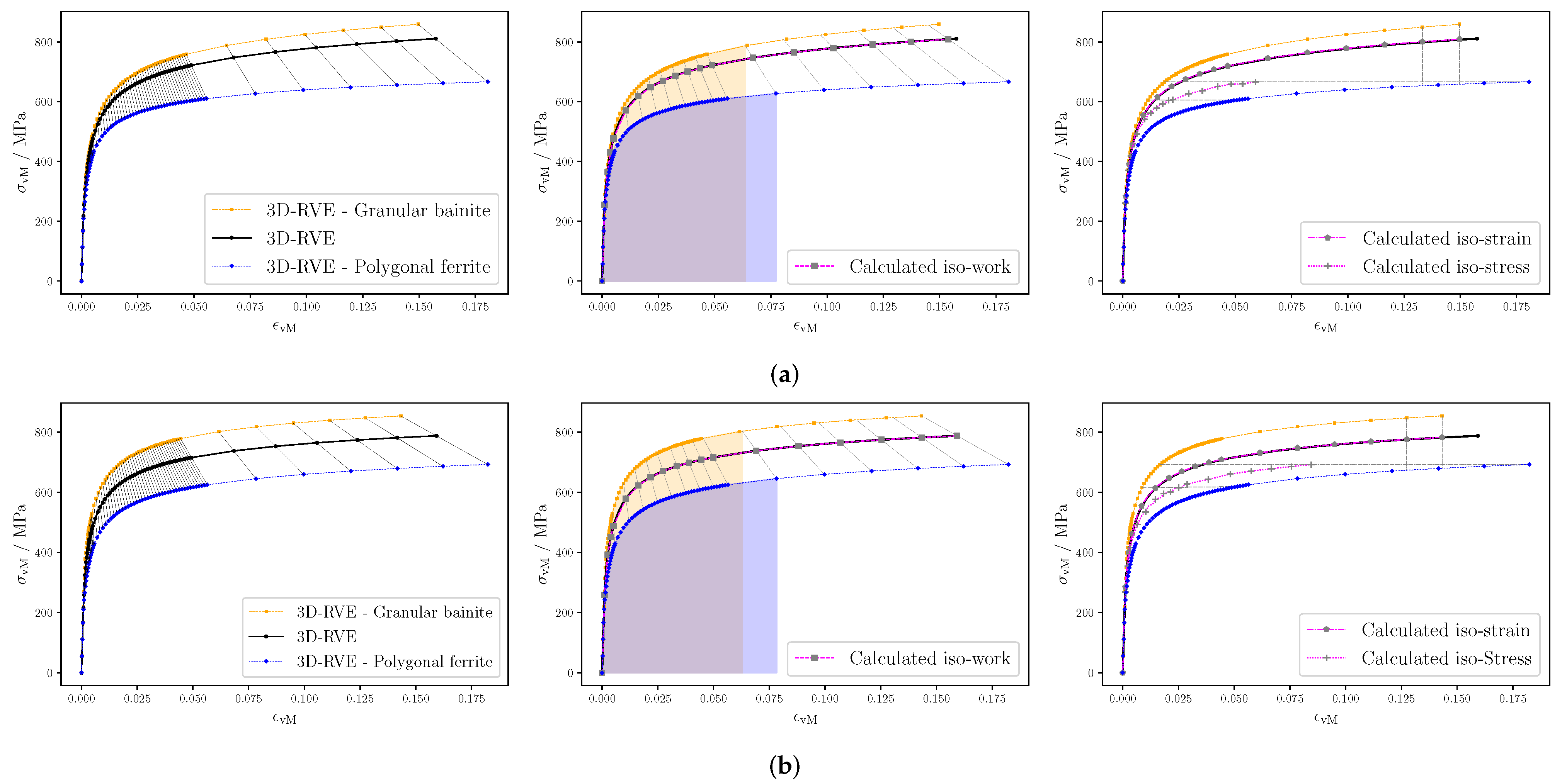
Finally, the results for the three different laws of mixtures, as introduced in Section 4.3, are shown in Figure 14. The left column of Figure 14 shows the results from the simulation output. The orange line corresponds to the average response among all points of GB. Analogously, the blue line corresponds to the response of PF. The black line, which is the stress–strain curve for the material, was calculated from the average response of all points at a given applied strain (gray line). In the middle and right columns of Figure 14, the stress–strain curves of the material (pink line with gray markers) were calculated using the individual stress–strain curve of each phase from the simulation output (blue and orange lines) and applying different assumptions (iso-work, iso-strain, and iso-stress). Some points of these calculated curves are shown with gray markers, and the weighted points considered are the ones at the end of the dashed gray lines. For the iso-work assumption, the sixth/fifth (S/S, respectively) point from last point is selected to show that the work done by each individual phase is the same (the shaded part is equal for both phases). Note that the blue and yellow points—represented by diamonds and squared markers, respectively—are the same throughout Figure 14.
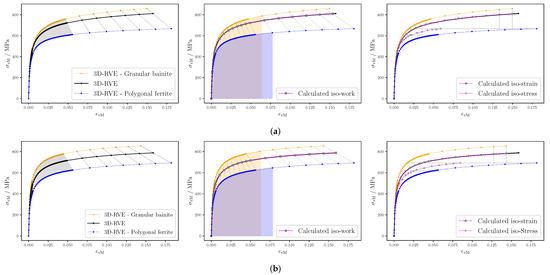
Figure 14.
Stress–strain curves for the simulation output (left column), for the iso-work assumption (middle), and for the iso-stress and iso-strain assumptions (right column) in materials (a) and (b).
The iso-stress assumption is the one that shows the greatest deviation in Figure 14. The iso-strain and iso-work stress–strain curves are very close to the simulation output, although they differ at the end point because the strain partitioning is not correctly described. The iso-strain assumption underestimates the PF deformation and overestimates it in GB for both materials. This is also the case for the iso-work assumption for S, although the misestimation is much less. On the other hand, for the iso-work assumption in S, the opposite is true, but also with a relatively small misestimation. Therefore, the iso-work assumption is proven to be the most accurate model within the ones studied here. This is a valuable finding as it allows to calculate the third stress–strain curve when the other two are known.
5.4. Microstructural Study of Ferritic Bainite
The macroscopic stress–strain curves are almost insensitive to the microstructural variations in this study. This is, however, not true for the local response, which is important for, e.g., damage initiation.
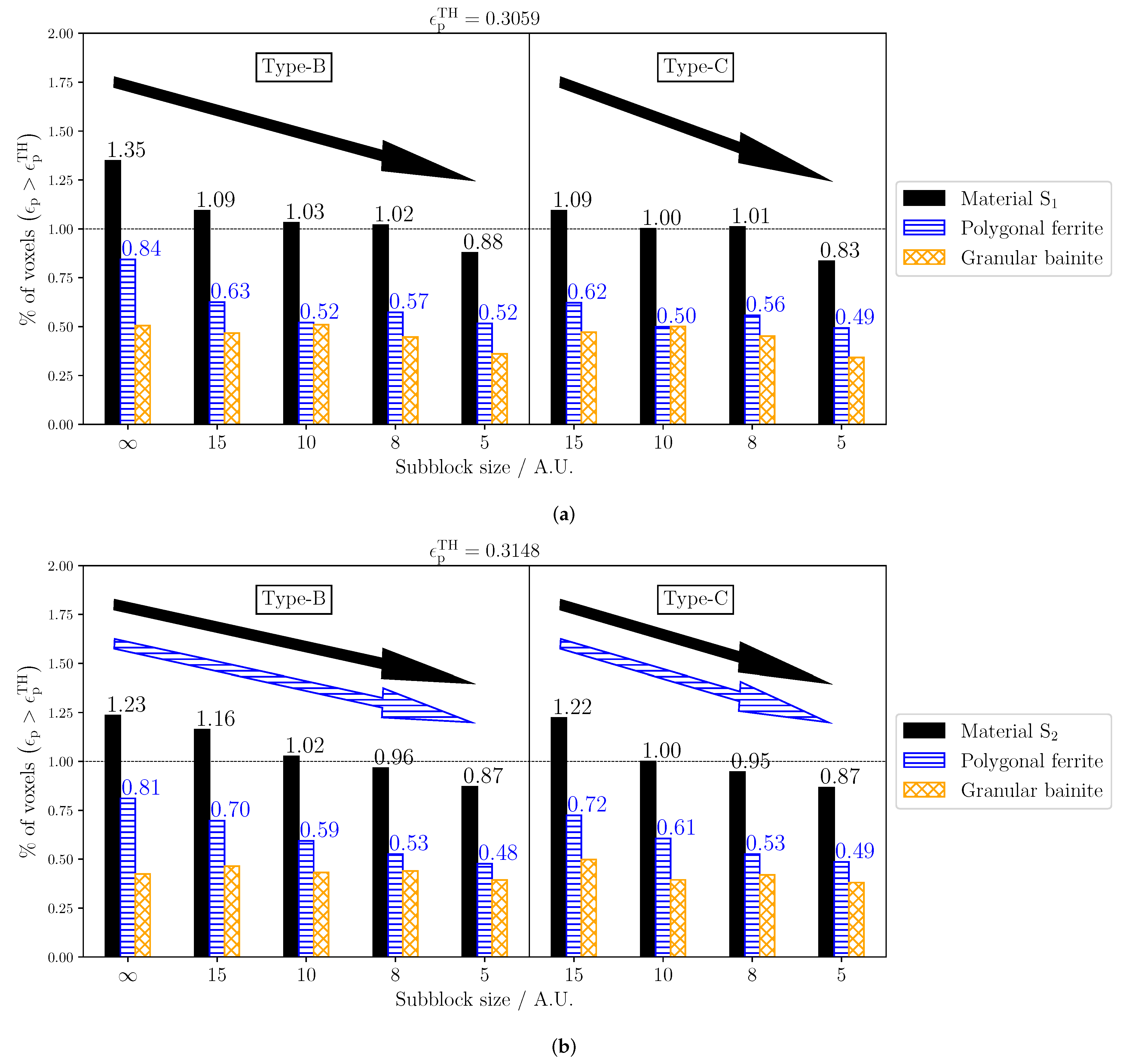
Damage initiation is represented by the fraction of points where the ductile damage parameter, , surpasses a certain threshold value at the final deformation stage. The threshold values were selected for each material to obtain results around 1%, and the results are shown in Figure 15 for both materials. Different thresholds to achieve 3% and 5% were also tested and the results obtained were qualitatively equivalent.
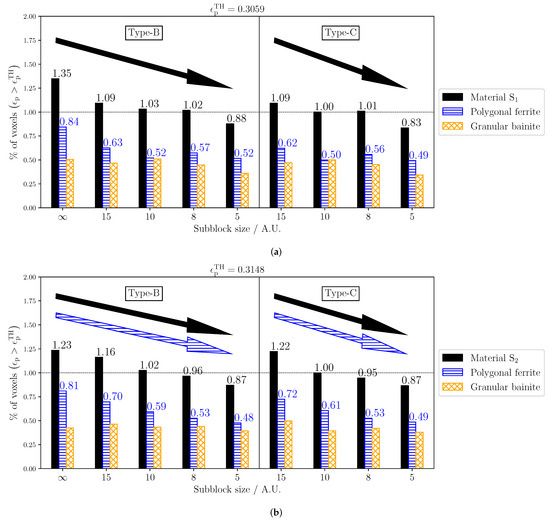
Figure 15.
The ductile damage parameter based on the equivalent plastic for RVEs with microstructural variations in materials (a) and (b).
The number of points with damage initiation in the whole material is proportional to the decrease in the sub-block size of the ferritic bainite. The contribution of both phases is significant. Note that, in all cases, the values for “type-B sb = X” are very similar to the ones in “type-C sb = X”. These two microstructures are almost the same and only differ inside the block structure, where the low-angle grain boundaries (LAGBs) are distributed differently. This variation in the placing of the LAGBs seems not to affect the damage initiation in this work. For GB (in orange without numeric data), no direct correlation can be seen between damage initiation and sub-block size. For PF, the trend is clearly shown in material , where the damage decreases with the sub-block size. In material , the trend is not so clear, since for a sub-block size of 10 the trend is broken, which can be attributed to statistical artifacts. The hypothesis that the substructure of GB affects the plasticity in polygonal ferrite is supported by these findings.
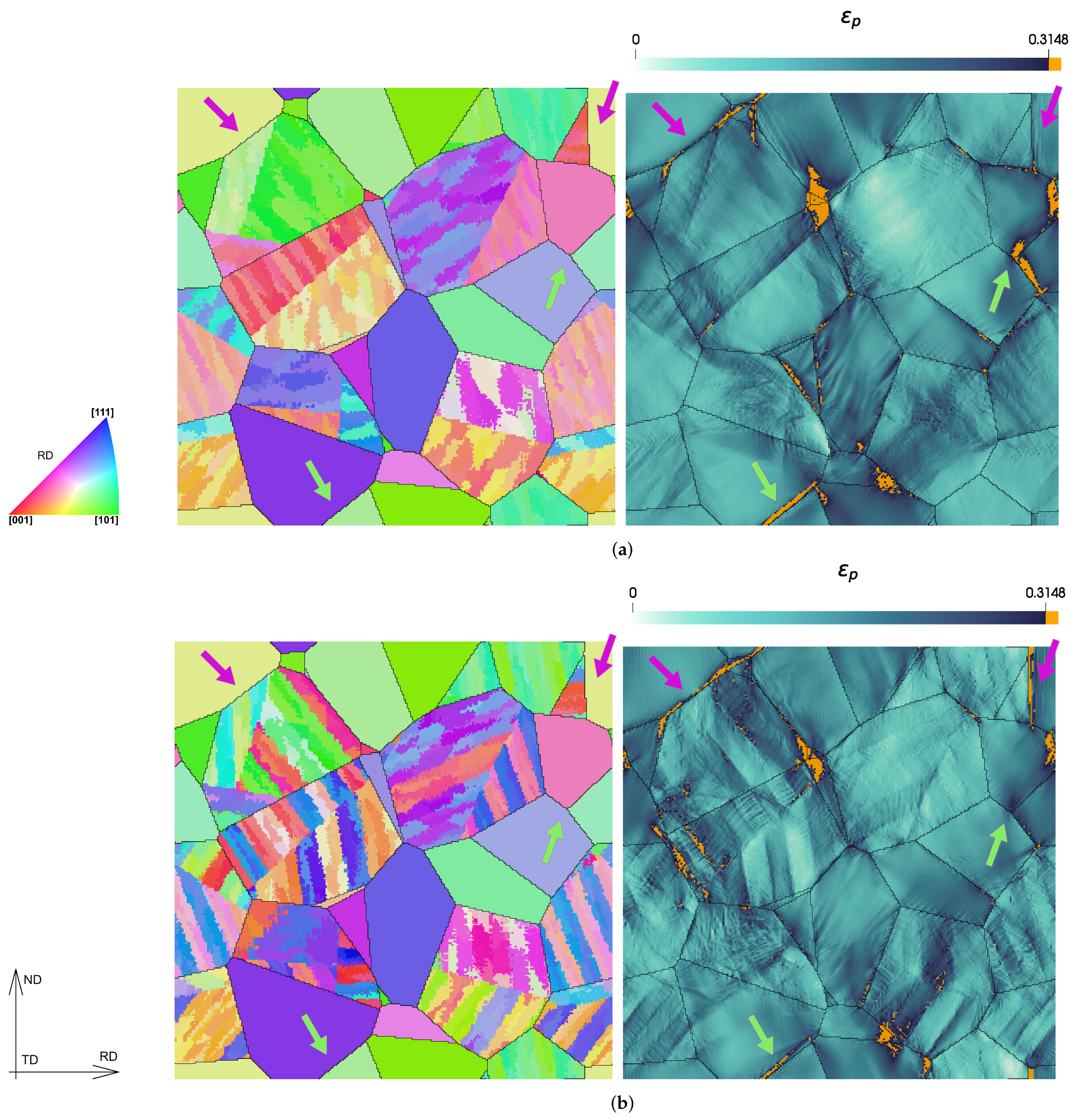
The spatially resolved results for are plotted in Figure 16 for one of the sections of material for the “type-B sb ” and “type-B sb = 5” RVEs. The high values, using the same threshold used as before, are colored in orange. From these images, one can observe that a high plastic strain in PF is situated at the PF boundaries. Note that for “type-B sb ”, there is a preference for the PF–PF boundaries (arrows colored in light green), which indicates the appearance of type-II voids. For “type-B sb = 5”, the preference is at the PF–GB boundaries (arrows colored in light green), which indicates the appearance of type-I voids. The finer the substructure of the ferritic bainite, the easier it is to accommodate the strain at the PF–GB boundaries. This is in agreement with what was shown experimentally by Tu et al. [14]. They demonstrated that high-angle grain boundaries (HAGBs) may allow slip transfer within a phase by evolving to medium-angle grain boundaries (MAGBs) or LAGBs to maintain a coordinated deformation behavior. This depended on the geometric orientation factor, and an example is shown in Figure 16, where some packet boundaries inside GB (which are HAGBs) accumulate a high plastic strain and others do not. However, in the case where an HAGB is situated at a phase boundary, the slip cannot be transferred across. In “type-B sb ”, the PF–GB boundary has a higher chance of being an HAGB since a packet of GB is only composed of two variants. Therefore, slip transfer between GB and PF is impeded. In “type-B sb = 5”, more variants appear at the PF–GB boundary, which has a higher chance of being—at least partially—an LAGB or an MAGB, which facilitates slip transfer across the phases.
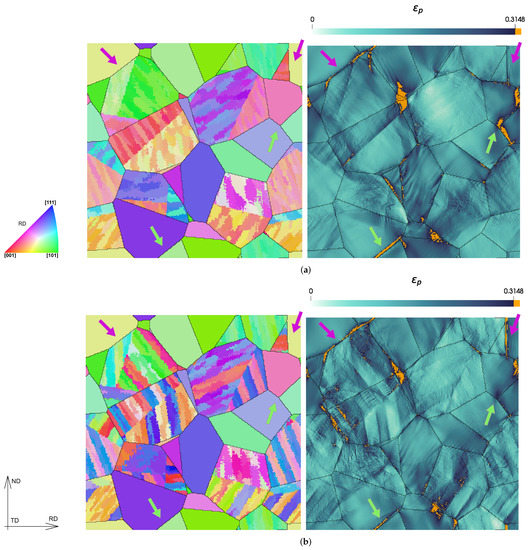
Figure 16.
IPF representation (left) and plastic strain map (right) for type-B sb (a) and Type-B sb = 5 (b) RVEs of material S. Two PF–PF boundaries are indicated with light green arrows. Two PF–GB boundaries are indicated with pink arrows.
It has been shown that the micro-voids of type-I may appear first and then the type-II, or vice versa depending on the bainitic microstructure.
The interpretation of these results applied to the materials S and S is here given. Material S (GB-41%PF) has a smaller grain size of and a lower ultimate elongation of 23% when compared to S (GB-25%PF) with a grain size of and an ultimate elongation of 26%. A finer bainitic substructure can be assumed for S considering the grain size. It has been shown that a finer substructure in GB is related to the preference of type-I (PF–GB) voids appearing first instead of type-II (PF–PF). Therefore, this could explain why S has a lower ultimate elongation, although it has a higher PF phase fraction. Material S is capable of fully utilizing the plastic capacity of PF, while material S is not.
6. Conclusions
Two different cooling rates are applied to a bainite dual-phase steel to obtain two materials, S and S, each containing polygonal ferrite (PF) and granular bainite (GB) in different proportions. The modeling of these two materials is performed by means of high-resolution crystal plasticity (CP) simulations with a phenomenological constitutive description. As a novelty, an RVE containing the substructure of bainite is used. The goals of the mechanical model developed are twofold: to investigate the differences in mechanical performance between the two different materials and to analyze other aspects of these steels which may be of interest.
The main results are summarized as follows:
- The CP parameters of PF and GB are determined for both materials. For GB, they are determined following an inverse modeling procedure based on measuring a post mortem nanoindentation imprint by atomic force microscopy and comparing it to a simulated one. For PF, they are determined by fitting the macroscopic stress–strain curves of the tensile tests.
- The heterogeneity of the microscopic results among the different RVEs is discussed. The von Mises stress–strain curves show no significant differences among the RVEs. This suggested that for the utilized CP model, the main inputs required to predict the macroscopic behavior are the phase fraction and the CP parameters of each phase. In contrast to the macroscopic response, the microscopic responses (stress distributions are shown) are clearly different for the different RVEs.
- The average stress and the plastic strain are analyzed for each phase of both materials. It is shown that the onset of the plastic deformation of PF is almost the same for both materials, but the GB plasticity is delayed for S, which contains a higher PF fraction.
- The contributions per slip plane family to the total cumulative plastic shear are calculated. The main difference in both materials is exhibited at the early stage of the deformation. For material S, the partioning of strain is made between {1 2 3} and {1 1 2}, while for material S, the {1 1 0} contributes 0.18% from the start.
- The strain partioning is calculated to be similar for both materials, except at the early stage of deformation, where material S2 is closer to iso-strain behavior while S1 is closer to iso-stress behavior. Both materials followed the iso-work assumption with only small deviations compared to the iso-strain and iso-stress which exhibited significant deviations.
- Ductile damage initiation is indicated by the fraction of points where the ductile damage parameter, , surpasses a certain threshold value at the final deformation stage. The contribution of both phases is shown to be significant. For GB, no direct correlation can be seen between damage initiation and sub-block size. For PF, the damage decreases with the sub-block size. It is shown that ductile damage initiation can be linked to a coarse bainitic substructure because of the accumulation of plastic strain at PF–PF boundaries (type-II voids).
- Material S has a higher PF phase fraction but a lower ultimate elongation compared to S. It is hypothesized that this can be explained by the preference of S to form type-I voids (PF–GB), which may interfere with the full utilization of the plastic capacity of PF.
Author Contributions
Conceptualization: F.-J.G.-B. Software development: F.-J.G.-B. Simulations and data analysis: F.-J.G.-B. Experiments: F.-J.G.-B. and R.M.J. Writing—original draft preparation: M.D., F.R. and F.-J.G.-B. Writing—review and editing: M.D. and F.-J.G.-B. Supervision: M.D., F.R., K.S. and S.S. All authors discussed the results and contributed to the final manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research is part of a collaboration between the Max–Planck–Institut für Eisenforschung and AG der Dillinger Hüttenwerke.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to its size.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ishikawa, N.; Shinmiya, T.; Shikanai, N.; Muraoka, R.; Kakihara, S. Recent advance in high strength linepipes for heavy sour service. In Proceedings of the Pipeline Technology Conference, Hannover, Germany, 22–23 April 2009; EITEP: Hannover, Germany, 2009; pp. 12–14. [Google Scholar]
- Kobayashi, K.; Omura, T.; Takahashi, N.; Minato, I.; Yamamoto, A. Advanced technologies for manufacturing high strength sour grade UOE line pipe. In Proceedings of the 2010 8th International Pipeline Conference, Calgary, AB, Canada, 27 September–1 October 2010; Volume 44212, pp. 289–297. [Google Scholar]
- Rosado, D.B.; Waele, W.D.; Vanderschueren, D.; Hertelé, S. Latest developments in mechanical properties and metallurgical features of high strength line pipe steels. Int. J. Sustain. Constr. Des. 2013, 4. [Google Scholar] [CrossRef] [Green Version]
- Javaheri, V.; Pohjonen, A.; Asperheim, J.I.; Ivanov, D.; Porter, D. Physically based modeling, characterization and design of an induction hardening process for a new slurry pipeline steel. Mater. Des. 2019, 182, 108047. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Bainite in Steels; Institute of Materials, IOM Communications Ltd.: London, UK, 2001. [Google Scholar]
- Entezari, E.; González-Velxaxzquez, J.L.; López, D.R.; Zúñiga, M.A.B.; Szpunar, J.A. Review of Current Developments on High Strength Pipeline Steels for HIC Inducing Service. Frat. Integrità Strutt. 2022, 16, 20–45. [Google Scholar] [CrossRef]
- Xu, X.N.; Tian, Y.; Ye, Q.B.; Misra, R.D.K.; Wang, Z.D. The Significant Impact of the Characteristics of Granular Structure and Granular Bainite on the Mechanisms Contributing to Strength–Ductility Combination. J. Mater. Eng. Perform. 2022, 30, 7479–7487. [Google Scholar] [CrossRef]
- Fang, H.-s.; Feng, C.; Zheng, Y.-k.; Yang, Z.-g.; Bai, B.-z. Creation of Air-Cooled Mn Series Bainitie Steels. J. Iron Steel Res. Int. 2008, 15, 1–9. [Google Scholar] [CrossRef]
- Akbarpour, M.R.; Ekrami, A. Effect of ferrite volume fraction on work hardening behavior of high bainite dual phase (DP) steels. Mater. Sci. Eng. A 2008, 477, 306–310. [Google Scholar] [CrossRef]
- Ishikawa, N.; Yasuda, K.; Sueyoshi, H.; Endo, S.; Ikeda, H.; Morikawa, T.; Higashida, K. Microscopic deformation and strain hardening analysis of ferrite–bainite dual-phase steels using micro-grid method. Acta Mater. 2015, 97, 257–268. [Google Scholar] [CrossRef]
- Tang, C.-j.; Liu, S.-l.; Shang, C.-j. Micromechanical behavior and failure mechanism of F/B multi-phase high performance steel. J. Iron Steel Res. Int. 2016, 23, 489–494. [Google Scholar] [CrossRef]
- Tu, X.; Ren, Y.; Shi, X.; Yan, W.; Shi, Q.; Shan, Y.; Li, C. Effect of distribution characters of ferrite/bainite on deformation compatibility in dual-phase pipeline steel: Experimental and numerical study. Mater. Today Commun. 2022, 33, 104923. [Google Scholar] [CrossRef]
- Tu, X.; Shi, X.; Shan, Y.; Yan, W.; Shi, Q.; Li, Y.; Li, C.; Yang, K. Tensile deformation damage behavior of a high deformability pipeline steel with a ferrite and bainite microstructure. Mater. Sci. Eng. A 2020, 793, 139889. [Google Scholar] [CrossRef]
- Tu, X.; Shi, X.; Yan, W.; Li, C.; Shi, Q.; Shan, Y.; Yang, K. Tensile deformation behavior of ferrite-bainite dual-phase pipeline steel. Mater. Sci. Eng. A 2022, 831, 142230. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization, and multiscale methods in crystal plasticity finite element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Roters, F. Advanced Material Models for the Crystal Plasticity Finite Element Method—Development of a General CPFEM Framework. Ph.D. Dissertation, RWTH Aachen, Aachen, Germany, 2011. [Google Scholar]
- Raabe, D.; Sachtleber, M.; Zhao, Z.; Roters, F.; Zaefferer, S. Micromechanical and macromechanical effects in grain scale polycrystal plasticity experimentation and simulation. Acta Mater. 2001, 49, 3433–3441. [Google Scholar] [CrossRef]
- Zaafarani, N.; Raabe, D.; Singh, R.N.; Roters, F.; Zaefferer, S. Three-dimensional investigation of the texture and microstructure below a nanoindent in a Cu single crystal using 3D EBSD and crystal plasticity finite element simulations. Acta Mater. 2006, 54, 1863–1876. [Google Scholar] [CrossRef]
- Raabe, D.; Roters, F. Using texture components in crystal plasticity finite element simulations. Int. J. Plast. 2004, 20, 339–361. [Google Scholar] [CrossRef]
- Tasan, C.C.; Hoefnagels, J.P.M.; Diehl, M.; Yan, D.; Roters, F.; Raabe, D. Strain localization and damage in dual phase steels investigated by coupled in situ deformation experiments-crystal plasticity simulations. Int. J. Plast. 2014, 63, 198–210. [Google Scholar] [CrossRef] [Green Version]
- Tasan, C.C.; Diehl, M.; Yan, D.; Zambaldi, C.; Shanthraj, P.; Roters, F.; Raabe, D. Integrated experimental-numerical analysis of stress and strain partitioning in multi-phase alloys. Acta Mater. 2014, 81, 386–400. [Google Scholar] [CrossRef]
- Roters, F.; Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Reuber, C.; Wong, S.L.; Maiti, T.; Ebrahimi, A.; Hochrainer, T.; Fabritius, H.-O.; et al. DAMASK—The Düsseldorf Advanced Material Simulation Kit for Modelling Multi-Physics Crystal Plasticity, Damage, and Thermal Phenomena from the Single Crystal up to the Component Scale. Comput. Mater. Sci. 2019, 158, 420–478. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. Lond. Ser. A 1976, 348, 101–127. [Google Scholar] [CrossRef]
- Jentner, R.M.; Srivastava, K.; Scholl, S.; Best, J.P.; Kirchlechner, C.; Dehm, G. Local strength of bainitic and ferritic HSLA steel constituents understood using correlative electron microscopy and microcompression testing. SSRN Electron. J. 2023. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4408322 (accessed on 5 April 2023).
- Jentner, R.M.; Tsai, S.-P.; Welle, A.; Srivastava, K.; Scholl, S.; Best, J.P.; Kirchlechner, C.; Dehm, G. Automated Classification of Granular Bainite and Polygonal Ferrite by Electron Backscatter Diffraction Verified through Local Structural and Mechanical Analyses. SSRN Electron. J. 2023. [Google Scholar] [CrossRef]
- Jentner, R.M.; Srivastava, K.; Scholl, S.; Gallardo-Basile, F.-J.; Best, J.P.; Kirchlechner, C.; Dehm, G. Unsupervised clustering of nanoindentation data for microstructural reconstruction: Challenges in phase discrimination. Materialia 2023, 28, 101750. [Google Scholar] [CrossRef]
- Bachmann, F.; Hielscher, R.; Schaeben, H. Texture Analysis with MTEX—Free and Open Source Software Toolbox. Solid State Phenom. 2010, 160, 63–68. [Google Scholar] [CrossRef] [Green Version]
- Gallardo-Basile, F.-J.; Roters, F.; Jentner, R.M.; Best, J.P.; Kirchlechner, C.; Srivastava, K.; Scholl, S.; Diehl, M. Application of a nanoindentation-based approach for parameter identification to a crystal plasticity model for bcc metals. MSEA, 2022; submitted. [Google Scholar]
- Groeber, M.A.; Jackson, M.A. DREAM.3D: A Digital Representation Environment for the Analysis of Microstructure in 3D. Integr. Mater. Manuf. Innov. 2014, 3, 56–72. [Google Scholar] [CrossRef] [Green Version]
- Ostoja-Starzewski, M. Material spatial randomness: From statistical to representative volume element. Probabilistic Eng. Mech. 2006, 21, 112–132. [Google Scholar] [CrossRef]
- Gallardo-Basile, F.-J.; Naunheim, Y.; Roters, F.; Diehl, M. Lath Martensite Microstructure Modeling: A High-Resolution Crystal Plasticity Simulation Study. Materials 2021, 14, 691. [Google Scholar] [CrossRef]
- EDAX. TSL OIM Analysis 7, Version 7.3.1; EDAX: Pleasanton, CA, USA, 2017.
- Bhadeshia, H.; Honeycombe, R. Formation of Martensite. In Steels: Microstructure and Properties; Butterworth-Heinemann: Oxford, UK; Elsevier: London, UK, 2017; pp. 135–177. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H.; Christian, J.W. Bainite in steels. Metall. Trans. A 1990, 21, 767–797. [Google Scholar] [CrossRef]
- Krauss, G. Martensite in steel: Strength and structure. Mater. Sci. Eng. A 1999, 273–275, 40–57. [Google Scholar] [CrossRef]
- Wayman, C.; Bhadeshia, H. Phase transformations, nondiffusive. In Physical Metallurgy; Butterworth-Heinemann: Oxford, UK; Elsevier: London, UK, 1996; pp. 1507–1554. [Google Scholar] [CrossRef]
- Murata, Y. Formation Mechanism of Lath Martensite in Steels. Mater. Trans. 2018, 59, 151–164. [Google Scholar] [CrossRef] [Green Version]
- Morito, S.; Tanaka, H.; Konishi, R.; Furuhara, T.; Maki, T. The morphology and crystallography of lath martensite in Fe-C alloys. Acta Mater. 2003, 51, 1789–1799. [Google Scholar] [CrossRef]
- Morito, S.; Huang, X.; Furuhara, T.; Maki, T.; Hansen, N. The morphology and crystallography of lath martensite in alloy steels. Acta Mater. 2006, 54, 5323–5331. [Google Scholar] [CrossRef]
- Maki, T.; Tsuzaki, K.; Tamura, I. The Morphology of Microstructure Composed of Lath Martensites in Steels. Trans. ISIJ 1980, 20, 207–214. [Google Scholar] [CrossRef] [Green Version]
- Nishiyama, Z. X-ray investigation of the mechanism of the transformation from face centered cubic lattice to body centered cubic. Sci. Rep. Tohoku Univ. 1934, 23, 637–664. [Google Scholar]
- Wassermann, G. Ueber den Mechanismus der α→γ-Umwandlung des Eisens. Mitt. K.-Wilh.-Inst. Eisenforsch. 1935, 17, 149–155. [Google Scholar]
- Kurdjumow, G.; Sachs, G. Über den mechanismus der stahlhärtung. Z. Phys. 1930, 64, 325–343. [Google Scholar] [CrossRef]
- Greninger, A.B.; Troiano, A.R. The mechanism of Martensite formation. JOM 1949, 1, 590–598. [Google Scholar] [CrossRef]
- Josefsson, B. Microscopy and Microanalysis of Bainitic Weld Metal. Ph.D. Dissertation, Chalmers University, Gothenburg, Sweeden, 1989. [Google Scholar]
- De-Castro, D.; Eres-Castellanos, A.; Vivas, J.; Caballero, F.G.; San-Martín, D.; Capdevila, C. Morphological and crystallographic features of granular and lath-like bainite in a low carbon microalloyed steel. Mater. Charact. 2022, 184, 111703. [Google Scholar] [CrossRef]
- Aaronson, H.I.; Wells, C. Sympathetic Nucleation of Ferrite. JOM 1956, 8, 1216–1223. [Google Scholar] [CrossRef]
- Chilton, J.; Barton, C.; Speich, G. Martensite transformation in low-carbon steels. J. Iron Steel Inst. 1970, 208, 184–193. [Google Scholar]
- Zhang, M.-X.; Kelly, P.M. Crystallography of carbide-free bainite in a hard bainitic steel. Mater. Sci. Eng. A 2006, 438–440, 272–275. [Google Scholar] [CrossRef]
- Davenport, E.S.; Bain, E.C. Transformation of austenite at constant subcritical temperatures. Metall. Mater. Trans. B 1970, 1, 3503–3530. [Google Scholar] [CrossRef]
- Davenport, A. The crystallography of upper bainite. Repub. Steel Res. Rep. Proj. 1974, 12051, 1–35. [Google Scholar]
- Landheer, H.; Offerman, S.E.; Petrov, R.H.; Kestens, L.A.I. The role of crystal misorientations during solid-state nucleation of ferrite in austenite. Acta Mater. 2009, 57, 1486–1496. [Google Scholar] [CrossRef]
- Abbasi, M.; Kim, D.-I.; Nelson, T.W.; Abbasi, M. EBSD and reconstruction of pre-transformation microstructures, examples and complexities in steels. Mater. Charact. 2014, 95, 219–231. [Google Scholar] [CrossRef]
- Tamura, M.O.I.; Tomota, Y. In Proceedings of the 3rd International Conference on the Strength of Metals and Alloys, Cambridge, UK, 20–25 August 1973.
- Voigt, W. Über die Beziehung zwischen den beiden Elastizitätskonstanten isotroper Körper. Ann. Phys. 1889, 38, 573–587. [Google Scholar] [CrossRef] [Green Version]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Und Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Bouaziz, O.; Buessler, P. Mechanical behaviour of multiphase materials: An intermediate mixture law without fitting parameter. Rev. Métall. 2002, 99, 71–77. [Google Scholar] [CrossRef]
- Furuhara, T.; Kawata, H.; Morito, S.; Maki, T. Crystallography of upper bainite in Fe–Ni–C alloys. Mater. Sci. Eng. A 2006, 431, 228–236. [Google Scholar] [CrossRef]
- Lou, Y.; Huh, H. Prediction of ductile fracture for advanced high strength steel with a new criterion: Experiments and simulation. J. Mater. Process. Technol. 2013, 213, 1284–1302. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).