Abstract
We studied a non-interacting /V-type dice model composed of three triangular sublattices. By considering the isotropic nearest-neighbor hoppings and the next-nearest-neighbor hoppings with the phase, as well as the quasi-staggered on-site potential, we acquired the full phase diagrams under the different fillings of the energy bands. There are abundant topological non-trivial phases with different Chern numbers , as well as higher ones and a metal phase in several regimes. In addition, we also checked the bulk–edge correspondence of the system by analyzing the edge-state energy spectrum.
1. Introduction
By means of an environment with a low temperature and strong magnetic field, Klitzing et al. discovered the quantum Hall effect in 1980 [1]. This discovery kicked off a wave of research on the quantum Hall effect, and a series of research on the topological features of condensed matter was inspired in the following decades [2,3,4]. These types of condensed matter are well classified according to their symmetry [5]. With these efforts, people have found some new topological quantum matter [6,7,8] with a quantum anomalous Hall effect (QAHE) [9], which releases the harsh condition of realizing a strong magnetic field.
A Chern insulator is a kind of insulator with QAHE that breaks the time-reversal symmetry. Its topological features can be directly reflected by the topological invariant, i.e., the Chern number (C). Thouless–Kohmoto–Nightingale–den Nijs (TKNN) first used the Chern number to describe the topological properties of a two-dimensional system [10]. In a gapped system, when the Fermi energy lies in a bulk band gap, the Chern number is always an integer and is equal to the quantized Hall conductance in units of [11,12,13]. Chern numbers can be used to distinguish whether or not a system has topological properties. In other words, () corresponds to the topological nontrivial (trivial) phase. Afterwards, by developing TKNN’s theory, Berry provided an alternative way to calculate the topological invariant with the Berry gauge field in the Brillouin zone [14]. Interestingly, the Chern numbers are linked to gapless edge states, forming the so-called bulk-edge correspondence [15]. The magnitude of the Chern number indicates the number of edge states.
In 1988, Haldane first theoretically pioneered the idea of breaking the time-reversal symmetry by applying a zero net magnetic flux through each unit cell in a hexagonal lattice and engineered a topological nontrivial model with , which is known as the Haldane model [16]. This model opens a gate for people to study QAHE and has more or less influenced other two-dimensional systems that appeared later, such as the Checkerboard lattice [17], Kagomé lattice [18,19,20,21] and Lieb lattice [22,23,24,25]. Moreover, by considering the long-range tunneling [26,27,28] or more a complex magnetic flux [29,30,31], one can obtain the topological phase with a higher Chern number.
Recently, people have realized the Haldane model by trapping ultracold atoms in an optical lattice formed by three standing-wave laser beams [32,33,34] or in a periodically modulated optical honeycomb lattice [35]. In addition to these experiments, there have been several works about the dice model [30,31] with a nonzero phase in the process of nearest-neighbor (NN) hoppings in the dice lattice [36,37,38,39,40,41,42,43]. In this paper, we will focus on a non-interacting dice model with a nonzero phase in the next-nearest-neighbor (NNN) term, but not in the NN term. We will consider a /V-type on-site potential, which will give us a more fruitful phase diagram and exciting topological phenomena.
By analyzing the dispersions of the bands, in this paper, we uncover that the system possesses two different phases—a metal phase and bulk insulating phase, which are both in the filling and filling cases. In the bulk insulating phase, the topological properties are further investigated. After calculating the Chern number, we find that there is a topological trivial phase with and topological nontrivial phases with , , and , which are separated by the band-crossing lines. Then, we obtain the full phase diagram and find that the metal phase and topological phases are symmetrically distributed within the phases. The relative positions of these phases in the phase diagram will be inverted when we change the filling from to , or vice verse. Finally, we also solve the edge-state spectrum and check the rule of bulk-edge correspondence.
This paper is organized as follows. In Section 2, we present the Hamiltonian of the dice model in both real and momentum space. In Section 3, we first analyze the band structures of the system. Next, we calculate the Chern numbers and numerically obtain the full phase diagram. Further, we check the bulk-edge correspondence through the edge-state spectrum. We summarize our work in the final section.
2. Model and Hamiltonian
Here, a non-interacting /V-type dice model is studied, and it is shown in Figure 1. There are three interpenetrating triangular sublattices, denoted by R (red dots), B (blue dots), and G (green dots). The lattice constant a is set as . The Hamiltonian of our model has three parts:
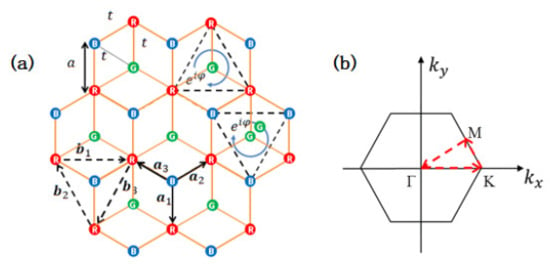
Figure 1.
(a) Geometry of the dice lattice. R, B, and G are sublattice sites, and are marked with red, blue, and green dots respectively. The lattice constant a is taken as . The vectors () link the nearest-neighbor sites that pertain to different sublattices. The vectors () link the nearest-neighbor R sites or B sites. The circle arrows represent the next-nearest-neighbor tunnelings accompanied by a phase . (b) The first Brillouin zone of the model. , K, and M are high-symmetry points in the high-symmetry path, and are connected by three red dashed lines.
The first part shows the isotropic hoppings with the same hopping amplitudes between nearest-neighbor sites, which pertain to various sublattices, and this part is presented as
in which t denotes the hopping amplitude, and it is regarded as the unit of energy, . are the fermionic annihilation operators, and , , and denote the coordinates of relevant sublattice sites R, B, and G, respectively. is the nearest-neighbor relation.
In the same R and B sublattices, we will consider the next-nearest-neighbor hoppings accompanied by a phase. Then, can be expressed as
in which is the hopping amplitude, where is the phase, and ± represents the direction of the hoppings (+ is the clockwise direction and − is the counterclockwise direction). References [30,31,32,33,34,44,45] tell us that the hopping terms in our toy models can be realized through laser-assisted tunneling. Moreover, the phase accompanied by the tunneling can be modulated with the momentum recoil. We think that this method is helpful in selectively engineering such a phase in specific hopping terms in experiments. At the very least, these are the most natural imperfections that may arise in the experimental implementation of such a model.
The final part describes the on-site potentials with a special configuration
in which denotes the potential at the R and B sublattice sites, and is the potential at the G sublattice sites. The configuration of the potential can be viewed as -type of three levels in a super atom, which is composed of three sites and forms a three-band model in the lattice case. This potential configuration differs from that in other dice models [30,31] and can also be realized by tuning single-beam lattice depths [34,35].
We consider a system that has discrete translational symmetry; thus, the single-particle Hamiltonian can be written in momentum space [46,47,48] as
where is a scalar, is a real vector with eight components, and denotes a vector consisting of Gell–Mann matrices [49]. As a matter of fact, the Chern number will not be affected by the scalar , and is only determined by . In order to obtain the , we need to perform a discrete Fourier transformation on the three-component basis :
After the derivation, we acquire the components of the vector , which are presented as
in which the six-unit vectors and (), which are shown in Figure 1a, are listed as
3. Results and Discussion
3.1. Band Structures
To begin, we study the band structures of the model described by Equation (1). The first Brillouin zone of this model is shown in Figure 1b, with , K, and M being the high-symmetry points [50]. Without loss of generality, in the following numerical calculation, we set . With the known components of in Equation (7), we can diagonalize and obtain its eigenvalues at each momentum . According to this strategy, we finally acquire the energy dispersions along the high-symmetry path --- with different and phase .
As a matter of fact, the energy at each band has a maximal value or a minimal value at a high-symmetry point. According to this obvious feature, we numerically analyze the energy gap between two adjacent energy bands, and finally uncover that the system consists of a bulk insulating phase and a metal phase. Figure 2 shows the metal–insulator phase diagram at 1/3 filling, and Figure 3 shows that for 2/3 filling. The green dots, which are marked as a, b, c, and d, are the four chosen typical parameter points. The terms 1/3 filling and 2/3 filling mean that the Fermi energies are selected to ensure that these three bands are filled just enough by and , respectively. There is no doubt that the system is in the metal phase (surrounded by the blue solid line and marked by M) when the gap is closed. The bulk insulating phase (marked by I) requires that the gap is be open. For instance, when the parameter is tuned to the a point, the gap is closed at 1/3 filling and is open at 2/3 filling. The consequence at the b point is the opposite of that at the a point. The system remains gapless at the c point and remains gapped at the d point. It is worth noting that the metal phase and bulk insulating phase are symmetrically distributed.
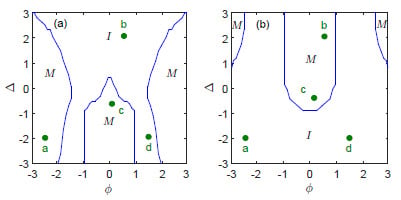
Figure 2.
The metal-insulator phase diagrams in the cases of filling (a) and filling (b). M refers to the metal phase and I refers to the bulk insulating phase. In each case, there are four chosen typical points, a, b, c, and d, which are marked by green dots and are discussed in the main text.
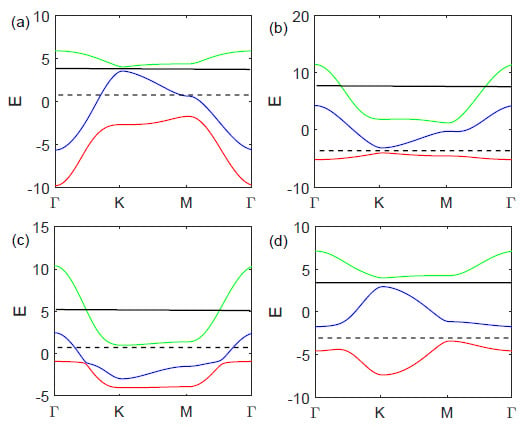
Figure 3.
Dispersions of the -type dice model along the high-symmetry path ---. (a) , , (b) , , (c) , , (d) , . The red, blue, and green solid lines show the dispersions. The lower Fermi energy (black dashed line) and higher Fermi energy (black solid line) show the cases of and filling, respectively.
Intuitively, the dispersion curves at these four chosen parameter points, , , , and , are plotted in Figure 3a–d, respectively. In these figures, we choose two Fermi energies to ensure the filling (black solid line) and the filling (black dashed line), respectively. In Figure 3a, because the top of the lowest band is higher than the bottom of the middle band, the Fermi energy crosses the middle band and forms a fully occupied lowest band and a partially occupied middle band. Accordingly, the system presents a metallic property in the filling case. If the Fermi energy is located at the filling line, the middle band is fully occupied and the highest band is empty. Then, in this case, the system will be in the bulk insulating phase. For the same reasons, one can easily comprehend that the system is a band insulator at filling and a metal at filling in the case shown in Figure 3b. Moreover, in Figure 3c,d, the system is stable in the metal phase and bulk insulating phase, respectively, no matter what the filling is. All of the results agree with our metal–insulator phase diagrams in Figure 2.
3.2. Chern Numbers and the Edge-State Spectrum
The nontrivial topological features of the Haldane model [16] and other dice models [30,31,43] motivate us to make it clear what topological phases exist in the bulk insulating region. According to the energy band theory [10,11,14], the n-th occupied band’s Chern number is defined as a contour integral along the boundary of the first Brillouin zone,
in which denotes the band index and , with being the associated eigenvector of . The ascending order of n indicates the band from the bottom to the top. The topological properties of this model can be reflected by two quantities, i.e., and , which satisfy and . We calculate the Chern number and obtain the full phase diagrams of the system, which are shown in Figure 4a,b for and filling of the system, respectively. There are several phase boundary lines in the bulk insulating phase, which are captured by the closing of the energy band. In Fact, the energy-crossing-lines also appear in the metal phase, but do not change the intrinsic properties of the metal phase. In each diagram, the black solid lines separate the topological nontrivial phase from the topological trivial phase, and the red solid lines distinguish the topological nontrivial phase with various and .
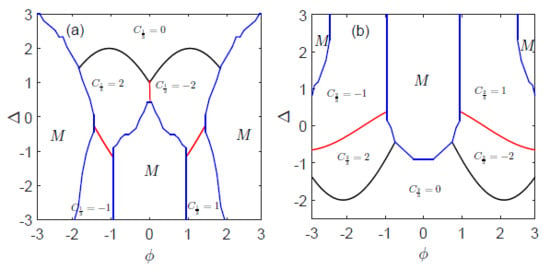
Figure 4.
Two full phase diagrams with (a) filling and (b) filling, respectively. The blue solid lines and axes surround the metallic region (M), and the bulk insulating region consists of several topological regions. The black solid lines separate the topological nontrivial phase from the topological trivial phase, and the red solid lines distinguish the topological nontrivial phase with various and .
As can be seen from the phase diagrams, abundant quantum phases exist in our model. In Figure 4a, intuitively, we know that, except for the metal phase, there are topological nontrivial phases with and , as well as the topological trivial phase with . A similar circumstance also appears in Figure 4. Furthermore, when the parameters are tuned continuously, the system will undergo abundant phases. We take as an example. As increases, at 2/3 filling, the system will undergo a closed circle with six different phases:
where M stands for the metal phase. The distribution of the phase diagram in Figure 4b ( filling) can be loosely regarded as the inversion of that with the filling. Similarly, the system can also undergo rich phases when we tune the Fermi energy.
In the following, we check the rule of the bulk–edge correspondence. We keep the x direction of the system periodic and make the system possess a zigzag edge along the y direction. Therefore, is a good quantum number. Finally, we solved the edge-state spectrum [4,15], which is plotted in Figure 5. We find that the system also obeys the rule of bulk–edge correspondence [15] for the reason that the magnitudes of and can be reflected from the intersections of the edge-state spectra. When we choose the parameter (, )=(), the edge-state spectrum intersects at (see Figure 5a), which means that there is only a pair of edge modes, corresponding to . The edge-state spectrum is gapped at 2/3 filling, which means that there are no edge modes, corresponding to . Meanwhile, at this parameter point, the Chern number of the lowest band is and that of the middle band is . In addition, it is known from the symmetry of the phase diagram that the Chern numbers become and at (, ) = (), and will also obtain the same edge-state spectrum as that in Figure 5a. When we select the parameter at (, ) = (), there are two different intersections at 1/3 filling (see Figure 5b), which means that there are two pairs of edge modes, corresponding to . The spectrum intersects at , which means that there is a pair of edge modes, corresponding to . By the definitions of and , we get and in this case. Similarly, when we take (, ) = (), we will know that and and we will obtain the same correspondence as that shown in Figure 5b.
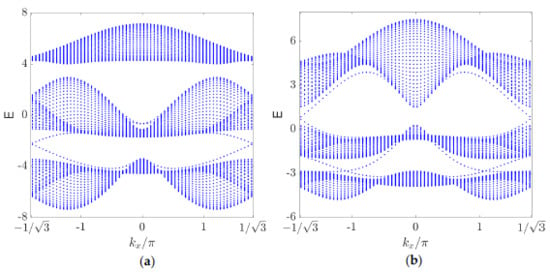
Figure 5.
Two edge-state spectra of a cylindrical geometry with a zigzag edge. (a) , . There is a pair of edge modes in the case of filling, corresponding to , while there are no edge modes in the case of filling, which corresponds to ; (b) , . There are two pairs of edge modes in the case of filling, which corresponds to , and there is only a pair of edge modes in the case of filling, which corresponds to .
4. Conclusions
To conclude, we have studied the band structures and topological properties of a /V-type dice model. First, we investigated the energy spectrum characteristics under filling and filling. In the - parameter space, the system can be divided into two parts: the metal phase and the bulk insulating phase. Furthermore, we calculated the Chern numbers according to the energy band theory in the bulk insulating phase and obtained a fruitful phase diagram. Interestingly, there are many topological nontrivial phases that are separated by some energy-level-crossing lines with different Chern numbers, such as , , and . Finally, by solving the edge-state spectrum, we found that the system obeys the rule of bulk-edge correspondence.
In spite of the existence of dice lattice structures in several electronic materials, such as [51], [52], and [53,54,55], the high free modulation of the parameters in cold-atom experiments will be convenient for us to study the topological phases by manipulating the neutral atoms, which never occurred in the aforementioned research. For this reason, we hope that our system can be realized in cold-atom experiments and that phases with higher Chern numbers will be observed.
Author Contributions
Conceptualization, X.G. and S.C.; methodology, X.G. and S.C.; software, X.G. and S.C.; validation, S.C.; formal analysis, S.C.; investigation, S.C.; resources, X.G.; data curation, S.C.; writing—original draft preparation, S.C.; writing—review and editing, X.G. and S.C.; visualization, X.G. and S.C.; supervision, X.G.; project administration, X.G.; funding acquisition, X.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NSFC under Grants No. 11835011 and No. 11774316.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the authors. The data are not publicly available due to intellectual property protection.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Klitzing, K.V.; Dorda, G.; Pepper, M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 1980, 45, 494. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Qi, X.-L.; Zhang, S.-C. Topological Insulators and Superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Shen, S.-Q. Topological Insulators; Springer: Berlin, Germany, 2012. [Google Scholar]
- Schnyder, A.P.; Ryu, S.; Furusaki, A.; Ludwig, A.W.W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 2008, 78, 195125. [Google Scholar] [CrossRef]
- Chang, C.-Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Li, K.; Ou, Y.; Wei, P.; Wang, L.-L.; et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 2013, 340, 167–170. [Google Scholar] [CrossRef]
- Chang, C.-Z.; Zhao, W.; Kim, D.Y.; Zhang, H.; Assaf, B.A.; Heiman, D.; Zhang, S.-C.; Liu, C.; Chan, M.H.W.; Moodera, J.S. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 2014, 14, 473–477. [Google Scholar] [CrossRef]
- Deng, Y.; Yu, Y.; Shi, M.Z.; Guo, Z.; Xu, Z.; Wang, J.; Chen, X.H.; Zhang, Y. Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. Science 2020, 367, 895–900. [Google Scholar] [CrossRef]
- Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H.; Ong, N.P. Anomalous Hall effect. Rev. Mod. Phys. 2010, 82, 1539. [Google Scholar] [CrossRef]
- Thouless, D.J.; Kohmoto, M.; Nightngale, M.P.; den Nijs, M. Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys. Rev. Lett. 1982, 49, 405. [Google Scholar] [CrossRef]
- Niu, Q.; Thouless, D.J.; Wu, Y.S. Quantized Hall conductance as a topological invariant. Phys. Rev. B 1985, 31, 3372. [Google Scholar] [CrossRef]
- Kohmoto, M. Topological Invariant and the Quantization of the Hall Conductance. Ann. Phys. 1985, 160, 343–354. [Google Scholar] [CrossRef]
- Kohmoto, M. Zero modes and the quantized Hall conductance of the two-dimensional lattice in a magnetic field. Phys. Rev. B 1989, 39, 11943. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. A 1984, 392, 45–57. [Google Scholar]
- Hatsugai, Y. Chern number and edge states in the integer quantum Hall effect. Phys. Rev. Lett. 1993, 71, 3697. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”. Phys. Rev. Lett. 1988, 61, 2015. [Google Scholar] [CrossRef]
- Sun, K.; Yao, H.; Fradkin, E.; Kivelson, S.A. Topological insulators and nematic phases from spontaneous symmetry breaking in 2D fermi systems with a quadratic band crossing. Phys. Rev. Lett. 2009, 103, 046811. [Google Scholar] [CrossRef]
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys. Rev. B 2000, 62, R6065. [Google Scholar] [CrossRef]
- Xiao, Y.; Pelletier, V.; Chaikin, P.M.; Huse, D.A. Landau levels in the case of two degenerate coupled bands: Kagomé lattice tight-binding spectrum. Phys. Rev. B 2003, 67, 104505. [Google Scholar] [CrossRef]
- Guo, H.M.; Franz, M. Topological insulator on the kagome lattice. Phys. Rev. B 2009, 80, 113102. [Google Scholar] [CrossRef]
- Liu, X.P.; Chen, W.C.; Wang, Y.F.; Gong, C.D. Topological quantum phase transitions on the kagomé and square–octagon lattices. J. Phys. Condens. Matter 2013, 25, 305602. [Google Scholar] [CrossRef]
- Weeks, C.; Franz, M. Topological insulators on the Lieb and perovskite lattices. Phys. Rev. B 2010, 82, 085310. [Google Scholar] [CrossRef]
- Apaja, V.; Hvrkas, M.; Manninen, M. Flat bands, Dirac cones, and atom dynamics in an optical lattice. Phys. Rev. A 2010, 82, 041402(R). [Google Scholar] [CrossRef]
- Goldman, N.; Urban, D.F.; Bercioux, D. Topological phases for fermionic cold atoms on the Lieb lattice. Phys. Rev. A 2011, 83, 063601. [Google Scholar] [CrossRef]
- Tsai, W.-F.; Fang, C.; Yao, H.; Hu, J. Interaction-driven topological and nematic phases on the Lieb lattice. New J. Phys. 2015, 17, 055016. [Google Scholar] [CrossRef]
- Yang, S.; Gu, Z.-C.; Sun, K.; Das Sarma, S. Topological flat band models with arbitrary Chern numbers. Phys. Rev. B 2012, 86, 241112. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Yao, H.; Gong, C.-D.; Sheng, D.N. Fractional quantum Hall effect in topological flat bands with Chern number two. Phys. Rev. B 2012, 86, 201101. [Google Scholar] [CrossRef]
- Sticlet, D.; Piėchon, F. Distant-neighbor hopping in graphene and Haldane models. Phys. Rev. B 2013, 87, 115402. [Google Scholar] [CrossRef]
- Hatsugai, Y.; Kohmoto, M. Energy spectrum and the quantum Hall effect on the square lattice with next-nearest-neighbor hopping. Phys. Rev. B 1990, 82, 8282. [Google Scholar] [CrossRef]
- Goldman, N.; Anisimovas, E.; Gerbier, F.; Öhberg, P.; Spielman, I.B.; Juzeliūnas, G. Measuring topology in a laser-coupled honeycomb lattice: From Chern insulators to topological semi-metals. New J. Phys. 2013, 15, 013025. [Google Scholar] [CrossRef][Green Version]
- Andrijauskas, T.; Anisimovas, E.; Račiūnas, M.; Mekys, A.; Kudriašov, V.; Spielman, I.B.; Juzeliūnas, G. Three-level Haldane-like model on a dice optical lattice. Phys. Rev. A 2015, 92, 033617. [Google Scholar] [CrossRef]
- Shao, L.B.; Zhu, S.-L.; Sheng, L.; Xing, D.Y.; Wang, Z.D. Realizing and Detecting the Quantum Hall Effect without Landau Levels by Using Ultracold Atoms. Phys. Rev. Lett. 2008, 101, 246810. [Google Scholar] [CrossRef]
- Alba, E.; Fernandez-Gonzalvo, X.; Mur-Petit, J.; Pachos, J.K.; Garcia-Ripoll, J.J. Seeing Topological Order in Time-of-Flight Measurements. Phys. Rev. Lett. 2011, 107, 235301. [Google Scholar] [CrossRef]
- Tarruell, L.; Greif, D.; Uehlinger, T.; Jotzu, G.; Essinger, T. Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice. Nature 2012, 483, 302–305. [Google Scholar] [CrossRef]
- Jotzu, G.; Messer, M.; Desbuquois, R.; Lebrat, M.; Uehlinger, T.; Greif, D.; Esslinger, T. Experimental realization of the topological Haldane model with ultracold fermions. Nature 2014, 515, 237–240. [Google Scholar] [CrossRef]
- Sutherland, B. Localization of electronic wave functions due to local topology. Phys. Rev. B 1986, 34, 5208. [Google Scholar] [CrossRef]
- Vidal, J.; Mosseri, R.; Doucot, B. Aharonov-Bohm Cages in Two-Dimensional Structures. Phys. Rev. Lett. 1998, 81, 5888. [Google Scholar] [CrossRef]
- Bercioux, D.; Urban, D.F.; Grabert, H.; Häusler, W. Massless Dirac-Weyl fermions in a T3 optical lattice. Phys. Rev. A 2009, 80, 063603. [Google Scholar] [CrossRef]
- Möller, G.; Cooper, N.R. Correlated Phases of Bosons in the Flat Lowest Band of the Dice Lattice. Phys. Rev. Lett. 2012, 108, 045306. [Google Scholar] [CrossRef]
- Rizzi, M.; Cataudella, V.; Fazio, R. Phase diagram of the Bose-Hubbard model with T3 symmetry. Phys. Rev. B 2006, 73, 144511. [Google Scholar] [CrossRef]
- Burkov, A.A.; Demler, E. Vortex-Peierls States in Optical Lattices. Phys. Rev. Lett. 2006, 96, 180406. [Google Scholar] [CrossRef]
- Bercioux, D.; Goldman, N.; Urban, D.F. Topology-induced phase transitions in quantum spin Hall lattices. Phys. Rev. A 2011, 83, 023609. [Google Scholar] [CrossRef]
- Cheng, S.; Yin, H.; Lu, Z.; He, C.; Wang, P.; Xianlong, G. Predicting large-Chern-number phases in a shaken optical dice lattice. Phys. Rev. A 2020, 101, 043620. [Google Scholar] [CrossRef]
- Dalibard, J.; Gerbier, F.; Juzeliūnas, G.; Ōhberg, P. Colloquium: Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 2011, 83, 1523. [Google Scholar] [CrossRef]
- Goldman, N.; Juzeliūnas, G.; Ōhberg, P.; Spielman, I.B. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 2014, 77, 126401. [Google Scholar] [CrossRef] [PubMed]
- Khanna, G.; Mukhopadhyay, S.; Simon, R.; Mukunda, N. Geometric phases for SU(3) representations and three level quantum systems. Ann. Phys. 1997, 253, 55–82. [Google Scholar] [CrossRef]
- Sachdev, S. Quantum Phase Transitions; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Barnett, R.; Boyd, G.R.; Galitski, V. SU(3) Spin-Orbit Coupling in Systems of Ultracold Atoms. Phys. Rev. Lett. 2012, 109, 235308. [Google Scholar] [CrossRef] [PubMed]
- Georgi, H. Lie Algebras In Particle Physics: From Isospin To Unified Theories; Benjamin/Cummings: Reading, MA, USA, 1982. [Google Scholar]
- Setyawan, W.; Curtarolo, S. High-throughput electronic band structure calculations: Challenges and tools. Comput. Mater. Sci. 2010, 49, 299–312. [Google Scholar] [CrossRef]
- Okamoto, S.; Xiao, D. Transition-Metal Oxide (111) Bilayers. J. Phys. Soc. Jpn. 2018, 87, 041006. [Google Scholar] [CrossRef]
- Rawl, R.; Lee, M.; Choi, E.S.; Li, G.; Chen, K.W.; Baumbach, R.; dela Cruz, C.R.; Ma, J.; Zhou, H.D. Magnetic properties of the triangular lattice magnets A4B′B2O12 (A=Ba, Sr, La; B′=Co, Ni, Mn; B=W, Re). Phys. Rev. B 2017, 95, 174438. [Google Scholar] [CrossRef]
- Schleid, T.; Meyer, G. Crystal structure of digadolinium monocarbide dichloride (1T type), Gd2CCl2. Z. Fur Krist. 1994, 209, 371. [Google Scholar] [CrossRef]
- Ryazanov, M.; Simon, A.; Mattausch, H. New synthesis route to and physical properties of lanthanum monoiodide. Inorg. Chem. 2006, 45, 2068–2074. [Google Scholar] [CrossRef]
- Schleid, T.; Meyer, G. Synthesis and crystal structures of hydrogen and carbon stabilized lutetium monochloride, LuClHx and Lu2Cl2C. Z. Fur Anorg. Undallgemeine Chem. 1987, 552, 90–96. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).