COMF: Comprehensive Model-Fitting Method for Simulating Isothermal and Single-Step Solid-State Reactions

Abstract

It is well known that the implementation of the conventional model-fitting (CMF) method leads to several indistinguishable ‘best’ candidate models (BCMs) for a single-step isothermal solid-state reaction (ISSR), meaning that subjective selection becomes unavoidable. Here, we developed a more robust comprehensive model-fitting method (COMF) which, while maintaining the mathematical simplicity of CMF, utilizes a ranking criterion that enables automatic and unambiguous determination of the BCM. For each model evaluated, COMF, like CMF, fits the integral reaction rate, but, unlike CMF, it also fits the experimental conversion fraction and reaction speed. From this, three different determination coefficients are calculated and combined to rank the considered models. To validate COMF, we used two sets of experimental kinetic data from the literature regarding the isothermal desolvation of pharmaceutical solvates: (i) tetrahydrofuran solvates of sulfameter, and (ii) methanol solvates of ciclesonide. Our results suggest that from an algorithmic perspective, COMF could become the model-fitting method of choice for ISSRs making the selection of BCM easier and more reliable.

1. Introduction

Solid-state reactions (SSRs) induced by heating occur in a broad range of processes such as the desolvation and dehydration of pharmaceutical crystals [1,2,3,4,5,6,7,8] or thermal decomposition of solids, e.g., pyrolysis [9,10,11,12,13]. To elucidate the mechanisms of chemical changes occurring when heating the solid reactants and to characterize the factors that control this process, various solid-state kinetic models have been developed [14,15,16,17,18]. The great challenge, when these models are implemented, is to accurately determine the so-called kinetic triplet, i.e., the kinetic model, activation energy and frequency factor, for a complete kinetic description of the overall reaction [19]. The kinetic analysis requires two main steps: (i) the collection of experimental thermal analysis data; and (ii) the appropriate computational techniques to calculate the kinetic triplet. Thermogravimetric analyzers are widely used to monitor weight changes of a solid sample, which undergoes heating at a constant temperature or heating rate, as a function of time and/or temperature. Additionally, there exist several methods for analyzing these kinetic data and performing mathematical analysis to determine the kinetic triplet [18,20]. Specifically, there are two main methods: (i) the conventional model-fitting method (CMF); (ii) and the iso-conversional or so-called model-free methods. Both can be used independently, in complement, or in a cross-validated manner depending on the nature of the thermogravimetric experiment and the requested outcome. So far, no single generic method capable of accurately calculating the kinetic triplet for any SSR has been developed [20,21].

We are interested in the CMF method, mainly due to its mathematical simplicity and straightforwardness for the determination of the kinetic triplet. Particularly, we are interested in using CMF for analyzing single-step isothermal solid-state reactions (ISSRs) [22], which usually take place during the drying process of pharmaceutical hydrates/solvates [1,2,3,4,21,23,24,25,26]. The most crucial step when performing CMF is to identify the ‘best’ candidate model (BCM) for a particular ISSR and then the complete kinetic triplet is calculated. This is done by fitting the integral reaction rate of each model explored with a straight line. The highest determination coefficient of these fits is the criterion that CMF relies on to finally chose the BCM. However, the implementation of CMF on real experimental data often leads to several indistinguishable BCMs that fit the kinetic data for a single ISSR equally well [15,21]. Therefore, the major drawback of CMF is that a subjective selection becomes unavoidable and thus the procedure of choosing the BCM is not automatic and possibly prone to user errors.

In this work, we improve CMF by developing a more robust comprehensive model-fitting method (COMF) for the case of single-step ISSRs. Our method maintains the mathematical simplicity of CMF, while it utilizes an alternative ranking criterion that enables automatic and unambiguous determination of the BCM. For each model considered, COMF similarly to CMF, fits the integral reaction rate, but, unlike CMF, also fits the experimental conversion fraction and reaction speed. Then, three different determination coefficients are calculated and combined to rank the evaluated models. We validated COMF on two sets of experimental kinetic data from the literature regarding the isothermal desolvation of pharmaceutical solvates: (i) tetrahydrofuran solvates of sulfameter [4] and (ii) methanol solvates of ciclesonide [3]. A brief reference for the CMF method follows, highlighting the most important elements that require improvement. Subsequently, the COMF method is introduced in detail followed by its implementation results. We conclude with a discussion of the results.

2. Theory

In solid-state kinetics, the mass loss of a reactant solid is always expressed in terms of the so-called extent of conversion or simply conversion fraction ($\alpha$), which ranges from 0 to 1 and is defined as [17]

$$\alpha =\frac{m_0-m_t}{m_0-m_{\infty }}$$

(1)

where $m_0$ is the initial sample weight, $m_t$ is the sample weight at time $t$ and $m_{\infty }$ is the final sample weight. The solid-state reaction speed for ISSRs is a function of both the reaction temperature and extent of the conversion and it is proportional to the product of the rate constant $k\left(T\right)$ with the differential reaction rate $f\left(\alpha \right)$:

$$\frac{d\alpha }{dt}=k\left(T\right)f\left(\alpha \right)$$

(2)

The rate constant is typically of Arrhenius type and can be expressed by

$$k\left(T\right)=A{e}^{-E_{\alpha }/RT}$$

(3)

where $A$ is the frequency factor, $E_{\alpha }$ is the activation energy, $T$ is the absolute temperature and $R$ is the ideal gas constant. The differential reaction rate, $f\left(\alpha \right)$, is a function of the conversion fraction and its form depends on the principal solid-state reaction mechanism, such as nucleation, diffusion, geometrical contraction, etc. [14,17,18,21,27]. By integrating Equation (2) over time, the so-called integral form of the reaction rate, $g\left(\alpha \right)$, is obtained:

$$\stackrel{g\left(\alpha \right)}{\overbrace{{\displaystyle \underset{0}{\overset{t}{\int }}\frac{1}{f\left(\alpha \right)}\frac{d\alpha }{dt}dt}}}=\stackrel{k}{\overbrace{A{e}^{-E_{\alpha }/RT}}}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\to g\left(\alpha \right)=kt$$

(4)

A variety of different models has been developed considering different reaction mechanisms [18]. Table 1 includes the most commonly used models found in the literature. The first column (left-hand side) of Table 1 includes the models’ names. All models used here are classified into four families, namely: nucleation, geometrical contraction, diffusion and reaction-order models. In the first column, we can therefore find each family (written in italic) and exactly below it the corresponding models. The models’ names, shown in Table 1, are represented by a letter attached to an integer number (e.g., A2). The letter reflects the model’s type, while the integer number is related with the reaction mechanism considered in each case. Specifically, the symbols P, A, R, D, F stand for Power Law, Avarami-Erofe’ev, Contraction, Diffusion and Reaction-Order, respectively. Details concerning all the different models used here, reaction mechanisms, and derivation of each model shown in Table 1 can be found in the literature [10,27,28,29]. Moreover, the second and third column of Table 1 include the forms of the so-called differential and integral reaction rates respectively for the various models. In fact, commonly in the literature, only the differential and integral rates for the various models are tabulated. However, in this work, we analytically solved the integral rate equation, $g\left(\alpha \right)=kt$, to obtain an expression for the conversion fraction itself for each model considering an arbitrary Arrhenius rate constant ($k$). These expressions are listed in the last column (right-hand side) of Table 1 accompanying their corresponding rates. Having the conversion fraction in a functional form is essential for our methodology as it is described below. Apparently, there are no analytical expressions of the conversion fraction for the diffusion models D2 and D4, for which the solution of the conversion fraction was obtained by numerical integration [30].

Table 1. Set of the various solid-state reaction models, which can potentially describe thermal transformations in solids. Solid-state reaction rates are presented in their differential and integral forms as well as the corresponding analytical expressions of the conversion fraction.

Models	Differential Form $\mathit{f}\left(\mathit{\alpha }\right)=\frac{1}{\mathit{k}}\frac{\mathit{d}\mathit{\alpha }}{\mathit{d}\mathit{t}}$	Integral Form $\mathit{g}\left(\mathit{\alpha }\right)=\mathit{k}\mathit{t}$	$\mathbf{Conversion}\mathbf{Fraction}\mathbf{Solution}\mathit{\alpha }=\left(\mathit{k};\mathit{t}\right)$
Nucleation
Power Law
P3	$2{\alpha }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$	${\alpha }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$	$k^2{t}^2$
P3	$3{\alpha }^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$	${\alpha }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$	$k^3{t}^3$
P4	$4{\alpha }^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}$	${\alpha }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}$	$k^4{t}^4$
Avarami-Erofe’ev
A2	$2\left(1-\alpha \right){\left[-\ln \left(1-\alpha \right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$	${\left[-\ln \left(1-\alpha \right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$	$1-\exp \left(-k^2{t}^2\right)$
A3	$3\left(1-\alpha \right){\left[-\ln \left(1-\alpha \right)\right]}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$	${\left[-\ln \left(1-\alpha \right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$	$1-\exp \left(-k^3{t}^3\right)$
A4	$4\left(1-\alpha \right){\left[-\ln \left(1-\alpha \right)\right]}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}$	${\left[-\ln \left(1-\alpha \right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}$	$1-\exp \left(-k^4{t}^4\right)$
Geometrical Contraction
R2 (Contracting area)	$2{\left(1-\alpha \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$	$1-{\left(1-\alpha \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$	$kt\left(2-kt\right)$
R3 (Contracting volume)	$3{\left(1-\alpha \right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$	$1-{\left(1-\alpha \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$	$kt\left(k^2{t}^2-3kt+3\right)$
Diffusion
D1 (1-D)	$\frac{1}{2}\alpha$	${\alpha }^2$	$\sqrt{kt}$
D2 (2-D)	${\left[-\ln \left(1-\alpha \right)\right]}^{-1}$	$\left(1-\alpha \right)\ln \left(1-\alpha \right)+\alpha$	-
D3 (3-D)	$\frac{3{\left(1-\alpha \right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{2\left[1-{\left(1-\alpha \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\right]}$	${\left[1-{\left(1-\alpha \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\right]}^2$	$\sqrt{kt\left(k^2{t}^2+6kt+9\right)}-3kt$
D4 (Ginstling-Brounshtein)	$\frac{3}{2}{\left[{\left(1-\alpha \right)}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}-1\right]}^{-1}$	$1-\frac{2\alpha }{3}-{(1-\alpha )}^{2/3}$	-
Reaction-order
F0 or R1 (Zero order)	$1$	$\alpha$	$kt$
F1 (First order)	$1-\alpha$	$-\ln \left(1-\alpha \right)$	$1-e^{-kt}$
F2 (Second order)	${\left(1-\alpha \right)}^2$	$\frac{1}{1-\alpha }-1$	$\frac{kt}{1+kt}$
F3 (Third order)	${\left(1-\alpha \right)}^3$	$\frac{1}{2}\left[{\left(1-\alpha \right)}^{-2}-1\right]$	$\frac{1+2kt-\sqrt{1+2kt}}{1+2kt}$

It is necessary to mention that there are numerous doubts regarding the validity of both the model-fitting and isoconversional methods, as well as the expressions for the reactions rate and rate constant, see Equations (2) and (3). The interested reader can go through the ICTAC projects [16,19,20,28,29,31,32,33,34] to understand the derivation, applicability, limitations and doubts regarding the methods used for calculating the kinetic triplet. As for the validity of the Arrhenius type rate constant in the case of heterogeneous reactions the reader is referred to the works of L’vov B. [35,36]. Although these doubts must be considered carefully, in our work we are interested in how the model-fitting method can be algorithmically more robust for identifying the BCM. We do not examine if this model is truly the best, that is already an open question in the literature, or its origins from a physicochemical point of view, but from an engineering point of view, this model can be used for simulating the mass loss or reaction rate of solid-state reactions at different temperatures than the ones experimentally tested.

3. Determination of the Kinetic Triplet via the CMF Method

To determine a kinetic triplet, first, one needs experimental data. It is recommended in the literature [20] that one should perform isothermal thermogravimetric experiments at least at three different temperatures ($T_1<T_2<\dots <T_n$). Considering the commonly used CMF approach, given the experimental conversion fraction values and following the integral reaction rate, $g\left(\alpha \right)$, measured at a certain temperature, the latter is fitted using the various solid-state models presented in Table 1. If the reaction is single-step and the model, which describes the reaction, exists, the integral rate, $g\left(\alpha \right)$, should be linearly dependent on time, see Equation (4), where the proportionality factor is the Arrhenius rate constant $k$. Consequently, the constant $k$ of the straight line $kt$, see Equation (4), is calculated using ordinary least-squares for each model by fitting $kt$ to each integral rate. The goodness of the fit, or the CMF’s model choice criterion, is measured using the determination coefficient $R^2$ (see Appendix A). The BCM to simulate that particular reaction is chosen to be the one which exhibits the highest $R^2$ value. The above steps are repeated for the whole range of temperatures experimentally used, resulting in the $k$ values calculated for each temperature. Consequently, following the procedure explained above, from a typical Arrhenius plot, see Equation (3), the activation energy and frequency factor are obtained using ordinary least-squares for fitting the $\ln \left(k\right)$ as a function of $1/T$, where the slope is equal to $-\raisebox{1ex}{$E_{\alpha }$}\!\left/ \!\raisebox{-1ex}{$R$}\right.$ and the intercept is equal to $\ln \left(A\right)$ [30].

CMF is significantly unreliable when it comes to unambiguously providing a single BCM, which describes a certain single-step ISSR. The reason for this is mainly the CMF’s model choice criterion described above [15,20]. Then, when several models exhibit comparable determination coefficients, the choice of the BCM relies on a “rather subjective discrimination” [3]. Additionally, since several models have to be tested at every experimentally used temperature, CMF might result in a selection of different BCMs for different temperatures, preventing thus the determination of a kinetic triplet. Therefore, the disadvantage of CMF that it cannot provide a single BCM for a particular ISSR or the fact that CMF might result in a BCM which is actually not the “best” may lead to a miscalculation of the corresponding Arrhenius constants and consequently to an incorrect estimation of the activation energy. That makes it necessary to look for the development of a more sophisticated algorithm for the determination of the BCM.

4. Development of a Comprehensive Model-Fitting (COMF) Method

Here, we attempt the development of a more comprehensive approach that minimizes any ad hoc selection of the BCM. The so-called comprehensive model-fitting method (COMF) is thus presented and its applicability is illustrated on two experimental kinetic data sets. Please note that we applied the method only in cases associated with single-step ISSRs. The workflow we developed and implemented is depicted step-by-step in the next scheme.

Similarly to the CMF method, we assume that one performs isothermal thermogravimetric experiments at at least three different temperatures. In the first step, given the experimental conversion fraction at a certain temperature, the integral reaction rate $g\left(\alpha \right)$ is evaluated using the various solid-state kinetics models from Table 1 (first process of STEP 1 in Scheme 1). The constant $k_g$ is evaluated for each model from the slope of a linear fit according to $k_{g}t$ using ordinary least-squares (OLS) (second process of STEP 1 in Scheme 1). The subscript $g$ indicates that the rate constant is derived from the fitting of the $g\left(\alpha \right)$ function. The coefficient of determination $R_g^2$ is calculated as a measure of the goodness of the fit.

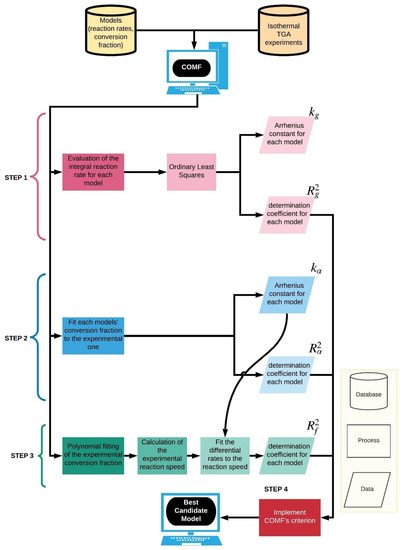
Scheme 1. An illustration of the step-by-step workflow COMF follows. The light-yellow framework on the right-hand side includes an explanation of the shapes used in the workflow.

In the second step, the experimental conversion fraction is fitted explicitly with the analytical expressions of the conversion fraction (first process of STEP 2 in Scheme 1) using non-linear least squares (NLLS) resulting in the rate constant $k_{\alpha }$ together with the corresponding coefficient of determination for each model $R_a^2$. Since there are no analytical expressions of the conversion fraction for the diffusion models D2 and D4, the differential reaction rate equation, see Equation (2), is solved numerically by explicit Euler time integration coupled with NLLS to calculate the fitting parameter [30], i.e., the rate constant $k_{\alpha }$.

In the third step, the so-called reaction speed, which is the time derivative of the conversion fraction $\frac{d\alpha }{dt}$, is calculated from the experimental data (second process of STEP 3 in Scheme 1) and it is fitted using the expressions $k_{\alpha }f\left(\alpha \right)$ with $k_{\alpha }$ obtained from the second step of the algorithm (third process of STEP 3 in Scheme 1). Therefore, given these constants we calculate the determination coefficients ($R_f^2$) for each fit. At this step, there is only one procedure which often might be cumbersome to implement, and this is the time derivation of the experimental conversion fraction (i.e., reaction speed). Mostly, the fitting of the reaction speed is hindered due to the nonsufficient smoothness of the derivative. In fact, its smoothness depends on the interval, at which the experimental conversion fraction was recorded. The smaller the recording interval, the smoother the derivative. Hence, if it is not small enough, the experimental conversion fraction must be first fitted with a polynomial, see Equation S1 in the Supplementary Materials, of a degree such that allows a smooth derivation (first process of STEP 3 in Scheme 1). Then, unlike the fittings implemented in the first and second step, the polynomial expression of the conversion fraction is used instead the corresponding experimental one.

The fourth step concerns the COMF’s model choice criterion. Since $R^2\in (-\infty ,1]$, where $R^2=1$ indicates the “best fit” from a statistical viewpoint, the determination coefficients of the BCM, ideally are $\left(R_{\alpha }^2,R_g^2,R_f^2\right)=\left(1,1,1\right)$. Therefore, we define the three-dimensional point $\left(R_{\alpha }^2,R_g^2,R_f^2\right)$ and the unit point $\left(1,1,1\right)$ in the coordinate system $R_{\alpha }^2,R_g^2,R_f^2$. The BCM will be the one that exhibits the minimum Euclidean distance between these two points. This criterion can be mathematically expressed as:

$$d\left(R_{\alpha }^2,R_g^2,R_f^2\right)=\sqrt{{\left(1-R_{\alpha }^2\right)}^2+{\left(1-R_g^2\right)}^2+{\left(1-R_f^2\right)}^2}\to 0$$

(5)

In the fifth step, the steps 1–4 are repeated for the whole range of temperatures experimentally tested. Finally, exactly as in the CMF method, given the calculated Arrhenius rate constants, see Equation (3), the activation energy and the frequency factor are obtained using ordinary least-squares.

Overall, regarding the implementation of COMF, we have to make clear that for a particular solid-state reaction, no matter what is the exact reaction mechanism, CMF and subsequently COMF can only be used in the case that the reaction speed can be considered of the form that Equation (2) states as well as when the activation energy does not vary significantly with the conversion (from an isoconversional plot). Therefore, as far as these two conditions hold, COMF can reliably determine the BCM for any reaction kinetics, as it shown below to the Results & Discussion section.

5. Results and Discussion

We validated COMF on two sets of experimental kinetic data from the literature regarding the isothermal desolvation of pharmaceutical solvates: (i) tetrahydrofuran solvates of sulfameter [4]; and (ii) methanol solvates of ciclesonide [3].

Figure 1, Figure 2, Figure 3 and Figure 4 concern the implementation of COMF onto data for the desolvation of tetrahydrofuran solvates of sulfameter [4] and Figure 5, Figure 6, Figure 7 and Figure 8 for the desolvation of methanol solvates of ciclesonide [3] at a single temperature. Due to the large amount of information, in Figure 1, Figure 2 and Figure 3 and Figure 5, Figure 6 and Figure 7 regarding the three different fittings, we show results associated with the four “best” models as ranked by COMF in a descending order. The results regarding the rest of the temperatures are shown in Tables S1–S7 and Figures S1–S4 for the methanol solvates of ciclesonide and Tables S8–S14 and Figures S5–S8 for the tetrahydrofuran solvates of sulfameter in the Supplementary Materials. In Figure 1, we present the fitting of the integral reaction rates for the four best models. Qualitatively, it is apparent, that for this single-step ISSR there is no model, which would give a perfectly linear integral reaction rate. Moreover, all of them are seemingly identical, with A2–A3 and R2–R3 having comparable time profiles of the integral reaction rate, respectively. Quantitatively, looking only at the $R_g^2$ coefficients (first column in Table 2), we observe that the first three highest ranked models, namely A2, R2, R3 are equally well fitted with coefficients very close to each other, while only A3 can be more easily discriminated based on its small $R_g^2$. If CMF was employed and we relied only on the ranking based on the highest $R_g^2$, we would obtain a set of four different BCMs (see Table 2). Particularly, following the CMF method, the BCM is the contracting volume (R3) with $R_g^2=0.9575$. Then, in descending order, come the 2nd order Avarami-Erofe’ev model (A2) with $R_g^2=0.9553$, the contracting area model (R2) with $R_g^2=0.9401$ and in the fourth position the 1st-order reaction model (F1) with $R_g^2=0.9214$. It is interesting that the models R3 & A2, although based on different principles, exhibit almost identical $R_g^2$ determination coefficients, which differ just in the third digit. Consequently, CMF’s model choice criterion does not suffice to determine the BCM and a subjective selection becomes unavoidable. The selection would come after looking at the simulated conversion fraction, which makes the algorithm non-automatic and not user-friendly. Additionally, determining the BCM based on CMF will also result in a corresponding Arrhenius constant, $k_g$, which does not necessarily ensure that using it to calculate the models’ conversion fraction, $\alpha \left(k_g;t\right)$, would match the experimental conversion fraction. Here lies the main improvement of our approach, COMF, which adds more comprehensive criteria associated with the overall behavior of the various models and makes the selection of BCM more straightforward and reliable.

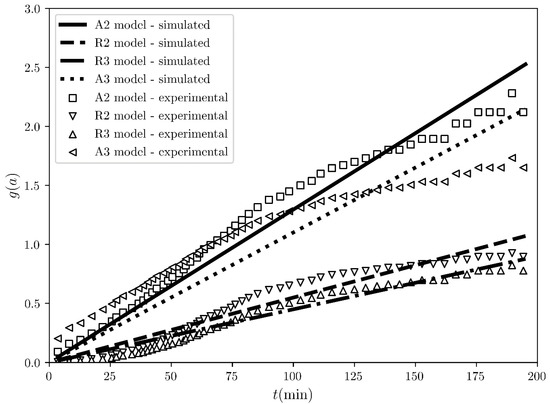
Figure 1. The integral reaction rate time evolution regarding the desolvation of the sulfameter solvate at 47.19 °C. The scatter plots represent the rates evaluated from the experimental conversion fraction measured by A. Khawam and D. Flanagan [4], while the solid and dashed black lines represent the straight line fits for the “best” four models ranked by COMF, i.e., A2, R2, R3 and A3 models.

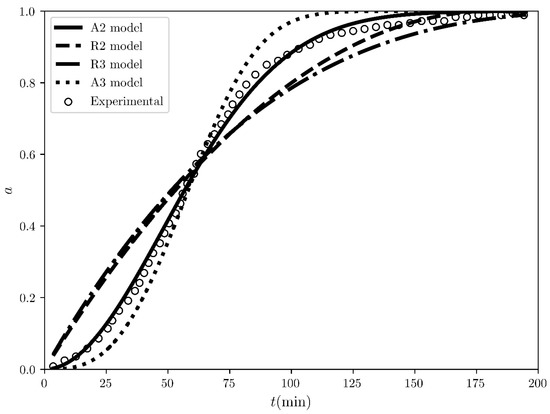
Figure 2. The conversion fraction time evolution regarding the desolvation of the sulfameter solvate at 47.19 °C. The scatter plots represent the experimental values measured by A. Khawam and D. Flanagan [4] while the solid and dashed black lines represent the simulated corresponding conversion fraction curves for the “best” four models ranked by COMF, i.e., A2, R2, R3 and A3 models.

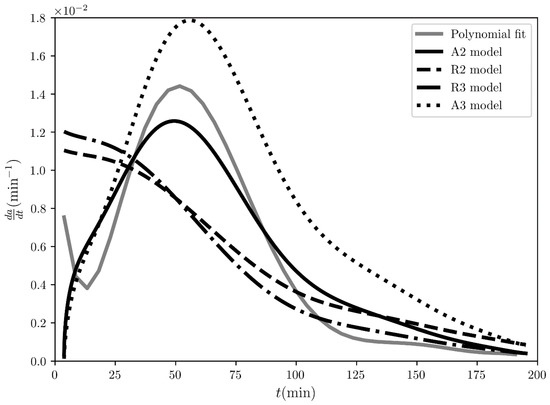
Figure 3. The reaction speed time evolution regarding the desolvation of the sulfameter solvate at 47.19 °C. The solid grey line represents the rate evaluated from the initial polynomial that fits the experimental conversion fraction measured by A. Khawam and D. Flanagan [4], while the solid and dashed black lines represent the fitting curves for the “best” four models ranked by COMF, i.e., A2, R2, R3 and A3 models.

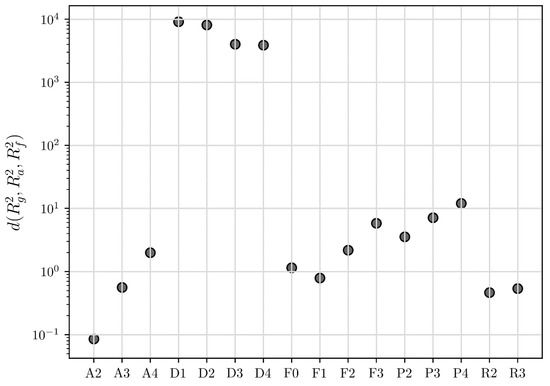
Figure 4. The calculated Euclidean distances via the COMF method for all the models presented in Table 1 in the case of the desolvation of the sulfameter solvate at 47.19 °C.

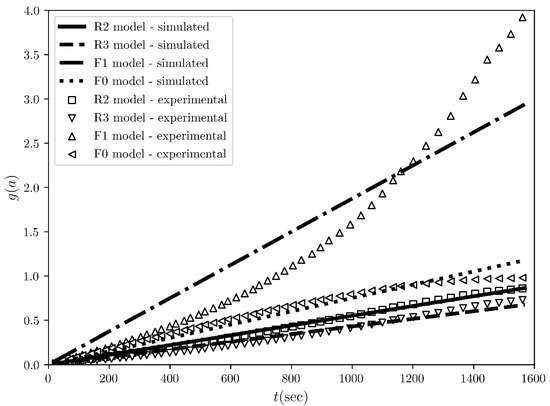
Figure 5. The integral reaction rate time evolution regarding the desolvation of the methanol solvates of ciclesonide at 115 °C. The scatter plots represent the rates evaluated from the experimental conversion fraction measured by L. Zhou et al. [3] while the solid and dashed black lines represent the straight line fits for the “best” four models ranked by COMF, i.e., R2, R3, F1 and F0 models.

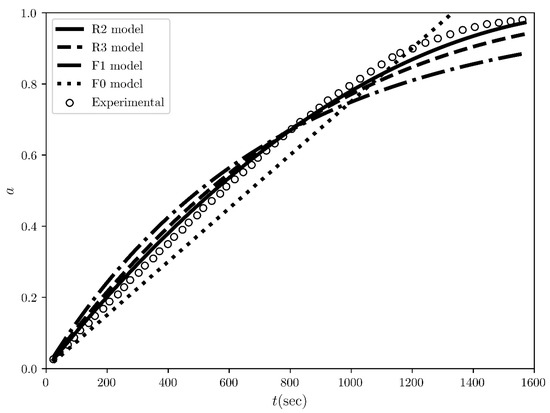
Figure 6. The conversion fraction time evolution regarding the desolvation of the methanol solvates of ciclesonide at 115 °C. The scatter plots represent the rates evaluated from the experimental conversion fraction measured by L. Zhou et al. [3] while the solid and dashed black lines represent the straight line fits for the “best” four models ranked by COMF, i.e., R2, R3, F1 and F0 models.

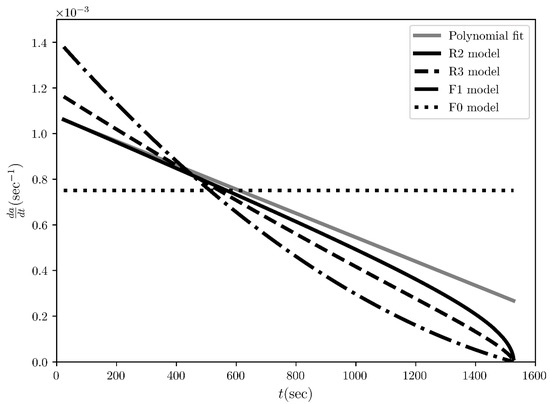
Figure 7. The reaction speed time evolution regarding the desolvation of the methanol solvates of ciclesonide at 115 °C. The solid grey line represents the rate evaluated from the initial polynomial that fits the experimental conversion fraction measured by L. Zhou et al. [3] while the solid and dashed black lines represent the fitting curves for the “best” four models ranked by COMF, i.e., R2, R3, F1 and F0 models.

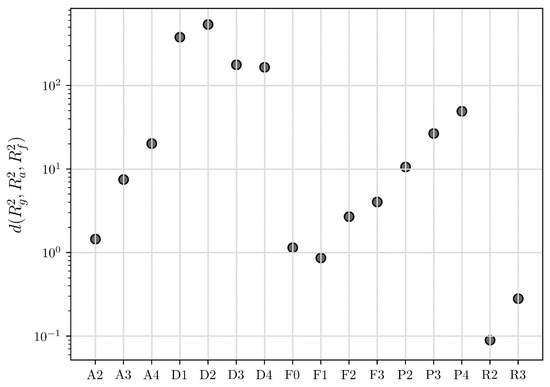
Figure 8. The calculated Euclidean distances via the COMF method for all the models presented in Table 1 in the case of the desolvation of the methanol solvates of ciclesonide at 115 °C.

Table 2. The determination coefficients calculated at every step of the COMF method in the case of the desolvation of sulfameter solvates at 47.19 °C.

Model	${\mathit{R}}_{\mathit{g}}^2$	${\mathit{R}}_{\mathit{\alpha }}^2$	${\mathit{R}}_{\mathit{f}}^2$
A2	0.9553	0.9967	0.9270
A3	0.6763	0.9790	0.5410
A4	0.1205	0.9401	−0.7909
D1	0.8885	0.8255	−9160.9528
D2	0.9002	0.8617	−8125.0876
D3	0.8565	0.8571	−4022.1314
D4	0.8964	0.9662	−3899.1707
F0	0.7936	0.7936	−0.1113
F1	0.9214	0.8803	0.2260
F2	0.4338	0.7173	−1.0845
F3	0.1598	0.5753	−4.7483
P2	0.1407	−0.0355	−2.2815
P3	−1.0664	−0.7823	−5.6033
P4	−2.8235	−1.3013	−10.1701
R2	0.9401	0.9426	0.5417
R3	0.9575	0.9261	0.4676

The fitting of the experimental conversion fraction itself with the analytical expressions of the various models tested (see Table 1) is shown in Figure 2. Qualitatively, this time, the 2nd order Avarami-Erofe’ev model (A2) model seems to perfectly overlap the experimental conversion fraction in comparison with the rest. This is also guaranteed quantitatively, where based only on the $R_{\alpha }^2$ coefficients, A2 is ranked as the BCM with $R_{\alpha }^2=0.9967$, while the rest have $R_{\alpha }^2\le 0.9426$ (see Table 2). These results so far prove to us that ranking the various models based on how linear the integral reaction rates exhibited are, meaning relying only on $R_g^2$, is not the optimal way to determine the BCM. On the other hand, the ranking based on the $R_{\alpha }^2$ coefficients is a more effective tool since the fitting is direct on the experimental conversion fraction. However, considering that in general, high determination coefficients and “best fit” are not in one-to-one correspondence, in COMF, we tried to incorporate all the possible fits in the context of model-fitting. The third type of fitting we performed is that of the reaction speed, shown in Figure 3. For this, the experimental conversion fraction was first fitted with a polynomial (see Figure S5 in the Supplementary Materials) and then this polynomial was used instead of the experimentally recorded conversion fraction to analytically calculate its derivative. Qualitatively, the models can be classified based on the shape of the modelled reaction speed curve. In Figure 3, the experimental reaction speed curve (black solid line) has a bell-like shape, which is approximated only by the 2nd and 3rd order Avarami-Erofe’ev models. Essentially, the fitting of the reaction speed has a very strong impact on ranking the various models, since only five out of the sixteen tested models exhibit positive $R_f^2$ coefficients (see the 3rd column in Table 2). Additionally, the highest ranked model based on $R_f^2$ is the 2nd order Avarami-Erofe’ev (A2) with $R_f^2=0.9270$, while second comes the contracting area (R2) model with $R_f^2=0.5417$. Apparently, the difference in between them is very large. Thus, the significance of incorporating the reaction speed’s fit into COMF is not only that it enhances the evaluation of the BCM, but it also sieves all the tested models and abruptly discards the models which do not have similar physical behavior in the reaction rate.

The three determination coefficients were then combined via the Euclidean distance, which is depicted in Figure 4. In the case of the desolvation of sulfameter solvates, we conclude that, even though the standard determination by CMF identifies contracting volume (R3) as the BCM, the correct BCM is actually the 2nd order Avarami-Erofe’ev (A2), which only becomes apparent by using COMF. To better understand the miscalculations of CMF, note that the conversion fraction of the desolvation of sulfameter solvates shows a sigmoidal curve shape, something that is only well predicted by COMF (see A2 model), while the contracting volume (R3) model (predicted by CMF) has a concave shape. To enhance the certainty that the BCM via the COMF method is the correct one, we can calculate the relative distances between BCM and the second highest ranked model using the formula:

$$\delta x=\frac{\left|x_{\#1}-x_{\#2}\right|}{\left|x_{\#1}\right|}$$

(6)

where $x=R_g^2$ or $x=d\left(R_{\alpha }^2,R_g^2,R_f^2\right)$ and $\#1$ and $\#2$ indicate the BCM and the second highest ranked model respectively. The BCM following the CMF method is the contracting volume (R3) with $R_g^2=0.9575$ and second comes the 2nd order Avarami-Erofe’ev model (A2) with $R_g^2=0.9553$, thus the relative distance between the first two ranked models is:

$$\delta R_g^2=\frac{\left|R_g^2{}_{\#1}-R_g^2{}_{\#2}\right|}{\left|R_g^2{}_{\#1}\right|}=\frac{\left|0.9575-0.9553\right|}{\left|0.9575\right|}=2.298\cdot {10}^{-3}$$

(7)

On the other hand, COMF ranks first the 2nd order Avarami-Erofe’ev model (A2) with $d\left(R_{\alpha }^2,R_g^2,R_f^2\right)=0.0857$ and second the contracting area model (R2) with $d\left(R_{\alpha }^2,R_g^2,R_f^2\right)=0.4658$ and thus:

$$\delta d\left(R_{\alpha }^2,R_g^2,R_f^2\right)=\frac{\left|d_{\#1}-d_{\#2}\right|}{\left|d_{\#1}\right|}=\frac{\left|0.0857-0.4658\right|}{\left|0.0857\right|}=4.4352$$

(8)

Following the COMF method, the relative distance between the BCM and the second highest ranked model is far larger, specifically three orders of magnitude, than the corresponding relative distance following the CMF method (see Figure 4).

The next experimental example is the desolvation of methanol solvate of ciclesonide, which was purposefully chosen for its difference to the first example of sulfameter. The conversion fraction time evolution for the sulfameter solvate has a sigmoidal shape (Figure 2), whereas it is concave for ciclesonide (Figure 6). Our purpose of choosing this data set was to test COMF on cases of various conversion fraction shapes. Differently from the case of sulfameter solvate, in the case of methanol solvate of ciclesonide, if we would rely on CMF to determine the BCM, we would notice that two “concave” models from the same family (R2 and R3) exbibit seemingly very similar linearity in their integral reaction rates (Figure 5). Even quantitatively, R2 and R3 models’ determination coefficients from the fitting of the integral rate are very close to each other (see Table 3) leading again to an uncertainty on how to choose the BCM. Thus, the necessity of exploiting more information from other fittings become apparent in Figure 6 and Figure 7, where the conversion fraction and reaction speed are presented respectively. These additional results concerning the desolvation of methanol solvate of ciclesonide (Figure 5, Figure 6, Figure 7 and Figure 8 and Table 3) and all the corresponding results included in the Supplementary Materials (see Tables S1–S7 and Figures S1–S4) prove that COMF can also distinguish the BCM from a list of models belonging to the same family (R2, R3). Moreover, based on our results, we observed that COMF, can reliably determine the BCM regardless the shape of the conversion fraction time evolution, proving thus that COMF remedies CMF for the determination of the BCM in cases of desolvation of different materials (i.e., different models).

Table 3. The determination coefficients calculated at every step of the COMF method in the case of the desolvation of methanol solvates of ciclesonide at 115 °C.

Model	${\mathit{R}}_{\mathit{g}}^2$	${\mathit{R}}_{\mathit{\alpha }}^2$	${\mathit{R}}_{\mathit{f}}^2$
A2	0.9509	0.9565	−0.4502
A3	0.5279	0.8349	−6.5056
A4	−0.3367	0.7256	−19.1669
D1	0.9407	0.8979	−378.3201
D2	0.8807	0.8453	−537.5531
D3	0.7495	0.9408	−175.7421
D4	0.8416	0.9016	−164.6580
F0	0.9526	0.9526	−0.1453
F1	0.8807	0.9528	0.1453
F2	0.4551	0.7748	−1.6390
F3	0.2457	0.4806	−2.9279
P2	0.2194	0.3723	−9.5523
P3	−1.3835	−0.2603	−25.5092
P4	−3.8410	−0.7606	−48.0887
R2	0.9942	0.9950	0.9103
R3	0.9739	0.9846	0.7194

6. Conclusions

The conventional model-fitting method (CMF) has been unreliable in uniquely determining the ‘best’ candidate model (BCM) for single-step isothermal solid-state reactions (ISSRs). Thus, we developed instead a comprehensive model-fitting method, which remedies the disadvantages of CMF while it sustains its mathematical simplicity. COMF utilizes a ranking criterion that enables the unique determination of the BCM. This criterion is the Euclidean distance between the calculated determination coefficients of three different types of fitting and their ideal values. The first fitting ranks the tested models based on how linear are the integral reaction rates that they exhibit. The second fitting ranks the models based on how well they describe the time evolution of the mass loss, while the third ranks them based on how well they describe the reaction speed. Their combination via the COMF’s model choice criterion proved essential and allowed us to automatically and unambiguously determine the BCM in the two tested experimental data sets regarding the desolvation of pharmaceutical solvates. Our results suggest that COMF can become the model-fitting method of choice for single-step ISSRs making the work of scientist needing to obtain kinetic parameters of isothermal solid-state reactions easier and more reliable.