Abstract
Ion exchange resins have many industrial applications, namely as sorbents and catalysts. In solid-catalyzed reactions, intraparticle reaction-diffusion competition is generally described by effectiveness factors calculated numerically or analytically in the case of isothermal particles and simple rate laws. Although robust, numerical calculations can be time-consuming, and convergence is not always guaranteed and lacks the flexibility of user-friendly equations. In this work, analytical equations for effectiveness factors of reversible reactions derived from the general scheme are developed and numerically validated. These effectiveness factors are analytically expressed in terms of an irreversible order Thiele modulus (specifically written for the order forward reaction), the thermodynamic equilibrium constant, the ratios of effective diffusivities, and the ratios of surface concentrations. The application of such analytical equations is illustrated for two liquid phase reactions catalyzed by Amberlyst-15, specifically the synthesis of ethyl acetate and acetaldehyde dimethyl acetal. For both reactions, the prediction of the concentration profiles in isothermal batch reactors achieved errors between 1.13% and 3.38% for six distinct experimental conditions. Finally, the impact of non-ideal behavior upon the multicomponent effective diffusivities, subsequently conveyed to the effectiveness factors, is enlightened.
1. Introduction
Catalysts are the backbone of chemical and petrochemical industries, with ca. 90% of its products being manufactured employing catalysts, whose market value represented 35.5 billion dollars in 2020, with a foreseen growth of 4.9% per year from 2021 to 2030 [1]. Heterogeneous catalysts predominate the market due to easier recovery from the reaction mixture and the possibility of reutilization, with or without regeneration steps. In addition, heterogeneous catalysts include a wide range of materials (such as ion exchange resins, zeolites, metal oxides, supported metals, and others) and are the basis for process intensification with multifunctional reactors [2]. Reactive distillation, reactive stripping, and chromatographic reactors are examples of such processes where ion exchange resins find frequent applications [3].
Ion exchange resins are cross-linked copolymers bearing acidic or basic functional groups that render them useful for many industrial applications, including as sorbents and catalysts for various reactions, e.g., esterification [4] and biomass conversion into biofuels [5]. In general, these resins can be easily regenerated and reused, but their low thermal resistance dictates that the reaction temperature cannot be too high (typically below 120 °C) [6]. Among the several types of ion exchange resins, Amberlyst, Amberlite, Dowex, Indion, and Nafion [7] stand out for their numerous catalytic applications. In particular, Amberlyst-15 is a versatile macroporous sulfonic acid resin originally developed by Rohm & Haas Co., (Philadelphia, PA, USA) [8] and a proven catalyst for esterification [4,9], etherification [10,11], hydration [11], and hydrolysis [12]. More recently, Amberlyst-15 has been employed as a catalyst to synthesize bioactive sulfur derivatives of birch bark triterpenoids [10] and complex heterocyclic compounds [13] within the Biorefinery and Green Chemistry context.
Despite the many advantages associated with heterogeneous catalysts, the design of catalytic systems can be challenging due to the presence of external and intraparticle mass transfer limitations. While the former can be overcome by increasing convective mass transfer between phases (e.g., using mechanical agitation and increasing the fluid velocity or recirculation), the latter can be reduced by employing smaller sizes of catalyst particles. However, for industrial applications, larger particles are preferred, as size reduction can lead to higher pressure drop in fixed-bed reactors, lower selectivity in the case of multiple reactions, and difficult solid-liquid separation for catalyst regeneration in slurry processes [14]. In the presence of intraparticle resistances, the concentration of any component inside the particle porous structure will be different from its concentration on the outer surface in direct contact with the reaction medium [15]. Thus, the rate of reaction will vary throughout the particle, and the observed rate of reaction will be an average of the rates at each point inside the catalyst.
The effectiveness factor, , which ranges from 0 to 1 under isothermal conditions, is a measure of the relative importance of internal diffusion and reaction kinetics [15]. Mathematically, it is defined as the ratio of the actual (or observed) rate of reaction in a porous catalyst to the reaction rate in the absence of particle diffusion resistance (i.e., at surface conditions). For a reference species ,
where and represent the observed rate of reaction of A and its rate at surface conditions, respectively. The reactor design equations can now be expressed in terms of the reaction kinetics at surface conditions multiplied by the effectiveness factor and determined by the local conditions within the reactor. Thereafter, different approaches can be used to evaluate the effectiveness factor and predict the reactor’s performance [16,17].
The effectiveness factor is expressed in terms of the Thiele modulus (), named after Ernest W. Thiele for his pioneering research in chemical reaction engineering [18], which depends on the kinetics and catalyst particle geometry. For a first-order irreversible reaction of type , the analytic solution of the steady state material balance for reactant diffusing and reacting in an isothermal porous catalyst particle yields the expression of the effectiveness factor, given by Equations (2) and (3) for slab or spherical shaped particles, respectively [19]:
The corresponding Thiele modulus is given by:
where and are the particles’ characteristic dimensions, i.e., the slab semi-thickness and the sphere radius, is the kinetic constant, is the intraparticle effective diffusivity of , and is the particle density. For higher-order irreversible reactions and diverse particle shapes, a generalized Thiele modulus is defined by [19]:
where and are the volume and outer surface area of the catalyst particle, respectively, is the reaction order, and is the surface concentration of . Bischoff [20] extended this concept to other types of reaction rate forms, even with adsorption terms, and later, Roberts and Satterfield [21,22] analyzed several cases of Langmuir–Hinshelwood kinetic expressions. The generalized Thiele modulus enables the use of Equation (2) to obtain an approximate value of the effectiveness factor for any particle shape. However, for spherical-shaped particles, it is preferable to use Equation (3) with defined by Equation (5) but using instead of .
For more complex kinetics (e.g., reversible reactions), the steady-state reaction-diffusion material balance equations for the key components in the catalyst particle must be solved numerically. Although robust and accessible, numerical methods can be time-consuming to implement, and convergence is not always guaranteed. Hence, analytical equations for are preferred to develop comprehensive and applicable models for the aforementioned processes. Analytical expressions of for first order reversible reactions of type were first reported by Carberry [23], and for several second-order reversible reaction schemes by Koopman and Lee [24], the latter being expressed as a function of various dimensionless parameters. Analytic or semi-analytic solutions for estimation are an ongoing quest, with Gottifredi and Gonzo [25] proposing a semi-analytic procedure to predict for irreversible power law kinetics, Jeyabarathi et al. [26] and Alopaeus [27] deriving approximate expressions for irreversible Langmuir–Hinshelwood–Hougen–Watson (LHHW) type kinetics, and Baur and Krishna [28] analyzing the influence of multicomponent diffusion for first order reversible reactions catalyzed by zeolites. Nkohla et al. [29] proposed an analytical expression of the effectiveness factor for photocatalytic reactors, which incorporates a parameter that accounts for the external mass transfer limitations.
In the present work, user-friendly equations of are proposed for reversible reactions of the first order, second order, and mixed first and second order, along with the procedure required to obtain similar expressions for higher order reversible reactions. These equations were used to compute the effectiveness factor and validated by comparison with numerical results for both slab and spherical catalyst particles, and with experimental data for two liquid-phase reactions catalyzed by Amberlyst-15 ion exchange resin. Such expressions can greatly facilitate the modeling and design of heterogeneous chemical reactors with diffusional resistances, given that the intraparticle mass balance differential equations do not need to be solved numerically.
2. Development of Analytical Expressions for Effectiveness Factors
This section presents the analytical expressions of for a set of seven reversible reaction schemes—see Table 1. First, the general procedure adopted to obtain these expressions is explained. Thereafter, the generalized Thiele modulus is applied to typical geometry-specific effectiveness factor equations to obtain the effectiveness factor without resorting to numerical methods.

Table 1.
List of reversible reactions and corresponding rate law equations for which generalized Thiele modulus equations were developed in this work.
2.1. Derivation of Generalized Thiele Modulus Expressions
The reversible reactions covered in this work are displayed in Table 1, along with the respective rate law equations, where is the rate of reaction, is the reaction rate constant, and is the equilibrium constant, both defined in terms of molar concentrations, and is the concentration of component , where .
For effectiveness factor calculations, can be obtained by steady-state material balance over the entire catalyst particle, equating the diffusion flow of reactant A at the particle surface with its disappearance rate by a chemical reaction in the particle. For a semi-infinite slab particle,
where is the position coordinate inside the slab. The derivative term in Equation (6) can be obtained by integration of the material balance for component ,
from the particle center () to the surface (), with the following limits:
where is the concentration of at the centerline. Accordingly, after manipulation, one obtains
The integration of Equation (9) requires to be written uniquely in terms of , which can be accomplished by equating the material balances for and any arbitrary species ,
where is the stoichiometric coefficient of component (positive for products, negative for reactants). Integrating Equation (10), and assuming constant effective diffusivities inside the particle, yields
From Equations (1), (6), and (9), the seminal equation for is obtained:
where is the rate law expressed uniquely in terms of
For slab-shaped particles and for any reaction for which the integral in Equation (12) has an analytical solution, the analytical equation of the effectiveness factor is expressed as a function of the Thiele modulus, the equilibrium constant, the surface concentration of the reference species A, and the ratios of surface concentrations and effective diffusivities of each species in relation to A,
where is the order of the forward reaction. For any of the specific rate equations presented in Table 1, the effectiveness factor is given by:
where the expressions for are given in Table 2 for each reaction type since they cannot be derived in a straightforward manner from the more general case (type I). Noteworthy, similar expressions can be obtained for any kinetic equation as long as the integration of in Equation (12) has an analytical solution. This can be accomplished with the aid of symbolic mathematics computation tools [30].

Table 2.
Expressions for the constants and necessary to compute the generalized Thiele modulus, Equation (15), for the reversible reactions presented in Table 1.
A major limitation of Equation (14) is that it requires concentration in the center of the particle (), which is usually unknown unless the mass balance equations are solved numerically. However, in the particular case of reversible reactions under strong intraparticle diffusion limitations, since the characteristic reaction time is much lower than the characteristic diffusion time, equilibrium is reached in the center, and thus, approaches the equilibrium concentration, . Then, in the regime of strong diffusional limitations (i.e., large values of the Thiele modulus), it is possible to define a generalized Thiele modulus as , by replacing with :
Although derived for semi-infinite slab particles, Equation (15) can be used to evaluate for any other particle shape substituting by and replacing by in Equation (2) to compute the effectiveness factor. However, in the case of spherical particles, it is preferable to use Equation (3), with defined by Equation (15) but using instead of .
2.2. Guide for Applying the Generalized Thiele Modulus Analytical Expressions
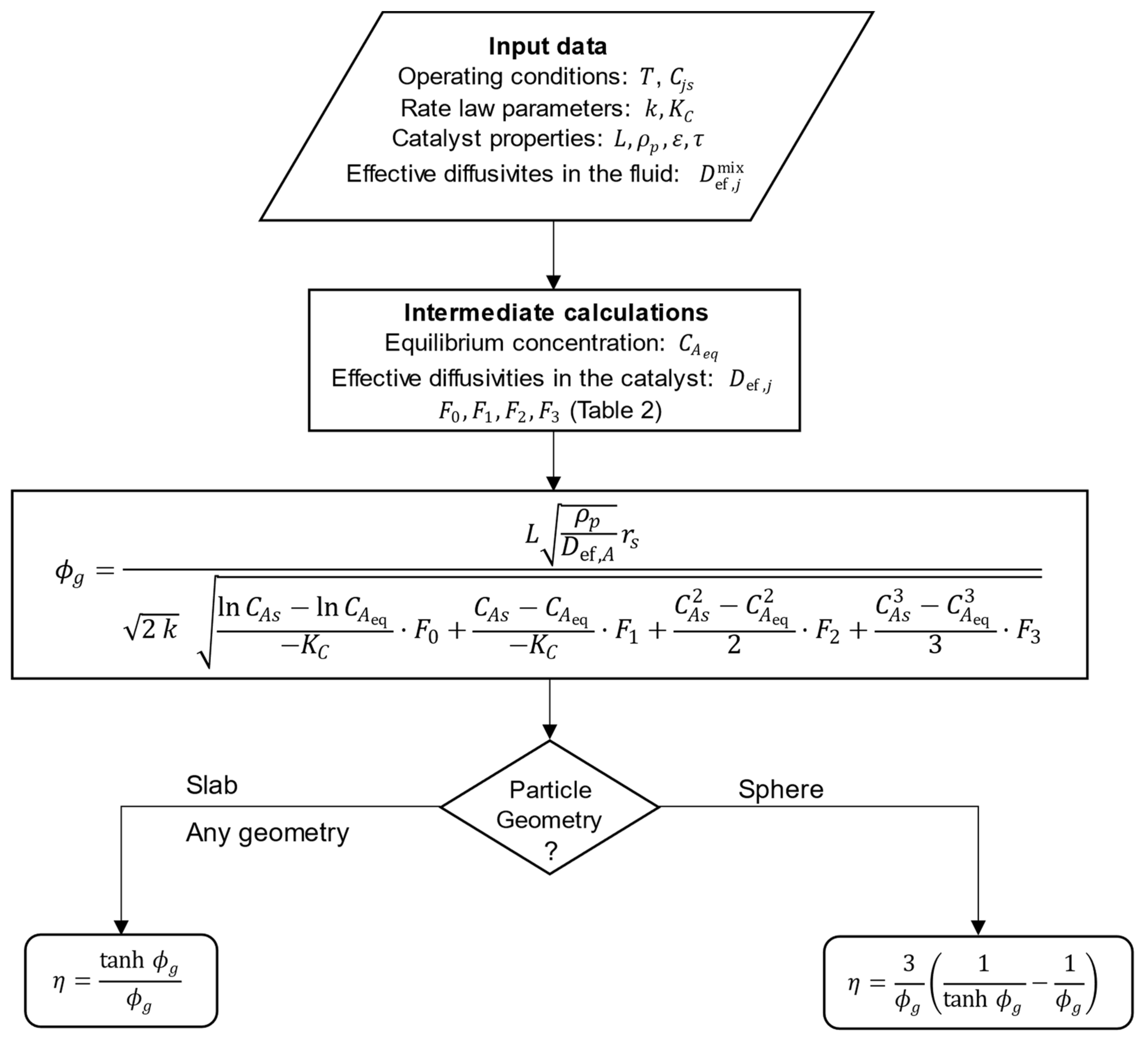
The steps necessary for the analytical calculation of the effectiveness factor using the generalized Thiele modulus derived in Section 2.1 (Equation (15) and Table 2) are listed below and schematized in Figure 1:
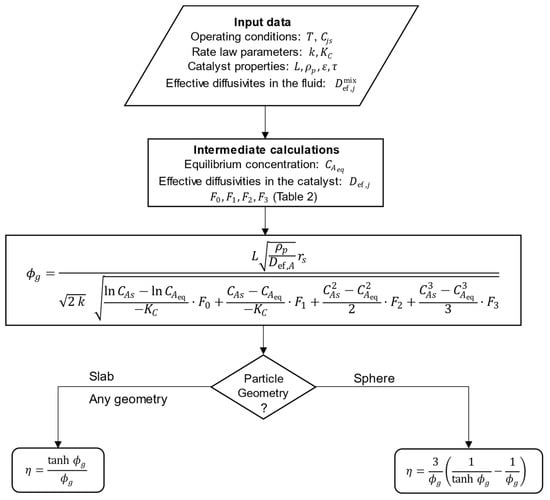
Figure 1.
Schematic diagram for the analytic calculation of effectiveness factors for isothermal porous catalyst particles. ( is the slab thickness, the sphere radius, or for any other shape).
- Identify the reaction type in Table 1;
- Gather the required input data, namely:
- Operating conditions: temperature and surface concentrations of all components ();
- Rate law parameters: kinetic constant ( and equilibrium constant () at the operating temperature;
- Catalyst properties: particle characteristic dimension (, or ), density (), porosity (), and tortuosity ();
- Effective diffusivities of all components in the reaction mixture () at the operating conditions;
- Calculate the equilibrium concentration of component , ;
- Calculate the effective diffusivities of all components in the porous catalyst, ;
- Calculate the constants and given by the specific expressions in Table 2;
- Calculate by Equation (15), using for the slab, for the sphere, or for any other catalyst shape;
- Calculate using Equation (2) for slab () or any geometry (with ) or Equation (3) for spherical particles.
It is worth noting that the surface concentrations, , are equal to the respective bulk concentrations only if external mass transfer limitations are negligible. Otherwise, they must be computed using the appropriate convective mass transfer coefficients.
The calculations of the equilibrium concentration and effective diffusivities of all species in the solution are described in Supplementary Material. The effective diffusivities in the porous catalyst, , were estimated in this work by the Wheeler model [19]:
For the particular case of catalysts with distinct pore sizes, for example, ion exchange resins with macro and micropores, different methods should be used [31,32].
3. Numerical Validation of the Analytical Calculations of the Effectiveness Factors
The effectiveness factors were calculated analytically (i.e., using the generalized Thiele expressions described in Section 2) and numerically were compared for all reaction types, aiming for the validation of the former. For illustration purposes, this comparison is explicitly presented for two very distinct reaction types, namely: in Figure 2, the second-order reversible reaction of Type I, which is the general case of Types I to VI (see Table 1); in Figure 3, reaction Type VII, whose rate law is the most different. The operating conditions are summarized in the captions of the figures, and further details are provided in the case studies discussed in Section 4.
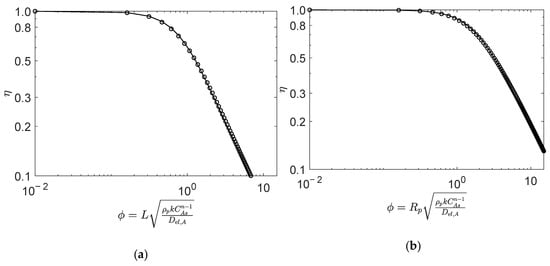
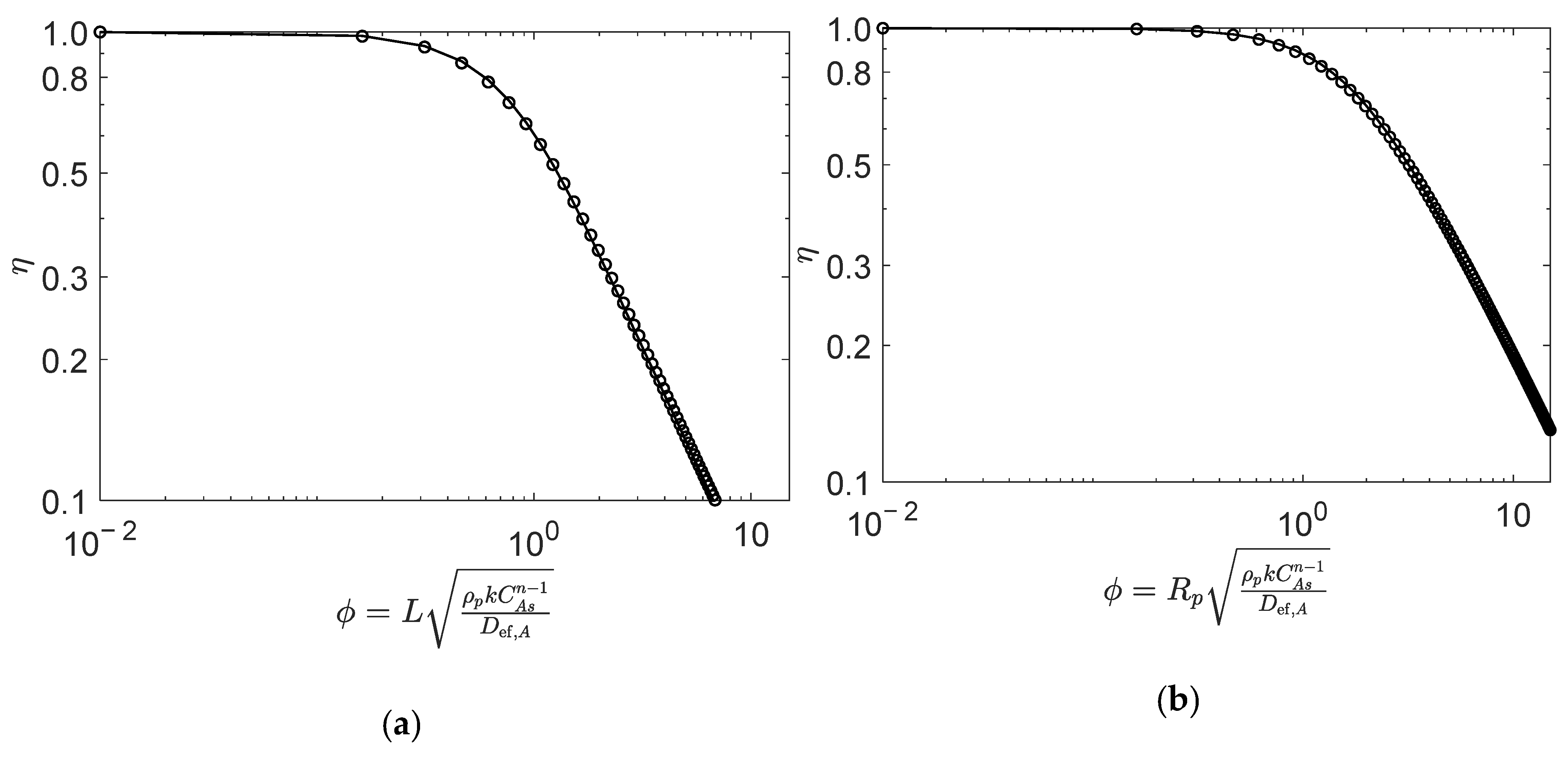
Figure 2.
Numerical (points) and analytical (line) effectiveness factors for reaction (Type I; in (a) slab, and (b) spherical porous catalyst particles. Figures were generated as function of for mol/dm3, mol/dm3, and , , (See details in Section 4.1).
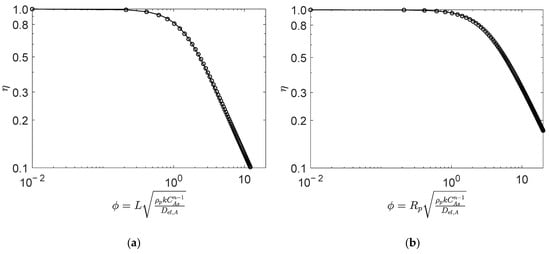
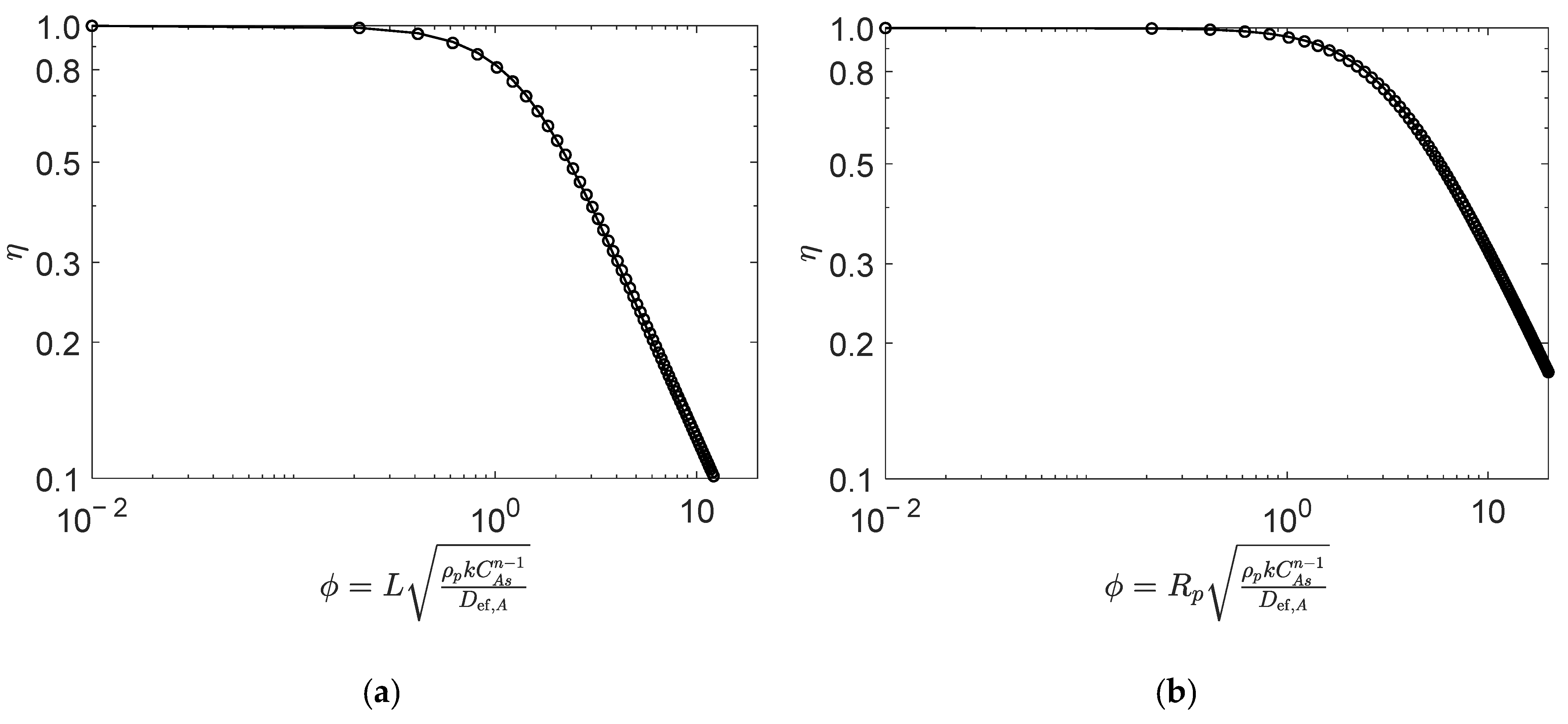
Figure 3.
Numerical (points) and analytical (line) effectiveness factors for reaction (type VII, ) in (a) slab, and (b) spherical porous catalyst particles. Figures were generated as function of for mol/dm3, mol/dm3, mol/dm3, and , , . (See details in Section 4.2).
Figure 2 illustrates the analytic and numeric values of the effectiveness factor versus Thiele modulus for Type I reaction (, see Table 1) with the equimolar feed of A and B, in the slab (Figure 2a) and spherical (Figure 2b) porous catalyst particles. The results clearly reveal the accuracy of the analytical calculations for both catalyst geometries, with average absolute relative deviations (AARD) of 1.7% (slab) and 1.1% (sphere), for from 0.01 to 15. The definition of AARD is given by
in which NP is the number of data points, and the superscripts represent the analytical and numeric effectiveness factors, respectively.
Figure 3 compares the numeric and analytic effectiveness factors for Type VII reaction (, see Table 1) with the stoichiometric feed of A and B, in the slab (Figure 2a) and spherical (Figure 2b) catalyst particles. Once again, the analytical results overlap with the numerical calculations over the entire Thiele modulus range, for both slab and spherical geometries, with an AARD of 1.1% and 0.7%, respectively, for from 0.01 to 20.
4. Case Studies
In this section, two case studies will be analyzed in detail to compare analytical effectiveness factors with experimental data. The first case is the synthesis of ethyl acetate by the Fisher esterification of acetic acid with ethanol (Type I reaction), and the second is the synthesis of acetaldehyde dimethyl acetal by reacting acetaldehyde with methanol (Type VII reaction). Both reactions occur in the liquid phase and are catalyzed by Amberlyst-15, an acidic ion exchange resin.
4.1. Case 1: Esterification of Acetic Acid with Ethanol (Type I Reaction)
4.1.1. Process Description and Data Compilation
The liquid phase acid-catalyzed esterification of acetic acid () with ethanol () is a bimolecular reversible reaction that yields ethyl acetate () and water (), and can be represented by:
which corresponds to Type I in Table 1. The reaction was experimentally studied in this work in a batch reactor operating at 78 °C, using an equimolar feed of both reactants (A and B) and different-sized spherical particles of Amberlyst-15 wet (Rohm and Haas, 39389-20-3) as catalysts. After preliminary tests, the stirring speed was adjusted to 900 rpm to guarantee the absence of external mass transfer limitations. The experimental procedure used to follow the reaction is similar to that described in the literature [33]. Compiled data pertaining to the experimental conditions are provided in Table 3.

Table 3.
Catalyst properties, rate law constants, and experimental conditions used to study the liquid phase esterification of acetic acid with ethanol in batch reactor.
4.1.2. Reactor Modelling and Effectiveness Factor Calculation
The reactor was modelled as a perfectly mixed isothermal batch reactor for which, in the absence of external mass transfer limitations (i.e., the acetic acid () material balance can be expressed by
where is the volume of the reaction mixture (which is essentially constant), and is the mass of the catalyst. Since the bulk and surface concentrations of all species are equal, they can be easily related with by:
where is the initial concentration of component in the batch reactor.
The constants of the rate law (Type I) at 78 °C were taken from Antunes et al. [33]: (i) for Amberlyst-15, dm6 mol−1 min−1 gcat−1; (ii) the concentration equilibrium constant is . The calculated equilibrium concentration of component A is mol/dm³ (details can be found in Section SM2 of the Supplementary Material).
The effectiveness factor was calculated via the generalized Thiele modulus analytical expressions developed in this work, as described in Section 2.2, using the data summarized in Table 3 and effective diffusivities estimated by the accurate model of Rios et al. [37] (details in Section SM1 of the Supplementary Material). The values of were then obtained by Equation (16).
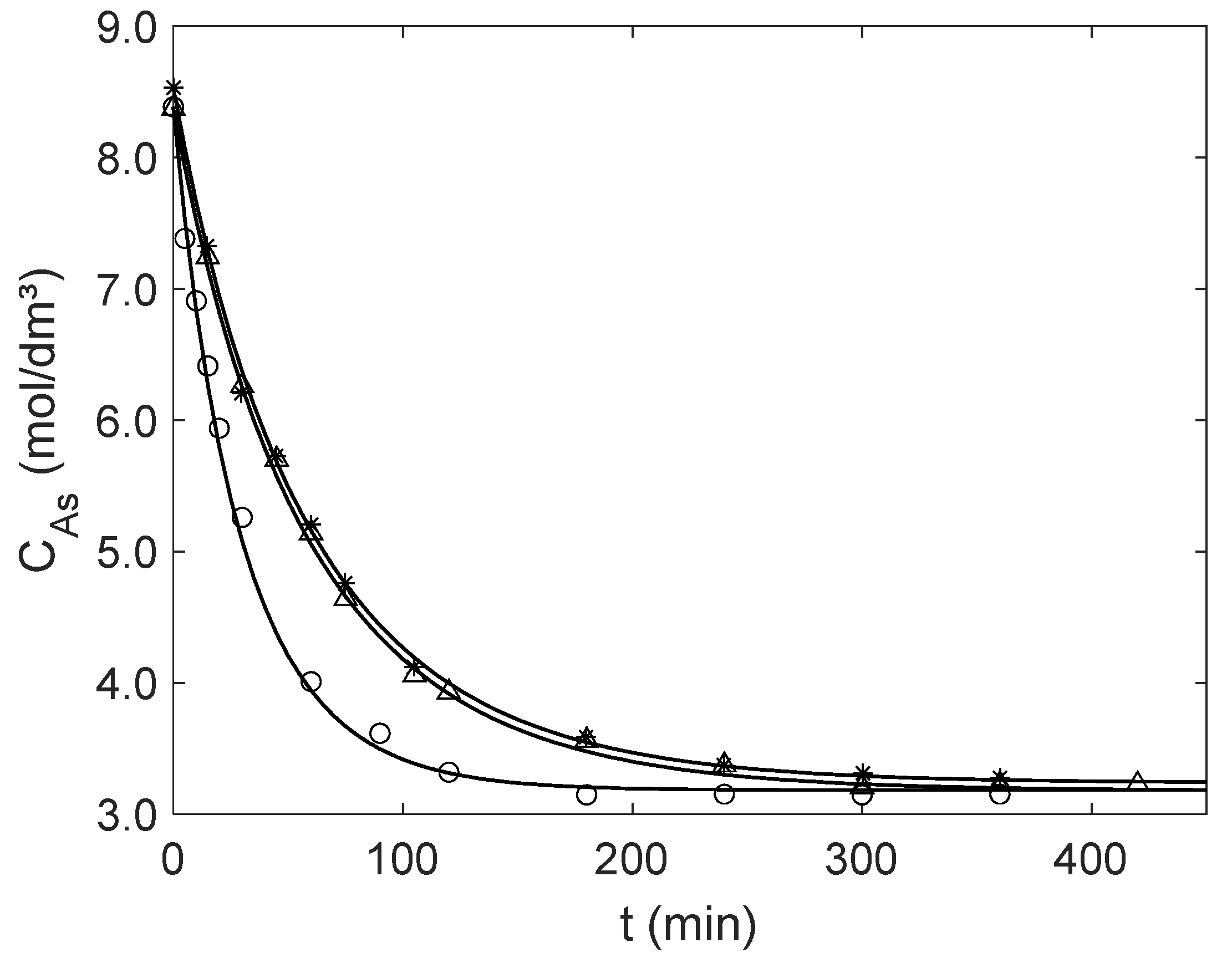
Once is computed by the new analytical expression, the concentration profile of over time, , is obtained by numerical integration of the material balance, Equation (19). The calculated and experimental results are presented in Figure 4, illustrating the accuracy of the proposed analytical equation. Table 4 presents the effectiveness factors calculated for initial conditions (see Table 3) and near equilibrium for both particle sizes, and the corresponding AARD values calculated with Equation (17) adapted for experimental and simulated concentrations. Overall, the effectiveness factors are close to one, increasing slightly along the reaction as diminishes, illustrating the efficiency of Amberlyst-15 as a catalyst for the liquid phase esterification of acetic acid. The small AARD values (1.13–2.20%) confirm the good performance of the modeling approach.
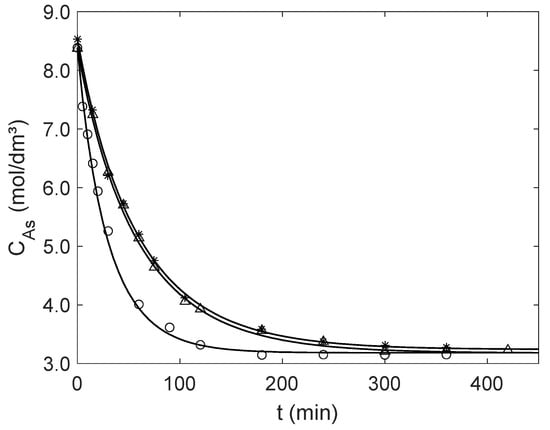
Figure 4.
Experimental (points) and modeling (curves) results for the catalytic esterification of acetic acid (A) with ethanol in a batch reactor for the operating conditions of Table 3. Mass and average diameter of Amberlyst-15 particles: Δ Exp. 1 (5.0058 g and μm); ○ Exp. 2 (10.0134 g and μm); and ✶ Exp. 3 (5.0024 g and μm).

Table 4.
Calculated effectiveness factors for the liquid phase Amberlyst-15 catalyzed esterification of acetic acid with ethanol for the operating conditions described in Table 3.
4.1.3. Impact of Effective Diffusivity Calculations on Effectiveness Factor Results
The effective diffusivities of each component in the solution, which are required to calculate the effective diffusivities in the catalyst (Equation (16)), were obtained by two distinct approaches: one considering the non-ideal behavior of the multicomponent reaction mixture, using the model proposed by Rios et al. [37], and the other considering ideal mixture and using the well-known equations by Bird et al. [38]. For the former, the activity coefficients were estimated by the UNIFAC model [39]. Table 5 presents the results obtained by both methods for the initial conditions described in Table 3.

Table 5.
Effective diffusivities in solution calculated for the initial conditions of reactor (see Table 3).
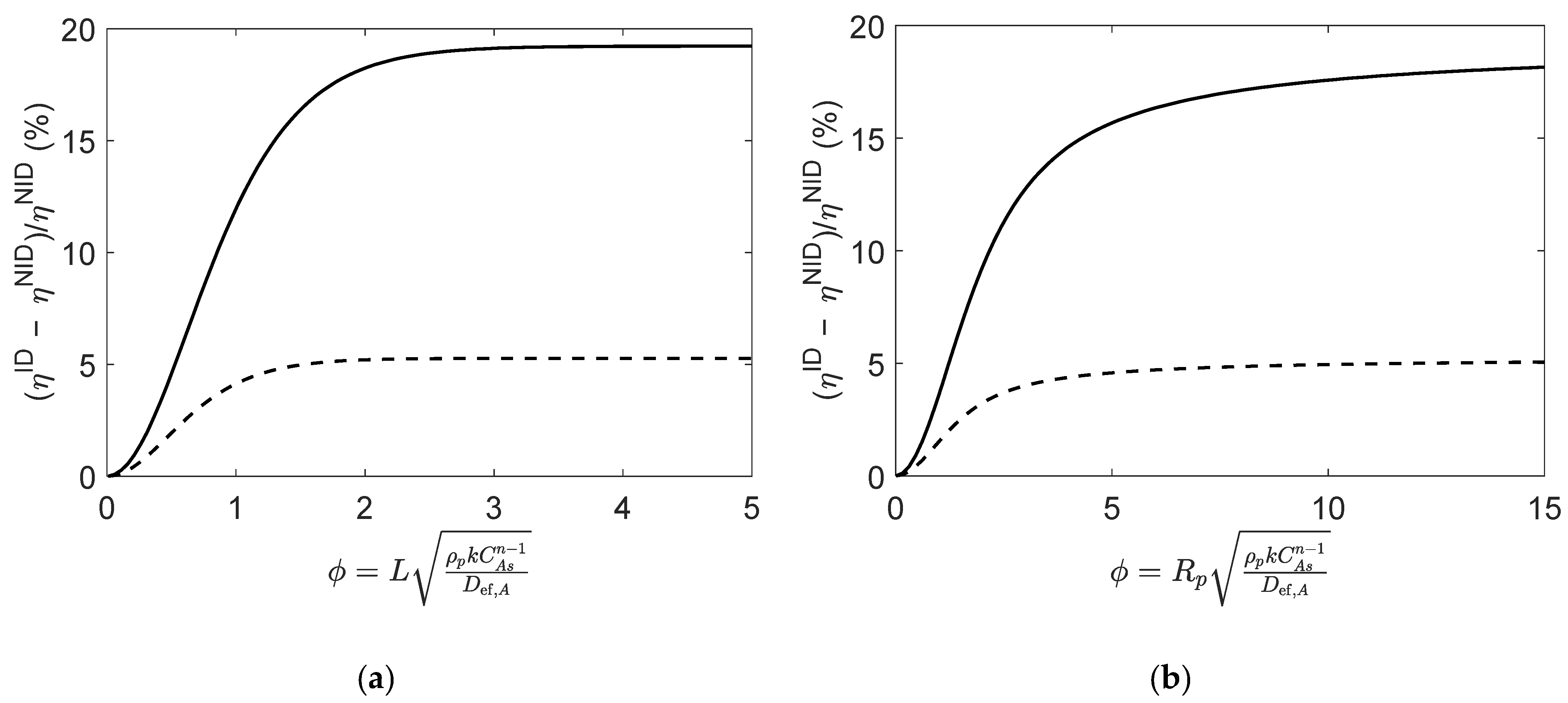
To ascertain the impact of the non-idealities, the effectiveness factors were analytically computed using ideal and non-ideal effective diffusivities, hereafter denoted by and , respectively. The results plotted in Figure 5 illustrate the relative deviations between and for both slab and spherical particles, for different values of Thiele modulus at initial conditions and near equilibrium. For both particle geometries, the results show that the non-ideal behavior impact on the effectiveness factor is negligible for very low values of Thiele modulus (). However, for larger values of the assumption of an ideal mixture produces significant deviations in the computed . These deviations are higher for the slab catalyst than for the spherical particles, and as the reaction progresses towards equilibrium, the deviations become smaller, as can be seen in Figure 5.
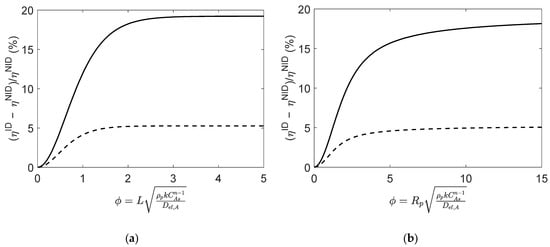
Figure 5.
Relative deviations between effectiveness factors computed using ideal and non-ideal effective diffusivities (i.e., and ), for reaction (Type I; in (a) slab and (b) spherical porous catalyst particles. Figures were generated as function of at initial conditions (solid line) and near equilibrium (dashed line).
Overall, these results enlighten the importance of adopting a rigorous approach to compute effective diffusivities when the reaction mixture evidences a non-ideal behavior.
4.2. Case 2: Acetal Synthesis (Type VII Reaction)
4.2.1. Process Description and Data Compilation
Acetaldehyde dimethyl acetal (referred to as acetal) can be synthesized in a liquid-phase acid-catalyzed reaction between methanol (A) and acetaldehyde (B), which corresponds to the Type VII reaction in Table 1. The reaction is represented by:
Gandi et al. [40] performed the reaction in a constant volume ( dm³) stirred batch reactor, operating at 20 °C, with agitation speed of 600 rpm to guarantee the absence of external mass transfer limitations, and using dry Amberlyst-15 resin (water content < 0.5 wt.%) with various particle sizes as a catalyst. The initial concentrations were mol/dm³ and mol/dm³. The catalyst properties and remaining data necessary to compute the analytical effectiveness factor are compiled in Table 6.

Table 6.
Catalyst properties, rate law constants and experimental conditions for Amberlyst-15 catalyzed acetal synthesis reaction in batch reactor [40].
4.2.2. Reactor Modelling and Effectiveness Factor Calculation
Gandi et al. [40] proposed an activity-based Langmuir–Hinshelwood–Hougen–Watson (LHHW) rate law for the Amberlyst-15 catalyzed reaction involving the equilibrium adsorption constant of water. However, at 20 °C, the adsorption term is negligible [40], and the rate law can be simplified, giving rise to the Type VII rate law equation (see Table 1). Since the original constants are reported for activities, the following manipulation was performed in this work:
where is the kinetic constant for the rate law expressed in terms of activities, and represent the activity and activity coefficient of component , respectively, is the total concentration, is the thermodynamic equilibrium constant, and are defined by Equation (23), and are the analogous quantities out of equilibrium defined in Equation (24). From Equation (22), the kinetic and equilibrium constants expressed in terms of concentrations are and . In this work, the activity coefficients embodied in Equation (22) and the equilibrium calculations were estimated by the UNIFAC model [39]. The computed equilibrium concentration for the conditions of Table 6 is mol/dm³.
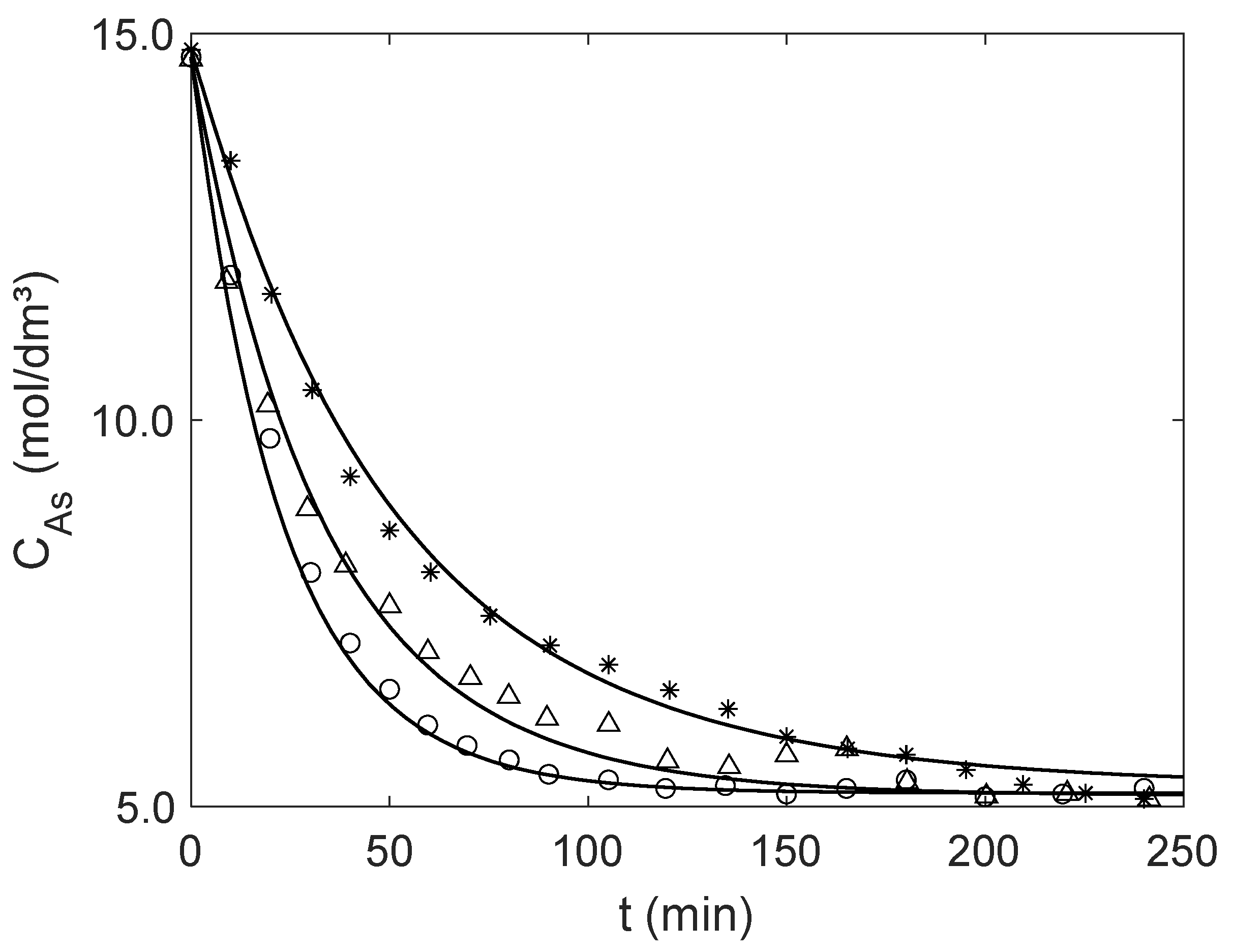
As in the previous case study (Section 4.1), the analytical effectiveness factors were calculated as described in Section 2.2, using the Rios et al. model [37] for the effective diffusivities in solution, . The reactor was modelled as a perfectly mixed isothermal batch reactor with no external mass transfer limitations. Hence, solving Equation (19) together with Equations (20) and (22)–(24) enables the prediction of the concentration profiles of methanol (A) over time. The experimental and calculated concentrations are presented in Figure 6. The overlapping of these results illustrates the accuracy of the analytical equations and modelling developed in this work (AARD between 1.23% and 3.38%).
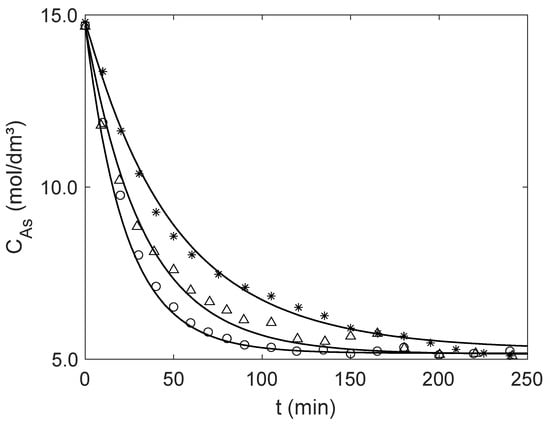
Figure 6.
Experimental data taken from Gandi et al. [40] (points) and modeling (curves) results for the catalyzed synthesis of acetal in batch reactor for the operating conditions of Table 6. Average diameter of Amberlyst-15 particles: ○ Exp. 1 ( μm); Δ Exp. 2 ( μm); and ✶ Exp. 3 (800 μm).
Table 7 summarizes the effectiveness factors values calculated for initial conditions and near equilibrium, along with the AARD of the curves. In both cases, the effectiveness factors are significantly lower than one, indicating the presence of relevant intraparticle diffusional resistances. Considering that the deviations between the experimental and calculated concentrations using the analytical are low (AARD < 3.38%), one may consider that the analytical procedure herein presented is once again validated as all calculations are pure predictions.

Table 7.
Calculated effectiveness factors for the liquid phase Amberlyst-15 catalyzed acetal synthesis for the conditions described in Table 6.
4.2.3. Impact of Effective Diffusivity Calculations on Effectiveness Factor Results
To ascertain the impact of the non-ideal behavior of the reaction system, the effectiveness factors were analytically computed using ideal and non-ideal effective diffusivities calculated with the Bird et al. [38] equations and the Rios et al. [37] model, respectively. Table 8 summarizes the results obtained by both methods for the initial conditions described in Table 6.

Table 8.
Effective diffusivities in solution calculated for the initial conditions described in Table 6.
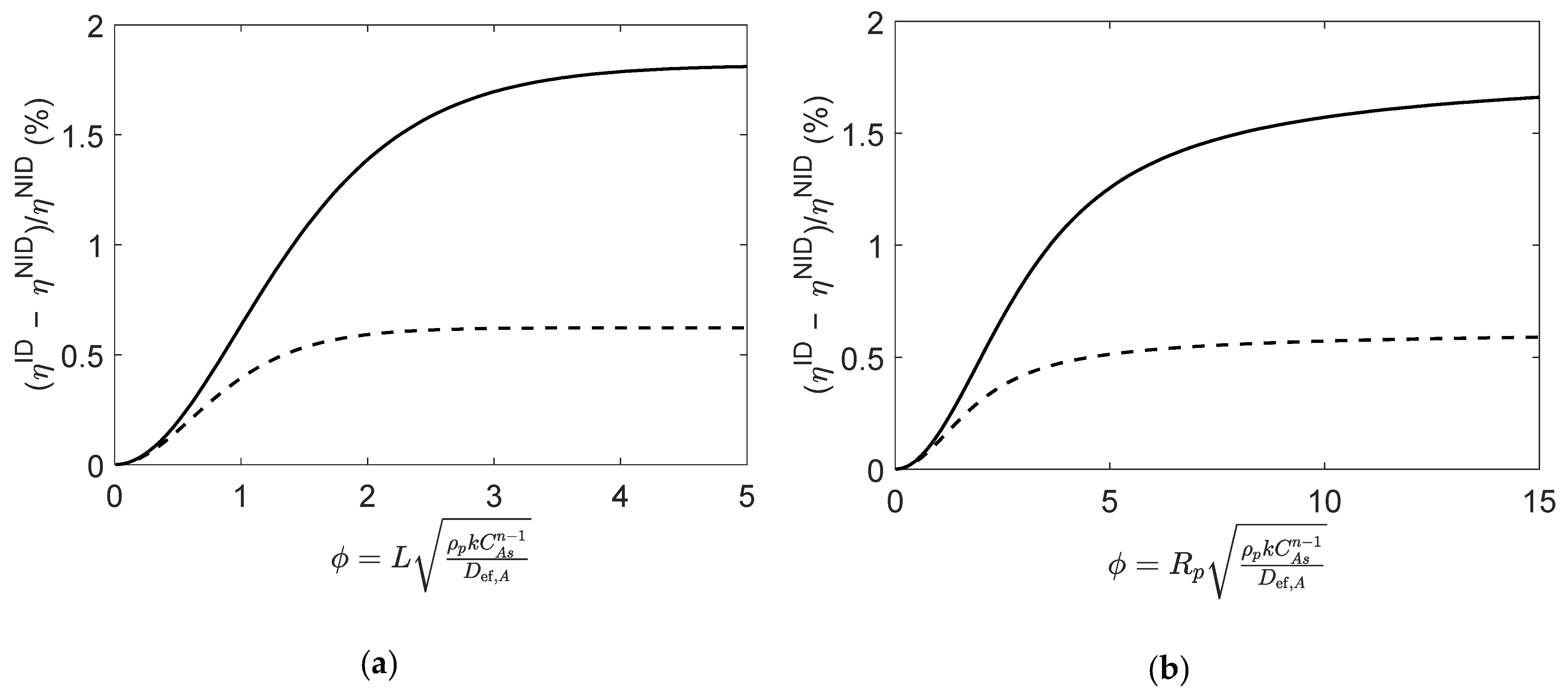
Although of the same magnitude, the different values of the effective diffusivities have a significant impact on the calculated effectiveness factors, as illustrated in Figure 7. For both particle geometries, the relative deviations between and show that the impact of the non-ideal behavior is negligible for very low values of Thiele modulus (), yet it increases for larger values of . As in Case 1 (Section 4.1.3), the assumption of an ideal mixture introduces important deviations in the computed that decrease as the reaction progresses towards equilibrium.
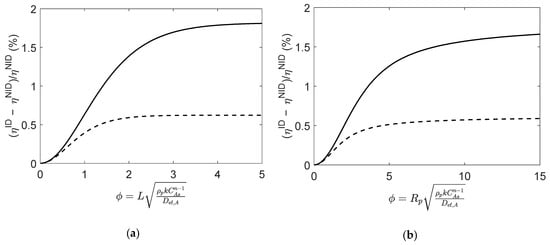
Figure 7.
Relative deviations between effectiveness factors computed using ideal and non-ideal effective diffusivities (i.e., and ), for reaction (Type VII; in (a) slab, and (b) spherical porous catalyst particles. Figures were generated as function of at initial conditions (solid line) and near equilibrium (dashed line).
5. Conclusions
Equations for the generalized Thiele modulus were developed for a set of seven reversible reactions occurring in isothermal porous catalyst particles, aiming for the analytical calculation of effectiveness factors. The proposed equations were numerically and experimentally validated for two distinct reversible liquid phase catalytic reactions. In both cases, the relative deviations between the numeric and analytical effectiveness factors were very low, revealing the accuracy of the analytical equations. Furthermore, the relative errors between the experimental and simulated concentration profiles in batch reactors were also very low, between 1.13% and 3.38%.
Additionally, a key finding of this work is the importance of selecting an accurate method to estimate the multicomponent effective diffusivities, especially when the system under analysis exhibits substantial deviations from ideal behavior. The deviations between the effectiveness factors computed assuming ideal behavior and non-ideal behavior reached 20% for the esterification of acetic acid with ethanol.
Despite the significant impact of the effective diffusivities on the computed effectiveness factor, several other potentially significant factors should be further investigated. Relevant areas may include analyses on the influence of catalyst parameters (e.g., tortuosity and porosity), the effects of not assuming equimolar counter diffusion inside the particle, and numerical studies for non-isothermal reaction conditions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/catal13050889/s1. It contains the effective diffusivity equations utilized in this work considering ideal and non-ideal liquid mixtures, as well as the iterative procedure to determine equilibrium concentrations. References [41,42] are cited in the supplementary materials.
Author Contributions
W.Q.R.: investigation, writing—original draft. B.A.: investigation, writing—original draft. A.E.R.: writing—review and editing, formal analysis. I.P.: supervision, methodology, resources, writing—review and editing, formal analysis. C.M.S.: conceptualization, methodology, resources, supervision, writing—review and editing, funding acquisition, formal analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This work is financed by Portugal 2020 through European Regional Development Fund (ERDF) in the frame of the Operational Competitiveness and Internationalization Programme (POCI) in the scope of the project CICECO—Aveiro Institute of Materials, UIDB/50011/2020 & UIDP/50011/2020 & LA/P/0006/2020, financed by national funds through the FCT/MEC (PIDDAC). This work was financially supported by LA/P/0045/2020 (ALiCE), UIDB/50020/2020 and UIDP/50020/2020 (LSRE-LCM), funded by national funds through FCT/MCTES (PIDDAC).
Data Availability Statement
Data are available in the article and in the Supplementary Material.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| AARD | average absolute deviation |
| activity of component | |
| concentration of component , mol/dm³ | |
| total concentration, mol/dm³ | |
| intraparticle effective diffusivity of component , dm²/min | |
| effective diffusivity of component in reaction medium, dm²/min | |
| Exp. | experiment |
| thermodynamic equilibrium constant | |
| equilibrium constant in terms of concentrations | |
| constant defined in Equation (23) | |
| constant defined in Equation (23) | |
| kinetic constant in terms of concentrations, dm6/(mol gcat min) | |
| kinetic constant in terms of activities, mol/(gcat min) | |
| catalyst characteristic dimension, dm | |
| molar flux of component A, mol/(dm² min) | |
| number of points | |
| order of forward reaction | |
| quotient of mole fractions out of equilibrium | |
| quotient of activity coefficients out of equilibrium | |
| particle radius, m | |
| rate of reaction, mol/(gcat min) | |
| rate of reaction at catalyst surface conditions, mol/(gcat min) | |
| observed reaction rate, mol/(gcat min) | |
| external surface area of the catalyst particle, dm² | |
| temperature, °C | |
| time, min | |
| catalyst volume, dm³ | |
| reactor mixture volume, dm³ | |
| liquid phase mole fraction | |
| mass of catalyst, gcat | |
| position coordinate inside slab, dm | |
| Greek Letters | |
| activity coefficient of component | |
| particle porosity | |
| effectiveness factor | |
| stoichiometric coefficient of component | |
| particle density, gcat/dm³ | |
| particle tortuosity | |
| Thiele modulus, dimensionless | |
| generalized Thiele modulus, dimensionless | |
| Subscripts | |
| 0 | catalyst center |
| direct | |
| effective | |
| equilibrium | |
| initial conditions | |
| arbitrary component in the mixture | |
| conditions at the catalyst surface or mixture bulk | |
| total | |
| Superscripts | |
| ID | refers to mixture effective diffusivities computed with the model by Bird et al. [38] |
| mixture | |
| NID | refers to mixture effective diffusivities computed with a non-ideal model [37] |
References
- Chidanand, N.M.; Eswara, P. Catalyst Market by Type (Zeolites, Metals, Chemical Compounds, Enzymes, and Organometallic Materials), Process (Recycling, Regeneration, and Rejuvenation), and Application (Petroleum Refining, Chemical Synthesis, Polymer Catalysis, and Environmental): Global Opportunity Analysis and Industry Forecast, 2021–2030; Allied Market Research: Portland, OR, USA, 2021; p. 580. [Google Scholar]
- Haase, S.; Tolvanen, P.; Russo, V. Process Intensification in Chemical Reaction Engineering. Processes 2022, 10, 99. [Google Scholar] [CrossRef]
- Mahajani, S.M.; Saha, B. Catalysis in Multifunctional Reactors. Phys. Sci. Rev. 2016, 1. [Google Scholar] [CrossRef]
- Osazuwa, O.U.; Abidin, S.Z. The Functionality of Ion Exchange Resins for Esterification, Transesterification and Hydrogenation Reactions. ChemistrySelect 2020, 5, 7658–7670. [Google Scholar] [CrossRef]
- Ramírez, E.; Bringué, R.; Fité, C.; Iborra, M.; Tejero, J.; Cunill, F. Role of Ion-Exchange Resins as Catalyst in the Reaction-Network of Transformation of Biomass into Biofuels. J. Chem. Technol. Biotechnol. 2017, 92, 2775–2786. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Sharma, M.M. Cationic Ion Exchange Resins as Catalyst. React. Polym. 1993, 20, 1–45. [Google Scholar] [CrossRef]
- Kidwai, M.; Chauhan, R.; Bhatnagar, S. Nafion-H®: A Versatile Catalyst for Organic Synthesis. Curr. Org. Chem. 2015, 19, 72–98. [Google Scholar] [CrossRef]
- Kunin, R.; Meitzner, E.A.; Oline, J.A.; Fisher, S.A.; Frisch, N. Characterization of Amberlyst 15. Macroreticular Sulfonic Acid Cation Exchange Resin. IEC Prod. Res. Dev. 1962, 1, 140–144. [Google Scholar] [CrossRef]
- Lilja, J.; Murzin, D.Y.; Salmi, T.; Aumo, J.; Mäki-Arvela, P.; Sundell, M. Esterification of Different Acids over Heterogeneous and Homogeneous Catalysts and Correlation with the Taft Equation. J. Mol. Catal. Chem. 2002, 182–183, 555–563. [Google Scholar] [CrossRef]
- Kazachenko, A.S.; Vasilieva, N.Y.; Fetisova, O.Y.; Sychev, V.V.; Elsuf’ev, E.V.; Malyar, Y.N.; Issaoui, N.; Miroshnikova, A.V.; Borovkova, V.S.; Kazachenko, A.S.; et al. New Reactions of Betulin with Sulfamic Acid and Ammonium Sulfamate in the Presence of Solid Catalysts. Biomass Convers. Biorefinery 2022, 1–12. [Google Scholar] [CrossRef]
- Sundmacher, K.; Zhang, R.-S.; Hoffmann, U. Mass Transfer Effects on Kinetics of Non-ideal Liquid Phase Ethyltert-Butyl Ether Formation. Chem. Eng. Technol. 1995, 18, 269–277. [Google Scholar] [CrossRef]
- Özgür, D.Ö.; Şimşek, T.; Özkan, G.; Akkuş, M.S.; Özkan, G. The Hydroloysis of Ammonia Borane by Using Amberlyst-15 Supported Catalysts for Hydrogen Generation. Int. J. Hydrogen. Energy 2018, 43, 10765–10772. [Google Scholar] [CrossRef]
- El-Nassan, H.B. Amberlyst 15®: An Efficient Green Catalyst for the Synthesis of Heterocyclic Compounds. Russ. J. Org. Chem. 2021, 57, 1109–1134. [Google Scholar] [CrossRef]
- Sie, S.T.; Krishna, R. Process Development and Scale Up: II. Catalyst Design Strategy. Rev. Chem. Eng. 1998, 14, 159–202. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 5th ed.; Prentice Hall: Boston, MA, USA, 2016; ISBN 978-0-13-388751-8. [Google Scholar]
- Shariff, H.; Al-Dahhan, M.H. Analyzing the Impact of Implementing Different Approaches of the Approximation of the Catalyst Effectiveness Factor on the Prediction of the Performance of Trickle Bed Reactors. Catal. Today 2020, 353, 134–145. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Q.; Kong, B.; Yang, C.; Fox, R.O. An Effectiveness Factor Model for Slurry Phase Olefin Polymerizations. Chem. Eng. Sci. 2022, 251, 117429. [Google Scholar] [CrossRef]
- Thiele, E.W. Relation between Catalytic Activity and Size of Particle. Ind. Eng. Chem. 1939, 31, 916–920. [Google Scholar] [CrossRef]
- Froment, G.F.; De Wilde, J.; Bischoff, K.B. Chemical Reactor Analysis and Design, 3rd ed.; Wiley: Hoboken, NJ, USA, 2011; ISBN 978-0-470-56541-4. [Google Scholar]
- Bischoff, K.B. Effectiveness Factors for General Reaction Rate Forms. AIChE J. 1965, 11, 351–355. [Google Scholar] [CrossRef]
- Roberts, G.W.; Satterfield, C.N. Effectiveness Factor for Porous Catalysts. Langmuir-Hinshelwood Kinetic Expressions. Ind. Eng. Chem. Fundam. 1965, 4, 288–293. [Google Scholar] [CrossRef]
- Roberts, G.W.; Satterfield, C.N. Effectiveness Factor for Porous Catalysts. Langmuir-Hinshelwood Kinetic Expressions for Bimolecular Surface Reactions. Ind. Eng. Chem. Fundam. 1966, 5, 317–325. [Google Scholar] [CrossRef]
- Carberry, J.J. The Micro-Macro Effectiveness Factor for the Reversible Catalytic Reaction. AIChE J. 1962, 8, 557–558. [Google Scholar] [CrossRef]
- Koopman, D.C.; Lee, H.H. Second-Order Reversible Reactions and Diffusion in a Slab-like Medium: An Application of the Weierstrass Elliptic PE-Function. Chem. Eng. Sci. 1991, 46, 1165–1177. [Google Scholar] [CrossRef]
- Gottifredi, J.C.; Gonzo, E.E. Approximate Expression for the Effectiveness Factor Estimation and a Simple Numerical Method for Concentration Profile Calculation in Porous Catalyst. Chem. Eng. J. 2005, 109, 83–87. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Rajendran, L.; Abukhaled, M.; Kannan, M. Semi-Analytical Expressions for the Concentrations and Effectiveness Factor for the Three General Catalyst Shapes. React. Kinet. Mech. Catal. 2022, 135, 1739–1754. [Google Scholar] [CrossRef]
- Alopaeus, V. Approximating Catalyst Effectiveness Factors with Reaction Rate Profiles. Catalysts 2019, 9, 255. [Google Scholar] [CrossRef]
- Baur, R.; Krishna, R. The Effectiveness Factor for Zeolite Catalysed Reactions. Catal. Today 2005, 105, 173–179. [Google Scholar] [CrossRef]
- Nkohla, M.A.; Godongwana, B.; Fester, V.G.; Caleb, O.J. An Analytical Solution of the Effectiveness Factor of Photocatalytic Reactors Based on Robin Boundary Conditions. Chem. Eng. J. Adv. 2023, 14, 100464. [Google Scholar] [CrossRef]
- Meurer, A.; Smith, C.P.; Paprocki, M.; Certık, O.; Kirpichev, S.B.; Rocklin, M.; Kumar, A.; Ivanov, S.; Moore, J.K.; Singh, S. SymPy: Symbolic Computing in Python. PeerJ Comput. Sci. 2017, 3, e103. [Google Scholar] [CrossRef]
- Doǧu, T. Diffusion and Reaction in Catalyst Pellets with Bidisperse Pore Size Distribution. Ind. Eng. Chem. Res. 1998, 37, 2158–2171. [Google Scholar] [CrossRef]
- Bensetiti, Z.; Schweich, D.; Abreu, C.A.M. The Sensitivity of the Catalyst Effectiveness Factor to Pore Size Distribution. Braz. J. Chem. Eng. 1997, 14, 3. [Google Scholar] [CrossRef]
- Antunes, B.M.; Cardoso, S.P.; Silva, C.M.; Portugal, I. Kinetics of Ethyl Acetate Synthesis Catalyzed by Acidic Resins. J. Chem. Educ. 2011, 88, 1178–1181. [Google Scholar] [CrossRef]
- Taddeo, F.; Vitiello, R.; Tesser, R.; Melchiorre, M.; Eränen, K.; Salmi, T.; Russo, V.; Di Serio, M. Nonanoic Acid Esterification with 2-Ethylhexanol: From Batch to Continuous Operation. Chem. Eng. J. 2022, 444, 136572. [Google Scholar] [CrossRef]
- Rehfinger, A.; Hoffmann, U. Kinetics of Methyl Tertiary Butyl Ether Liquid Phase Synthesis Catalyzed by Ion Exchange Resin—II. Macropore Diffusion of Methanol as Rate-Controlling Step. Chem. Eng. Sci. 1990, 45, 1619–1626. [Google Scholar] [CrossRef]
- Badia, J.H.; Fité, C.; Bringué, R.; Ramírez, E.; Iborra, M. Relevant Properties for Catalytic Activity of Sulfonic Ion-Exchange Resins in Etherification of Isobutene with Linear Primary Alcohols. J. Ind. Eng. Chem. 2016, 42, 36–45. [Google Scholar] [CrossRef]
- Rios, W.Q.; Antunes, B.; Rodrigues, A.E.; Portugal, I.; Silva, C.M. Accurate Effective Diffusivities in Multicomponent Systems. Processes 2022, 10, 2042. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Diffusivity and the Mechanisms of Mass Transport. In Transport Phenomena; Wiley: New York, NY, USA, 2002; ISBN 978-0-471-41077-5. [Google Scholar]
- Elliott, J.R.; Lira, C.T. Introductory Chemical Engineering Thermodynamics, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2012; ISBN 978-0-13-606854-9. [Google Scholar]
- Gandi, G.K.; Silva, V.M.T.M.; Rodrigues, A.E. Process Development for Dimethylacetal Synthesis: Thermodynamics and Reaction Kinetics. Ind. Eng. Chem. Res. 2005, 44, 7287–7297. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2001; ISBN 978-0-07-011682-5. [Google Scholar]
- Biffis, A.; Corain, B.; Zecca, M.; Corvaja, C.; Jerabek, K. On the Macromolecular Structure and Molecular Accessibility of Swollen Microporous Resins: A Combined ESR-ISEC Approach. J. Am. Chem. Soc. 1995, 117, 1603–1606. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).