Abstract
Many companies try to access personal information to discriminate among consumers. We analyse how privacy regulations affect the acquisition and disclosure of information in a simple game of persuasion. Theory predicts that no data will be acquired with Disclosure Duty of collected data whereas Consent Law with perfect privacy results in complete information acquisition. Imperfect privacy, i.e., an environment in which leaks of collected data are possible, gives rise to multiple equilibria. Results from a laboratory experiment confirm the qualitative differences between Consent Law and Disclosure Duty and show that imperfect privacy does not stop people from collecting personal information.
JEL Classification:
C90; D80; D82; I10
1. Introduction
In modern economies information is key. People collect data every minute and share it frequently with third parties. People collect data on their GPS location through their smartphones or use wearables to keep track of their personal health status. Such information is on the one hand valuable to the individual and, on the other hand, valuable to companies. So far, the behavioural literature on preferences for privacy has mainly focused on information transmission, i.e., on when and why people share their personal data (see for instance [1,2,3,4,5,6,7]). This research has informed policy makers from which privacy regulations individuals may benefit or suffer. In this paper we argue that it not only important to understand under which conditions people are willing to share personal data but, even more so, to investigate how privacy regulations affect the willingness to acquire such information in the first place, as this may have severe consequences for individuals as well as aggregate market outcomes and welfare (see also [8]).
Studying how privacy regulations affect the acquisition of personal information can inform policy makers under which conditions information asymmetries arise and is of great importance to judge institutional consequences for rent distributions and welfare. One particularly important example for an environment with asymmetric information are health markets. On the one hand, keeping track of one’s personal health status by using wearables, visiting the doctor regularly or undertaking specific medical tests (e.g., tests for chronic diseases, sexually transferable diseases (STDs) or genetic tests) benefits the individual. It offers possibilities of prevention and early interventions of serious diseases, and may as well benefit the individual through preferable rates for insurance. On the other hand, these documentations and tests generate data that are valuable for insurers. Insurers can benefit from access to such data, as it is in insurers’ interest to discriminate among different health types.1 However, anticipating such discrimination, patients may become reluctant to collect personal health data or forego specific medical tests and thereby also potential benefits from information acquisition.2
Across the world, different data privacy regulations have been proposed and implemented. Some of them explicitly involve a risk of discrimination when acquiring personal data. For instance, Disclosure Duty, a regulatory rule used for genetic testing in New Zealand, the UK and Germany (see [11]) creates such a risk, as under Disclosure Duty patients have to disclose collected information when contracting with an insurer. Other institutions, such as Consent Law3 (implemented for genetic testing e.g., in the Netherlands and Switzerland, [10]) aim at leaving patients in full control of their collected data and let patients themselves decide whether or not to disclose them.4
There exist several studies that have theoretically discussed the welfare implications of different regulatory institutions in the context of insurance markets (see e.g., [11,13,14,15,16]) and matching markets (see e.g., [17,18]).5 However, causal empirical evidence on the consequences of privacy institutions for information acquisition is missing. Further, the theoretical literature has so far neglected a central aspect concerning privacy regulations: Perfect privacy—as assumed under Consent Law—cannot always be guaranteed; in particular not for centrally collected health data.6
Imperfect Privacy may result for at least two reasons. First, information about personal health attributes has often to be generated through the help of third parties (e.g., doctors and laboratories conducting medical tests, wearables and smartphone apps etc.) and thus patients are not in full control of their personal data. Second, recent incidents of leakage and data breaches, e.g., in 2007, where hundreds of thousands of UK National Health Service patients’ details were lost (see [24]), have remembered the public that perfect control over personal data cannot be taken for granted. Further, technological advances have increased the possibilities of health and genetic testing such that more and more data can be collected, stored and accessed.
The aim of this article is twofold. First, we extend the theoretical discussion about the consequences of Perfect Privacy and Disclosure Duty for testing and disclosing information (see also [25]) by asking how people’s behaviour should change when Perfect Privacy cannot be guaranteed due to a positive probability of involuntary data transfer (e.g., data leakage).7 Second, we enrich the so far theoretical discussion of privacy regulations by providing experimental evidence on the relation of privacy institutions, information acquisition and information disclosure. We provide a novel and parsimonious laboratory experiment that allows for the identification of causal effects of three different privacy institutions (Disclosure Duty, Consent Law with Perfect Privacy and Imperfect Privacy, i.e., a Consent Law environment where patients are not in full control of their collected data).8 The experiment is closely linked to our simple model and provides additional guidance on behaviour for institutional environments with multiple equilibria.
Both, our theoretical framework and our experiment build on a simplified game of persuasion that captures the main incentive structures people face in the context of acquisition and disclosure of personal health data. In the main model, we focus on the individual benefits from testing for insurance premiums.9 Patients decide whether to collect information about their own health status—which can be good or bad. Thereafter they decide whether or not to disclose the collected information to persuade an insurer to offer a contract. The information transferred affects the prospects for a contract with the insurer, because the insurer’s profits depend on the patient’s health status. The insurer will contract with an identified good health type but will refuse to contract with an identified bad type.10 Because the insurer cannot directly identify whether a test has been conducted, it depends on the institutional setting whether or not the insurer will contract with an unknown type.
We focus on the decision to take tests which reveal information that is valuable to the insurer, e.g., information about people’s unchangeable health attributes (such as results from tests for chronic diseases or genetic tests). In contrast to more complex models (see e.g., [11,15,16]), we do not explicitly focus on genetic testing as an informative action for the patient in our simple game. Instead, we follow the approach for STD testing and protection by Philipson and Posner [18] (which abstains from modelling benefits from testing explicitly) but extend our theoretical analysis by providing a discussion on the robustness of our results with respect to explicit costs and benefits from testing.
Mirroring the logic of propositions 1 and 2 in the model Matthews and Postlewaite [25], we show that given insurers are ex ante willing to contract with unknown health types, the only Proper Equilibrium [26] for Disclosure Duty is a pooling equilibrium in pure strategies, in which patients will not collect information. The only Proper Equilibrium for Perfect Privacy is a separating equilibrium in pure strategies with full information acquisition. For Imperfect Privacy, we show that there exist, both, the separating equilibrium with complete information acquisition and the pooling equilibrium without information acquisition (as well as a proper mixed strategy equilibrium with incomplete information acquisition).11
Due to the existence of multiple equilibria under Imperfect Privacy our theoretical model does not provide clear guidance with respect to whether imperfect data privacy stops people from collecting personal information. Further, behavioural biases may affect whether or not people acquire and disclose information on their type. Therefore, we investigate which outcomes result from actual behaviour in a laboratory experiment. Participants of the laboratory experiment played a neutrally framed version of the simple persuasion game. We parameterize the game such that insurers were ex ante willing to contract with unknown health types and implemented three different treatments reflecting the privacy institutions described above. The experimental results show that behaviour in Perfect Privacy and Imperfect Privacy almost coincides. Thus, imperfect data privacy does not stop people from collecting personal information. Only under Disclosure Duty information acquisition is reduced (and contracting with unknown types becomes common).
2. Theory
2.1. The Model
Our theory builds on a simple game of persuasion which reflects the idea of an insurance market in which a patient (player 1) persuades an insurer (player 2) to contract by providing certified information about her health type. Player 2 can contract (from now on match) with player 1 and both may benefit from the match. A match is always profitable for player 1. However, player 2’s payoff depends on player 1’s type. Player 1 can be a good (type G) or a bad type (type B). A match with a good type increases player 2’s payoff. A match with a bad type decreases his payoff (e.g., costs for medical treatments to be paid by the insurer). A match results in payoff M for each player. However, if player 1 is a bad type, player 2 additionally incurs a loss of I.12 We assume M > 0, I > 0, and I > M. The last assumption describes the fact that a match with a bad type decreases player 2’s payoff. Let 0 < b < 1 be the share of bad types in the population of players 1. Further, for the main model, we assume both players to be risk neutral.13
Importantly, player 1 does not know her type ex-ante, but she can test and disclose her type to player 2 before player 2 decides on whether to match. Testing and disclosing is costless.14 The action of testing (not testing) is denoted by . Results from such tests reveal relevant information as soon as they have been taken (irrespective of whether the test is taken several times) such that the decision to test reflects a one-shot decision of an inexperienced actor. The action of voluntarily disclosing (not voluntarily disclosing) the test result to player 2 is denoted by . Let be the probabilities that type G and type B voluntarily disclose their type after testing.
Player 2 can learn player 1’s type only if player 1 had herself tested. After a test, player 1 might disclose her type voluntarily. However, player 2 might learn the test result although player 1 decided against disclosing with probability . Therefore, reflects Disclosure Duty, reflects Perfect Privacy and reflects Imperfect Privacy. Note that the action of testing itself cannot be observed. Hence for p < 1, if player 2 does not learn player 1’s type, he also does not learn whether player 1 had herself tested or not. Let U (unknown) denote the fact that player 2 does not know player 1’s type. denotes player 2’s decision to match (not to match) and si denotes the strategy of player i. All decisions are binary.
We are now ready to describe the existence of equilibria under the different privacy institutions. For all institutions, player 2 will match with an identified type G and will never match with an identified type B. Whether player 2 will match with an unidentified type U, depends on the data privacy institution (i.e., on ) as well as on the relative size of gains from a match () and expected losses (). In the following, we present equilibria in pure strategies for each institution separately followed by a short intuitive reasoning.15
Proposition 1.
(Disclosure Duty)
- (a)
- For andis a pure strategy equilibrium (complete information acquisition).
- (b)
- For andis a pure strategy equilibrium (no information acquisition).
Because all test results are revealed under Disclosure Duty, an unknown type has to be an untested player. The expected payoff of a match with an untested player is non-positive as long as . Therefore, for player 2 will not match with untested players and player 1 can only gain from testing. For the expected payoff of a match with an untested player is non-negative. Therefore, player 2 will match with untested players and player 1 will not test.
Proposition 2.
(Perfect Privacy)
- (a)
- Foris a pure strategy equilibrium (complete information acquisition).
- (b)
- For andis a pure strategy equilibrium (no information acquisition).
If player 2 does not match with unknown types, it is worthwhile to test for player 1. Also, it will be worthwhile for player 1 to disclose her test result if the test reveals that she is of type G. Type B is indifferent whether or not to disclose her type. In turn, as everybody tests and type G discloses her type, player 2 will not match with unknown types (who are all of type B).
Given player 2 matches with type G and unknown types U, player 1 is (in expectation) not better of when testing and hence does not deviate from her strategy of not testing.
Proposition 3.
(Imperfect Privacy)
- (a)
- Foris a pure strategy equilibrium (complete information acquisition).
- (b)
- For andis a pure strategy equilibrium (no information acquisition).
The intuition for the equilibrium with complete information acquisition (3a) is the same as for (2a). The intuition for the equilibrium with no information acquisition (3b) is that given player 2 matches with type G and unknown types U, it is clearly worthwhile to forgo collecting information as long as data privacy is not guaranteed ( > 0) because not collecting information prevents involuntary disclosure of being a bad type. If nobody tests, the set of untested players and the set of players of unknown types coincide. Thus, matching with unknown types will be worthwhile (or at least not harmful) for player 2 for .
In addition to the pure strategy equilibria there exist several mixed strategy equilibria in which information acquisition is incomplete. We relegate the derivation of these equilibria to Appendix B (but report the existence of these equilibria along with refined pure strategy equilibria in Figure 1).
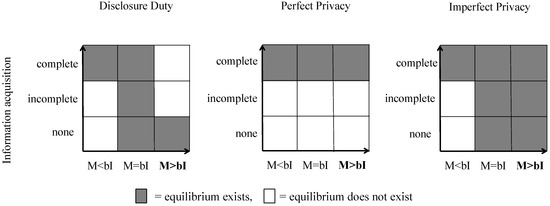
Figure 1.
Proper equilibria in the different privacy institutions.
2.2. Robustness: Risk Aversion, Costs and Benefits from Testing and Equilibrium Refinements
2.2.1. Risk Aversion
Let us briefly discuss the robustness of the different equilibria with respect to our assumption of risk neutral players. For all institutions, equilibria without information acquisition and incomplete information acquisition do not exists if player 2 (the insurer) is sufficiently risk averse because in this case player 2 will only match with identified good types. The equilibrium with full information acquisition holds also for risk averse players, since player 2 chooses the save option (matching with tested good types only) in equilibrium and player 1 has, in equilibrium, nothing to lose by playing the “lottery of testing.”16
2.2.2. Costs and Benefits from Testing
We abstained from modelling costs and benefits from testing explicitly. In this section, we briefly discuss how the introduction of costs and benefits affects the existence of the different equilibria. We will consider both, costs and benefits from testing that do not depend on the outcome of the test (costs of the test) and costs that depend on the testing outcome (psychological costs).17
First, it is clear that pure strategy equilibria in which people decide to test and reveal will still exist, if we introduce benefits from testing (both outcome dependent and outcome independent benefits), because benefits make testing even more attractive. Second and analogously, pure strategy equilibria without information acquisition and matching with unknown types will still exist, if we introduce costs from testing (for both types of costs). Third, it can be shown that the equilibria with full information acquisition also hold with explicit costs from testing as long as the expected gains from testing outweigh the costs. Equilibria with no information acquisition still hold for as long as the benefits from testing for Player 1 are smaller or equal to the expected loss of a match due to the revelation of a bad test outcome. However, under Perfect Privacy (), the equilibrium without information acquisition does not hold as soon as there are benefits from testing. Player 1 will test because collecting benefits from testing is riskless, if privacy is guaranteed.
2.2.3. Equilibrium Refinements
We derived multiple equilibria for each institutional setting. In this subsection we briefly discuss whether the number of equilibria may be reduced by applying the equilibrium refinement concept of Proper Equilibrium [26]. The notion of Proper Equilibrium has been introduced by Myerson [26] and is a further refinement of Selten’s [27] Trembling-Hand Perfect Equilibrium. Proper Equilibria consider the possibility that players play also non-equilibrium strategies with positive but very small probability such that decision errors are possible. The main idea of the Proper Equilibrium concept is that the likelihood of an error depends on the costs of making the error, i.e., making a costlier error can never be more likely than making a less costly error.
Applying this idea to our propositions it can be shown that for Perfect Privacy () the equilibrium without and incomplete information acquisition are no Proper Equilibria.
All equilibria we derived for Imperfect Privacy and Disclosure Duty remain. Figure 1 summarizes these findings. The figure illustrates that privacy institutions do not matter for testing if M < bI. Here only equilibria with complete information acquisition are possible. Since M = bI is a very unlikely assumption, we focus on the most interesting case (M > bI) where matches are ex-ante profitable for all agents in expected terms. Here, were find a unique Proper Equilibrium with no information acquisition in Disclosure Duty, and a unique Proper Equilibrium with complete information acquisition in Perfect Privacy. However, there exist multiple Proper Equilibria for Imperfect Privacy (for M > bI). Hence, the model does not provide a clear prediction with respect to the question whether Imperfect Privacy stops people from collecting information. Our experiment allows us to investigate whether behaviour under Imperfect Privacy coincides rather with behaviour under Perfect Privacy or Disclosure Duty.
3. Experiment
3.1. Experimental Design (Parameters and Treatments)
We chose the following parameter values for the experiment which fulfil the condition M > bI: The share of bad types B within players 1 was . A match M yielded 10 points for both players. A match with type B additionally decreased player 2’s payoff by 15 points (I = 15). At the beginning of the experiment, each player received an endowment of 10 points to prevent negative payoffs. Half of the participants were randomly assigned to the role of player 1 and half to the role of player 2. Then, player 1 and 2 were randomly assigned to a pair. Player 1 decided whether to test for her type and, depending on the treatment, whether to disclose the test result. Testing and disclosure was costless. Player 2 (potentially) learned the test result and decided whether or not to match.
We implemented three values of as treatment conditions in a between-subjects design: (Disclosure Duty), (Perfect Privacy) and (Imperfect Privacy). After as test, the test result was displayed to both players automatically in Disclosure Duty whereas in Perfect Privacy, player 1 first learned the test result and then decided whether to display the result to player 2. In Imperfect Privacy, after a test, player 1 first learned the test result and second decided whether to display the result to player 2. However, if player 1 decided to test she ran the risk of involuntary disclosure of the test result. If a player 1 had decided to test but not to transfer the information to the other player, a random device determined whether the test result was, nevertheless, shown on player 2’s screen.18 Note that player 2 only received information about the type of player 1 but not about whether or not this information was voluntarily revealed. Disclosing test results was costless and the test result displayed to both players was true in all treatments.19 The experiment consisted of two parts.
3.2. Part 1 (One-Shot)
In Part 1, the game was played once. This condition reflects on the one hand the idea that many specific tests (such as genetic tests) are usually not taken repeatedly and frequently taking a test once is sufficient that the information created by the test can be assessed by others (e.g., insurers) and on the other hand, that the decision to buy a specific insurance, e.g., disability insurance, is usually non-repeated. After participants made their decisions they were informed about their profit and player 1’s type.
3.3. Experimental Design for Part 2 (Repeated)
To control for potential decision errors and learning, we added a second part to the experiment, in which participants decided in ten periods whether or not to test (and disclose) or match. To exclude individual reputation building across periods and parts, we used a perfect stranger design (i.e., no participant interacted with the same person more than once and this was common knowledge). In the second part, participants were informed about player 1’s type, and their profit after every round.
3.4. Experimental Procedures
Each player sat at a randomly assigned and separated computer terminal and was given a copy of written instructions.20 At the beginning of the experiment participants were informed that the experiment consists of two independent parts. Participants received the instructions for the second part only after they finished the first part. Participants knew that it would be randomly determined at the end of the experiment which part would be payoff relevant. In case part two was selected, one randomly determined period was payoff relevant. The experiment was neutrally framed, i.e., we did not use the term patient or insurer or expressions such as “good” or “bad” types. Participants acted as player 1 or 2 and player 1 was either of type A or B. A set of control questions was provided to ensure that participants understood the game. If any participant repeatedly failed to answer correctly, the experimenter provided an oral explanation. No form of communication between the players was allowed during the experiment. We conducted ten sessions at the LakeLab (University of Konstanz, Germany) in June 2015 with a total number of 258 participants (NPerfect Privacy = 76, NImperfect Privacy = 102, NDisclosure Duty = 80). We computerized the experiment using z-Tree [30]. We recruited participants from the local subject pool using the online recruiting tool ORSEE [31]. In all treatments participants decided in one role, either as player 1 and or player 2 and kept that role for the whole experiment. To avoid testing out of general curiosity, players were informed ex ante that they will learn their type ex post (after decisions by both players were made). Further, participants were informed about all decisions and payoffs after every round. Procedures and parameters were common knowledge. Our experiment lasted 1 h. 10 points were equivalent to 6 euros. Participants received a 4 Euro show-up fee and earned 13.60 euros on average ($15.23 at that point in time). Participants also answered a short post-experimental questionnaire on their socio-economic background and their risk attitudes.
3.5. Experimental Results
3.5.1. Testing, Disclosing and Matching (Part 1: One-Shot)
Panel A of Figure 2 presents testing frequencies for all treatments in Part 1. Testing in Perfect Privacy is significantly more likely than in Disclosure Duty (χ2-test, p-value = 0.001). Also, testing in Imperfect Privacy is significantly more likely than in Disclosure Duty (χ2-test, p-value = 0.001). Testing frequencies in Perfect Privacy and Imperfect Privacy do not significantly differ (χ2-test, p-value = 0.631). Hence, only if data loss is certain, a significant share of players stops collecting information. We summarize this finding in Result 1.
Result 1
Testing frequencies in Perfect Privacy and Imperfect Privacy are higher than in Disclosure Duty. Testing frequencies in Perfect Privacy and Imperfect Privacy do not differ.
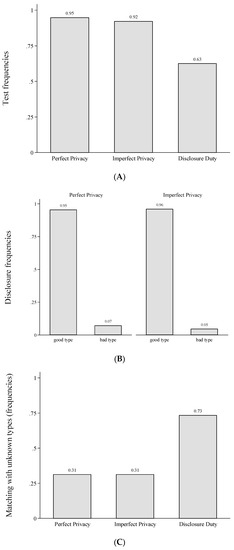
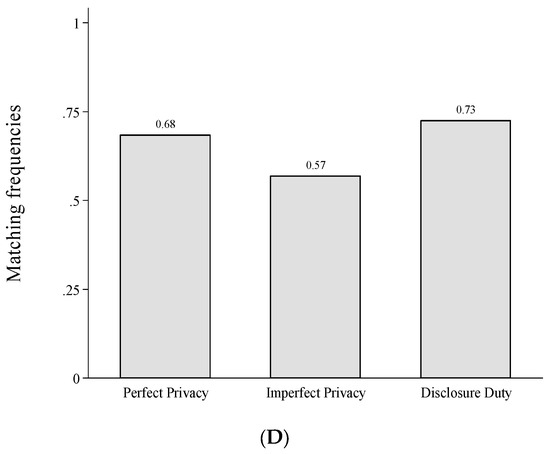
Figure 2.
Testing, disclosure, matching and frequency of matches in Part 1. (A) Test frequencies across treatments in Part 1; (B) Disclosure frequencies when tested; (C) Matching with unknown type (# participants matching with an unknown type/# participants facing an unknown type); (D) Total frequencies of matches.
Panel B of Figure 2 shows that almost all tested good types disclosed their type in Perfect Privacy and Imperfect Privacy,21 whereas voluntary disclosure of bad types is rare.22 Following, almost all players in Perfect Privacy and (almost all players in) Imperfect Privacy who did not disclose their type, are tested bad types or untested players.
Result 2
Disclosure behaviour in Perfect Privacy and Imperfect Privacy does not differ. Good types disclose their type, bad types are highly unlikely to do so.
Given that in Imperfect Privacy and Perfect Privacy players 1 test and good types disclose their type but fewer players test in Disclosure Duty, we should observe fewer matches with unknown types in Imperfect Privacy and Perfect Privacy compared to Disclosure Duty. As Panel C of Figure 2 shows, this is indeed the case: In Disclosure Duty 73 percent of players facing an unknown type decide to match whereas only 31 percent do so in Perfect Privacy (Fisher’s exact test, p-value = 0.001) and in Imperfect Privacy (Fisher’s exact test, p-value = 0.014). However, players 2 behaviour does not coincide with best responses of a risk neutral player given actual testing and disclosure rates (i.e., always matching with an unknown type in Disclosure Duty and never matching with an unknown type in Perfect Privacy and Imperfect Privacy).
However, participants rarely make errors when matching with disclosed types. Out of 65 disclosed good types 63 received a match. All 17 disclosed bad types received no match. We summarize these findings in Result 3.
Result 3
Matching with unknown types is not more likely in Imperfect Privacy than in Perfect Privacy but significantly more likely in Disclosure Duty.
Finally, we analyse whether efficiency varies across the different privacy institutions. As each match generates a surplus, we can measure efficiency by the total frequency of matches. According to our parameters and the Proper equilibria in Figure 1 we should ex ante expect 100% matching in Disclosure Duty and 66.67% matching in Perfect Privacy. In Imperfect Privacy, the matching probability depends on the equilibrium that is selected. In the equilibrium with no information acquisition we should expect 100% matching, in the equilibrium with full information acquisition we should observe 66.67%. The mixed equilibrium strategies result in 68.57% matching for our parameter values. However, since information acquisition and transmission does not significantly differ in the two privacy institutions and people rarely make errors when matching with disclosed types in the behavioural data, differences in efficiency between Imperfect Privacy and Perfect Privacy are expected to be small. If at all we should expect slightly fewer matches (and thus lower efficiency) in Imperfect Privacy, because insurers can identify some tested but undisclosed bad health types in Imperfect Privacy, given data is disclosed involuntarily. As can be seen in Panel D of Figure 2, we find that matching tends to be less likely in Imperfect Privacy compared to Perfect Privacy (57 vs. 68 percent) but does not differ significantly (χ2-test, p-value = 0.267). Disclosure Duty yields the highest level of efficiency, since it results in the most matches but also fails to differ significantly from the other two institutions (Disclosure Duty vs. Imperfect Privacy, χ2-test, p-value = 0.124 and Disclosure Duty vs. Perfect Privacy, χ2-test, p-value = 0.693).
Result 4
Efficiency levels do not significantly differ across treatments.
3.5.2. Testing, Disclosing and Matching (Part 2: Repeated)
Table 1 presents regression analyses for behaviour in Part 2, where participants made testing, disclosure and matching decisions repeatedly with new partners in each round. The results are very similar to the results from part 1: Testing frequencies in Model (1) between Perfect Privacy and Imperfect Privacy do not differ and testing frequencies are significantly lower in Disclosure Duty compared to Perfect Privacy and Imperfect Privacy (see model (1), Wald-Test comparing coefficients of Imperfect Privacy and Disclosure Duty, χ2 = 18.25, p < 0.001). Further, we find if at all a weak positive time trend in testing frequencies (see also Figure 3). Model (1) further shows that participants who are generally more willing to take risks and older participants tend to test less frequently for their type.

Table 1.
Random effects probit regressions (marginal effects), robust standard errors in parentheses (clustered on sessions), *** p < 0.01, ** p < 0.05, * p < 0.1.
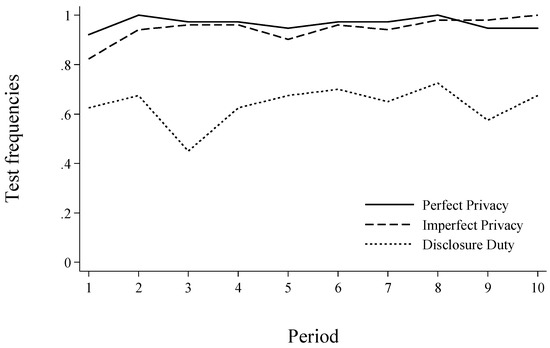
Figure 3.
Test frequencies over periods across treatments (Part 2).
Model (2) focuses on disclosure behaviour. We find that bad types disclose their type significantly less often than good types. Imperfect Privacy does not affect the decision to disclose information when tested. As in part 1, matching with unknown types is more likely in Disclosure Duty as compared to Perfect Privacy and Imperfect Privacy (see model (3), Wald-Test comparing coefficients of Disclosure Duty and Imperfect Privacy, χ2 = 20.61, p < 0.001). However, in part 2, matching with unknown types is also significantly more likely in Imperfect Privacy as compared to Perfect Privacy. Besides, there is a weak negative time trend in matching with unknown types Efficiency, measured in terms of unconditional matching in Model (4), does not significantly differ between Perfect Privacy and Imperfect Privacy and between Perfect Privacy and Disclosure Duty but is slightly less frequent in Disclosure Duty (0.59) compared to Imperfect Privacy (0.65, Wald-Test comparing coefficients of Imperfect Privacy and Disclosure Duty in model (4), χ2 = 2.25, p < 0.097).
To summarize, our results from the repeated setting (Part 2) are consistent with the main findings in Part 2. Testing frequencies in Perfect Privacy and Imperfect Privacy are higher than in Disclosure Duty but do not differ between Perfect Privacy and Imperfect Privacy. Disclosure behaviour is similar across treatments. Matching with unknown types occurs more frequently in Disclosure Duty as compared to Perfect Privacy but efficiency does not differ strongly.
4. Discussion and Conclusions
We study theoretically and experimentally whether imperfect data privacy stops people from collecting personal information about their health type. Our theory does not provide a clear answer to this question, as it allows for multiple equilibria if the privacy institution is imperfect. The behavioural results from our laboratory experiment, however, show that people collect information irrespective of whether data privacy is perfect or imperfect—even in an abstract environment that renders the potential consequences of involuntary disclosure salient.
Information acquisition and disclosure behaviour in Imperfect and Perfect Privacy almost coincide. Two possible reasons may explain why behaviour does not differ in the two privacy institutions: First, at the testing stage in Imperfect Privacy participants may simply not take into account the probability and consequences of involuntary disclosure. Second, participants may expect that only identified good types revive a match, although (at least in the repeated version of the game) matching with unknown types is significantly more likely when privacy is imperfect compared to perfect.
Our findings provide insights relevant to policy makers for economic environments in which individuals can acquire personal information that is useful to insurers. First, we find that even when privacy cannot be guaranteed, people still acquire personal information under Consent Law. Second, we contrast information acquisition and disclosure across different privacy institutions. Thereby our results inform policy makers about the causal consequences of these different institutions. Depending on the ultimate goal of the social planner, different institutions are attractive. From a perspective of equal opportunities, a social planner might be interested in maximizing the number of insured persons. For this goal, Disclosure Duty where matching with unknown types is theoretically most likely, is preferable. Consent Law is instead advantageous if the social planner is interested in increasing information acquisition (e.g., because of benefits from early preventions), even when perfect privacy cannot be guaranteed.
An alternative interpretation of the incentive structure in our game relates to matching markets. Namely, one may interpret our game as a reduced form of a matching market in which (un)infected persons look for a sexual partner. Instead of modelling two potential partners in a symmetric way, our game simplifies the decision framework such that one partner always wants to match but might be infected (player 1) whereas the other is not infected and only wants to match with healthy partners (player 2). A policy maker interested in maximizing the number of tests and thereby eventually minimizing the frequency of infections (mismatches) will prefer Perfect Privacy.23 As in Perfect Privacy, almost all players in Imperfect Privacy test and the good types disclose their test result whereas in Disclosure Duty the most matches with unknown types occur.24
Finally, we want to note that behaviour in the experiment corresponds to qualitative differences of our theoretical predictions (more information acquisition and fewer matches with unknown types in Perfect Privacy than Disclosure Duty). However, actual behaviour does not coincide with the point predictions of the model. While testing frequencies in Perfect Privacy and Imperfect Privacy almost perfectly correspond to the theoretical prediction, testing is observed far too frequently in Disclosure Duty. Such behaviour may be driven by inequality aversion25, assumptions about other players’ risk aversion, curiosity or simple decision errors. While our design does not allow to distinguish between inequality aversion and beliefs about other players’ risk aversion, curiosity and decision errors are unlikely to explain frequent testing. First, all participants knew that they would learn their own type at the end of the experiment (irrespective of their testing decision). Second, the results from the second part of the experiment do not indicate any learning patterns in Disclosure Duty. Further, we observe more matches with unknown types in Perfect Privacy and Imperfect Privacy than predicted in the proper equilibrium with complete information acquisition. This may also be a result of efficiency concerns, since a match always increased the total surplus. Future research may try to further disentangle which of the reasons discussed above explain the observed behaviour.
Acknowledgments
We would like to thank Katharine Bendrick, Lisa Bruttel, Gerald Eisenkopf, Urs Fischbacher, Konstantin von Hesler, Pascal Sulser, Katrin Schmelz, Irenaeus Wolff and the participants of the PET 2013 in Lisbon, the International ESA Meeting 2012 at NYU, the Thurgau Experimental Economics Meeting THEEM 2012 in Kreuzlingen for helpful thoughts and comments.
Author Contributions
Simeon Schudy and Verena Utikal conceived, designed and performed the experiments, analyzed the data and wrote the paper jointly.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proofs of Propositions 1 to 3
We provide proofs of propositions 1 to 3 for risk-neutral players. However, note that the propositions also hold as long as expected utility of matches with unknown types are sufficiently high or the utility function is not too concave.
Note that denotes player i’s expected payoff.
Proof of Proposition 1
- (a)
- Assume player 2 will not match with unknown types and . If , player 1 will test, i.e., , because . Player 2’s best response is and if , because and .
- (b)
- Assume player 2 will match with unknown types and . If player 1 will not have herself tested, i.e., player 1 will automatically be disclosed and in case of a bad test result, player 1 would not receive a match. Player 2’s best response is and if because and .
Proof of Proposition 2
- (a)
- Assume player 2 will not match with unknown types and . If , player 1 will disclose her type after a good test result because . After a bad test result player 1 is indifferent whether to disclose her type with because Player 2’s best response is because and for all M.
- (b)
- Assume = 0. Assume further that player 1 will never test and player 2 will match with unknown types. Clearly, player 1 cannot gain from testing if player 2 matches with unknown types. The same holds for player 2’s matching strategy and because and .
Proof of Proposition 3
- (a)
- Analogous to proposition 2a.
- (b)
- Assume player 2 will match with unknown type, i.e., and . If a tested player 1’s best response will be because and because . It follows that. Player 2’s best response is and if because and .
Appendix B. Incomplete Information Acquisition (Mixed Strategy Equilibria)
Let m denote the probability that player 2 matches with an unknown type and t the probability that player 1 tests.
Incomplete information acquisition under Disclosure Duty
For and .
is a mixed strategy equilibrium.
Proof
Assume . Player 1 is indifferent between testing and not testing because . Player 2 is indifferent between matching and not matching with unknown types because .
Incomplete information acquisition under Perfect Privacy
For and
is a mixed strategy equilibrium.
Proof
If player 2 matches with unknown types, a tested good type is indifferent whether to disclose her type, i.e., and indifferent whether to test as long as player 2 matches with unknown types. Player 2 matches with unknown types if
The left side of the equation derives from the fact that the fraction of undisclosed players consists of all players with bad type, untested good types, and tested but undisclosed good types.
Incomplete information acquisition under Imperfect Privacy
For and
is a mixed strategy equilibrium.
Proof
Assume with . If 0 < < 1, player 1 is indifferent whether to test as long as . For player 2, a match with an unknown player yields:
The left side of the equation derives from the fact that the fraction of undisclosed players consists of 1 − t untested players and t(1 − p)b tested but undisclosed players with bad type.
Appendix C. Instructions
One-shot experiment (translated from German)
We cordially welcome you to this economic experiment. In this experiment, your decisions and possibly other participants’ decisions will influence your payoff. It is therefore important that you read these instructions carefully. For the entire experiment, it is not allowed to communicate with other participants. If you have questions, please have a second look at the instructions. If you then still have questions, please raise your hand. We will then come to you and answer your question in private. Today’s experiment consists of two independent parts (i.e., neither your decisions nor other participants’ decisions from Part 1 are relevant for your or other participants’ payoff in Part 2. Also, in Part 2 you will not interact with the same participant as in Part 1.) Both parts are equally likely to be payoff relevant. Which part will be payoff relevant will be determined after Part 2. The participant with seat number 12 will roll a six-sided die. If the die shows a  ,
,  , or
, or  Part 1 will be payoff relevant. If the die shows a
Part 1 will be payoff relevant. If the die shows a  ,
,  , or
, or  , Part 2 will be payoff relevant. Your payoff in the experiment will be calculated in points and later converted into euros. The points you achieve in the payoff relevant part will be converted to Euros and paid out at the end of the experiment. The exchange rate we will use is 10 points = 6 Euros. On the following pages, we will explain the procedures of Part 1. All participants received the same instructions. You will receive the instructions for Part 2 shortly after Part 1 has ended. Before the experiment starts, we will summarize the procedures verbally. After Part 2 we kindly ask you to answer a short questionnaire.
, Part 2 will be payoff relevant. Your payoff in the experiment will be calculated in points and later converted into euros. The points you achieve in the payoff relevant part will be converted to Euros and paid out at the end of the experiment. The exchange rate we will use is 10 points = 6 Euros. On the following pages, we will explain the procedures of Part 1. All participants received the same instructions. You will receive the instructions for Part 2 shortly after Part 1 has ended. Before the experiment starts, we will summarize the procedures verbally. After Part 2 we kindly ask you to answer a short questionnaire.
 ,
,  , or
, or  Part 1 will be payoff relevant. If the die shows a
Part 1 will be payoff relevant. If the die shows a  ,
,  , or
, or  , Part 2 will be payoff relevant. Your payoff in the experiment will be calculated in points and later converted into euros. The points you achieve in the payoff relevant part will be converted to Euros and paid out at the end of the experiment. The exchange rate we will use is 10 points = 6 Euros. On the following pages, we will explain the procedures of Part 1. All participants received the same instructions. You will receive the instructions for Part 2 shortly after Part 1 has ended. Before the experiment starts, we will summarize the procedures verbally. After Part 2 we kindly ask you to answer a short questionnaire.
, Part 2 will be payoff relevant. Your payoff in the experiment will be calculated in points and later converted into euros. The points you achieve in the payoff relevant part will be converted to Euros and paid out at the end of the experiment. The exchange rate we will use is 10 points = 6 Euros. On the following pages, we will explain the procedures of Part 1. All participants received the same instructions. You will receive the instructions for Part 2 shortly after Part 1 has ended. Before the experiment starts, we will summarize the procedures verbally. After Part 2 we kindly ask you to answer a short questionnaire.The Experiment
Summary
In this experiment two participants (participant 1 and participant 2) will be randomly matched. Whether you are a participant 1 or 2 will be randomly determined. As soon as the experiment starts the computer screen shows you whether you are participant 1 or 2. Each of the two participants receives 10 points.
Participant 1 is either a type A or type B. Whether participant 1 is a type A or type B depends on chance. For each participant 1 the probability of being a type A is exactly 2/3 (or 66.66%). The probability of being a type B for participant 1 is exactly 1/3 (or 33.33%). Participant 2 has no special type.
Participant 2 decides whether he would like to interact with participant 1. If no interaction takes place, points do not change. An interaction changes both participants’ points.
- An interaction yields additional 10 points for participant 1.
- How an interaction affects participant 2 depends on participant 1’s type. If participant 1 is a type A, participant 2 receives additional 10 points. If participant 1 is a type B, participant 2’s points are reduced by 5 points.
- If there is no interaction, points do not change.
Procedure in Detail
- One participant 1 and one participant 2 will be randomly assigned to each other. Participant 1 as well as participant 2 receive 10 points. Participant 1 does not know whether he is of type A or of type B. Participant 2 also does not know participant 1’ type.
- Participant 1 decides whether she wants to learn her type.
- [This bullet point was only included in Perfect Privacy]
- If participant 1 has decided to learn her type, she decides whether to inform participant 2. Please note: If participant 1 knows her type and decided to inform participant 2, participant 2 will learn participant 1’s true type. If participant 1 knows her type but did not inform participant 2, participant 2 will not learn participant 1’s type. If participant 1 does not know her type, participant 2 will also not learn participant 1’s type. If participant 2 does not learn participant 1’s type, she will also not learn whether participant 1 herself knows her type. If participant 2 learns participant 1’s type, he also knows that participant 1 knows her type.
- [This bullet point was only included in Imperfect Privacy]
- If participant 1 decided to learn his type, she decides whether to inform participant 2 about her type. If participant 1 decided to learn her type, but does not inform participant 2, a random mechanism determines whether player 2 learns player 1’s type nevertheless. In this case player 2 learns player 1’s type with a probability of 50%.Please note: If participant 1 knows her type and decided to inform participant 2, participant 2 will learn participant 1’s true type. If participant 1 knows her type but did not inform participant 2, participant 2 will learn participant 1’s type with a probability of 50%. In both cases participant 2 does not know whether he was informed about the type randomly or directly by participant 1. In all other cases, participant 2 does not receive any information about participant 1’s type, i.e., if participant 1 does not know her type, participant 2 will also not learn participant 1’s type. If participant 2 does not learn participant 1’s type, he will also not learn whether participant 1 knows her type. If participant 2 learns participant 1’s type, he also knows that participant 1 knows her type.
- [This bullet point was only included in Disclosure Duty]If participant 1 decides to learn her type, participant 2 will learn participant 1’s type too.Please note: If participant 1 knows that she is type B, participant 2 will also learn that participant 1’s type is B. If participant 1 knows that she is type A, participant 2 will also learn that participant 1’s type is A. If participant 1 does not know her type, participant 2 will also not learn participant 1’s type. But participant 2 knows that participant 1 is of Type A with probability 2/3 (66%) and of Type B with probability 1/3 (33%)
- Participant 2 decides whether he wants to interact with participant 1.
- If participant 2 decides to interact, participant 1 receives an extra 10 points. Participant 2’s points depend on participant 1’ type. If participant 1 is of type A, participant 2 receives an extra 10 points. If participant 1 is of type B, participant 2’s points are reduced by 5 points.
- If participant 2 does decides NOT to interact, both participants receive no extra points, so each of the participants has the 10 points received at the beginning.
- After all participants have made their decision you will receive information about your earnings. At the same time the type of participant 1 and whether an interaction took place will be shown to participants 1 and 2.
Procedure on-Screen
Participant 1 will see the following screen.
Let’s assume that participant 1 would like to learn his type. Participant 1 selects “yes,” clicks on OK, and learns his type.
[This section was only included in Imperfect Privacy and Perfect Privacy]
Then participant 1 decides whether she wants to inform participant 2 about his type. Participant 1 will see the following screen (we assume in the example that participant 1 is a type A):
[This section was only included in Imperfect Privacy]
If participant 1 knows his type but did not inform participant 2, a random (50% probability) mechanism determines whether participant 2 learns participant 1’s type. For the random mechanism, the participant with ID number 12 will roll a die. You will learn the detailed procedure on screen.
Afterwards, participant 2 will see the following screen and decide whether he would like to interact with participant 1. (On the example screen we assume that participant 2 does not know participant 1’s type.)
The experiment ends after participant 2 has taken his decision.
At the end of the experiment, all participants 1 learn their type. All participants 2 learn their participant 1’s type—no matter whether they have learned the type before. Also, all participants are informed whether an interaction took place and how many points each of the two participants received.
Comprehension Questions: (correct answers in parentheses, DD = Disclosure Duty, PP = Perfect Privacy, IP = Imperfect Privacy)
True or False?
☐T ☐F Participant 1 always learns her type at the beginning of the experiment. (F)
☐T ☐F If participant 1 learned her type participant 2 learns it as well. (DD: T, PP & IP: F)
☐T ☐F Participant 2 always learns whether participant 1 knows her type. (F)
☐T ☐F At the end of the experiment all participants 1 learn their type. (T)
☐T ☐F At the end of the experiment all participants 2 learn their participant 1’s type. (T)
Further Questions:
How many points do you receive before each decision? (10)
What is the probability that participant 1 is of type A? (2/3)
What is the probability that participant 1 is of type B? (1/3)
What is the probability that a participant 1 who didn’t want to learn his type is of type A? (2/3)
What is the probability that a participant 1 who didn’t want to learn his type is of type B? (1/3)
If participant 1 learned his type [only in PP and IP: “but did not inform participant 2”], what is the probability that participant 2 learns the type nevertheless? (DD: 1, PP: 0 IP: 1/2)
If participant 1 DID NOT learn his type, what is the probability that participant 2 learns the type nevertheless before deciding whether or not to interact? (0)
Please fill in the Blanks:
- If participant 2 decided to interact and participant 1 is of type A, participant 2 receives___ (10) points.
- If participant 2 decided to interact and participant 1 is of type B, participant 2 loses ___ (5) points.
- If participant 2 decided to interact, participant 1 receives an extra ___ (10) points.
- If participant 2 refused to interact, participant 1 receives an extra ___ (0) points and participant 2 an extra ___ (0) points.
Repeated Experiment (Translated from German)
[These instructions were distributed after the end of Part 1.]
The Experiment—Summary
- Experiment 2 consists of 10 periods.
- Every period has the same procedure and rules as Experiment 1.
- You have the same role (participant 1 or participant 2) as in Experiment 1 in all 10 periods.
- Participant 1 decides whether she wants to learn her type (A or B).
- [This bullet point was only included in Perfect Privacy and Imperfect Privacy]. If participant 1 decided to learn her type, she decides whether to inform participant 2 about her type.
- Participant 2 decides whether to interact with participant 1.
Important:
- In every period, you will be matched with another participant, i.e., with a participant you have not been matched with before (neither in Part 1 or Part 2).
- In every period for every participant 1 it will be randomly determined whether she is type A or B. The probability to be type A or B are the same as in Part 1.
- ⚪
- The probability of being a type A is 2/3 (or 66.66%).
- ⚪
- The probability of being a type B is 1/3 (or 33.33%).
- At the end of Part 2, i.e., after period 10, one period will be randomly determined to be payoff relevant for Part 2. For this, the participant with seat number 12 will roll a ten-sided die.
- Afterwards, the participant with seat number 12 will roll a six-sided die to determine whether participants will receive their earnings from part 1 or Part 2.
[After reading the instructions for Part 2, participants had to fill in the following on-screen control questions.]

References
- Acquisti, A.; John, L.K.; Loewenstein, G. What is privacy worth? J. Legal Stud. 2013, 42, 249–274. [Google Scholar] [CrossRef]
- Beresford, A.R.; Kübler, D.; Preibusch, S. Unwillingness to pay for privacy: A field experiment. Econ. Lett. 2012, 117, 25–27. [Google Scholar] [CrossRef]
- Grossklags, J.; Acquisti, A. When 25 Cents is Too Much: An Experiment on Willingness-to-Sell and Willingness-to-Protect Personal Information; WEIS: Pittsburg, PA, USA, 2007. [Google Scholar]
- Huberman, B.A.; Adar, E.; Fine, L.R. Valuating privacy. IEEE Secur. Priv. 2005, 3, 22–25. [Google Scholar] [CrossRef]
- Tsai, J.Y.; Egelman, S.; Cranor, L.; Acquisti, A. The effect of online privacy information on purchasing behavior: An experimental study. Inf. Syst. Res. 2011, 22, 254–268. [Google Scholar] [CrossRef]
- Benndorf, V.; Normann, H.T. The willingness to sell personal data. Scand. J. Econ. 2017. [Google Scholar] [CrossRef]
- Schudy, S.; Utikal, V. ‘You must not know about me’—On the willingness to share personal data. J. Econ. Behav. Organ. 2017, 141, 1–13. [Google Scholar] [CrossRef]
- Hall, J.; Fiebig, D.G.; King, M.T.; Hossain, I.; Louviere, J.J. What influences participation in genetic carrier testing?: Results from a discrete choice experiment. J. Health Econ. 2006, 25, 520–537. [Google Scholar] [CrossRef] [PubMed]
- 5 Steps to Get More out of Your New Oscar Plan. Available online: https://www.hioscar.com/faq/5-steps-to-get-more-out-of-your-new-Oscar-plan (accessed on 2 March 2018).
- Hirshleifer, J. The private and social value of information and the reward to inventive activity. Am. Econ. Rev. 1971, 61, 561–574. [Google Scholar]
- Barigozzi, F.; Henriet, D. Genetic information: Comparing alternative regulatory approaches when prevention matters. J. Pub. Econ. Theory 2011, 13, 23–46. [Google Scholar] [CrossRef]
- Viswanathan, K.S.; Lemaire, J.; Withers, K.; Armstrong, K.; Baumritter, A.; Hershey, J.C.; Pauly, M.V.; Asch, D.A. Adverse selection in term life insurance purchasing due to the brca1/2 genetic test and elastic demand. J. Risk Insur. 2007, 74, 65–86. [Google Scholar] [CrossRef]
- Doherty, N.A.; Thistle, P.D. Adverse selection with endogenous information in insurance markets. J. Pub. Econ. 1996, 63, 83–102. [Google Scholar] [CrossRef]
- Hoy, M.; Polborn, M. The value of genetic information in the life insurance market. J. Pub. Econ. 2000, 78, 235–252. [Google Scholar] [CrossRef]
- Bardey, D.; De Donder, P.; Mantilla, C. Adverse Selection vs Discrimination Risk with Genetic Testing: An Experimental Approach. CESifo Working Paper Series No. 5080. 2014. Available online: http://ssrn.com/abstract=2532921 (accessed on 2 March 2018).
- Peter, R.; Richter, A.; Thistle, P. Endogenous information, adverse selection, and prevention: Implications for genetic testing policy. J. Health Econ. 2017, 55, 95–107. [Google Scholar] [CrossRef] [PubMed]
- Caplin, A.; Eliaz, K. Aids policy and psychology: A mechanism-design approach. RAND J. Econ. 2003, 34, 631–646. [Google Scholar] [CrossRef]
- Philipson, T.J.; Posner, R.A. A theoretical and empirical investigation of the effects of public health subsidies for std testing. Q. J. Econ. 1995, 110, 445–474. [Google Scholar] [CrossRef]
- Tabarrok, A. Genetic testing: An economic and contractarian analysis. J. Health Econ. 1994, 13, 75–91. [Google Scholar] [CrossRef]
- Bardey, D.; De Donder, P. Genetic testing with primary prevention and moral hazard. J. Health Econ. 2013, 32, 768–779. [Google Scholar] [CrossRef] [PubMed]
- Hoel, M.; Iversen, T. Genetic testing when there is a mix of compulsory and voluntary health insurance. J. Health Econ. 2002, 21, 253–270. [Google Scholar] [CrossRef]
- Kierkegaard, P. Electronic health record: Wiring europe’s healthcare. Comput. Law Secur. Rev. 2011, 27, 503–515. [Google Scholar] [CrossRef]
- Peppet, S.R. Unraveling privacy: The personal prospectus and the threat of a full-disclosure future. Northwest. Univ. Law Rev. 2011, 105, 1153. [Google Scholar]
- Nine NHS Trusts Lose Patient Data. Available online: http://news.bbc.co.uk/2/hi/uk_news/7158019.stm (accessed on 1 March 2018).
- Matthews, S.; Postlewaite, A. Quality testing and disclosure. RAND J. Econ. 1985, 16, 328–340. [Google Scholar] [CrossRef]
- Myerson, R.B. Refinements of the nash equilibrium concept. Int. J. Game Theory 1978, 7, 73–80. [Google Scholar] [CrossRef]
- Selten, R. Reexamination of the perfectness concept for equilibrium points in extensive games. Int. J. Game Theory 1975, 4, 25–55. [Google Scholar] [CrossRef]
- Rosar, F.; Schulte, E. Imperfect Private Information and the Design of Information–Generating Mechanisms. Discussion Paper. 2010. Available online: http://www.sfbtr15.de/uploads/media/Rosar_Schulte.pdf (accessed on 5 March 2018).
- Schweizer, N.; Szech, N. Optimal revelation of life-changing information. Manag. Sci. 2018. [Google Scholar] [CrossRef]
- Fischbacher, U. Z-tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef]
- Greiner, B. An online recruitment system for economic experiments. In Forschung und Wissenschaftliches Rechnen GWDG Bericht 63; Kremer, K., Macho, V., Eds.; Gesellschaft für Wissenschaftliche Datenverarbeitung: Göttingen, Germany, 2004; pp. 79–93. [Google Scholar]
- Engelhardt, B.; Kurt, M.R.; Polgreen, P.M. Sexually transmitted infections with semi-anonymous matching. Health Econ. 2013, 22, 1295–1317. [Google Scholar] [CrossRef] [PubMed]
| 1 | Apart from test based, type specific premiums, insurances nowadays also offer rebates, bonuses (or penalties) based on personal health data collected through health trackers or third parties (see e.g., [9]). |
| 2 | For a similar argument see also Hirshleifer [10]. |
| 3 | Consent Law describes the situation in which consumers “are not required to divulge genetic tests results. But, if they do, insurers may use this information” [12]. |
| 4 | In addition to Consent Law and Disclosure Duty, several other approaches have been discussed in the context of genetic testing. Barigozzi and Henriet [11] consider further the “Laissez-Faire approach”, under which insurers can access test results and require additional tests and “Strict Prohibition” of the use of test results. |
| 5 | For further work on genetic testing see also Tabarrok [19], Bardey and De Donder [20] and Hoel and Iversen [21]. |
| 6 | See also Kierkegaard [22] who discuss the merits and weaknesses of a centralized European health record system as planned by the European Commission’s Directive 2011/24/EU and Peppet [23] for a discussion with respect to legal aspects of privacy institutions. |
| 7 | Matthews and Postlewaite [25] focus on sellers’ testing behavior in the context of product quality when disclosure of test results is mandatory or voluntary and test results may be beneficial to consumers. For Perfect Privacy and Disclosure Duty our model mirrors the logic of their analysis and can be understood as a simplified version of their framework. However, our analysis differs in terms of who acquires information, what quality types are available and includes the additional environment of Imperfect Privacy. |
| 8 | Recently in a different setting, Bardey, De Donder and Mantilla [15] complement their theoretical analysis on different regulatory institutions for genetic testing with an experiment. However, their experimental design focuses on the joint decision of choosing a privacy institution and testing for one’s type using a series of individual lottery choice tasks. |
| 9 | In Section 2.2.2 we provide a robustness analysis on how psychological costs and prevention benefits affect the existence of equilibria derived in the simple model. |
| 10 | Our framework may also be interpreted as a situation in which the insurer offers two tariffs, one for good and one for bad health types. |
| 11 | While these results are derived by modelling patients and insurers as risk neutral and abstaining from modelling direct costs or benefits from testing, we discuss below whether these Proper Equilibria are robustness to common assumptions concerning risk aversion of patients and risk neutrality of insurers. Further, we discuss also the robustness of the different equilibria concerning costs and benefits from testing. |
| 12 | We refrain from modeling a partial internalization of the loss of utility (from a match with a bad type) of player 2 by player 1. Nevertheless modelling this internalization as a loss of I’ for player 1 does not change the model’s predictions as long as for player 1 I’ < M. We thank an anonymous referee for highlighting this aspect. |
| 13 | We discuss the robustness of our results with respect to risk aversion in Section 2.2.1. |
| 14 | We discuss the impact of explicit testing costs in Section 2.2.2. |
| 15 | We relegate formal proofs of all propositions as well as the derivation of mixed strategy equilibria to the appendix. |
| 16 | Assuming a risk neutral insurer but a risk averse consumer (as [13], equilibria with complete information or no information still exist for all institutions. Equilibria with incomplete information acquisition exist only for Disclosure Duty and Imperfect Privacy. |
| 17 | By doing so we implicitly deal with benefits from knowing to be the good type (which are in our model mathematically equivalent to costs from knowing to be the bad type) and costs from not knowing to be the good type (which are mathematically equivalent to benefits from knowing to be the bad type). |
| 18 | One randomly selected participant rolled a six-sided die to determine whether a test result was involuntarily displayed (depending on whether the number was odd or even). The participant was monitored and announced the number publicly. |
| 19 | For a discussion on imperfect testing devices see e.g., Caplin and Eliaz [17] or Rosar and Schulte [28] and more recently Schweizer and Szech [29]. |
| 20 | A copy of translated instructions can be found in Appendix C. |
| 21 | We cannot reject the hypothesis that disclosure behavior of tested good types is identical in Privacy and Imperfect Privacy (Fisher’s exact test, p-value = 0.926). |
| 22 | We cannot reject the hypothesis that disclosure behavior of tested bad types is identical in Perfect Privacy and Imperfect Privacy (Fisher’s exact test, p-value = 0.740). |
| 23 | More testing eventually reduces the number of mismatches. Engelhardt, et al. [32] for instance argue that on internet platforms for semi-anonymous encounters, provision of information about the own HIV status might result in a directed search and reduce the transmission rate by separating the uninfected and infected, e.g., through the use of condoms. |
| 24 | We carefully note that in the context of HIV testing, social preferences may matter strongly and many people may test and report their result, irrespective of the institutional setup. |
| 25 | Inequality aversion might also be the reason why some players 1 disclose their bad type. By this means they prevent player 2 from matching which would lead to an unequal allocation. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).