Strictly Dominated Strategies in the Replicator-Mutator Dynamics

Abstract

The replicator-mutator dynamics is a set of differential equations frequently used in biological and socioeconomic contexts to model evolutionary processes subject to mutation, error or experimentation. The replicator-mutator dynamics generalizes the widely used replicator dynamics, which appears in this framework as the extreme case where replication is perfectly precise. This paper studies the influence of strictly dominated strategies on the location of the rest points of the replicator-mutator dynamics, at the limit where the mutation terms become arbitrarily small. It can be proved that such limit rest points for small mutation are Nash equilibria, so strictly dominated strategies do not occur at limit stationary points. However, we show through a simple case how strictly dominated strategies can have an influence on the location of the limit rest points for small mutation. Consequently, the characterization of the limit rest points of the replicator-mutator dynamics cannot in general proceed safely by readily eliminating strictly dominated strategies.

1. Introduction

The continuous time selection mutation equation [1], usually called Replicator-Mutator Dynamics (RMD) [2], is a set of differential equations frequently used in biological and socioeconomic contexts to model evolutionary processes subject to mutation or experimentation. Among other applications, the replicator-mutator has been used to study molecular reactions [3], the evolution of viral variants [4], the evolution of cooperation [5], the evolution of language [6–8], signaling games [9,10] and, with some modifications over the standard version, carcinogenesis and tumor progression [11]. Formally, the replicator-mutator dynamics reads:

$${ẋ}_i=\text{∑}_{j=1}^n{x}_j{f}_j{\mu }_{ji}-x_i\overline{f},i=1,\dots ,n$$

Here x_i represents the fraction of individuals in a large (infinite) population using pure strategy i (i = 1,…, n) and μ_ij is the probability that strategy i generates an offspring using strategy j (therefore, Σ_j μ_ij =1). The payoff or fitness matrix is A = [a_ij], where a_ij ≥ 0 is the payoff that an i-strategist obtains in an interaction with a j-strategist. The fitness of strategy i is f_i = Σ_j x_j a_ij and the average fitness is f̄ = Σ_i x_if_i.

In the replicator-mutator dynamics, the unit simplex Δ_n = {(x₁,…,x_n)∈ℜⁿ: Σ_i x_i = 1 and x_i ≥ 0 }is forward invariant: if the state vector x = (x₁,…,x_n) starts in the unit simplex, it remains there; existence and uniqueness of trajectories can be proved by the Picard-Lindelöf theorem; and the existence of at least one stationary point (in the interior of the simplex if μ_ij > 0) can be proved using Brouwer's fixed point theorem. Results for the extension of the replicator-mutator to an infinite number of possibly mixed strategies are provided by Bomze and Bürger [12].

For the particular case of symmetric payoff matrices (which corresponds to the standard population-genetic model of natural selection on a large diploid population) and mutation rates μ_ji = μ_i for i ≠ j (an assumption introduced by Kingman [13] in his “house of cards” model), a global Lyapunov function can be found which excludes cyclic behavior and guarantees that all orbits converge to the set of fixed points [1,9]. However, this “nice” behavior is not the general case [1,3,14].

A well-known particular instance of the Replicator-Mutator Dynamics is the widely-used replicator dynamics. The Replicator Dynamics (RD) appears in this framework as the extreme case where replication is perfectly precise, i.e., where i-strategists can only give birth to i-strategists, leaving no room for mutation, error or experimentation. A crucial point in this regard is to note the difference between an evolutionary process without mutation (i.e., the RD or, equivalently, the RMD with μ_ij = 0 for i ≠ j) and an evolutionary process subject to arbitrarily rare mutations, which can be studied using the limit of the RMD when μ_ij → 0 for i ≠ j. Any property of the RD that does not hold in the small mutation limit of the RMD is a property that vanishes if only arbitrarily small departures from the perfect model could happen; thus the importance of studying discrepancies between the RD and the RMD with small mutation. Bomze and Bürger [12] show that an important difference between the RD and the RMD is that, in general, the effect of introducing mutation in the RD is to dissolve continua of neutrally stable equilibria into isolated asymptotically stable ones.

In this paper we focus on the influence of strictly dominated strategies on the location of the rest points of the RMD in the limit of small mutation. Following Samuelson [15], we will refer to the limit of the stationary states of the RMD, as the mutation terms become arbitrarily small, as “limit stationary states”. The limit stationary states of the RMD constitute a subset of the stationary points of the RD. For the sake of completeness, we start by reviewing the results concerning weakly dominated strategies.

It is well known that weakly dominated strategies in the RD may remain present forever [16-18]. While at any point in the interior of the simplex a weakly dominated strategy obtains a strictly lower payoff than some alternative (pure or mixed) strategy, the dynamics may lead the process “quickly” towards the boundary of the simplex, where the selection pressure over weakly dominated strategies may disappear.

In the RMD with μ_ij > 0, where a persistent form of mutation, migration or noise guarantees that all strategies enjoy a minimum inflow into the system (i.e., the process is pushed away from the boundaries of the simplex towards its interior), weakly dominated strategies always earn a strictly lower payoff than some other strategy. Thus, one could expect that this permanent selection pressure against weakly dominated strategies would keep them at minimal levels (i.e., those strictly induced by the mutation), and therefore, that in the small mutation limit (i.e., when those minimal levels tend to zero) weakly dominated strategies would be asymptotically wiped out. However, rather surprisingly, it has been shown that weakly dominated strategies are not wiped out in the limit of the RMD, or in more general perturbed selection dynamics [15,19,20].

Let us now turn to strictly dominated strategies. In the RD, starting from any interior point, strictly dominated strategies are asymptotically wiped out [20,21]. This result has been extended to some more general selection dynamics [22], but it has also been shown not to hold for many other common dynamics [23]. The disappearance of strictly dominated strategies along interior trajectories in the RD suggests the (stronger) conjecture that, in order to calculate the set of points to which these trajectories converge, strictly dominated strategies can be safely removed from the analysis. In any case, we show in this paper that this conjecture does not hold for the limit stationary points of the RMD.

For the RMD with μ_ij > 0 and a_ii > ∀ i, j = 1,…n, (from now on we will assume that these conditions hold) it can be proved—by the same arguments put forward by Samuelson [15] (Proposition 4.7) or Samuelson and Zhang [20] (Theorem 9)—that the limit stationary states for small mutation are Nash equilibria, so strictly dominated strategies are also absent from any limit stationary state. However, we show in this paper that strictly dominated strategies, even though they disappear at the limit stationary states of the RMD, can completely modify their position, thus changing the set of limit stationary points that correspond to trajectories that begin in the interior of the simplex. Strictly dominated strategies can dramatically alter the position of even asymptotically stable rest points. As a result, when analyzing the asymptotic dynamics of this kind of process for low mutation rates, and particularly the set of limit points, one should not readily dispose of strictly dominated strategies.

A biological implication of this result is that, in an evolutionary system in which the flow of mutations between behaviors, species or varieties is small, a very poorly fit and very rarely observed behavior in an ecosystem can be the main force explaining, predicting or controlling the observed proportions of the other behaviors or species. The impact of the poorly fit behavior can be more profound than the mere selection of a particular point within a set of neutrally stable equilibria subject to random drift (like in the RD): in the RMD with arbitrarily rare mutations, the poorly fit behavior may modify the location of a unique asymptotically stable point. Below, we use an example to show that equilibria that, in the RD, would be subject to random drift within a large range of values, can actually be stabilized at a precise particular level which is influenced by the scarce appearance of strictly dominated strategies or entrants.

The dependence of limit stationary states of the RMD on strictly dominated strategies is not as disheartening as it may seem: there are some cases where one can safely calculate the limit stationary states of the RMD with relation to the stationary states of the RD [15,19]. For instance, if we are dealing with a hyperbolic stationary state z of the RD, then the RMD has a rest point close to z which moves arbitrarily close to z as the mutation term becomes arbitrarily small, and has the same stability properties as z [24]. Bomze and Bürger [12,25], Stadler and Nuno [26] and Stadler and Schuster [3] provide further results on the relation between stationary states of the RD and the RMD, and some particular cases have been studied in detail [27].

2. Results

We study a replicator-mutator system with three strategies, one of which is strictly dominated, and we provide an analytical formula for the limit of its stationary state as the mutation rate goes to zero. The limit stationary state is shown to depend on the parameters that correspond to the strictly dominated strategy.

Let μ be the total fraction of mutants or entrants in the population, and let m_i be the fraction of mutants that adopt strategy i, so that μ_ji = μ_i for j ≠ i, where μ_i = μ_i ·m_i, with m_i > 0 and Σ_i m_i = 1. Then the persistence rate equals μ_ii = 1 — μ (1 — m_i). The replicator-mutator equation for this case can be written as:

$${ẋ}_i=x_i\left[\left(1-\mu \right)f_i-\overline{f}\right]+{\mu }_i\overline{f}$$

(1)

Assuming a_ii > 0, Equation (1) is equivalent (via a change in speed) to

$${ẋ}_i=x_i\left(1-\mu \right)\frac{f_i-\overline{f}}{\overline{f}}+\mu \left(m_i-x_i\right)$$

(2)

and, considering that, for x_i = 0, the first term in the right-hand side of Equation (2) is null, it is straightforward to see that, for μ_i = μ·m_i > 0, any stationary state of this system must be interior and a solution to

$$x_i{f}_i=\frac{\overline{f}}{1-\mu }\left(x_i-\mu ·m_i\right)$$

(3)

Let us now consider the payoff matrix

$$A=\left[\begin{array}{ccc}1& 1& a_{13}\\ 1& 1& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]$$

where strategy 3 is strictly dominated by the other two strategies:

$$0\le a_{31}<1;0\le a_{32}<1;0<a_{33}<min(a_{13},a_{23})$$

Let $x^{*}=\left[x_1^{*},x_2^{*},x_3^{*}\right]$ be a stationary state of the replicator-mutator Equation (3) for matrix A. We show in the appendix that ${lim}_{\mu \to 0}{x}_3^{*}=0$ and that x* satisfies the equation

$$m_3\left(a_{13}-a_{23}\right)x_1^{*}\left(x_1^{*}-1\right)+\left[1-a_{32}-\left(a_{31}-a_{32}\right)x_1^{*}\right]\left[\left(m_1+m_2\right)x_1^{*}-m_1\right]=O\left(x_3^{*}\right)$$

where $O\left(x_3^{*}\right)$ is a term that goes to zero as $x_3^{*}\to 0$, more precisely,

$$\exists M,\delta >0:\left|x_3^{*}\right|<\delta \Rightarrow \left|\text{O}\left(x_3^{*}\right)\right|\le M\left|x_3^{*}\right|$$

Consequently, for small μ, x* must be in a small neighborhood of some point l = [l ₁, 1 − l ₁, 0]which satisfies

$$g\left(l_1\right)=m_3\left(a_{13}-a_{23}\right)l_1\left(l_1-1\right)+\left[1-a_{32}-\left(a_{31}-a_{32}\right)l_1\right]\left[\left(m_1+m_2\right)l_1-m_1\right]=0$$

Note that g(l ₁) is a quadratic function. Given that g(0) = −m ₁(1 − a₃₂) < 0 and g(1) = m₂(1 − a₃₁) > 0, there is a unique solution to the equation g(l ₁) = 0 in l₁ ∈[0,1], which proves that there is a unique limit stationary state l. This solution is given by

$$l_1=\{\begin{array}{cc}\frac{\sqrt{b^2-4ac}-b}{2a}& \text{if}a\ne 0\\ -\frac{c}{b}& \text{if}a=0\end{array}$$

(4)

where

$$\begin{array}{c}a=m{}_3(a_{13}-a{}_{23})-(m{}_1+m_2)(a_{31}-a_{32}),\\ b=(m{}_1+m_2)(1-a_{32})-m_3(a_{13}-a_{23})+m_1(a_{31}-a_{32}),\text{and}\\ c=-m_1(1-a_{32})\end{array}$$

Note also that the limit stationary state does not depend on the payoff a₃₃, and the analysis is locally valid dropping the constraint a₃₃ < min(a₁₃, a₂₃), as there would still be an ε > 0 such that f ₃ < f₂ and f₃ < f₁, for x₃ < ε.

Finally, notice that, without mutation, the 3-strategy case we have selected presents a connected component of critical points along the edge where the strictly dominated strategy is null (x₃ = 0). In this neutral component the other two strategies are payoff-equivalent (f₁ = f₂). Thus, the selection of one single limit stationary point within this neutral component is necessarily due to the second-order forces induced by mutations [28]. Our results show that, at least in such situations where first-order selection forces vanish and second-order forces come into play, regardless of the number of strategies involved, strictly dominated strategies may influence the location of the limit stationary states of the RMD.

3. Example

Consider the case

$$A=\left[\begin{array}{ccc}1& 1& \alpha \\ 1& 1& \beta \\ \alpha & \beta & \gamma \end{array}\right]$$

with strategy 3 being strictly dominated: 0≤α< 1, 0≤β< 1, and 0 < γ < max(α, β). A is a symmetric matrix, so in this case, and with μ_ji = μ_i for j ≠ i, all orbits converge to the set of fixed points [1,9]. The fixed points are the solutions to

$$x_i{f}_i=\frac{\overline{f}}{1-\mu }(x_i-{\mu }_i)$$

For small mutation the limit stationary state l = [l ₁, 1 − l ₁, 0] can be calculated according to Equation (4). In the particular case m₁ =m₂ = m₃ = 1/3, this leads to

$$l_1=\{\begin{array}{cc}\frac{\left(1-\beta \right)-\sqrt{\left(1-\beta \right)\left(1-\alpha \right)}}{\alpha -\beta }& \text{if}\alpha \ne \beta \\ 1/2& \text{if}\alpha =\beta \end{array}$$

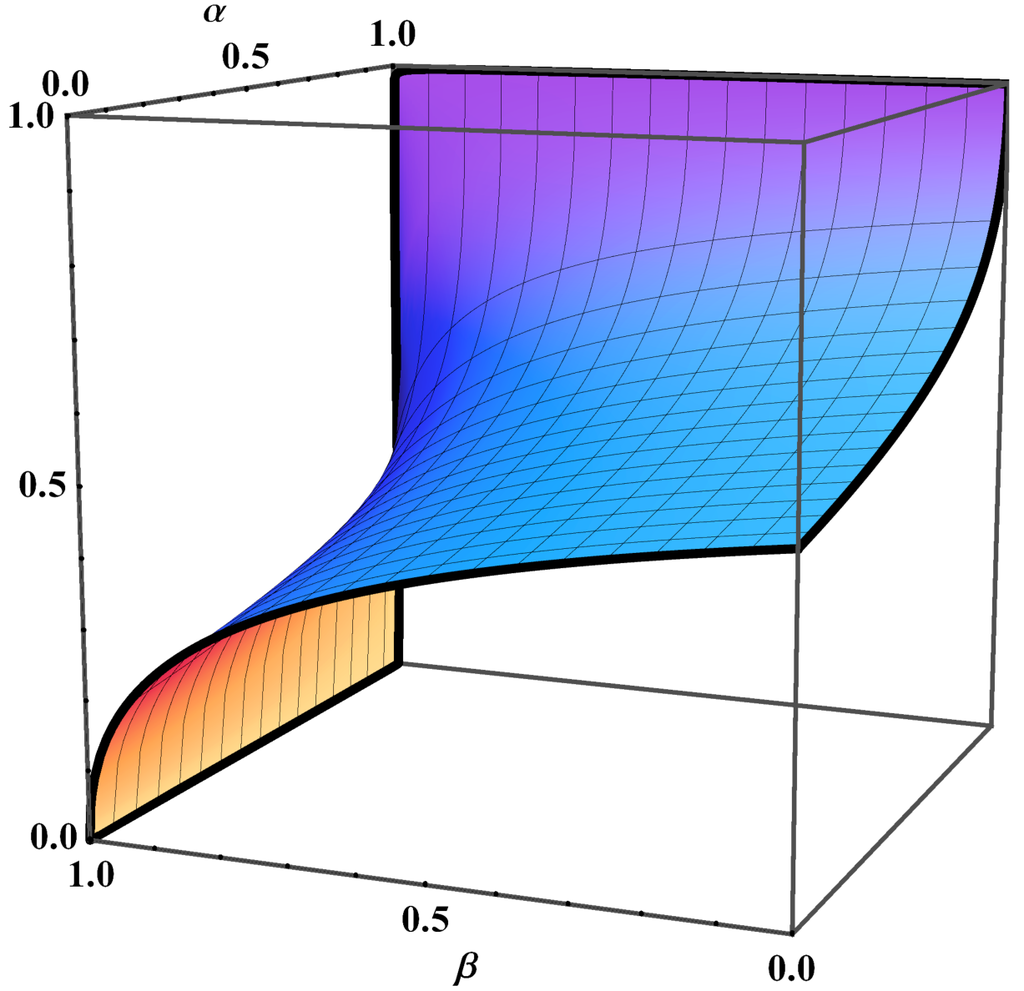
Figure 1 represents l₁ as a function of α and β. It can be seen how the limit stationary state l = [l ₁, 1 − l ₁, 0] can vary from one extreme to the other with the parameters α and β that correspond to the strictly dominated strategy. Figure 2 shows the limit stationary state in the unit simplex corresponding to three different combinations of values of α and β. Figure 2 can be reproduced using the Mathematica® computer program provided as supplementary material. This program can be run with Wolfram CDF Player, which is freely available on the Web.

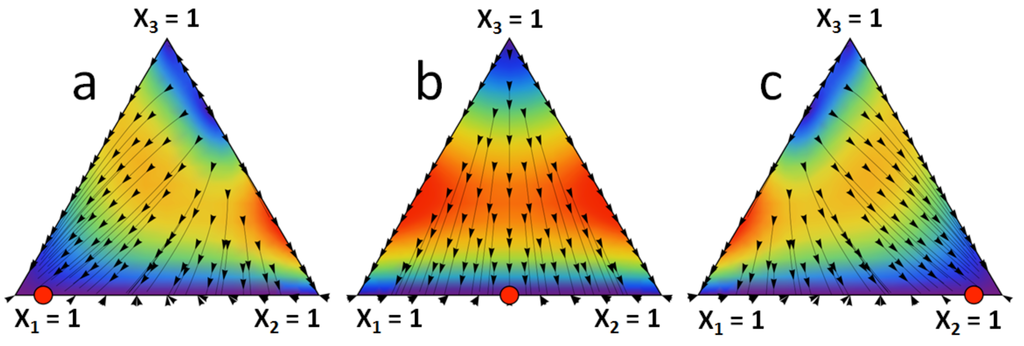
It might be thought that which particular point is selected out of a continua of RD equilibria, such as the line x₁ + x₂ = 1 in this example, is not very relevant, given that strategy 1 and strategy 2 are equivalent in the absence of other strategies. Note, however, that the response of this system to shocks or perturbations can be very different depending on the proportions of strategy 1 and strategy 2. Suppose, for instance, that the model corresponds to the coexistence of three species in an ecosystem, and the system is resting at the stationary point where x₁ + x₂ ≈ 1. If a small fraction x₄ of individuals of a fourth species arrives at this ecosystem, and this fourth species rates poorly against species 1, but well against species 2 and against itself, needing a minimal value of x₂ in order to proliferate (i.e., in order to obtain enough fitness), it is clear that both the short-run and the long-run behavior of this system in response to the potential invasion can be completely different depending on the initial proportions of species 1 and 2.

4. Conclusions

The limit stationary points of the RMD constitute a subset of the stationary points of the RD. Bomze and Bürger [12] show that the effect of introducing mutation in the RD (in a framework which admits mixed strategies) is to dissolve continua of neutrally stable equilibria into isolated asymptotically stable ones. This paper provides a formula to calculate a limit stationary point of the RMD for a simple kind of game and illustrates that, in general, the location of a limit stationary point of the RMD depends not only on the surviving strategies at that point and their mutation rates, but it can also depend on the non-surviving strategies, including strictly dominated strategies. It also shows as a corollary that, in order to calculate the set of limit stationary points of the RMD, strictly dominated strategies cannot be readily eliminated.