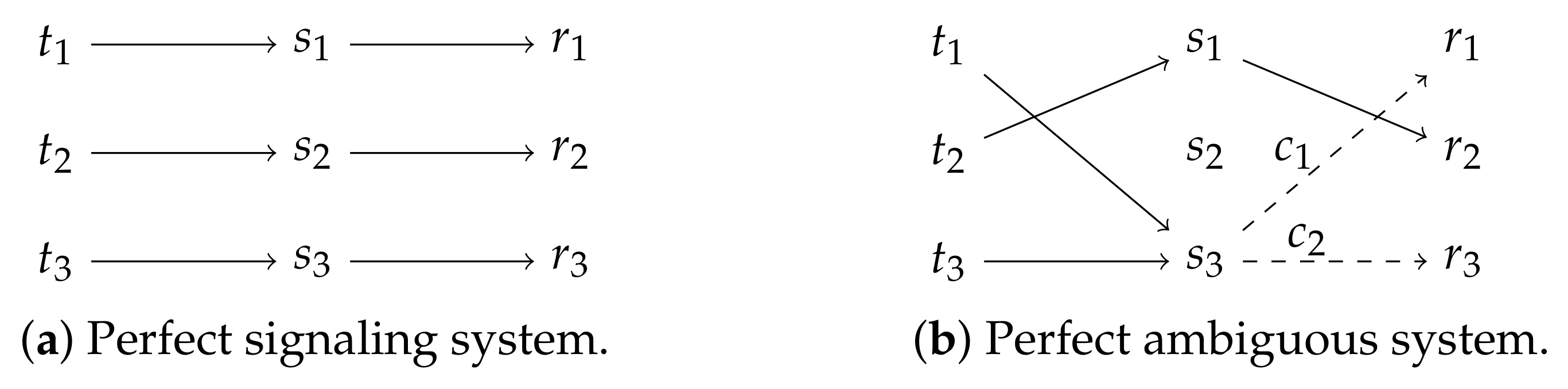Abstract
We study an extended version of a sender–receiver signaling game—a context-signaling (CS) game that involves external contextual cues that provide information about a sender’s private information state. A formal evolutionary analysis of the investigated CS game shows that ambiguous signaling strategies can achieve perfect information transfer and are evolutionarily stable. Moreover, a computational analysis of the CS game shows that such perfect ambiguous systems have the same emergence probability as non-ambiguous perfect signaling systems in multi-agent simulations under standard evolutionary dynamics. We contrast these results with an experimental study where pairs of participants play the CS game for multiple rounds with each other in the lab to develop a communication system. This comparison shows that unlike virtual agents, human agents clearly prefer perfect signaling systems over perfect ambiguous systems.
1. Introduction
David Lewis [1] developed a game-theoretic model to study how conventional communicative patterns can evolve through emerging regularities of communicative behavior, giving rise to a (common interest) sender–receiver signaling game. In the vanilla variant of such a signaling game, the expected utilities for sender and receiver are optimal if and only if their strategies form perfect signaling systems: one-to-one mappings between information states, signals and actions. Only such mappings guarantee perfect information transfer. Previous research into most variants of the signalling game has shown that perfect signaling systems (i) are the most expected outcome under evolutionary dynamics, including dynamics on a population level as well as imitation and learning dynamics in agent-based models [2,3,4], and (ii) display the highest level of evolutionary stability in comparison to non-perfect signaling strategies, such as pooling strategies that represent ambiguous signaling [5,6].
The superiority of perfect signaling systems over ambiguous signaling does not necessarily hold for modified versions of the signaling game. For example, the context-signaling game is an extension of the standard Lewis signaling game, which involves contextual cues, i.e., clues that reveal the sender’s information state to the receiver. It can be shown that in such a game, ambiguous signaling can ensure perfect information transfer: the sender’s and the receiver’s strategies form a perfect ambiguous system, wherein the receiver uses contextual cues for disambiguation [7,8].
In this article, we look into a context-signaling (CS) game where the evolutionary expediency of perfect signaling systems and perfect ambiguous systems is equivalent. More concretely, in this CS game, the probability for the emergence of a perfect signaling system or a perfect ambiguous system is identical, starting from a random initial population state. Apart from the CS game, we will study two benchmark games: the standard Lewis signaling (LS) game, and a variant of the context-signaling game with an information bottleneck, which we call the context bottleneck (CB) game. We study these games (i) in computer simulations where agents repeatedly interact and update their behavior according to an imitation dynamics protocol; and (ii) in the laboratory, where pairs of participants repeatedly play the games with each other. Our main finding is that humans behave differently from bots: in particular, the results for the CS game show that while, under evolutionary dynamics, perfect signaling systems and perfect ambiguous systems emerge with the same frequency, human participants in the lab are much more likely to arrive at perfect signaling systems. We briefly discuss the implications of this finding in the conclusion.
1.1. Related Work
In this paper, we are interested in how human communicative behavior changes under dynamics of cultural evolution and how this leads to the emergence of communicative conventions and norms. There is a large body of literature that studies communicative (or more generally, signaling) behavior under evolutionary dynamics, using the tools from evolutionary game theory for formal analyses [5,6,9,10] and computational models for dynamic analyses [4,11,12,13,14]. The computational part of our study considers repeatedly played variants of the signaling game and the role of ambiguity in decision making. The repeated game structure has been studied extensively with respect to signaling games [2,3,11,15,16,17,18,19] as well as other classical games, for example, the Prisoner’s Dilemma game or the Stag Hunt game [20,21,22,23,24]. In particular, [25] looks into the role of ambiguity in strategic choices in the Prisoner’s Dilemma game and the Matching Pennies game.
In contrast to the abundance of the formal and computational studies on signaling games, very few studies are available that compare these mathematical results with actual human behavior as studied in the laboratory, and only recently such computational research has been complemented with signaling game experiments with human participants [26,27,28,29]. This work includes one study related specifically to the role of ambiguity in signaling games played in the lab [30]. Both the computational and the experimental parts of our study involve the context-signaling game, where successful strategies have to be able to cope with changing contexts. This idea is related to a number of previous studies that explored the role of changing contexts in games and their impact on strategic behavior, see, e.g., the research on reflexive games [31,32] or stochastic games [33,34]. The context-signaling game itself has been studied formally and computationally [7,8,18,35,36]. However, there is no work to date that studies context-signaling games experimentally.
With this study, we want to start bridging this gap and thereby initiate a research program that aims at using tools from experimental economics for addressing questions in philosophy [27,28,37]. The primary focus of this novel approach lies in the juxtaposition of mathematical predictions with experimental data, both derived from the same underlying game model. As Bruner et al. [37] argue: “[...], these [experimental] studies are important complements to the theoretical work that inspired them. They lend credence to evolutionary game-theoretic predictions, both in specific cases and as a general tool for predicting human communicatory behavior. In this way, they play a double epistemic role, telling us something about human behavior as well as about our other methods for understanding human behavior. In sum, we argue that these experimental methods have much to offer to experimental philosophy, for extending and improving existing game-theoretic explorations in philosophy, as well as for any inquiry into the nature of strategic interaction—cooperation, altruism, communication, social coordination, social learning, etc., -in humans.”
1.2. Structure of the Article
The article is structured as follows. In Section 2, we introduce the game models of the three types of signaling games. In Section 3, we analyze the three signaling games (i) by deriving their strategy spaces and equilibria, particularly with respect to evolutionary stability (static analysis), and (ii) by computing emergence rates of equilibria in simulation experiments, where a population of agents repeatedly play one of the signaling games and update their behavior according to an imitation update rule (dynamic analysis). In Section 4, we present the results of an online experiment with human participants who play repeatedly one of the three signaling games and contrast these results with the outcome of the simulations. In Section 5, we present a conclusion, and in Section 6 we point to possible directions of developing this research program.
2. The Game Models
We consider three different games, which we will call the Lewis signaling (LS) game, the context-signaling (CS) game, and the context bottleneck (CB) game. Table 1 shows an overview of notations required for the definition of (context) signaling games.

Table 1.
Notations for the definition of (context) signaling games.
2.1. Lewis Signaling Game
The first game is a standard sender–receiver signaling game. This game type has been extensively studied in many different fields, e.g., philosophy [1,3], economics [38,39], linguistics [40,41], and theoretical biology [42,43]. In the following, we will call this game type a Lewis signaling (LS) game, after one of its earliest formulations by Lewis [1].
A LS game is a game-theoretic model that outlines information transfer between the sender and the receiver. An LS game is given by a tuple , where T is a set of states, each of which represents the private information of the sender; S is a set that contains signals that the sender transfers to the receiver, and R is a set that contains response actions that the receiver can choose. Furthermore, is a utility function that determines how well a state matches a response action. In all of the games that we consider in the article, there is exactly one optimal action for any state, notified by the same indices. More precisely, the utility function is defined as if , or otherwise 0. In this paper, we consider a variant of the LS game that has three states, three signals and three actions: , , and .
One round of the LS game is played as follows: first, a state is randomly chosen. Then, the sender communicates state t by choosing a signal . Afterwards, the receiver chooses a response . Communication is successful if and only if s matches r, which results in an optimal utility of 1 for both players, or otherwise 0.
The game determines the relationship between states and response actions through its utility function, but it does not determine any relationship between signals and states or signals and actions. Thus, as a consequence of the definition of the model itself, signals are meaningless. However, signals can become meaningful due to the regularities in sender and receiver behavior. Such behavior can be described in terms of strategies. A sender strategy is defined by a function , and a receiver strategy is defined by a function . We describe agents’ communicative behavior by a combination of a sender strategy and a receiver strategy. Therefore, a communicative strategy is defined as a strategy pair of sender strategy and receiver strategy , thus .
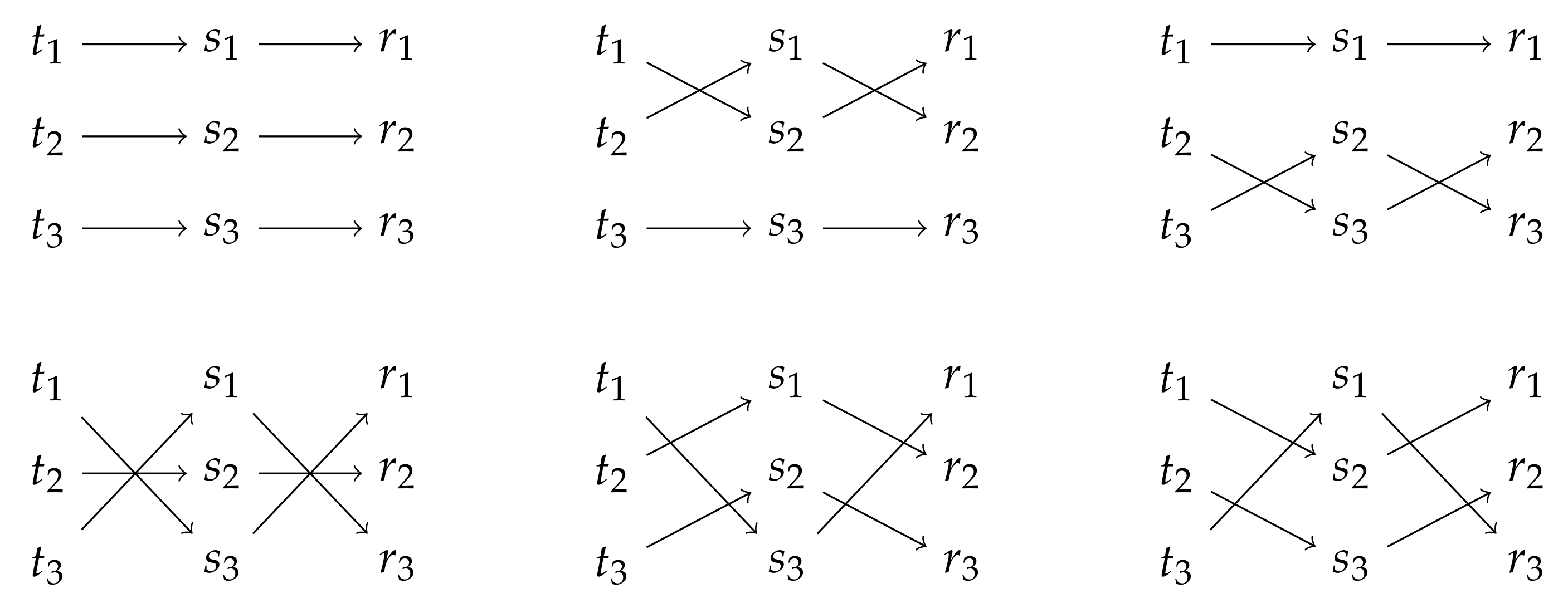
The LS game entails sender strategies and receiver strategies, resulting in 729 communicative strategies. Only 6 strategies guarantee perfect communication. These 6 strategies enable a one-to-one mapping between states and signals. In the Lewisean diction, these strategies are called perfect signaling systems. Figure 1 shows the six strategy pairs that form perfect signaling systems. These are the only strategy pairs that achieve a perfect expected utility of 1 against themselves, which is equivalent to perfect information transfer.
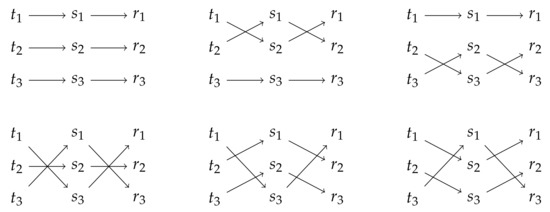
Figure 1.
The six perfect signaling systems of the Lewis signaling game.
2.2. Context-Signaling Game
The context-signaling (CS) game is an extended version of the LS game. It is defined by a tuple . It has the same components as the LS game plus a set C of contextual cues and a probability function that maps probabilities of states onto contextual cues, as described below. The idea here is that states can correlate with contextual cues, and receiver strategies can access these cues to construe the very same signal differently given different contexts. This allows the receiver to disambiguate signals that are ambiguously used by the sender [7,8]. In other words, some ambiguous signaling systems can guarantee perfect information transfer, provided that a reliable contextual cue delivers the necessary additional information (something that is not possible in LS games, where ambiguous signaling systems can never achieve perfect information transfer). Examples of such perfect ambiguous systems will be given below.
In this paper, we consider a variant of the CS game that has three states, three signals, three actions, and two contextual cues: , , , and . Moreover, we reconsider a CS game where the information states occur with the following probabilities:
- ,
- ,
- ,
In other words, the state only appears with , the state only appears with , and the state appears with or , each with the same probability.
To give an idealized example that is represented by this game, one can imagine using alarm signals in the communication of animals such as monkeys. In this simplified example, a group of monkeys uses three alarm signals to distinguish between different predator types, and for each predator type there is a different optimal response action, such as hiding in a bush or climbing a tree. In our example, there are three different types of predators, represented by the information states , and . Accordingly, is the optimal response actions for an attack by , . The relevant contextual cues are daytime () and nighttime () since predator type is only active at daytime, predator type is only active at nighttime and predator type can potentially attack at any time. By assuming daytime and nighttime to be equally likely, this results in the probabilities , as defined above. Finally, three different signals are at the individuals’ disposal: , and . Note that in this example, a perfect ambiguous system would have (i) the sender using the same signal for the daytime predator and the nighttime predator, and (ii) the receiver arriving at the right response action upon this signal by taking into account whether it is daytime or nighttime.
Formally, one round of the CS game is played as follows: first, a contextual cue is chosen randomly. Then, a state is chosen with probability . Then, the sender communicates the given state by choosing a signal . Afterwards, the receiver chooses a response . Importantly, the receiver knows the current contextual cue c and can use this information for adjusting her behavior. Communication is successful if and only if the state matches the response action, which results in an optimal utility of 1 for both players, else 0.
As in the LS game, a CS game’s sender strategy is defined by a function . However, a receiver strategy is defined by a function since the receiver can also make use of the contextual cue to organize her behavioral pattern. Again, we describe agents’ communicative behavior by a combination of sender and receiver strategy .
The CS game has a much greater strategic space than the LS game (concrete numbers below). Moreover, the CS game has two different types of strategies that guarantee perfect communication, which we will call perfect signaling systems (as defined before) and perfect ambiguous systems. Note that the perfect ambiguous systems of the CS game only use two signals, one of which can be successfully disambiguated by the receiver through contextual cues. Figure 2a shows an exemplary perfect signaling system and Figure 2b, an exemplary perfect ambiguous system. In total, the CS game, as defined here, has 54 different perfect signaling systems and 54 different perfect ambiguous systems.
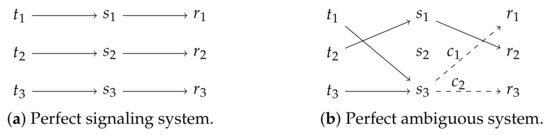
Figure 2.
A perfect signaling system of the CS game is shown in (a), and a perfect ambiguous system of the CS game is shown in (b). Both achieve an expected utility of 1.
2.3. Context Bottleneck Game
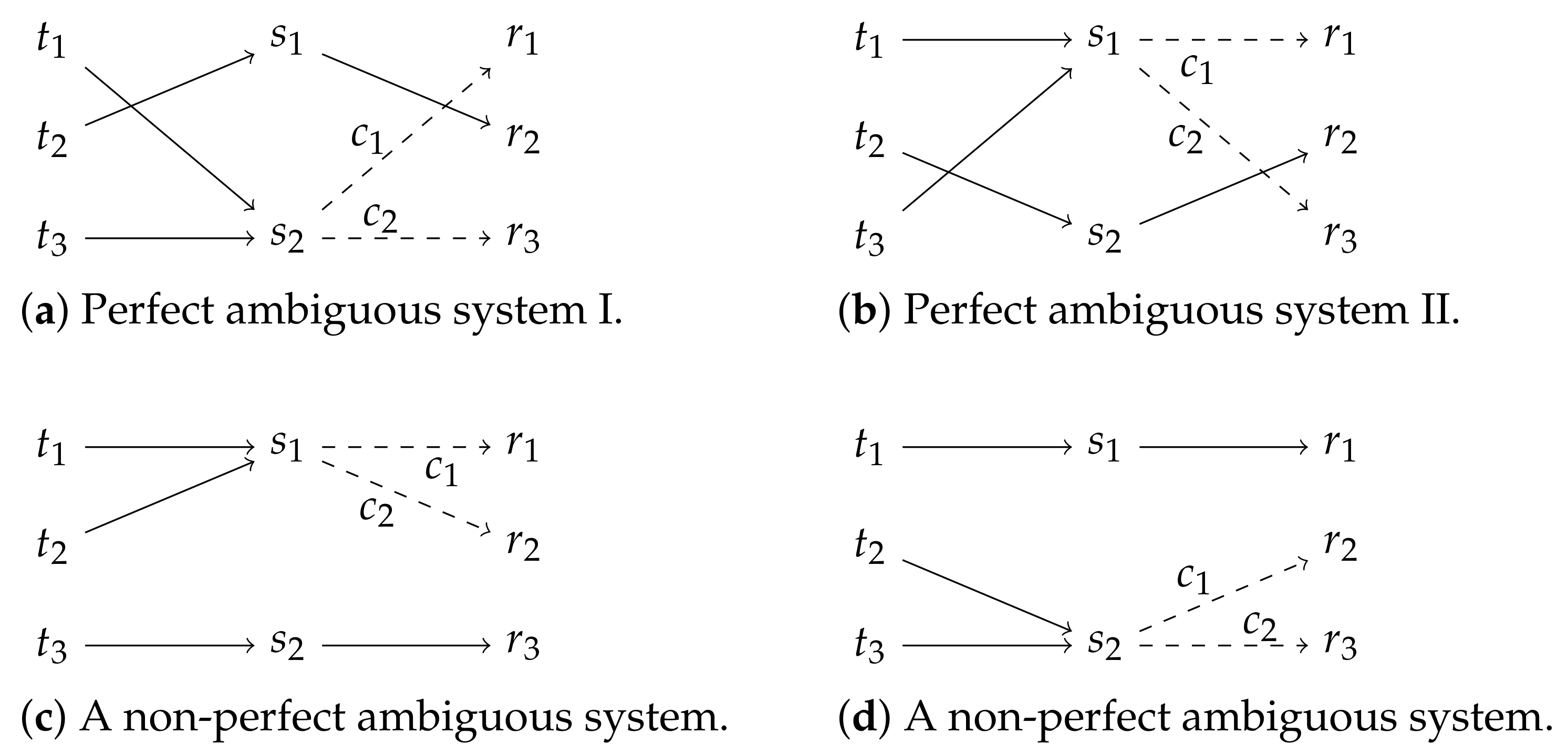
The context bottleneck (CB) game is a CS game with a particular property: it has fewer signals than states. Formally, a CB game and its communicative strategies are defined exactly like for the CS game before, with the only difference in that it has a smaller signal space: . Therefore, without contextual cues, it would be impossible to achieve perfect information transfer since it is impossible to distinguish between different states with different signals. However, the CB game entails ambiguous systems that achieve perfect information transfer. All in all, the CB game has two such perfect ambiguous systems, as shown in Figure 3a,b.
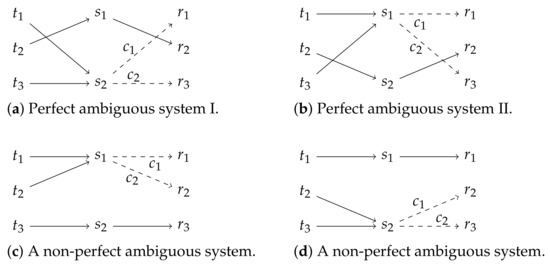
Figure 3.
The two perfect ambiguous systems of the CB game are shown in (a,b), both of which achieve an expected utility of 1. Two (of 12) exemplary non-perfect but evolutionarily stable pooling systems of the CB game are shown in (c,d), both of which achieve an expected utility of .
Moreover, the CB game has non-perfect ambiguous systems that achieve very high communicative success of . Two of such systems are shown in Figure 3c,d. For example, in the system in Figure 3c, communication only fails when appears in context . This case appears with a probability since , and the probability that is given at all is since contextual cues are drawn randomly. In the remaining cases, which therefore appear with a probability , communication is always successful. Setting probabilities off against utilities yields .
These non-perfect ambiguous systems are relevant for the following study since they are evolutionarily stable (a concept that we introduce below). Note that the CB game and the CS game both have evolutionarily stable non-perfect ambiguous systems, whereas in the LS game only perfect signaling systems are evolutionarily stable. An overview of the three games and their properties is shown in Table 2.

Table 2.
Properties of the three games studies in this articles.
3. Formal and Computational Analysis
In this section, we will study formal properties and evolutionary aspects of the three games. For the evolutionary analysis, we look at so-called expected utility (EU) tables that contain all the expected utility (EU) values over all communicative strategies of a game G. Moreover, here values assume agents to be in the sender and receiver role with the same frequency. Formally, the expected utility with and is defined as follows:
whereby is the communicative utility of using a sender strategy against a receiver strategy . The communicative utility is defined as follows for the LS game:
For the CS game and CB game, is defined slightly differently due to taking contextual cues into consideration and is defined as follows:
Studying EU tables is a standard practice in evolutionary game theory (EGT), particularly when it comes to signaling games [3]. An EU table as defined here is a symmetric normal form representation of the game and enables the detection of evolutionary properties, particularly evolutionarily stable strategies [44,45], a central concept in EGT. For a symmetric normal form game with strategy set and utility function , a strategy is an evolutionarily stable strategy (ESS) if and only if the following two conditions hold:
- for all
- If for some , then
ESSs are equilibria with an invasion barrier: when a whole population plays an ESS then the population cannot be invaded by a (small) number of mutants. More concretely, if mutants appear, and if their number is below a particular threshold, then the evolutionary dynamics wipe out the mutants and the population swings back to the state where everyone plays the ESS. The size of an invasion barrier can differ from ESS to ESS and can be approximated through other means, as pointed out in Section 3.2. In the next section, we will specify the games’ startegy spaces and evolutionary equilibria.
3.1. Strategy Spaces and Equilibria
The LS game has 27 sender strategies and 27 receiver strategies, resulting in 729 communicative strategies, out of which 6 strategies ( of the strategy space) form perfect signaling systems. It has been proven in [6] that perfect signaling systems are the only ESS for any signaling game with n information states, n signals and n response actions, . Therefore, the 6 strategy pairs (see Figure 1) are the only ESS of the LS game, but it has also been shown that particular ambiguous strategies (so-called pooling strategies) have attraction potential under evolutionary dynamics [6,13,46].
While Lewis signaling games have been extensively studied in the past, the evolutionary aspects of context-signaling games have been the focus of only two recent studies [7,8]. The CS game as defined here has not been studied at all. The CS game has 27 sender strategies and 729 receiver strategies, which results in communicative strategies. A computational analysis of the whole strategy space showed that the CS game entails 54 perfect signaling systems ( of the strategy space), such as depicted in Figure 2a, and 54 perfect ambiguous systems ( of the strategy space), such as depicted in Figure 2b. Moreover, it can be shown that both strategy types have the same attraction potential under evolutionary dynamics, such as the replicator dynamics [47]–a standard dynamics in EGT. In other words, starting from a random population distribution, it is equally likely that a perfect signaling system or a perfect ambiguous system emerges under evolutionary dynamics. Finally, the CS game has a number of non-perfect ambiguous strategies that form evolutionarily stable sets [48]. The analysis of these sets would go beyond the scope of this paper, but note that the strategies therein are similar to the two exemplary strategies of the CB game in Figure 3c,d.
The CB game has sender strategies and 81 receiver strategies, which results in 648 communicative strategies. As already mentioned, the CB game strategies cannot form perfect signaling systems due to its bottleneck property of having fewer signals than states/actions. However, the CB game has two perfect ambiguous systems ( of the strategy space), which are both shown in Figure 3a,b. Moreover, the CB game has 12 non-perfect ambiguous strategies that form two evolutionarily stable sets [48]. Two of them are shown in Figure 3c,d. As already indicated, all of these non-perfect ambiguous systems achieve a communicative success of .
Table 3 shows an overview of the strategy spaces and their evolutionary aspects of all three games.

Table 3.
Strategic/evolutionary properties of the three games.
3.2. Emergence Rates under Evolutionary Dynamics
As indicated at the beginning of this section, the detection of evolutionarily stable states is a static analysis, which helps one to understand what kind of strategies are expected to persist and hence are hard to be replace with other strategies. However, knowing that a strategy is an ESS does not tell us anything about processes that make a population end up in a state where everyone plays . Evidently, ESSs are very often endpoints of an evolutionary process, but how likely it is for such endpoints to be reached under evolutionary dynamics must be determined by adynamic analysis.
A very common approach of such a dynamic analysis is as follows: we start with a population of agents, each of whom is randomly attributed a strategy. Then, we simulate an iterated interaction process, where agents update their behavior according to an evolutionary dynamics protocol until a stable endpoint is reached. In general, such an endpoint corresponds to a stable equilibrium, very often an ESS. When we reproduce the simulation process multiple times, we obtain emergence rates of such equilibria, which approximate the size of their basins of attraction (the basin of attraction of an equilibrium is the range of population states that lead to under the evolutionary dynamics.). In other words, these emergence rates are indicators for how likely an equilibrium is to emerge under the tested evolutionary dynamics, starting from a randomly selected population state.
For the computation of emergence rates, we applied an algorithm that accomplishes imitation dynamics with the decision method ‘pairwise difference imitation’ (PDI). It can be shown that the PDI dynamics constitute one of the multiple agent-based protocols that approximate replicator dynamics [49]. Moreover, the PDI dynamics constitute a more realistic model for an agent-based perspective, since (i) they consider a finite population, and (ii) their members do not need to have global knowledge (such as knowing the average utility of a population, which e.g., has to be taken into account for an agent-based interpretation of the replicator dynamics) but only local knowledge about one interlocutor’s performance in making strategy updates. The details of this PDI dynamics algorithm are described as Python-similar pseudo code in Appendix A.
We carried out three simulation experiments, one for each game. In each experiment, we conducted 1000 simulation runs. Each simulation run started with a population of 100 agents, initially attributing a communicative strategy randomly drawn from the set of all strategies . The simulation ended when all agents had adopted the same strategy.
The results were as follows. For the LS game, agents eventually adopt a perfect signaling system in of all runs. In the remaining , so-called partial pooling equilibria emerge, which are non-perfect ambiguous systems that achieve a communicative success of . This result is in line with related studies that investigate the LS game with other evolutionary dynamics. For example, Skyrms [3] reports for the LS game that under replicator dynamics, perfect signaling systems emerge in of all runs, whereas in the remaining partial pooling equilibria emerge. Moreover, Barrett [2] shows that when two agents play the LS game repeatedly and update their probabilistic choices via reinforcement learning, perfect signaling systems emerge in of all runs, whereas in the remaining partial pooling equilibria emerge. Taken together, all these studies show that across different evolutionary dynamics, in a vast majority of runs perfect signaling equilibria emerge.
For the CB game, perfect ambiguous systems emerge less often than non-perfect ambiguous systems ( to ). Note that all non-perfect ambiguous systems that have emerged are those that have achieved a communicative success of (example strategies are shown in Figure 3c,d) and are evolutionarily stable (see discussion in Section 2.3 and Section 3.1). Finally, for the CS game, we also see the emergence of non-perfect ambiguous systems (), all of which achieve a communicative success of . Perfect signaling systems and perfect ambiguous systems emerge with almost the same frequency ( vs. ). The results are outlined in Table 4.

Table 4.
Results of the imitation dynamics: 100 agents, no mutation, 100 runs.
In sum, we see that results differ across games. The LS game has only one type of strategy that is evolutionarily stable: the perfect signaling system. Not surprisingly, this strategy type emerges in a vast majority of runs. The CB game, however, has two types of evolutionarily stable strategy types: perfect and non-perfect ambiguous systems. It turns out that only these two types emerge, and the non-perfect ambiguous systems emerge slightly more often. Finally, for the CS game, all three types are evolutionarily stable, and all three types emerge with roughly the same frequency.
4. Online Experiments
Common models of evolutionary dynamics, such as the PDI dynamics, formalize evolutionary processes driven by the principles of random trial-and-error and utility maximization. These principles constitute a reasonable assumption for modeling biological evolution (where utility represents fitness), but do they also constitute a reasonable assumption for cultural evolution? We argue that cultural evolution might involve more complex principles, such as biased trial-and-error processes (instead of completely random ones), that pay respect to higher cognitive skills of the individuals. This leads us to the general research question of this section: do human participants in the lab behave differently than virtual agents under evolutionary dynamics when playing the signaling games discussed in this paper? To study this question, we present an experimental study where participants in the lab play the three games repeatedly for a number of rounds with a fixed partner. We use design protocols from experimental economics, where game payoff is transferred into real money, which is payed out after the experiment on top of to the participation fee.
With the lab experiment we want to test four hypotheses, which are motivated by the results of the simulation experiments (see Table 4) and assumptions about the difference between adaptive dynamic and rational decision making. Note that under evolutionary dynamics, optimal communication systems emerge with a frequency of across the three games ( for the LS game, for the CB game, and for the CS game). We assume that participants in the lab learn perfect communication systems with higher frequencies for at least one reason: since the evolutionary dynamics produce a randomly initiated process of trial-and-error, populations can potentially get trapped in a sub-optimal local optimum. However, the behavior of participants in the lab is more likely driven by rational considerations of optimization, and perfect communication systems are the preferred endpoint of such an optimization-guided learning process. Therefore, we state the following first hypothesis:
Hypothesis 1.
For the LS, CS and CB games, perfect communication systems emerge more often in the laboratory under a fixed partner protocol than in simulation runs under adaptive (PDI) dynamics.
From Hypothesis 1, we can derive more specific hypotheses that relate to the specific outcome of each game. The hypothesis about the LS game is as follows.
Hypothesis 2.
Playing the LS game, in the vast majority of experimental runs, participants establish a perfect signaling system in the laboratory under a fixed partner protocol.
For the CB game, we see that the perfect ambiguous system emerged slightly less often than . However, assuming that participants arrive at a better rate in the laboratory experiments, we put forward the following hypothesis:
Hypothesis 3.
Playing the CB game, in the majority of experimental runs, participants establish a perfect ambiguous system in the laboratory under a fixed partner protocol.
Finally, we see that for the CS game, perfect communication systems emerge . Moreover, we know that perfect signaling systems and perfect ambiguous systems both emerge with roughly the same frequency ( vs. ), and we also know that both types of communication systems have the same basin of attraction sizes under evolutionary dynamics. We assume that this relationship can be reproduced in the laboratory experiments; therefore, we put forward the following hypothesis:
Hypothesis 4.
Playing the CS game, in the majority of experimental runs, participants establish a perfect communication system in the laboratory under a fixed partner protocol, whereby perfect signaling systems and perfect ambiguous systems emerge with roughly the same frequency.
4.1. Experimental Setup
We conducted five experimental sessions with 10 participants each. In each session, five pairs of participants played one of the three signaling games (LS game, CS game and CB game) for a sequence of 30 rounds. For reasons that we describe below, we partitioned the sequence into five blocks of six rounds each, so that Block 1 includes the Rounds 1–6, Block 2 includes the Rounds 7–12, and so on. The role of both participants alternated for each round, so that in the even round numbers, player 1 was sender and player 2 was receiver, and in the odd round numbers it was exactly the other way around. Each experiment had a fixed sequence of information states that where presented to the sender. This sequence was designed in a way that in every block, each of the participants was exposed to each of the three information states exactly one time. A block of a sequence could, for example, look as follows:
- player 1 is sender, information state is ;
- player 2 is sender, information state is ;
- player 1 is sender, information state is ;
- player 2 is sender, information state is ;
- player 1 is sender, information state is ;
- player 2 is sender, information state is .
This structure is useful for analyzing the communication protocol because we can deduce from the participants’ behavior of every block if (i) both participants use the same protocol and (ii) the protocol reproduces one of the perfect communication strategies as introduced earlier.
We recorded the behavior of all participants to evaluate how the communicative success changes and if the participants manage to establish perfectly working communication protocol at the end of the experiment. The experimental design was developed for being used in online experiments. Participants received a url that directed them to a waiting room where they waited to be paired with another participant. For four of the five sessions, we recruited participants via the crowdsourcing platform Prolific, and for the remaining one we recruited participants from an online seminar via an invitation link. An overview of the five sessions is depicted in Table 5.

Table 5.
Overview of the experimental sessions with 50 participants in total.
We conducted two sessions (II and III) for the CS game and two sessions (IV and V) for the CB game. For the LS game, we conducted solely one session (Session I) because this game has been studied frequently elsewhere [26,27,29], and one session was sufficient to confirm that the results are in line with findings of former studies with similar settings. More details about the software for the experimental design and the procedure and structure of an experimental run can be found in Appendix B.
4.2. Experimental Results
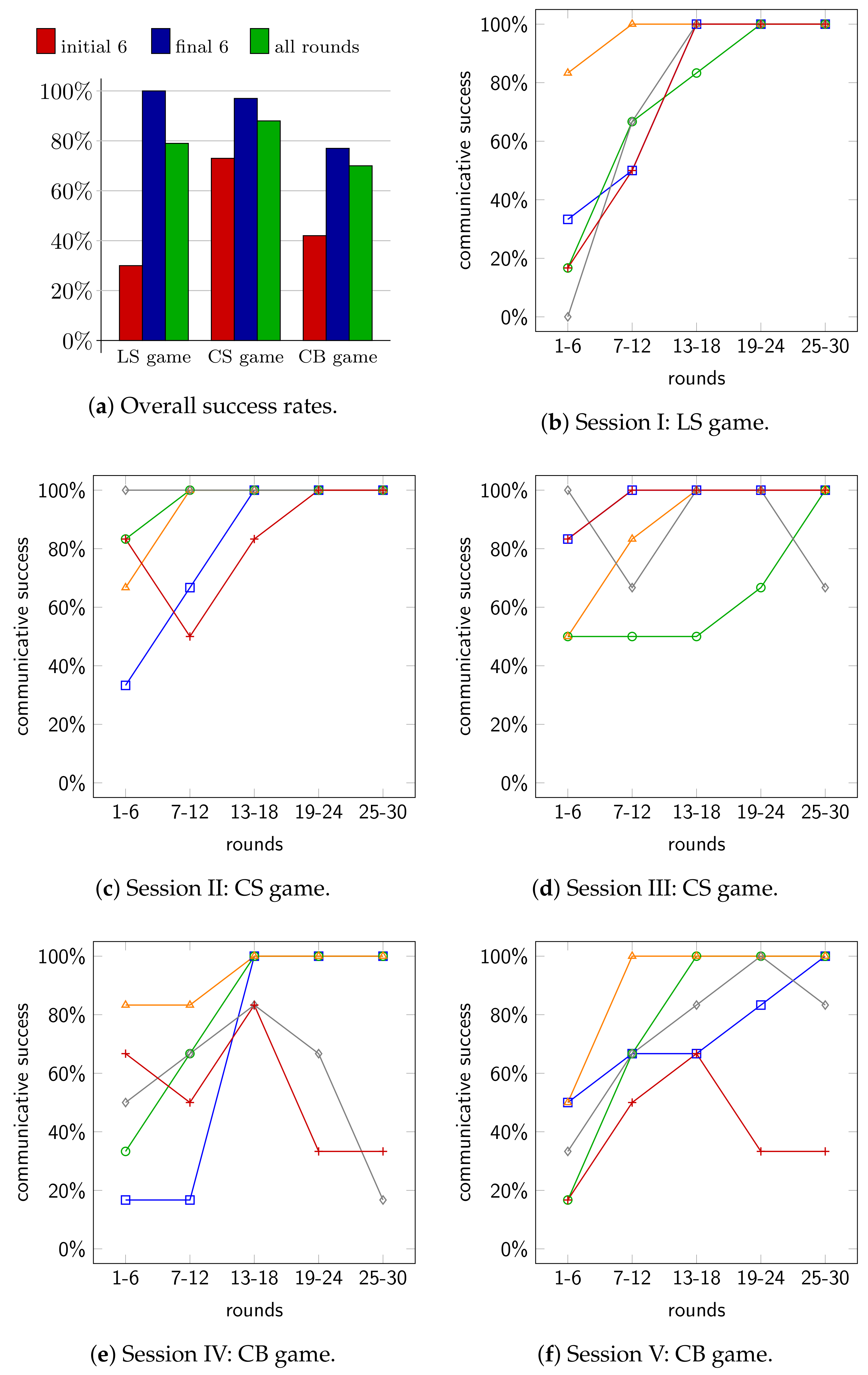
In the first analysis step, we computed the communicative success (CoS) rates for every six rounds. Figure 4b–f show CoS rates over blocks for all five pairs of participants of each session, where each data plot represents a pair of participants. Figure 4b shows the result for the LS game. It shows that initially the CoS rates are below , but they increase over time, and in all five sessions the participants communicate with a CoS rate during the last block of the experiment. Figure 4c,d show the results for both sessions with the CS game. Additionally, here almost all CoS rates are below at the beginning. Moreover, CoS rates mostly increase so that in 9 of 10 runs participants communicate with a CoS rate at the last block of the experiment. Finally, Figure 4e,f show the results for both sessions with the CB game. Here, all CoS rates are below at the beginning. In 6 of 10 runs, participants communicate with a CoS rate during the last block of the experiment, and in one run the CoS rate is near (gray line of Session V). In three runs, however, CoS rates are below during the last block.
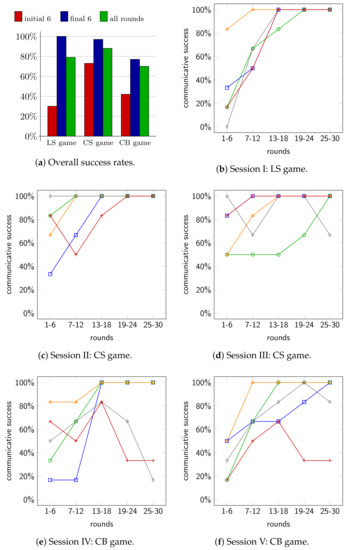
Figure 4.
Communicative success (CoS) rates of the experiments. (a) shows the CoS rates over initial 6, final 6 and all rounds, averaged over all participants for each game type. (b–f) show the CoS rates over blocks of all participant pairs for Sessions I to V, respectively.
Figure 4a summarizes the results for each game type, showing the CoS rates averaged over all participants for the initial 6 rounds, the final 6 rounds, and all the rounds. The results show that the tendencies are the same in all three games: the CoS rates are initially lower, and they increase over time (on average), but with different magnitudes across the three game types. Not surprisingly, the LS game has the lowest initial CoS rates since the expected communicative success is for a random guess, whereas for the CS ans CB game it is due to the contextual cues. Moreover, the CB game has the lowest final CoS rates. As we will see, this is due to the bottleneck property that makes it harder for participants to establish a successful communication protocol.
In a next step, we analyzed the participants’ behavior in the last six rounds to establish what kind of communication protocol they might have developed. The results are as follows: for the LS game (Session I), all five pairs of participants have established a perfect signaling system in the final six rounds (or even earlier). Here, both players use exactly the same protocol, which is characterized by on of the signaling systems as shown in Figure 1.
For the CS game (Sessions II and III), in 8 of 10 runs participants established a perfect signaling system in the final six rounds. In one run (green data plot of Figure 4d), participants established a non-perfect ambiguous system that did not always achieve a CoS rate of , although in this particular run it did. Finally, in another run (gray data plot of Figure 4d), participants tried to establish a pooling system that only considered contextual cues but failed in doing so, so that the communicative success broke down eventually.
For the CB game (Sessions IV and V), in 7 out of 10 runs participants established a perfect ambiguous system. In one of these runs (gray data plot of Figure 4f), the CoS rate was not during the last block, due to the fact that one of the players made a mistake. However, the communication protocol of these six rounds and former rounds show that the participants used a perfect ambiguous system. In the remaining three runs (red and gray line of Figure 4e, red line of Figure 4f), participants failed to establish any efficient communication protocol.
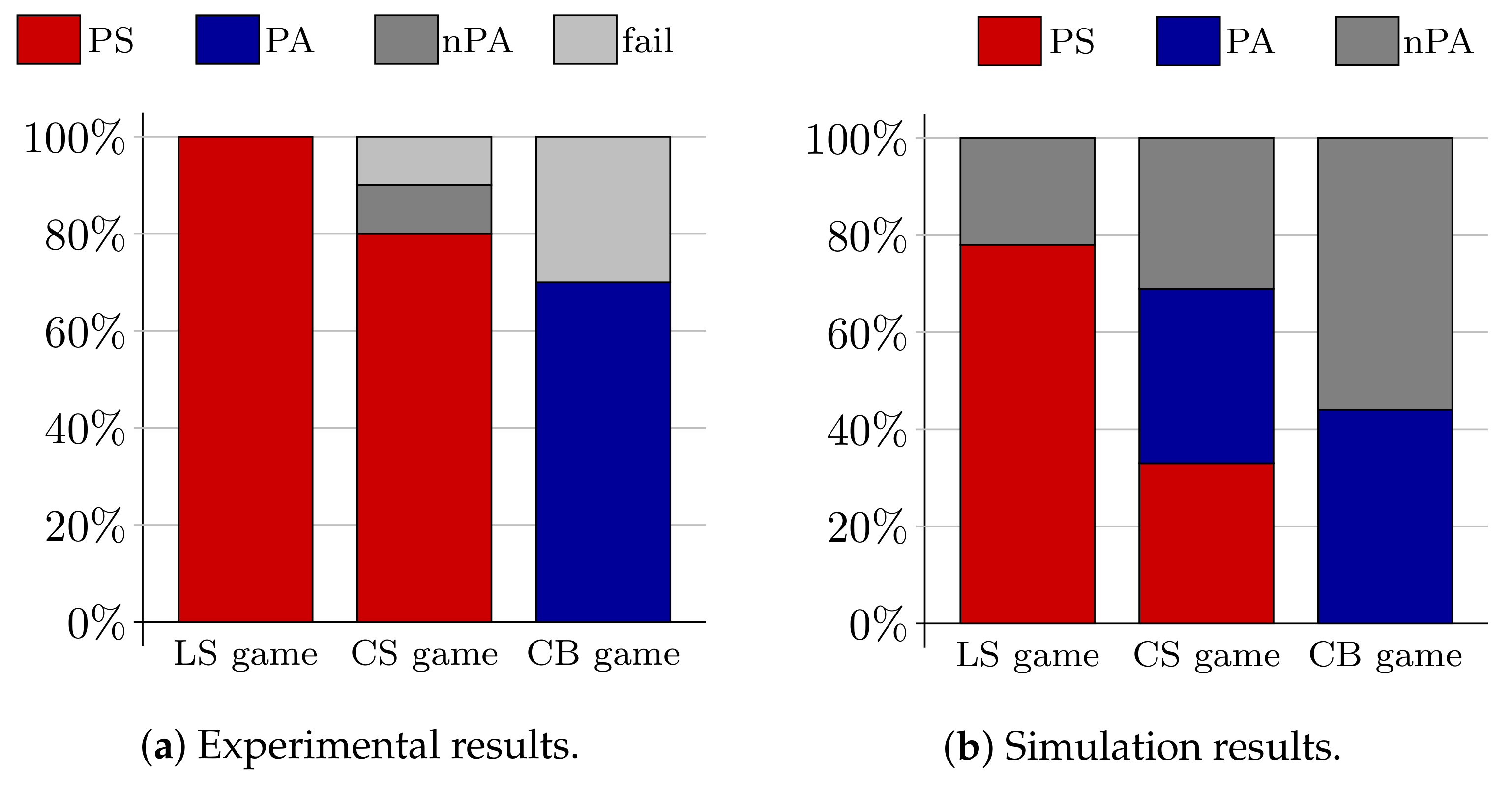
A bar plot of the frequencies of emerged communication protocol types for the three different games is shown in Figure 5a.
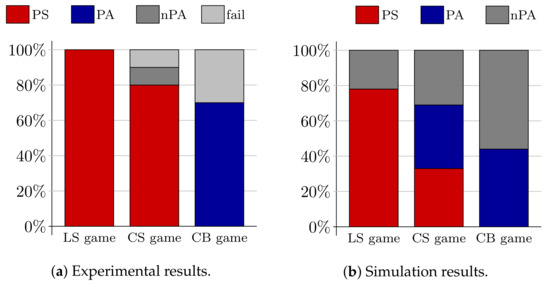
Figure 5.
Frequency of types of communication systems that emerged in the laboratory experiments (a) and in the simulation runs under evolutionary dynamics (b). Perfect signaling systems (PS) are coded red, perfect ambiguous systems (PA) are coded blue and non-perfect ambiguous systems (nPA) are coded darkgray. Experimental runs where participants failed to establish a joint communication protocol after 30 rounds are coded lightgray.
4.3. Discussion
Figure 5a,b juxtapose the experimental results and the simulation results (values of Table 4). The figures highlight that the results are in line with Hypothesis 1. On average across the three games, perfect communication systems emerged in the lab in 20 of 25 experimental runs, and thus in of all runs, whereas they emerged in of all simulation runs under imitation dynamics. Moreover, perfect communication systems emerged more frequently in the lab for every single game type, namely, versus for the LS game, versus for the CS game, and versus for the CB game (cf. Figure 5).
Furthermore, the experimental results (i) are in line with Hypothesis 2 since perfect signaling systems emerged in all experimental sessions with the LS game, and (ii) confirm Hypothesis 3 since perfect ambiguous systems emerged in the majority () of all sessions with the CB game. The experimental results only partially confirm Hypothesis 4. It is true that in the majority () of all sessions with the CS game, participants established a perfect communication system. However, whenever they established one, it was always a perfect signaling system. This result goes against Hypothesis 4, where we assumed that perfect signaling systems and perfect ambiguous systems emerge roughly with the same frequency, as was the case in the simulation study. This discrepancy is clearly visible by comparing the middle bars of Figure 5a,b.
Why do we find this difference in the emergence of communication systems under evolutionary dynamics relative to with participants in the lab? One aspect that we expect to play a role here is the underlying mechanism of decision making. Note that low-level evolutionary dynamics, such as imitation dynamics, simulate a trial-and-error process: “If what I do works, I stick to it, otherwise I adopt what works better.” These dynamics do not incorporate any higher-order mechanisms of decision making, in contrast to what we believe the human participants did in the lab sessions. Human players incorporate their knowledge about the situation and, in particular, their predictions on how the other player will act in this situation. This makes them prefer establishing a communication system that is based on communicated signals only over one that involves additionally external contextual cues.
Let us make this point more precise. In the CS game, a CoS rate of can be achieved with a perfect signaling system or a perfect ambiguous system. The success of perfect signaling is not dependent on contextual cues but only on the behavior of the other player. Since participants know that the other player is exactly in the same situation (they both want to communicate successfully to maximize utility), one can rely on the other’s behavior. In other words: perfect signaling systems are very attractive as the circumstances—particularly that both participants’ interests are perfectly aligned—make the behavior of the other player reliable. In Section 6, we will propose a number of factors that are expected to change the circumstances in a way such that perfect signaling might become less, and ambiguous signaling more attractive.
5. Conclusions
The central game of our study is the CS game, where the evolutionary expediency of perfect signaling systems and perfect ambiguous systems is equivalent, as shown in computer simulations of populations of agents playing the CS game repeatedly and updating strategies according to the PDI protocol. However, when human participants in the lab repeatedly play the game with each other, they arrive at perfect signaling systems in the vast majority of experimental runs, which clearly shows that they disprefer the utilizations of contextual cues for establishing perfect ambiguous systems.
The discrepancy between the emergence rates of communication strategies in simulations under evolutionary dynamics and in experiments in the lab is the main finding of this study. We believe that this is most probably due to a difference in the sophistication level (low-level vs. high-level) of decision making or preexisting cognitive biases. This insight is not new but is also discussed with respect to other games. For example, Skyrms [50] studies a Stag Hunt game with pre-play signaling. He shows that under low-level evolutionary dynamics, agents very frequently (around ) establish an interaction protocol where the whole population plays the cooperative stag strategy upon receiving any signal, much more often than without pre-play signaling. Skyrms refers to paper by Aumann [51], who discusses the same scenario and argues that high-level rational agents would establish a communication protocol with meaningless signals, which makes pre-play communication completely ineffecitve. Here, high-level sophistication is assumed to be disadvantageous for establishing a more cooperative, more beneficial convention.
Therefore, one must be careful with taking any adaptive low-level dynamics as a good model for cultural evolution. For any phenomenon under investigation, one must factor in the following question: how much sophistication, rationality and recognition of the situation is necessarily involved in the decision-making processes of agents in a society? Models of cultural evolution must take these aspects into consideration, with an immediate goal of having a nuanced picture of the particular phenomenon under investigation, and with a long-term goal of developing a broader set of evolutionary dynamics that are properly sensitive to the different levels of agents’ sophistication in their decision making. (For example, when we look at learning in games, we find two very prominent learning models that involve quite different levels of sophistication: reinforcement learning [52] and fictitious play [53]. While the former one is a low-level learning model where agents do not even need to know the payoff structure of the game or even the existence of another player, the latter one assumes a higher level of sophistication, where agents have to know that exact payoff structure of the game and form beliefs about how other players will behave, based on past experiences.)
6. Outlook
The results of this experiment invite follow-up studies with context-signaling games to determine the conditions that promote ambiguity and access to contextual cues. As we showed in this study with the CB game, one such condition is an information bottleneck, but we believe there are more such relevant factors. Another one might be alignment of interests: when we change the underlying condition that interests of both players are completely aligned to one where they are only partially aligned, then we might expect that participants will prefer to exploit contextual cues, due to the fact that such cues then have a higher reliability than signals from a interlocutor with competing interests. (See Blume et al. [26] and Rubin et al. [28] for experimental studies with signaling games with partially aligned interests.) A further condition is signaling costs: when it is very costly for the sender to learn or use a large number of signals, then reducing the number is beneficial for the sender, as long as there is a way that communication is still successful; for example, through a disambiguation effort taken by the receiver through the use of contextual cues. (See Santana [7] and Mühlenbernd [8] for formal and computational analyses with context-signaling games that involve signaling costs. Both studies show that signaling costs promote the emergence of perfect ambiguous systems.)
Finally, contextual cues might be exploited more when we have a larger group of participants. For example, Bruner et al. [27] conducted experiments with a Lewis signaling games played over 60 rounds by a group of 12 participants under random matching protocol. Here, perfect signaling systems emerged much less frequently, only in 3 out of 10 sessions, whereas in the other sessions non-perfect ambiguous systems emerged. (See also Blume et al. [26] for a similar study where participants more frequently establish perfect signaling systems.) It is reasonable to assume that in such a setting, contextual cues are helpful since receivers can rely on them to turn a non-perfect into a perfect ambiguous system. The role of these and many other factors should be tested in future studies to see their effect on the evolution of ambiguity in the laboratory.
Author Contributions
Formal analysis, R.M.; Funding acquisition, R.M.; Investigation, R.M.; Project administration, R.M., S.W. and P.Ż.; Resources, R.M.; Software, R.M.; Writing—original draft, R.M., S.W. and P.Ż.; Writing—review & editing, R.M., S.W. and P.Ż. All authors have read and agreed to the published version of the manuscript.
Funding
Roland Mühlenbernd was funded by the Polish National Agency for Academic Exchange (NAWA) under grant agreement PPN/ULM/2019/1/00222, and by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG)—SFB 1412 Register, 416591334.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are openly available in FigShare at figshare.com/articles/dataset/Experimental_data/19187747 accessed on 8 October 2021, (doi:10.6084/m9.figshare.19187747).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CS game | context-signaling game |
| LS game | Lewis signaling game |
| CB game | context bottleneck game |
| expected utility | |
| communicative utility | |
| EGT | evolutionary game theory |
| ESS | evolutionarily stable strategy |
| PDI | pairwise difference imitation |
| CoS | communicative success |
| PS | perfect signaling |
| PA | perfect ambiguity |
| nPA | non-perfect ambiguity |
Appendix A. Pairwise Differential Imitation (PDI) Dynamics
A pseudo code (based on Python) of the PDI dynamics is given in Figure A1:

Figure A1.
Pseudo Python code of the ‘pairwise difference’ imitation algorithm.
Figure A1.
Pseudo Python code of the ‘pairwise difference’ imitation algorithm.

The input parameters are a set of agents, a signaling game G, a set S of sender strategies, a set R of receiver strategies, and a breaking condition B (lines 1–5). First, all agents are initialized with a random sender strategy and a random receiver strategy (lines 6–8). Then, a number of simulation steps are accomplished until the breaking condition is reached (line 9). In each simulation step, every agent interacts with every other agent by playing game G, one as sender, the other as receiver. After each interaction, the sender agent’s accumulated sender utility (ASU) and the receiver agent’s accumulated receiver utility (ARU) are incremented by the utility they scored in the game, and , respectively (interaction part, lines 10–14). Afterwards, each agent is attributed to another random agent (lines 15–16). If agent has a lower ASU value than , she adopts the sender strategy of the other agent with a probability that equals the difference of both agents’ ASU values (lines 17–19); the same happens independently for the ARU values (lines 20–22). Finally, all agents’ ASU and ARU values will be reset for starting a new round (lines 23–25).
Appendix B. Experimental Procedure
The experimental design was created with LabVanced. Participants started the experiments via a link, which they either received via eMail invitation (Session II) or on the Crowdsourcing platform Prolific (Sessions I, III, IV and V). Upon clicking this link, participants waited in a virtual lobby to get matched with another participant. After matching, participants saw a screen with the following general instructions:
- In this experiment you will play a communication game with an other participant for a number of 30 rounds.
- In each round you both can score 10 points if you play successfully, otherwise you both receive 0 points.
- Your final total score will be converted into real money (100 points = 1£) and added to your participation fee.
- Please take your time and play carefully. Press ’Next’ to go to the video tutorial (<2 min) that explains how to play the game.
Afterwards, participants saw a short tutorial video (less than 2 min) that demonstrates how to play the communication game (cf. Figure A2).

Figure A2.
Screenshots of an exemplary interaction round for the LS game, with the green agent as sender and the blue agent as receiver. (a) Initial perspective of the green agent in sender role. Her private information state is ’banana’ (alternatives: ’apple’, ’grapes’), and she has to pick a signal, $, & or §. (b) Perspective of the blue agent (receiver role) after the sender has picked signal &. He cannot see the information state of the green agent and has to guess an information state as response: ’apple’, ’banana’ or ’grapes’. (c) Perspective of both agents after the receiver has picked ’grapes’ as response. Communication failed in this example, and both don’t score.
Figure A2.
Screenshots of an exemplary interaction round for the LS game, with the green agent as sender and the blue agent as receiver. (a) Initial perspective of the green agent in sender role. Her private information state is ’banana’ (alternatives: ’apple’, ’grapes’), and she has to pick a signal, $, & or §. (b) Perspective of the blue agent (receiver role) after the sender has picked signal &. He cannot see the information state of the green agent and has to guess an information state as response: ’apple’, ’banana’ or ’grapes’. (c) Perspective of both agents after the receiver has picked ’grapes’ as response. Communication failed in this example, and both don’t score.
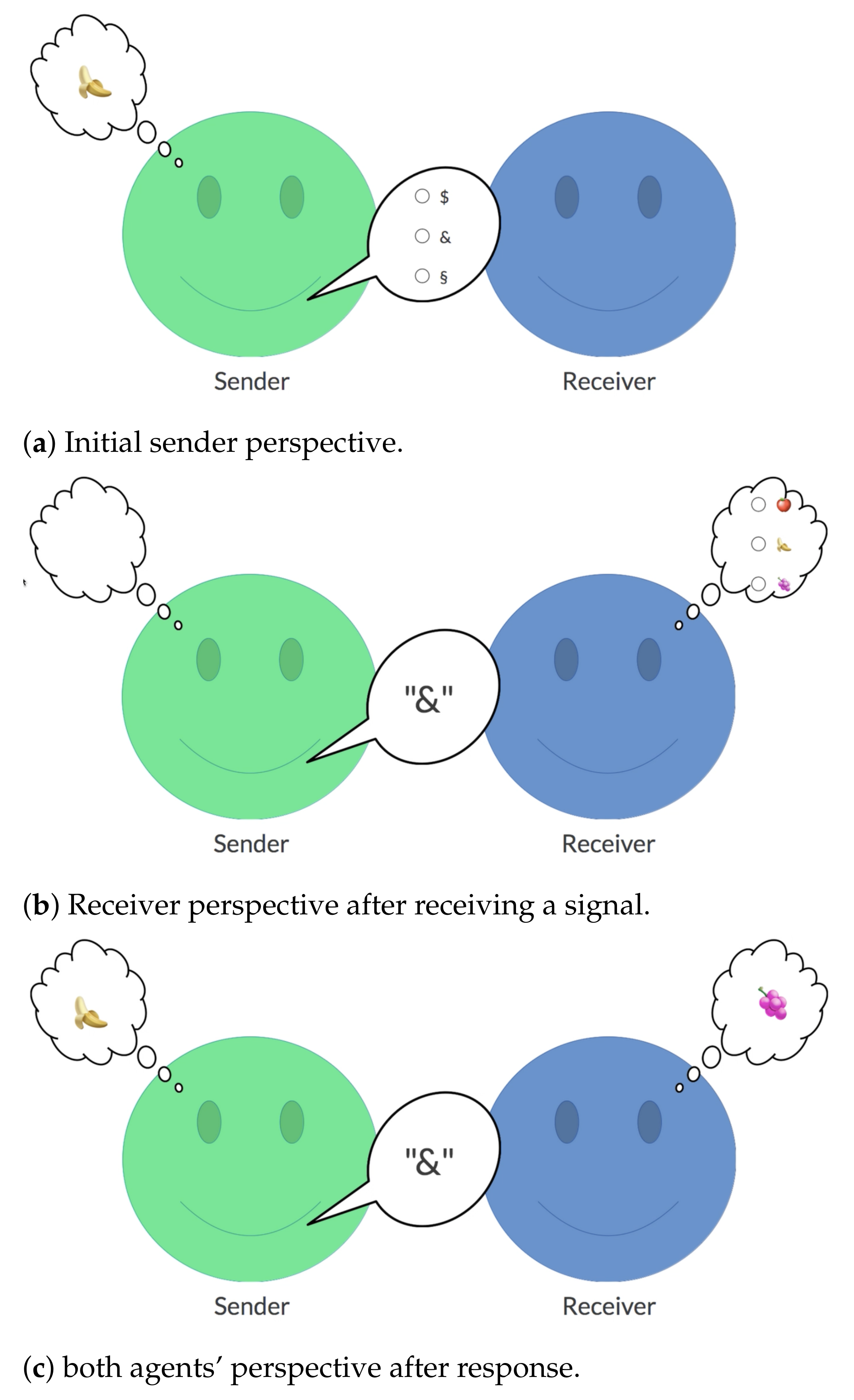
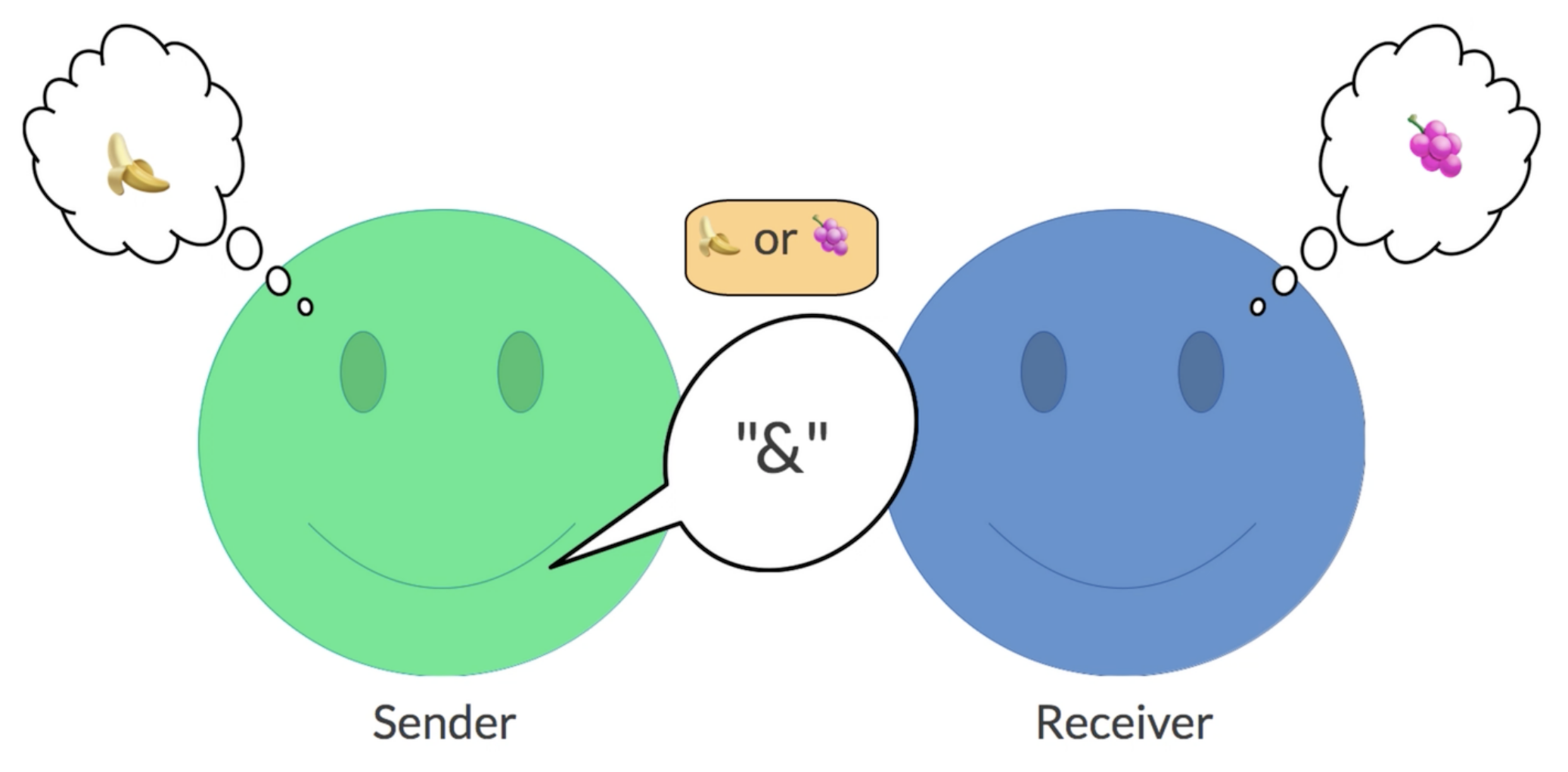
Then, the experiment started. For each pair of participants, one player was inaugurated as the ’blue agent’ and the other as the ’green agent’, represented by a blue or green smiley face, respectively. Both participants played the communication game for 30 rounds, thereby alternating between sender role and receiver role. The three information states were represented by the fruit icons ’apple’, ’banana’ and ’grapes’. The signals were represented by diverse characters, for example, the $-symbol or the &-symbol. The contextual cues in the SC game and the CB game were represented by an orange box that contains a disjunction of two information states. Figure A2 shows the screenshots of an exemplary interaction round for the LS game, with the green agent as sender and the blue agent as receiver. Figure A3 shows the final screen of an exemplary interaction round for the CS game to illustrate the contextual cue representation.

Figure A3.
Screenshots of the final screen of an exemplary interaction round for the CS game. The contextual cue is presented as a disjunction of two information states, of which one is true.
Figure A3.
Screenshots of the final screen of an exemplary interaction round for the CS game. The contextual cue is presented as a disjunction of two information states, of which one is true.
References
- Lewis, D. Convention. A Philosophical Study; Blackwell: Cambridge, MA, USA, 1969. [Google Scholar]
- Barrett, J.A. Numerical Simulations of the Lewis Signaling Game: Learning Strategies, Pooling Equilibria, and the Evolution of Grammar; Technical Report; Institute for Mathematical Behavioral Sciences, University of California: Irvine, UK, 2006. [Google Scholar]
- Skyrms, B. Signals: Evolution, Learning and Information; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Huttegger, S.M.; Zollman, K.J.S. Signaling Games: Dynamics of Evolution and Learning. In Language, Games, and Evolution; Benz, A., Ebert, C., Jäger, G., van Rooij, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 160–176. [Google Scholar]
- Wärneryd, K. Cheap Talk, Coordination, and Evolutionary Stability. Games Econ. Behav. 1993, 5, 532–546. [Google Scholar] [CrossRef]
- Huttegger, S.M. Evolution and the Explanation of Meaning. Philos. Sci. 2007, 74, 1–27. [Google Scholar] [CrossRef]
- Santana, C. Ambiguity in Cooperative Signaling. Philos. Sci. 2014, 81, 398–422. [Google Scholar] [CrossRef]
- Mühlenbernd, R. Evolutionary stability of ambiguity in context-signaling games. Synthese 2021, 198, 11725–11753. [Google Scholar] [CrossRef]
- Skyrms, B. Evolution of the Social Contract; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Skyrms, B.; Pemantle, R. A dynamic model of social network formation. Proc. Natl. Acad. Sci. USA 2000, 97, 9340–9349. [Google Scholar] [CrossRef] [Green Version]
- Zollman, K.J.S. Talking to Neighbors: The Evolution of Regional Meaning. Philos. Sci. 2005, 72, 69–85. [Google Scholar] [CrossRef] [Green Version]
- Hofbauer, J.; Huttegger, S.M. Feasibility of communication in binary signaling games. J. Theor. Biol. 2008, 245, 843–849. [Google Scholar] [CrossRef]
- Pawlowitsch, C. Why Evolution does not always lead to an optimal signaling system. Games Econ. Behav. 2008, 63, 203–226. [Google Scholar] [CrossRef]
- Barrett, J.A.; Zollman, K.J.S. The Role of Forgetting in the Evolution and Learning of Language. J. Exp. Theor. Artif. Intell. 2009, 21, 293–309. [Google Scholar] [CrossRef]
- Mühlenbernd, R. Learning with Neighbours. Synthese 2011, 183, 87–109. [Google Scholar] [CrossRef]
- Mühlenbernd, R.; Franke, M. Meaning, evolution and the structure of society. In Proceedings of the European Conference on Social Intelligence, Barcelona, Spain, 3–5 November 2014; Herzig, A., Lorini, E., Eds.; Volume 1283, pp. 28–39. [Google Scholar]
- Mühlenbernd, R.; Nick, J. Language change and the force of innovation. In Pristine Perspectives on Logic, Language, and Computation; Katrenko, S., Rendsvig, K., Eds.; Springer: Heidelberg, Germany; New York, NY, USA, 2014; Volume 8607, pp. 194–213. [Google Scholar]
- Mühlenbernd, R.; Enke, D. The grammaticalization cycle of the progressive—A game-theoretic analysis. Morphology 2017, 27, 497–526. [Google Scholar] [CrossRef]
- Mühlenbernd, R. The change of signaling conventions in social networks. AI Soc. 2019, 34, 721–734. [Google Scholar] [CrossRef]
- Macy, M.W.; Flache, A. Learning dynamics in social dilemmas. Proc. Natl. Acad. Sci. USA 2002, 99, 7229–7236. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skyrms, B. The Stag Hunt and the Evolution of Social Structure; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lorini, E.; Mühlenbernd, R. The long-term benefits of following fairness norms under dynamics of learning and evolution. Fundam. Inform. 2018, 158, 121–148. [Google Scholar] [CrossRef]
- LiCalzi, M.; Mühlenbernd, R. Categorization and cooperation across games. Games 2019, 10, 5. [Google Scholar] [CrossRef] [Green Version]
- Harré, M. Utility, Revealed Preferences Theory, and Strategic Ambiguity in Iterated Games. Entropy 2017, 19, 201. [Google Scholar] [CrossRef] [Green Version]
- Blume, A.; DeJong, D.V.; Kim, Y.G.; Sprinkle, G.B. Evolution of Communication with Partial Common Interest. Games Econ. Behav. 2001, 37, 79–120. [Google Scholar] [CrossRef] [Green Version]
- Bruner, J.; O’Connor, C.; Rubin, H.; Huttegger, S.M. David Lewis in the lab: Experimental results on the emergence of meaning. Synthese 2018, 195, 603–621. [Google Scholar] [CrossRef]
- Rubin, H.; Bruner, J.; O’Connor, C.; Huttegger, S.M. Communication without common interest: A signaling experiment. Stud. Hist. Philos. Sci. Part C Stud. Hist. Philos. Biol. Biomed. Sci. 2020, 83, 101295. [Google Scholar] [CrossRef]
- Blume, A.; Lai, E.; Lim, W. Strategic information transmission: A survey of experiments and theoretical foundations. In Handbook of Experimental Game Theory; Capra, C.M., Croson, R., Rigdon, M., Rosenblat, T., Eds.; Edward Elgar Publishing: Cheltenham, UK; Northampton, MA, USA, 2020; pp. 311–347. [Google Scholar]
- Rohde, H.; Seyfarth, S.; Clark, B.; Jaeger, G.; Kaufmann, S. Communicating with cost-based implicature: A game-theoretic approach to ambiguity. In Proceedings of the 16th Workshop on the Semantics and Pragmatics of Dialogue, Paris, France, 19–21 September 2012. [Google Scholar]
- Schumann, A. Payoff Cellular Automata and Reflexive Games. J. Cell. Autom. 2014, 9, 287–313. [Google Scholar]
- Schumann, A. Towards Context-Based Concurrent Formal Theories. Parallel Process. Lett. 2015, 25, 1540008. [Google Scholar] [CrossRef]
- Mertens, J.F.; Neyman, A. Stochastic games. Internatioanl J. Game Theory 1981, 10, 53–66. [Google Scholar] [CrossRef]
- Hilbe, C.; Štěpán, Š.; Chatterjee, K.; Nowak, M.A. Evolution of cooperation in stochastic games. Nature 2018, 559, 246–249. [Google Scholar] [CrossRef] [PubMed]
- Jäger, G. Evolutionary Game Theory and Typology. A Case Study. Language 2007, 83, 74–109. [Google Scholar] [CrossRef]
- Deo, A. The semantic and pragmatic underpinnings of grammaticalization paths: The progressive to imperfective shift. Semant. Pragmat. 2015, 8, 1–52. [Google Scholar] [CrossRef] [Green Version]
- Bruner, J.; O’Connor, C.; Rubin, H. Experimental economics for philosophers. In Methodological Advances in Experimental Philosophy; Fischer, M.C.E., Ed.; Bloomsbury Academic: New York, NY, USA, 2019. [Google Scholar]
- Spence, M. Job market signaling. Q. J. Econ. 1973, 87, 355–374. [Google Scholar] [CrossRef]
- Farrell, J.; Rabin, M. Cheap Talk. J. Econ. Perspect. 1996, 10, 103–118. [Google Scholar] [CrossRef]
- Jäger, G. Applications of Game Theory in Linguistics. Lang. Linguist. Compass 2008, 2/3, 408–421. [Google Scholar]
- Mühlenbernd, R.; Quinley, J. Language change and network games. Lang. Linguist. Compass 2017, 11, e12235. [Google Scholar] [CrossRef]
- Grafen, A. Biological signals as handicaps. J. Theor. Biol. 1990, 144, 517–546. [Google Scholar] [CrossRef]
- Maynard Smith, J. The concept of information in biology. Philos. Sci. 2000, 67, 177–194. [Google Scholar] [CrossRef]
- Maynard Smith, J.; Price, G. The Logic of Animal Conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Maynard Smith, J. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Nowak, M.A.; Krakauer, D.C. The evolution of language. Proc. Natl. Acad. Sci. USA 1999, 96, 8028–8033. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taylor, P.D.; Jonker, L.B. Evolutionarily Stable Strategies and Game Dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Balkenborg, D.; Schlag, K.H. Evolutionarily stable sets. Int. J. Game Theory 2001, 29, 571–595. [Google Scholar] [CrossRef]
- Izquierdoy, L.R.; Izquierdoz, S.S.; Sandholm, W.H. An Introduction to ABED: Agent-Based Simulation of Evolutionary Game Dynamics. Games Econ. Behav. 2019, 118, 434–462. [Google Scholar] [CrossRef]
- Skyrms, B. Signals, evolution and the explanatory power of transient information. Philos. Sci. 2002, 69, 407–428. [Google Scholar] [CrossRef] [Green Version]
- Aumann, R. Nash equilibria are not self-enforcing. In Economic Decision Making, Games, Econometrics and Optimization; Gabzewicz, J.J., Richard, J.F., Wolsey, L.A., Eds.; North Holland: Amsterdam, The Netherlands, 1990; pp. 201–206. [Google Scholar]
- Roth, A.E.; Erev, I. Learning in Extensive-Form Games: Experimental Data and Simple Dynamic Models in the Intermediate Term. Games Econ. Behav. 1995, 8, 164–212. [Google Scholar] [CrossRef]
- Fudenberg, D.; Levine, D.K. The Theory of Learning in Games; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).