Dynamic Durable Goods Monopoly and Market Power

Abstract

We analyze a vertically differentiated market for an imperfectly durable good served by a monopolist in an infinite-horizon, discrete-time game. Our goal is to identify the Markov perfect stationary equilibria where the seller can maintain his monopoly power. We establish that the set of parameters supporting a monopoly outcome is larger when the seller offers different quality versions of the same product. Hence, our results suggest that, when the innate durability of a product is high, the seller should offer different quality versions of the product.

1. Introduction

The time-inconsistency problem of durable goods monopolist has been aggressively studied since [1] conjectured that the sequence of prices (or outputs) of a monopolist selling a perfectly durable good does not maximize his overall profitability. The monopolist cannot exercise his market power as rational consumers anticipate the seller’s pricing strategy. When the market clears at the current prices, the monopolist cannot sell more unless he lowers the price of the product. Then, consumers are reluctant to purchase the product at the current prices. Additionally, when the monopolist can adjust the prices frequently, the market price immediately drops to the competitive level and hence the monopolist cannot extract any consumer surplus. However, in real markets, a durable goods seller can charge prices greater than the marginal cost of production and make significant profits.

Our study is motivated by the discrepancy between the real-life markets and the Coase conjecture, supported by the theoretical studies in the literature. We want to understand whether the strategies we observe in real-life enable the sellers to maintain their market power. Durable goods sellers follow ingenious strategies to make some buyers pay more than others. One of the strategies we often observe in durable goods markets is related to the quality of the product. While some customers care a great deal about high-end products, others are satisfied with simpler products at lower prices. Many durable goods sellers offer different quality versions of the same product to the market. Even in some cases, durable goods sellers deliberately cripple their product to damage the product and produce a lower quality version of it at a higher unit cost. Student versions of software, printers with slower speed, and scratch ’n’ dent sales are some examples of this deliberate product damaging. The main reason for a profit-seeking seller to manufacture a lower quality product is to increase his own profits. Because, even though all customers prefer the higher quality version over the lower one, they do not value these products at the same amount. This difference in valuation creates a room for the seller to discriminate customers by offering different quality versions at different prices. Hence, the monopolist seller is able to attain a higher profit by sorting customers with vertical product differentiation. We want to understand whether this strategy also helps the monopolist seller to alleviate the time-inconsistency problem. The intuition behind this idea is simple. Once all lower valuation customers have a lower quality product, the monopolist has less incentive to lower the price of the higher quality version as the price cut of the high-quality product must be sufficiently high to make lower valuation customers’ low-quality products obsolete.

We examine quality differentiation as a strategy to alleviate the commitment problem of a durable goods monopolist and study whether the simultaneous introduction of vertically differentiated goods enables the monopolist to maintain his market power. We study a monopolistic market for an imperfectly durable good. The product depreciates stochastically. We consider an infinite-horizon, discrete-time game. In each period, the monopolist can sell two versions, the high- and low-quality, of the durable good. We establish that quality differentiation may enhance the market power of a durable goods monopolist and alleviate the commitment problem. In particular, when the product’s innate durability is high, to credibly commit to the monopoly prices, the monopolist must introduce a lower quality product.

Early studies analyzing a monopolist selling a perfectly durable good establish that if buyers condition their strategies on the payoff-relevant part of the histories, Coase’s prediction holds. Reference [2] studies a durable goods monopolist in a two-period model and shows that the optimum price charged by the monopolist is strictly less than the static monopoly price. Intuitively, unless the monopolist credibly pre-commit to a production plan, consumers anticipate that the monopolist will produce additional units to exploit the residual demand which decreases the present value of the durable good. Therefore, since consumers are reluctant to pay the static monopoly price in the first period, in response to the expectations of the consumers, the monopolist cuts the price of the product. Reference [3] extends [2]’s setting into an infinite-horizon setting. Reference [3] establishes that there exists an equilibrium that satisfies the Coase conjecture. This equilibrium is the limit of the unique equilibrium of the finite version of her model. Similarly, reference [4] show that, even though a continuum of subgame perfect equilibria may exist in an infinite-horizon model, the Coase conjecture is verified for Markov strategies. Reference [5] extends these initial analyses by considering a market for a perfectly durable good in which demand expands over time. His study also verifies Coase’s prediction for Markov strategies. Intuitively, if the monopolist charges the static monopoly price forever, as new consumers enter the market the number of low-valuation customers grows and the price cutting strategy becomes inevitable.

On the contrary to the early studies, reference [6] shows that, if buyers condition their strategies on not only payoff-relevant part of the histories but the past actions as well, there exist equilibria in which the monopolist creates a reputation and maintains some or all market power when the marginal cost of production is no less than the lowest buyer valuation. In addition to establishing a reputation, product depreciation can also help a durable goods monopolist to avoid the time-inconsistency problem. Reference [7] show that, in a discrete-time, infinite-horizon game when the good depreciates, the replacement sales may deter the monopolist from cutting the price as long as the time period between successive offers of the monopolist is nonzero. However, in the limit, as the length of the time period approaches zero, the competitive outcome is achieved and the Coase conjecture holds. Reference [8], on the other hand, by using a continuous-time model with replacement sales constructs continuous-time equilibria in which the monopolist can earn profits above the competitive level. However, reference [8] also shows the existence of an equilibrium that verifies the Coase conjecture. Then, reference [8,9] characterize the effect of the depreciation rate on the market outcome of a durable goods monopoly when agents follow Markov strategies. They conclude that, below a certain level of durability, there exists a unique stationary equilibrium in which the monopolist charges the static monopoly price in each period and the equilibrium continues to exist even when the seller becomes highly impatient. Intuitively, when the product depreciates, the replacement sales become more profitable than penetrating the market by cutting the price of the good. We extend their single good setting into a setting of a vertically differentiated market to analyze the effect of quality differentiation on the commitment problem of a durable goods monopolist.

There are several studies on durable goods monopolies revolve around the issue of quality improvements. References [10,11,12] consider this issue in two-period models. A finite horizon model, however, is insufficient to capture the time inconsistency problem. References [13,14,15,16,17] consider planned obsolescence and show that a durable goods monopolist cannot maintain market power as the higher quality products lower the value of used ones. Our study establishes that the simultaneous introduction of the different versions of a product increases the profit when the product is not sufficiently perishable. Similar to our study, reference [18] analyzes a discrete-time, infinite horizon game. A perfectly durable goods monopolist can vary the quality of the good over time. Reference [18] shows that, when the marginal cost of production is sufficiently low, the Coase conjecture holds in all subgame perfect equilibria.

Reference [19] studies quality differentiation of a perfectly durable product in an infinite-horizon model and establishes that introducing a lower quality good mitigates the time inconsistency problem. Reference [20] studies a durable goods monopolist who can offer perfectly durable goods in different qualities in an infinite-horizon model and shows that, when the monopolist becomes extremely flexible in adjusting the prices and qualities, he immediately loses his monopoly power and the competitive outcome is achieved. Reference [21] studies the role of quality in a finite-time model and offers a Coasian explanation for product differentiation. In all these models, when a buyer purchases the product, she leaves the market. In our study, buyers are allowed to re-enter the market as often as they wish. We establish that the set of the parameters supporting the monopoly equilibrium is larger when the monopolist produces a lower quality good as well.

The rest of the paper proceeds as follows. Section 2 introduces the model. Section 3 describes the dynamic optimization problem. Section 4 characterizes the steady states and identifies the stationary Markov perfect equilibria. Section 5 concludes. All proofs are relegated to the Appendix A.

2. Model

Consider a monopolist serving an indivisible and imperfectly durable good to a market. The monopolist is able to manufacture two different quality versions of the same product and offer high-quality (H) and low-quality (L) versions for sale simultaneously at discrete points in time. The durable good with quality level $i\in \{H,L\}$ is referred to as durable good i.

There exists a unit mass of infinitely-lived buyers indexed by $b\in [0,1]$. Buyers are segmented into two groups: high-valuation buyers with $b\in [0,\widehat{b}]$ and low-valuation buyers with $b\in (\widehat{b},1]$. The reservation value of a high-valuation buyer from good i is ${\overline{u}}^i$ and the reservation value of a low-valuation buyer from good i is ${\underline{u}}^i$. The flow payoff of buyer b for acquiring one unit of good i is represented by $f^i(b)={\overline{u}}^i$ for $b\in [0,\widehat{b}]$ and $f^i(b)={\underline{u}}^i$ for $b\in (\widehat{b},1]$.1 The high-valuation buyer assigns a higher value to good i than the low-valuation buyer, i.e., ${\overline{u}}^i>{\underline{u}}^i$ holds valid for all i. The difference between the highest and the lowest reservation value is higher for the high-quality product, i.e., ${\overline{u}}^H-{\underline{u}}^H>{\overline{u}}^L-{\underline{u}}^L$ holds valid.2 Buyers are allowed to trade with each other in a perfectly competitive second-hand market. A buyer can always access the markets. Additionally, each buyer is able to possess at most one unit of the durable good. The marginal cost of production is assumed to be zero. The length of the time-period between successive price changes is $z>0$. Both versions of the durable good depreciate stochastically at the same rate. The probability that a product is still working after a length of time z is $e^{-\lambda z}$. Hence, with probability $\mu \equiv 1-e^{-\lambda z}$, the good fails between successive price changes.

Sales occur only at discrete points in time, $t=0,z,2z,\dots ,nz,\dots$ in all markets. The time $nz$ is referred to as period n. All agents (buyers and the monopolist) are risk neutral and have the same discount factor $\delta \equiv e^{-rz}$. In each period, the game runs as follows. First, the monopolist sets the price of the goods. Then, buyers choose whether or not to hold a good and which version to hold. Trade simultaneously occurs in all markets accordingly. The game repeats itself in the next period. The objective of the monopolist is to maximize the present value of his expected profits and while a buyer seeks to maximize the present value of her expected payoffs as a function of the current state of the market.

We seek to derive stationary Markov perfect equilibria of this game in which agent strategies only depend on the current state. Let $\sigma$ and ${\tau }_b$ be the strategies of the monopolist and buyer b, respectively. A strategy of the buyer with index b is denoted by ${\tau }_b:{\Re }_{+}^2\to \{0,1,2\}$, where decision 0 indicates that the buyer prefers not holding any good in the current period, decision 1 indicates that the buyer prefers holding the low-quality good, and decision 2 indicates that the buyer prefers holding the high-quality good in the current period. Since there exists a perfectly competitive second-hand market, strategies of a buyer are independent of her holding status and depend only on the current prices. It follows that the monopolist can specify his strategy as a function of the current stock of the goods in the market rather than prices. Hence, the prices of the monopolist in a period are determined by $\sigma :\mathsf{\Omega }\times \mathsf{\Omega }\to {\Re }_{+}^2$, where $\mathsf{\Omega }$ is the Borel sigma algebra on $[0,1]$. The strategy profile $\{\sigma ,\tau \}$ generates a stationary path of prices and stock of goods that can be derived recursively. We restrict our attention to equilibria in which deviations by sets of measure zero buyers change neither the actions of the monopolist nor the actions of the other buyers. Hence, in such equilibria, buyers behave as price takers.

3. Dynamic Optimization Problem

In this section, first, we represent the objective function of the monopolist. Next, we derive the reservation valuation of a customer for each version of the product. Then, by taking into account the incentive compatibility and the participation constraints, we identify the maximum possible prices at each state of the market. Finally, we characterize the structure of the stationary equilibria.

The stock of the durable good i before trade is denoted by $x^i$ and the stock of the durable good i after trade is denoted by $y^i$. Both versions of the product depreciate at an individual level. We, however, consider the stock of goods in the market as the state variable. If we did not have a second-hand market, the state variable cannot be the stock of goods in the market. It must be the distribution of the customers. The product either stops working or its value stays the same. This implies that prices in the second-hand market are the same as the ones in the primary market. Buyers holding a lower quality good can upgrade the product at a lower cost by selling the current version in the second-hand market. Then, the value function of the monopolist becomes

$$R(x^H,x^L)=\underset{y^i\in [x^i,1],\forall i}{max}\{P^H(y^H,y^L)(y^H-x^H)+P^L(y^H,y^L)(y^L-x^L)+\delta R((1-\mu )y^H,(1-\mu )y^L)\},$$

(1)

where $P^i(·)$ is the price of durable good i, and $R(·)$ is the continuation value.

We need to derive the reservation valuations for these two goods to identify the prices. The reservation valuation of buyer b from good i is represented by $V^i(b)$ which is derived from buyer b’s inter-temporal optimization that requires buyer b to be indifferent between purchasing the good today at the price $V^i(b)$ and waiting one period to purchase it. Then, $V^i(b)$ becomes

$$V^i(b)=(1-\rho )f^i(b)+\rho {\acute{p}}^i$$

(2)

where $\rho \equiv \delta (1-\mu )$ and ${\acute{p}}^i$ is the expected price of good i in the next period. Since $f^i(·)$ is monotone and deviations of measure zero buyers do not affect the equilibrium, $V^i\left(·\right)$ is a non-increasing left-continuous function. When the stock of the goods after a trade is $(y^H,y^L)$, the price of the high-quality good is derived from the incentive compatibility constraint of the marginal buyer of the high-quality good

$$P^H(y^H,y^L)\le V^H(y^H)-V^L(y^H)+P^L(y^H,y^L)$$

(3)

and the price of the low-quality good is derived from the participation constraint of the marginal buyer of the low-quality good

$$P^L(y^H,y^L)\le V^L(y^H+y^L)$$

(4)

where $V^L(y^H)-P^L(y^H,y^L)$ is the payoff of buyer $y^H$ if she purchases the low-quality good at the price $P^L(y^H,y^L)$.

The argmax correspondence of the objective function is denoted by $T(·)$. By the generalized theorem of the maximum and the contraction mapping theorem, there exists a unique continuous function $R(·)$, and $T(·)$ is a non-empty and compact valued correspondence.3 Moreover, the supermodularity of the objective function implies that $T(·)$ is non-decreasing with respect to each argument. It follows that there exists at most countable number of points for which $T(·)$ is multi-valued.

Proposition 1.

The monopolist does not randomize along any equilibrium path unless it is the initial period.

Hence, given a state $(x^H,x^L)$, the equilibrium output choice of the monopolist is $t(x^H,x^L)=minT(x^H,x^L)$. Moreover, the output function, $t^i(·):[0,1-\mu ]\times [0,1-\mu ]\to {\Re }_{+}$, is nondecreasing since $T(x^H,x^L)$ is a monotone correspondence.

An equilibrium is represented by $\{P^H(·),P^L(·),t^H(·),t^L(·),R(·)\}$. The structure of a stationary path is as follows. In the initial period, the monopolist selects prices, $P^H(y_0)$ and $P^L(y_0)$. All buyers $b\le y_0^H$ purchase the high-quality good and all buyers $y_0^H<b\le y_0^H+y_0^L$ purchase the low-quality good.4 At the beginning of the next period, the stock of the high-quality good is $x_1^H=(1-\mu )y_0^H$ and the stock of the low-quality good is $x_1^L=(1-\mu )y_0^L$. The monopolist selects prices, $P^H(y_1)=P^H(t(x_1))$ and $P^L(y_1)=P^L(t(x_1))$, and all buyers $b\le y_1^H$ choose to hold the high-quality good and all buyers $y_1^H<b\le y_1^H+y_1^L$ choose to hold the low-quality good. This continues until a steady state is reached. Once a steady state is reached, the monopolist continues by selling to the replacement demands. In order to construct equilibria of this game, the solution method introduced by [9] is followed. First, we prove the existence of a steady state in any equilibrium. Then, we characterize all possible steady states. Finally, we derive all stationary paths that reach a steady state by using backward induction from the steady state.

We focus on the nontrivial case where $\widehat{b}{\overline{u}}^H>{\underline{u}}^H$. Otherwise, the unique stationary steady state would be the static monopoly outcome where the monopolist sets a price so that all buyers purchase the high-quality good immediately and from then on the monopolist sells to the replacement demand.

4. Analysis

In this section, first, we establish the existence of a steady state in any equilibrium. Then, we characterize all possible steady states that may coexist when the monopolist sells the high-quality good to the high-valuation buyers. Finally, we identify the set of parameters supporting monopoly equilibria.

The steady state stock levels of durable goods $(y_s^H,y_s^L)$ must satisfy $t^H((1-\mu )y_s)=y_s^H$ and $t^L((1-\mu )y_s)=y_s^L$, where $(t^H(·),t^L(·))$ is the argmax correspondence of the objective function. We establish that any equilibrium has a steady state.

Proposition 2.

Any equilibrium has at least one steady state, and the steady state prices satisfy $P^H\left(y_s^H,y_s^L\right)=f^H\left(y_s^H\right)-f^L\left(y_s^H\right)+f^L\left(y_s^H+y_s^L\right)$ and $P^L\left(y_s^H,y_s^L\right)=f^L\left(y_s^H+y_s^L\right)$.

The economic intuition behind the steady state prices is as follows. At a steady state $(y_s^H,y_s^L)$, the marginal buyer of the high-quality good is $y_s^H$ and the marginal buyer of the low-quality good is $y_s^H+y_s^L$ in each period. Buyer $y_s^H+y_s^L$ is indifferent between today’s and tomorrow’s offer for the low-quality good when the price of the low-quality good is $f^L(y_s^H+y_s^L)$. Similarly, buyer $y_s^H$ is indifferent between today’s and tomorrow’s offer for the high-quality good when the price of the high-quality good is $f^H(y_s^H)$. However, when the price of the low-quality good is $f^L\left(y_s^H+y_s^L\right)$, buyer $y_s^H$’s net surplus from the low-quality good is $f^L(y_s^H)-f^L(y_s^H+y_s^L)$. Hence, to sell the high-quality good to buyer $y^H$, the monopolist has to leave an information rent no less than $f^L(y_s^H)-f^L(y_s^H+y_s^L)$ to the high-valuation buyers. Therefore, at the steady state, the price of the high-quality good is $f^H(y_s^H)-f^L(y_s^H)+f^L(y_s^H+y_s^L)$ and the price of the low-quality good is $f^L(y_s^H+y_s^L)$.

We consider equilibria in which the monopolist credibly commits not to selling the high-quality good to low-valuation buyers. The monopoly steady states of such equilibria are $(\widehat{b},0)$ and $(\widehat{b},1-\widehat{b})$. In the first one, the monopolist sells the high-quality good to the high-valuation buyers and there is no low-quality good in the market. This steady state is called static monopoly steady state. We call the corresponding equilibrium static monopoly equilibrium. In the second one, the monopolist segments the market by selling the high-quality good to the high-valuation buyers and by selling the low-quality good to the low-valuation buyers. This steady state is called segmented monopoly steady state. We call the corresponding equilibrium segmented monopoly equilibrium.

Proposition 3.

Let S denote the set of steady states. In any equilibrium, where the monopolist sells the high-quality good to high-valuation buyers, one of the following holds:

1.

$S=\{(\widehat{b},1-\widehat{b}),(\widehat{b},0)\}$;

2.

$S=\{(\widehat{b},1-\widehat{b}),(\widehat{b},0),(1,0)\}$

3.

$S=\{(\widehat{b},1-\widehat{b}),(1,0)\}$.

We establish that, when a monopolist produces two versions of a durable good, there exist three possible steady states in a monopoly equilibrium: $(1,0)$, $(\widehat{b},0)$, $(\widehat{b},1-\widehat{b})$. At the steady state $(1,0)$, all buyers hold the high-quality good after the trade and the monopolist serves their replacement demand in each period. This steady state is called the Coase conjecture steady state. We prove that the static monopoly steady state always coexists with the segmented monopoly steady state. Depending on the magnitude of $\mu$, the Coase conjecture steady state $(1,0)$ may coexist with the monopoly steady states. We now identify the sets of $\mu$ supporting these three cases established in Proposition 3.

The necessary conditions for the existence of the static monopoly equilibrium are as follows. First, when the state before trade is $((1-\mu )\widehat{b},0)$, the monopolist must prefer selling the high-quality good to the high-valuation buyers’ replacement demand $\mu \widehat{b}$ at the price ${\overline{u}}^H$ thereafter to selling the high-quality good to buyers who do not hold the high-quality good $(1-($$1-\mu )$$\widehat{b})$ at the price $P^H(1,0)$ and continuing by selling the high-quality good to all buyers’ replacement demand $\mu$ at the price $P^H(1,0)$ thereafter. If

$$\frac{\mu \widehat{b}{\overline{u}}_H}{1-\delta }\ge (1-(1-\mu )\widehat{b})P^H(1,0)+\frac{\delta \mu }{1-\delta }{P}^H(1,0)$$

(5)

holds, the monopolist never cuts the price of the high-quality good to $P^H(1,0)$ to serve the high-quality good to all buyers. Since $P^H(1,0)\le {\underline{u}}^H$, (5) holds for all $\mu \ge \frac{(1-\delta )(1-\widehat{b}){\underline{u}}^H}{\widehat{b}({\overline{u}}^H-{\underline{u}}^H)-\delta (1-\widehat{b}){\underline{u}}^H}\equiv {\underline{\mu }}^{st}(\delta )$. Second, when the state before trade is $((1-\mu )\widehat{b},0)$, the monopolist must prefer selling the high-quality good to the high-valuation buyers’ replacement demand $\mu \widehat{b}$ at the price ${\overline{u}}^H$ forever to selling the high-quality good to the high-valuation buyers’ replacement demand $\mu \widehat{b}$ at the price $P^H(\widehat{b},1-\widehat{b})$ thereafter and selling the low quality good to the low-valuation buyers $1-\widehat{b}$ at the price $P^L(\widehat{b},1-\widehat{b})$ and continuing by selling the low-quality good to their replacement demand $\mu (1-\widehat{b})$ at the price $P^L(\widehat{b},1-\widehat{b})$ thereafter. If

$$\frac{\mu \widehat{b}{\overline{u}}^H}{1-\delta }\ge \frac{\mu \widehat{b}}{1-\delta }{P}^H(\widehat{b},1-\widehat{b})+(1-\widehat{b})P^L(\widehat{b},1-\widehat{b})+\frac{\delta \mu (1-\widehat{b})}{1-\delta }{P}^L(\widehat{b},1-\widehat{b})$$

(6)

holds, the monopolist never cuts the price of the low-quality good to $P^L(\widehat{b},1-\widehat{b})$ to serve the low-quality good to the low-valuation buyers. Since $P^H(\widehat{b},1-\widehat{b})\le {\overline{u}}^H-{\overline{u}}^L+P^L(\widehat{b},1-\widehat{b})$ and $P^L(\widehat{b},1-\widehat{b})\le {\underline{u}}^L$, (6) holds if $\mu \ge {\underline{\mu }}^{st}(\delta )$. Therefore, the monopolist does not deviate from the static monopoly steady state $(\widehat{b},0)$ when $\mu \ge {\underline{\mu }}^{st}(\delta )$.

The necessary conditions for the existence of the segmented monopoly equilibrium are as follows. When the state before trade is $((1-\mu )\widehat{b},(1-\mu )(1-\widehat{b}))$, the monopolist must prefer selling the high-quality good to the high-valuation buyers’ replacement demand $\mu \widehat{b}$ at the price ${\overline{u}}^H-{\overline{u}}^L+{\underline{u}}^L$ and selling the low-quality good to the low-valuation buyers’ replacement demand $\mu (1-\widehat{b})$ at the price ${\underline{u}}^L$ thereafter to penetrating the entire market with the high-quality good by charging $P^H(1,(1-\mu )(1-\widehat{b}))$ and continuing by selling the high-quality good to all buyers’ replacement demand $\mu$ at the price $P^H(1,x^L)$ thereafter. If

$$\frac{\mu \widehat{b}({\overline{u}}^H-{\overline{u}}^L+{\underline{u}}^L)}{1-\delta }+\frac{\mu (1-\widehat{b}){\underline{u}}^L}{1-\delta }\ge (1-(1-\mu )\widehat{b})P^H({1,x}^L)+\frac{\delta \mu }{1-\delta }{P}^H(1,x^L)$$

(7)

holds, the monopolist never cuts the price of the high-quality good to $P^H({1,x}^L)$ to serve the high quality good to all buyers. Since $P^H(1,x^L)\le {\underline{u}}^H-{\underline{u}}^L$ for all $x^L>0$, (7) holds if $\mu \ge \frac{(1-\delta )(1-\widehat{b})({\underline{u}}^H-{\underline{u}}^L)}{\widehat{b}(({\overline{u}}^H-{\overline{u}}^L)-({\underline{u}}^H-{\underline{u}}^L))-\delta (1-\widehat{b})({\underline{u}}^H-{\underline{u}}^L)+{\underline{u}}^L}\equiv {\underline{\mu }}^{sg}(\delta )$. Therefore, the monopolist does not deviate from the segmented monopoly steady state $(\widehat{b},1-\widehat{b})$ for $\mu \ge {\underline{\mu }}^{sg}(\delta )$. Moreover, since $P^H(1,0)>P^H(1,x^L)$ for all $x^L>0$, ${\underline{\mu }}^{sg}(\delta )<{\underline{\mu }}^{st}(\delta )$ must hold. Figure 1 represents these threshold values as a function of $\delta$.

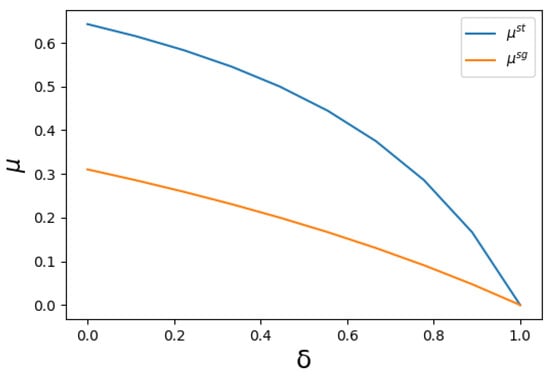
Figure 1. The threshold values for the failure probability $\mu$.

It is established that the necessary condition for the existence of a monopoly equilibrium, $\mu \ge$${\underline{\mu }}^{sg}(\delta )$, is also sufficient for the existence and the uniqueness of the equilibrium.

Theorem 1.

There exists at most one monopoly equilibrium iff $\mu \ge {\underline{\mu }}^{sg}(\delta )$ for a given δ. The monopoly steady states of such equilibrium are

• $\left\{(\widehat{b},1-\widehat{b})\right\}$ at the equilibrium and $\{(\widehat{b},1-\widehat{b}),(1,0)\}$ upon deviation for ${\underline{\mu }}^{sg}(\delta )\le \mu <{\underline{\mu }}^{st}(\delta )$,
• $\left\{(\widehat{b},0)\right\}$ at the equilibrium and $\{(\widehat{b},0),(\widehat{b},1-\widehat{b}),(1,0)\}$ upon deviation for $\mu \ge {\underline{\mu }}^{st}(\delta )$

where ${\underline{\mu }}^{st}(\delta )\equiv \frac{(1-\delta )(1-\widehat{b}){\underline{u}}^H}{\widehat{b}({\overline{u}}^H-{\underline{u}}^H)-\delta (1-\widehat{b}){\underline{u}}^H}$ and ${\underline{\mu }}^{sg}(\delta )\equiv \frac{(1-\delta )(1-\widehat{b})({\underline{u}}^H-{\underline{u}}^L)}{\widehat{b}(({\overline{u}}^H-{\overline{u}}^L)-({\underline{u}}^H-{\underline{u}}^L))-\delta (1-\widehat{b})({\underline{u}}^H-{\underline{u}}^L)+{\underline{u}}^L}$.

In such an equilibrium, for $\mu \ge {\underline{\mu }}^{st}(\delta )$, the monopolist initially charges ${\overline{u}}^H$ for the high-quality good and charges a price for the low-quality good high enough that none of the buyers purchase it. Hence, from the initial state $(0,0)$, the monopolist brings the state to $(\widehat{b},0)$ by selling the high-quality good to all high-valuation buyers. He then continues to serve the replacement demand of the high-valuation buyers for the high-quality good. For ${\underline{\mu }}^{sg}(\delta )\le \mu <{\underline{\mu }}^{st}(\delta )$, the monopolist initially charges ${\overline{u}}^H-{\overline{u}}^L+{\underline{u}}^L$ for the high-quality good and ${\underline{u}}^L$ for the low-quality good. Hence, from the initial state $(0,0)$, the monopolist brings the state to $(\widehat{b},1-\widehat{b})$ by selling the high-quality good to all high-valuation and the low-quality good to all low-valuation buyers. He then continues to charge the segmented monopoly prices to serve the replacement demands.

If the monopolist deviates from a monopoly steady state by selling more in an attempt to increase profits, the movement of the states in a monopoly equilibrium is as follows. The sequence of states ${\left\{({\tilde{x}}_{k,j}^H,{\tilde{x}}_{k,j}^L)\right\}}_{k=0}^{m_j+1}$ is constructed such that when that state is $({\tilde{x}}_{k,j}^H,{\tilde{x}}_{k,j}^L)$, the monopolist is indifferent between bringing the next period’s state to $({\tilde{x}}_{k-1,j}^H,{\tilde{x}}_{k-1,j}^L)$ by charging $({\tilde{p}}_{k-1,j}^H,{\tilde{p}}_{k-1,j}^L)$ and staying at $({\tilde{x}}_{k,j}^H,{\tilde{x}}_{k,j}^L)$ by charging $({\tilde{p}}_{k,j}^H,{\tilde{p}}_{k,j}^L)$ forever. The prices are driven recursively. If the market is saturated with the low-quality good, the price of the low-quality version of the product becomes zero. If some, but not all, low-valuation customers hold the low-quality version, then its price would be equal to ${\underline{u}}_L$. Hence, while constructing the price path for the high-quality product, one needs to take into account the incentive compatibility constraint.

There exist three paths, $j\in \{1,2,3\}$, depending on the state of the low-quality good. On all paths, the initial value of the state of the high-quality good is ${\tilde{x}}_{0,j}^H=(1-\mu )\widehat{b}$ and its end value is ${\tilde{x}}_{m_j+1,j}^H\le 1-\mu$. On the first path $j=1$, none of the buyers hold the low-quality good. That is, ${\tilde{x}}_{k,1}^L=0$ for all k. Then, the price of the low-quality good becomes ${\tilde{p}}_{k,1}^L\ge {\underline{u}}^L+{\rho }^k({\overline{u}}^H-{\underline{u}}^H)$. The price of the high-quality good due to the incentive compatibility constraint becomes ${\tilde{p}}_{k,1}^H={\underline{u}}^H+{\rho }^k({\overline{u}}^H-{\underline{u}}^H)$ for all k. On the second path, some buyers hold the low-quality good. As the low-valuation buyers anticipate that the price of the low quality good will be eventually equal to ${\underline{u}}^L$, the monopolist cannot charge more than ${\underline{u}}^L$ for the low quality good. Hence, ${\tilde{p}}_{k,2}^L={\underline{u}}^L$ for all k. Then, the price of the high-quality good becomes ${\tilde{p}}_{k,2}^H={\underline{u}}^H+{\rho }^k(({\overline{u}}^H-{\overline{u}}^L)-({\underline{u}}^H-{\underline{u}}^L))$ for all k. On path 3, there exists an excess supply of the low-quality good. Hence, ${\tilde{p}}_{k,3}^L=0$ for all k. Then, the price of the high-quality good is ${\tilde{p}}_{k,3}^H=({\underline{u}}^H-{\underline{u}}^L)+{\rho }^k(({\overline{u}}^H-{\overline{u}}^L)-({\underline{u}}^H-{\underline{u}}^L))$ for all k.

If the good is sufficiently perishable, the monopolist will return to a monopoly steady state from any state of the high-quality good above $(1-\mu )\widehat{b}$. Hence, we have ${\tilde{x}}_{m_j+1,j}^H=1-\mu$. Otherwise, the Coase conjecture steady state $(1,0)$ coexists with monopoly steady states. In this case, we have ${\tilde{x}}_{m_j+1,j}^H<1-\mu$. Hence, when the state is $({\tilde{x}}_{m_j+1,j}^H,{\tilde{x}}_{m_j+1,j}^L)$, the monopolist is indifferent between bringing the state to $({\tilde{y}}_{m_j,j}^H,{\tilde{y}}_{m_j,j}^L)$ and fully penetrating the market by selling the high-quality good to all buyers and continuing by serving the replacement demand $\mu$ for the high-quality good thereafter. It follows that the monopolist strictly prefers penetrating the market with the high-quality good when the state of the high-quality good is greater than ${\tilde{x}}_{m_j+1,j}^H$.

Figure 2 illustrates how states move to a monopoly steady state when the good is sufficiently perishable. The arrows indicate the direction of movement of the state at any $(y^H,y^L)$. For all $(y^H,y^L)$, the state goes back to a monopoly steady state. If $y^L=0$, then the corresponding steady state is the static monopoly steady state $(\widehat{b},0)$; otherwise, it is the segmented monopoly steady state $(\widehat{b},1-\widehat{b})$. Figure 3 illustrates how states move to a monopoly steady state when the goods are not sufficiently perishable. The arrows indicate the direction of movement of the state at any $(y^H,y^L)$. If $y^H$ is low, the states move towards a monopoly steady state; otherwise, the states move towards the Coase conjecture steady state.

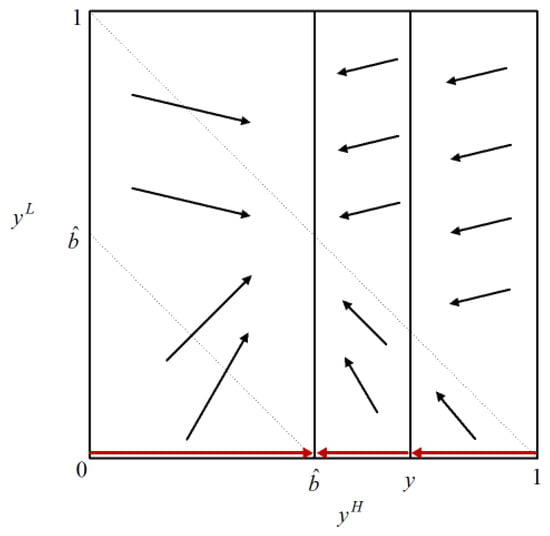
Figure 2. The Monopoly Equilibrium I.

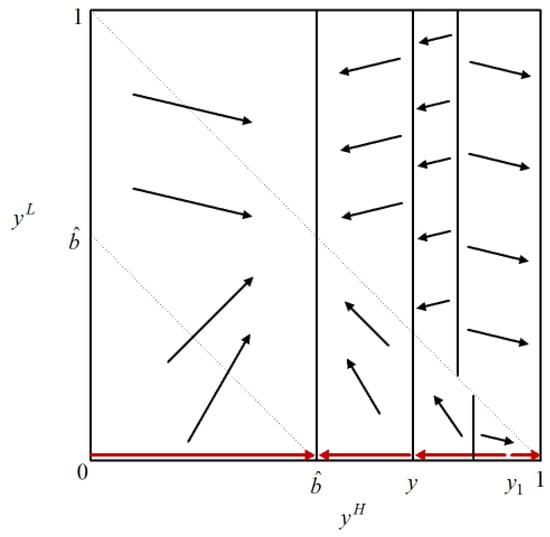
Figure 3. The Monopoly Equilibrium II.

Let ${\underline{\mu }}^s\left(\delta \right)$ be the threshold when a monopolist produces a single version of a durable good, a monopoly equilibrium exists for all $\mu >{\underline{\mu }}^s(\delta )$ for a given $\delta$. It is established that

Corollary 1.

The set of parameters supporting a monopoly equilibrium expands when the monopolist produces vertically differentiated products.

We show that the threshold failure probability supporting the static monopoly steady state is a function of $\delta$ such that ${\underline{\mu }}^{st}(\delta )={\underline{\mu }}^s(\delta )$ holds for all $\delta$. Since the segmented monopoly steady state is supported for ${\underline{\mu }}^{sg}(\delta )\le \mu <{\underline{\mu }}^{st}(\delta )$, the segmented monopoly equilibrium exists when the static one does not. If we compare the steady state profits, we can observe that the monopolist reaches the highest possible profit with static monopoly equilibrium. The profit of the monopolist becomes ${\mathsf{\Pi }}^{st}=\widehat{b}{\overline{u}}^H(1+\frac{\delta \mu }{1-\delta })$. However, unless the product is sufficiently perishable, this profit is not attainable. When the segmented equilibrium exists, ${\underline{\mu }}^{sg}(\delta )\le \mu <{\underline{\mu }}^{st}(\delta )$, the profit of the monopolist under this equilibrium becomes ${\mathsf{\Pi }}^{sg}=(\widehat{b}{\overline{u}}^H-(\widehat{b}{\overline{u}}^L-{\underline{u}}^L))(1+\frac{\delta \mu }{1-\delta })$. The segmented equilibrium profit, ${\mathsf{\Pi }}^{sg}$, is strictly higher than the profit that the monopolist would get under the Coase conjecture outcome, ${\mathsf{\Pi }}^{cc}=\widehat{b}{\underline{u}}^H(1+\frac{\delta \mu }{1-\delta })$. Hence, for the set of failure probability ${\underline{\mu }}^{sg}(\delta )\le \mu <{\underline{\mu }}^{st}(\delta )$, the monopolist can attain a higher profit with vertical product differentiation than the profit the monopolist would get under the single product case.

Consider an example to observe how the production of a low-quality good affects the parameters consistent with each type of equilibrium. Let $\widehat{b}=0.7$, ${\overline{u}}^H=3{\overline{u}}^L$, ${\underline{u}}^H=3{\underline{u}}^L$, $0.6({\overline{u}}^H-{\overline{u}}^L)={\underline{u}}^H-{\underline{u}}^L$, and $\delta =0.60$ Then, the threshold depreciation rates become ${\underline{\mu }}^{sg}=0.15$, and ${\underline{\mu }}^{st}=0.42$, Therefore, if the monopolist only produces the high-quality good, the monopoly equilibrium exists when the expected life time is less than 2 years. However, if the monopolist produces the low quality good as well as the high-quality good, the monopoly equilibrium exists when the expected lifetime is less than six years. Figure 4 represents the steady state profits as well as the Coase conjecture profit when ${\underline{\mu }}^{sg}=0.15$, and ${\underline{\mu }}^{st}=0.42$.

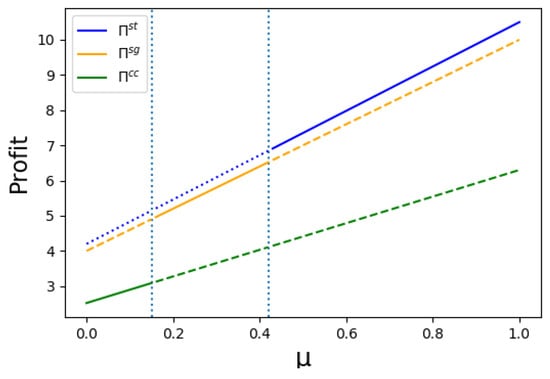
Figure 4. The steady state profits versus the Coase conjecture profit.

Now, consider the structure of the stationary path as the time period between successive offers of the monopolist diminishes. For $x^H>(1-\mu )\widehat{b}$, the state either immediately moves to the Coase conjecture steady state or slowly goes back to a monopoly steady state. It is established that the rate at which a monopoly steady state is reached is independent of the state of the low-quality good.

Corollary 2.

As the length of the time period between successive price changes approaches zero, the state of the high-quality good moves towards a monopoly steady state at the rate of ${\dot{x}}^H=\lambda x^H\left(1-\frac{{\underline{u}}^H}{{\overline{u}}^L}{\left(\frac{y^H}{\widehat{b}}\right)}^{\frac{\lambda +r}{\lambda }}\right)$ for $x^H>(1-\mu )\widehat{b}$.

If the monopolist deviates from a monopoly steady state by selling more in an attempt to increase profits, when the good is sufficiently perishable, the state goes back to a monopoly steady state. If $x^L=0$, then the corresponding steady state is the static monopoly steady state $(\widehat{b},0)$; otherwise, it is the segmented monopoly steady state $(\widehat{b},1-\widehat{b})$. When the good is not sufficiently perishable for low values of $x^H$, the state moves towards a monopoly steady state. For high values of $x^H$, however, the state moves towards the Coase conjecture steady state.

5. Conclusions

This study analyzes the effect of quality differentiation on the commitment problem of a durable goods monopolist. We consider a monopolist selling an imperfectly durable good available in two quality levels in an infinite-horizon, discrete-time game. We characterize the stationary Markov perfect equilibria where the seller can maintain his market power as a function of the common discount rate, the common depreciation rate of the goods, the length of the time period between successive price changes, and the quality levels of the goods. We show that, if the depreciation rate is sufficiently high, the monopoly equilibrium exists. This result survives even when the agents become extremely patient. We also establish that the set of parameters supporting the monopoly equilibrium is larger when the monopolist can produce a lower quality good.

This study establishes that quality differentiation may enhance the market power of a durable goods monopolist and alleviate the commitment problem. In particular, when the innate durability of a good is high, to credibly commit to the monopoly prices of the good the monopolist will produce a lower quality good as well.