Erev, I. et al. A Choice Prediction Competition for Market Entry Games: An Introduction. Games 2010, 1, 117-136

Ido Erev; Eyal Ert; Alvin E. Roth

doi:10.3390/g1030221

,

and

¹

Max Wertheimer Minerva Center for Cognitive Studies, Faculty of Industrial Engineering and Management, Technion, Haifa 32000, Israel

²

Computer Laboratory for Experimental Research, Harvard Business School, Boston, MA, 02163, USA

³

Department of Economics, 308 Littauer, Harvard University, Cambridge, MA 02138, USA

⁴

Harvard Business School, 441 Baker Library, Boston, MA 02163, USA

Games2010, 1(3), 221-225;https://doi.org/10.3390/g1030221

This article belongs to the Special Issue Predicting Behavior in Games

Version Notes

Order Reprints

Ion Juvina found an error in our manuscript published in Games [1]. The error led to overestimation (by about 3%) of the alternation rate presented in Table 2 (in page 120). The correction does not change the main conclusions, but it slightly changes five exhibits. The corrected exhibits are presented below, and in the competition website (http://sites.google.com/site/gpredcomp).

Table 2. The 40 market entry games that were studied in the estimation experiment. At each trial, each of 4 players has to decide (individually) between “entering a risky market”, or “staying out” (a safer prospect). The payoffs depended on a realization of a binary gamble (the realization at trial t is denoted G_t, and yields “H with probability Ph; and L otherwise”), the number of entrants (E), and two additional parameters (k and S). The exact payoff for player i at trial t is:

V_{i} (t) = {_{{round(G}_{t} /S) with p= {.5; -round(G}_{t} /S) otherwise   if i does not enter}^{{10-k(E)+G}_{t} if i enters}}

The left hand-columns present the exact value of the different parameters in the 40 games, the right hand columns present the equilibrium predictions, and the main experimental results in the first and second block (B1 and B2).

**Table 2.** **The 40 market entry games that were studied in the estimation experiment.** At each trial, each of 4 players has to decide (individually) between “entering a risky market”, or “staying out” (a safer prospect). The payoffs depended on a realization of a binary gamble (the realization at trial t is denoted G_t, and yields “H with probability Ph; and L otherwise”), the number of entrants (E), and two additional parameters (k and S). The exact payoff for player i at trial t is: $V_{i} (t) = {_{{round(G}_{t} /S) with p= {.5; -round(G}_{t} /S) otherwise if i does not enter}^{{10-k(E)+G}_{t} if i enters}}$ The left hand-columns present the exact value of the different parameters in the 40 games, the right hand columns present the equilibrium predictions, and the main experimental results in the first and second block (B1 and B2).
								Experimental results
The games						Entry at eq.		Entry rates		Efficiency		Alternations
#	K	ph	H	L	S	pure	symmetric	B1	B2	B1	B2	B1	B2
1	2	0.04	70	-3	5	1.00	1.00	0.71	0.80	2.77	2.66	0.16	0.16
2	2	0.23	30	-9	4	1.00	1.00	0.55	0.62	2.64	2.75	0.25	0.23
3	2	0.67	1	-2	3	1.00	1.00	0.88	0.94	2.39	2.24	0.10	0.04
4	2	0.73	30	-80	4	1.00	1.00	0.71	0.64	2.58	2.57	0.28	0.27
5	2	0.80	20	-80	5	1.00	1.00	0.66	0.67	2.50	2.67	0.29	0.27
6	2	0.83	4	-20	3	1.00	1.00	0.73	0.82	2.45	2.50	0.24	0.18
7	2	0.94	6	-90	5	1.00	1.00	0.86	0.87	2.34	2.38	0.13	0.11
8	2	0.95	1	-20	5	1.00	1.00	0.86	0.91	2.48	2.31	0.12	0.08
9	2	0.96	4	-90	3	1.00	1.00	0.87	0.90	2.36	2.34	0.14	0.08
10	3	0.10	70	-8	4	0.75	0.77	0.42	0.48	1.22	1.11	0.29	0.25
11	3	0.90	9	-80	4	0.75	0.77	0.80	0.73	-0.33	0.29	0.18	0.25
12	3	0.91	7	-70	6	0.75	0.77	0.76	0.83	0.10	-0.41	0.19	0.12
13	4	0.06	60	-4	2	0.50	0.50	0.42	0.41	0.52	0.84	0.22	0.15
14	4	0.20	40	-10	4	0.50	0.50	0.48	0.46	-0.34	0.04	0.31	0.31
15	4	0.31	20	-9	4	0.50	0.50	0.49	0.44	-0.07	0.30	0.34	0.38
16	4	0.60	4	-6	2	0.50	0.50	0.56	0.58	-0.27	-0.26	0.22	0.26
17	4	0.60	40	-60	3	0.50	0.50	0.58	0.55	-0.96	-0.20	0.28	0.25
18	4	0.73	3	-8	2	0.50	0.50	0.57	0.55	-0.29	0.09	0.24	0.20
19	4	0.80	20	-80	2	0.50	0.50	0.64	0.63	-1.30	-1.21	0.28	0.27
20	4	0.90	1	-9	6	0.50	0.50	0.53	0.48	0.12	0.63	0.21	0.16
21	4	0.96	3	-70	3	0.50	0.50	0.65	0.62	-0.84	-0.38	0.23	0.18
22	5	0.02	80	-2	3	0.25	0.33	0.36	0.31	0.24	0.64	0.17	0.17
23	5	0.07	90	-7	3	0.25	0.33	0.39	0.24	-0.81	0.34	0.19	0.13
24	5	0.53	80	-90	5	0.25	0.33	0.65	0.58	-3.41	-2.44	0.27	0.36
25	5	0.80	1	-4	2	0.25	0.33	0.45	0.42	-0.31	0.11	0.20	0.18
26	5	0.88	4	-30	3	0.25	0.33	0.52	0.49	-0.95	-0.57	0.22	0.21
27	5	0.93	5	-70	4	0.25	0.33	0.57	0.57	-1.63	-1.43	0.27	0.20
28	6	0.10	90	-10	5	0.25	0.22	0.26	0.27	-0.13	0.07	0.22	0.19
29	6	0.19	30	-7	3	0.25	0.22	0.39	0.32	-1.35	-0.45	0.27	0.26
30	6	0.29	50	-20	3	0.25	0.22	0.47	0.48	-2.74	-2.43	0.38	0.36
31	6	0.46	7	-6	6	0.25	0.22	0.38	0.34	-0.90	-0.38	0.23	0.24
32	6	0.57	6	-8	4	0.25	0.22	0.44	0.39	-1.56	-0.59	0.26	0.27
33	6	0.82	20	-90	3	0.25	0.22	0.63	0.55	-5.33	-3.14	0.26	0.21
34	6	0.88	8	-60	4	0.25	0.22	0.57	0.50	-3.30	-1.96	0.16	0.19
35	7	0.06	90	-6	4	0.25	0.14	0.31	0.35	-1.40	-1.43	0.29	0.21
36	7	0.21	30	-8	3	0.25	0.14	0.39	0.31	-2.20	-1.04	0.30	0.23
37	7	0.50	80	-80	5	0.25	0.14	0.51	0.55	-4.18	-4.78	0.34	0.32
38	7	0.69	9	-20	5	0.25	0.14	0.46	0.34	-2.62	-0.88	0.25	0.23
39	7	0.81	7	-30	2	0.25	0.14	0.41	0.34	-2.25	-0.93	0.22	0.21
40	7	0.91	1	-10	2	0.25	0.14	0.34	0.27	-0.71	-0.30	0.19	0.17
Means						0.51	0.51	0.56	0.54	-0.39	0.04	0.23	0.21
Estimated error variance								.0016	.0015	.1370	.1188	.0012	.0015

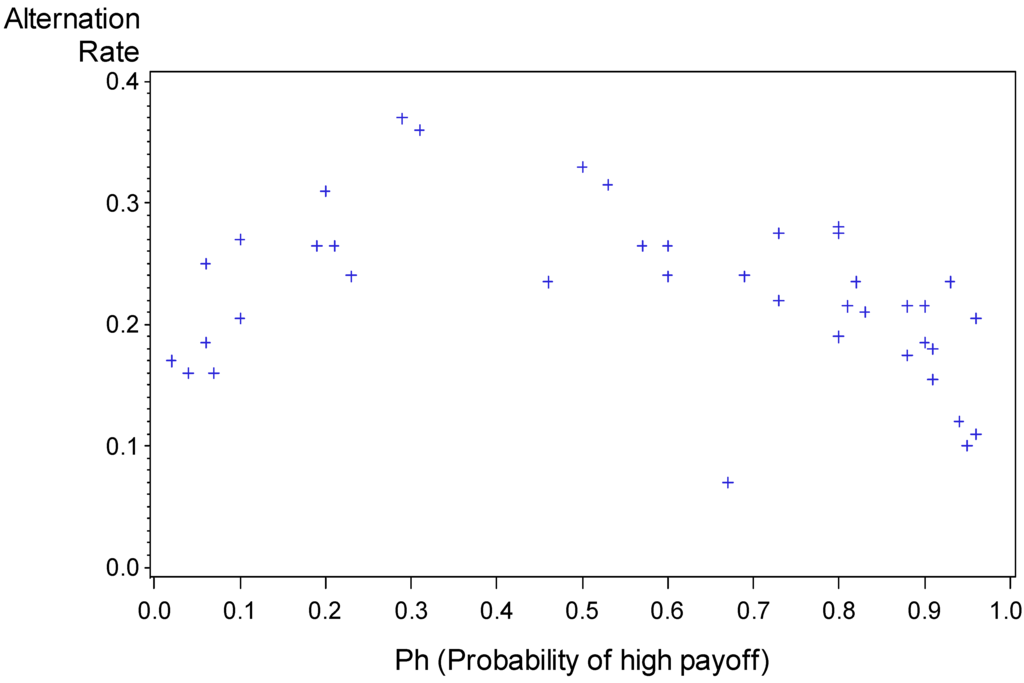
Figure 1. Proportion of alternation as a function of Ph. Each data point summarizes the results of one game. The outlier (alternation rate of 0.07 when Ph = 0.67) is Problem 3: The problem with the lowest payoff variance, and the only problem in which entry cannot lead to losses.

Table 3. Summary of correlation analyses that examine the possibility of consistent individual differences. The summary scores are based on 180 correlation analyses (180 pairs of games) for each of the four variables.

**Table 3.** **Summary of correlation analyses that examine the possibility of consistent individual differences.** The summary scores are based on 180 correlation analyses (180 pairs of games) for each of the four variables.
Variable	Mean correlation	Proportion of positive correlations
Entry rate	0.249	0.844
Maximization	0.058	0.611
Alternation	0.415	0.983
Recency	0.281	0.888

Table 4. The baseline models, the estimated parameters, and the implied normalized MSD scores by statistic and block.

**Table 4.** **The baseline models, the estimated parameters, and the implied normalized MSD scores by statistic and block**.
Model	Fitted parameters	Normalized Mean Squared Deviation Scores by statistic and block
		Entry rates		Efficiency		Alteration		Mean
	Block:	1	2	1	2	1	2
Pure		26.52	21.56	39.41	28.01	49.50	35.26	33.38
Symmetric		29.57	25.11	21.13	13.24	30.59	25.95	24.26
RL	λ = 4, w = 0.01	8.57	16.37	5.19	8.84	19.14	12.22	11.72
NRL	λ = 12, w = 0.025	6.36	14.03	3.59	7.35	4.58	1.53	6.24
SFP	λ = 1.5, w = 0.1	5.91	5.36	9.37	14.99	6.53	3.79	7.66
NFP	λ = 4, w = 0.15	4.75	4.16	3.60	6.13	2.70	3.80	4.19
EWA	λ = 0.7, φ = 0.8, δ = 0.5, ρ = 0.4	10.06	8.91	4.69	9.22	4.38	2.49	6.62
SAW	ε_i ~ U[0,0.02], w_i ~ U[0,1], ρ_i ~ U[0,0.02], and µ_i = {1, 2, or 3}.	3.93	2.49	1.87	2.04	4.18	5.37	3.31
I-SAW	ε_i ~ U[0,0.24], w_i ~ U[0,0.8], ρ_i ~ U[0,0.2], π_i ~ U[0,0.6], and µ_i = {1, 2, or 3}.	1.56	1.19	1.37	1.47	1.43	1.30	1.38

Table 5. The predictions of the best baseline models (I-SAW): The lowest row presents the correlation with the experimental results by statistic.

**Table 5.** **The predictions of the best baseline models (I-SAW):** The lowest row presents the correlation with the experimental results by statistic.
The games						Entry rates		Efficiency		Alternations
#	K	Ph	h	l	Sf	B1	B2	B1	B2	B1	B2
1	2	0.04	70	-3	5	0.78	0.81	2.60	2.56	0.17	0.13
2	2	0.23	30	-9	4	0.58	0.62	2.39	2.62	0.24	0.22
3	2	0.67	1	-2	3	0.90	0.91	2.33	2.32	0.10	0.08
4	2	0.73	30	-80	4	0.64	0.64	2.47	2.59	0.26	0.25
5	2	0.80	20	-80	5	0.67	0.67	2.47	2.61	0.24	0.23
6	2	0.83	4	-20	3	0.77	0.78	2.49	2.57	0.20	0.18
7	2	0.94	6	-90	5	0.82	0.82	2.39	2.49	0.15	0.14
8	2	0.95	1	-20	5	0.84	0.85	2.42	2.47	0.13	0.11
9	2	0.96	4	-90	3	0.84	0.86	2.35	2.43	0.13	0.11
10	3	0.10	70	-8	4	0.42	0.45	0.97	1.23	0.23	0.21
11	3	0.90	9	-80	4	0.74	0.75	-0.06	0.11	0.19	0.18
12	3	0.91	7	-70	6	0.76	0.76	-0.15	0.05	0.18	0.17
13	4	0.06	60	-4	2	0.41	0.43	0.22	0.34	0.24	0.22
14	4	0.20	40	-10	4	0.43	0.44	-0.04	0.25	0.27	0.25
15	4	0.31	20	-9	4	0.48	0.49	-0.22	0.01	0.29	0.28
16	4	0.60	4	-6	2	0.52	0.52	-0.20	-0.05	0.30	0.28
17	4	0.60	40	-60	3	0.55	0.55	-0.78	-0.47	0.29	0.28
18	4	0.73	3	-8	2	0.53	0.52	-0.20	-0.08	0.29	0.27
19	4	0.80	20	-80	2	0.65	0.64	-1.65	-1.23	0.24	0.24
20	4	0.90	1	-9	6	0.52	0.52	0.07	0.06	0.25	0.23
21	4	0.96	3	-70	3	0.61	0.59	-0.80	-0.51	0.21	0.19
22	5	0.02	80	-2	3	0.35	0.35	-0.08	0.06	0.23	0.20
23	5	0.07	90	-7	3	0.31	0.32	-0.42	-0.05	0.21	0.19
24	5	0.53	80	-90	5	0.52	0.52	-2.03	-1.59	0.29	0.28
25	5	0.80	1	-4	2	0.40	0.40	-0.24	-0.10	0.25	0.23
26	5	0.88	4	-30	3	0.47	0.46	-0.89	-0.73	0.25	0.22
27	5	0.93	5	-70	4	0.51	0.50	-1.43	-1.08	0.24	0.21
28	6	0.10	90	-10	5	0.31	0.31	-1.08	-0.63	0.22	0.20
29	6	0.19	30	-7	3	0.36	0.36	-1.28	-0.90	0.26	0.24
30	6	0.29	50	-20	3	0.42	0.42	-2.05	-1.62	0.29	0.27
31	6	0.46	7	-6	6	0.35	0.35	-0.86	-0.67	0.27	0.24
32	6	0.57	6	-8	4	0.36	0.35	-0.94	-0.70	0.27	0.25
33	6	0.82	20	-90	3	0.60	0.57	-4.69	-3.73	0.25	0.24
34	6	0.88	8	-60	4	0.47	0.46	-2.20	-1.83	0.25	0.22
35	7	0.06	90	-6	4	0.26	0.26	-1.19	-0.68	0.20	0.18
36	7	0.21	30	-8	3	0.34	0.33	-1.77	-1.32	0.26	0.24
37	7	0.50	80	-80	5	0.49	0.48	-4.31	-3.61	0.29	0.28
38	7	0.69	9	-20	5	0.37	0.36	-1.84	-1.52	0.26	0.24
39	7	0.81	7	-30	2	0.37	0.36	-1.81	-1.50	0.26	0.23
40	7	0.91	1	-10	2	0.29	0.28	-0.76	-0.58	0.22	0.19
Means						0.525	0.526	-0.270	-0.011	0.234	0.215
Correlation with the experimental results						0.973	0.979	0.982	0.970	0.750	0.834

References and Notes

Erev, I.; Ert, E.; Roth, A.E. A choice prediction competition for market entry games: An introduction. Games 2010, 1, 117–136. [Google Scholar]

© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).

Erev, I. et al. A Choice Prediction Competition for Market Entry Games: An Introduction. Games 2010, 1, 117-136

References and Notes

Article Metrics

Citations

Article Access Statistics