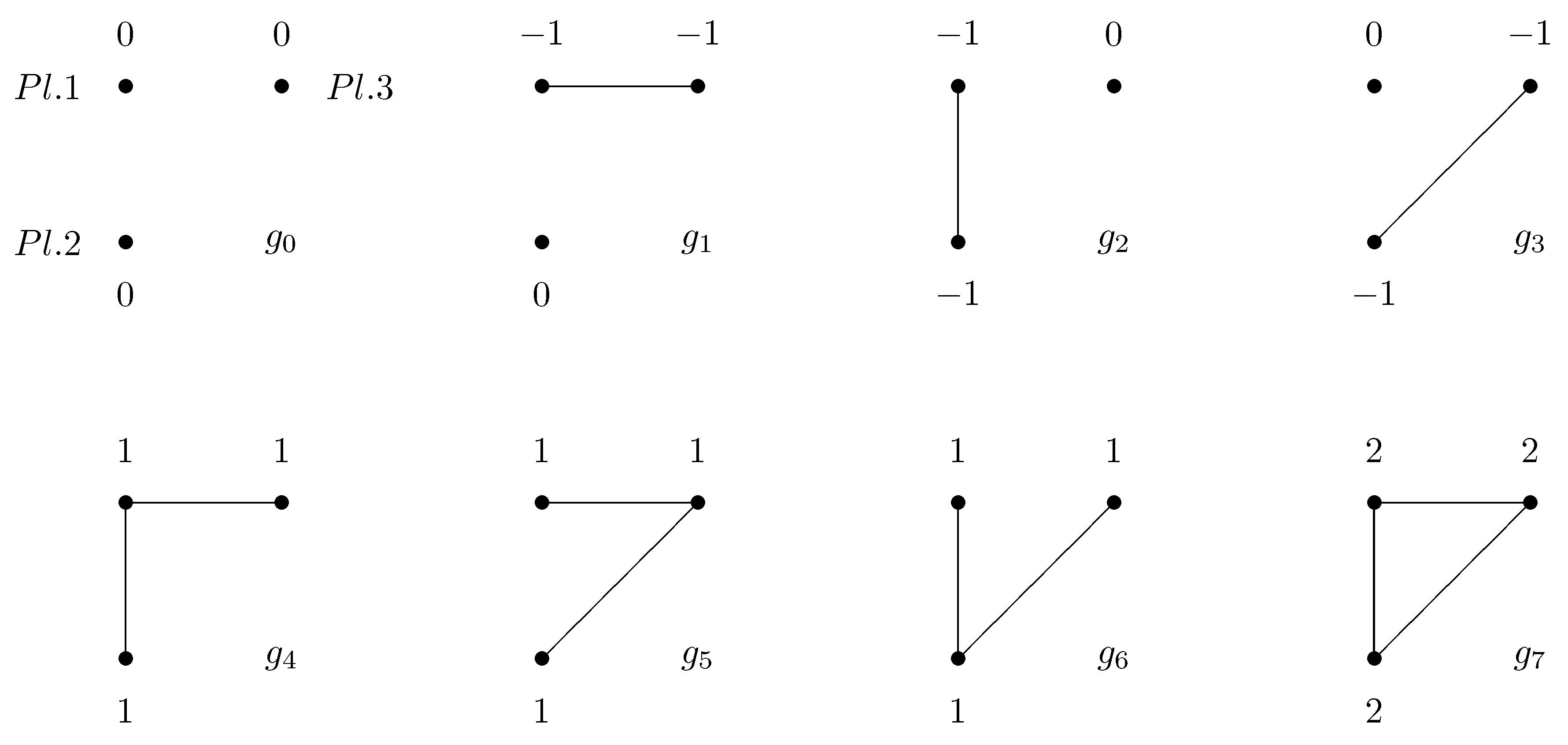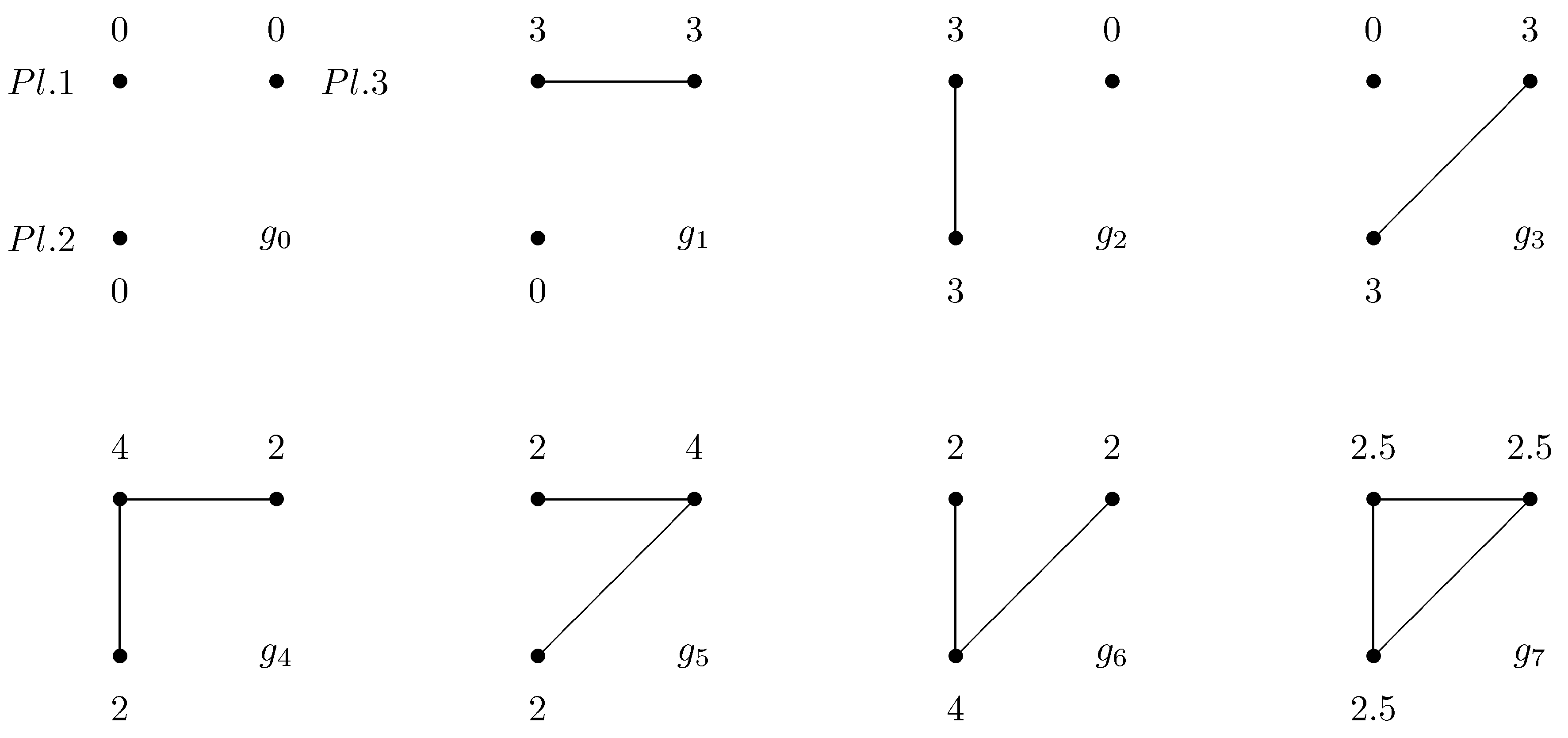A Characterization of Farsightedly Stable Networks

Abstract

We study the stability of social and economic networks when players are farsighted. We first provide an algorithm that characterizes the unique pairwise and groupwise farsightedly stable set of networks under the componentwise egalitarian allocation rule. We then show that this set coincides with the unique groupwise myopically stable set of networks but not with the unique pairwise myopically stable set of networks. We conclude that, if groupwise deviations are allowed then whether players are farsighted or myopic does not matter; if players are farsighted then whether players are allowed to deviate in pairs only or in groups does not matter.

1. Introduction

The organization of agents into networks and groups or coalitions plays an important role in the determination of the outcome of many social and economic interactions.1 A simple way to analyze the networks that one might expect to emerge in the long run is to examine the requirement that players do not benefit from altering the structure of the network. An example of such a condition is the pairwise stability notion defined by Jackson and Wolinsky [5]. A network is pairwise stable if no player benefits from severing one of her links and no two players benefit from adding a link between them. Pairwise stability is a myopic definition. Players are not farsighted in the sense that they do not forecast how others might react to their actions. For instance, the adding or severing of one link might lead to subsequent addition or severing of another link. If players have very good information about how others might react to changes in the network, then these are things one wants to allow for in the definition of the stability concept. For instance, a network could be stable because players might not add a link that appears valuable to them given the current network, as that might in turn lead to the formation of other links and ultimately lower the payoffs of the original players.

In this paper we address the question of which networks one might expect to emerge in the long run when players are either farsighted or myopic. Herings, Mauleon and Vannetelbosch [6] have first extended the Jackson and Wolinsky pairwise stability notion to a new set-valued solution concept, called the pairwise myopically stable set. A set of networks G is pairwise myopically stable (i) if all possible myopic pairwise deviations from any network $g\in G$ to a network outside the set are deterred by the threat of ending worse off or equally well off, (ii) if there exists a myopic improving path from any network outside the set leading to some network in the set, and (iii) if there is no proper subset of G satisfying Conditions (i) and (ii). The pairwise myopically stable set is non-empty, unique and contains all pairwise stable networks. They have then introduced the pairwise farsightedly stable set, to predict which networks may be formed among farsighted players.2 The definition corresponds to the one of a pairwise myopically stable set with myopic deviations and myopic improving paths replaced by farsighted deviations and farsighted improving paths. A farsighted improving path is a sequence of networks that can emerge when players form or sever links based on the improvement the end network offers relative to the current network. Each network in the sequence differs by one link from the previous one. If a link is added, then the two players involved must both prefer the end network to the current network. If a link is deleted, then it must be that at least one of the two players involved in the link prefers the end network. Similarly, it is straightforward to define the notions of groupwise myopically stable sets and of groupwise farsightedly stable sets for situations in which players can deviate in group. Herings, Mauleon and Vannetelbosch [6] have shown that a non-empty pairwise (groupwise) farsightedly stable set always exists. In addition, they have provided necessary and sufficient conditions for a set to be a unique pairwise (groupwise) farsightedly stable set of networks.

We first provide an algorithm that characterizes the unique pairwise and groupwise farsightedly stable set of networks under the componentwise egalitarian allocation rule. We then show that this set coincides with the unique groupwise myopically stable set of networks but not with the unique pairwise myopically stable set of networks. We conclude that, if groupwise deviations are allowed then whether players are farsighted or myopic does not matter; if players are farsighted then whether players are allowed to deviate in pairs only or in groups does not matter. In addition, we show that alternative notions of farsighted stability also single out the same set as the unique farsighted stable set.

The paper is organized as follows. In Section 2 we introduce some notations and basic properties. In Section 3 we define the notions of myopically stable sets and of farsightedly stable sets. In Section 4 we characterize the unique farsightedly stable set of networks under the componentwise egalitarian allocation rule. In Section 5 we consider other concepts of farsighted stability. In Section 6 we conclude.

2. Networks

Let $N=\{1,\dots ,n\}$ be the finite set of players who are connected in some network relationship. The network relationships are reciprocal and the network is thus modeled as a non-directed graph. Individuals are the nodes in the graph and links indicate bilateral relationships between individuals. Thus, a network g is simply a list of which pairs of individuals are linked to each other. We write $ij\in g$ to indicate that i and j are linked under the network g. Let $g^S$ be the set of all subsets of $S\subseteq N$ of size 2.3 So, $g^N$ is the complete network. The set of all possible networks or graphs on N is denoted by $\mathbb{G}$ and consists of all subsets of $g^N.$ The network obtained by adding link $ij$ to an existing network g is denoted $g+ij$ and the network that results from deleting link $ij$ from an existing network g is denoted $g-ij$. Let

$${g|}_S=\{ij\mid ij\in g\text{and}i\in S,j\in S\}$$

Thus, ${g|}_S$ is the network found deleting all links except those that are between players in S. For any network g, let $N\left(g\right)=\{i\mid \exists j$ such that $ij\in g\}$ be the set of players who have at least one link in the network g. A path in a network $g\in \mathbb{G}$ between i and j is a sequence of players $i_1,\dots ,i_K$ such that $i_k{i}_{k+1}\in g$ for each $k\in \{1,\dots ,K-1\}$ with $i_1=i$ and $i_K=j$. A network g is connected if for each pair of agents i and j such that $i\ne j$ there exists a path in g between i and j. A non-empty network $h\subseteq g$ is a component of g, if for all $i\in N\left(h\right)$ and $j\in N\left(h\right)\setminus \left\{i\right\},$ there exists a path in h connecting i and j, and for any $i\in N\left(h\right)$ and $j\in N\left(g\right)$, $ij\in g$ implies $ij\in h$. The set of components of g is denoted by $C\left(g\right)$. Knowing the components of a network, we can partition the players into groups within which players are connected. Let $\Pi \left(g\right)$ denote the partition of N induced by the network g.

A value function is a function $v:\mathbb{G}\to \mathbb{R}$ that keeps track of how the total societal value varies across different networks. The set of all possible value functions is denoted by $\mathcal{V}$. An allocation rule is a function $Y:\mathbb{G}\times \mathcal{V}\to {\mathbb{R}}^N$ that keeps track of how the value is allocated among the players forming a network. It satisfies ${\sum }_{i\in N}{Y}_i(g,v)=v\left(g\right)$ for all v and g.

Jackson and Wolinsky [5] have proposed a number of basic properties of value functions and allocation rules. A value function is component additive if $v\left(g\right)={\sum }_{h\in C\left(g\right)}v\left(h\right)$ for all $g\in \mathbb{G}$. Component additive value functions are the ones for which the value of a network is the sum of the value of its components. For a component additive v and network g, the componentwise egalitarian allocation rule $Y^{ce}$ is such that for any $h\in C\left(g\right)$ and each $i\in N\left(h\right)$, $Y_i^{ce}(g,v)=v\left(h\right)/\#N\left(h\right)$. For a v that is not component additive, $Y^{ce}(g,v)=v\left(g\right)/n$ for all g; thus, $Y^{ce}$ splits the value $v\left(g\right)$ equally among all players if v is not component additive.

Which networks are likely to emerge in the long run? The game-theoretic approach to network formation uses two different notions of a deviation by a coalition. Pairwise deviations (Jackson and Wolinsky [5]) are deviations involving a single link at a time. That is, link addition is bilateral (two players that would be involved in the link must agree to adding the link), link deletion is unilateral (at least one player involved in the link must agree to deleting the link), and network changes take place one link at a time. Groupwise deviations (Jackson and van den Nouweland [14]) are deviations involving several links within some group of players at a time. Link addition is bilateral, link deletion is unilateral, and multiple link changes can take place at a time. Whether a pairwise deviation or a groupwise deviation makes more sense will depend on the setting within which network formation takes place. The definitions of stability we consider allow for a deviation by a coalition to be valid only if all members of the coalition are strictly better off, and in doing so we deviate from the original definitions by Herings, Mauleon and Vannetelbosch [6] where it is sufficient that at least one coalition member is strictly better off while all other members are at least as well off.

3. Definitions of Stable Sets of Networks

3.1. Myopic Definitions

We first introduce the notion of pairwise myopically stable sets of networks due to Herings, Mauleon and Vannetelbosch [6] which is a generalization of Jackson and Wolinsky [5] pairwise stability notion.4 Pairwise stable networks do not always exist. A pairwise myopically stable set of networks is a set such that from any network outside this set, there is a myopic improving path leading to some network in the set, and each deviation outside the set is deterred because the deviating players do not prefer the resulting network. The notion of a myopic improving path was first introduced in Jackson and Watts [15]. A myopic improving path is a sequence of networks that can emerge when players form or sever links based on the improvement the resulting network offers relative to the current network. Each network in the sequence differs by one link from the previous one. If a link is added, then the two players involved must both prefer the resulting network to the current network. If a link is deleted, then it must be that at least one of the two players involved in the link prefers the resulting network.

Formally, a pairwise myopic improving path from a network g to a network $g^{\prime }\ne g$ is a finite sequence of networks $g_1,\dots ,g_K$ with $g_1=g$ and $g_K=g^{\prime }$ such that for any $k\in \{1,\dots ,K-1\}$ either: (i) $g_{k+1}=g_k-ij$ for some $ij$ such that $Y_i(g_{k+1},v)>Y_i(g_k,v)$ or $Y_j(g_{k+1},v)>Y_j(g_k,v)$, or (ii) $g_{k+1}=g_k+ij$ for some $ij$ such that $Y_i(g_{k+1},v)>Y_i(g_k,v)$ and $Y_j(g_{k+1},v)>Y_j(g_k,v)$. For a given network g, let $m\left(g\right)$ be the set of networks that can be reached by a pairwise myopic improving path from g.

Definition 1.

A set of networks $G\subseteq \mathbb{G}$ is pairwise myopically stable with respect v and Y if

$\left(\mathbf{i}\right)$

∀$g\in G$,

$\left(\mathbf{ia}\right)$

∀$ij\notin g$ such that $g+ij\notin G$, $Y_i(g+ij,v)\le Y_i(g,v)$ or $Y_j(g+ij,v)\le Y_j(g,v)$,

$\left(\mathbf{ib}\right)$

∀$ij\in g$ such that $g-ij\notin G$, $Y_i(g-ij,v)\le Y_i(g,v)$ and $Y_j(g-ij,v)\le Y_j(g,v)$,

$\left(\mathbf{ii}\right)$

$\forall g^{\prime }\in \mathbb{G}\setminus G,$$m\left(g^{\prime }\right)\cap G\ne \varnothing ,$

$\left(\mathbf{iii}\right)$

∄$G^{\prime }⊊G$ such that $G^{\prime }$ satisfies Conditions (ia), (ib), and (ii).

Conditions (ia) and (ib) in Definition 1 capture deterrence of external deviations. In Condition (ia) the addition of a link $ij$ to a network $g\in G$ that leads to a network outside G is deterred because the two players involved do not prefer the resulting network to network g. Condition (ib) is a similar requirement, but then for the case where a link is severed. Condition (ii) requires external stability. External stability asks for the existence of a pairwise myopic improving path from any network outside G leading to some network in G. Condition (ii) implies that if a set of networks is pairwise myopically stable, it is non-empty. Condition (iii) is the minimality condition.

Jackson and Watts [15] have defined the notion of a closed cycle. A set of networks C is a cycle if for any $g\in C$ and $g^{\prime }\in C\setminus \left\{g\right\},$ there exists a pairwise myopic improving path connecting g to $g^{\prime }.$ A cycle C is a maximal cycle if it is not a proper subset of a cycle. A cycle C is a closed cycle if no network in C lies on a pairwise myopic improving path leading to a network that is not in C. A closed cycle is necessarily a maximal cycle. Herings, Mauleon and Vannetelbosch [6] have shown that the set of networks consisting of all networks that belong to a closed cycle is the unique pairwise myopically stable set.

The notion of pairwise myopically stable set only considers deviations by at most a pair of players at a time. It might be that some group of players could all be made better off by some complicated reorganization of their links, which is not accounted for under pairwise myopic stability. A network $g^{\prime }\in G$ is obtainable from $g\in G$ via deviations by group $S\subseteq N$ if (i) $ij\in g^{\prime }$ and $ij\notin g$ implies $\{i,j\}\subseteq S$, and (ii) $ij\in g$ and $ij\notin g^{\prime }$ implies $\{i,j\}\cap S\ne ⌀$.

A groupwise myopic improving path from a network g to a network $g^{\prime }\ne g$ is a finite sequence of networks $g_1,\dots ,g_K$ with $g_1=g$ and $g_K=g^{\prime }$ such that for any $k\in \{1,\dots ,K-1\}$ : $g_{k+1}$ is obtainable from $g_k$ via deviations by $S_k\subseteq N$ and $Y_i(g_{k+1},v)>Y_i(g_k,v)$ for all $i\in S_k$. For a given network g, let $M\left(g\right)$ be the set of networks that can be reached by a groupwise myopic improving path from g.

Definition 2.

A set of networks $G\subseteq \mathbb{G}$ is groupwise myopically stable with respect v and Y if

$\left(\mathbf{i}\right)$

∀$g\in G$, $S\subseteq N$, $g^{\prime }\notin G$ that is obtainable from g via deviations by S, there exists $i\in S$ such that $Y_i(g^{\prime },v)\le Y_i(g,v)$,

$\left(\mathbf{ii}\right)$

$\forall g^{\prime }\in \mathbb{G}\setminus G,$ $M\left(g^{\prime }\right)\cap G\ne \varnothing ,$

$\left(\mathbf{iii}\right)$

∄$G^{\prime }⊊G$ such that $G^{\prime }$ satisfies Conditions (ia), (ib), and (ii).

Replacing the notion of pairwise improving path by the notion of groupwise improving path in the definition of a closed cycle, we have that the set of networks consisting of all networks that belong to a closed cycle is the unique groupwise myopically stable set. The notion of groupwise myopically stable set is a generalization of Dutta and Mutuswami [16] strong stability notion.5 In Figure 1 we have depicted an example where the unique pairwise myopically stable set is $\{g_0,g_7\}$ while the unique groupwise myopically stable set is $\left\{g_7\right\}$. The networks $g_0$ and $g_7$ are pairwise stable but only $g_7$ is strongly stable, and there are no closed cycles of networks consisting of more than one network when players can modify their links either in pairs or in groups. There is no network such that there is a pairwise myopic improving path from any other network leading to it: $m\left(g_0\right)=\varnothing$, $m\left(g_1\right)=\{g_0,g_4,g_5,g_7\}$, $m\left(g_2\right)=\{g_0,g_4,g_6,g_7\}$, $m\left(g_3\right)=\{g_0,g_5,g_6,g_7\}$, $m\left(g_4\right)=\left\{g_7\right\}$, $m\left(g_5\right)=\left\{g_7\right\}$, $m\left(g_6\right)=\left\{g_7\right\}$, and $m\left(g_7\right)=\varnothing$. Hence, a set formed by the empty network $g_0$ and the complete network $g_7$ is a pairwise myopically stable set. However, the groupwise myopically stable set consists only of the complete network since $g_7\in M\left(g\right)$ $\forall g\ne g_7$ and $M\left(g_7\right)=⌀$. Indeed, we have $M\left(g_0\right)=\{g_4,g_5,g_6,g_7\}$, $M\left(g_1\right)=\{g_0,g_4,g_5,g_6,g_7\}$, $M\left(g_2\right)=\{g_0,g_4,g_5,g_6,g_7\}$, $M\left(g_3\right)=\{g_0,g_4,g_5,g_6,g_7\}$, $M\left(g_4\right)=\left\{g_7\right\}$, $M\left(g_5\right)=\left\{g_7\right\}$, $M\left(g_6\right)=\left\{g_7\right\}$, and $M\left(g_7\right)=\varnothing$.

Figure 1. An example with three players.

Figure 1. An example with three players.

In Figure 2 we have depicted Jackson and Wolinsky co-author model with three players. It is easy to verify that the complete network $g_7$ is the unique pairwise stable network and that the pairwise myopically stable set is $\left\{g_7\right\}$. However, there is no strongly stable network. The groupwise myopically stable set is $\{g_1,g_2,g_3,g_4,g_5,g_6,g_7\}$ and consists only of networks that belong to a cycle. Indeed, we have $M\left(g_0\right)=\{g_1,g_2,g_3,g_4,g_5,g_6,g_7\}$, $M\left(g_1\right)=\{g_1,g_2,g_3,g_4,g_5,g_6,g_7\}$, $M\left(g_2\right)=\{g_1,g_2,g_3,g_4,g_5,g_6,g_7\}$, $M\left(g_3\right)=\{g_1,g_2,g_3,g_4,g_5,g_6,g_7\}$, $M\left(g_4\right)=\{g_1,g_2,$ $g_3,g_4,g_5$, $g_6,g_7\}$, $M\left(g_5\right)$ $=\{g_1,g_2,g_3,g_4,g_5,g_6,g_7\}$, $M\left(g_6\right)=\{g_1,g_2,g_3,g_4,g_5,g_6,g_7\}$, and $M\left(g_7\right)=\{g_1,g_2,g_3,g_4,g_5,g_6,g_7\}$.

Figure 2. The co-author model with three players.

Figure 2. The co-author model with three players.

3.2. Farsighted Definitions

A pairwise farsighted improving path is a sequence of networks that can emerge when players form or sever links based on the improvement the end network offers relative to the current network. Each network in the sequence differs by one link from the previous one. If a link is added, then the two players involved must both strictly prefer the end network to the current network. If a link is deleted, then it must be that at least one of the two players involved in the link prefers the end network. Formally, a pairwise farsighted improving path from a network g to a network $g^{\prime }\ne g$ is a finite sequence of networks $g_1,\dots ,g_K$ with $g_1=g$ and $g_K=g^{\prime }$ such that for any $k\in \{1,\dots ,K-1\}$ either: (i) $g_{k+1}=g_k-ij$ for some $ij$ such that $Y_i(g_K,v)>Y_i(g_k,v)$ or $Y_j(g_K,v)>Y_j(g_k,v)$, or (ii) $g_{k+1}=g_k+ij$ for some $ij$ such that $Y_i(g_K,v)>Y_i(g_k,v)$ and $Y_j(g_K,v)>Y_j(g_k,v)$. For a given network g, let $f\left(g\right)$ be the set of networks that can be reached by a pairwise farsighted improving path from g.

We now give the definition of a pairwise farsightedly stable set due to Herings, Mauleon and Vannetelbosch [6].6

Definition 3.

A set of networks $G\subseteq \mathbb{G}$ is a pairwise farsightedly stable set with respect v and Y if

$\left(\mathbf{i}\right)$

∀$g\in G$,

$\left(\mathbf{ia}\right)$

∀$ij\notin g$ such that $g+ij\notin G$, $\exists g^{\prime }\in f(g+ij)\cap G$ such that $Y_i(g^{\prime },v)\le Y_i(g,v)$ or $Y_j(g^{\prime },v)\le Y_j(g,v)$,

$\left(\mathbf{ib}\right)$

∀$ij\in g$ such that $g-ij\notin G$, $\exists g^{\prime },g^{\prime \prime }\in f(g-ij)\cap G$ such that $Y_i(g^{\prime },v)\le Y_i(g,v)$ and $Y_j(g^{\prime \prime },v)\le Y_j(g,v)$,

$\left(\mathbf{ii}\right)$

$\forall g^{\prime }\in \mathbb{G}\setminus G,$$f\left(g^{\prime }\right)\cap G\ne \varnothing .$

$\left(\mathbf{iii}\right)$

∄$G^{\prime }⊊G$ such that $G^{\prime }$ satisfies Conditions (ia), (ib), and (ii).

Condition (i) in Definition 3 requires the deterrence of external deviations. Condition (ia) captures that adding a link $ij$ to a network $g\in G$ that leads to a network outside of $G,$ is deterred by the threat of ending in $g^{\prime }.$ Here $g^{\prime }$ is such that there is a pairwise farsighted improving path from $g+ij$ to $g^{\prime }.$ Moreover, $g^{\prime }$ belongs to $G,$ which makes $g^{\prime }$ a credible threat. Condition (ib) is a similar requirement, but then for the case where a link is severed. Condition (ii) in Definition 3 requires external stability and implies that the networks within the set are robust to perturbations. From any network outside of G there is a farsighted improving path leading to some network in G. Condition (ii) implies that if a set of networks is pairwise farsightedly stable, it is non-empty. Condition (iii) is the minimality condition. Herings, Mauleon and Vannetelbosch [6] have shown that a pairwise farsightedly stable set of networks always exists.

Figure 3. Another example with three players.

Figure 3. Another example with three players.

In Figure 3 we have depicted another example with three players. We have that $f\left(g_0\right)=\{g_1,g_2,g_3,g_4$, $g_5,g_6,g_7\}$, $f\left(g_1\right)=\{g_2,g_4,g_5,g_6,g_7\}$, $f\left(g_2\right)=\{g_3,g_4,g_5,g_6,g_7\}$, $f\left(g_3\right)=\{g_1,g_4,g_5,g_6,g_7\}$, $f\left(g_4\right)=\{g_5,g_{6,}{g}_7\}$, $f\left(g_5\right)=\{g_4,g_6,g_7\}$, $f\left(g_6\right)=\{g_4,g_5,g_7\}$, and $f\left(g_7\right)=\{g_4,g_5,g_6\}$. Theorem 4 in Herings, Mauleon and Vannetelbosch [6] states that a set $\left\{g\right\}$ is a pairwise farsightedly stable set if and only if for every $g^{\prime }\in \mathbb{G}\setminus \left\{g\right\}$ we have $g\in f\left(g^{\prime }\right)$. It follows that $\left\{g_4\right\}$, $\left\{g_5\right\}$, $\left\{g_6\right\}$ and $\left\{g_7\right\}$ are pairwise farsightedly stable sets. The network $g_4$ is not pairwise stable but it is farsightedly stable because the profitable deviation to $g_7$ is deterred by the threat of ending back to $g_4$. Indeed, $g_4\in f\left(g_7\right)$. For instance, $(g_7,g_6,g_3,g_0,g_1,g_4)$ is a farsighted improving path starting in $g_7$ and ending in $g_4$.

A groupwise farsighted improving path from a network g to a network $g^{\prime }\ne g$ is a finite sequence of networks $g_1,\dots ,g_K$ with $g_1=g$ and $g_K=g^{\prime }$ such that for any $k\in \{1,\dots ,K-1\}$ : $g_{k+1}$ is obtainable from $g_k$ via deviations by $S_k\subseteq N$ and $Y_i(g_K,v)>Y_i(g_k,v)$ for all $i\in S_k$. For a given network g, let $F\left(g\right)$ be the set of networks that can be reached by a groupwise farsighted improving path from g.

Definition 4.

A set of networks $G\subseteq \mathbb{G}$ is groupwise farsightedly stable with respect v and Y if

$\left(\mathbf{i}\right)$

∀$g\in G$, $S\subseteq N$, $g^{\prime }\notin G$ that is obtainable from g via deviations by S, there exists $g^{″}\in F\left(g^{\prime }\right)\cap G$ such that $Y_i(g^{″},v)\le Y_i(g,v)$ for some $i\in S$,

$\left(\mathbf{ii}\right)$

$\forall g^{\prime }\in \mathbb{G}\setminus G,$$F\left(g^{\prime }\right)\cap G\ne \varnothing ,$

$\left(\mathbf{iii}\right)$

∄$G^{\prime }⊊G$ such that $G^{\prime }$ satisfies Conditions (ia), (ib), and (ii).

Let us reconsider the co-author model with three players depicted in Figure 2. No singleton set is pairwise farsightedly stable. Indeed, there is no network such that there is a farsighted improving path from any other network leading to it. More precisely, $f\left(g_0\right)=\{g_1,g_2,g_3,g_4,g_5,g_6\}$, $f\left(g_1\right)=\{g_4,g_5\}$, $f\left(g_2\right)=\{g_4,g_6\}$, $f\left(g_3\right)=\{g_5,g_6\}$, $f\left(g_4\right)=\left\{g_7\right\}$, $f\left(g_5\right)=\left\{g_7\right\}$, $f\left(g_6\right)=\left\{g_7\right\}$, and $f\left(g_7\right)=\varnothing$. Theorem 3 in Herings, Mauleon and Vannetelbosch [6] states that if for every $g^{\prime }\in \mathbb{G}\setminus G$ we have $f\left(g^{\prime }\right)\cap G\ne ⌀$ and for every $g\in G$, $f\left(g\right)\cap G=⌀$, then G is a pairwise farsightedly stable set. Hence, $\{g_1,g_2,g_3,g_7\}$ is a pairwise farsightedly stable set. However, a set formed by the complete and two star networks is also a pairwise farsightedly stable set of networks. Indeed, $\{g_4,g_5,g_7\}$, $\{g_4,g_6,g_7\}$, and $\{g_5,g_6,g_7\}$ are pairwise farsightedly stable sets in the co-author model with three players. Suppose that we allow now for groupwise deviations. Then, we have $F\left(g_0\right)=\{g_1,g_2,g_3,g_4,g_5,g_6,g_7\}$, $F\left(g_1\right)=\{g_4,g_5\}$, $F\left(g_2\right)=\{g_4,g_6\}$, $F\left(g_3\right)=\{g_5,g_6\}$, $F\left(g_4\right)=\{g_3,g_7\}$, $F\left(g_5\right)=\{g_2,g_7\}$, $F\left(g_6\right)=\{g_1,g_7\}$, and $F\left(g_7\right)=\{g_1,g_2,g_3\}$. Hence, $\{g_1,g_2,g_3\}$ becomes a groupwise farsightedly stable set. But, this is not the unique groupwise farsightedly stable set. The others are $\{g_1,g_2,g_4,g_5,g_6\}$, $\{g_1,g_3,g_4,g_5,g_6\}$, $\{g_2,g_3,g_4,g_5,g_6\}$, $\{g_4,g_5,g_6,g_7\}$.

4. Farsighted Stability under the Componentwise Egalitarian Allocation Rule

We now investigate whether the pairwise or groupwise farsighted stability coincide with the pairwise or groupwise myopically stability under the componentwise egalitarian allocation. Let

$$g(v,S)=\left\{g\subseteq g^S\left|\frac{v\left(g\right)}{\#N\left(g\right)}\ge \frac{v\left(g^{\prime }\right)}{\#N\left(g^{\prime }\right)}\forall g^{\prime }\subseteq g^S,g^{\prime }\ne ⌀\right.\right\}$$

be the set of networks with the highest per capita value out of those that can be formed by players in $S\subseteq N$. Given a component additive value function v, find a network $g^v$ through the following algorithm due to Banerjee [17]. Pick some $h_1\in g(v,N)$. Next, pick some $h_2\in g(v,N\setminus N\left(h_1\right))$. At stage k pick some $h_k\in g(v,N\setminus {\cup }_{i\le k-1}N\left(h_i\right))$. Since N is finite this process stops after a finite number K of stages. The union of the components picked in this way defines a network $g^v$. We denote by $G^v$ the set of all networks that can be found through this algorithm. More than one network may be picked up through this algorithm since players may be permuted or even be indifferent between components of different sizes.

Lemma 1 tells us that there is no pairwise or groupwise farsighted improving path emanating from each $g\in G^v$.

Lemma 1.

Consider any component additive value function v. For all $g\in G^v$ we have $f\left(g\right)=⌀$ and $F\left(g\right)=⌀$ under the componentwise egalitarian allocation rule $Y^{ce}$.

Take any $g\in G^v$ where $g{=}_{k=1}^K{h}_k$ with $h_k\in g\left(v,N\setminus {\cup }_{i\le k-1}N\left(h_i\right)\right)$. Players belonging to $N\left(h_1\right)$ in g who are looking forward will never engage in a move since they can never be strictly better off than in g given the componentwise egalitarian allocation rule $Y^{ce}$. Players belonging to $N\left(h_2\right)$ in g who are forward looking will only engage in a move if they can end up in some h such that $v\left(h\right)/\#N\left(h\right)>v\left(h_2\right)/\#N\left(h_2\right)$. Suppose there exists some h such that $v\left(h\right)/\#N\left(h\right)>v\left(h_2\right)/\#N\left(h_2\right)$. Since $h_2\in g\left(v,N\setminus N\left(h_1\right)\right)$ it follows that $N\left(h\right)\cap N\left(h_1\right)\ne ⌀$. Given that players in $N\left(h_1\right)$ will never engage in a move, players belonging to $N\left(h_2\right)$ can never end up strictly better off than in g under the componentwise egalitarian allocation rule $Y^{ce}$. So, players belonging to $N\left(h_2\right)$ in g will never engage in a move. Players belonging to $N\left(h_k\right)$ in g who are forward looking will only engage in a move if they can end up in some h such that $v\left(h\right)/\#N\left(h\right)>v\left(h_k\right)/\#N\left(h_k\right)$. Suppose there exists some h such that $v\left(h\right)/\#N\left(h\right)>v\left(h_k\right)/\#N\left(h_k\right)$. Since $h_k\in g\left(v,N\setminus {\cup }_{i\le k-1}N\left(h_i\right)\right)$ it follows that $N\left(h\right)\cap \left\{{\cup }_{i\le k-1}N\left(h_i\right)\right\}\ne ⌀$. Given that players in ${\cup }_{i\le k-1}N\left(h_i\right)$ will never engage in a move, players belonging to $N\left(h_k\right)$ can never end up strictly better off than in g under the componentwise egalitarian allocation rule $Y^{ce}$. So, players belonging to $N\left(h_k\right)$ in g will never engage in a move; and so on. Thus, $f\left(g\right)=⌀$ and $F\left(g\right)=⌀$.

From Lemma 1 it follows that there is no pairwise or groupwise myopic improving path emanating from each $g\in G^v$.

Corollary 1.

Consider any component additive value function v. For all $g\in G^v$ we have $m\left(g\right)=⌀$ and $M\left(g\right)=⌀$ under the componentwise egalitarian allocation rule $Y^{ce}$.

Lemma 2 tells us that from any $g^{\prime }\notin G^v$ there is some pairwise farsighted improving path going to some $g\in G^v$. Hence, from any $g^{\prime }\notin G^v$ there is some groupwise farsighted improving path going to some $g\in G^v$.

Lemma 2.

Consider any component additive value function v. For all $g^{\prime }\notin G^v$ there exists $g\in G^v$ such that $g\in f\left(g^{\prime }\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$.

We show in a constructive way that for all $g^{\prime }\notin G^v$ there exists $g\in G^v$ such that $g\in f\left(g^{\prime }\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$. Take any $g^{\prime }\notin G^v$.

Step 1:

If there exists some $h_1\in g(v,N)$ such that $h_1\in C\left(g^{\prime }\right)$ then go to Step 2 with $g_1=g^{\prime }$. Otherwise, two cases have to be considered. (A) There exists $h\in C\left(g^{\prime }\right)$ such that $h_1⊊h$ for some $h_1\in g(v,N)$. Then, take $h_1\in g(v,N)$ such that there does not exist $h_1^{\prime }\in g(v,N)$ with $h_1⊊h_1^{\prime }⊊h$. From $g^{\prime }$, let the players who belong to $N\left(h_1\right)$ and who look forward to $g\in G^v$ delete successively their links that are not in $h_1$ to reach $g_1=g^{\prime }-\{ij\mid i\in N\left(h_1\right)$ and $ij\notin h_1\}$. Along the sequence from $g^{\prime }$ to $g_1$ all players who are moving always prefer the end network g to the current network. (B) There does not exist $h\in C\left(g^{\prime }\right)$ such that $h_1⊊h$ with $h_1\in g(v,N)$. Pick $h_1\in g(v,N)$ such that there does not exist $h_1^{\prime }\in g(v,N)$ with $h_1^{\prime }⊊;h_1$. From $g^{\prime }$, let the players who belong to $N\left(h_1\right)$ and who are looking forward to $g\in G^v$ such that $h_1\in C\left(g\right)$ first delete successively their links not in $h_1$ and then build successively the links in $h_1$ that are not in $g^{\prime }$ leading to $g_1=g^{\prime }-\{ij\mid i\in N\left(h_1\right)$ and $ij\notin h_1\} + \{ij\mid i\in N\left(h_1\right)$, $ij\in h_1$ and $ij\notin g^{\prime }\}$. Along the sequence from $g^{\prime }$ to $g_1$ all players who are moving always prefer the end network g to the current network. Once $g_1$ and $h_1$ are formed, we move to Step 2.

Step 2:

If there exists some $h_2\in g(v,N\setminus N\left(h_1\right))$ such that $h_2\in C\left(g_1\right)$ then go to Step 3 with $g_2=g_1$. Otherwise, two cases have to be considered. (A) There exists $h\in C\left(g^{\prime }\right)$ such that $h_2⊊h$ for some $h_2\in g(v,N\setminus N\left(h_1\right))$. Then, take $h_2\in g(v,N\setminus N\left(h_1\right))$ such that there does not exist $h_2^{\prime }\in g(v,N\setminus N\left(h_1\right))$ with $h_2⊊h_2^{\prime }⊊h$. From $g_1$ let the players who belong to $N\left(h_2\right)$ and who look forward to $g\in G^v$ such that $h_1\in C\left(g\right)$ and $h_2\in C\left(g\right)$ delete successively all their links that are not in $h_2$ to reach $g_2=g_1-\{ij\mid i\in N\left(h_2\right)$ and $ij\notin h_2\}$. Along the sequence from $g_1$ to $g_2$ all players who are moving always prefer the end network g to the current network. (B) There does not exist $h\in C\left(g^{\prime }\right)$ such that $h_2⊊h$ with $h_2\in g(v,N\setminus N\left(h_1\right))$. Pick $h_2\in g(v,N\setminus N\left(h_1\right))$ such that there does not exist $h_2^{\prime }\in g(v,N\setminus N\left(h_1\right))$ with $h_2^{\prime }⊊h_2$. From $g_1$ let the players who belong to $N\left(h_2\right)$ and who are looking forward to $g\in G^v$ such that $h_1\in C\left(g\right)$ and $h_2\in C\left(g\right)$ first delete successively their links not in $h_2$ and then build successively the links in $h_2$ that are not in $g_1$ leading to $g_2=g_1-\{ij\mid i\in N\left(h_2\right)$ and $ij\notin h_2\} + \{ij\mid i\in N\left(h_2\right)$, $ij\in h_2$ and $ij\notin g_1\}$. Along the sequence from $g_1$ to $g_2$ all players who are moving always prefer the end network g to the current network. Once $g_2$ and $h_2$ are formed, we move to Step 3.

Step k:

If there exists some $h_k\in g(v,N\setminus \{N\left(h_1\right)\cup ...\cup N(k-1)\})$ such that $h_k\in C\left(g_{k-1}\right)$ then go to Step $k+1$ with $g_k=g_{k-1}$. Otherwise, two cases have to be considered. (A) There exists $h\in C\left(g^{\prime }\right)$ such that $h_k⊊h$ for some $h_k\in g(v,N\setminus \{N\left(h_1\right)\cup ...\cup N(k-1)\})$. Then, take $h_k\in g(v,N\setminus \{N\left(h_1\right)\cup ...\cup N(k-1)\})$ such that there does not exist $h_k^{\prime }\in g(v,N\setminus \{N\left(h_1\right)\cup ...\cup N(k-1)\})$ with $h_k⊊h_k^{\prime }⊊h$. ¿From $g_{k-1}$ let the players who belong to $N\left(h_k\right)$ and who look forward to $g\in G^v$ such that $h_1\in C\left(g\right)$, $h_2\in C\left(g\right)$, ..., $h_k\in C\left(g\right)$ delete successively their links not in $h_k$ to reach $g_k=g_{k-1}-\{ij\mid i\in N\left(h_k\right)$ and $ij\notin h_k\}$. Along the sequence from $g_{k-1}$ to $g_k$ all players who are moving always prefer the end network g to the current network. (B) There does not exist $h\in C\left(g^{\prime }\right)$ such that $h_k⊊h$ with $h_k\in g(v,N\setminus \{N\left(h_1\right)\cup ...\cup N(k-1)\})$. Pick $h_k\in g(v,N\setminus \{N\left(h_1\right)\cup ...\cup N(k-1)\})$ such that there does not exist $h_k^{\prime }\in g(v,N\setminus \{N\left(h_1\right)\cup ...\cup N(k-1)\})$ with $h_k^{\prime }⊊h_k$. ¿From $g_{k-1}$ let the players who belong to $N\left(h_k\right)$ and who are looking forward to $g\in G^v$ such that $h_1\in C\left(g\right)$, $h_2\in C\left(g\right)$, ..., $h_k\in C\left(g\right)$ first delete successively their links not in $h_k$ and then build successively the links in $h_k$ that are not in $g_{k-1}$ leading to $g_k=g_{k-1}-\{ij\mid i\in N\left(h_k\right)$ and $ij\notin h_k\} + \{ij\mid i\in N\left(h_k\right)$, $ij\in h_k$ and $ij\notin g_{k-1}\}$. Along the sequence from $g_{k-1}$ to $g_k$ all players who are moving always prefer the end network g to the current network. Once $g_k$ and $h_k$ are formed, we move to Step $k+1$; and so on until we reach the network $g{=}_{k=1}^K{h}_k$ with $h_k\in g(v,N\setminus {\cup }_{i\le k-1}N\left(h_i\right))$. Thus, we have build a pairwise farsightedly improving path from $g^{\prime }$ to g; $g\in f\left(g^{\prime }\right)$. Since $f\left(g^{\prime }\right)\subseteq F\left(g^{\prime }\right)$, we also have that for all $g^{\prime }\notin G^v$ there exists $g\in G^v$ such that $g\in F\left(g^{\prime }\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$.

The next proposition tells us that once players are farsighted it does not matter whether groupwise or only pairwise deviations are feasible. Both pairwise farsighted stability and groupwise farsighted stability single out the same unique set.

Proposition 1.

Consider any component additive value function v. The set $G^v$ is both the unique pairwise farsightedly stable set and the unique groupwise farsightedly stable set under the componentwise egalitarian allocation rule $Y^{ce}$.

Consider any anonymous and component additive value function v. From Lemma 1 we know that $f\left(g\right)=⌀$ and $F\left(g\right)=⌀$ for all $g\in G^v$ under the componentwise egalitarian allocation rule $Y^{ce}$. From Lemma 2 we have that for all $g^{\prime }\notin G^v$ there exists $g\in G^v$ such that $g\in f\left(g^{\prime }\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$. Using Theorem 5 in Herings, Mauleon and Vannetelbosch [6] which says that G is the unique pairwise farsightedly stable set if and only if $G=\{g\in \mathbb{G}\mid f(g)=⌀\}$ and for every $g^{\prime }\in \mathbb{G}\setminus G$, $f\left(g^{\prime }\right)\cap G\ne ⌀$, we have that $G^v$ is the unique pairwise farsightedly stable set. In case of groupwise deviations, Theorem 5 says that G is the unique groupwise farsightedly stable set if and only if $G=\{g\in \mathbb{G}\mid F(g)=⌀\}$ and for every $g^{\prime }\in \mathbb{G}\setminus G$, $F\left(g^{\prime }\right)\cap G\ne ⌀$. Since $f\left(g\right)\subseteq F\left(g\right)$ $\forall g\in \mathbb{G}$, we have that $G^v$ is also the unique groupwise farsightedly stable set.

Lemma 3 tells us that from any $g^{\prime }\notin G^v$ there is some groupwise myopic improving path going to some $g\in G^v$.

Lemma 3.

Consider any component additive value function v. For all $g^{\prime }\notin G^v$ there exists $g\in G^v$ such that $g\in M\left(g^{\prime }\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$.

We show in a constructive way that for all $g^{\prime }\notin G^v$ there exists $g\in G^v$ such that $g\in M\left(g^{\prime }\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$. Take any $g^{\prime }\notin G^v$.

Step 1:

If there exists some $h_1\in g(v,N)$ such that $h_1\in C\left(g^{\prime }\right)$ then go to Step 2 with $g_1=g^{\prime }$. Otherwise, pick some $h_1\in g(v,N)$. In $g^{\prime }$ all players are strictly worse off than the players belonging to $N\left(h_1\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$. Then, we have that all members of $N\left(h_1\right)$ have incentives to deviate from $g^{\prime }$ to $g_1=g^{\prime }{|}_{N\setminus N\left(h_1\right)}\cup h_1$. Indeed, $g_1$ is obtainable from $g^{\prime }$ via deviations by $N\left(h_1\right)\subseteq N$ and $Y_i(g_1,v)>Y_i(g^{\prime },v)$ for all $i\in N\left(h_1\right)$. In words, players who belong to $N\left(h_1\right)$ delete their links in $g^{\prime }$ with players not in $N\left(h_1\right)$ and build the missing links of $h_1$. Once $g_1$ and $h_1$ are formed, we move to Step 2.

Step 2:

If there exists some $h_2\in g(v,N\setminus N\left(h_1\right))$ such that $h_2\in C\left(g_1\right)$ then go to Step 3 with $g_2=g_1$. Otherwise, pick some $h_2\in g(v,N\setminus N\left(h_1\right))$. In $g_1$ all the remaining players who are belonging to $N\setminus N\left(h_1\right)$ are strictly worse off than the players belonging to $N\left(h_2\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$. Then, we have that all members of $N\left(h_2\right)$ have incentives to deviate from $g_1$ to $g_2=g_1{|}_{N\setminus N\left(h_2\right)}\cup h_2$. Indeed, $g_2$ is obtainable from $g_1$ via deviations by $N\left(h_2\right)\subseteq N$ and $Y_i(g_2,v)>Y_i(g_1,v)$ for all $i\in N\left(h_2\right)$. Once $g_2$ and $h_2$ are formed, we move to Step 3.

Step k:

If there exists some $h_k\in g(v,N\setminus \{N\left(h_1\right)\cup ...\cup N(k-1)\})$ such that $h_k\in C\left(g_{k-1}\right)$ then go to Step $k+1$ with $g_k=g_{k-1}$. Otherwise, pick some $h_k\in g(v,N\setminus \{N\left(h_1\right)\cup ...\cup N(k-1)\})$. In $g_{k-1}$ all the remaining players who are belonging to $N\setminus \{N\left(h_1\right)\cup ...\cup N(k-1)\}$ are strictly worse off than the players belonging to $N\left(h_k\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$. Then, we have that all members of $N\left(h_k\right)$ have incentives to deviate from $g_{k-1}$ to $g_k=g_{k-1}{|}_{N\setminus N\left(h_k\right)}\cup h_k$. Indeed, $g_k$ is obtainable from $g_{k-1}$ via deviations by $N\left(h_k\right)\subseteq N$ and $Y_i(g_k,v)>Y_i(g_{k-1},v)$ for all $i\in N\left(h_k\right)$. Once $g_k$ and $h_k$ are formed, we move to Step $k+1$; and so on until we reach the network $g{=}_{k=1}^K{h}_k$ with $h_k\in g(v,N\setminus {\cup }_{i\le k-1}N\left(h_i\right))$. Thus, we have build a groupwise myopically improving path from $g^{\prime }$ to g; $g\in M\left(g^{\prime }\right)$.

The next proposition tells us that groupwise myopic stability singles out the same unique set as pairwise and groupwise farsighted stability do.

Proposition 2.

Consider any component additive value function v. The set $G^v$ is the unique groupwise myopically stable set under the componentwise egalitarian allocation rule $Y^{ce}$.

Since the set of networks consisting of all networks that belong to a closed cycle is the unique groupwise myopically stable set, we have to show that the set of all networks that belong to a closed cycle is $G^v$. From Lemma 3 we know that for all $g^{\prime }\notin G^v$ there exists $g\in G^v$ such that $g\in M\left(g^{\prime }\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$. By Corollary 1 we have that $M\left(g\right)=⌀$ for all $g\in G^v$. Thus, it follows that each $g\in G^v$ is a closed cycle, all closed cycles belong to $G^v$, and $G^v$ is the unique groupwise myopically stable set.

Notice that all networks belonging to $G^v$ are pairwise stable networks in a strict sense. However, the pairwise myopically stable set may include networks that do not belong to $G^v$. Thus, if players are myopic it matters whether groupwise or only pairwise deviations are feasible. So, pairwise farsighted stability, groupwise farsighted stability and groupwise myopic stability refines the notion of pairwise stability under $Y^{ce}$ when deviations are valid only if all deviating players are strictly better off.

In the example of Figure 1, the value function is component additive and the allocation rule is the componentwise egalitarian one. Using the algorithm we obtain that $G^v=\left\{g_7\right\}$. Hence, $\left\{g_7\right\}$ is the unique pairwise (groupwise) farsightedly stable set and the unique groupwise myopically stable set.

5. Other Notions of Farsighted Stability

In this section we show that other notions of farsighted stability also single out the set $G^v$. 7 The largest consistent set is a concept that has been defined in Chwe [7] for general social environments. By considering a network as a social environment, we obtain the definition of the largest consistent set.

Definition 5.

G is a consistent set if ∀$g\in G$, $S\subseteq N$, $g^{\prime }\in \mathbb{G}$ that is obtainable from g via deviations by S, there exists $g^{″}\in G$, where $g^{″}=g^{\prime }$ or $g^{″}\in F\left(g^{\prime }\right)\cap G$ such that $Y_i(g^{″},v)\le Y_i(g,v)$ for some $i\in S$. The largest consistent set is the consistent set that contains any consistent set.

Proposition 3.

Consider any component additive value function v. The set $G^v$ is the largest consistent set under the componentwise egalitarian allocation rule $Y^{ce}$.

First, we show in a constructive way that any $g^{\prime }\notin G^v$ cannot belong to a consistent because there always exists a deviation which is not deterred. Take any $g^{\prime }\notin G^v$.

Suppose $\nexists h_1\in g(v,N)$ such that $h_1\in C\left(g^{\prime }\right)$. Then, in $g^{\prime }$ all players are strictly worse off than the players belonging to $N\left(h_1\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$. We have that the deviation by all members of $N\left(h_1\right)$ from $g^{\prime }$ to $g^{″}=g^{\prime }{|}_{N\setminus N\left(h_1\right)}\cup h_1$ cannot be deterred. Indeed, $g^{″}$ is obtainable from $g^{\prime }$ via deviations by $N\left(h_1\right)\subseteq N$ and $Y_i(g^{″},v)>Y_i(g^{\prime },v)$ for all $i\in N\left(h_1\right)$. In words, players who belong to $N\left(h_1\right)$ delete their links in $g^{\prime }$ with players not in $N\left(h_1\right)$ and build the missing links of $h_1$. In addition, for any $g^{*}\ne g^{″}$, we have that $Y_i(g^{″},v)\ge Y_i(g^{*},v)$ for all $i\in N\left(h_1\right)$. So, for any $g^{‴}\in F\left(g^{″}\right)$ we have $Y_i(g^{\prime },v)<Y_i(g^{″},v)=Y_i(g^{‴},v)$ for all $i\in N\left(h_1\right)$. Thus, $g^{\prime }$ cannot belong to a consistent set.

Suppose that $\exists h_1\in g(v,N)$ such that $h_1\in C\left(g^{\prime }\right)$ but $\nexists h_2\in g(v,N\setminus N\left(h_1\right))$ such that $h_2\in C\left(g^{\prime }\right)$. Then, in $g^{\prime }$ all players who belong to $N\setminus N\left(h_1\right)$ are strictly worse off than the players belonging to $N\left(h_2\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$. Then, we have that the deviation by all members of $N\left(h_2\right)$ from $g^{\prime }$ to $g^{″}=g^{\prime }{|}_{N\setminus N\left(h_2\right)}\cup h_2$ cannot be deterred. Indeed, $g^{″}$ is obtainable from $g^{\prime }$ via deviations by $N\left(h_2\right)\subseteq N$ and $Y_i(g^{″},v)>Y_i(g^{\prime },v)$ for all $i\in N\left(h_2\right)$. In addition, for any $g^{*}\ne g^{″}$, $g^{*}\subseteq g^{N\setminus N\left(h_1\right)}$, we have that $Y_i(g^{″},v)\ge Y_i(g^{*},v)$ for all $i\in N\left(h_2\right)$. So, for any $g^{‴}\in F\left(g^{″}\right)$ we have $Y_i(g^{\prime },v)<Y_i(g^{″},v)=Y_i(g^{‴},v)$ for all $i\in N\left(h_2\right)$. Thus, $g^{\prime }$ cannot belong to a consistent set.

Suppose that $\exists h_1,h_2,h_3,...,h_{k-1}$ with $h_l\in g(v,N\setminus \{N\left(h_1\right)\cup ...\cup N\left(h_{l-1}\right)\})$, $l=2,...,k-1$, and $h_l\in C\left(g^{\prime }\right)$ but $\nexists h_k\in C\left(g^{\prime }\right)$ such that $h_k\in g(v,N\setminus \{N\left(h_1\right)\cup ...\cup N\left(h_{k-1}\right)\})$. Then, in $g^{\prime }$ all players who are belonging to $N\setminus \{N\left(h_1\right)\cup ...\cup N\left(h_{k-1}\right)\}$ are strictly worse off than the players belonging to $N\left(h_k\right)$ under the componentwise egalitarian allocation rule $Y^{ce}$. Then, we have that the deviation by all members of $N\left(h_k\right)$ from $g^{\prime }$ to $g^{″}=g^{\prime }{|}_{N\setminus N\left(h_k\right)}\cup h_2$ cannot be deterred. Indeed, $g^{″}$ is obtainable from $g^{\prime }$ via deviations by $N\left(h_k\right)\subseteq N$ and $Y_i(g^{″},v)>Y_i(g^{\prime },v)$ for all $i\in N\left(h_k\right)$. In addition, for any $g^{*}\ne g^{″}$, $g^{*}\subseteq g^{N\setminus \{N\left(h_1\right)\cup ...\cup N\left(h_{k-1}\right)}$, we have that $Y_i(g^{″},v)\ge Y_i(g^{*},v)$ for all $i\in N\left(h_k\right)$. So, for any $g^{‴}\in F\left(g^{″}\right)$ we have $Y_i(g^{\prime },v)<Y_i(g^{″},v)=Y_i(g^{‴},v)$ for all $i\in N\left(h_k\right)$. Thus, $g^{\prime }$ cannot belong to a consistent set. And so forth.

Second, we have from Lemma 1 that $F\left(g\right)=⌀$∀$g\in G^v$. Hence, each $\left\{g\right\}$ with $g\in G^v$ is a consistent set. Thus, $G^v$ is the largest consistent set under the componentwise egalitarian allocation rule $Y^{ce}$.

The von Neumann-Morgenstern stable set (von Neumann and Morgenstern [18]) imposes internal and external stability. Incorporating the notion of farsighted improving paths into the original definition of the von Neumann-Morgenstern stable set, we obtain the von Neumann-Morgenstern farsightedly stable set. von Neumann-Morgenstern farsightedly stable sets do not always exist. Corollary 5 in Herings, Mauleon and Vannetelbosch [6] tells us that if G is the unique pairwise (groupwise) farsightedly stable set, then G is the unique von Neumann-Morgenstern pairwise (groupwise) farsightedly stable set. Hence, the set $G^v$ is both the unique von Neumann-Morgenstern pairwise farsightedly stable set and the unique von Neumann-Morgenstern groupwise farsightedly stable set under the componentwise egalitarian allocation rule $Y^{ce}$.8

The definitions of stability we have considered allow for a deviation by a coalition to be valid only if all members of the coalition are strictly better off. On the contrary, if we require that at least one coalition member is strictly better off while all other members are at least as well off, then it is not excluded that there are pairwise (groupwise) farsighted improving paths emanating from networks belonging to $G^v$ going to other networks belonging to $G^v$. Then, it follows that $G^v$ is no more a von Neumann-Morgenstern pairwise farsightedly stable set since internal stability is violated, and from Theorem 5 in Herings, Mauleon and Vannetelbosch [6] we have that $G^v$ is no more the unique pairwise and groupwise farsightedly stable set.

6. Conclusions

We have studied the stability of social and economic networks when players are farsighted. We have provided an algorithm that characterizes the unique pairwise and groupwise farsightedly stable set of networks under the componentwise egalitarian allocation rule. We have then shown that this set coincides with the unique groupwise myopically stable set of networks but not with the pairwise myopically stable set. Thus, if group deviations are allowed then whether players are farsighted or myopic does not matter, or if players are farsighted then whether players are allowed to deviate in pairs only or in groups does not matter.