Improved Hybrid Bagging Resampling Framework for Deep Learning-Based Side-Channel Analysis

Abstract

As cryptographic implementations leak secret information through side-channel emissions, the Hamming weight (HW) leakage model is widely used in deep learning profiling side-channel analysis (SCA) attacks to expose the leaked model. However, imbalanced datasets often arise from the HW leakage model, increasing the attack complexity and limiting the performance of deep learning-based SCA attacks. Effective management of class imbalance is vital for training deep neural network models to achieve optimized and improved performance results. Recent works focus on either improved deep-learning methodologies or data augmentation techniques. In this work, we propose the hybrid bagging resampling framework, a two-pronged strategy for tackling class imbalance in side-channel datasets, consisting of data augmentation and ensemble learning. We show that adopting this framework can boost attack performance results in a practical setup. From our experimental results, the SMOTEENN ensemble achieved the best performance in the ASCAD dataset, and the basic ensemble performed the best in the CHES dataset, with both contributing over $70\%$ practical improvements in performance compared to the original imbalanced dataset, and accelerating practical attack space in comparison to the classical setup of the attack.

1. Introduction

Cryptography plays a vital role in modern digital systems, supporting the mechanisms used to protect the confidentiality, integrity, and authenticity of information. Decades of meticulous design and analysis have yielded cryptographic protocols and primitives that offer strong theoretical security guarantees [1,2]. However, a critical distinction must be drawn between the theoretical security of cryptographic algorithms and the practical realities of their implementation. Even rigorously designed ciphers, when implemented on physical devices such as microcontrollers, FPGAs and ASICs, become susceptible to information leakage. This fundamental vulnerability enables a powerful class of cryptanalytic approaches known as side-channel attacks.

Side-channel attacks represent a formidable class of cryptanalytic techniques that subvert cryptographic algorithms by exploiting implementation-specific characteristics rather than targeting their inherent mathematical structure. Every implementation of a cipher, either in software or hardware, generates side-channel leakages. These unintended emanations can include, but are not limited to, device power consumption, timing information, electromagnetic emissions, acoustic signals, or patterns in cache access [3]. Adversaries, equipped with the ability to collect and analyze these side-channel traces, can infer relationships between the observed leakage patterns and the secret data (such as a cryptographic key) used within the device. By combining side-channel analysis with traditional cryptanalytic approaches, attackers can compromise cryptographic implementations with an efficiency that far exceeds brute force methods [4,5,6].

Machine learning (ML) has become an indispensable tool within the attacker’s arsenal, transforming the field of side-channel analysis. Initially, methods such as random forests (RF) and support vector machines (SVM) were prevalent [7,8,9,10,11,12,13]. However, deep learning (DL) has since emerged as the dominant paradigm due to its superior predictive capabilities. Neural network architectures, including multilayer perceptrons (MLP) and convolutional neural networks (CNN), have become instrumental in side-channel attack methodologies [14,15]. A key advantage of deep learning lies in its ability to automatically learn relevant features from raw side-channel traces, eliminating the need for laborious manual feature engineering.

The authors of [16] introduced a technique that leverages models generated during hyperparameter tuning to improve the generalization of deep learning methods. By ensembling these models, their approach demonstrates a significant enhancement in attack performance against the AES-128 cipher. This attack was evaluated using well-established datasets, including Piñata SW AES, DPAv4, ASCAD, and CHES CTF 2018. The methodology involves conducting a hyperparameter search to train multiple deep-learning models on the same profiling dataset. These models are then ranked according to their performance in the validation data. Subsequently, an ensemble composed of the best-performing models is created, yielding superior results compared to the selection of a single best model. However, Perin et al. did not investigate the possible impact of dataset balance (or imbalance) on the generalization capabilities of such ensembles [16]. A balanced dataset implies an equal representation of all output classes, and its role in ensemble generalization warrants further exploration.

The dataset imbalance is a prevalent issue in profiled side-channel analysis. Using leakage models such as the Hamming weight (HW) often results in an imbalanced dataset [11,17]. This imbalance comes from the calculation of bit transitions by the HW model from 0 to 1 [18]. For example, in an eight-bit number, there exist eight different configurations with an HW of 1 (a single bit set to 1), while only one configuration has an HW of 8 (all bits set to 1). This pattern extends to the HW values between 1 and 7, resulting in their over-representation compared to the hamming weight of 0 and 8.

Picek et al. [11] investigated the resilience of various machine learning techniques to imbalanced datasets in the context of attacking AES-128 implementations on an AVR microcontroller and FPGA. They proposed the use of the Synthetic Minority Oversampling Technique (SMOTE) and other data resampling methods to artificially increase the representation of underrepresented classes, leading to a more balanced dataset [19]. However, their work did not explore the potential benefits of ensembles with these techniques. Ensembles, composed of multiple ML models, inherently introduce a degree of balance [20]. Combining ensemble methods with SMOTE could potentially lead to further performance improvements.

Existing literature offers valuable insights into the application of deep learning models in side-channel attacks, including the use of ensemble methods [16]. Researchers have also addressed the practical challenge of imbalanced datasets in profiled side-channel attacks, often employing SMOTE as an oversampling technique to mitigate imbalance. However, a notable gap remains: the potential of model ensembles to directly address dataset imbalance or to enhance the effectiveness of oversampling techniques like SMOTE has yet to be thoroughly explored. This work proposes a hybrid bagging ensemble deep learning side-channel attack framework that successfully formulates and integrates bagging ensemble and data enhancement techniques as an additional tuning layer to tackle dataset imbalance, thereby building highly discriminative deep learning models.

1.1. Related Works

Many papers in side-channel analysis (SCA) have focused on hyperparameter tuning methods for training efficient neural networks for SCA, while only a few have considered strategies that address SCA class imbalance. Perin et al. explored ensembles of machine learning models to improve attack performance [16]. The authors boosted machine learning attack performance by combining the predictions of complementary predictors. On the other hand, Llavata et al. proposed a stacking ensemble methodology that can relieve a security evaluator from a laborious hyperparameter tuning process [21]. By using stacking as an aggregation method, the authors built a meta-model that learns the best way to combine the output class probabilities of the ensemble models. Some works have used ensembles as a method to tackle class imbalance. Zhang et al. proposed an SCA multilabel classification from a bit-to-byte methodology [22]. By predicting bit-by-bit and training a machine learning model for each bit, model complexity is greatly reduced, and the dataset for each bit is uniformly distributed, thus effectively tackling imbalance while the class prediction is an ensemble of each monobit model. Gao et al. provided an ensemble learning method that consists of data enhancement methods such as SMOTE and machine learning techniques [23]. The authors used data enhancement methods to address the imbalanced class distribution and subsequently utilized a random forest machine-learning technique to recover the mask value. Finally, they used the recovered mask value to predict the secret key. Furthermore, some methods have applied generative adversarial networks as a tool for imbalanced data scenarios. Wang et al. utilized a conditional generative adversarial network (CGAN) to simulate new traces, thereby balancing the data and consequently predicting the secret key with greater performance [24]. Additionally, Mukhtar et al. explored an efficient deep learning-based attack methodology integrated with an analysis framework to improve the side-channel attacks on imbalanced leakage datasets [25]. They achieved this through the combination of dimensionality reduction and the SMOTE class balancing technique along with a proposed simple ConvNet model. On the other hand, other methods have focused purely on data enhancement techniques to improve generalization. Picek et al. used various balancing techniques to address data imbalance and concluded that the SMOTE technique was the most effective [11,26]. Similarly, Won et al. proposed techniques to boost the efficiency of current SCA deep learning architectures [27]. They reported that SMOTE variant balancing techniques outperformed data augmentation procedures by a significant margin. The method proposed in [27] does not sufficiently explore other data balancing techniques. Furthermore, there is insufficient evidence on the specific impact that bagging ensembles have on enhancing the performance of SCA when dealing with imbalanced datasets. The summary of the related work is presented in

Table 1. Summary of related work in side-channel analysis (SCA) and class imbalance strategies.

Authors	Method	Description	Outcome
Perin et al. [16]	Ensemble Learning	Boosted machine learning attack performance by combining the predictions of complementary predictors.	Improved attack performance through ensemble methods.
Llavata et al. [21]	Stacking Ensemble	Proposed a stacking ensemble methodology to relieve a security evaluator from laborious hyperparameter tuning. Built a meta-model to combine output class probabilities of ensemble models.	Effective aggregation method to improve model performance, easing the hyperparameter tuning process.
Zhang et al. [22]	Multilabel Classification from Bit-to-Byte Methodology	Proposed an SCA multilabel classification by predicting bit-by-bit and training a machine learning model for each bit, resulting in uniformly distributed datasets.	Tackled class imbalance effectively while reducing model complexity.
Gao et al. [23]	Ensemble Learning with Data Enhancement	Combined data enhancement methods like SMOTE with machine learning techniques, using random forest to recover the mask value and predict the secret key.	Addressed imbalanced class distribution and improved key prediction accuracy.
Wang et al. [24]	Conditional Generative Adversarial Network (CGAN)	Used CGAN to simulate new traces for balancing data, enhancing the performance of key prediction.	Balanced data effectively, leading to better performance in secret key prediction.
ine Mukhtar et al. [25]	Deep Learning-Based Attack with Dimensionality Reduction and SMOTE	Combined dimensionality reduction and SMOTE class balancing technique with a simple ConvNet model for improved side-channel attacks on imbalanced leakage datasets.	Enhanced attack performance on imbalanced datasets through a combined approach.
Picek et al. [11,26]	Various Balancing Techniques	Used several balancing techniques to address data imbalance, concluding that SMOTE was the most effective.	SMOTE found to be the most effective balancing technique for improving generalization.
Won et al. [27]	Efficiency Boosting Techniques for SCA Deep Learning Architectures	Proposed techniques to boost efficiency, reporting that SMOTE variant balancing techniques outperformed data augmentation procedures.	SMOTE variants significantly improved the efficiency of deep learning architectures for SCA.
Current Study	Bagging Resampling Framework	Introduces a hybrid approach that integrates data augmentation and bagging ensembles to handle class imbalance in SCA.

.

1.2. Contributions

In this work, we carried out an in-depth investigation into improving SCA performance by tackling class imbalance.

• To the best of our knowledge, we are the first to propose a hybrid bagging resampling framework specifically for deep learning-based SCA. We conducted comparisons with models trained on imbalanced datasets, and our proposed method consistently performed well and better than basic models trained on imbalanced data. The results demonstrate that our approach not only addresses class imbalance effectively but also provides superior performance, making it a strong alternative for scenarios involving imbalanced data distributions.
• By leveraging the benefits and improved performance associated with data augmentation and oversampling techniques, our work successfully formulates and integrates a hybrid method that overcomes class imbalance through a data oversampling ensemble approach.
• We carry out experiments with well-established datasets and present a comparative study that examines various data sampling approaches within the context of the bagging ensemble method as well as distinguishing MLP and CNN performances.
• We evaluate our framework against state-of-the-art methods, showing significant improvements in performance, robustness and efficiency in side-channel attacks, proving it superior to current methodologies.

1.3. Paper Organization

The rest of this paper is organized as follows: Section 2 describes the background. Section 3 discusses the methodology, data enhancement and data augmentation mechanisms. Section 4 explains the side-channel analysis attack framework. Section 5 discusses the experimental setup, and analyzes the test cases and results. Section 6 wraps up with future considerations and conclusion of our findings.

2. Background

2.1. Profiled Side-Channel Analysis

Profiled side-channel attacks represent a powerful class of cryptanalytic adversaries that leverage information leakage from cryptographic implementations to compromise secrets. A schematic representation of a power trace and profile attack is given in Figure 1. These attacks operate in two distinct phases:

Profiling (Training) Phase: The adversary possesses a device identical to the target. This device allows them to obtain extensive side-channel measurements (e.g., power consumption traces) under various plaintext inputs and known or controlled key configurations [28]. The adversary leverages this dataset to model the relationship between the device’s side-channel leakage and internal values sensitive to secret key material.

In SCA, a divide-and-conquer strategy is employed to recover the full secret key. This approach typically involves the analysis and extraction of individual bytes within the key. Accordingly, the leakage model and attack techniques presented here are tailored to the extraction of a single subkey byte at a designated point in time. By iterating this analysis, subsequent bytes of the subkey can be recovered, ultimately leading to the retrieval of the complete secret key.

The training data consist of N side-channel traces, where each trace, $X_i$, is a vector of sample points based on the sampling rate of the measurement device. The trace $X_i$, is the measurement of the power leakage of encryption of a plaintext $P_i$ with the known or chosen secret key $K_i$. The power trace is modeled on the basis of a leakage model that is dependent on the secret key. The validation data consist of V, a subset of training data to evaluate the generalizability of the model [29].

Attack Phase: The adversary targets a similar device, obtaining side-channel measurements while it operates with an unknown secret key. The trained model is applied to infer likely key hypotheses based on the observed characteristics of the side-channel. The attack data consist of Q traces from the target device with unknown key ${\mathcal{K}}^{*}$.

During the attack, a probabilistic approach is typically used. For each possible key hypothesis k (one byte), a log-likelihood score is calculated:

$$S\left(k\right)=log{P}_k^{\mathrm{Q}}=\sum _{i=1}^{Q}log{P}_{i,j}$$

where $j=HW(PT,k)$, with HW denoting the Hamming Weight function, $PT$ is plaintext and k is the hypothesis key. Therefore, j represents the intermediate state values that result from the Hamming Weight applied to plaintext byte PT and hypothesis key k. Thus in our context, j spans over all possible values of the intermediate state for the given key hypothesis.

For each trace i, given the model and the corresponding plaintext, the adversary first predicts the intermediate value (e.g., S-box output) sensitive to the key. Then, use the leakage model to estimate which predicted value class (j) best matches the side-channel observation by calculating $P_{i,j}$ (the probability of the observation given the key hypothesis and the predicted value) and incorporate it into the log-likelihood.

The secret key byte predicted $\tilde{k}$ is the key hypothesis that maximizes log-likelihood:

$$\tilde{k}=arg\underset{k}{max}log{P}_k^{\mathrm{Q}}$$

2.2. Hamming Weight (HW) Leakage Model

The leakage model provides a matching representation between the secret key that we aim to predict with our machine-learning model and observable side-channel measurements. Thus, a power leakage model is a theoretical or empirical representation of how the power consumption of a cryptographic device relates to the data it processes, especially its secret information (like encryption keys). A good leakage model provides guidance on what features of a power trace are most likely to reveal sensitive information, aiding feature engineering for machine learning SCA. We are using the HW model in this work, which is one of the simplest and most common models. It assumes that the power consumption of a device is roughly proportional to the number of bits in a register that change state (from 0 to 1 or vice versa) during an operation. Usually, in SCA, one byte is attacked at a time. Therefore, the HW ranges from 0 to 8, resulting in 9 different classes. This offers the advantage of reduced training complexity in SCA. However, the drawback is that it introduces a class imbalance in our datasets, which is what our proposed hybrid bagging resampling framework is tackling in this research.

2.3. Deep Learning Classifiers in Profiled Side-Channel Analysis

With the HW model providing profiling data, the next phase is to train machine learning models that learn which bit computations result in certain power consumption profiles. In profiled side-channel analysis (SCA), deep learning techniques, particularly multilayer perceptrons (MLPs) and convolutional neural networks (CNNs) have emerged as powerful tools. Their key advantage lies in their ability to learn discriminative patterns directly from raw side-channel measurements (e.g., power or EM traces). This minimizes the reliance on hand-crafted features and domain-specific preprocessing, simplifying the analysis process. Additionally, they often demonstrate a degree of robustness against common SCA countermeasures such as masking and hiding. Their capacity to learn complex, nonlinear relationships allows them to identify subtle leakage patterns that might be obscured by these countermeasures. As a result, the SCA community has embraced these techniques to enhance the performance and efficiency of side-channel attack methodologies.

2.3.1. Multi-Layer Perceptrons

Multi-layer perceptrons (MLP) are a class of artificial neural networks composed of multiple layers of interconnected perceptrons, also known as neurons. Each perceptron in a layer receives input, computes a weighted sum, applies an activation function, and outputs a result to the next layer. The architecture typically consists of an input layer, one or more hidden layers, and an output layer. These layers form the hyperparameters of the MLP. The hidden layers consist of neurons that consist of trainable weights that usually diminish or amplify the effect of certain features at each layer toward estimating the score for the output vector. These trainable weights are adjusted accordingly during training to reduce loss and improve accuracy. The following expression illustrates MLP:

$${\mathbf{Y}}_i=f\left(\sum _{j=1}^n{W}_{ij}·x_i+b_j\right)$$

where $x_i$ is the i-th input trace to a neuron, $W_{ij}$ is the weight connecting the i-th input to the j-th neuron, $b_j$ is the bias vector, f is the activation function, and ${\mathbf{Y}}_i$ is the output vector for the i-th trace. In SCA, MLPs are trained with supervised learning, usually through the backpropagation algorithm. This iterative algorithm involves forward propagation, error calculation, gradient computation, and weight and bias updates.

2.3.2. Convolutional Neural Network

Convolutional Neural Networks (CNNs) are designed to excel in processing data with grid-like structures, making them remarkably effective for SCA. Side-channel traces can be viewed as 1D (power over time) or 2D representations (power variations across time and frequency). CNNs leverage the inherent spatial and temporal dependencies [30,31,32] within these traces through convolutional layers, pooling layers and fully connected layers. The following expression illustrates CNN:

$${\mathbf{Y}}_i=f\left(\sum _{m=1}^M\sum _{n=1}^N{W}_{ijmn}·x_{i,m,n}+b_j\right)$$

where $x_{i,m,n}$ represents the input data at position $(m,n)$ for the i-th trace, $W_{ijmn}$ is the weight matrix at position $(m,n)$ of the kernel connecting the i-th input channel to the j-th output channel, $b_j$ is the bias vector for the j-th layer, f the activation function and ${\mathbf{Y}}_i$ is the corresponding output vector for the i-th trace. In this work, we employ MLP and CNN to train classifiers on the ASCAD and CHES datasets. To further enhance performance, we apply ensemble techniques as outlined in [16].

2.4. Performance Metrics

While standard machine learning metrics provide insights into model performance, their direct application in side-channel analysis (SCA) presents limitations. This section explores these limitations and introduces metrics specifically designed to evaluate the effectiveness of SCA attacks.

2.4.1. Accuracy and Loss: Contextual Limitations

In machine learning, accuracy and loss (or error) are fundamental performance indicators. Accuracy denotes the proportion of correct predictions made by the model, while loss quantifies the degree of error and serves as an optimization target during training. Machine learning models aim to minimize loss, thus improving their predictive accuracy on the training set. The model parameters and hyperparameters are iteratively adjusted to achieve this optimization [33]. Given that our SCA attack involves multi-class predictions made trace by trace, we have employed the categorical cross-entropy loss function to effectively handle this classification challenge. This helps us optimize the model during training to improve its ability to distinguish between different key candidates based on the side-channel traces.

Within side-channel analysis, the overarching goal differs from conventional machine learning. Here, the focus is not merely on classifying traces, but on extracting specific secret information (e.g., cryptographic keys) by exploiting hardware-specific leakage patterns in power consumption, timing, or electromagnetic emanations. That is, given a test set of 1000 traces, the end goal is to use all the traces to predict a secret key associated with the 1000 traces rather than classifying each trace as in conventional machine learning. Consequently, achieving high accuracy on a dataset may not directly translate into a successful SCA attack. Therefore, the effectiveness of side-channel attacks is measured by their ability to accurately infer the secret key, rather than just classifying individual traces correctly. In this context, we adopt the well-established SCA metric of Guessing Entropy to evaluate the effectiveness of our attack methods.

2.4.2. Guessing Entropy (GE)

In SCA, guessing entropy (GE) provides a rigorous metric to quantify the effort required by an adversary to correctly identify the secret key [3]. It represents the average number of key candidates that an attacker must explore after conducting an SCA attack. The overarching aim of SCA is to correctly distinguish the secret key within a manageable number of traces, minimizing computational overhead. After analyzing each trace, the keys are ranked in descending order of probability. GE, therefore, reflects the average ranking of the correct key among these ordered probabilities across multiple experiments (or analyzed traces). Due to its reliability, GE is a widely adopted performance metric in side-channel research.

For a side-channel attack that uses Q traces, the adversary generates a key guess vector $\mathcal{G}$ where each possible key is arranged in descending order according to their likelihood. GE quantifies the average rank of the correct key ${\mathcal{K}}^{*}$ within this vector after multiple iterations of the attack. An efficient SCA technique strives to minimize GE, with the ideal outcome being a GE of one, signifying immediate and consistent key recovery using a minimal number of traces.

Consider a key guessing experiment where an adversary receives Q traces and produces a key guess vector $\mathcal{G}=[g_1,g_2, \dots ,g_{\left|\mathcal{K}\right|}]$, where $\left|\mathcal{K}\right|$ represents the keyspace size for a given encryption scheme $E_{K^{*}}\left(\right)$. Let $g{k}_x=i$ denote the position of the correct key byte within $\mathcal{G}$ for the x-th experiment. Upon repeating this experiment E times, GE is calculated as:

$$\mathrm{GE}={\displaystyle \frac{1}{E}}·\sum _{x=1}^{E}g{k}_x$$

2.4.3. Accuracy vs. Guessing Entropy/Success Rate

In machine learning, accuracy is a predominant metric used to analyze model performance. It is defined as the ratio of the number of correct predictions to the total number of predictions made.

In side-channel analysis (SCA), guessing entropy (GE) and success rate (SR) are the primary metrics used to evaluate the effectiveness of SCA techniques. When applying machine learning techniques to SCA, determining the appropriate metrics is crucial.

The authors in [11] addressed this question, and we briefly summarize their findings for completeness. They highlighted the main differences between accuracy and GE/SR. Accuracy measures each label prediction in the test set independently, whereas SR and GE are computed with respect to a fixed secret key. Specifically, accuracy is calculated based on class labels averaged over samples, while SR and GE are measured with respect to the secret key, accumulated over samples and averaged over experiments.

Additionally, SR and GE consider the exact value of the output probability of each class, whereas accuracy only considers which class has the highest output probability. There are instances where a model can have an accuracy of 0% but achieve an SR of 100% with more samples.

In this work, GE serves as our primary evaluation metric for SCA performance.

2.5. Datasets

In this work, we utilize two publicly available datasets that are extensively used in SCA research. We briefly describe the ASCAD and CHES CTF 2018 datasets.

2.5.1. ASCAD Dataset

The ASCAD dataset, a publicly accessible resource, contains measurements derived from a software implementation of AES-128 on an 8-bit AVR microcontroller. Boolean masking countermeasures were used in this implementation [28]. Our analysis uses the fixed-key ASCAD variant consisting of 50,000 training traces and 1000 testing traces, each with 700 sample points (features). Attacks specifically target the processing of the third S-Box within the initial round.

2.5.2. CHES CTF Dataset

AES CHES CTF dataset is a publicly available dataset released in 2018 for the Conference on Cryptographic Hardware and Embedded Systems (CHES). It is available in [34]. This dataset reflects a software-based AES-128 implementation on a 32-bit STM microcontroller with masking countermeasures. This dataset also utilizes a fixed key. Hereafter, we refer to this dataset as the CHES dataset. Our analysis uses 43,000 training traces and 1000 testing traces, each trace containing 2200 features. Importantly, the methodologies and analyses outlined in this work are extensible to alternative forms of side-channel measurements.

Table 2. Side-Channel Datasets.

Dataset	Training	Validation	Test	Features	Countermeasures
ASCAD	50,000	500	500	700	Masking
CHES CTF 2018	43,000	1000	1000	2200	Masking

provides a summary of the key characteristics of the dataset.

3. Techniques to Handle Imbalanced Data

In SCA, the HW leakage model is widely employed to model the relationship between sensitive intermediate values and observable side-channel emanations (e.g., power consumption). However, a significant challenge arises due to the inherent class imbalance introduced by this model.

Specifically, assuming an 8-bit architecture, the probability of encountering an intermediate value with HW of 4 is approximately 70 times higher than the probability of encountering a value with HW of 0 or 8. This disparity stems from the binomial distribution governing the number of ‘1’ bits in a random byte. Addressing this class imbalance is crucial, and we briefly discuss the various data sampling techniques used in this paper.

3.1. Synthetic Minority Oversampling Technique (SMOTE)

The Synthetic Minority Oversampling Technique (SMOTE) is a well-established oversampling method designed to address class imbalance in datasets [19,35]. It works by generating synthetic samples for minority classes, effectively augmenting their representation.

The core mechanism of SMOTE can be described as follows: For each minority class sample, its k nearest neighbors within the minority class are identified, with the value of k commonly set to 5 as a hyperparameter. Synthetic samples are then generated by randomly selecting one of the k nearest neighbors for each minority sample and interpolating between the original sample and the selected neighbor, typically through a linear combination of feature values. The degree of oversampling is controlled by a parameter, which allows the minority class to either fully equalize with the majority class or reach a specified target size.

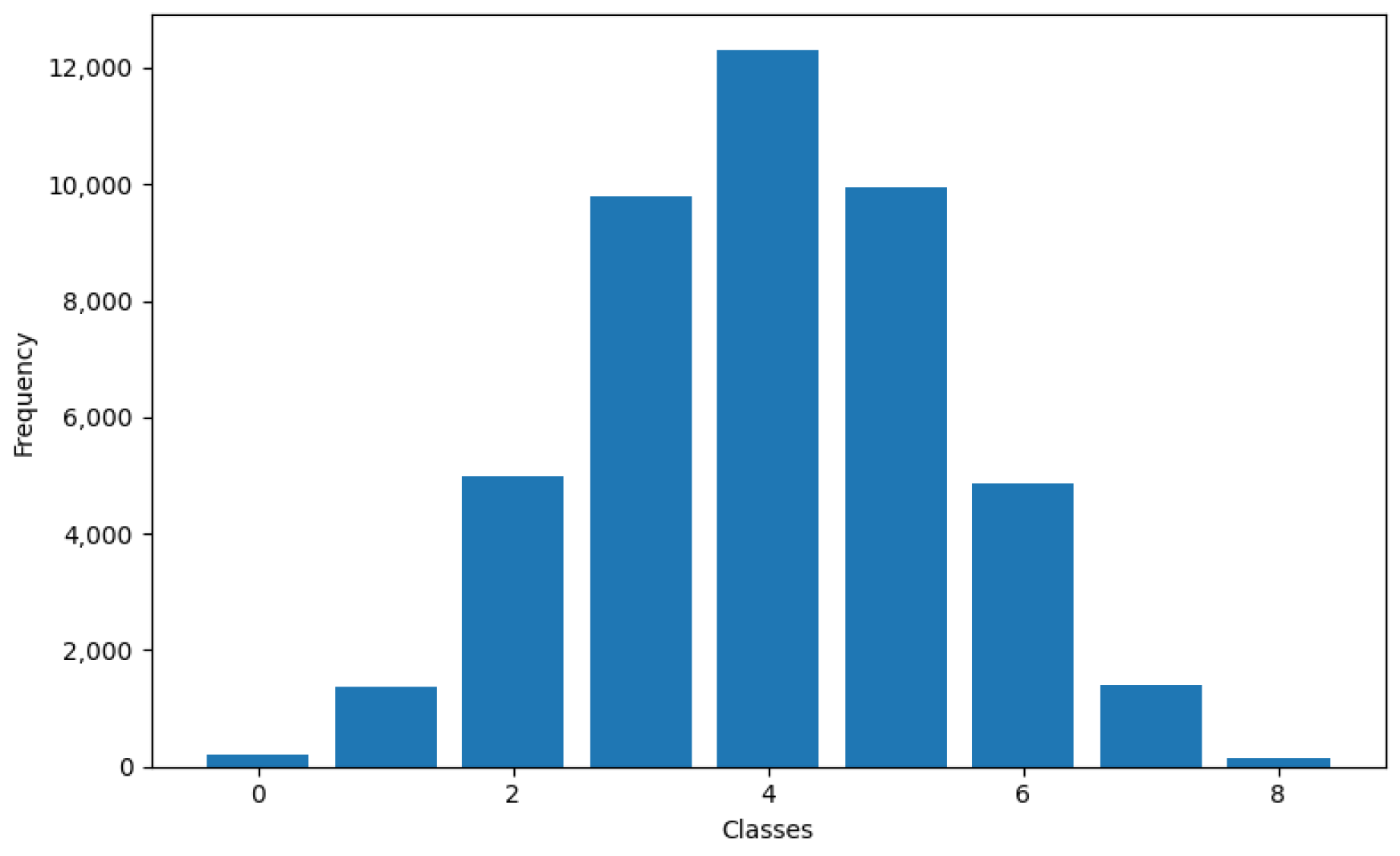
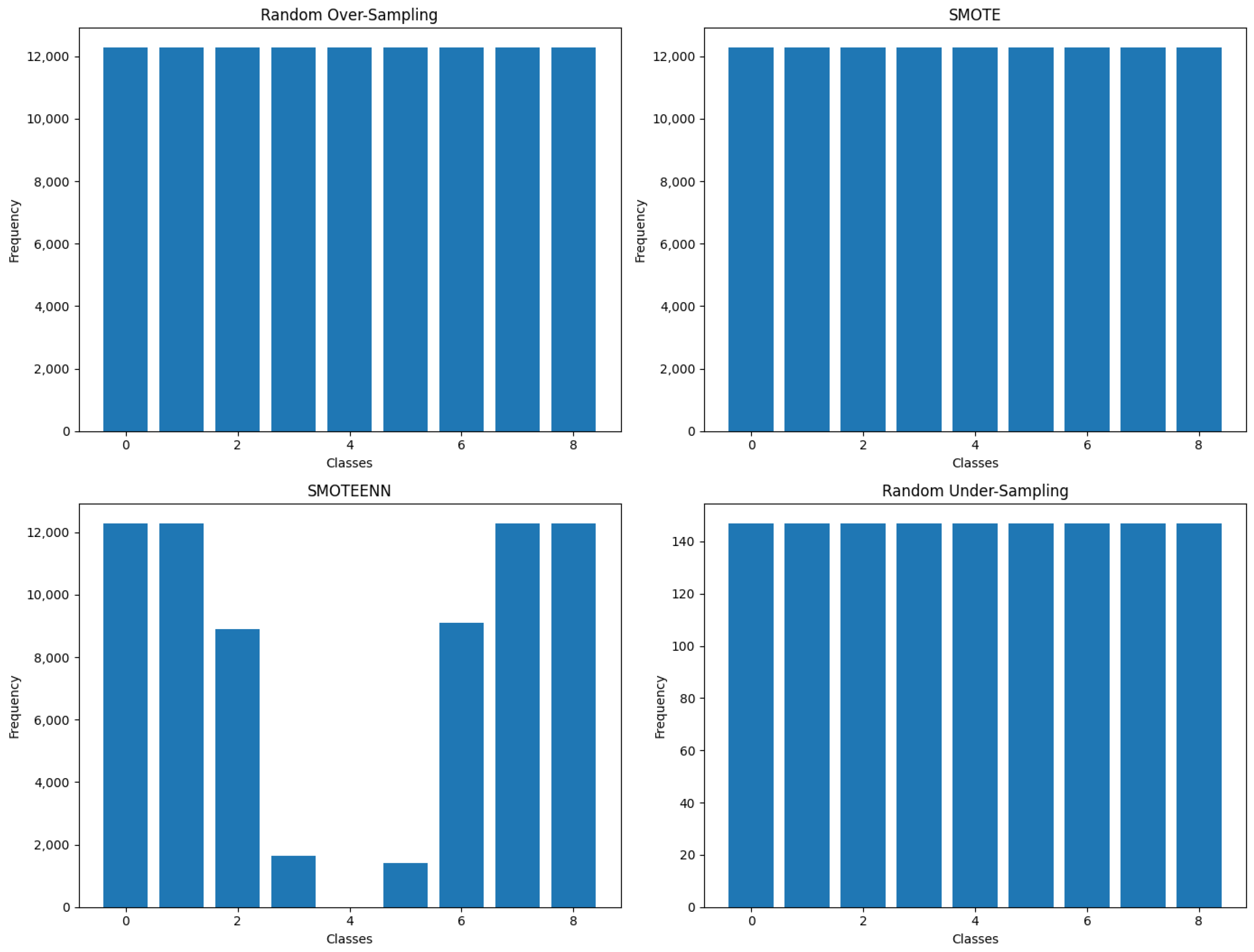
To demonstrate SMOTE’s effect, consider the CHES dataset in the context of side-channel analysis. Figure 2 depicts its inherent class imbalance. Applying SMOTE to this dataset yields a new distribution as shown in Figure 3, where the class sizes are more balanced, with each class approaching approximately 14,000 instances.

3.2. Synthetic Minority Oversampling Technique with Edited Nearest Neighbor (SMOTEENN)

SMOTEENN combines two techniques to address class imbalance and potential noise within a dataset. First, SMOTE generates synthetic samples for minority classes to augment their representation. Then, the Edited Nearest Neighbor (ENN) algorithm identifies and removes samples whose class label differs from at least two of their k nearest neighbors, with a common choice for k being 3. This process aims to smoothen decision boundaries and reduce the impact of noisy or mislabeled instances across all classes.

The SMOTEENN process begins with the application of SMOTE to create synthetic minority class samples, initially achieving class balance. Subsequently, ENN meticulously examines all classes and removes potentially mislabeled or noisy samples. While this cleaning phase helps to refine the dataset by eliminating noise, it also has the potential to reintroduce a degree of imbalance.

To illustrate with the CHES dataset as shown in Figure 3, if it exhibits a natural imbalance with a dominant class 4, SMOTEENN’s oversampling step would generate synthetic minority examples. However, the ENN stage might remove a significant portion of class 4 due to feature overlap or noise, potentially resulting in near-zero instances of that class.

It is important to note that SMOTEENN’s sequential design could lead to a reintroduction of class imbalance after the cleaning phase. Exploring different orders of operation or iterative applications may be necessary for optimal results. Furthermore, the algorithm is particularly effective when datasets contain noisy data, as the ENN component helps mitigate the negative impact of such inconsistencies.

3.3. Random Oversampling

Random oversampling offers a straightforward approach to mitigating class imbalance by randomly replicating samples from minority classes with replacement, aiming to increase their representation to a size comparable to the largest class in the dataset. This method is characterized by its simplicity, being computationally efficient and easy to implement. However, it carries the potential risk of overfitting, as models may over-adapt to specific, duplicated instances. Unlike methods such as SMOTE, random oversampling does not generate new synthetic data points, relying solely on existing samples.

Consider the CHES dataset in its naturally imbalanced state, as shown in Figure 2. The application of random oversampling leads to a modified distribution as shown in Figure 3. In this oversampled version, all classes now possess around 14,000 instances, representing the original size of the largest class.

Although random oversampling can improve class balance, its potential for overfitting deserves careful consideration. Alternative techniques, such as SMOTE, which introduce synthetic samples to expand the distribution of the minority class, may sometimes be a more robust choice. The most suitable oversampling method depends on the specific characteristics of the dataset and the machine learning models used.

3.4. Random Undersampling

Random undersampling offers a direct approach to addressing class imbalance by reducing the representation of majority classes. It involves randomly selecting a subset of samples from each majority class, without replacement, until they match the size of the smallest (minority) class. The core mechanism of this method is straightforward to implement, making it simple and computationally efficient. However, the primary drawback of random undersampling lies in the potential loss of valuable information from the majority classes. This reduction could hinder the model’s ability to learn a comprehensive representation of these classes.

In the example of the CHES dataset, applying random undersampling as shown in Figure 3 results in all the classes being reduced to the smallest original class size (160 instances). This demonstrates how random undersampling, despite achieving class balance, can lead to the loss of potentially significant data from larger classes [11].

3.5. Noise Addition for Regularization

The introduction of Gaussian noise within hidden layers can act as a powerful regularization technique to combat overfitting in MLP and CNN architectures. This approach is supported by previous research that demonstrates its ability to improve generalization, particularly in scenarios involving small and imbalanced datasets [36]. Similar to data augmentation, the injection of Gaussian noise creates perturbations, compelling the model to learn more robust feature representations that generalize better to unseen data.

The primary mechanism of noise injection as a regularization technique lies in its implicit expansion of the training dataset. By forcing the model to continuously adapt to slightly modified inputs, it encourages the learning of robust features that generalize better. Strategic placement of noise within batch normalization layers can amplify its effectiveness due to the sensitivity of normalization to input variations. It is important to note that, unlike traditional data augmentation, noise injection relies on perturbing existing data rather than explicitly creating new, transformed instances.

The potential of noise addition for improving generalization holds a particular interest in SCA, where class imbalance is often present. Its ability to improve the robustness of the model could improve the classification of underrepresented sensitive value classes.

3.6. Hybrid Bagging Resampling Framework

Algorithm 1 illustrates our proposed hybrid bagging resampling deep learning SCA framework in a pseudocode form.

Algorithm 1 Pseudo-code for Hybrid Bagging Resampling DL-SCA

//method = [‘basic’, ‘smote’, ‘smoteenn’, ‘random oversampling’, ‘random under sampling’, ‘noise addition’]

//dlearning = [‘MLP’, ‘CNN’]

Step 1: Start

Step 2: Set $n=50$, the total number of ML models to train

Step 3: Select an arbitrary hyperparameter combination

Step 4: Initialize $k=0$, index of the sampling method to start with

Step 5: while $k<\mathrm{length}\left(\mathrm{method}\right)$ do

Step 6:     Apply data enhancement technique using method[k]

Step 7:     Initialize $m=0$, index of the deep learning method to start with

Step 8:     while $m<\mathrm{length}\left(\mathrm{dlearning}\right)$ do

Step 9:        Using the profiling dataset, train n models of type dlearning[m] using random search of hyperparameter combinations

Step 10:        Rank the models based on performance and form ensembles of 5, 10, and 20 models, resulting in ensemble sizes of [1, 5, 10, 20, 50] models

Step 11:        Use the ensembles to attack the validation dataset and select the best ensemble

Step 12:        Use the best ensemble to attack the test dataset and predict the secret key

Step 13:        Output the predicted key value

Step 14:        $m=m+1$

Step 15:     end while

Step 16:     $k=k+1$

Step 17: end while

Step 18: End

4. Hybrid Bagging Resampling for Deep Learning-Based Side-Channel Analysis

This section presents and analyzes the experimental findings from our investigation of the ASCAD and CHES datasets. We employed ensemble deep learning techniques, including multi-layer perceptrons (MLPs) and convolutional neural networks (CNNs), to perform SCA attacks on these datasets, which were balanced using various data sampling techniques.

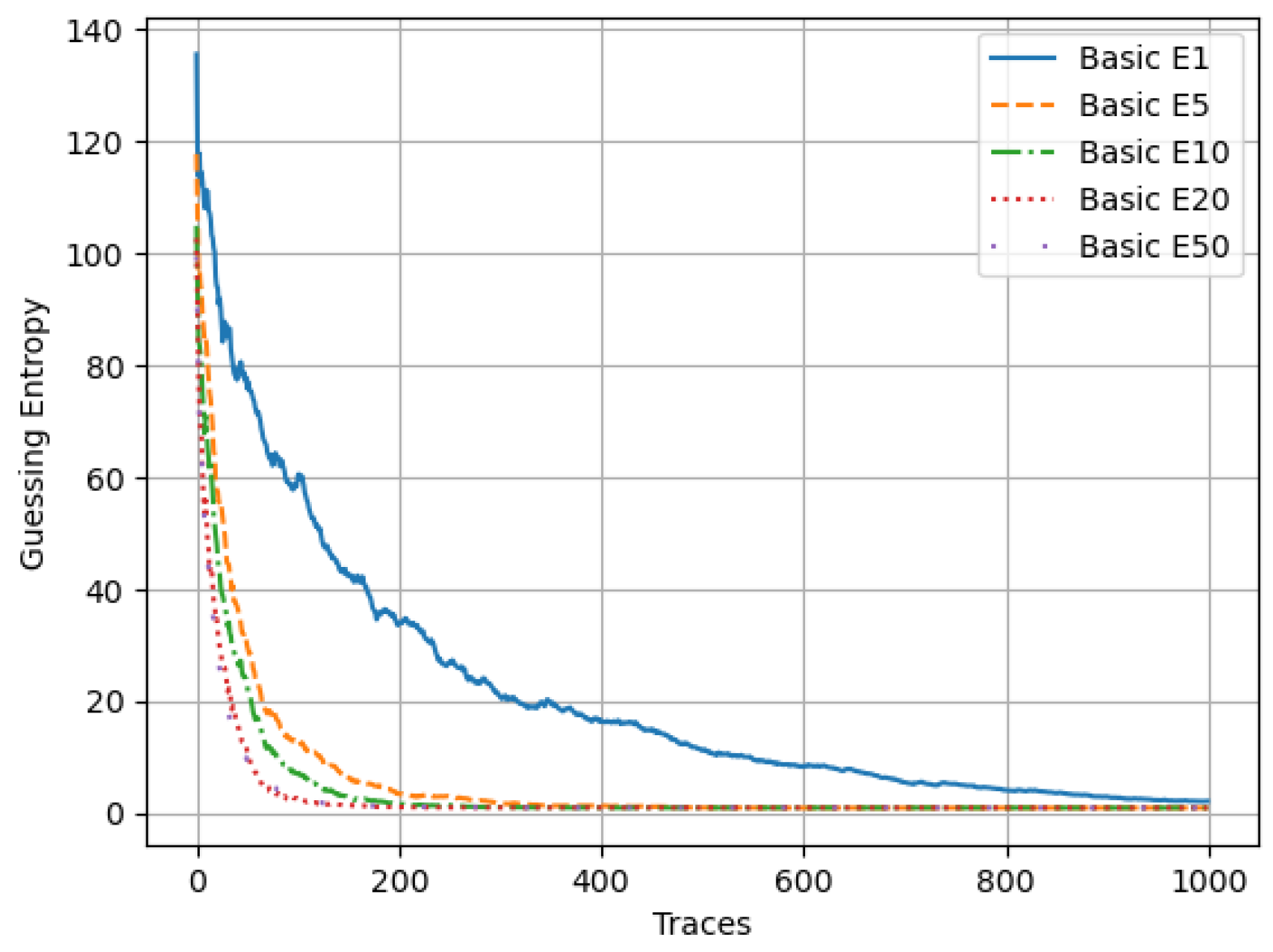
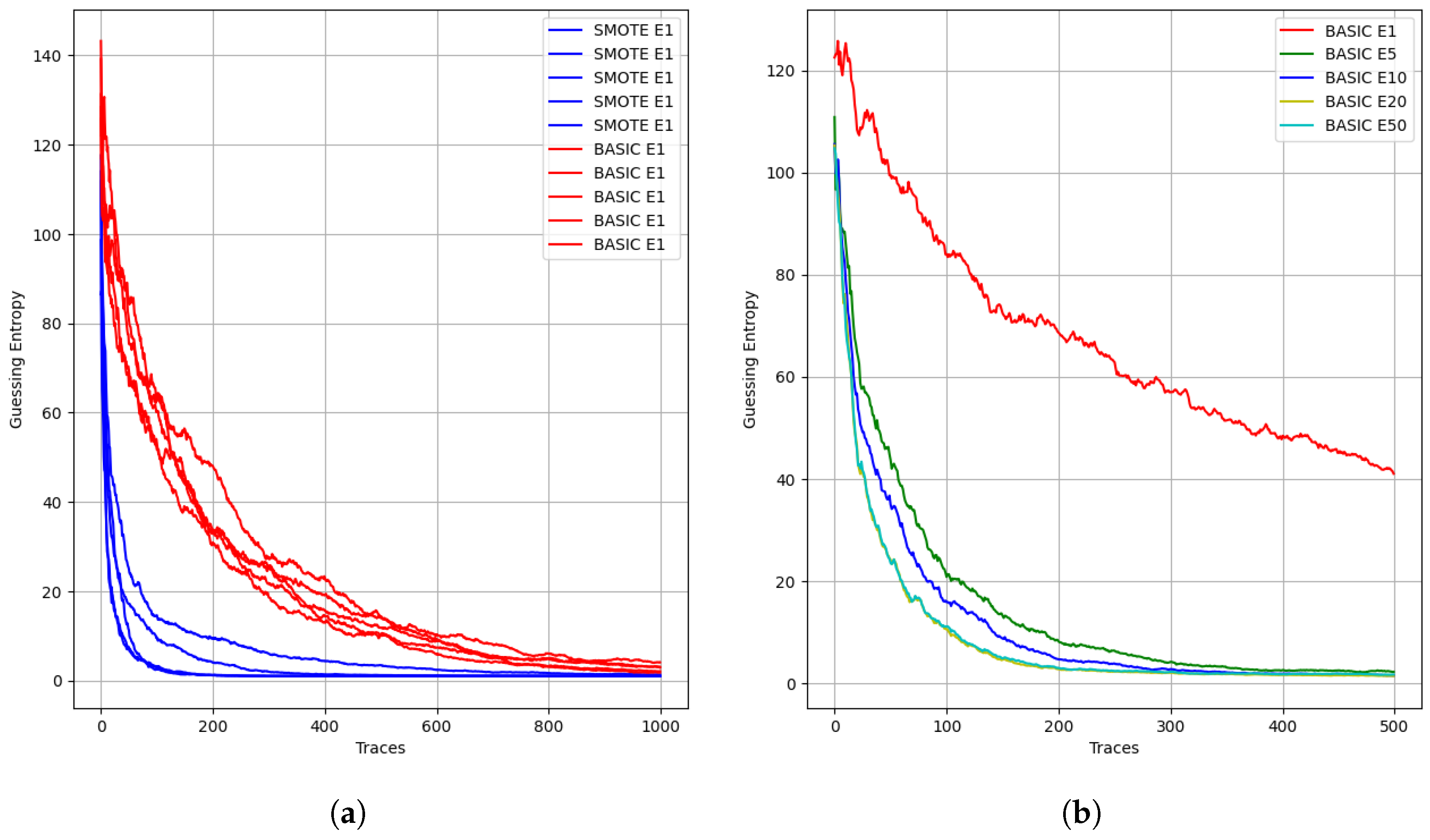
Before conducting our proposed experiments, we demonstrated the research problem by investigating the impact of class imbalance on ML model performance. Our proposed hybrid bagging ensemble combines data enhancement and ensemble methods. Prior to the experimental section, we independently assessed the effectiveness of each method in addressing dataset imbalance. One of these methods, SMOTE, was used to balance the imbalanced dataset. We selected SMOTE as the data enhancement method and trained fifty ML models, referred to as SMOTE E1 models. Similarly, we trained fifty ML models on the naturally imbalanced dataset, referred to as BASIC E1 models. Overall, the SMOTE E1 models outperformed the BASIC E1 models in terms of attack performance, requiring fewer than 200 traces to break the secret key, compared to 1000 traces for the BASIC models. To facilitate visualization, Figure 4a shows the performance curves of the five best models from both the SMOTE E1 and BASIC E1 groups. In other words, the imbalanced dataset required over 1000 traces to predict the secret key, as shown in Figure 4a, whereas a balanced dataset required around 200 traces, demonstrating a five-fold improvement in performance. This preliminary investigation helped us understand the effectiveness of each method in addressing data imbalance.

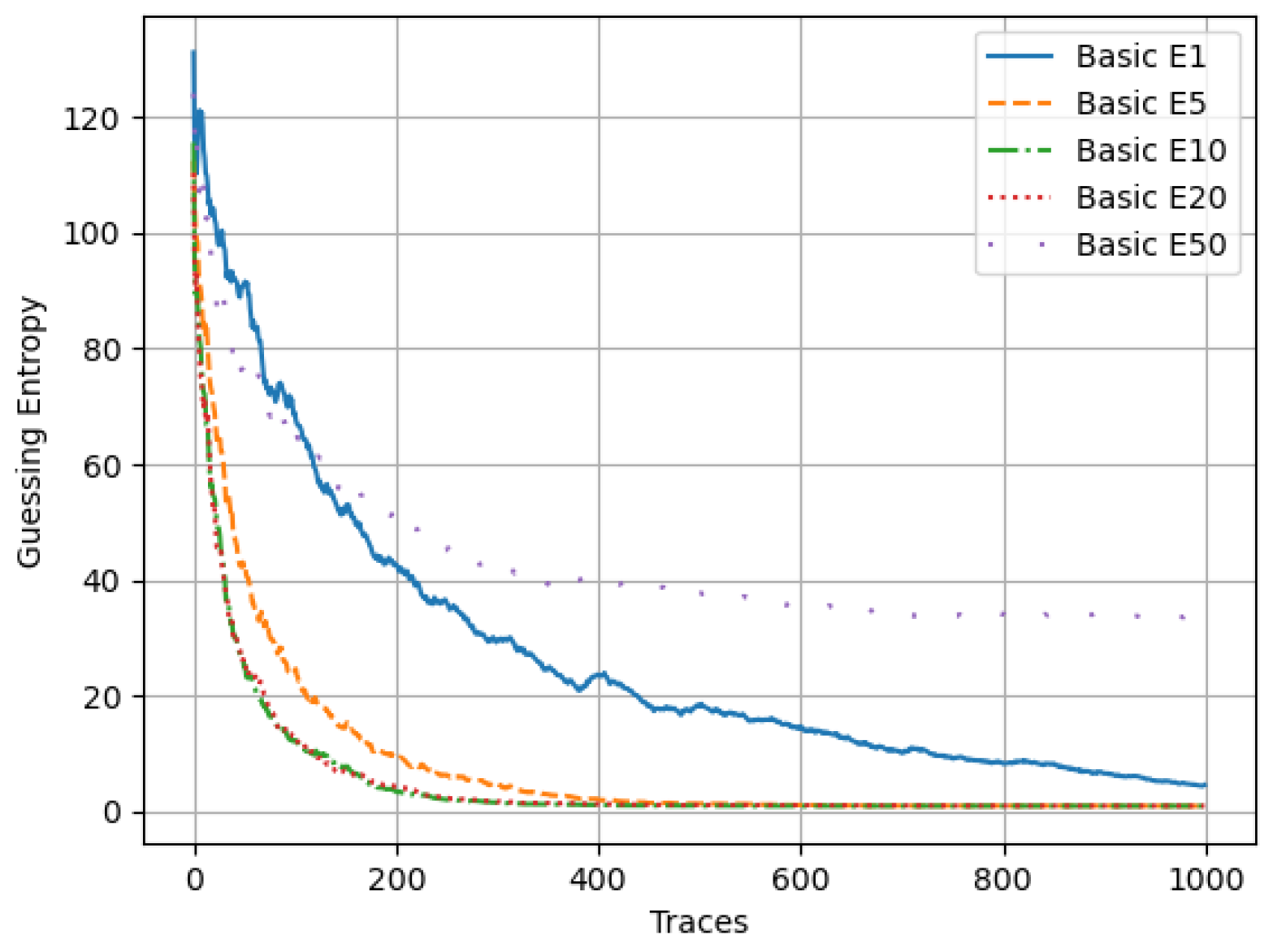
In the same vein, we also compare traditional non-ensemble methods with ensemble methods. From the plots displayed in Figure 4b, we observe that the poorest performing model is the traditional single model, which we have named E1. This single model never attained a GE of 1. In contrast, all the ensemble models successfully predicted the secret key, requiring a maximum of 400 traces to do so. In summary, addressing data imbalance is crucial for enhancing model efficiency and accuracy. This paves the way for further experimentation and detailed analysis in the next section.

4.1. Experimental Setup

In this section, we will describe the experimental setup for this project. Our main objective is to investigate the performance of the deep learning bagging data resampling methodology on established SCA attacks. Specifically, we focus on the HW leakage model of the ASCAD and CHES datasets, which are known to exhibit class imbalances. These imbalances present a challenge that our technique aims to overcome.

To address these imbalances, we employ a variety of data enhancement techniques in the initial stage, including SMOTE, SMOTEENN, random oversampling, random undersampling, and noise techniques. These methods are applied to mitigate the class imbalance within the datasets. In the second phase, we utilize the enhanced datasets to conduct profiled attacks using deep learning models, specifically MLP and CNN. We implement a bagging approach, which involves training multiple models on the entire training data and combining their predictions to improve overall performance and robustness. By employing this two-stage methodology, we aim to demonstrate the effectiveness of our proposed bagging data resampling approach in improving the accuracy and reliability of SCA attacks on imbalanced datasets. We illustrate all these steps in the pseudo-code contained in Algorithm 1.

On the training set, we conduct a five-fold cross-validation. We use the averaged results of individual folds to select the best classifier parameters. We report results from the testing phase only, as these are more relevant for assessing the actual classification strength of the constructed models. This focus ensures that our evaluation reflects the model’s performance on unseen data, providing a more accurate measure of its effectiveness and robustness in real-world scenarios. Furthermore, we carried out the experiment for each test case fifty times and then averaged the results to ensure statistical significance and reliability.

Our computational infrastructure consisted of nodes equipped with 16 GB NVIDIA Tesla V100 SXM2 GPUs, each offering performance comparable to 100 CPUs. The experiments were implemented using the TensorFlow framework and conducted with the scikit-learn library in Python.

For MLP-based attacks, we employed the Adam optimizer for training over 50 epochs with learning rates ranging from 0.0001 to 0.01 and minibatch sizes between 50 and 2000. MLP architectures varied from three to eight dense layers, containing 50 to 2000 neurons per layer. We evaluated several activation functions, including ReLU, Tanh, and SELU.

For the CNN-based model, we utilized minibatch sizes ranging from 500 to 1000, with two to eight dense layers containing 500 to 800 neurons each. We incorporated one or two convolutional layers with filter sizes between 8 and 32, employing 1-D convolution due to the one-dimensional nature of our data. We explored ReLU, Tanh, ELU, and SELU activation functions, with learning rates set at either 0.0001 or 0.001. Kernel sizes ranged from 10 to 20, and strides from 5 to 10.

4.2. Methodology

In this experiment, we demonstrate the potency of our proposed hybrid bagging resampling framework for datasets subjected to data balancing and data enhancement techniques. For each data enhancement method, we trained 50 models with a random search hyperparameter tuning. We then selected the top 1, 5, 10, 20, and 50 models to form ensembles labeled $E1$, $E5$, $E10$, $E20$, and $E50$, respectively. These ensemble models were evaluated in profiling attacks, and their performance was measured using GE. The $E1$ model is a commonly used single model and is not an ensemble model. It provides a performance benchmark against which ensemble models are compared.

In our analysis, we independently examined each individual data sampling technique, determining which ensemble models performed best for that technique using CNN and MLP classifiers on the ASCAD and CHES datasets. The results and code are available on our GitHub page (https://github.com/Hoda-alkhzaimi/EMARATSEC-sidechannels-analytics-/tree/main) (accessed on 9 August 2024).

5. Results for Proposed Resampling Ensemble

This work investigates the impact of bagging ensemble on six data enhancement techniques for CNN and MLP architectures on ASCAD and CHES datasets. Our goal is to determine how these hybrid two-stage techniques can improve the performance of SCA attacks.

5.1. ASCAD Dataset

The GE results for the ASCAD dataset are presented with up to 500 traces only, as the addition of more traces does not result in a significant change in GE. Thus, after 500 traces, the GE attains a steady state across all models. Overall, the Basic and Noise addition ensemble techniques demonstrate very strong performance when using MLP, highlighting the significant benefits of the bagging ensemble.

We will provide an overview of the results obtained before delving into the details. First, it is important to clarify that the technique named Basic refers to the case where no sampling was carried out, leaving the dataset in its naturally imbalanced state. The Noise technique represents the scenario where the dataset has been regularized by the addition of Gaussian noise.

Over 50 runs of experiments, the mean performance of MLP and CNN ensemble models for each sampling technique on the ASCAD dataset are shown in

Table 3. ASCAD: Ensemble model of MLP performance. RO: Random Oversampling; RU: Random Undersampling.

Sampling Technique	Best Ensemble	Mean Traces	Mean GE
Basic	$E20$	83	1
Noise	$E20$	102	1
SMOTE	$E50$	250	1
SMOTEENN	$E20$	94	1
RO	$E20$	400	1
RU	$E10$	255	5

and

Table 4. ASCAD: Ensemble model of CNN performance. RO: Random Oversampling; RU: Random Undersampling.

Sampling Technique	Best Ensemble	Mean Traces	Mean GE
Basic	$E20$	304	1
Noise	$E10$	203	1
SMOTE	$E20$	−	4.24
SMOTEENN	$E50$	154	1
RO	$E20$	900	1
RU	$E10$	−	4.51

Note: The minus (−) sign indicates that the model did not converge to a solution.

. The table has four columns, with the first column listing the names of sampling techniques. The Ensemble column shows the ensemble that yields the best test performance for that particular sampling technique. The traces column contains the number of traces a sampling technique needed to predict a GE of 1. The last column, GE, shows the final trace after attacking the test set. For a successful attack, the GE is 1. In summary, the best models are the ones that require the least amount of traces to obtain a GE of 1. If a model never attained a GE of 1, then the traces column will be empty.

In the Basic unsampled dataset, MLP ensembles have exceptional performance. On the contrary, CNN ensembles show performance degradation beyond a certain count, with $E20$ being the optimal configuration. Similar results emerge with the Noise addition method, with MLP performance consistently strong. However, a surprising observation is that the $E50$ ensemble of CNN becomes the worst performer within this dataset. This emphasizes that blindly increasing model counts for CNN in noise-infused data can produce diminishing returns, with $E10$ demonstrating the best balance for this scenario.

SMOTE ensemble results are more variable among MLP and CNN techniques. Performance generally improves with the ensemble count up to a point (often E20), followed by a decrease. In the SMOTE-sampled ASCAD dataset, MLP performs better than CNN across all ensembles. The SMOTEENN technique consistently demonstrated competitive performance compared to Basic, and Noise ensembles. Within SMOTEENN, MLP performance tends to improve with increasing ensemble size, while CNN sees gains in GE with more models. However, this improvement plateaus for CNN models equally at E20.

Random Oversampling (RO) results lack consistency. Its CNN models performance ranks fourth out of six models with Basic, Noise and SMOTEENN enhancement techniques demonstrating better performances. Lastly, Random Undersampling (RU) leads to the worst performance in both MLP and CNN techniques across all ensemble models. This highlights the importance of careful data sampling choices for SCA.

SMOTEENN attained the best result overall in the ASCAD dataset, followed by the Basic, Noise and RO methods, respectively. Detailed performance analysis of each sampling technique on the ASCAD dataset is provided in the following sections.

5.1.1. Basic Ensemble

The GE for all ensemble models of the MLP technique in the basic ASCAD dataset is shown in Figure 5. Our analysis indicates that all ensemble models, with the exception of model $E1$, exhibit strong performance. Models $E20$ and $E50$ achieve a GE of 1.00, while $E10$ attains a GE of 1.01, and $E5$ achieves a GE of 1.53. $E1$ model demonstrates the weakest performance with a GE of 14.73. These results suggest that ensemble techniques significantly enhance the performance of MLP-based SCA compared to the single-model baseline ($E1$). Optimal performance is observed with $E20$, and further increasing the ensemble size yields comparable performance at a higher computational cost.

The GE for all ensemble models of the CNN technique in the basic ASCAD dataset is shown in Figure 6. The $E10$ model demonstrates the optimal performance with a GE of 1, closely followed by the $E20$ model with a GE of 1.05. The $E5$ model has a GE of 1.1. As expected, the $E1$ model has a weak performance with a GE of 4. Surprisingly, the $E50$ model also performs poorly, demonstrating a GE of 41. These findings suggest that ensemble techniques generally enhance the performance of CNN-based SCA on the basic unsampled ASCAD dataset compared to the single-model baseline. However, increasing the ensemble size beyond 20 leads to a significant decline in performance, with the potential to obtain worse performance than the single model $E1$.

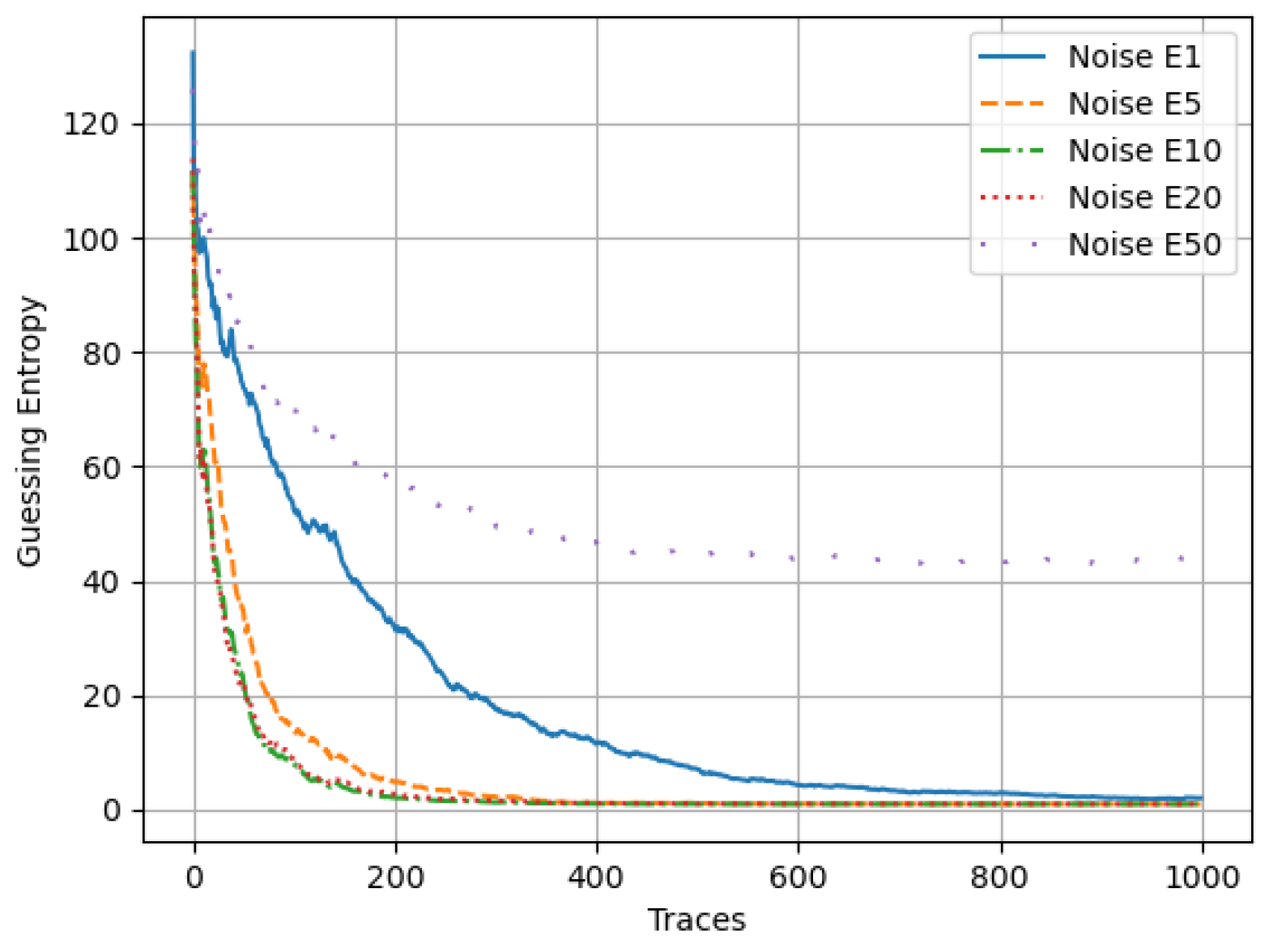
5.1.2. Noise Ensemble

The GE for all ensemble models of the MLP technique in the noise-infused ASCAD dataset is shown in Figure 7. All ensemble models, with the exception of $E1$, demonstrate robust performance. $E50$, $E20$, $E10$, and $E5$ all achieved the GE of 1. $E50$ achieved the best attack performance, requiring only 102 traces to predict the secret key. As anticipated, the $E1$ model demonstrates the weakest performance with a GE of 3.86. These results conclusively indicate that ensemble techniques significantly improve the performance of MLP-based SCA on the noise-infused ASCAD dataset.

The GE for all ensemble models of the CNN technique in the noise-infused ASCAD dataset is shown in Figure 8. Unexpectedly, $E50$ exhibits the weakest performance among all ensemble models with a GE of 1. The remaining models, including $E1$, demonstrate significantly lower GE values. The $E10$ model achieves optimal performance with a GE of 1 requiring 203 traces, closely followed by $E20$, $E5$, and $E1$ also having a GE of 1. To carry out key prediction, the $E20$ and $E5$ models require 250 and 300 traces, respectively. $E1$ after 1000 traces only attained a GE of 2.5. These findings suggest that increasing the ensemble size beyond $E20$ dramatically degrades the performance of CNN-based SCA on the noise-infused ASCAD dataset, potentially resulting in outcomes significantly worse than the single-model $E1$.

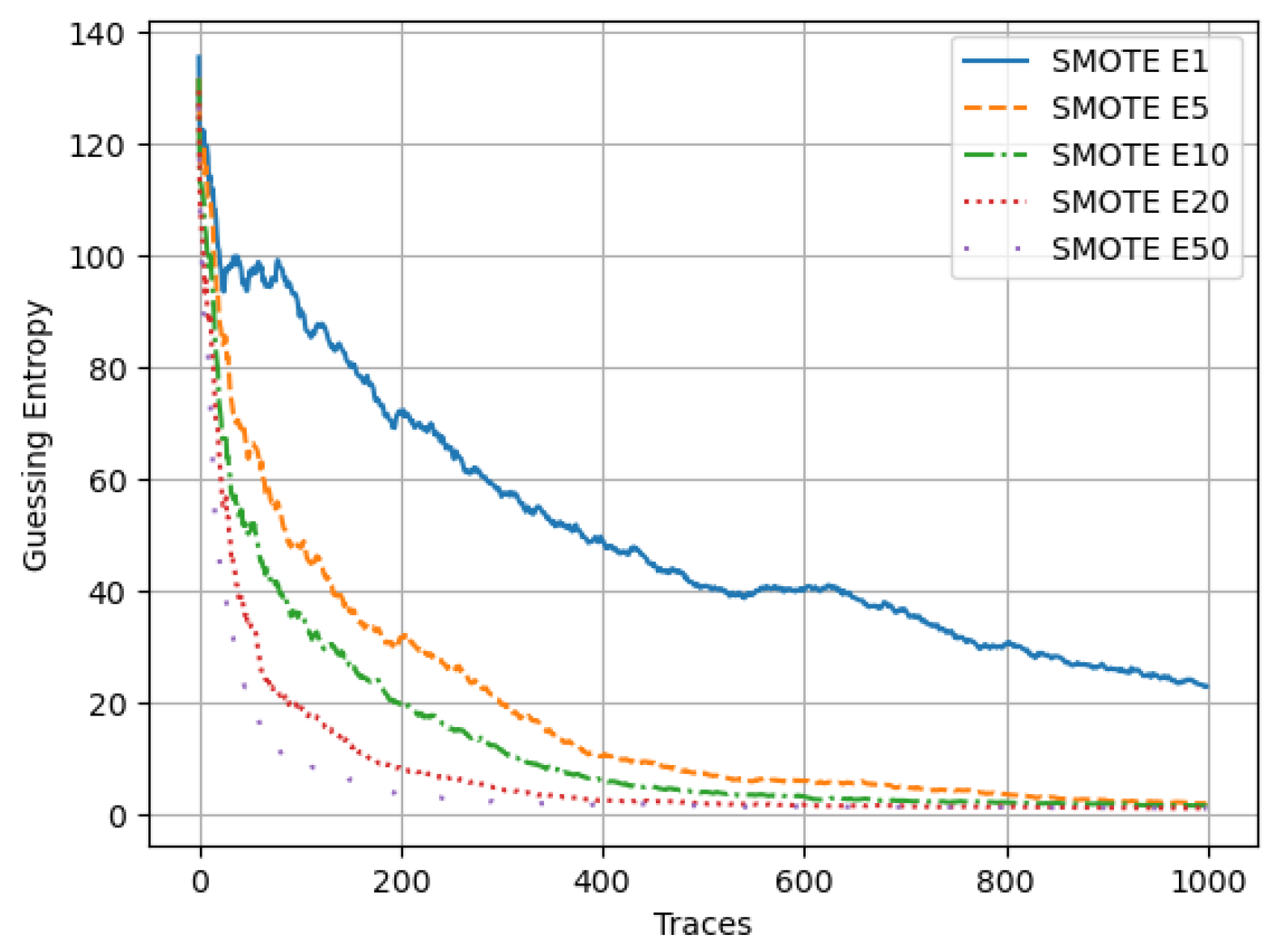
5.1.3. SMOTE Ensemble

The GE for all ensemble models of the MLP technique in the ASCAD dataset resampled with SMOTE is shown in Figure 9. The $E1$ model exhibits the weakest performance with a GE of 21. Performance significantly improves with increased ensembling: the $E5$ model achieves a GE of 1 in 850 traces, the $E10$ model attains a GE of 1 in 450 traces, the $E20$ model attains a GE of 1 in 303 traces while the $E50$ attains the optimal performance, requiring 250 traces to attain GE of 1. This suggests that increasing the ensemble size up to $E50$ improves the performance of MLP-based side-channel analysis on the SMOTE-sampled ASCAD dataset.

The GE for all ensemble models of the CNN technique in the ASCAD dataset resampled with the SMOTE is shown in Figure 10. The $E1$ model demonstrates the weakest performance with a GE of 39. Performance improves significantly as the ensemble count increases: the $E5$ model has a GE of 9, the $E10$ model has a GE of 6, and the $E20$ has a GE of 4. Thus, the $E20$ model achieves optimal performance. However, further increasing the ensemble size leads to performance degradation, as observed in the $E50$ model’s GE of 18.5. This trend contrasts the behavior of MLP models, suggesting that ensembling beyond $E20$ can positively impact the performance of MLP models but degrade CNN-based SCA on the SMOTE-sampled ASCAD dataset.

5.1.4. SMOTEENN Ensemble

The GE for all ensemble models of the MLP technique in the ASCAD dataset resampled with the SMOTEENN technique is shown in Figure 11. Overall, the SMOTEENN data sampling technique appears vastly effective for SCA compared to Basic, or Noise ensembles. However, within the context of SMOTEENN, the $E50$ model achieves the best performance, attaining GE of 1 in 94 traces, followed by $E20$, $E10$, and $E5$, requiring 180, 250, and 600 races, respectively. The $E1$ model exhibits the weakest performance with a GE of 14. These results suggest that increasing the ensemble size beyond $E20$ degrades the performance of MLP-based SCA in the SMOTEENN-sampled ASCAD dataset.

The GE for all ensemble models of the CNN technique in the ASCAD dataset resampled with the SMOTEENN technique is shown in Figure 12. Consistent with the MLP results, the SMOTEENN data sampling technique generally demonstrates similar performance for CNN-based SCA compared to Basic, Noise, or SMOTE techniques. However, a unique trend emerges within the SMOTEENN context: performance improves as the ensemble size increases. The $E50$ model achieves optimal performance with a GE of 1 in 154 traces, followed by $E20$, $E10$ and $E5$ with all having GE of 1 in 270, 300 and 420 traces, respectively. As expected, the $E1$ model has the weakest performance with a GE of 4. This pattern suggests that, while increasing the ensemble size does enhance the performance of CNN models on the SMOTEENN-sampled ASCAD dataset, it likely comes at a significant computational cost.

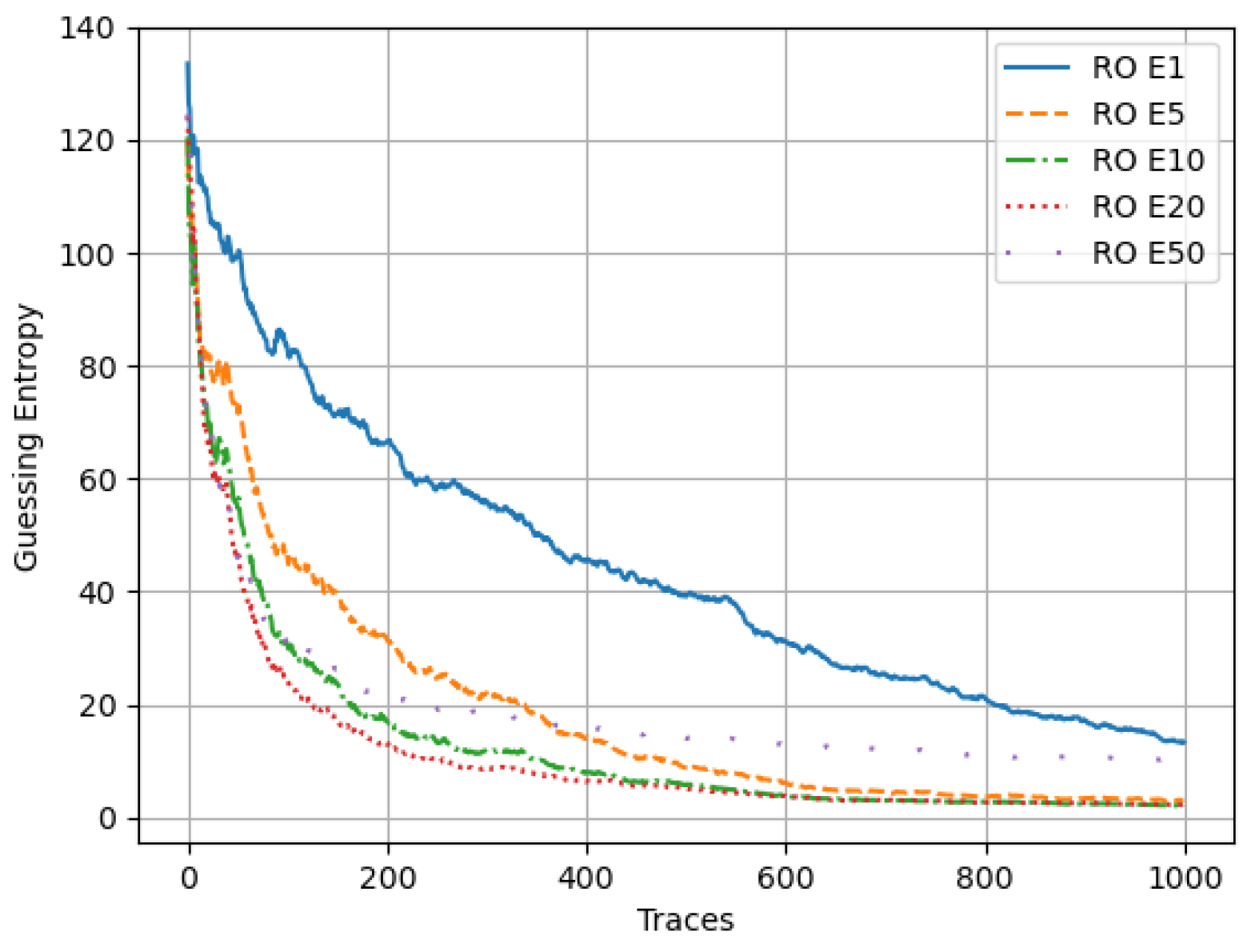
5.1.5. Random Oversampling (RO) Ensemble

The GE for all ensemble models of the MLP technique in the ASCAD dataset resampled with the Random Oversampling (RO) technique is shown in Figure 13. In general, the RO data sampling technique does not perform as well compared to the Basic, Noise, or SMOTEENN techniques. However, within the RO technique, $E50$ has the best GE of 1 in 400 traces, followed by $E20$ with a GE of 1 in 420 traces. $E10$ and $E5$ follow next with a GE of 1, requiring 650 and 900 traces. The $E1$ model demonstrates the worst performance with a GE of 17. RO sampling performance using the MLP technique increases with the number of models in the ensemble.

The GE for all ensemble models of the CNN technique in the ASCAD dataset resampled with the RO technique is shown in Figure 14. Overall, the RO data sampling technique exhibits lower performance in SCA compared to Basic, Noise or SMOTEENN techniques. The $E1$ model demonstrates the weakest performance with a GE of 17. Performance improves with increasing ensemble count, reaching an optimal point with $E20$, which achieves a GE of 3.62. However, further increasing the ensemble size leads to a significant decline in performance, as evidenced by the $E50$ model’s GE of 12. This indicates that the performance of CNN-based SCA on the RO-sampled ASCAD dataset is negatively impacted by excessive ensembling, beyond $E20$.

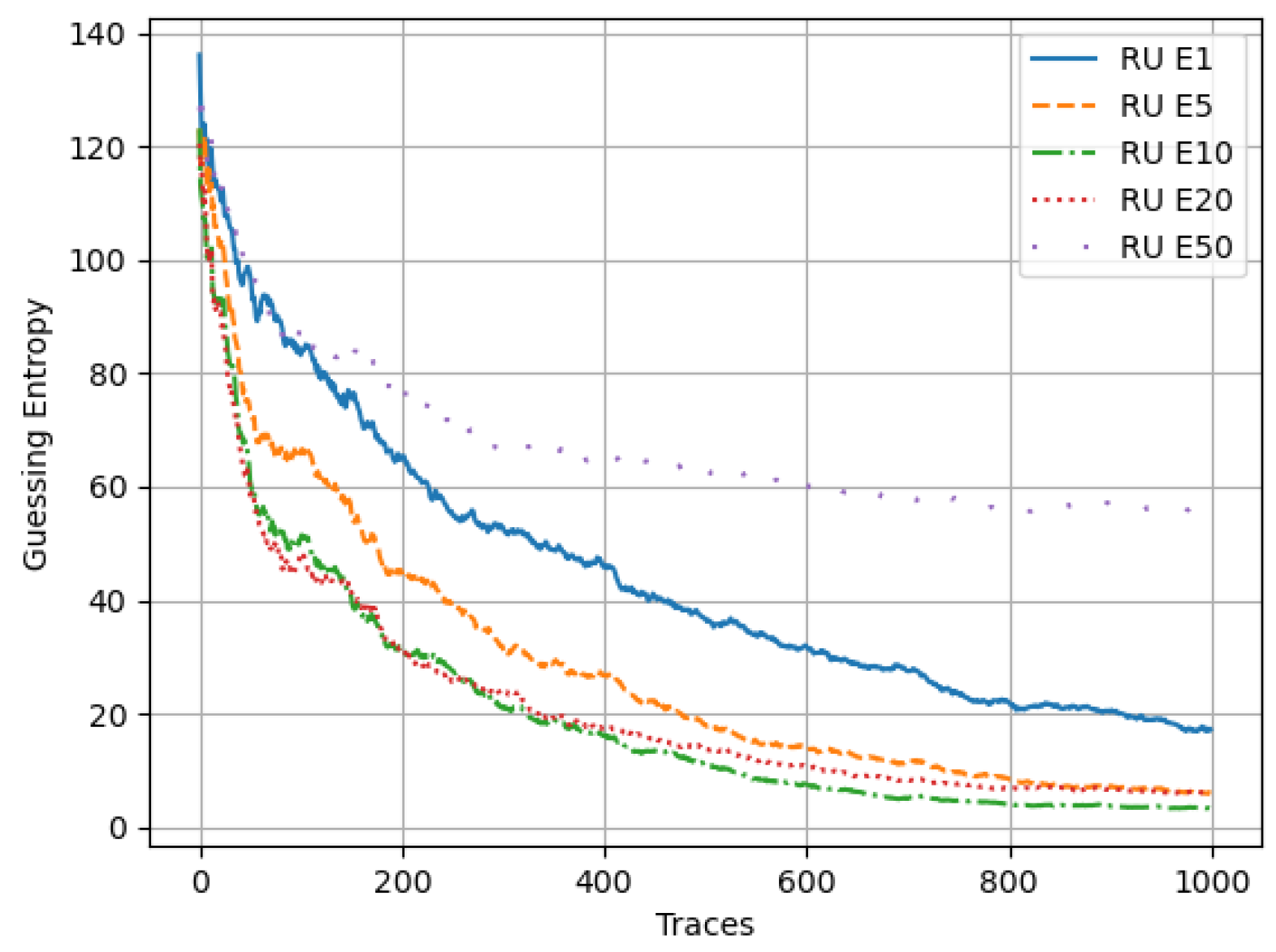
5.1.6. Random Undersampling Ensemble

The GE for all ensemble models of the MLP technique in the ASCAD dataset resampled with the Random Undersampling (RU) technique is shown in Figure 15. In general, the RU data sampling technique does not perform as well compared to Basic, Noise, SMOTE, SMOTEENN and RO techniques. All the models have GE greater than 15. $E50$ performed the worst with a GE of 78 while $E10$ performed the best with a GE of 9. Overall, RU sampling with MLP demonstrates the worst performance in all analyzed techniques.

The GE for all ensemble models of the CNN technique in the ASCAD dataset resampled with the Random Undersampling (RU) technique is shown in Figure 16. RU sampling with CNN demonstrates a better performance than the MLP version. The $E1$ model has a GE of 20. Performance improves with increasing ensemble count, with $E5$ and $E20$ achieving the best GE at 7. $E10$ achieved the best performance at a GE of 4.

5.2. Comparison with Results from Literature

Additionally, we compared the results of our proposed hybrid bagging resampling framework with methods from the literature and provided a summary of the results in

Table 5. ASCAD: comparison with methods from literature.

Sampling Technique	[37]	[38]	Proposed Bagging Resampling MLP	Proposed Bagging Resampling CNN
Complexity	5566	1,388,457	2,145,000	4,870,400
Trace to reach GE of 1	906	447	83	154

. Our proposed framework is highly competitive compared to [37,38] in terms of the number of traces and complexity, i.e., the number of operations per sample per training and the time taken to reach a GE of 1, surpassing existing methods. Our proposed methods outperform [37] by almost 11 times in performance and over five times in performance compared to [38]. The complexity of our method is comparatively more; however, the realized performance compensates for this. Ways to preserve performance and reduce complexity will be the focus of further research.

5.3. Analysis of the CHES Dataset

We have also applied our proposed bagging resampling framework to the CHES dataset. The plots we obtained in this dataset closely matched the ASCAD dataset results. In this analysis, we have summarized the results in

Table 6. CHES: Ensemble model of MLP performance. RO: Random Oversampling; RU: Random Undersampling.

Sampling Technique	Best Ensemble	Mean Traces	Mean GE
Basic	$E20$	90	1
Noise	$E20$	103	1
SMOTE	$E20$	320	1
SMOTEENN	$E20$	266	1
RO	$E10$	280	1
RU	$E10$	−	103

Note: The minus (−) sign indicates that the model did not converge to a solution.

and

Table 7. CHES: Ensemble model of CNN performance. RO: Random Oversampling; RU: Random Undersampling.

Sampling Technique	Best Ensemble	Mean Traces	Mean GE
Basic	$E20$	46	1
Noise	$E20$	68	1
SMOTE	$E20$	489	1
SMOTEENN	$E20$	143	1
RO	$E20$	130	1
RU	$E5$	−	67

Note: The minus (−) sign indicates that the model did not converge to a solution.

. We will, therefore, be analyzing these results.

A key observation within the CHES dataset is the generally superior performance of CNN ensemble models compared to MLP models, with the exception of Random Undersampling. CHES containing 2200 features versus 700 in ASCAD can be attributed to why CNN performance was stronger. Furthermore, with Basic (unsampled) data, the performance of the CNN ensemble is particularly strong. In MLP ensembles, the $E1$ model consistently exhibits the worst performance, highlighting the significant benefits of ensembling.

The Noise infusion technique yields a pattern similar to that of basic sampling. CNN models achieve GE values below 10, while ensembling significantly boosts the performance of MLP relative to the single model scenario ($E1$). This suggests that ensembling offers a greater relative improvement for MLP compared to CNN within the noise-infused CHES dataset.

SMOTE sampling shows an increase in performance for both MLP and CNN ensembles up to a certain count (often $E20$), followed by a decline. This highlights the value of ensembling on SMOTE-sampled CHES data for both model architectures to a certain extent only.

In the SMOTEENN-sampled CHES dataset, performance gains for both MLP and CNN ensembles level off beyond a certain ensemble count. Although $E20$ appears as an ideal configuration for both types of models, CNN demonstrates consistently better performance than MLP on SMOTEENN sampled data.

RO in the CHES dataset follows a pattern similar to SMOTEENN. Performance improvements for both MLP and CNN, then plateau beyond a certain ensemble count, with $E20$ again being a suitable configuration. However, CNN outperforms MLP within this sampling scenario.

Finally, RU yields significantly poor performance across both CNN and MLP ensembles within the CHES dataset. These results strongly suggest that this data sampling technique is not recommended for SCA tasks.

The basic ensemble achieved a GE of 1 with 110 traces, representing a 67% performance improvement over the CHES original dataset, which required 350 traces. Overall, the basic method attained the best results on the CHES dataset, followed by the noise method, SMOTEENN, and random oversampling methods. Interestingly, these top four methods also performed best on the ASCAD dataset. In the ASCAD dataset, the SMOTEENN ensemble reduced the GE to 85 traces, a 72% improvement over the original dataset’s 300 traces. This indicates that generating new samples significantly benefited the model’s performance. Conversely, in the CHES dataset, the basic and noise methods, which do not generate new samples, performed the best. These results highlight the importance of selecting resampling techniques tailored to each dataset’s specific characteristics. While SMOTEENN excelled in the ASCAD dataset, the basic and noise methods were more effective in the CHES dataset, demonstrating the varying impacts of sample generation on model performance.

Our proposed hybrid bagging resampling deep learning models have demonstrated superior performance in learning both simple and complex statistical models for side-channel leakages in imbalanced datasets. However, achieving this performance required larger hyperparameters, leading to decreased interpretability and increased complexity in the hyperparameter tuning process [39,40]. Hence, there exists a trade-off between interpretability and performance. To address the interpretability drawback inherent in our deep learning models, we conducted additional experiments utilizing Shapley Distribution Networks. These networks explain the predictions of complex machine learning models by decomposing the model’s output into contributions from each feature, thereby identifying the relevant regions of the side channel traces that leak information using a 1D heatmap plot [41,42,43]. The Shapley heatmap for our considered model ensembles is provided in Figure 17a,b.

From all the plots provided, Figure 17a depicting the ensemble of one model displayed the fewest number of peaks at 3, indicating minimal participation of the traces in the model output prediction. With an increase in the number of models in the ensemble, the number of peaks in the plots also increased, signifying a greater contribution of side-channel traces. Notably, the ensemble of 20 models in Figure 17b demonstrated the most balanced performance, with eight peaks and the highest peak at approximately $-0.0025$. Thus, the Shapley values plot aligns with our previous findings and establishes the additional benefit of employing an ensemble of machine learning models in SCA attacks.

5.4. Statistical Significance Test of Results

We will be calculating p-values to determine the statistical significance of the results of our experiment. Before proceeding with the calculation of p-values, we have provided Figure 18a,b to offer a visual comparison of imbalanced versus resampled data and imbalanced versus ensemble of models, respectively. This approach aligns with the fundamental machine learning principle of addressing class imbalance through data enhancement techniques or compensatory training methods. These figures clearly demonstrate that both resampled data and ensemble models yield improved predictive performance in machine learning.

To assess the statistical significance of our findings, we follow a systematic approach involving hypothesis testing, calculation of test statistics, computation of p-values and interpretation of p-values. Here, is a detailed explanation of our process:

1. Define Hypotheses:

• Null Hypothesis ($H_0$): There is no significant difference between the performance of models trained with SMOTE and those trained with the imbalanced dataset, or between a single model and an ensemble of models.
• Alternative Hypothesis ($H_1$): There is a significant difference between the performance of models trained with SMOTE and those trained with the imbalanced dataset, or between a single model and an ensemble of models.

2. Select a Test: We use an independent t-test to compare the means of two independent groups. For instance, we compare SMOTE-trained models against BASIC-trained models and a single model against an ensemble of models.

3. Calculate Test Statistic: The t-test statistic is calculated using the following formula:

$$t={\displaystyle \frac{{\overline{X}}_1-{\overline{X}}_2}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}}$$

where ${\overline{X}}_1$ and ${\overline{X}}_2$ are the sample means of the two groups, $s_1^2$ and $s_2^2$ are the sample variances of the two groups, $n_1$ and $n_2$ are the sample sizes of the two groups.

4. Determine p-value: The p-value is derived from the t-test statistic using the t-distribution. It indicates the probability of observing our results, or more extreme results if the null hypothesis is true. For a two-tailed test, the p-value is computed as:

$$p=2·P(T\ge |t\left|\right)$$

where $P(T\ge |t\left|\right)$ is the probability that the t-distribution with $df=n_1+n_2-2$ degrees of freedom is greater than or equal to the absolute value of the calculated t-statistic.

5. Interpret p-value: We compare the p-value to a predefined significance level (typically $\alpha =0.05$). If the p-value is less than the significance level, we reject the null hypothesis, concluding that our findings are statistically significant. We followed the above procedures setting up two hypothesis tests as follows:

• Ensemble Method Performance:

  –

  Null Hypothesis ($H_0$): The single model predictor performs equally well as the ensemble method.

  –

  Alternative Hypothesis ($H_1$): The ensemble method provides better performance.

• Data Resampling Technique:

  –

  Null Hypothesis ($H_0$): The naturally imbalanced dataset performs equally well as the resampled dataset.

  –

  Alternative Hypothesis ($H_1$): The resampled dataset provides better performance.

Aiming to provide strong statistical evidence that our ensemble methods and resampling techniques significantly improve performance we, therefore, calculated the p-values for these tests. We have used the number of traces it takes to reach GE of 1 to form our sampled data. For both of our experiments, $\alpha$ was approximately 0, indicating that the observed difference is statistically significant and not by chance. This result is in tandem with our plots in Figure 18. Based on the obtained results, our proposed ensemble methods demonstrate superior performance compared to the traditional single-model predictor. Additionally, our data resampling technique yields better performance than using the naturally imbalanced dataset.

6. Discussion

Our proposed hybrid bagging resampling method was successfully applied to attack two widely accepted datasets in the SCA community. For the ASCAD dataset, MLPs demonstrated superior attack performance compared to CNNs. Conversely, for the CHES dataset, CNNs outperformed MLPs. This variation in performance is likely due to the difference in the number of features, with ASCAD having 700 features and CHES having 2200 features. Therefore, our proposed hybrid bagging resampling framework trains both MLP and CNN deep learning models to leverage their respective strengths. In addition, our hypothesis testing results indicated that data resampling significantly improved the performance of our ML models. The results obtained from our experiments demonstrated that no single resampling method was consistently superior across all the four test cases we considered.

For example, in the ASCAD MLP test case, the Basic resampling method had the best performance, while in the ASCAD CNN test case, SMOTEENN was the top performer. In the CHES MLP and CNN test cases, the Basic resampling method again showed the best results. Out of the four test cases, SMOTEENN was the best in only one, indicating that SMOTEENN is not the optimal choice 75% of the time. This variation establishes that the effectiveness of resampling techniques can be highly context-dependent. Therefore, our bagging resampling framework incorporates the use of multiple resampling techniques together with ensembles to determine the configuration that will yield the best performance. By doing so, we ensure that our approach remains flexible and adaptable to different datasets and model architectures, ultimately enhancing the robustness and generalizability of our framework.

The proposed framework represents a significant advancement over traditional SCA techniques in both efficiency and effectiveness. Traditional methods, such as those based on statistical correlation and simple machine learning models, often face limitations in handling complex leakage patterns and large datasets efficiently. In contrast, our framework integrates advanced deep learning techniques with a hybrid bagging resampling approach. This integration improves both efficiency and effectiveness. Specifically, the use of ensemble methods and sophisticated resampling techniques enhances the framework’s ability to manage imbalanced datasets and extract meaningful patterns from noisy data, which traditional techniques often struggle with [44].

Our framework’s efficiency is demonstrated through its ability to handle large volumes of side-channel data with reduced computational overhead compared to traditional methods. To reduce complexity while maintaining performance gains, several strategies can be employed. One approach is to implement parallel training of models, which can significantly cut down the time required if sufficient computational resources are available [45]. Another method is to perform a sensitivity analysis to determine the minimum number of models needed to achieve the desired performance, thereby reducing unnecessary computational overhead. Additionally, techniques such as model pruning, which involves removing less important weights, and knowledge distillation, where a simpler model is trained to mimic a more complex one, can help maintain performance while lowering computational demands. These methods are scalable, accommodating larger datasets and more complex models, and are flexible enough to be adapted for various types of data and applications. Overall, while traditional techniques are foundational, our proposed framework leverages modern advancements to achieve greater accuracy and operational efficiency.

As datasets grow larger and SCA attacks become more complex, computational constraints become more significant. Larger datasets increase the training time and memory requirements, and more complex attacks may require more sophisticated models or larger ensembles. The practical implications of our findings suggest that for applications where training time and computational resources are critical factors, such as rapid model deployment scenarios, a single model approach might be more suitable. On the other hand, in environments where prediction accuracy is paramount and models are trained less frequently, our proposed bagging ensemble framework’s longer training time can be justified by its superior performance.

Our proposed hybrid bagging resampling framework was developed for the AES-128 cipher, and many cryptographic algorithms share similar side-channel leakages based on the presence of S-boxes and round functions. These similarities indicate that our methods can extend beyond AES-128. Presently, similar tests on other algorithms, such as the DES cipher, show encouraging performance, indicating potential for wider application [46]. However, different ciphers involve varying mathematical operations, resulting in distinct leakage patterns. For instance, the leakage patterns differ among RSA, AES-128, and SIMON ciphers. Adapting our techniques to new cryptographic standards and evolving SCA attack techniques will require addressing these varying leakage models and different levels of imbalance. Thus, our framework’s adaptability hinges on incorporating rigorous data preprocessing steps and comprehensive deep learning hyperparameter tuning tailored to each algorithm. By employing these steps, our approach can be fine-tuned to effectively handle different leakage patterns and evolving attack vectors.

Our work mainly focuses on AES-128 due to its widespread use and well-documented SCA data. However, this focus presents a limitation in the generalization of our findings to other cryptographic algorithms. While initial tests on algorithms such as DES and SIMON ciphers have shown promising results, further validation is needed for a broader range of cryptographic systems. Other performance limitations include the computational costs associated with training ensemble models and the scalability of our methods to larger datasets or more complex cryptographic algorithms.

Recent research highlights the need for machine learning models to adapt to diverse data conditions beyond just addressing class imbalance. Our framework is specifically designed to be robust against variations in dataset characteristics, such as noise and different leakage models. Our proposed framework, though targeted for class imbalance, includes extensive data augmentation and bagging stages that enhance its robustness to variations in side-channel data. Additionally, we acknowledge that different leakage models may require tailored approaches. For instance, variations in noise levels can be mitigated through regularization methods, as seen in prior research, ensuring that the framework remains effective even when faced with challenging dataset characteristics. While our framework has demonstrated resilience, we also recognize that extreme variations in leakage models or noise could necessitate further refinement, particularly through specialized preprocessing steps or adjustments in the deep learning architecture. This adaptability is a key strength of our approach, allowing it to maintain performance across diverse scenarios.

Furthermore, integrating our hybrid bagging resampling ensemble framework with advanced machine learning models or architectures, such as transformers, is a promising direction to further improve performance. Incorporating advanced architectures like transformers holds great potential for enhancing the effectiveness and robustness of SCA. Transformers, known for their self-attention mechanisms, excel at capturing long-range dependencies in sequential data, which is particularly beneficial for SCA where capturing intricate patterns in power consumption traces is crucial. Models like EstraNet, a novel transformer-based model, have demonstrated remarkable performance in SCA by achieving linear time and memory complexity, making them highly effective in diverse scenarios [47]. While integrating transformers and advanced models into our framework offers significant benefits, it also presents challenges such as substantial computational resources and trade-offs between accuracy and efficiency.

As post-quantum cryptography becomes increasingly relevant, it is crucial to adapt our framework to these new algorithms. Future research should focus on tailoring our ensemble and resampling techniques to the unique leakage characteristics of post-quantum cryptographic schemes. This includes developing new feature extraction methods capable of handling the complex and diverse leakage profiles associated with algorithms like lattice-based or hash-based cryptography. Additionally, evaluating the performance of the proposed framework on these algorithms will be essential for understanding its generalizability and effectiveness in the post-quantum context [48,49].

7. Conclusions and Future Work

In this work, we proposed a hybrid bagging resampling deep learning SCA framework designed to address imbalanced class distribution in SCA datasets. Our technique integrates a two-stage hybrid approach that includes a data enhancement phase and a bagging ensemble phase. Through our experiments, we demonstrated that our framework has over 50% performance improvement over previous methods, although the optimal resampling technique varied depending on the dataset. The key insight from our study is that both sampling and bagging techniques can improve model performance on imbalanced datasets by more than three times compared to the initial performance. While the SMOTEENN ensemble achieved the best performance in the ASCAD dataset, the Basic ensemble performed the best in the CHES dataset, both contributing to over a $70\%$ improvement in performance. This reinforces the importance of selecting appropriate methods tailored to the specific characteristics of each dataset. Our findings suggest several avenues for future research, including exploring additional resampling techniques, applying our framework to a broader range of datasets, and integrating it with other machine learning models and cryptographic algorithms, such as those in post-quantum computing. Advanced neural network architectures like transformers, known for handling sequential data and capturing long-range dependencies, could further enhance SCA performance. While our framework shows significant potential, there are areas for improvement. Future work should address the computational overhead of complex resampling methods and the impact of extreme imbalance levels. Tackling these issues could enhance the framework’s effectiveness and efficiency, paving the way for more robust solutions. Ultimately, our bagging resampling framework offers a robust, efficient, and less complex solution for optimizing methodologies on imbalanced datasets, laying the groundwork for further advancements in the field.