Design and Modeling of a 2-DOF Micro-Positioning Stage for Vibration-Assisted Polishing
Abstract
1. Introduction
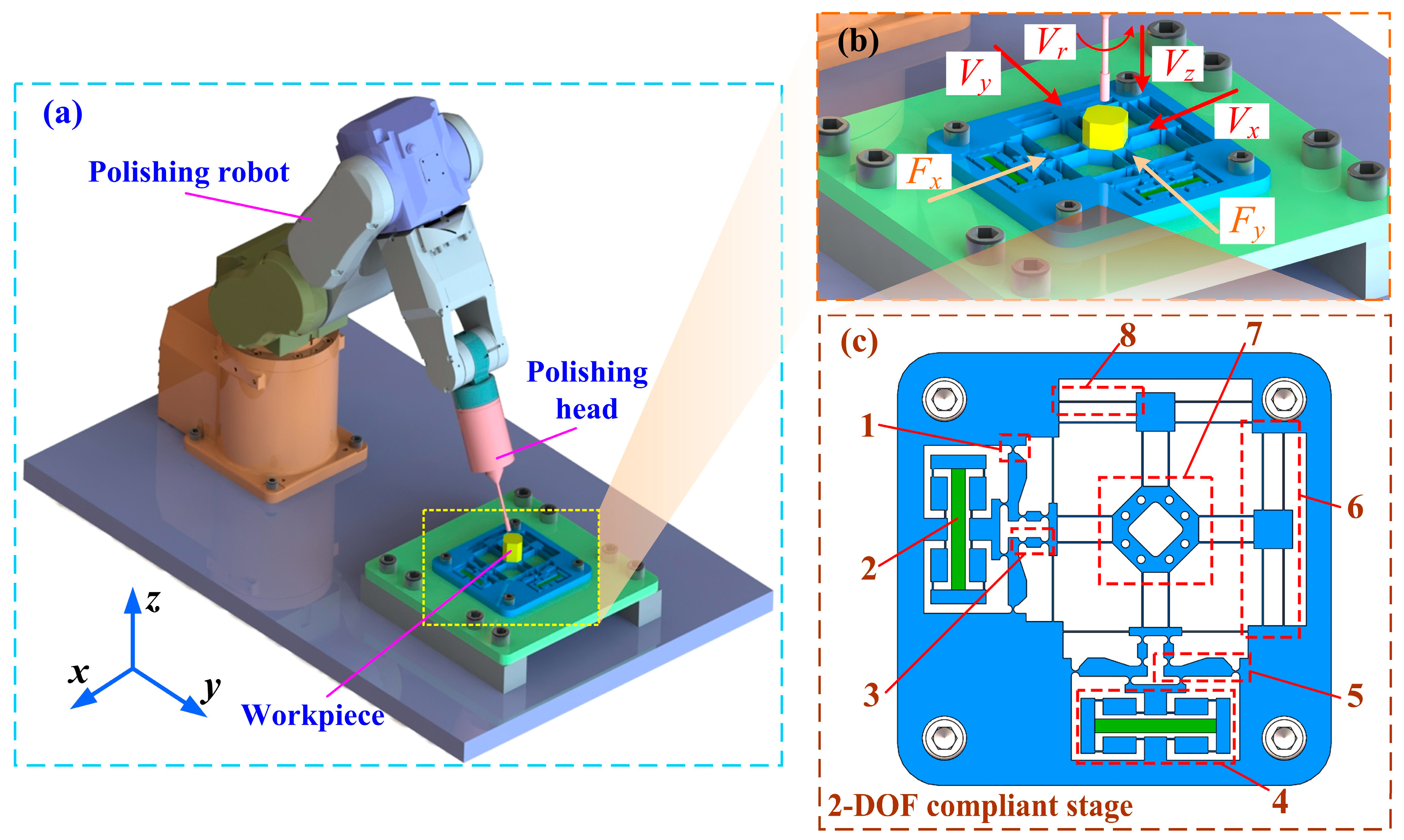
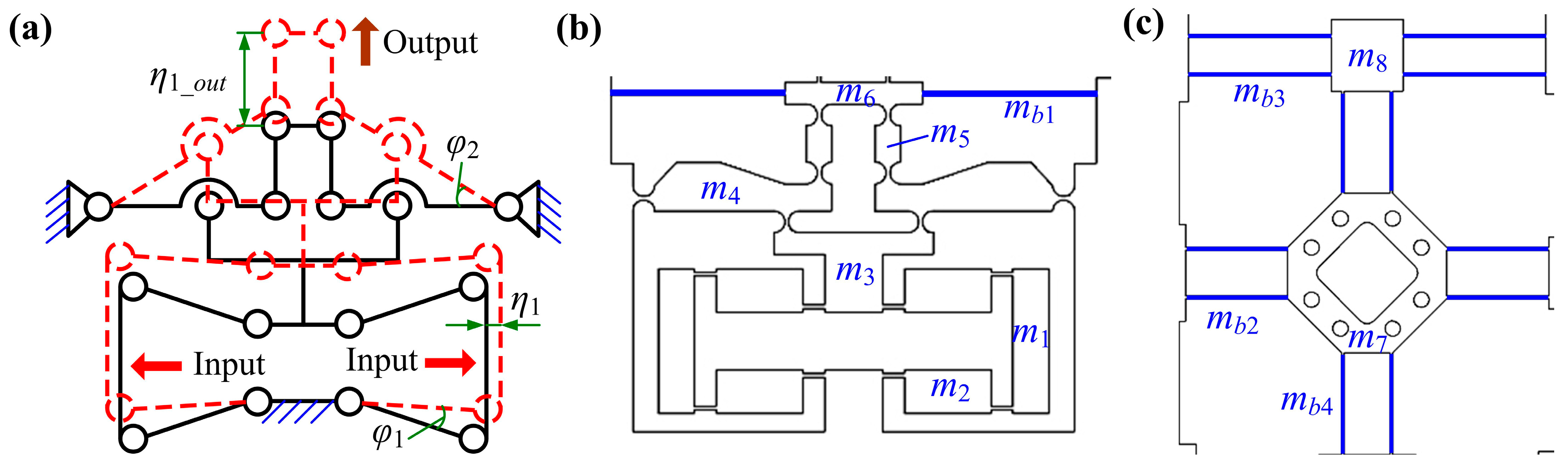
2. Mechanism Design
3. Static Modeling Analysis
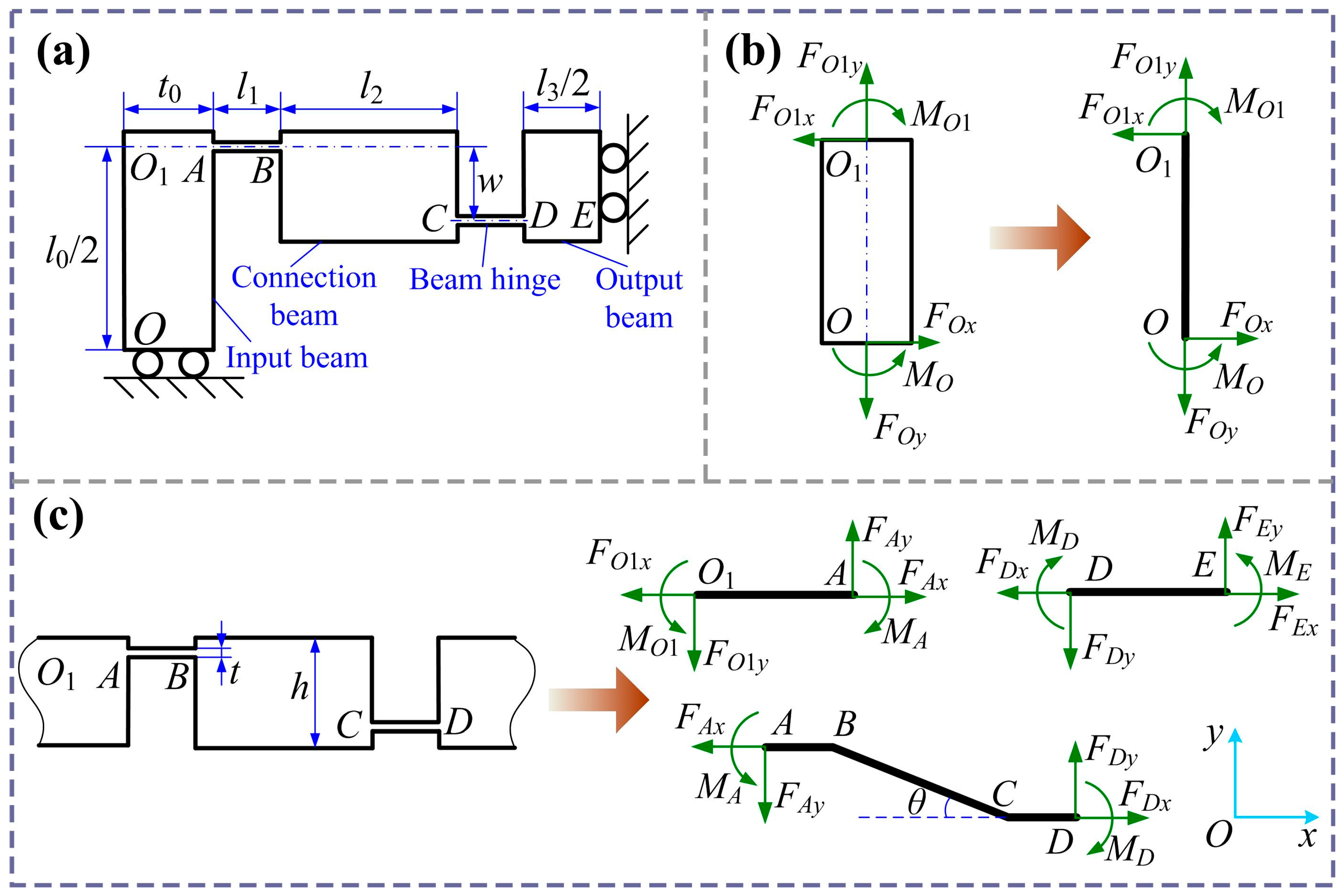
3.1. Static Modeling of Bridge Mechanism
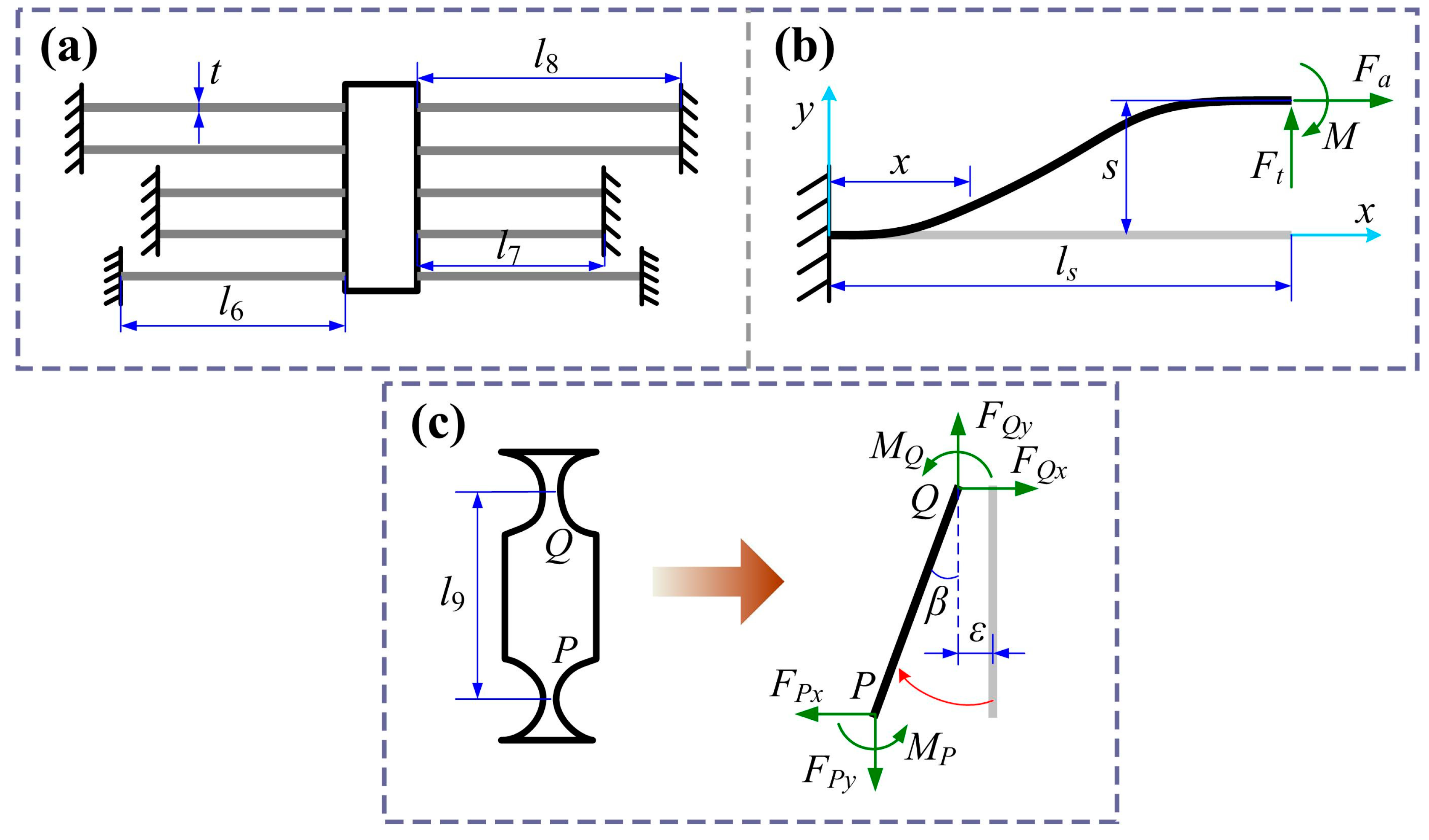
3.2. Static Modeling of Lever Mechanism
3.3. Static Modeling of Guiding Mechanisms
3.4. Static Modeling of the Stage
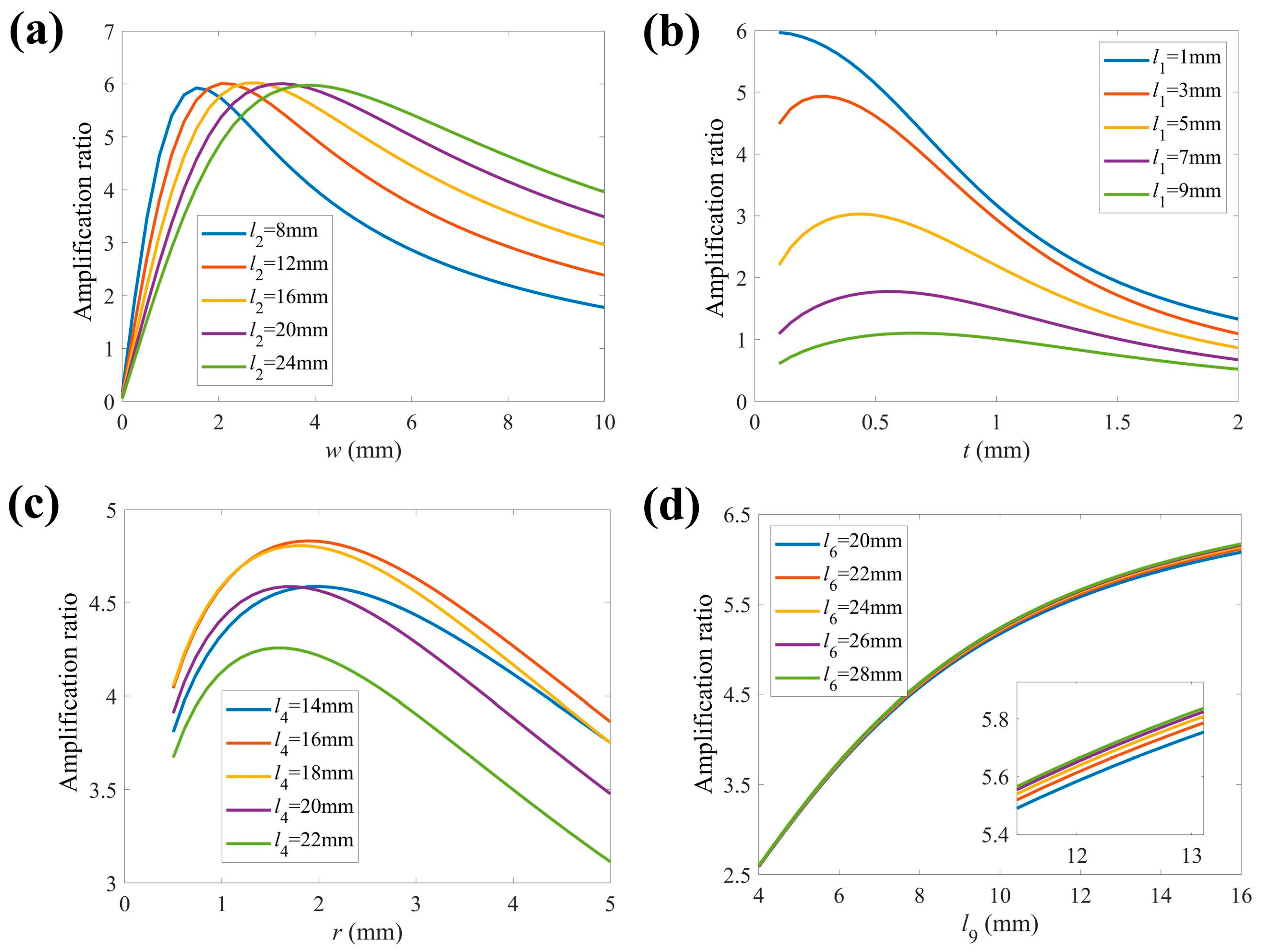
3.5. Parameter Analysis
4. Dynamic Modeling Analysis
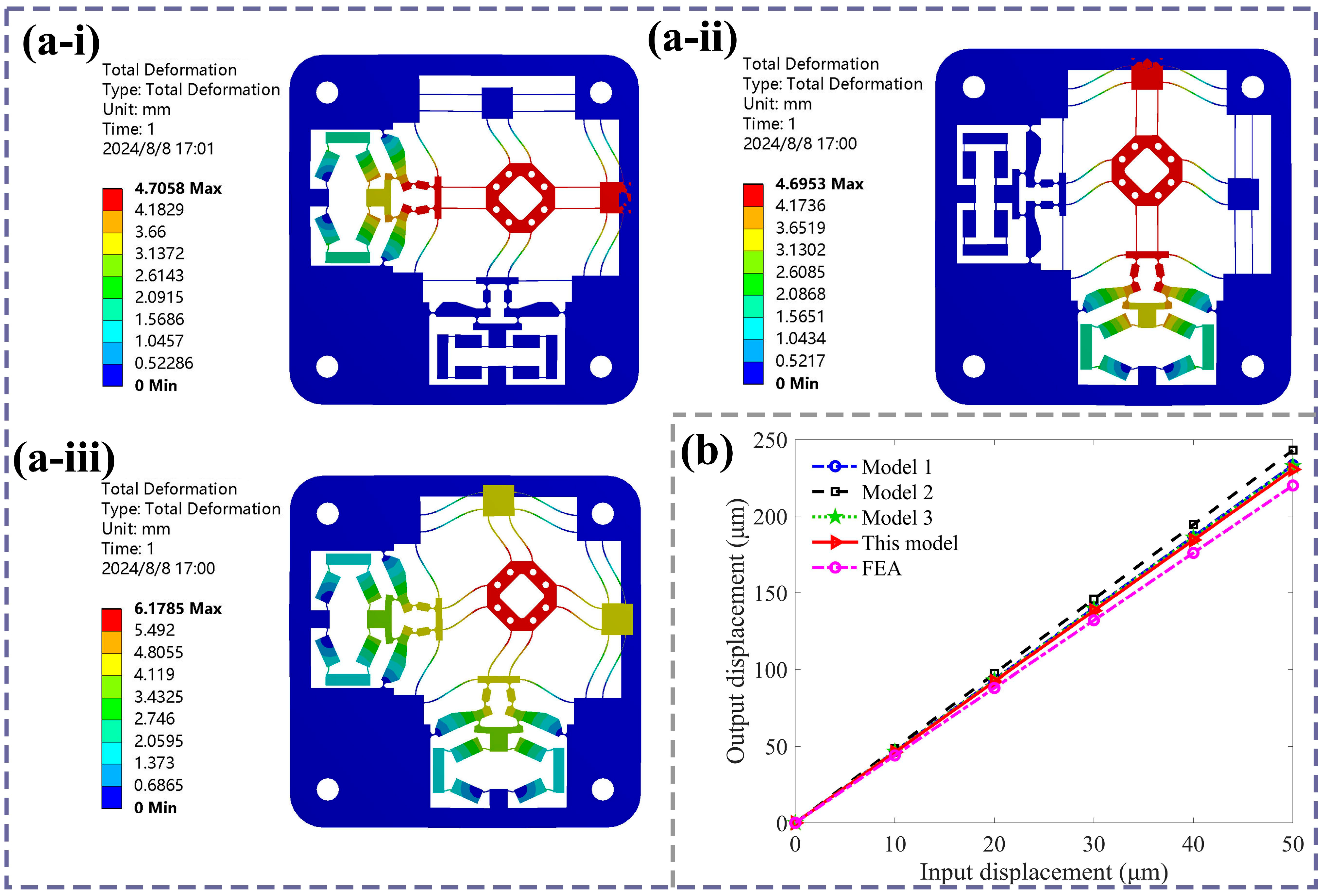
5. Simulation Analysis
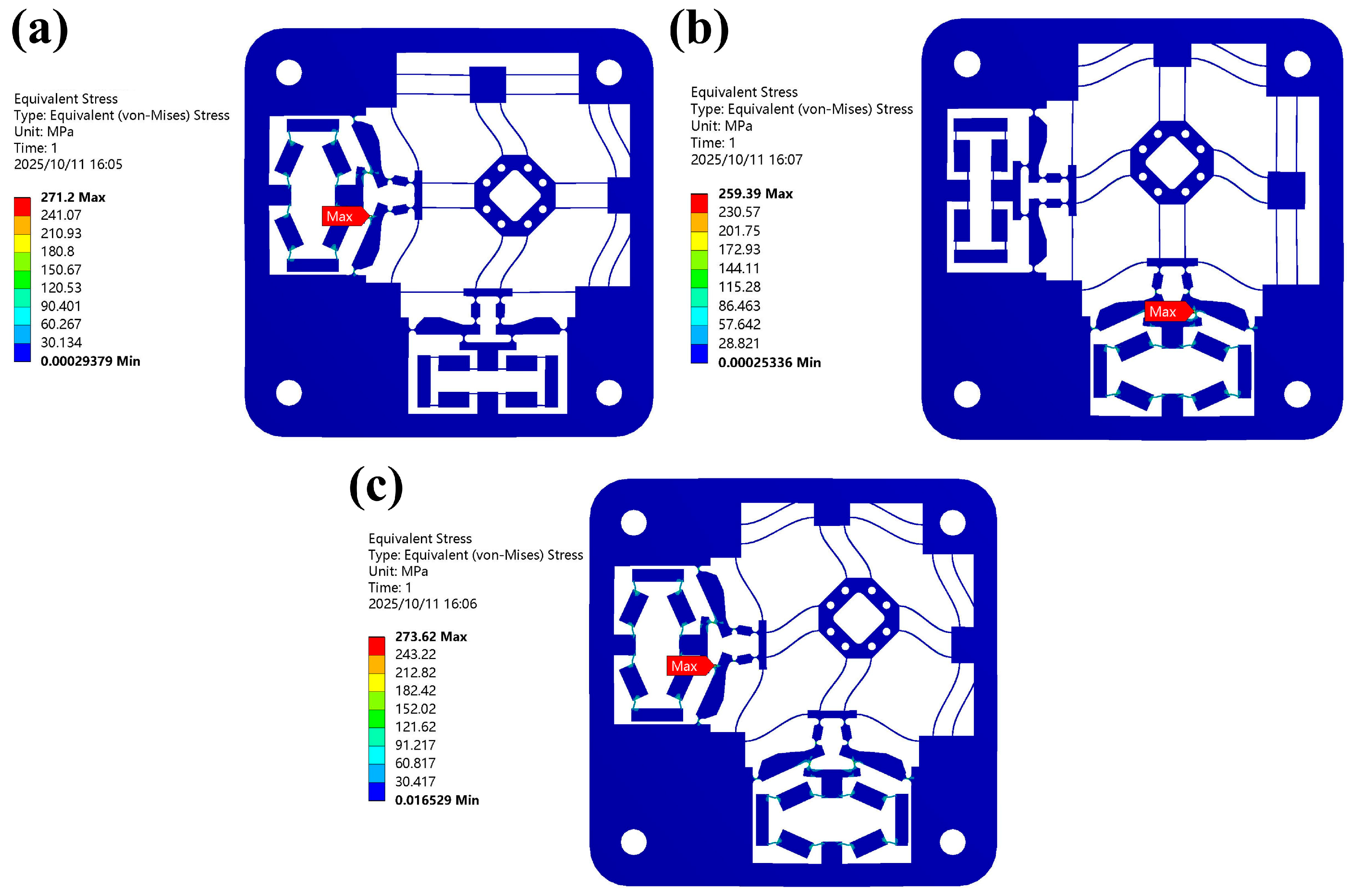
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| F, M | Force and moment |
| O, O1, A, B, C, D, E | Ends of beams in bridge mechanism |
| l0, t0, l2, h, l1, t, l3, w | Length and width of the input beam; length and width of the connection beam; length of the output beam; length and width of the straight beam’s hinge; horizontal distance between the two hinges in bridge mechanism |
| , , , | Axial tensile stiffness of the input beam; beam flexible hinges; connection beam and output beam |
| , , , | Rotational stiffness of the input beam; beam flexible hinges; connection beam and output beam |
| xin, xout | Input and output displacements of the bridge mechanism |
| kb-in, kb_out, λB | Input stiffness, output stiffness, and amplification ratio of the bridge mechanism |
| H, I, J | Flexible hinges in lever mechanism |
| l4, l5, r, t, b, α, δ | Horizontal distance between hinges H and I; horizontal distance between hinges H and J; circular radius; minimum width and thickness of the circular hinge; rotational angle of hinge H; and deviation displacement of center of hinge H in lever mechanism |
| kHb, kJb, kHt, kIt, kJt | Bending stiffness of flexible hinges H and J and torsion stiffness of flexible hinges H, I, and J |
| kL, λL | Stiffness and amplification ratio of the lever mechanism |
| ts, ls, ks, | Thickness, length, and bending stiffness of a single beam |
| l6, l7, l8 | Length of beams in guiding mechanism |
| kg | Stiffness of guiding mechanism |
| P, Q | Flexible hinges in transmitting mechanism |
| l9 | Vertical distance between hinges P and Q |
| β, ε | Rotational angle and axial drift displacement of hinge Q |
| kPb, kQb, kPt, kQt | Bending stiffness of flexible hinges P and Q and torsion stiffness of flexible hinges P and Q |
| kd | Stiffness of the transmission mechanism |
| Kload, Kamp, Kstage | Stiffness of elastic load, overall stiffness of the amplification mechanism, and amplification ratio of the compliant stage |
| ηi, φi, T, V, mi, f | Movement, rotational angle, kinetic energy, potential energy, mass, and frequency |
| E, b | Young’s modulus and out-of-plane width of the compliant stage |
References
- Tsegaw, A.A.; Shiou, F.J.; Lin, S.P. Ultra-precision polishing of N-Bk7 using an innovative self-propelled abrasive fluid multi-jet polishing tool. Mach. Sci. Technol. 2015, 19, 262–285. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Han, J.; Xu, Q.; Guo, Y. Evaluating subsurface damage in optical glasses. J. Eur. Opt. Soc.-Rapid Publ. 2011, 6, 11001. [Google Scholar] [CrossRef]
- Yu, T.; Li, H.; Wang, W. Experimental investigation on grinding characteristics of optical glass BK7: With special emphasis on the effects of machining parameters. Int. J. Adv. Manuf. Technol. 2016, 82, 1405–1419. [Google Scholar] [CrossRef]
- Zhao, Q.; Sun, Z.; Guo, B. Material removal mechanism in ultrasonic vibration assisted polishing of micro cylindrical surface on SiC. Int. J. Mach. Tools Manuf. 2016, 103, 28–39. [Google Scholar] [CrossRef]
- Riemer, O.; Elsner-Dörge, F. Investigation of material removal in vibration polishing of NiCo alloys with millimetre-sized tools. Int. J. Adv. Manuf. Technol. 2017, 92, 3117–3122. [Google Scholar] [CrossRef]
- Zhao, H.; Yan, L.; Hou, Z.; Lin, J.; Zhao, Y.; Ji, Z.; Wang, Y. Error Analysis Strategy for Long-term Correlated Network Systems: Generalized Nonlinear Stochastic Processes and Dual-Layer Filtering Architecture. IEEE Internet Things J. 2025, 12, 33731–33745. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, J.; Xing, D.; Zhao, Y. A study of surface roughness variation in ultrasonic vibration-assisted milling. Int. J. Adv. Manuf. Technol. 2012, 58, 553–561. [Google Scholar] [CrossRef]
- Chen, X.; Gu, Y.; Lin, J.; Yi, A.; Kang, M.; Cang, X. Study on subsurface damage and surface quality of silicon carbide ceramic induced by a novel non-resonant vibration-assisted roll-type polishing. J. Mater. Process. Technol. 2020, 282, 116667. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, X.; Zheng, L.; Xue, D. High-performance grinding of a 2-m scale silicon carbide mirror blank for the space-based telescope. Int. J. Adv. Manuf. Technol. 2017, 89, 463–473. [Google Scholar] [CrossRef]
- Suzuki, H.; Hamada, S.; Okino, T.; Kondo, M.; Yamagata, Y.; Higuchi, T. Ultraprecision finishing of micro-aspheric surface by ultrasonic two-axis vibration assisted polishing. CIRP Ann. 2010, 59, 347–350. [Google Scholar] [CrossRef]
- Suzuki, H.; Moriwaki, T.; Okino, T.; Ando, Y. Development of ultrasonic vibration assisted polishing machine for micro aspheric die and mold. CIRP Ann. 2006, 55, 385–388. [Google Scholar] [CrossRef]
- Lin, J.; Lu, H.; Gu, Y.; Zhou, X.; Xin, C.; Kang, M.; Cang, X. A new vibration device applied for two-dimensional ultrasonic polishing of biomaterials. IEEE Access 2019, 7, 92838–92849. [Google Scholar] [CrossRef]
- Gu, Y.; Duan, X.; Lin, J.; Yi, A.; Kang, M.; Jiang, J.; Zhou, W. Design, analysis, and testing of a novel 2-DOF vibration-assisted polishing device driven by the piezoelectric actuators. Int. J. Adv. Manuf. Technol. 2020, 111, 471–493. [Google Scholar] [CrossRef]
- Gu, Y.; Zhou, Y.; Lin, J.; Yi, A.; Kang, M.; Lu, H.; Xu, Z. Analytical prediction of subsurface damages and surface quality in vibration-assisted polishing process of silicon carbide ceramics. Materials 2019, 12, 1690. [Google Scholar] [CrossRef] [PubMed]
- Jia, D.; Li, C.; Zhang, Y.; Yang, M.; Zhang, X.; Li, R.; Ji, H. Experimental evaluation of surface topographies of NMQL grinding ZrO2 ceramics combining multiangle ultrasonic vibration. Int. J. Adv. Manuf. Technol. 2019, 100, 457–473. [Google Scholar] [CrossRef]
- Fu, H.; Tian, J.; Chin, C.L.; Liu, H.; Yuan, J.; Tang, S.; Mai, R.; Wu, X. Axial compression behavior of GFRP-steel composite tube confined seawater sea-sand concrete intermediate long columns. Eng. Struct. 2025, 333, 120157. [Google Scholar] [CrossRef]
- Ding, B.; Li, X.; Li, C.; Li, Y.; Chen, S.-C. A survey on the mechanical design for piezo-actuated compliant micro-positioning stages. Rev. Sci. Instrum. 2023, 94, 101502. [Google Scholar] [CrossRef] [PubMed]
- Dong, W.; Chen, F.; Gao, F.; Yang, M.; Sun, L.; Du, Z.; Tang, J.; Zhang, D. Development and analysis of a bridge-lever-type displacement amplifier based on hybrid flexure hinges. Precis. Eng. 2018, 54, 171–181. [Google Scholar] [CrossRef]
- Ding, B.; Yang, Z.; Li, Y. Design of flexure-based modular architecture micro-positioning stage. Microsyst. Technol. 2020, 26, 2893–2901. [Google Scholar] [CrossRef]
- Ling, M.; Yuan, L.; Lai, J.; Wei, H.; Zhang, X. Compliance and precision modeling of general notch flexure hinges using a discrete-beam transfer matrix. Precis. Eng. 2023, 82, 233–250. [Google Scholar] [CrossRef]
- Dao, T.P.; Huang, S.C. Optimization of a two degrees of freedom compliant mechanism using Taguchi method-based grey relational analysis. Microsyst. Technol. 2017, 23, 4815–4830. [Google Scholar] [CrossRef]
- Gu, Y.; Zhou, Y.; Lin, J.; Lu, M.; Zhang, C.; Chen, X. Design, analysis, and testing of a flexure-based vibration-assisted polishing device. AIP Adv. 2018, 8, 055113. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, A.; Lin, J.; Chen, X.; Lu, F.; Sun, E. Development of decoupling device for vibration-assisted roller polishing of silicon carbide ceramics. IEEE Access 2020, 8, 219098–219113. [Google Scholar] [CrossRef]
- Van Le, H.; Le, H.G.; Dao, T.P. Kinetostatic and dynamic analysis for a new 2-DOF compliant mechanism for potential application in vibration-assisted polishing. Int. J. Adv. Manuf. Technol. 2024, 135, 2413–2436. [Google Scholar] [CrossRef]
- Chee, S.; Suzuki, H.; Okada, M.; Yano, T.; Higuchi, T.; Lin, W.M. Precision polishing of micro mold by using piezoelectric actuator incorporated with mechanical amplitude magnified mechanism. Adv. Mater. Res. 2011, 325, 470–475. [Google Scholar] [CrossRef]
- Chee, S.; Suzuki, H.; Uehara, J.; Yano, T.; Higuchi, T.; Lin, W. A Low Contact Force Polishing System for Micro Molds that Utilizes 2-Dimensional Low Frequency Vibrations (2DLFV) with Piezoelectric Actuators (PZT) and a Mechanical Transformer Mechanism. Int. J. Autom. Technol. 2013, 7, 71–82. [Google Scholar] [CrossRef]
- Guo, J.; Suzuki, H. Effects of process parameters on material removal in vibration-assisted polishing of micro-optic mold. Micromachines 2018, 9, 349. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Guo, F.; Wang, Y.; Wang, Z.; Li, C.; Ling, M.; Hao, G. Design and modeling of a compact compliant stroke amplification mechanism with completely distributed compliance for ground-mounted actuators. Mech. Mach. Theory 2022, 167, 104566. [Google Scholar] [CrossRef]
- Gu, G.; Zhu, L.; Su, C.; Ding, H.; Fatikow, S. Modeling and control of piezo-actuated nanopositioning stages: A survey. IEEE Trans. Autom. Sci. Eng. 2014, 13, 313–332. [Google Scholar] [CrossRef]
- Yong, Y.K.; Moheimani, S.R.; Kenton, B.J.; Leang, K.K. Invited review article: High-speed flexure-guided nanopositioning: Mechanical design and control issues. Rev. Sci. Instrum. 2012, 83, 121101. [Google Scholar] [CrossRef]
- Aabid, A.; Raheman, M.A.; Ibrahim, Y.E.; Anjum, A.; Hrairi, M.; Parveez, B.; Parveen, N.; Zayan, J.M. A systematic review of piezoelectric materials and energy harvesters for industrial applications. Sensors 2021, 21, 4145. [Google Scholar] [CrossRef] [PubMed]
- Yong, Y.K.; Aphale, S.S.; Moheimani, S.R. Design, identification, and control of a flexure-based XY stage for fast nanoscale positioning. IEEE Trans. Nanotechnol. 2008, 8, 46–54. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, J.; Shen, X.; Xiao, Q.; Huang, J.; Wang, Y. Design, modeling, and testing of a novel XY piezo-actuated compliant micro-positioning stage. Micromachines 2019, 10, 581. [Google Scholar] [CrossRef]
- Tian, Y.; Shirinzadeh, B.; Zhang, D.; Alici, G. Development and dynamic modelling of a flexure-based Scott–Russell mechanism for nano-manipulation. Mech. Syst. Signal Process. 2009, 23, 957–978. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, M.; Cheng, Y.; Zheng, D.; Peng, Y. A stick-slip/inchworm hybrid rotary piezo motor based on a symmetric triangular driving mechanism. Appl. Phys. Lett. 2019, 115, 131904. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Jiang, Z.; Lin, J. Modular kinematics and statics modeling for precision positioning stage. Mech. Mach. Theory 2017, 107, 274–282. [Google Scholar] [CrossRef]
- Sun, X.; Chen, W.; Tian, Y.; Fatikow, S.; Zhou, R.; Zhang, J.; Mikczinski, M. A novel flexure-based microgripper with double amplification mechanisms for micro/nano manipulation. Rev. Sci. Instrum. 2013, 84, 085002. [Google Scholar] [CrossRef]
- Gu, Y.; Chen, X.; Lin, J.; Lu, M.; Lu, F.; Zhang, Z.; Yang, H. Vibration-assisted roll-type polishing system based on compliant micro-motion stage. Micromachines 2018, 9, 499. [Google Scholar] [CrossRef]
- Cera, M.; Cirelli, M.; Colaiacovo, L.; Valentini, P.P. Second-order approximation pseudo-rigid model of circular arc flexure hinge. Mech. Mach. Theory 2022, 175, 104963. [Google Scholar] [CrossRef]
- Ding, B.; Li, Y.; Xiao, X.; Tang, Y.; Li, B. Design and analysis of a 3-DOF planar micromanipulation stage with large rotational displacement for micromanipulation system. Mech. Sci. 2017, 8, 117–126. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, J.; Peng, Y.; Pu, H.; Yang, Y. A novel amplification ratio model of a decoupled XY precision positioning stage combined with elastic beam theory and Castigliano’s second theorem considering the exact loading force. Mech. Syst. Signal Process. 2020, 136, 106473. [Google Scholar] [CrossRef]
- Wu, Z.; Li, Y.; Hu, M. Design and optimization of full decoupled micro/nano-positioning stage based on mathematical calculation. Mech. Sci. 2018, 9, 417–429. [Google Scholar] [CrossRef]
- Lou, Y.; Liu, W. Analysis of the displacement of distributed compliant parallel-guiding mechanism considering parasitic rotation and deflection on the guiding plate. Mech. Mach. Theory 2014, 80, 151–165. [Google Scholar] [CrossRef]
- Ma, H.; Yao, S.; Wang, L.; Zhong, Z. Analysis of the displacement amplification ratio of bridge-type flexure hinge. Sens. Actuators A Phys. 2006, 132, 730–736. [Google Scholar] [CrossRef]
- Qi, K.; Xiang, Y.; Fang, C.; Zhang, Y.; Yu, C. Analysis of the displacement amplification ratio of bridge-type mechanism. Mech. Mach. Theory 2015, 87, 45–56. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Zeng, M.; Lin, J.; Inman, D.J. Enhanced mathematical modeling of the displacement amplification ratio for piezoelectric compliant mechanisms. Smart Mater. Struct. 2016, 25, 075022. [Google Scholar] [CrossRef]




| Parameter | Value (mm) | Parameter | Value (mm) |
|---|---|---|---|
| l0 | 18.5 | b | 10 |
| l1 | 3 | w | 4.5 |
| l2 | 12 | t0 | 5 |
| l3 | 8 | t | 0.5 |
| l4 | 19.75 | h | 6 |
| l5 | 24.25 | r | 1.5 |
| l6 | 24 | l7 | 20 |
| l8 | 28 | l9 | 8 |
| Young’s Modulus | Poisson’s Ratio | Yield Strength | Density |
|---|---|---|---|
| 72 GPa | 0.33 | 503 MPa | 2810 kg/m3 |
| Parameter | Value (kg) | Parameter | Value (kg) |
|---|---|---|---|
| m1 | 0.0028 | m7 | 0.013 |
| m2 | 0.002 | m8 | 0.0055 |
| m3 | 0.0037 | mb1 | 0.0003 |
| m4 | 0.0036 | mb2 | 0.0002 |
| m5 | 0.0005 | mb3 | 0.0004 |
| m6 | 0.0016 | mb4 | 0.0002 |
| Method | Amplification Ratio | Error |
|---|---|---|
| Model 1 [44] | 4.67 | 6.1% |
| Model 2 [45] | 4.86 | 10.4% |
| Model 3 [46] | 4.65 | 5.6% |
| This model | 4.61 | 4.6% |
| FEA | 4.40 | / |
| Resonant Frequency | Theoretical Value | Simulation Value | Error |
|---|---|---|---|
| f | 334.61 Hz | 370.23 Hz | 9.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Li, Y. Design and Modeling of a 2-DOF Micro-Positioning Stage for Vibration-Assisted Polishing. Micromachines 2025, 16, 1250. https://doi.org/10.3390/mi16111250
Chen P, Li Y. Design and Modeling of a 2-DOF Micro-Positioning Stage for Vibration-Assisted Polishing. Micromachines. 2025; 16(11):1250. https://doi.org/10.3390/mi16111250
Chicago/Turabian StyleChen, Panpan, and Yangmin Li. 2025. "Design and Modeling of a 2-DOF Micro-Positioning Stage for Vibration-Assisted Polishing" Micromachines 16, no. 11: 1250. https://doi.org/10.3390/mi16111250
APA StyleChen, P., & Li, Y. (2025). Design and Modeling of a 2-DOF Micro-Positioning Stage for Vibration-Assisted Polishing. Micromachines, 16(11), 1250. https://doi.org/10.3390/mi16111250







