Abstract
In order to improve the response speed and output force of the camera focusing mechanism, the authors proposed a novelty micro focusing mechanism based on piezoelectric driving, which has the characteristics of rapid response, high precision positioning and large displacement focusing. In this paper, the operating principle of the proposed focusing mechanism is presented. Using the piezoelectric output characteristic, the movable tooth drive theory and the screw drive theory, the electromechanical coupling mechanical model and equations of the piezoelectric focusing mechanism are established. Through MATLAB simulation, the output characteristics of the piezoelectric focusing mechanism are calculated. The results indicate that the maximum thrust force of the lens and the maximum output torque of the movable tooth drive for the piezoelectric focusing mechanism are 562.5 N and 1.16 Nm, respectively. Furthermore, the driving voltage directly affects the output performance of the piezoelectric focusing mechanism. These results can be utilized both to optimize the dimensions and improve the overall performance of the piezo-driven focusing mechanism.
1. Introduction
The rapid development of intelligent manufacturing has propelled electromechanical and microelectromechanical systems to pursue high precision, integration and intelligence [1,2,3,4]. At the same time, higher requirements of anti-interference, anti-impact and anti-vibration are put forward for various precise transmission devices and mechanisms [5,6,7]. Focusing mechanism is an electromechanical drive system used to adjust the focal length of a camera. As the focal length of the lens changes, the scope of the target to be photographed varies, and the effect of the photo is quite different. Hence, the accuracy and quick response characteristics of the focusing mechanism have a significant influence on the performance of the camera [8,9].
Piezoelectric element has many excellent performances, such as fast response, small size, large output force and no electromagnetic interference. As a result, it has been successfully used in the field of robot actuating, precision positioning, energy harvesting and vibration reduction [10,11,12,13].
The driving of the camera focusing mechanism is an important application of piezoelectric actuation in the precise positioning field. Numerous achievements on improving the performance of the focusing system have been done by researchers. As early as 1987, Canon Company applied its independently developed annular piezoelectric ultrasonic motor to the focusing system of the EOS camera. The application of piezoelectric driving not only enables the camera to focus quickly, but also simplifies the camera structure and reduces its weight. Currently, Canon has installed piezoelectric motors in more than 30 types of cameras [14]. Burhanettin et al. [15], scholars from Pennsylvania State University, developed a single-phase piezoelectric ultrasonic motor driven by the bending vibration mode of metal cylinders, which was successfully applied to the focusing system of mobile phone cameras by Samsung Company. Subsequently, Sigma, Nikon, Pantex and other companies also use piezoelectric drive to achieve camera focusing. In recent years, the study of using piezoelectric to drive the various optical lenses focusing mechanism has gradually increased. Japanese researcher Masahiko et al. [16] applied a spherical piezoelectric ultrasonic motor to achieve the positioning and driving of the camera inside the tube. With this driving method, the camera can rotate 360 degrees along the tube. With eight piezoelectric films, Australian Michael et al. [17] designed an actuator used for out-of-plane movement of the microlens. Compared with other lens-driven mechanisms, this mechanism can achieve higher response frequency and is suitable for rapid action. Based on piezoelectric driving, Nazmul et al. [18] in US designed a kind of adjustable focusing adaptive glasses, which has practical value for improving the visual degradation of people. According to the characteristics of high controllability and automatic focusing required by mobile phone cameras, Korean Hyun-Phill et al. [19] developed a piezoelectric actuator for automatic focusing of mobile phone cameras. When focusing, the response time of the piezoelectric actuator is only 1% of the automatic focusing time, and it consumes energy only when working. The average instantaneous power is only 65 mW, which is far higher than the traditional electromagnetic mechanism in terms of energy conversion efficiency. What is more, since in the laser direct writing equipment the focusing mechanism with high resolution is needed to focus the photoresist objective lens, Chinese researcher Liu et al. [20] developed a focusing servo mechanism for laser direct writing equipment based on piezoelectric driving. As the proposed focusing mechanism has the characteristics of 10 nm resolution, 10 μm travel and 1.37" guiding accuracy, so it is an ideal focusing mechanism that is suitable for nanometer positioning. Chen et al. [21] developed a piezoelectric screw micromotor for the automatic focusing and zooming of the micro camera. The system uses the hollow piezoelectric stator as the nut stator, and the hollow rotor is connected with the lens as the stud to generate the spiral motion along the axial direction.
For the piezoelectric-driven focusing system, the performance of the control system is one of the key factors that affects its response speed and stability. Therefore, scholars have done a lot of research on improving the control performance of the focusing system. Teo et al. [22] constructed a PI tracking controller based on the integral force feedback, and verified the control effect of the controller through the piezoelectric objective locator. The results showed that its frequency tracking bandwidth could reach 255 Hz. Michael et al. [23] used a feedback system consisting of an optical displacement sensor, a 90° phase shifter with feedback gain and a forward path actuator to drive the fast piezoelectric microlens actuator. When the driving frequency was 750 Hz, the minimum switching time of the driver was only 2.5 ms. In order to improve the beam writing quality in confocal differential parallel laser direct writing, Zong et al. [24] designed a leveling focusing servo control system. Though using the differential astigmatism detection method and proportional integral differential (PID) feedback algorithm, the error of light source and external interference is reduced. By means of dynamic focusing, the elongation of piezoelectric ceramics can be guaranteed within the range of focal depth, the discrimination accuracy of the focal position can be nanoscale, and the tilt angle and pitch angle of the focusing platform are around 1 × 10−5 rad. Using traditional proportional integral differential control (PID) and fuzzy control, Pan et al. [25] proposed the parallel switching control strategy of the electric objective lens driven by an ultrasonic motor. The predictive control method of macro and micro phase fusion is established to realize the high precision and fast switching control of the objective lens converter. Addditionally, the repeated positioning error of the electric objective lens converter is less than 0.015°. For the drive system of the piezoelectric objective lens in digital confocal microscopy, Chen et al. [26] analyzed the control performance of the fuzzy PID controller and proposed the idea of off-line optimization. The optimized initial parameters are configured in the fuzzy PID control, the system is adjusted online and in real time, and the control system is driven by step positioning, which improves the response speed of the system.
From the above studies, scholars have made many valuable achievements in the field of piezoelectric-driven focusing. Various focusing mechanisms have been developed. However, there are still some problems such as slow response speed, small range of lens movement, small output force and poor stability that exist in focusing mechanisms, which seriously restrict the application of the focusing mechanism in the field of precise focusing and macro focusing. Meanwhile, previous research mainly uses piezoelectric ceramic as the driving source, so the driving force and output displacement of the piezoelectric ceramic plate are small. What is more, the friction mechanism between the stator and rotor of traditional piezoelectric actuation makes the transmission ratio unstable. In order to realize the rapid response, high precision positioning and large displacement focusing of the focusing mechanism, a cylindrical macro focusing mechanism based on piezoelectric drive, is proposed in this paper. In the proposed mechanism model, the stacked piezoelectric actuator is used as the driving source, which can output larger force and displacement than the piezoelectric ceramic. At the same time, the application of movable teeth makes the contact of the transmission mechanism as point contact, which greatly reduces the friction between the transmission mechanisms and makes the transmission ratio adjustable. Therefore, the novel piezoelectric focusing mechanism proposed by the author has important innovations.
Electromechanical coupling characteristic is an important factor of the focusing mechanism, which will affect the driving precision and overall performance of the system. Hence, in this paper, the electromechanical coupling mechanical model and equations of the proposed focusing mechanism are established. The output performance of the focusing mechanism is analyzed as well. What is more, the effect of parameters on output performance is investigated. The research results lay a theoretical foundation for the application of piezoelectric drive in the focusing mechanism.
2. Operating Principle of the Piezo-Driven Focusing Mechanism
The operating principle of the proposed piezo-driven focusing mechanism is shown in Figure 1. In the structure diagram, the focusing mechanism consists of the lens moving mechanism, micro movable tooth mechanism and displacement amplifier (or harmonic generator), and integrates piezoelectric drive, harmonic drive, precision gear drive and screw drive. Compared with other piezoelectric focusing mechanisms, the piezoelectric focusing system proposed in this paper has the advantages of large lens displacement, adjustable moving speed, large driving force, integrated drive and deceleration, rolling contact between stator and tooth carrier and between the lens connecting support and guide rail and long service life. Hence, it is suitable for macro focusing of micro target shooting. Through simulation analysis, the output torque of the movable tooth drive system and thrust force of the moving lens are 1.16 Nm and 562.5 N under the driven by four 5 × 5 × 20 mm3 piezoelectric actuators. In Ref. [27], the largest output torque of a harmonic piezo-drive motor with eight 5 × 5 × 50 mm3 piezoelectric actuators is only 0.75 Nm. Thus, the torque density of the proposed piezoelectric focusing mechanism is more than three times larger than that of the harmonic piezo-drive motor.
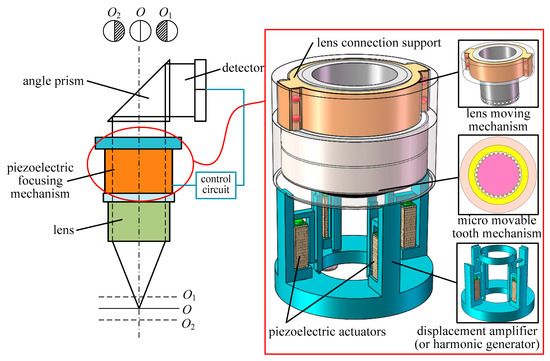
Figure 1.
Operating principle of the piezo-driven focusing mechanism.
During the operation of the focusing system, when the image beam enters the lens focus, it is received by the detector through the reflection of the angle prism for signal calculation and amplification. The signal is transmitted to the macro focusing system, causing the lens to twitch up and down for dynamic defocusing compensation. In Figure 1, Position O is the image obtained by focusing, and the light flux in the two quadrants is equal. The positions O1 and O2 are in the near-focus and far-focus images, and the light flux in the two quadrants is not equal.
The piezoelectric focusing system is driven by four sinusoidal signals whose phases differ by π/2 in turn. As the stacked type piezoelectric actuator is selected in this paper, the actuator is made of several piezoelectric ceramic plates bonded together with fixing glue. For exposed piezoelectric ceramics, once the tension is applied, the adhesive between the ceramic plates breaks. Hence, the piezoelectric ceramic does not resist tension, and the piezoelectric actuators can only apply positive voltages. The driving signals that applied for the piezoelectric actuators are shown in Figure 2. The equations of the driving signals can be expressed by:
where U1, U2, U3, U4 are the voltage that is applied to the piezoelectric actuators; Up is the peak value of the voltage; f is the driving frequency.
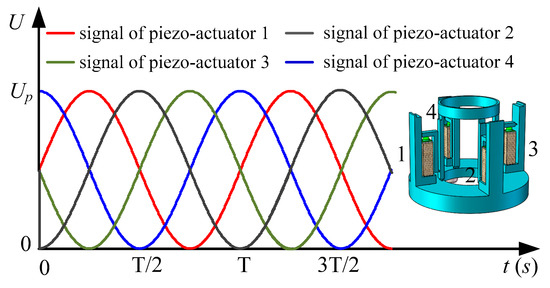
Figure 2.
Driving signals of piezoelectric actuators.
Driven by four signals, the harmonic wave is generated on the top surface of the harmonic generator, which is shown in Figure 3. Here, branch Figure 3a–d represent the initial position (or 360° position), 90° position, 180° position and 270° position of harmonic wave, respectively. However, when the order of input signals for piezoelectric actuators changes in Equation (2), the rotational motion turns in the opposite direction.
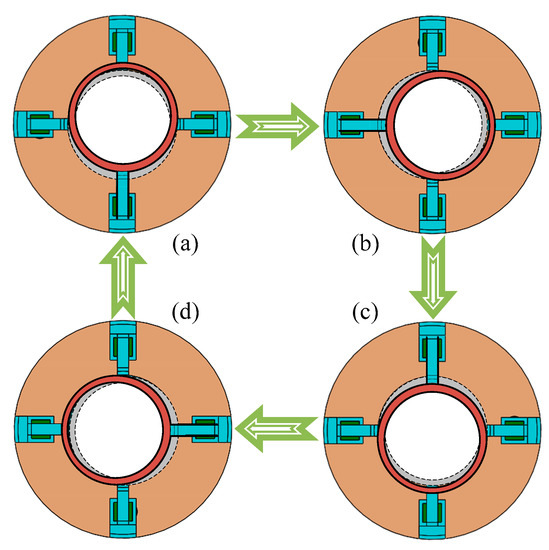
Figure 3.
Working principle of the harmonic generator. (a) Initial position and 360° position; (b) 90° position; (c) 180° position; (d) 270° position.
Hence, the reverse drive signals of piezoelectric actuators can be written as:
The harmonic forces push the movable teeth to mesh with the tooth profile of the central gear, and the motion of movable teeth drive the tooth carrier to generate a small angle. The equations and diagram of the tooth profile of central gear and trajectory of movable tooth [28] are presented in Equations (3) and (4) and Figure 4:
where is the rotational angle of the tooth carrier; ψ is the angle between the normal of the moving tooth center and x axis; a is the wave generator offset; b = rs+rp, rs and rp are the radius of the wave generator and the movable tooth; icp is the transmission ratio of the movable tooth system; αj is the angle between center of the j-th movable tooth and geometric center of the center gear.
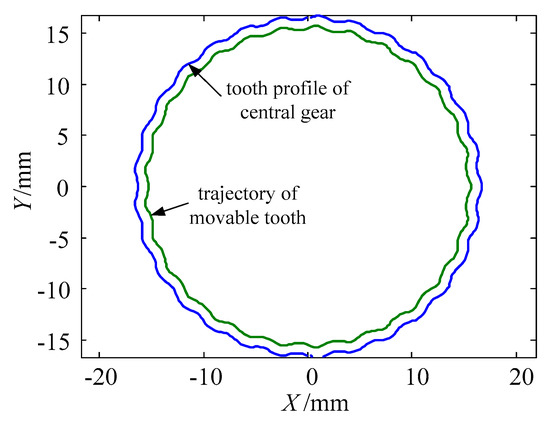
Figure 4.
The tooth profile of the central gear and trajectory of the movable tooth.
Under the action of four continuous signals, the tooth carrier realizes continuous rotation. With screw drive, the rotational motion of the tooth carrier is converted into the linear motion of the lens. The proposed piezo-driven focusing mechanism can achieve the function of the large displacement of the lens, adjustable movement speed and low friction force.
3. Electrochemical Coupled Models and Equations
The driving forces of the proposed micro piezo-driven focusing mechanism come from four piezoelectric actuators. As the piezoelectric actuator selected here is elongated along the axis and its working mode is d33 (piezoelectric strain constant), so the working mode of d33 is adopted in this paper. Except the d33 mode can meet the work requirements, other modes of piezoelectric actuators can also meet the requirements. Here, only one working mode is utilized for analysis. The output strain of each piezoelectric actuator varies with time, its expression is:
where s33 is the elastic flexibility coefficient of the piezoelectric actuator; P1, P2, P3 and P4 are preloads of the piezoelectric actuators; Sp is the sectional area of the piezoelectric actuator; hp is thickness of the piezoelectric layer.
Hence, the output forces of piezoelectric actuators can be written as:
where c33 is elastic modulus of the piezoelectric actuator.
Figure 5 shows the forces of the displacement amplification mechanism, where Fpi is the output force of the piezoelectric actuators, Fhi is the force that applied to the wave generator, Mi1 and Mi2 are torsional moment of the flexible hinge, di1 and di2 are length dimension, and i = 1, 2, 3, 4. According to theoretical mechanics, establishing the force balance equation as follows:
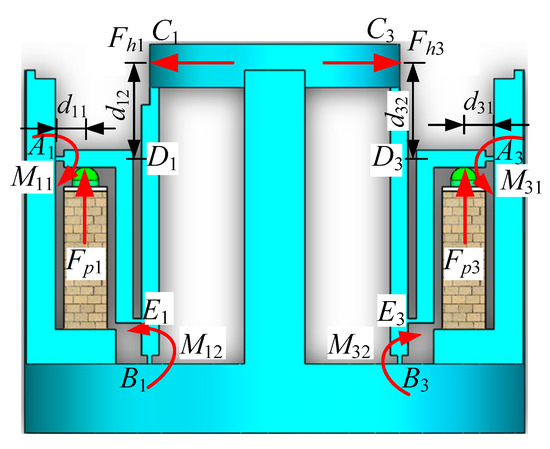
Figure 5.
Force diagram of displacement amplification mechanism.
Rotational angle of flexible hinge Ai can be expressed by:
where is total deformation of the piezoelectric actuator; is length from A1 to D1; n is the number of the piezoelectric layer for the actuator.
Similarly, the rotational angle of the flexible hinge Bi can be expressed by:
where is the intermediate variable; is the length from Bi to Ei; is the length from Di to Ei.
According to the torque calculation formula of the flexure hinge [29], the torsional moment of the flexure hinge can be written as:
From Equations (6)–(9), the force that applied to the wave generator can be deduced as follows:
The forces of a selected single movable are shown in Figure 6, where Oc and Os represent the center of the central gear and harmonic generator, γj is the angle between the tangent line of the center track of the movable tooth and the x-axis, Fcj, Frj and Fsj are the forces of the movable tooth that are applied by the central gear, tooth carrier and harmonic generator, respectively.
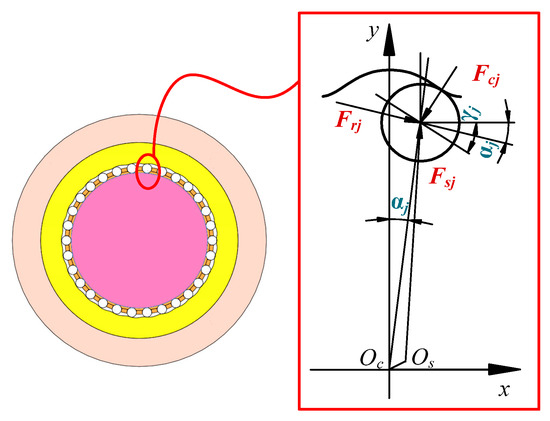
Figure 6.
Forces of a selected single movable tooth.
The force equilibrium equations of the single movable teeth along x and y directions can be written as:
By decomposing the forces of the movable tooth received from the wave generator along x and y axis, it can be obtained:
where is the initial position angle of the tooth carrier.
Therefore, the output torque of the tooth carrier can be obtained as the following form:
When the piezoelectric focusing mechanism works, the output torque of the tooth carrier is transferred to the screw drive mechanism to realize the linear motion of the lens. Figure 7 shows the force diagram of the screw drive mechanism, where Fq and Ft are axial pushing force and horizontal pushing force, supporting force FN and frictional force Ff constitute the opposite force FR, Ψ and ζ are the helix angle and frictional angle of the screw drive.
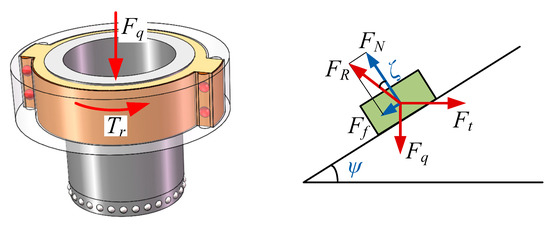
Figure 7.
Force diagram of the screw drive mechanism.
Establishing the equilibrium equations in the horizontal and vertical directions, it can be obtained:
From Equation (15), it can be deduced that:
where is the frictional coefficient.
As horizontal pushing force is provided by the output torque of the tooth carrier, so the relationship between Ft and Tr can be written as:
where dm is the effective diameter of the thread.
Hence, according to above equations, the output characteristic of the proposed piezo-driven focusing mechanism can be acquired. Furthermore, the electromechanical coupling relationship between output force and input voltage is established.
4. Results and Discuss
4.1. Output Forces of Piezoelectric Actuator
For the proposed piezo-driven focusing mechanism, a dimension of 5 × 5 × 20 mm3 of the piezoelectric actuator is selected to drive the focusing mechanism. Meanwhile, a 100 N preload is applied to the piezoelectric actuator. Applying those conditions and Equation (6), the output forces of the piezoelectric actuator are investigated as shown in Figure 8, where sub-figure a shows the output forces of the different piezo-actuator, whereas Figure 8b–f represent the changes of output forces with different peak voltage, piezoelectric strain constant, elastic modulus of piezoelectric actuator, thickness of piezoelectric layer and sectional area of piezoelectric actuator. Based on Figure 8, one can draw the conclusions:
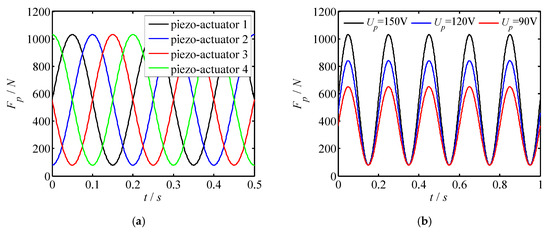
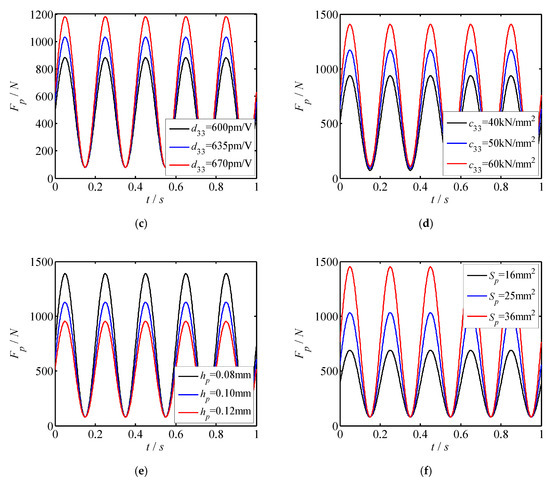
Figure 8.
Output forces of the piezoelectric actuator. (a) Force changes with different piezo-actuator; (b) force changes with Up; (c) force changes with d33; (d) force changes with c33; (e) force changes with hp; (f) force changes with Sp.
(1) The forces acting on the piezoelectric actuator vary sinusoidal with time. The phase difference of the force curve for each piezoelectric actuator is π/2. Besides, when the peak voltage of each piezoelectric actuator is the same, the maximum output force of each piezoelectric actuator is the same as well.
(2) As the driving voltage Up increases, the output forces of the piezoelectric actuator increase linearly. Therefore, the output force of the piezoelectric actuator can be adjusted by changing the driving voltage.
(3) The variation law of the output force with d33, c33 and Sp is similar to that with Up. The output force is proportional to the change of parameters.
(4) The output force of the piezoelectric actuator decreases with the thickness of the piezoelectric layer increasing. Hence, a small thickness of the piezoelectric layer benefits to obtain a large output force of the piezoelectric actuator, and then gets better output performance.
4.2. Forces of Movable Tooth Drive
According to Equation (11), the harmonic force of the wave generator has been deduced. Using MATLAB simulation software, the harmonic force under different input signals and its variation with voltage and time are studied as shown in Figure 9. From Figure 9, it can be observed that:
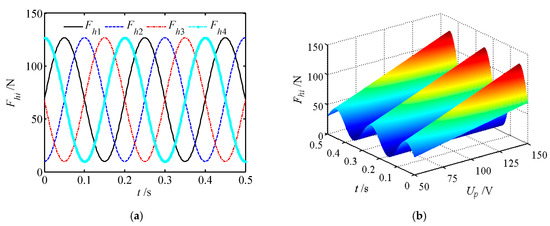
Figure 9.
Harmonic force of the wave generator. (a) Harmonic under different input signals; (b) harmonic force varies with input voltage and time.
(1) The maximum harmonic force is 126.8 N, which is only 1/8 of the output force of the piezoelectric actuator. It can thus be seen that the displacement is amplified 8 times by the action of the displacement amplifier.
(2) What is more, the harmonic force increases linearly with the input voltage at a certain time, whereas it changes sinusoidal with time when the input voltage is constant.
The movable tooth drive system is an important part of the proposed piezoelectric focusing mechanism, and its mechanical characteristics affect the stable output characteristics of the system. Therefore, the force of movable teeth is analyzed in this section, where 30 movable teeth are selected to mesh with 29 teeth of the central gear. Table 1 shows the number of the meshing movable teeth of different positions in a period. Figure 10, Figure 11 and Figure 12 depict the forces of the movable tooth. From Table 1 and Figure 10, Figure 11 and Figure 12, it is known that:

Table 1.
Number of meshing movable teeth of different positions in a period.
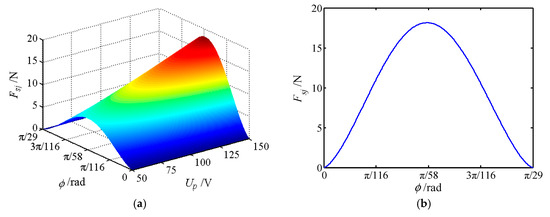
Figure 10.
The force of movable tooth Fsj. (a) The force varies with rotational angle and voltage; (b) force sectional view at Up = 150 V.
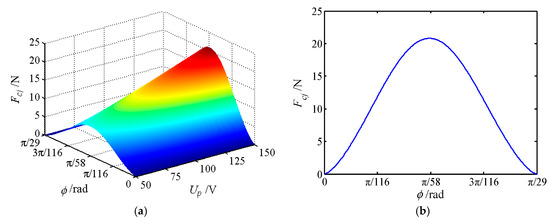
Figure 11.
The force of movable tooth Fcj. (a) The force varies with rotational angle and voltage; (b) force sectional view at Up = 150 V.
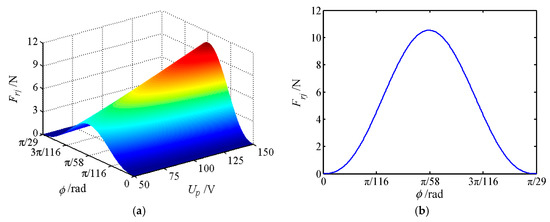
Figure 12.
The force of movable tooth Frj. (a) The force varies with rotational angle and voltage; (b) force sectional view at Up = 150 V.
(1) For every π/870 angle that the tooth carrier rotates, one of the movable tooth contacts the tooth tip or root of the central gear. Once again at an angle of π/870, one of the movable teeth falls out of meshing, so π/870 is the dividing point between the movable teeth entering and exiting meshing.
(2) At any given moment, all movable teeth are acted upon by the force from the wave generator Fsj, the central rotation force Fcj and the tooth carrier force Frj. With the change of the rotating angle of the tooth carrier, the force of each movable tooth will change correspondingly, but its maximum force maintains constant.
(3) The forces Fsj, Fcj and Frj of a single movable tooth change significantly with the voltage. When the movable gear rotates at an angle of π/58, the force exerted on the movable tooth reaches the maximum value, and the force exerted on the movable tooth is most sensitive to the change of voltage. Forces Fsj, Fcj and Frj show the tendency of increasing first and then decreasing with the increase of the rotational angle of the tooth carrier.
(4) When the voltage is constant, the peak value of Fcj is the largest, whereas the peak value of Fsj is the smallest. Therefore, the meshing force between the center gear and the movable teeth is the largest. At the same time, the magnitude of force Fcj directly affects the magnitude of Frj.
4.3. Thrust Force of Piezo-Driven Focusing Mechanism
Base on the forces of the movable teeth, the torque of the movable tooth drive system can be calculated by using Equation (14), and then the thrust force of the moving lens can be obtained by solving Equation (17). Figure 13 shows the output torque and thrust force vary with peak value of the driving voltage Up. Figure 14, Figure 15, Figure 16 and Figure 17 depict the output torque and thrust force change with the piezoelectric strain constant d33, elastic modulus of piezoelectric actuator c33, thickness of piezoelectric layer hp and sectional area of piezoelectric actuator Sp. From Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, it can be concluded that:
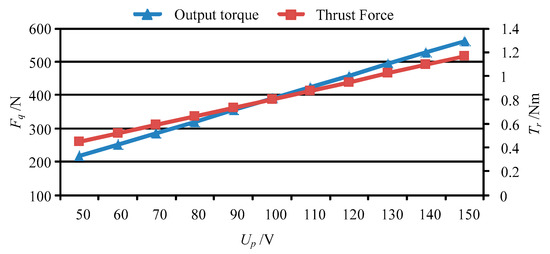
Figure 13.
The output torque and thrust force vary with Up.
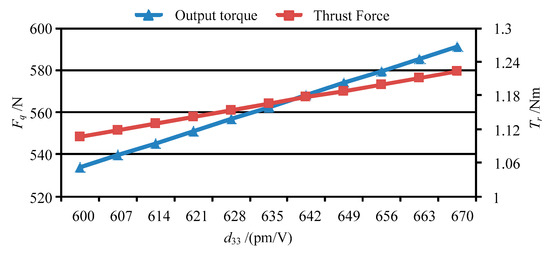
Figure 14.
The output torque and thrust force vary with d33.
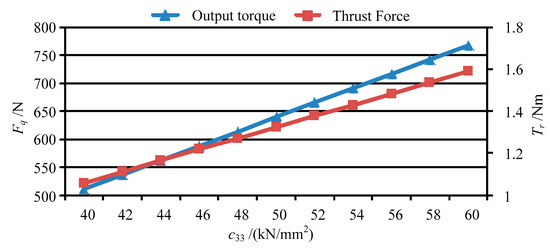
Figure 15.
The output torque and thrust force vary with c33.
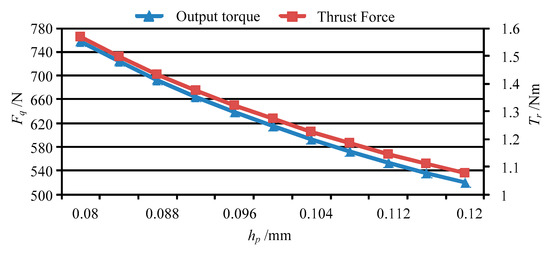
Figure 16.
The output torque and thrust force vary with hp.
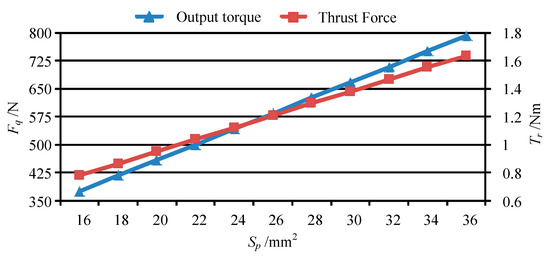
Figure 17.
The output torque and thrust force vary with Sp.
(1) With the increase of driving voltage, the output torque of the movable tooth drive system and thrust force of moving lens increase linearly. Therefore, the driving voltage is a decisive factor that affects the output performance of the piezoelectric focusing system.
(2) At Up = 150 V, the output torque of the movable tooth drive system and thrust force of moving lens are 1.16 Nm and 562.5 N under the driven by four 5 × 5 × 20 mm3 piezoelectric actuators. In Ref. [23], the largest output torque of a harmonic piezo-drive motor with eight 5 × 5 × 50 mm3 piezoelectric actuators is only 0.75 Nm. Thus, the torque density of the proposed piezoelectric focusing mechanism is more than three times larger than that of the harmonic piezo-drive motor.
(3) The variation of output torque and thrust force with d33, c33 and Sp is similar to that with driving voltage Up. That is, the output torque and thrust force increase in direct proportion to those parameters.
(4) As the thickness of the piezoelectric layer hp increases, the output torque and thrust force decrease nonlinearly. Therefore, the smaller the thickness of the piezoelectric layer, the better the performance of the piezo-driven focusing mechanism.
In short, through theoretical simulation analysis, the proposed micro piezoelectric focusing mechanism has a large driving torque and thrust force, which has an important application prospect in the field lens focusing.
4.4. Finite Element Analysis
The finite element analysis (FEA) of the system is carried out by ANSYS software. In the FEA model, the density of the piezoelectric material is 7740 Kg/m3, while the stiffness matrix c, dielectric constant matrix ε and piezoelectric stress constant e matrix are respectively as follows:
Other parts of the piezo-driven focusing mechanism are made of structural steel. Its material density is 7850 Kg/m3, the Young’s modulus and Poisson’s ratio are 2 × 1011 Pa and 0.3, respectively. In addition, the compressive yield strength and tensile ultimate strength of this material are 2.5 × 108 Pa and 4.6 × 108 Pa, respectively.
During the finite element analysis, the APDL language of ANSYS is used to program the finite element analysis of the piezoelectric actuator. Then, the analysis results of the piezoelectric actuator are imported into ANSYS Workbench for the finite element analysis of the whole structure of the piezoelectric focusing mechanism. The mesh size was set as 2 mm, and the structure was meshed by free partition type. The finite element analysis process is shown in Figure 18.
Figure 18.
Process of the finite element analysis.
Figure 19 shows the FEA results of the piezoelectric actuator. Its Figure 19a,b give voltage load that applied on the piezoelectric actuator and deformation displacement of the piezoelectric actuator, where a 150 V voltage is applied on it. Figure 19c,d present transient responses at 1000 and 5713 Hz (natural frequency of piezoelectric actuator) of exciting frequency. Figure 20 shows stress analysis results at different times, where a half period time (T/2 in Figure 2) of the exciting signal is selected to illustrate the stress of the displacement magnifying mechanism in different operating conditions. Figure 21 shows the modal analysis results of the piezoelectric focusing mechanism. From Figure 19, Figure 20 and Figure 21, it is known that:
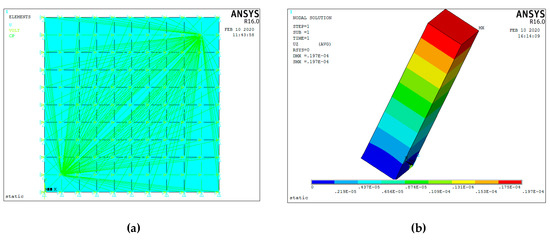
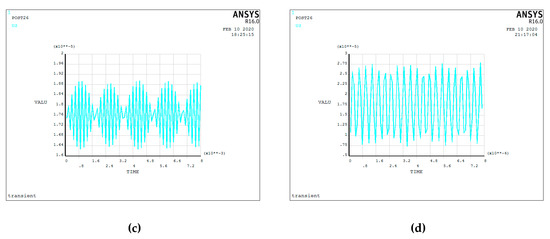
Figure 19.
Finite element analysis results of piezoelectric actuator. (a) Voltage load applied on the piezoelectric actuator; (b) deformation displacement of the piezoelectric actuator; (c) transient response at 1000 Hz of the exciting frequency; (d) transient response at 5713 Hz of the exciting frequency.
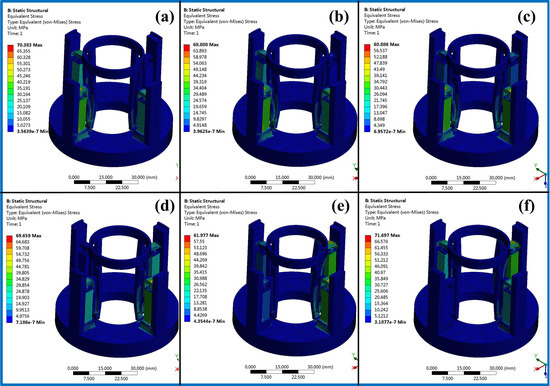
Figure 20.
Stress analysis results at different times. (a) At t = 0 s; (b) at t = 0.01 s; (c) at t = 0.025 s; (d) at t = 0.05 s; (e) at t = 0.075 s; (f) at t = 0.1 s.
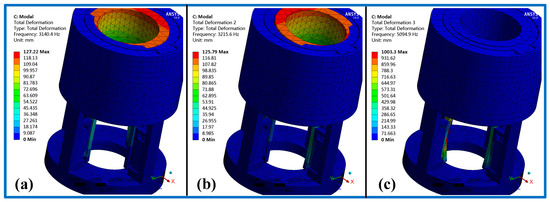
Figure 21.
Modal analysis results of the piezoelectric focusing mechanism. (a) First-order mode; (b) second-order mode; (c) third-order mode.
(1) Driven by a voltage of 150 V, the maximum deformation displacement of the piezoelectric actuator is 19.7 μm, which is consistent with the actual output. At the excitation frequency of 1000 Hz, the transient response peak of the piezoelectric actuator is 19 μm. However, this value is 28 μm when the excitation frequency is the natural frequency value 5713 Hz. Thus, the response displacement of the piezoelectric actuator increases greatly when resonance occurs.
(2) According to the stress diagram in Figure 20, the stress of each piezoelectric actuator and magnifying branch changes at different times. The maximum stress occurs at t = 0, 0.05 s and 0.1 s. The reason for this is that the voltage of the drive signals of the piezoelectric drivers 1, 2 and 4 reaches the maximum peak at these moments.
(3) The natural frequency values of the first three orders are 3140.4, 3215.6 and 5094.9 Hz. Their corresponding vibration modes are Y swing of the tooth carrier, X swing of the tooth carrier and bending vibration of the displacement amplification mechanism. Since the driving frequency of the piezoelectric focusing mechanism is less than 100 Hz, which is far lower than the natural frequency, thus the resonance has little influence on the system.
In conclusion, the FEM simulation verifies that the response displacement of the piezoelectric actuator is consistent with the actual output, the maximum stress at different moments is within the allowable range, and the operating frequency of the system is lower than the natural frequency.
4.5. Principium Experiment
In order to verify the characteristics of the piezoelectric output, the output displacement of the piezoelectric actuator was tested. Figure 22 shows the output displacement test of the piezoelectric actuator, where the XMT piezoelectric power supply is used as the driving signal and power amplifier, and the OptoMET laser vibrometer is applied to test the displacement of the piezoelectric actuator. From the test results in Figure 22b, it is known that:
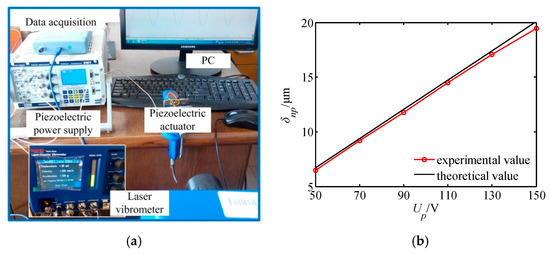
Figure 22.
Output displacement test of the piezoelectric actuator. (a) Experimental device structure; (b) test results.
The tested displacement is very close to the theoretical displacement, and the maximum error is 2.6% when the voltage is 150 V. The output displacement experiment of the piezoelectric actuator lays a foundation for the development of the prototype.
At the same time, in order to verify the feasibility of the design scheme in this paper, the first generation prototype is used to carry out the principium experiment. For the first generation principium prototype, its design principle is the same as that shown in Figure 1. The difference is that the first prototype is driven by two piezoelectric actuators and can only output rotational motion, without a screw drive. The exploded view of the principium prototype and test scheme for the principium experiment are shown in Figure 23, where the control system can output two sinusoidal signals with different phases and positive bias. Table 2 presents the output rotational speed of the principium prototype with different driving voltages. The test results show:
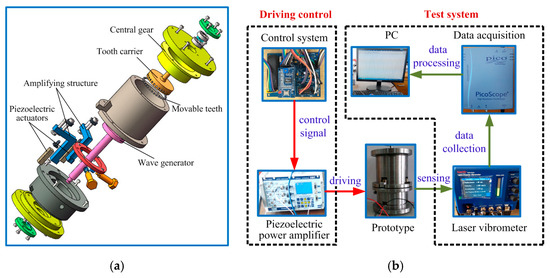
Figure 23.
Principium experiment of the piezo-driven focusing mechanism. (a) Exploded view of the principium prototype; (b) test scheme.

Table 2.
The prototype rotational speed with different driving voltages (r/min).
(1) When the peak value of the driving voltage exceeds 100 V, the prototype starts to rotate, and the speed increases slowly with the increase of the voltage. When the peak value of the voltage exceeds 120 V, the speed of the prototype gradually tends to be stable. When the peak value of the voltage is 150 V, the speed of the prototype does not change with the change of the voltage.
(2) When the driving frequency increases, the error between the test speed and the theoretical speed increases. It is because when the driving speed is high, the loss of teeth increases. Therefore, the lower the driving frequency is, the more favorable it is for the system transmission, and the prototype system is more suitable for low-speed work.
In a word, the experimental test verifies the feasibility and reasonability of the piezoelectric drive structure designed in this paper.
4.6. Future Work Prospects
Based on the findings of existing studies [30,31] and results of this paper, a static–dynamic hybrid optimization method can be proposed to optimize the performance of the piezoelectric focusing mechanism for future work. The specific steps are as follows:
(1) Based on the results of this paper, a system optimization model will be established to analyze the static performance of single-objective static optimization.
(2) Find out the dynamic objective function, optimize the single objective with dynamic characteristics of the piezoelectric focusing mechanism, and analyze the sensitivity of parameters to dynamic optimization.
(3) Combining static and dynamic optimization goals, establish the static–dynamic multi-objective optimization mathematical model. Compare the difference and relation between the results of multi-objective optimization and single-objective optimization.
Therefore, by using the research results of this paper, the performance optimization of the piezoelectric focusing system can be realized by establishing a multi-objective optimization mathematical model.
5. Conclusions
In this paper, a micro piezo-driven focusing mechanism is proposed and its working principle is presented. Using the piezoelectric theory, the movable tooth drive theory and the screw drive theory, the electromechanical coupling mechanical model of the piezoelectric focusing mechanism is established. Through MATLAB simulation, the output characteristics of the piezoelectric focusing mechanism are calculated. The results indicate that:
(1) The driving voltage directly affects the output performance of the piezoelectric focusing mechanism, and the thrust force is proportional to the voltage.
(2) The maximum thrust force of the lens of the piezoelectric focusing mechanism is 562.5 N, and the maximum output torque of the movable tooth drive is 1.16 Nm.
(3) A small thickness of the piezoelectric layer of the piezoelectric actuator benefits to obtain a large output force of the focusing mechanism.
(4) The experiment verifies the displacement output characteristic of the piezoelectric actuator and the feasibility of the proposed piezoelectric drive structure.
These results can be used for improving the output performance of the proposed micro piezo-driven focusing mechanism.
Author Contributions
Conceptualization, C.L.; Investigation, K.L. and W.Z.; Validation, J.F.; Writing—original draft, C.L. and Y.Z.; Writing-review & editing, L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China [grant No. 51905228, 51705217, 51805214], China Postdoctoral Science Foundation [grant No. 2018M640515], Natural Science Foundation of the Jiangsu Higher Education Institutions [grant No. 18KJB460008] and Science and Technology Innovation Project of Jiangsu University of Science and Technology for Youth [grant No. 1022921801].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhu, Y.; Tang, S.; Quan, L.; Jiang, W.; Zhou, L. Extraction method for signal effective component based on extreme-point symmetric mode decomposition and Kullback-Leibler divergence. J. Braz. Soc. Mech. Sci. 2019, 41, 100. [Google Scholar] [CrossRef]
- Wang, C.; He, X.; Cheng, L.; Luo, C.; Xu, J.; Chen, K.; Jiao, W. Numerical simulation on hydraulic characteristics of nozzle in waterjet propulsion system. Processes 2019, 7, 915. [Google Scholar] [CrossRef]
- Zhu, Y.; Qian, P.; Tang, S.; Jiang, W.; Li, W.; Zhao, J. Amplitude-frequency characteristics analysis for vertical vibration of hydraulic AGC system under nonlinear action. AIP Adv. 2019, 9, 035019. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, S.; Wang, C.; Jiang, W.; Yuan, X.; Lei, Y. Bifurcation characteristic research on the load vertical vibration of a hydraulic automatic gauge control system. Processes 2019, 7, 718. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.X.; Qiu, N.; Zhu, Y.; Shi, W. Numerical and experimental study on the pressure fluctuation, vibration, and noise of multistage pump with radial diffuser. J. Braz. Soc. Mech. Sci. 2018, 40, 481. [Google Scholar] [CrossRef]
- Li, W.; Li, E.; Ji, L.L.; Zhou, L.; Shi, W.; Zhu, Y. Mechanism and propagation characteristics of rotating stall in a mixed-flow pump. Renew. Energy 2020, 153, 74–92. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, S.; Wang, C.; Jiang, W.; Zhao, J.; Li, G. Absolute stability condition derivation for position closed-loop system in hydraulic automatic gauge control. Processes 2019, 7, 766. [Google Scholar] [CrossRef]
- Gaunekar, A.S.; Widdowson, G.P.; Srikanth, N.; Guangneng, W. Design and development of a high precision lens focusing mechanism using flexure bearings. Precis. Eng. 2005, 29, 81–85. [Google Scholar] [CrossRef]
- Wang, L.; Ishikawa, M. Dynamic response of elastomer-based liquid-filled variable focus lens. Sensors 2019, 19, 4624. [Google Scholar] [CrossRef]
- Zhu, X.B.; Wen, Z.J.; Chen, G.Z.; Liang, J.; Liu, P. A decoupled flexure-based rotary micropositioning stage with compact size. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4167–4179. [Google Scholar] [CrossRef]
- Yang, Y.L.; Lou, J.Q.; Wu, G.H.; Wei, Y.; Fu, L. Design and position/force control of an S-shaped MFC microgripper. Sens. Actuators A Phys. 2018, 282, 63–78. [Google Scholar] [CrossRef]
- Yoon, S.; Kim, J.; Cho, K.; Ko, Y.-H.; Lee, S.-K.; Koh, J.-H. Piezoelectric energy generators based on spring and inertial mass. Materials 2018, 11, 2163. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.X.; Niu, S.K.; Hu, Y.T. A periodic piezoelectric smart structure with the integrated passive/active vibration-reduction performances. Smart Mater. Struct. 2017, 26, 065015. [Google Scholar] [CrossRef]
- Xia, C.L.; Shi, T.N.; Wang, T.Y. The Development and future applicaton of piezoelectric ultrasonic motors. Chin. J. Sci. Instrum. 2001, 22, 390–391. [Google Scholar]
- Koc, B.; Cagatay, S.; Uchino, K. A piezoelectric motor using two orthogonal bending modes of a hollow cylinder. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 495–500. [Google Scholar] [CrossRef]
- Hoshina, M.; Mashimo, T.; Fukaya, N.; Matsubara, O.; Toyama, S. Spherical ultrasonic motor drive system for camera orientation in pipe inspection. Adv. Robot. 2013, 27, 199–209. [Google Scholar] [CrossRef]
- Michael, A.; Kwok, C.Y. Piezoelectric micro-lens actuator. Sens. Actuators A Phys. 2015, 236, 116–129. [Google Scholar] [CrossRef]
- Nazmul, H.; Aishwaryadev, B.; Hanseup, K. Tunable-focus lens for adaptive eyeglasses. Opt. Express 2017, 25, 1221–1233. [Google Scholar]
- Hyun-Phill, K.; Hoseop, J.; Burhanettin, K. Piezoelectric actuator for mobile auto focus camera applications. J. Electroceram. 2009, 23, 530–535. [Google Scholar]
- Liu, W.; Zhang, J.H. Focusing-servo mechanism with nanometer resolution for laser direct writing device. J. Harbin Inst. Technol. 2004, 36, 310–312. [Google Scholar]
- Chen, X.; Li, X.; Shan, L.; Sun, W.; Wang, X.; Xie, T.; Dong, S. A spiral motion piezoelectric micromotor for autofocus and auto zoom in a medical endoscope. Appl. Phys. Lett. 2016, 108, 052902. [Google Scholar] [CrossRef]
- Teo, Y.R.; Russell, D.; Aphale, S.S. Optimal integral force feedback and ftructured PI tracking control: Application for objective lens positioner. Mechatronics 2014, 24, 701–711. [Google Scholar] [CrossRef]
- Michael, A.; Chen, S.S.; Kwok, C.Y. Feedback driven fast piezoelectric micro-lens actuator. Procedia Eng. 2016, 168, 1492–1495. [Google Scholar] [CrossRef]
- Zong, Y.; Zhou, C.; Ma, J.; Wang, J.; Lu, Y. Optimized design of leveling and focusing servo control system. Acta Opt. Sin. 2017, 37, 261–270. [Google Scholar]
- Pan, S.; Jian, L.; Huang, W. The control method of ultrasonic motor direct driving motorized revolving nosepiece. J. Vib. Meas. Diagn. 2016, 36, 796–800. [Google Scholar]
- Chen, H.; Dong, Z.; Lin, G. PID controller of piezoceramic objective-lens actuator system based on offline optimization. Trans. Beijing Inst. Technol. 2013, 33, 976–979. [Google Scholar]
- Barth, O. Harmonic Piezodrive—Miniaturized Servo Motor. Mechatronics 2000, 10, 545–554. [Google Scholar] [CrossRef]
- Li, C.; Xing, J.; Xu, L.; Sun, L. Nonlinear dynamics of a piezoelectric precision drive system used for robot joint. Int. J. Appl. Electromagnet. Mech. 2018, 58, 57–77. [Google Scholar] [CrossRef]
- Li, C. Design and mechanical analysis of a mesh-type rotary harmonic piezoelectric motor. Int. J. Appl. Electromagnet. Mech. 2018, 56, 461–478. [Google Scholar] [CrossRef]
- Li, C.; Xing, J.C. Dynamic optimization of an electromechanical integrated harmonic piezoelectric motor. J. Mech. Sci. Technol. 2018, 32, 2517–2526. [Google Scholar] [CrossRef]
- Nabavi, S.; Zhang. L. Frequency Tuning and Efficiency Improvement of Piezoelectric MEMS Vibration Energy Harvesters. J. Microelectromech. Syst. 2019, 28, 77–87. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).