Estimating Fraction of Absorbed Photosynthetically Active Radiation of Winter Wheat Based on Simulated Sentinel-2 Data under Different Varieties and Water Stress
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Ground Data Collection
2.2.1. Data
2.2.2. Spectral Reflectance Data
2.3. Sentinel-2 Data
2.4. Vegetation Indices
2.5. Accuracy Assessment
3. Results
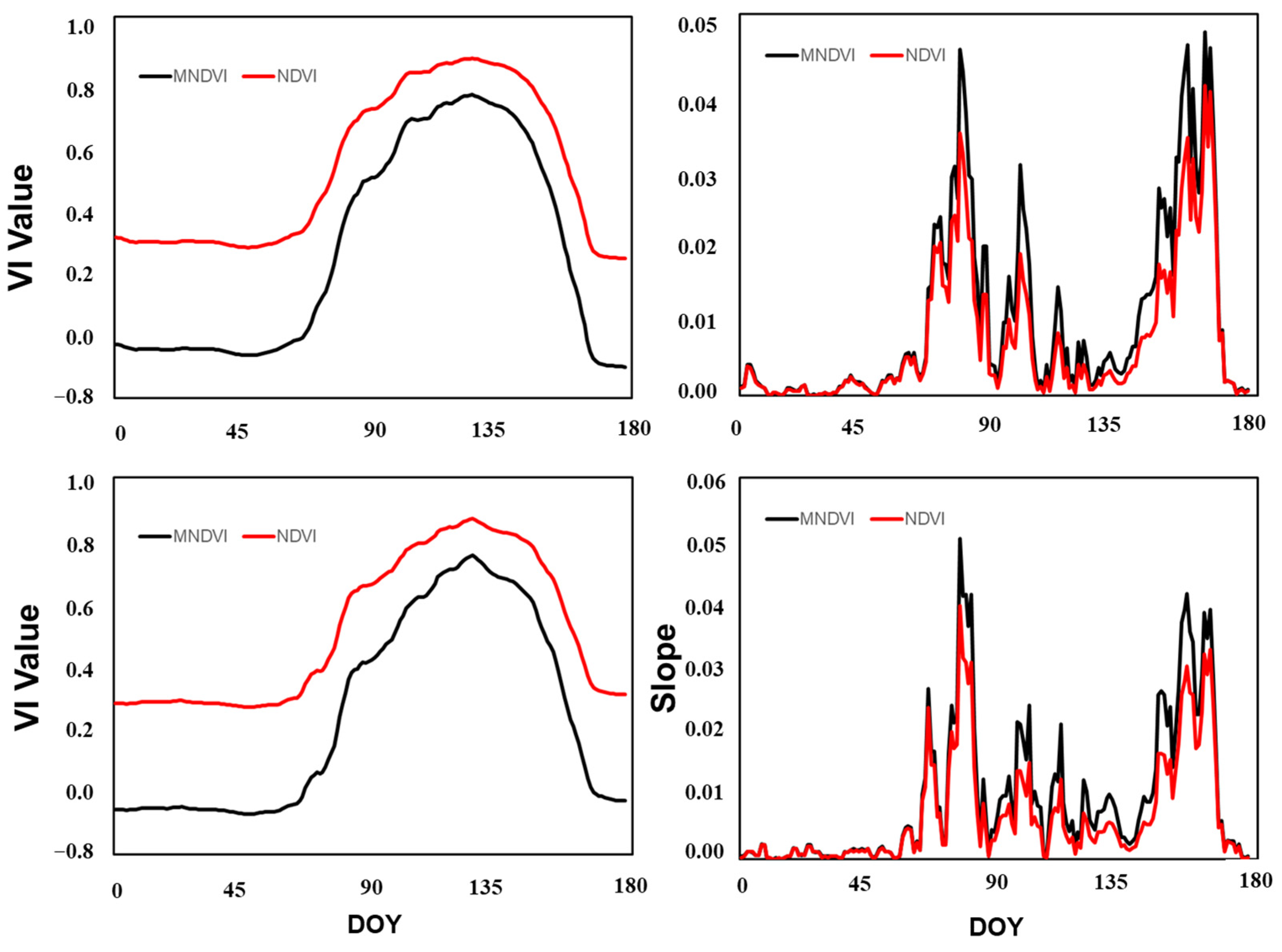
3.1. Correlation between Vegetation Indices at Different Phenological Stages
3.2. Comparison of the Estimation Ability of Vegetation Index for fPAR at the Entire Crop Season
3.3. Stability Test of MNDVI Estimation for fPAR
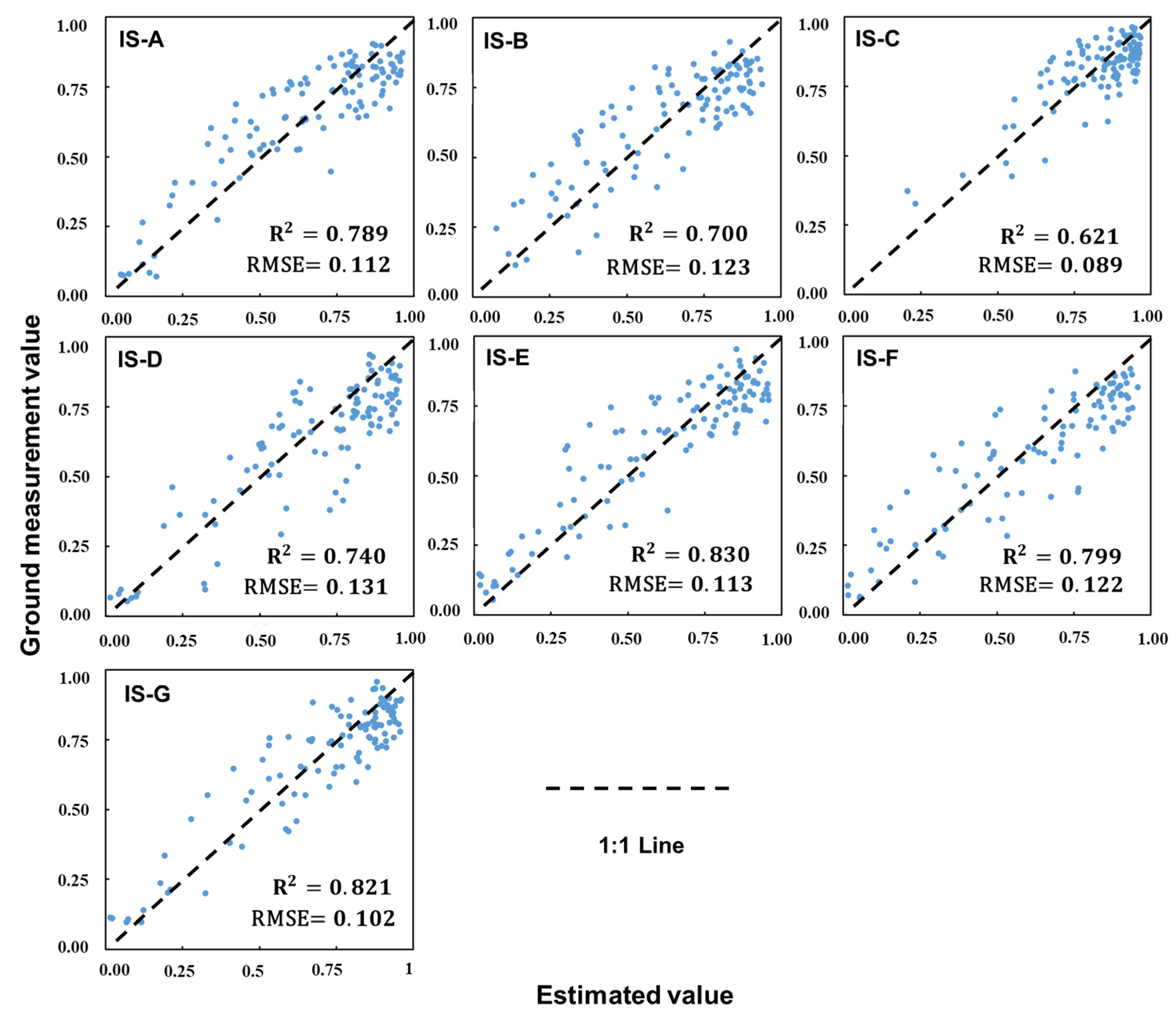
3.3.1. Accuracy Assessment Based on Different Varieties
3.3.2. Accuracy Assessment Based on Different Lighting Conditions
3.3.3. Accuracy Assessment Based on Different Irrigation Scheme
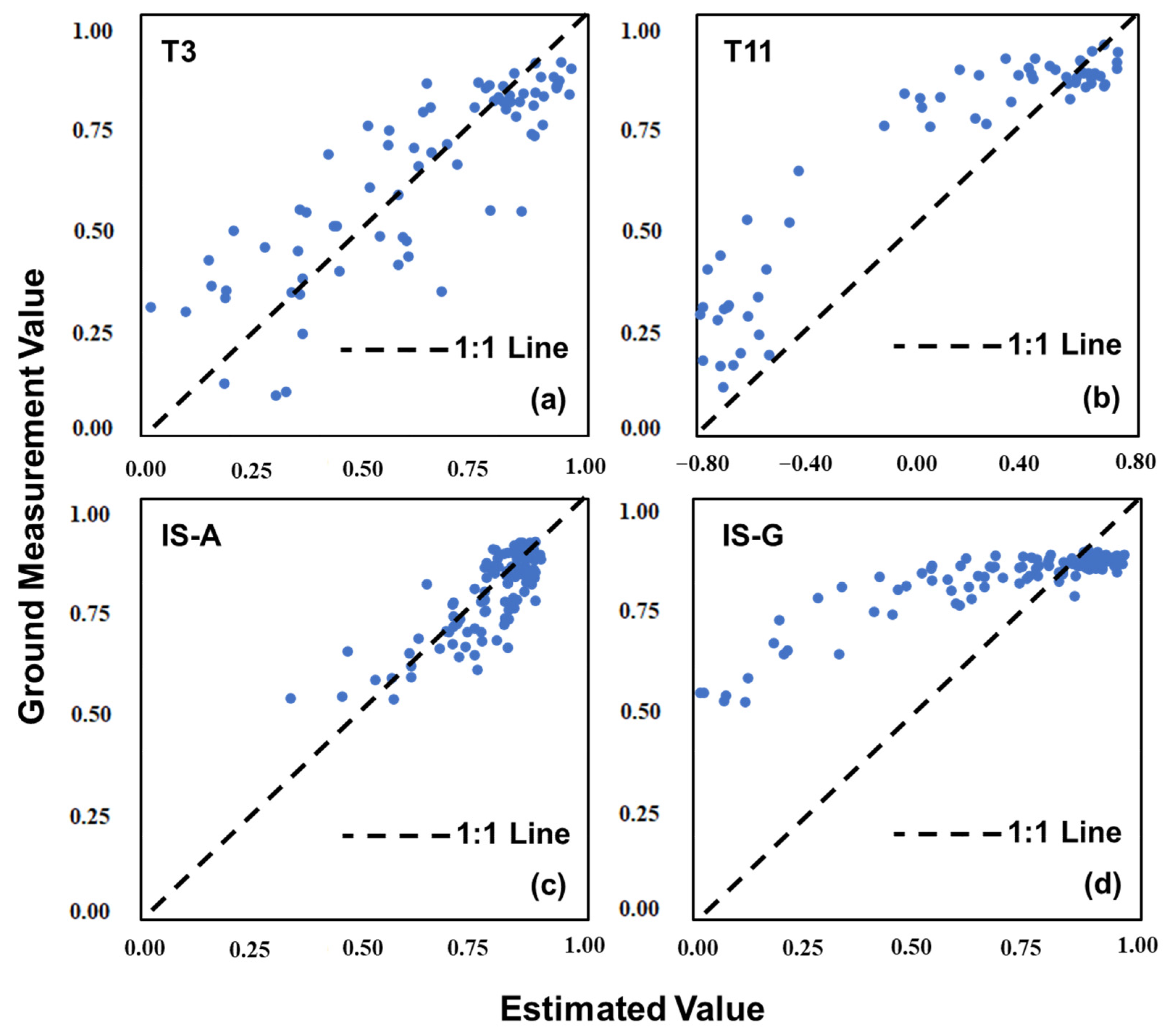
3.3.4. Accuracy Assessment at Satellite Scale
4. Discussion
4.1. The Necessity of Considering Variety and Water Stress
4.2. Sensitivity Analysis of MNDVI
4.3. The Potential of MNDVI in Estimating Winter Wheat Yield
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| No. Band | Band Name | Central Wavelength (nm) | Bandwidth (nm) | ASD Range (nm) | Spatial Resolution (m) |
|---|---|---|---|---|---|
| B2 | Blue | 492.5 | 65 | 460–525 | 10 |
| B3 | Green | 559.5 | 35 | 542–577 | 10 |
| B4 | Red | 664.5 | 31 | 649–680 | 10 |
| B5 | RE-1 | 704 | 14 | 697–711 | 20 |
| B6 | RE-2 | 740 | 14 | 733–747 | 20 |
| B7 | RE-3 | 781.5 | 19 | 772–791 | 20 |
| B8 | NIR | 833 | 104 | 781–885 | 10 |
| B8A | NIR2 | 864.5 | 21 | 854–875 | 20 |
| B9 | Water vapor | 944 | 20 | 934–954 | 60 |
| B10 | SWIR–Cirrus | 1375.5 | 29 | 1361–1390 | 60 |
| B11 | SWIR-1 | 1612 | 92 | 1566–1658 | 20 |
| B12 | SWIR-2 | 2194 | 180 | 2104–2284 | 20 |
Appendix C
| Abbreviation of Vegetation Index | The Full Name of Vegetation Index | Abbreviation of Vegetation Index | The Full Name of Vegetation Index |
|---|---|---|---|
| NDVI | Normalized Difference Vegetation Index | MNDVI | Modified Normalized Difference Vegetation Index |
| EVI | Enhanced Vegetation Index | SAVI | Soil Adjusted Vegetation Index |
| EVI2 | Enhanced Vegetation Index 2 | OSAVI | Optimized Soil Adjusted Vegetation Index |
| NDPI | Normalized Difference Phenology Index | CIG | Chlorophyll Index Green |
| GCVI | Green Chlorophyll Vegetation Index | CIR | Chlorophyll Index Red |
| RVI | Ratio Vegetation Index | MNDWI | Modified Normalized Difference Water Index |
| DVI | Difference Vegetation Index | NDBI | Normalized Difference Built-up Index |
| LSWI-b8b11 | Land Surface Water Index-b8b11 | GNDVI | Green Normalized Difference Vegetation Index |
| LSWI-b8b12 | Land Surface Water Index-b8b12 | NIRV | Near-Infrared Radiance of Vegetation |
| LSWI-b8Ab11 | Land Surface Water Index-b8Ab11 | MTCI | Meris Terrestrial Chlorophyll Index |
| LSWI-b8Ab12 | Land Surface Water Index-b8Ab12 |
References
- Tripathi, A.; Tripathi, D.K.; Chauhan, D.K.; Kumar, N.; Singh, G.S. Paradigms of climate change impacts on some major food sources of the world: A review on current knowledge and future prospects. Agric. Ecosyst. Environ. 2016, 216, 356–373. [Google Scholar] [CrossRef]
- Khan, S.; Hanjra, M.A.; Mu, J. Water management and crop production for food security in China: A review. Agric. Water Manag. 2009, 96, 349–360. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, X. Mapping crop phenology in near real-time using satellite remote sensing: Challenges and opportunities. J. Remote Sens. 2021, 14, 8379391. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Liu, C.A.; Chen, Z.X.; Yun, S.H.A.O.; Chen, J.S.; Hasi, T.; Pan, H.Z. Research advances of SAR remote sensing for agriculture applications: A review. J. Integr. Agric. 2019, 18, 506–525. [Google Scholar] [CrossRef]
- Sun, L.; Gao, F.; Anderson, M.C.; Kustas, W.P.; Alsina, M.M.; Sanchez, L.; Sams, B.; McKee, L.; Dulaney, W.; White, W.; et al. Daily Mapping of 30 m LAI and NDVI for Grape Yield Prediction in California Vineyards. Remote Sens. 2017, 9, 317. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Q.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Moore, B., III; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Huang, J.; Ma, H.; Sedano, F.; Lewis, P.; Liang, S.; Wu, Q.; Zhu, D. Evaluation of regional estimates of winter wheat yield by assimilating three remotely sensed reflectance datasets into the coupled WOFOST–PROSAIL model. Eur. J. Agron. 2019, 102, 1–13. [Google Scholar] [CrossRef]
- Xiao, G.; Zhang, X.; Niu, Q.; Li, X.; Li, X.; Zhong, L.; Huang, J. Winter wheat yield estimation at the field scale using Sentinel-2 data and deep learning. Comput. Electron. Agric. 2024, 216, 108555. [Google Scholar] [CrossRef]
- Wang, X.; Huang, J.; Feng, Q.; Yin, D. Winter Wheat Yield Prediction at County Level and Uncertainty Analysis in Main Wheat-producing Regions of China with Deep Learning Approaches. Remote Sens. 2020, 12, 1744. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Yu, G.; Bonnefond, J.-M.; Chen, J.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F.; et al. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef]
- D’Odorico, P.; Gonsamo, A.; Pinty, B.; Gobron, N.; Coops, N.; Mendez, E.; Schaepman, M.E. Intercomparison of fraction of absorbed photosynthetically active radiation products derived from satellite data over Europe. Remote Sens. Environ. 2014, 142, 141–154. [Google Scholar] [CrossRef]
- Pei, Y.; Dong, J.; Zhang, Y.; Yuan, W.; Doughty, R.; Yang, J.; Zhou, D.; Zhang, L.; Xiao, X. Evolution of light use efficiency models: Improvement, uncertainties, and implications. Agric. For. Meteorol. 2022, 317, 108905. [Google Scholar] [CrossRef]
- Prince, S.D.; Goward, S.N. Global primary production: A remote sensing approach. J. Biogeogr. 1995, 22, 815–835. [Google Scholar] [CrossRef]
- Peng, D.; Zhang, B.; Liu, L. Comparing spatiotemporal patterns in Eurasian FPAR derived from two NDVI-based methods. Int. J. Digit. Earth 2012, 5, 283–298. [Google Scholar] [CrossRef]
- Chen, J.M. Canopy architecture and remote sensing of the fraction of photosynthetically active radiation absorbed by boreal conifer forests. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1353–1368. [Google Scholar] [CrossRef]
- Zhou, G.; Liu, X.; Zhao, S.; Liu, M.; Wu, L. Estimating FAPAR of rice growth period using radiation transfer model coupled with the WOFOST model for analyzing heavy metal stress. Remote Sens. 2017, 9, 424. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Sun, R.; Wang, J.; Jiang, B. Estimating the fraction of absorbed photosynthetically active radiation from the MODIS data based GLASS leaf area index product. Remote Sens. Environ. 2015, 171, 105–117. [Google Scholar] [CrossRef]
- Zhou, Q.; Fellows, A.; Flerchinger, G.N.; Flores, A.N. Examining interactions between and among predictors of net ecosystem exchange: A machine learning approach in a semi-arid landscape. Sci. Rep. 2019, 9, 2222. [Google Scholar] [CrossRef] [PubMed]
- Myneni, R.; Knyazikhin, Y. MODIS/Terra+Aqua Leaf Area Index/FPAR 4-Day L4 Global 500 m SIN Grid. Available online: https://lpdaac.usgs.gov/products/mcd15a3hv061/ (accessed on 15 January 2020).
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of general regression neural networks for generating the GLASS leaf area index product from time-series MODIS surface reflectance. IEEE Trans. Geosci. Remote Sens. 2013, 52, 209–223. [Google Scholar] [CrossRef]
- Jin, H.; Li, A.; Liang, S.; Ma, H.; Xie, X.; Liu, T.; He, T. Generating high spatial resolution GLASS FAPAR product from Landsat images. Sci. Remote Sens. 2022, 6, 100060. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Martonchik, J.V.; Myneni, R.B.; Diner, D.J.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res. Atmos. 1998, 103, 32257–32275. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Aussedat, O.; Taberner, M.; Faber, O.; Mélin, F.; Lavergne, T.; Robustelli, M.; Snoeij, P. Uncertainty estimates for the FAPAR operational products derived from MERIS—Impact of top-of-atmosphere radiance uncertainties and validation with field data. Remote Sens. Environ. 2008, 112, 1871–1883. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, Y.; Zhang, Y.; El-Saleous, N.; Knyazikhin, Y.; Vermote, E.; Myneni, R.B. Investigation of product accuracy as a function of input and model uncertainties: Case study with SeaWiFS and MODIS LAI/FPAR algorithm. Remote Sens. Environ. 2001, 78, 299–313. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Lacaze, R.; Camacho, F.; Makhmara, H.; Pacholcyzk, P.; Smets, B. GEOV1: LAI and FAPAR essential climate variables and FCOVER global time series capitalizing over existing products. Part1: Principles of development and production. Remote Sens. Environ. 2013, 137, 299–309. [Google Scholar] [CrossRef]
- Tian, D.; Fan, W.; Ren, H. Progress of fraction of absorbed photosynthetically active radiation retrieval from remote sensing data. J. Remote Sens. 2020, 24, 1307–1324. [Google Scholar] [CrossRef]
- Cheng, Y.B.; Zhang, Q.; Lyapustin, A.I.; Wang, Y.; Middleton, E.M. Impacts of light use efficiency and fPAR parameterization on gross primary production modeling. Agric. For. Meteorol. 2014, 189, 187–197. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Park, T.; Zhu, P.; Huete, A.; Myneni, R.; Knyazikhin, Y.; Qi, J.; Nemani, R.R.; Li, F.; et al. Structural complexity biases global vegetation greenness measures. Nat. Ecol. Evol. 2023, 7, 1790–1798. [Google Scholar] [CrossRef]
- Chen, Z.; Shao, Q.; Liu, J.; Wang, J. Analysis of net primary productivity of terrestrial vegetation on the Qinghai-Tibet Plateau, based on MODIS remote sensing data. Sci. China Earth Sci. 2012, 55, 1306–1312. [Google Scholar] [CrossRef]
- Pei, Y.; Dong, J.; Zhang, Y.; Yang, J.; Zhang, Y.; Jiang, C.; Xiao, X. Performance of four state-of-the-art GPP products (VPM, MOD17, BESS and PML) for grasslands in drought years. Ecol. Inform. 2020, 56, 101052. [Google Scholar] [CrossRef]
- Ding, L.; Li, Z.; Shen, B.; Wang, X.; Xu, D.; Yan, R.; Yan, Y.; Xin, X.; Xiao, J.; Li, M.; et al. Spatial patterns and driving factors of aboveground and belowground biomass over the eastern Eurasian steppe. Sci. Total Environ. 2022, 803, 149700. [Google Scholar] [CrossRef]
- Dong, T.; Meng, J.; Shang, J.; Liu, J.; Wu, B. Evaluation of chlorophyll-related vegetation indices using simulated Sentinel-2 data for estimation of crop fraction of absorbed photosynthetically active radiation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4049–4059. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, N.; Liu, X.; Wu, S. Estimation of Harvest Index of Winter Wheat Based on Simulated Sentinel-2A Reflectance Data and Its Real Remote Sensing Imagery. Trans. Chin. Soc. Agric. Mach. 2022, 53, 231–243. [Google Scholar]
- Dong, J.; Lu, H.; Wang, Y.; Ye, T.; Yuan, W. Estimating winter wheat yield based on a light use efficiency model and wheat variety data. ISPRS J. Photogramm. Remote Sens. 2020, 160, 18–32. [Google Scholar] [CrossRef]
- Jenkins, J.P.; Richardson, A.D.; Braswell, B.H.; Ollinger, S.V.; Hollinger, D.Y.; Smith, M.L. Refining light-use efficiency calculations for a deciduous forest canopy using simultaneous tower-based carbon flux and radiometric measurements. Agric. For. Meteorol. 2007, 143, 64–79. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Sun, L.; Gao, F.; Xie, D.; Anderson, M.; Chen, R.; Yang, Y.; Yang, Y.; Chen, Z. Reconstructing daily 30 m NDVI over complex agricultural landscapes using a crop reference curve approach. Remote Sens. Environ. 2021, 253, 112156. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- Gitelson, A.A. Remote estimation of fraction of radiation absorbed by photosynthetically active vegetation: Generic algorithm for maize and soybean. Remote Sens. Lett. 2019, 10, 283–291. [Google Scholar] [CrossRef]
- Yebra, M.; Van Dijk, A.I.; Leuning, R.; Guerschman, J.P. Global vegetation gross primary production estimation using satellite-derived light-use efficiency and canopy conductance. Remote Sens. Environ. 2015, 163, 206–216. [Google Scholar] [CrossRef]
- Wang, S.; Ibrom, A.; Bauer-Gottwein, P.; Garcia, M. Incorporating diffuse radiation into a light use efficiency and evapotranspiration model: An 11-year study in a high latitude deciduous forest. Agric. For. Meteorol. 2018, 248, 479–493. [Google Scholar] [CrossRef]
- Tan, C.; Samanta, A.; Jin, X.; Tong, L.; Ma, C.; Guo, W.; Knyazikhin, Y.; Myneni, R.B. Using hyperspectral vegetation indices to estimate the fraction of photosynthetically active radiation absorbed by corn canopies. Int. J. Remote Sens. 2013, 34, 8789–8802. [Google Scholar] [CrossRef]
- Ogutu, B.O.; Dash, J. An algorithm to derive the fraction of photosynthetically active radiation absorbed by photosynthetic elements of the canopy (FAPAR ps) from eddy covariance flux tower data. New Phytol. 2013, 197, 511–523. [Google Scholar] [CrossRef]
- Cristiano, P.M.; Posse, G.; Di Bella, C.M.; Jaimes, F.R. Uncertainties in fPAR estimation of grass canopies under different stress situations and differences in architecture. Int. J. Remote Sens. 2010, 31, 4095–4109. [Google Scholar] [CrossRef]
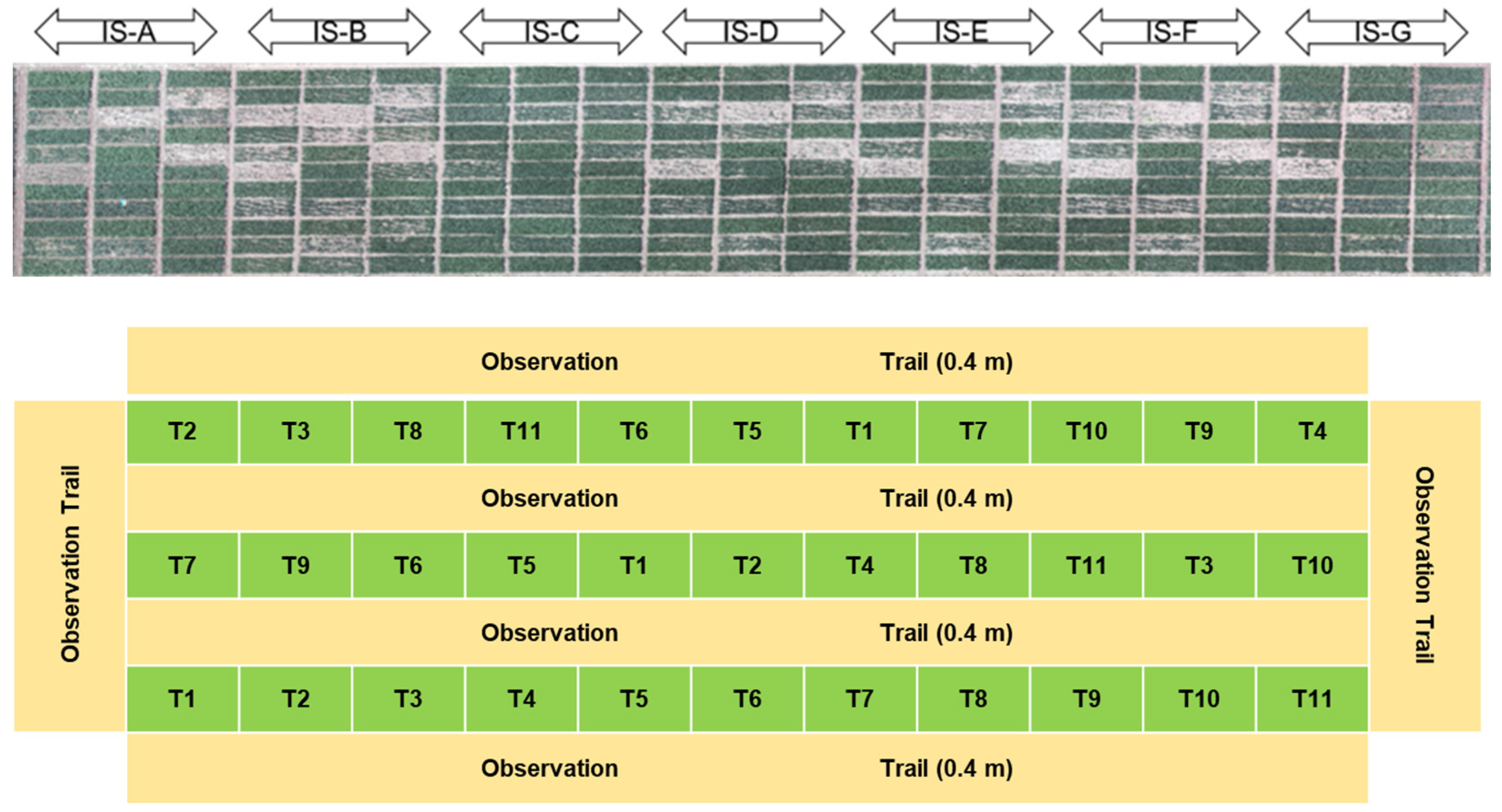
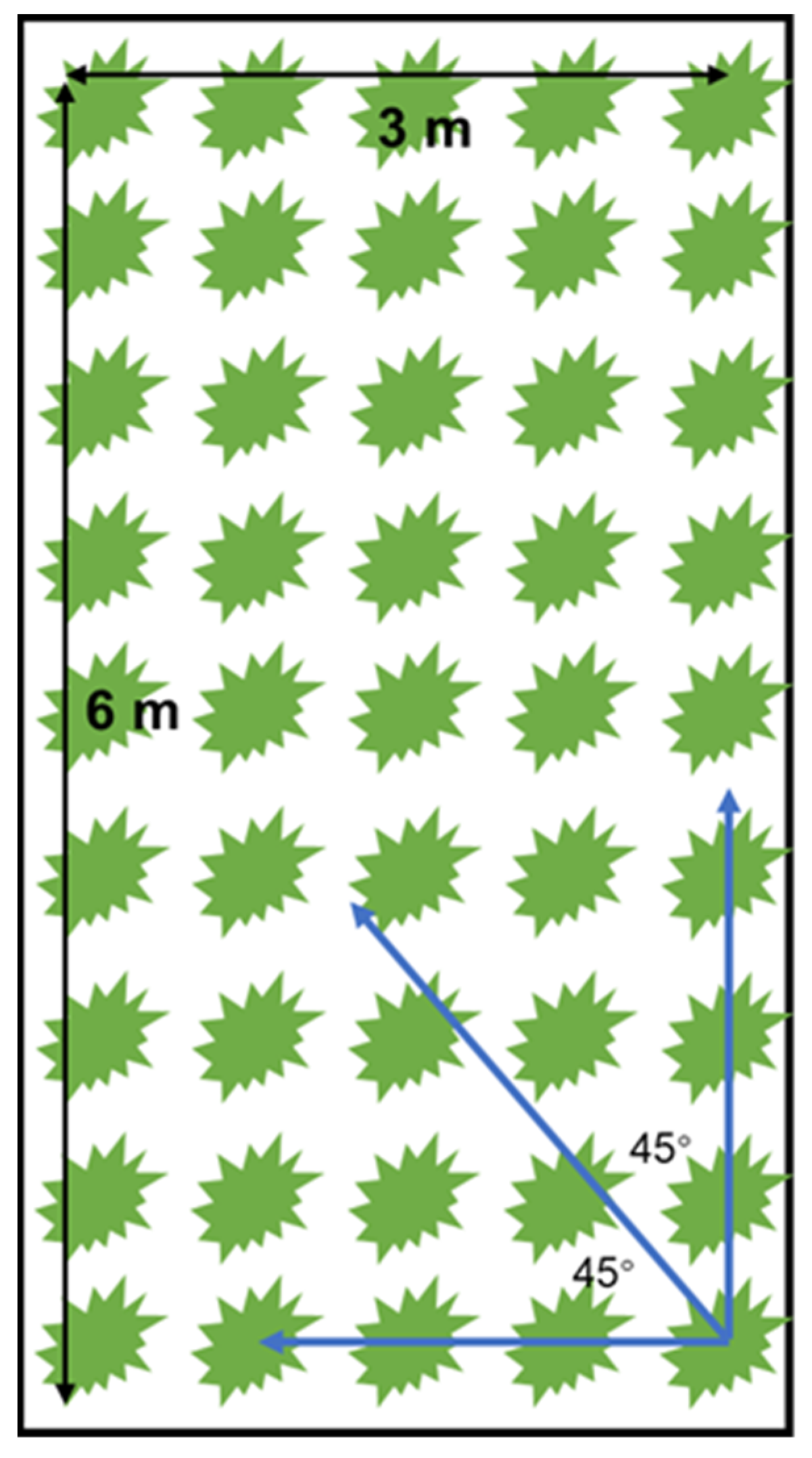
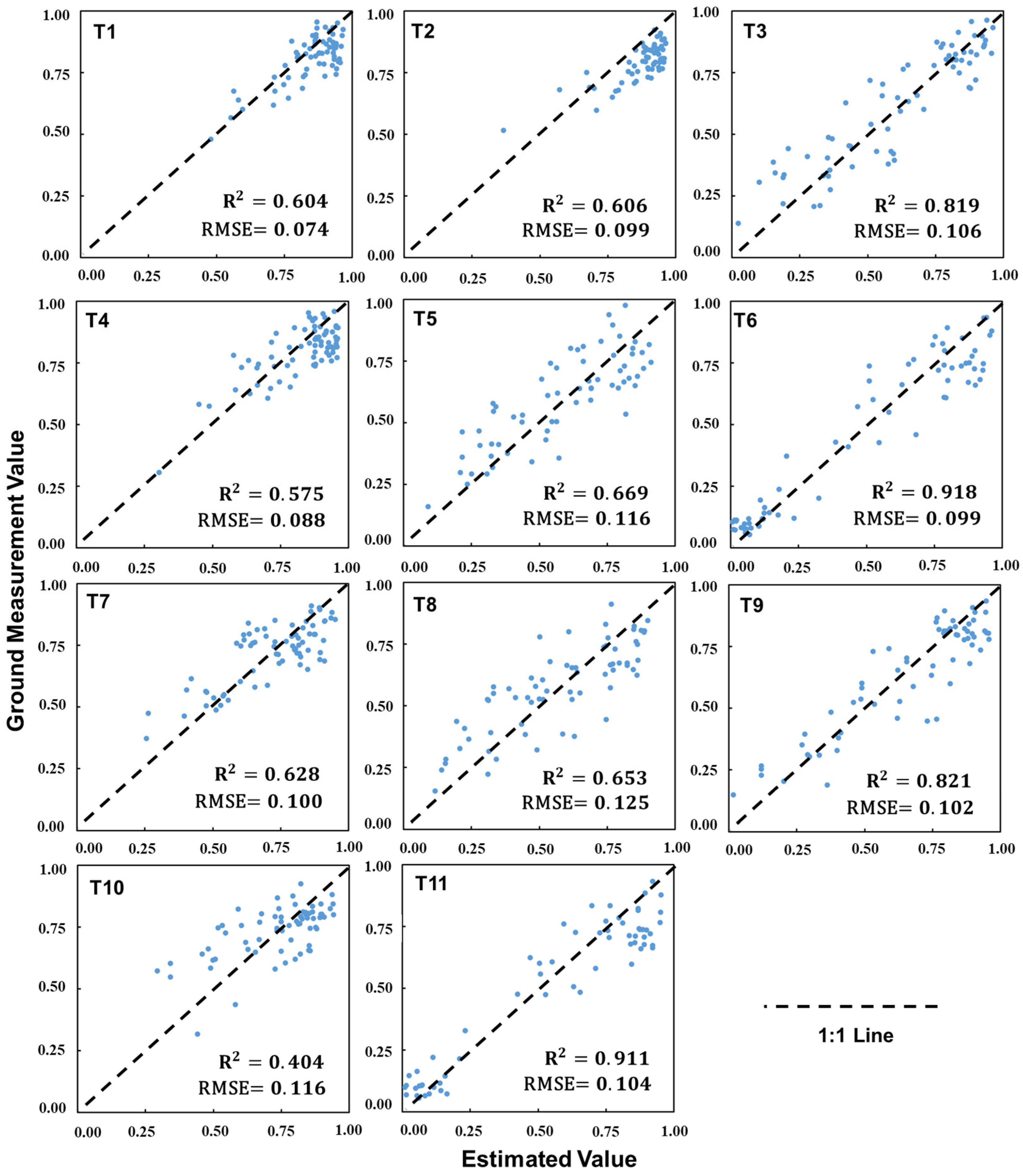
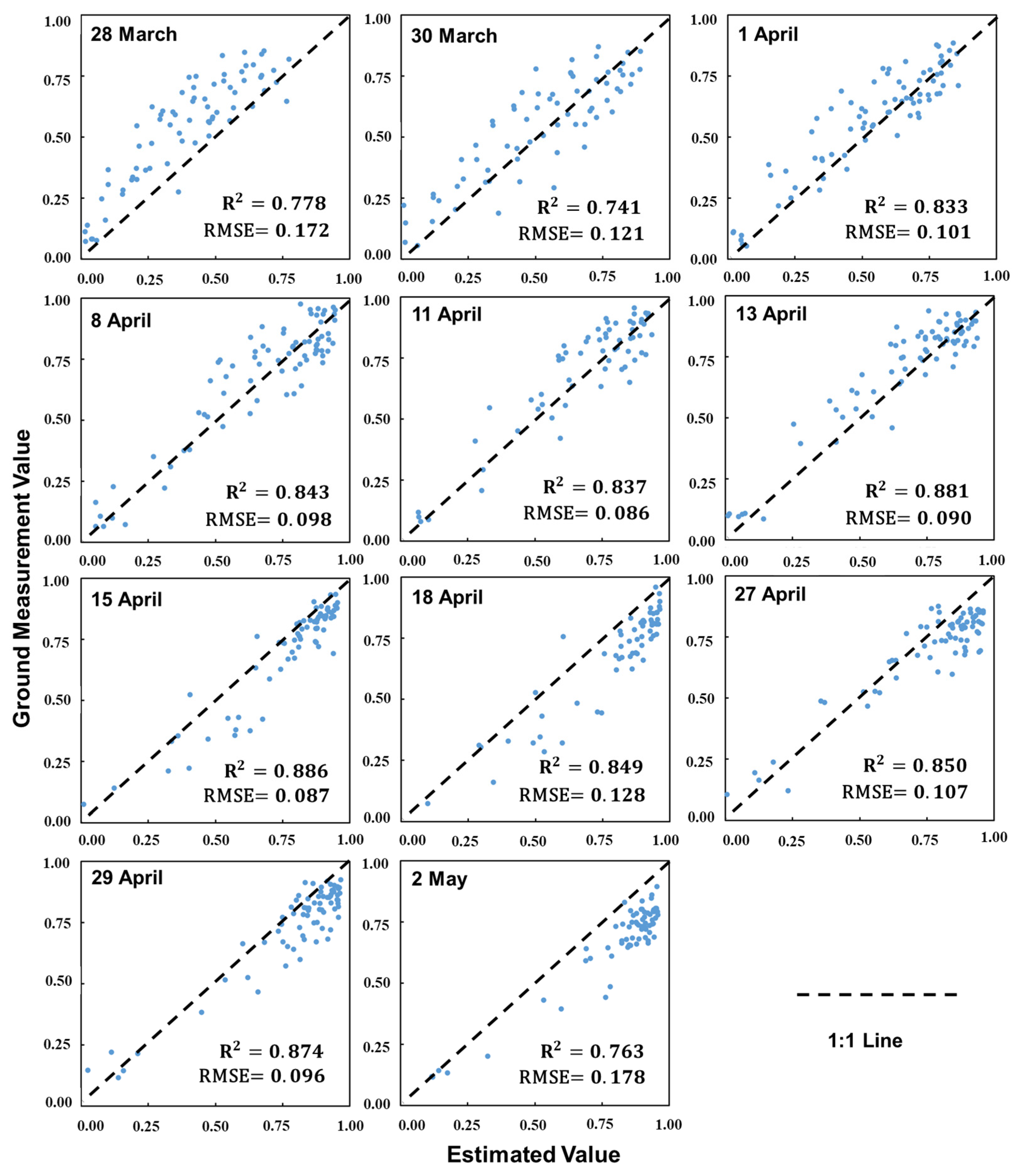

| Irrigation Scheme | Irrigation Data | Phenological Phase | Total Irrigation Volume (m3 ha−1) |
|---|---|---|---|
| IS-A | 2 April 2023 | Jointing Flowering | 1500 |
| IS-B | None | None | 0 |
| IS-C | 28 November 2022 | Overwintering | 750 |
| IS-D | 7 March 2023 | Regreen | 750 |
| IS-E | 2 April 2023 | Jointing | 750 |
| IS-F | 9 April 2023 | Jointing | 750 |
| IS-G | 16 April 2023 | Booting | 750 |
| Date | 28 March | 30 March | 1 April | 8 April | 11 April | 13 April | 15 April | 18 April | 27 April | 29 April | 2 May |
|---|---|---|---|---|---|---|---|---|---|---|---|
| √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |
| Reflec. | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Weather 1 | C | C/S | S | S/R | S | C | C | C | C/S | S | C/R |
| Index Name | Definition of Indices 1 | Index Name | Definition of Indices 1 |
|---|---|---|---|
| NDVI | MNDVI | ||
| EVI | SAVI | ||
| EVI2 | OSAVI | ||
| NDPI | CIG | ||
| GCVI | CIR | ||
| RVI | MNDWI | ||
| DVI | NDBI | ||
| LSWI-b8b11 | GNDVI | ||
| LSWI-b8b12 | NIRV | ||
| LSWI-b8Ab11 | MTCI | ||
| LSWI-b8Ab12 |
| Date | 28 March | 30 March | 1 April | 8 April | 11 April | 13 April | 15 April | 18 April | 27 April | 29 April | 2 May |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NDPI | 0.583 | 0.659 | 0.621 | 0.719 | 0.621 | 0.742 | 0.812 | 0.828 | 0.324 | 0.550 | 0.919 |
| NDVI | 0.588 | 0.643 | 0.685 | 0.721 | 0.612 | 0.758 | 0.821 | 0.839 | 0.500 | 0.681 | 0.917 |
| MNDVI | 0.596 | 0.674 | 0.695 | 0.732 | 0.652 | 0.761 | 0.830 | 0.840 | 0.498 | 0.679 | 0.911 |
| LSWIB8B12 | 0.523 | 0.607 | 0.442 | 0.616 | 0.567 | 0.632 | 0.733 | 0.760 | 0.183 | 0.364 | 0.899 |
| LSWIB8aB12 | 0.520 | 0.607 | 0.439 | 0.615 | 0.567 | 0.630 | 0.729 | 0.758 | 0.180 | 0.365 | 0.899 |
| OSAVI | 0.672 | 0.648 | 0.725 | 0.741 | 0.636 | 0.717 | 0.835 | 0.812 | 0.570 | 0.740 | 0.897 |
| NDWI | 0.506 | 0.602 | 0.565 | 0.728 | 0.622 | 0.640 | 0.817 | 0.809 | 0.375 | 0.516 | 0.882 |
| LSWIB8B11 | 0.541 | 0.658 | 0.438 | 0.632 | 0.572 | 0.630 | 0.720 | 0.756 | 0.160 | 0.371 | 0.878 |
| NDBI | 0.541 | 0.658 | 0.438 | 0.632 | 0.572 | 0.630 | 0.720 | 0.756 | 0.160 | 0.371 | 0.878 |
| LSWIB8aB11 | 0.536 | 0.658 | 0.434 | 0.629 | 0.570 | 0.627 | 0.714 | 0.753 | 0.155 | 0.372 | 0.877 |
| SAVI | 0.715 | 0.646 | 0.705 | 0.703 | 0.622 | 0.630 | 0.799 | 0.726 | 0.431 | 0.661 | 0.837 |
| EVI2 | 0.725 | 0.655 | 0.698 | 0.687 | 0.626 | 0.612 | 0.785 | 0.699 | 0.412 | 0.640 | 0.808 |
| EVI | 0.720 | 0.652 | 0.659 | 0.639 | 0.605 | 0.560 | 0.770 | 0.674 | 0.316 | 0.573 | 0.779 |
| NIRV | 0.731 | 0.644 | 0.640 | 0.634 | 0.582 | 0.536 | 0.726 | 0.611 | 0.357 | 0.588 | 0.742 |
| DVI | 0.712 | 0.616 | 0.565 | 0.589 | 0.526 | 0.466 | 0.675 | 0.543 | 0.314 | 0.541 | 0.683 |
| CIG | 0.501 | 0.545 | 0.486 | 0.600 | 0.589 | 0.597 | 0.772 | 0.701 | 0.321 | 0.432 | 0.639 |
| CIR | 0.590 | 0.632 | 0.616 | 0.580 | 0.617 | 0.670 | 0.767 | 0.664 | 0.421 | 0.556 | 0.636 |
| GCVI | 0.492 | 0.541 | 0.481 | 0.594 | 0.582 | 0.594 | 0.769 | 0.695 | 0.321 | 0.432 | 0.631 |
| RVI | 0.585 | 0.631 | 0.614 | 0.577 | 0.614 | 0.669 | 0.767 | 0.660 | 0.422 | 0.556 | 0.631 |
| MNDWI | 0.150 | 0.307 | 0.237 | 0.574 | 0.536 | 0.146 | 0.418 | 0.679 | 0.261 | 0.318 | 0.238 |
| MTCI | 0.550 | 0.502 | 0.497 | 0.646 | 0.587 | 0.617 | 0.661 | 0.573 | 0.437 | 0.354 | 0.361 |
| Date | 28 March | 30 March | 1 April | 8 April | 11 April | 13 April | 15 April | 18 April | 27 April | 29 April | 2 May |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NDVI | 0.667 | 0.686 | 0.719 | 0.766 | 0.794 | 0.755 | 0.814 | 0.777 | 0.510 | 0.704 | 0.912 |
| NDPI | 0.640 | 0.655 | 0.642 | 0.731 | 0.775 | 0.720 | 0.792 | 0.765 | 0.336 | 0.569 | 0.887 |
| MNDVI | 0.668 | 0.686 | 0.721 | 0.765 | 0.804 | 0.753 | 0.817 | 0.775 | 0.506 | 0.699 | 0.885 |
| OSAVI | 0.732 | 0.661 | 0.750 | 0.769 | 0.789 | 0.711 | 0.816 | 0.755 | 0.550 | 0.748 | 0.867 |
| LSWIB8B12 | 0.571 | 0.564 | 0.453 | 0.616 | 0.724 | 0.610 | 0.710 | 0.705 | 0.196 | 0.385 | 0.861 |
| LSWIB8aB12 | 0.560 | 0.563 | 0.449 | 0.614 | 0.724 | 0.607 | 0.706 | 0.703 | 0.193 | 0.386 | 0.861 |
| NDWI | 0.542 | 0.492 | 0.571 | 0.714 | 0.770 | 0.616 | 0.790 | 0.750 | 0.379 | 0.520 | 0.854 |
| LSWIB8B11 | 0.573 | 0.563 | 0.442 | 0.599 | 0.668 | 0.593 | 0.681 | 0.696 | 0.171 | 0.384 | 0.807 |
| NDBI | 0.563 | 0.563 | 0.442 | 0.599 | 0.668 | 0.593 | 0.681 | 0.696 | 0.171 | 0.384 | 0.807 |
| LSWIB8aB11 | 0.559 | 0.561 | 0.437 | 0.596 | 0.665 | 0.590 | 0.676 | 0.692 | 0.166 | 0.384 | 0.806 |
| SAVI | 0.751 | 0.618 | 0.718 | 0.713 | 0.737 | 0.622 | 0.769 | 0.675 | 0.407 | 0.658 | 0.788 |
| EVI2 | 0.750 | 0.605 | 0.703 | 0.683 | 0.711 | 0.601 | 0.748 | 0.646 | 0.386 | 0.633 | 0.747 |
| EVI | 0.745 | 0.596 | 0.671 | 0.648 | 0.700 | 0.558 | 0.739 | 0.625 | 0.293 | 0.571 | 0.733 |
| NIRV | 0.734 | 0.559 | 0.628 | 0.614 | 0.624 | 0.524 | 0.678 | 0.561 | 0.332 | 0.575 | 0.669 |
| DVI | 0.704 | 0.514 | 0.558 | 0.572 | 0.568 | 0.456 | 0.631 | 0.501 | 0.291 | 0.528 | 0.614 |
| CIG | 0.493 | 0.410 | 0.448 | 0.485 | 0.550 | 0.544 | 0.701 | 0.619 | 0.314 | 0.414 | 0.531 |
| GCVI | 0.484 | 0.406 | 0.443 | 0.512 | 0.542 | 0.541 | 0.697 | 0.614 | 0.313 | 0.413 | 0.522 |
| CIR | 0.568 | 0.549 | 0.554 | 0.492 | 0.536 | 0.605 | 0.686 | 0.570 | 0.411 | 0.531 | 0.505 |
| RVI | 0.564 | 0.548 | 0.552 | 0.490 | 0.532 | 0.603 | 0.686 | 0.567 | 0.411 | 0.530 | 0.499 |
| MNDWI | 0.165 | 0.137 | 0.223 | 0.537 | 0.556 | 0.143 | 0.404 | 0.612 | 0.234 | 0.284 | 0.235 |
| MTCI | 0.571 | 0.462 | 0.473 | 0.602 | 0.602 | 0.601 | 0.570 | 0.541 | 0.502 | 0.344 | 0.348 |
| Date | 28 March | 30 March | 1 April | 8 April | 11 April | 13 April | 15 April | 18 April | 27 April | 29 April | 2 May |
|---|---|---|---|---|---|---|---|---|---|---|---|
| LSWIB8aB12 | 0.509 | 0.498 | 0.434 | 0.604 | 0.522 | 0.627 | 0.730 | 0.767 | 0.177 | 0.358 | 0.970 |
| NDPI | 0.568 | 0.563 | 0.611 | 0.704 | 0.578 | 0.737 | 0.810 | 0.838 | 0.321 | 0.543 | 0.897 |
| NDVI | 0.574 | 0.568 | 0.674 | 0.704 | 0.573 | 0.752 | 0.814 | 0.847 | 0.498 | 0.674 | 0.891 |
| OSAVI | 0.657 | 0.551 | 0.713 | 0.724 | 0.599 | 0.711 | 0.833 | 0.822 | 0.572 | 0.733 | 0.882 |
| LSWIB8B12 | 0.511 | 0.498 | 0.437 | 0.606 | 0.521 | 0.629 | 0.739 | 0.769 | 0.181 | 0.357 | 0.869 |
| LSWIB8aB11 | 0.519 | 0.513 | 0.426 | 0.619 | 0.506 | 0.626 | 0.724 | 0.768 | 0.152 | 0.362 | 0.859 |
| LSWIB8B11 | 0.522 | 0.515 | 0.431 | 0.621 | 0.502 | 0.629 | 0.729 | 0.772 | 0.156 | 0.361 | 0.858 |
| MNDVI | 0.568 | 0.560 | 0.672 | 0.698 | 0.559 | 0.749 | 0.817 | 0.855 | 0.494 | 0.666 | 0.848 |
| SAVI | 0.702 | 0.519 | 0.695 | 0.688 | 0.589 | 0.624 | 0.802 | 0.737 | 0.436 | 0.655 | 0.832 |
| EVI2 | 0.711 | 0.513 | 0.689 | 0.672 | 0.591 | 0.606 | 0.793 | 0.713 | 0.417 | 0.636 | 0.809 |
| EVI | 0.706 | 0.488 | 0.648 | 0.623 | 0.570 | 0.553 | 0.775 | 0.687 | 0.321 | 0.568 | 0.774 |
| NIRV | 0.718 | 0.476 | 0.632 | 0.622 | 0.551 | 0.530 | 0.744 | 0.630 | 0.366 | 0.586 | 0.752 |
| CIR | 0.542 | 0.547 | 0.629 | 0.592 | 0.599 | 0.668 | 0.838 | 0.768 | 0.417 | 0.565 | 0.725 |
| RVI | 0.548 | 0.552 | 0.628 | 0.593 | 0.602 | 0.670 | 0.840 | 0.761 | 0.420 | 0.566 | 0.719 |
| DVI | 0.705 | 0.439 | 0.561 | 0.582 | 0.506 | 0.461 | 0.692 | 0.556 | 0.322 | 0.541 | 0.693 |
| CIG | 0.474 | 0.409 | 0.491 | 0.609 | 0.568 | 0.601 | 0.820 | 0.756 | 0.320 | 0.440 | 0.688 |
| GCVI | 0.466 | 0.407 | 0.487 | 0.604 | 0.562 | 0.599 | 0.818 | 0.749 | 0.321 | 0.440 | 0.682 |
| MTCI | 0.533 | 0.507 | 0.495 | 0.634 | 0.566 | 0.608 | 0.672 | 0.580 | 0.414 | 0.346 | 0.359 |
| VI Name | Correlation | Equation | RMSE | |
|---|---|---|---|---|
| NDVI | Linear | 0.5926 | 0.1460 | |
| Exponential | 0.6639 | 0.1350 | ||
| Logarithmic | 0.5350 | 0.1479 | ||
| EVI | Linear | 0.3183 | 0.1896 | |
| Exponential | 0.2793 | 0.2039 | ||
| Logarithmic | 0.3312 | 0.1812 | ||
| EVI2 | Linear | 0.3710 | 0.1878 | |
| Exponential | 0.3271 | 0.1976 | ||
| Logarithmic | 0.3795 | 01810 | ||
| NDPI | Linear | 0.6174 | 0.1314 | |
| Exponential | 0.5993 | 0.1379 | ||
| Logarithmic | 0.5595 | 0.1418 | ||
| GCVI | Linear | 0.5601 | 0.1513 | |
| Exponential | 0.4554 | 0.1846 | ||
| Logarithmic | 0.6191 | 0.1408 | ||
| RVI | Linear | 0.5625 | 0.1510 | |
| Exponential | 0.4403 | 0.1900 | ||
| Logarithmic | 0.6569 | 0.1342 | ||
| DVI | Linear Exponential Logarithmic Linear Exponential Logarithmic | 0.2292 | 0.2510 | |
| 0.2056 | 0.2608 | |||
| 0.2492 | 0.2342 | |||
| LSWI-b8b11 | 0.4828 | 0.1643 | ||
| 0.5029 | 0.1641 | |||
| 0.4309 | 0.1722 | |||
| LSWI-b8b12 | Linear | 0.5099 | 0.1598 | |
| Exponential | 0.5252 | 0.1704 | ||
| Logarithmic | 0.4498 | 0.1698 | ||
| LSWI-b8Ab11 | Linear | 0.5899 | 0.1465 | |
| Exponential | 0.5437 | 0.1615 | ||
| Logarithmic | 0.5147 | 0.1593 | ||
| LSWI-b8Ab12 | Linear | 0.5065 | 0.1603 | |
| Exponential | 0.5718 | 0.1610 | ||
| Logarithmic | 0.4486 | 0.1693 | ||
| MNDVI | Linear | 0.6184 | 0.1413 | |
| Exponential | 0.6649 | 0.1340 | ||
| Logarithmic | 0.4507 | 0.1697 | ||
| SAVI | Linear | 0.3939 | 0.1789 | |
| Exponential | 0.3550 | 0.1921 | ||
| Logarithmic | 0.3926 | 0.1791 | ||
| OSAVI | Linear | 0.5131 | 0.1602 | |
| Exponential | 0.5088 | 0.1642 | ||
| Logarithmic | 0.4815 | 0.1642 | ||
| CIG | Linear | 0.5663 | 0.1503 | |
| Exponential | 0.4619 | 0.1874 | ||
| Logarithmic | 0.6229 | 0.1401 | ||
| CIR | Linear | 0.5652 | 0.1504 | |
| Exponential | 0.4432 | 0.1925 | ||
| Logarithmic | 0.6545 | 0.1346 | ||
| MNDVI | Linear | 0.3038 | 0.1908 | |
| Exponential | 0.2924 | 0.1981 | ||
| NDBI | Linear | 0.5951 | 0.1445 | |
| Exponential | 0.5490 | 0.1983 | ||
| NDWI | Linear | 0.6097 | 0.1423 | |
| Exponential | 0.6166 | 0.149 3 | ||
| NIRV | Linear | 0.2966 | 0.1924 | |
| Exponential | 0.2582 | 0.2182 | ||
| Logarithmic | 0.3228 | 0.1890 | ||
| MTCI | Linear | 0.5749 | 0.1490 | |
| Exponential | 0.4807 | 0.1845 | ||
| Logarithmic | 0.6001 | 0.1464 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Sun, L.; Liu, Y.; Li, Y.; Crusiol, L.G.T.; Chen, R.; Wuyun, D. Estimating Fraction of Absorbed Photosynthetically Active Radiation of Winter Wheat Based on Simulated Sentinel-2 Data under Different Varieties and Water Stress. Remote Sens. 2024, 16, 362. https://doi.org/10.3390/rs16020362
Sun Z, Sun L, Liu Y, Li Y, Crusiol LGT, Chen R, Wuyun D. Estimating Fraction of Absorbed Photosynthetically Active Radiation of Winter Wheat Based on Simulated Sentinel-2 Data under Different Varieties and Water Stress. Remote Sensing. 2024; 16(2):362. https://doi.org/10.3390/rs16020362
Chicago/Turabian StyleSun, Zheng, Liang Sun, Yu Liu, Yangwei Li, Luís Guilherme Teixeira Crusiol, Ruiqing Chen, and Deji Wuyun. 2024. "Estimating Fraction of Absorbed Photosynthetically Active Radiation of Winter Wheat Based on Simulated Sentinel-2 Data under Different Varieties and Water Stress" Remote Sensing 16, no. 2: 362. https://doi.org/10.3390/rs16020362
APA StyleSun, Z., Sun, L., Liu, Y., Li, Y., Crusiol, L. G. T., Chen, R., & Wuyun, D. (2024). Estimating Fraction of Absorbed Photosynthetically Active Radiation of Winter Wheat Based on Simulated Sentinel-2 Data under Different Varieties and Water Stress. Remote Sensing, 16(2), 362. https://doi.org/10.3390/rs16020362










