Adaptive Basis Function Method for the Detection of an Undersurface Magnetic Anomaly Target
Abstract
1. Introduction
2. Target Signal Modeling Using ABFs
3. Detection and Location
3.1. Data Preprocessing
3.2. Target Signal Detection
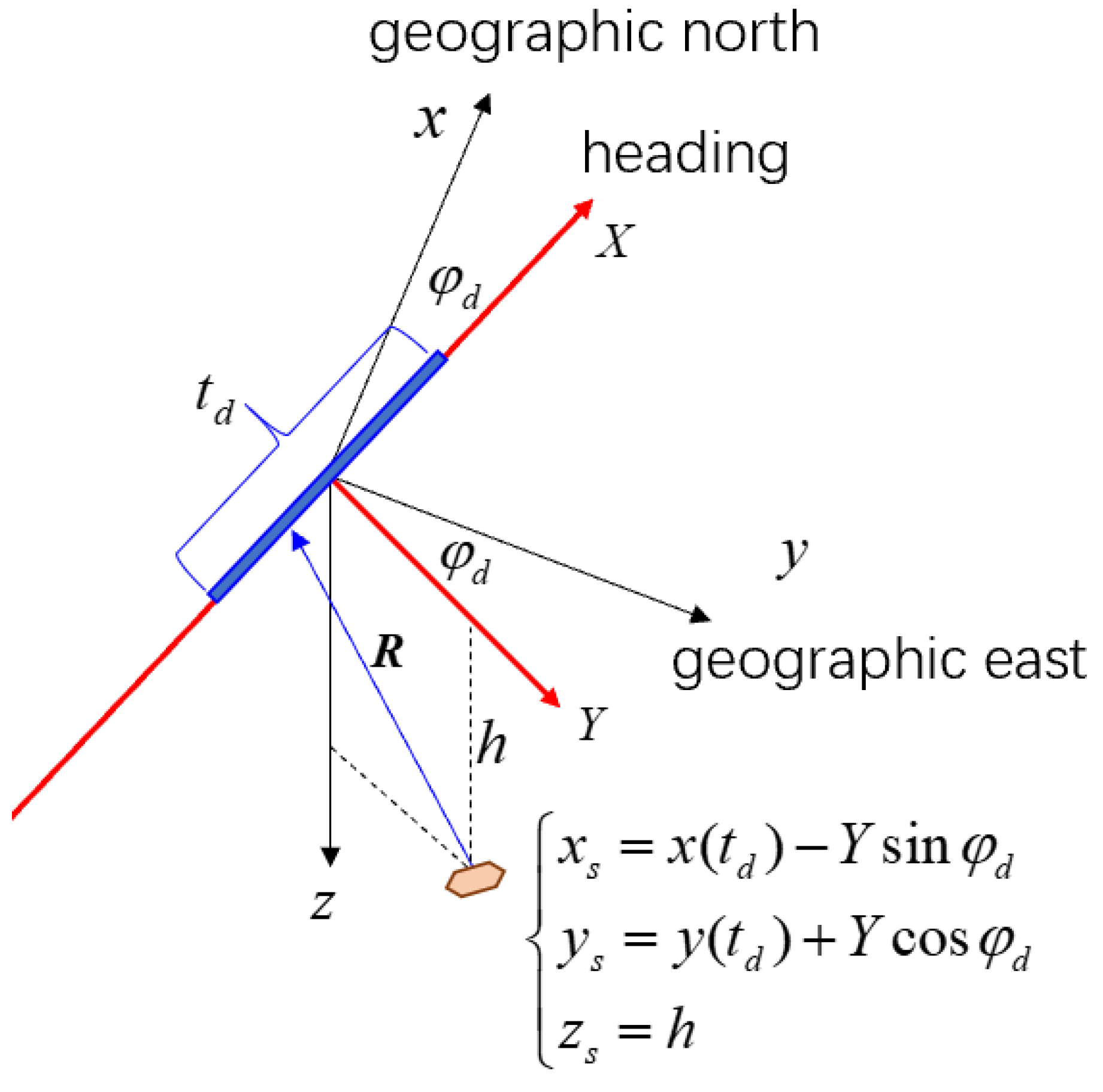
3.3. Target Locating and Imaging

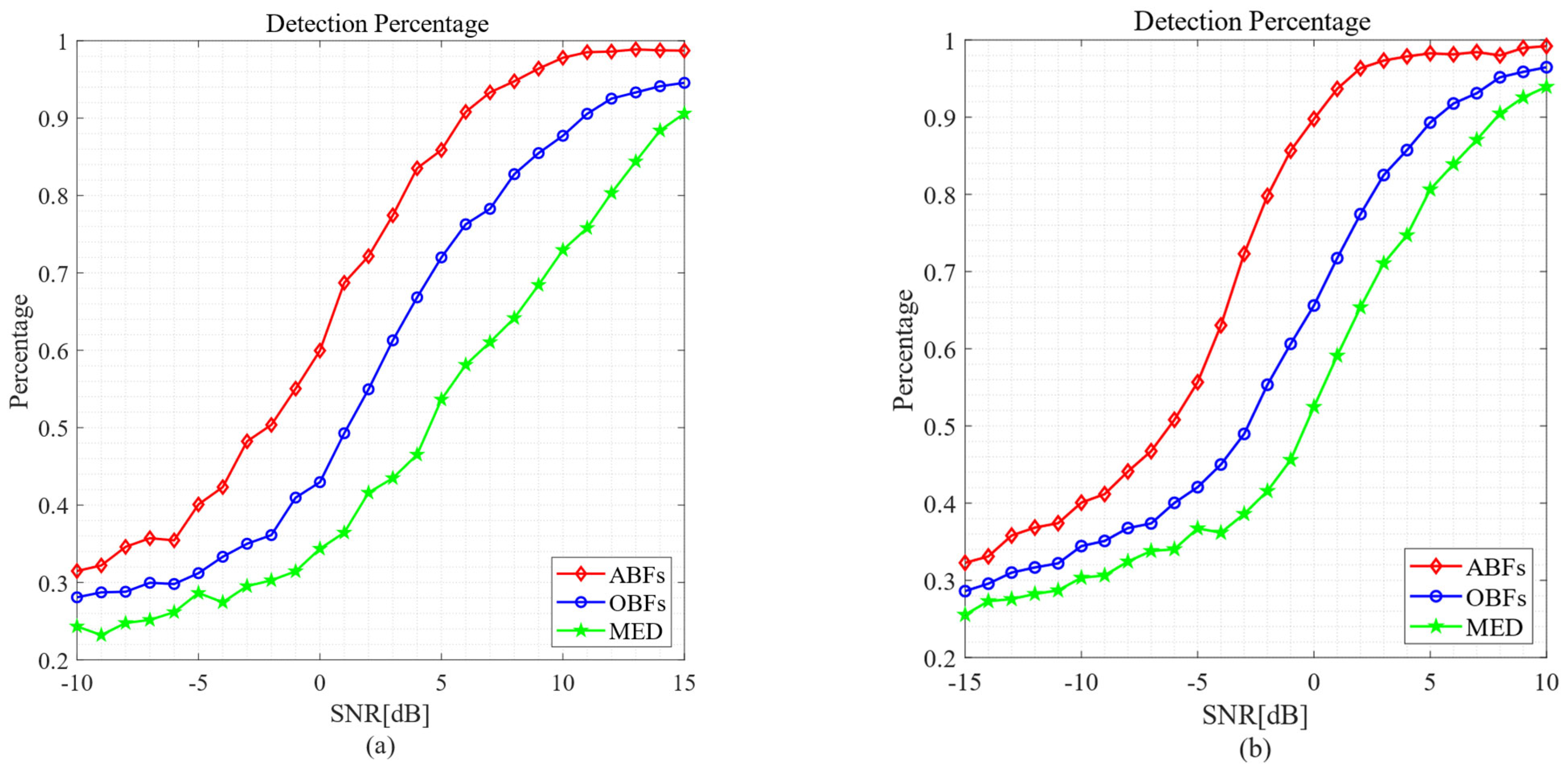
4. Experiment Validation
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Zhang, X.; Dong, H.; Liu, Z.; Hu, X. Theories, Applications, and Expectations for Magnetic Anomaly Detection Technology: A Review. IEEE Sens. J. 2023, 23, 17868–17882. [Google Scholar] [CrossRef]
- Wiegert, R. System and Method Using Magnetic Anomaly Field Magnitudes for Detection, Localization, Classification and Tracking of Magnetic Objects. U.S. Patent 7,932,718, 26 April 2011. [Google Scholar]
- Birsan, M. Recursive Bayesian method for magnetic dipole tracking with a tensor gradiometer. IEEE Trans. Magn. 2010, 47, 409–415. [Google Scholar] [CrossRef]
- Sithiravel, R.; Balaji, B.; Nelson, B.; McDonald, M.K.; Tharmarasa, R.; Kirubarajan, T. Airborne maritime surveillance using magnetic anomaly detection signature. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3476–3490. [Google Scholar] [CrossRef]
- Kolster, M.E.; Wigh, M.D.; Lima Simões da Silva, E.; Bjerg Vilhelmsen, T.; Døssing, A. High-speed magnetic surveying for unexploded ordnance using UAV systems. Remote Sens. 2022, 14, 1134. [Google Scholar] [CrossRef]
- Zalevsky, Z.; Bregman, Y.; Salomonski, N.; Zafrir, H. Resolution enhanced magnetic sensing system for wide coverage real time UXO detection. J. Appl. Geophys. 2012, 84, 70–76. [Google Scholar] [CrossRef]
- Yoo, L.S.; Lee, J.H.; Ko, S.H.; Jung, S.K.; Lee, S.H.; Lee, Y.K. A drone fitted with a magnetometer detects landmines. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2035–2039. [Google Scholar] [CrossRef]
- Yoo, L.S.; Lee, J.H.; Lee, Y.K.; Jung, S.K.; Choi, Y. Application of a drone magnetometer system to military mine detection in the demilitarized zone. Sensors 2021, 21, 3175. [Google Scholar] [CrossRef]
- Hirota, M.; Furuse, T.; Ebana, K.; Kubo, H.; Tsushima, K.; Inaba, T.; Shima, A.; Fujinuma, M.; Tojyo, N. Magnetic detection of a surface ship by an airborne LTS SQUID MAD. IEEE Trans. Appl. Supercond. 2001, 11, 884–887. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, L.H.; Sun, F. Underwater continuous localization based on magnetic dipole target using magnetic gradient tensor and draft depth. IEEE Geosci. Remote Sens. Lett. 2013, 11, 178–180. [Google Scholar] [CrossRef]
- Eppelbaum, L.V. Study of magnetic anomalies over archaeological targets in urban environments. Phys. Chem. Earth Parts A/B/C 2011, 36, 1318–1330. [Google Scholar] [CrossRef]
- Merlat, L.; Naz, P. Magnetic localization and identification of vehicles. In Proceedings of the SPIE 5090, Unattended Ground Sensor Technologies and Applications V, Orlando, FL, USA, 18 September 2003; Volume 5090, pp. 174–185. [Google Scholar]
- Liu, D.; Xu, X.; Fei, C.; Zhu, W.; Liu, X.; Yu, G.; Fang, G. Direction identification of a moving ferromagnetic object by magnetic anomaly. Sens. Actuators A Phys. 2015, 229, 147–153. [Google Scholar] [CrossRef]
- Soheilian, A.; Tehranchi, M.M.; Ranjbaran, M. Detection of magnetic tracers with Mx atomic magnetometer for application to blood velocimetry. Sci. Rep. 2021, 11, 7156. [Google Scholar] [CrossRef]
- Jin, R.; Jung, B. Magnetic tracking system for heart surgery. IEEE Trans. Biomed. Circuits Syst. 2022, 16, 275–286. [Google Scholar] [CrossRef]
- Yarotsky, V.A. Optimum detection of magnetic dipoles. Electromagn. Meas. 1992, 35, 43–45. [Google Scholar] [CrossRef]
- Ginzburg, B.; Frumkis, L.; Kaplan, B.Z. Processing of magnetic scalar gradiometer signals using orthonormalized functions. Sens. Actuators A Phys. 2002, 102, 67–75. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.Y.; Pan, M.C.; Zhang, Q.; Chen, D.X.; Wan, C.B.; Hu, G.; Zhang, D.W.; Chen, Z. Magnetic anomaly signal space analysis and its application in noise suppression. IEEE Geosci. Remote Sens. Lett. 2018, 16, 130–134. [Google Scholar]
- Sheinker, A.; Shkalim, A.; Salomonski, N.; Ginzburg, B.; Frumkis, L.; Kaplan, B.Z. Processing of a scalar magnetometer signal contaminated by 1/fa noise. Sens. Actuators A Phys. 2007, 138, 105–111. [Google Scholar] [CrossRef]
- Hu, M.K.; Du, C.P.; Wang, H.D.; Xia, M.Y.; Peng, X.; Guo, H. Optimized basis functions under gaussian color noise for magnetic target signal detection. IEEE Geosci. Remote Sens. Lett. 2020, 18, 806–810. [Google Scholar] [CrossRef]
- Zhao, G.; Han, Q.; Tong, X.; Guo, H. Adaptive filtering method for magnetic anomaly detection. J. Appl. Remote Sens. 2018, 12, 025003. [Google Scholar] [CrossRef]
- Wan, C.; Pan, M.; Zhang, Q.; Chen, D.; Pang, H.; Zhu, X. Performance improvement of magnetic anomaly detector using Karhunen–Loeve expansion. IET Sci. Meas. Technol. 2017, 11, 600–606. [Google Scholar] [CrossRef]
- Sheinker, A.; Salomonski, N.; Ginzburg, B.; Frumkis, L.; Kaplan, B.Z. Magnetic anomaly detection using entropy filter. Meas. Sci. Technol. 2008, 19, 045205. [Google Scholar] [CrossRef]
- Sheinker, A.; Ginzburg, B.; Salomonski, N.; Dickstein, P.A.; Frumkis, L.; Kaplan, B.Z. Magnetic anomaly detection using high-order crossing method. IEEE Trans. Geosci. Remote Sens. 2011, 50, 1095–1103. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, W.; Wu, P.; Fei, C.; Fang, G. Magnetic anomaly detection algorithm based on fractal features in geomagnetic background. J. Electron. Inf. Technol. 2019, 41, 332–340. [Google Scholar]
- Wan, C.; Pan, M.; Zhang, Q.; Wu, F.; Pan, L.; Sun, X. Magnetic anomaly detection based on stochastic resonance. Sens. Actuators A Phys. 2018, 278, 11–17. [Google Scholar] [CrossRef]
- Qin, T.; Zhou, L.; Chen, S.; Chen, Z. The novel method of magnetic anomaly recognition based on the fourth order aperiodic stochastic resonance. IEEE Sens. J. 2022, 22, 17043–17053. [Google Scholar] [CrossRef]
- Liu, D.; Xu, X.; Huang, C.; Zhu, W.; Liu, X.; Yu, G.; Fang, G. Adaptive cancellation of geomagnetic background noise for magnetic anomaly detection using coherence. Meas. Sci. Technol. 2014, 26, 015008. [Google Scholar] [CrossRef]
- Fan, L.; Kang, C.; Wang, H.; Hu, H.; Zhang, X.; Liu, X. Adaptive magnetic anomaly detection method using support vector machine. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Hu, M.; Jing, S.; Du, C.; Xia, M.; Peng, X.; Guo, H. Magnetic dipole target signal detection via convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Fan, L.; Hu, H.; Zhang, X.; Wang, H.; Kang, C. Magnetic anomaly detection using one-dimensional convolutional neural network with multi-feature fusion. IEEE Sens. J. 2022, 22, 11637–11643. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Z.; Liu, S.; Zhang, Q.; Pan, M.; Hu, J.; Chen, D.; Liu, Z. Magnetic anomaly detection using multifeature fusion-based neural network. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Wu, X.; Huang, S.; Li, M.; Deng, Y. Vector magnetic anomaly detection via an attention mechanism deep-learning model. Appl. Sci. 2021, 11, 11533. [Google Scholar] [CrossRef]
- Xu, X.; Huang, L.; Liu, X.; Fang, G. Deepmad: Deep learning for magnetic anomaly detection and denoising. IEEE Access 2020, 8, 121257–121266. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Q.; Zhan, D.; Li, Q. Magnetic anomaly detection network with adaptive time-frequency feature expression. IEEE Sens. J. 2023, 23, 21620–21630. [Google Scholar] [CrossRef]
- Wynn, W.; Frahm, C.; Carroll, P.; Clark, R.; Wellhoner, J.; Wynn, M. Advanced superconducting gradiometer/magnetometer arrays and a novel signal processing technique. IEEE Trans. Magn. 1975, 11, 701–707. [Google Scholar] [CrossRef]
- Du, C.P.; Xia, M.Y.; Huang, S.X.; Xu, Z.H.; Peng, X.; Guo, H. Detection of a moving magnetic dipole target using multiple scalar magnetometers. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1166–1170. [Google Scholar] [CrossRef]
- Dassot, G.; Blanpain, R.; Flament, B.; Jauffret, C. Process for Determining the Position of a Moving Object Using Magnetic Gradientmetric Measurements. U.S. Patent 6,539,327, 25 March 2003. [Google Scholar]
- Hu, S.; Tang, J.; Ren, Z.; Chen, C.; Zhou, C.; Xiao, X.; Zhao, T. Multiple underwater objects localization with magnetic gradiometry. IEEE Geosci. Remote Sens. Lett. 2018, 16, 296–300. [Google Scholar] [CrossRef]
- Davis, K.; Li, Y.; Nabighian, M. Automatic detection of UXO magnetic anomalies using extended Euler deconvolution. Geophysics 2010, 75, G13–G20. [Google Scholar] [CrossRef]
- Ibraheem, I.M.; Aladad, H.; Alnaser, M.F.; Stephenson, R. IAS: A new novel phase-based filter for detection of unexploded ordnances. Remote Sens. 2021, 13, 4345. [Google Scholar] [CrossRef]
- Alimi, R.; Geron, N.; Weiss, E.; Ram-Cohen, T. Ferromagnetic mass localization in check point configuration using a Levenberg Marquardt algorithm. Sensors 2009, 9, 8852–8862. [Google Scholar] [CrossRef] [PubMed]
- Ge, J.; Wang, S.; Dong, H.; Liu, H.; Zhou, D.; Wu, S.; Luo, W.; Zhu, J.; Yuan, Z.; Zhang, H. Real-time detection of moving magnetic target using distributed scalar sensor based on hybrid algorithm of particle swarm optimization and Gauss–Newton method. IEEE Sens. J. 2020, 20, 10717–10723. [Google Scholar] [CrossRef]
- Sheinker, A.; Lerner, B.; Salomonski, N.; Ginzburg, B.; Frumkis, L.; Kaplan, B.Z. Localization and magnetic moment estimation of a ferromagnetic target by simulated annealing. Meas. Sci. Technol. 2007, 18, 3451. [Google Scholar] [CrossRef]
- Alimi, R.; Weiss, E.; Ram-Cohen, T.; Geron, N.; Yogev, I. A dedicated genetic algorithm for localization of moving magnetic objects. Sensors 2015, 15, 23788–23804. [Google Scholar] [CrossRef] [PubMed]
- Mu, Y.; Zhang, X.; Xie, W.; Zheng, Y. Automatic detection of near-surface targets for unmanned aerial vehicle (UAV) magnetic survey. Remote Sens. 2020, 12, 452. [Google Scholar] [CrossRef]
- Cárdenas, J.; Denis, C.; Mousannif, H.; Camerlynck, C.; Florsch, N. Magnetic anomalies characterization: Deep learning and explainability. Comput. Geosci. 2022, 169, 105227. [Google Scholar] [CrossRef]
- Leliak, P. Identification and evaluation of magnetic-field sources of magnetic airborne detector equipped aircraft. IRE Trans. Aerosp. Navig. Electron. 1961, ANE-8, 95–105. [Google Scholar] [CrossRef]
- Jo, K.; Lee, M.; Sunwoo, M. Fast GPS-DR sensor fusion framework: Removing the geodetic coordinate conversion process. IEEE Trans. Intell. Transp. Syst. 2015, 17, 2008–2013. [Google Scholar] [CrossRef]

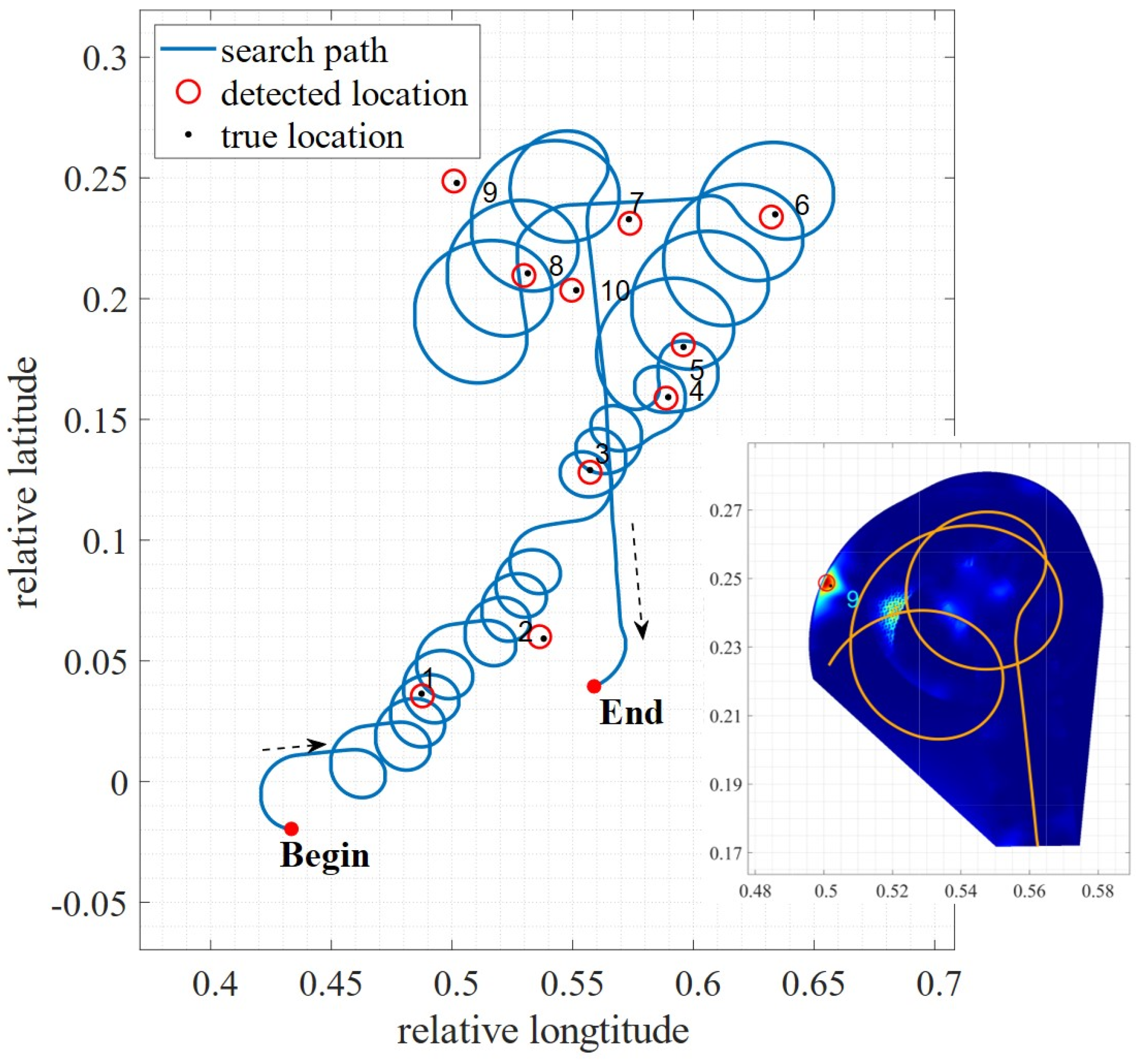

| No. | Detected Longitude | Detected Latitude | True Longitude | True Latitude | Positioning Error (Unit: m) |
|---|---|---|---|---|---|
| 1 | 0.4877 | 0.0355 | 0.4874 | 0.0364 | 104.99 |
| 2 | 0.5363 | 0.0600 | 0.5380 | 0.0592 | 200.54 |
| 3 | 0.5572 | 0.1281 | 0.5572 | 0.1290 | 100.08 |
| 4 | 0.5887 | 0.1588 | 0.5896 | 0.1592 | 104.99 |
| 5 | 0.5958 | 0.1809 | 0.5959 | 0.1800 | 100.64 |
| 6 | 0.6323 | 0.2338 | 0.6339 | 0.2349 | 208.61 |
| 7 | 0.5737 | 0.2312 | 0.5733 | 0.2329 | 193.71 |
| 8 | 0.5298 | 0.2096 | 0.5314 | 0.2105 | 196.42 |
| 9 | 0.5008 | 0.2487 | 0.5020 | 0.2479 | 154.84 |
| 10 | 0.5496 | 0.2035 | 0.5515 | 0.2035 | 200.71 |
| Average | 156.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Yuan, Z.; Du, C.; Peng, X.; Guo, H.; Xia, M. Adaptive Basis Function Method for the Detection of an Undersurface Magnetic Anomaly Target. Remote Sens. 2024, 16, 363. https://doi.org/10.3390/rs16020363
Liu X, Yuan Z, Du C, Peng X, Guo H, Xia M. Adaptive Basis Function Method for the Detection of an Undersurface Magnetic Anomaly Target. Remote Sensing. 2024; 16(2):363. https://doi.org/10.3390/rs16020363
Chicago/Turabian StyleLiu, Xingen, Zifan Yuan, Changping Du, Xiang Peng, Hong Guo, and Mingyao Xia. 2024. "Adaptive Basis Function Method for the Detection of an Undersurface Magnetic Anomaly Target" Remote Sensing 16, no. 2: 363. https://doi.org/10.3390/rs16020363
APA StyleLiu, X., Yuan, Z., Du, C., Peng, X., Guo, H., & Xia, M. (2024). Adaptive Basis Function Method for the Detection of an Undersurface Magnetic Anomaly Target. Remote Sensing, 16(2), 363. https://doi.org/10.3390/rs16020363






