Cooperative Navigation for Heterogeneous Air-Ground Vehicles Based on Interoperation Strategy

Abstract

This paper focuses on the cooperative navigation of heterogeneous air-ground vehicle formations in a Global Navigation Satellite System (GNSS) challenged environment and proposes a cooperative navigation method based on motion estimation and a regionally optimal path planning strategy. In air-ground vehicle formations, unmanned ground vehicles (UGVs) are equipped with low-precision inertial navigation measurement units and wireless range sensors, which interact with unmanned aerial vehicles (UAVs) equipped with high-precision navigation equipment for cooperative measurement information and use the UAVs as aerial benchmarks for cooperative navigation. Firstly, the Interacting Multiple Model (IMM) algorithm is used to predict the next moment’s motion position of the UGVs. Then regional real-time path optimization algorithms are introduced to design the motion position of the high-precision UAVs so as to improve the formation’s configuration and reduce the geometric dilution of precision (GDOP) of the configuration. Simulation results show that the Dynamic Optimal Configuration Cooperative Navigation (DOC-CN) algorithm can reduce the GDOP of heterogeneous air-ground vehicle formations and effectively improve the overall navigation accuracy of the whole formation. The method is suitable for the cooperative navigation environment of heterogeneous air-ground vehicle formations under GNSS-challenged conditions.

1. Introduction

With many advantages of low loss, zero casualties, and high mobility, unmanned motion vehicles are widely used in military and civilian fields, such as reconnaissance and strike, search and rescue, environmental monitoring, and resource exploration [1,2,3]. The characteristics and advantages of various unmanned vehicles are different. Fixed-wing UAVs have fast maneuverability, a wide field of view, and are not restricted by terrain [4]. Rotary-wing UAVs have a simple structure, low cost, good concealment, and are easy to transport and deploy on a large scale [5]. Unmanned ground vehicles (UGV) have the characteristics of considerable size and strong carrying capacity [6]. The formation composed of UAVs and UGVs can cooperate in complex, unknown, and dynamic environments to accomplish tasks through multidimensional sensing, information interaction, and collaborative interoperability. At present, various countries are conducting research on cross-domain collaboration projects, including the SHERPA project proposed by the European Union, which aims to build a system for searching and rescuing people in mountainous areas using aerial and ground-based unmanned platforms [7]. The ROBOSAMPLER project funded by Portugal aims to use rotary-wing UAVs and UGVs to build a hazardous substance sampling platform suitable for complex wild environments [8]. In offensive swarm-enabled tactics, the United States uses a multi-platform unmanned swarm system composed of UGVs, fixed-wing, and rotary-wing UAVs to conduct reconnaissance on targets in a simulated urban environment [9]. Heterogeneous air-ground vehicle formations have good development potential in various fields, among them, formation navigation and positioning technology is an important part of the formation control system. This paper proposes a cooperative navigation algorithm for air-ground vehicles to ensure the overall positioning performance of formations and takes into account the respective advantages and shortcomings of different unmanned vehicles in environmental perception and movement characteristics. We construct a heterogeneous air-ground cooperative system through aerial UAVs for wide-range high-altitude observation and UGVs for close reconnaissance, which has the advantages of distributed functions, high system survival rate, and high efficiency [10,11,12]. The cooperative navigation algorithm can reduce the number of sensors carried by the vehicles and reduce the performance requirements of the navigation system on the on-board computing platform. Meanwhile, the use of distributed cooperative navigation architecture can overcome the problems of poor scalability and weak anti-destruction capability of traditional centralized navigation architecture and reduce the communication burden among vehicles.

Accurate positioning information is the critical factor affecting heterogeneous air-ground vehicle formations’ ability to execute various tasks. Satellite navigation is the primary method used by air-ground vehicle formations to achieve their respective positioning. Nevertheless, GNSS-challenged situations may occur in air-ground vehicle formations when executing missions in areas, such as buildings and jungles, caused by occlusion [13,14]. The GNSS system is easily interfered within the complex battlefield environment due to low signal power [15]. The positioning accuracy of ordinary GNSS equipment cannot meet the intended requirements of the navigation system, and in some situations, requiring high accuracy need to be equipped with high precision satellite navigation equipment such as Real Time Kinematic (RTK). However, equipping each vehicle with such a device is too expensive and difficult to implement. Satellite independent navigation means currently include scene matching, terrain matching, astronomical navigation, visual navigation, and so on [16,17,18,19], but the above navigation sensors are no longer applicable under the high dynamic motion characteristics, lower computational performance, and complex environmental constraints of unmanned vehicles. Therefore, improving the positioning accuracy through cooperative navigation methods has become the current research hotspot for air-ground vehicle formations navigation [20,21,22].

In order to improve the overall localization performance of motion vehicle formations, many scholars have researched multi-source fusion algorithms. Vetrella et al. proposed a cooperative navigation method that incorporates inertial, magnetometer, available satellite pseudorange, cooperative UAV position, and monocular camera information, effectively improving the navigation performance of UAV swarms in GPS-constrained situations [23]. Indelman et al. proposed a method for distributed vision-aided cooperative localization and navigation of multiple inter-communicating autonomous vehicles based on three-view geometric constraints, allowing localization when different vehicles observe the same scene [24]. GAO et al. proposed an on-board cooperative positioning scheme based on integrated ultra-wideband (UWB) and GNSS that can obtain better positioning accuracy than the decimeter level [25]. Xiong et al. integrated the use of satellites, ground stations, inertial, inter-node ranging and speed measurement, and random signal sources to achieve cooperative positioning between vehicles [26].

Under the computational performance constraint of the navigation platform, the positioning accuracy can be improved by the preferential selection of the available cooperative navigation information. Therefore, numerous scholars have conducted corresponding research on the influence of the position distribution of each vehicle in the cooperative navigation system on positioning accuracy. Chen et al. proposed a cooperative dilution of precise (C-DOP) calculation method combining ranging error, clock error, and position error of cooperative UAVs to analyze the positioning error of UAV swarm under different formations [27]. Heng et al. proposed a generalized theory where lower bound on expectation of average geometric DOP (LB-E-AGDOP) can be used to quantify positioning accuracy and demonstrated a strong link between LB-E-AGDOP and best achievable accuracy [28]. Huang et al. used the collaborative dilution of precision (CDOP) model to specify the effect of relative distance measurement accuracy, the number of users, and their distribution on localization [29]. Causa et al. proposed a concept of the generalized accuracy factor and investigated the accuracy calculation method of cooperative configuration based on visual measurement. The experimental results showed that the UAV swarm could achieve meter-level positioning accuracy with the aid of visual measurement under the appropriate cooperative configuration [30]. Sivaneri et al. used the UGV to assist another UAV for positioning, thus improving the positioning geometry of the UAV with a low number of satellites [31]. Although there are numerous studies on cooperative navigation systems, they mainly focus on the acquisition and fusion methods of navigation information. There is no in-depth research on improving the cooperative navigation accuracy of air-ground vehicle formations through the configuration optimization of formations.

A new approach for cooperative navigation of heterogeneous air-ground vehicle formations is proposed in this paper. Firstly, we use the IMM algorithm to predict the motion state of UGVs, then construct a cost function based on the GDOP value of the whole air-ground vehicle formation. Then, it traverses the motion range of UAVs and selects the position where the minimum cost is located as the position where UAVs should arrive at the next moment. Finally, the UGVs localization calculation is completed by fusing the cooperative range values through the Kalman Filter. The simulation results show that the method proposed in this paper can achieve the effect of real-time optimization of configuration, reduce the error of cooperative navigation, and provide guidelines for the deployment and mission execution of heterogeneous air-ground vehicle formations.

2. Measurement Model

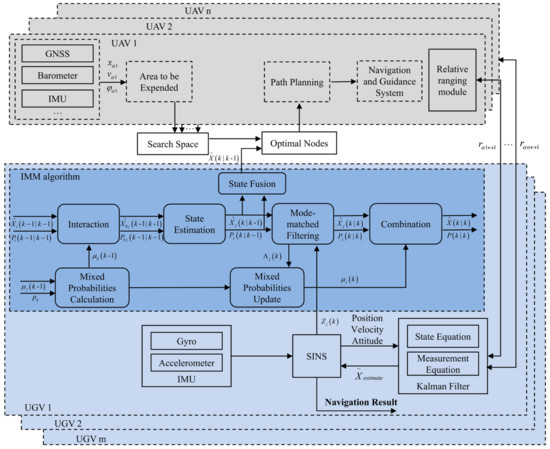
The following scenario is considered in this paper, as shown in Figure 1, heterogeneous air-ground vehicle formations execute missions in complex scenarios (e.g., urban areas, forests, canyons, etc.). In the above scenario, the GNSS signal received by UGV is easily interrupted and deceived due to obstacle blockage and active jamming, so the regional navigation and positioning system is constructed by UAVs to provide positioning service for UGVs. The UGVs accept the absolute position information of the UAVs and the inter-range information broadcasted by the air reference, then complete their own positioning calculation through the spatial geometry constraint relationship. In terms of navigation sensor configuration, UAVs flying at higher altitude are equipped with high-precision navigation equipment, such as high-precision IMU, differential GPS, and altimeters. UGVs that execute missions in urban alleyways carry lower accuracy IMU and other navigation equipment. Navigation data and sensor data are shared between all vehicles via a wireless network.

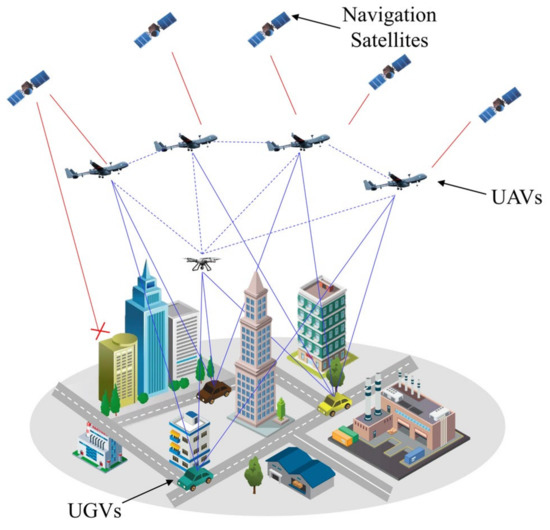
Figure 1. Schematic of cooperative navigation.

For the cooperative navigation system shown in Figure 1, we can introduce two navigation coordinate systems: Earth-Centered, Earth-Fixed (ECEF) and geographic coordinate system, denoted by $e$ and $g$, respectively. All high-altitude UAVs are denoted by $\mathrm{H}$; ground-based UGVs are denoted by $\mathrm{G}$. The position parameters of vehicles $i,{\alpha }_n$ are denoted as ${\mathit{p}}_i=[x_i{y}_i{z}_i]$ ${\mathit{p}}_{{\alpha }_n}=[x_{{\alpha }_n}{y}_{{\alpha }_n}{z}_{{\alpha }_n}]$, where $i\in \mathrm{G}$ ${\alpha }_n\in \mathrm{H}$. The speed parameters are denoted as ${\mathit{v}}_i=[v_{i,x}{v}_{i,y}{v}_{i,z}]$ ${\mathit{v}}_{{\alpha }_n}=[v_{{\alpha }_n,x}{v}_{{\alpha }_n,y}{v}_{{\alpha }_n,z}]$.

Wireless ranging exists now with many kinds of measurement methods, such as Time of Arrival (TOA), Time Difference of Arrival (TDOA), Received Signal Strength Indication (RSSI), and so on. For the distance measurement error, the RSSI measurement method distance measurement error is generally modeled as a log-normal distribution [32]. Most of the TOA-based methods are modeled as zero-mean Gaussian random variables in the line-of-sight case [33]. In the non-line-of-sight (NLOS) case, the ranging error is generally modeled as the superposition of the distance difference, measurement noise, and NLOS error due to clock error [34].

Assuming a zero-mean Gaussian distribution for the range error and perfect clock synchronization for all the high-altitude UAVs, the range values in this paper are of the following form.

$$\begin{array}{l}{r}_{{\alpha }_n\leftrightarrow i}=d_{{\alpha }_n\leftrightarrow i}+c{t}_{{\alpha }_n}+n_i\\ d_{{\alpha }_n\leftrightarrow i}=\sqrt{{(x_{{\alpha }_n}^e-x_i^e)}^2+{(y_{{\alpha }_n}^e-y_i^e)}^2+{(z_{{\alpha }_n}^e-z_i^e)}^2}\end{array}$$

(1)

where $d_{{\alpha }_n\leftrightarrow i}$ denotes the actual distance between vehicle $i$ and vehicle ${\alpha }_n$; $c$ is the speed of light; $t_{{\alpha }_n}$ is the clock error; $n_i\sim N(0,{\delta }^2)$ is Additive White Gaussian Noise with mean zero and variance ${\delta }^2$; the superscript $e$ indicates the ECEF coordinate system.

The problem of localization in NLOS environments is described in the literature [35,36] and is not analyzed in this paper.

3. Cooperative Navigation System

For the cooperative navigation scenario depicted in Figure 1, high-altitude fixed-wing UAVs and rotary-wing UAVs can provide cooperative navigation information assistance to UGVs, and the accuracy of the final cooperative navigation is not only related to the accuracy of the navigation sensors but also to the flight configuration of the UAVs. Since different types of vehicles have different speeds and states during movement, UGVs need to adjust their driving state according to the actual environment, such as bypassing obstructions. The whole heterogeneous air-ground vehicle formations cannot execute the mission in a fixed configuration. UAVs need to adjust the flight configuration in real-time according to the position of the UGVs.

The merit of the configuration can be measured by Dilution of precision (DOP), which can correlate the configuration with the positioning accuracy, and the DOP based on inter-vehicles wireless range is calculated as follows.

Set the approximate position of the vehicle $i$ as ${\tilde{\mathit{p}}}_i^e=[{\tilde{x}}_i^e{\tilde{y}}_i^e{\tilde{z}}_i^e]$ and the approximate clock difference as ${\tilde{t}}_{{\alpha }_n}$, after neglecting the measurement noise and NLOS error in Equation (1), the Taylor expansion at ${\tilde{\mathit{x}}}_i^e$ and retaining the first-order term yields, $\mathsf{\Delta }{r}_{{\alpha }_n\leftrightarrow i}$ can be denoted as follows.

$$\mathsf{\Delta }{r}_{{\alpha }_n\leftrightarrow i}=h_{x{\alpha }_n}\mathsf{\Delta }{x}_i^e+h_{y{\alpha }_n}\mathsf{\Delta }{y}_i^e+h_{z{\alpha }_n}\mathsf{\Delta }{z}_i^e-c\mathsf{\Delta }{t}_{{\alpha }_n}$$

(2)

where $(h_{x{\alpha }_n}{h}_{y{\alpha }_n}{h}_{z{\alpha }_n})$ is the direction cosine of the vehicle ${\alpha }_n$ to vehicle $i$; $(\mathsf{\Delta }{x}_i^e\mathsf{\Delta }{y}_i^e\mathsf{\Delta }{z}_i^e)$ is the difference between the approximate position of the vehicle $i$ and the actual position; $\mathsf{\Delta }{t}_{{\alpha }_n}$ is the deviation between the accurate and approximate clock difference.

Equation (2) can be extended to the following form.

$$\begin{array}{l}\left[\begin{array}{c}\mathsf{\Delta }{r}_{{\alpha }_1\leftrightarrow i}\\ \mathsf{\Delta }{r}_{{\alpha }_2\leftrightarrow i}\\ \dots \\ \mathsf{\Delta }{r}_{{\alpha }_n\leftrightarrow i}\end{array}\right]=\left[\begin{array}{cccc}{h}_{x{\alpha }_1}& h_{y{\alpha }_1}& h_{z{\alpha }_1}& 1\\ h_{x{\alpha }_2}& h_{y{\alpha }_2}& h_{z{\alpha }_2}& 1\\ \dots & \dots & \dots & \dots \\ h_{x{\alpha }_n}& h_{y{\alpha }_n}& h_{z{\alpha }_n}& 1\end{array}\right]\left[\begin{array}{c}\mathsf{\Delta }{x}_i^e\\ \mathsf{\Delta }{y}_i^e\\ \mathsf{\Delta }{z}_i^e\\ -c\mathsf{\Delta }{t}_{{\alpha }_n}\end{array}\right]\\ =H_i\mathsf{\Delta }{\mathit{x}}_i^e\end{array}$$

(3)

Based on Equation (3), the position and clock deviation vectors of the vehicle can be obtained as:

$$\mathsf{\Delta }{\mathit{x}}_i^e={(H_i^{\mathrm{T}}{H}_i)}^{-1}{H}_i^{\mathrm{T}}\mathsf{\Delta }\mathit{r}$$

(4)

The error covariance of the deviation vector can be defined as:

$$\begin{array}{l}\mathrm{cov}(\delta \mathsf{\Delta }{\mathit{x}}_i^e)\\ ={(H_i^{\mathrm{T}}{H}_i)}^{-1}{H}_i^{\mathrm{T}}\mathrm{cov}(\delta \mathsf{\Delta }\mathit{r}){[{(H_i^{\mathrm{T}}{H}_i)}^{-1}{H}_i^{\mathrm{T}}]}^{\mathrm{T}}\\ ={(H_i^{\mathrm{T}}{H}_i)}^{-1}{\delta }^2\end{array}$$

(5)

GDOP is then defined as the square root of the trace of ${(H_i^{\mathrm{T}}{H}_i)}^{-1}$. The GDOP of all UAVs with respect to the vehicle $i$ is defined as:

$$\mathrm{GDOP}\triangleq \sqrt{tr{(H_i^{\mathrm{T}}{H}_i)}^{-1}}$$

(6)

For the whole cooperative navigation system, each UGV calculates its position by IMU and fuses the cooperative information from UAVs by the Kalman filter. At the $k-1$ moment, the UGVs need to predict their position at the $k$ moment by the IMM algorithm; so as to judge the position that UAVs should reach when the sum of GDOP corresponds to all UGVs at the $k$ moment is the smallest; so that the configuration of the whole cooperative navigation system can be adjusted in real-time to provide the UGVs with the optimal cooperative information. Therefore, the cooperative navigation algorithm proposed in this paper is divided into three main parts: position prediction of UGVs, cost function calculation and optimal position selection of the high-altitude UAVs, and inertial/co-ranging value fusion of UGVs.

3.1. Position Prediction of UGVs

In order to carry out the route planning of high-altitude UAVs, the position of UGVs at the $k-1$ moment needs to be estimated first. Ground unmanned vehicles have strong mobility on the ground, and the rapid switching of their movement modes leads to drastic changes in parameters, such as heading, velocity, and acceleration, etc. The traditional single-model filter has a slow convergence speed and poor stability in the accuracy of state estimation and prediction for targets in a highly dynamic motion state, and this paper introduces multi-model filters to predict the position of UGVs at the $k$ moment.

The core of the IMM algorithm lies in describing the target’s maneuver using a set of models and filters working in parallel, corresponding to different maneuver states, switching between models follows a known Markov process, and the final estimate is a weighted value of all model state estimates [37,38]. The commonly used models are mainly the uniform velocity model, uniform acceleration model, current statistical model, Singer model, and so on [39,40]. In order to effectively characterize the maneuvering characteristics of the unmanned vehicle in ground motion, and to improve the robustness of the IMM filter and reduce the computational effort of the system, the uniform velocity model and uniform acceleration model are used to describe the motion state of each ground vehicle in this paper. The specific steps of the IMM algorithm designed in this paper are as follows.

Step 1 Input interaction module. $\forall i,j\in [1\mathrm{for}\mathrm{CV}\mathrm{model},2\mathrm{for}\mathrm{CA}\mathrm{model}]$, $k\in [1,\dots ,K]$

A. Mixing Probability Calculation.

$$\begin{array}{l}{\mu }_{i|j}(k-1|k-1)=p_{ij}{\mu }_i(k-1)/{\overline{c}}_j\\ {\overline{c}}_j={\displaystyle \sum _{i=1}^2{p}_{ij}{\mu }_i(k-1)}\end{array}$$

(7)

where ${\mu }_{i|j}(k-1|k-1)$ represents the transition probability of the state estimation of model $i$ at the $k-1$ moment to model $j$ at the $k$ moment,${\mu }_i(k-1)$ denotes the model probability of model $i$ at the $k-1$ moment, ${\overline{c}}_j$ is the normalization factor, $p_{ij}$ is the transfer probability from model $i$ to model $j$.

B. Mixing state estimation and Covariance matrix Calculation.

$$\begin{array}{l}{\widehat{\mathit{x}}}_{0j}(k-1|k-1)={\displaystyle \sum _{i=1}^2{\widehat{\mathit{x}}}_i(k-1|k-1)}{\mu }_{i|j}(k-1|k-1)\\ {\widehat{\mathit{P}}}_{0j}(k-1|k-1)={\displaystyle \sum _{i=1}^2{\mu }_{i|j}(k-1|k-1)\{{\mathit{P}}_i(k-1|k-1)}\\ +[{\widehat{\mathit{x}}}_i(k-1|k-1)-{\widehat{\mathit{x}}}_{0j}(k-1|k-1)]\cdot \\ {[{\widehat{\mathit{x}}}_i(k-1|k-1)-{\widehat{\mathit{x}}}_{0j}(k-1|k-1)]}^{\mathrm{T}}\}\end{array}$$

(8)

where ${\widehat{\mathit{x}}}_i(k-1|k-1)$ and ${\mathit{P}}_i(k-1|k-1)$ are the state estimation and the covariance matrix of model $i$ at the $k-1$ moment, respectively.

Step 2 Model filter estimation module.

A. one-step prediction for sub-model

$$\begin{array}{l}{\widehat{\mathit{x}}}_j(k|k-1)=\mathit{F}{\widehat{\mathit{x}}}_{0j}(k-1|k-1)\\ {\widehat{\mathit{P}}}_j(k|k-1)=\mathit{F}{\widehat{\mathit{P}}}_{0j}(k-1|k-1){\mathit{F}}^{\mathrm{T}}+\mathit{G}\mathit{Q}(k){\mathit{G}}^{\mathrm{T}}\end{array}$$

(9)

where $\mathit{F},\mathit{G}$ are the state transfer matrix and the system noise matrix of the model, respectively, and the state equations of the uniform velocity model and the uniform acceleration model are shown in the literature [41]. $\mathit{Q}(k)$ is the variance matrix of the system noise.

B. position prediction

$$\widehat{\mathit{x}}(k|k-1)={\displaystyle \sum _{j=1}^2{\widehat{\mathit{x}}}_j(k|k-1){\mu }_j(k-1)}$$

(10)

where $\widehat{\mathit{x}}(k|k-1)$ is the estimated value of the position of UGV at the $k$ moment.

Step 3 Update of model probability module. $(j=1,2)$

A. Filtered residuals

$$\begin{array}{l}{\mathit{\nu }}_j(k)={\mathit{Z}}_j(k)-{\mathit{H}}_j{\widehat{\mathit{x}}}_j(k|k-1)\\ {\mathit{S}}_j(k)={\mathit{H}}_j{\widehat{\mathit{P}}}_j(k|k-1){\mathit{H}}_j^{\mathrm{T}}+{\mathit{R}}_j\end{array}$$

(11)

where ${\mathit{Z}}_j(k)$ is the position output obtained by fusing the IMU/co-ranging values of the vehicle at the $k$ moment, as described in Section 3.3, and ${\mathit{H}}_j$ is the measurement matrix.

B. Kalman filter gain calculation

$${\mathit{K}}_j={\widehat{\mathit{P}}}_j(k|k-1){\mathit{H}}_j^{\mathrm{T}}{({\mathit{S}}_j(k))}^{-1}$$

(12)

C. Sub-model measurement update

$$\begin{array}{l}{\widehat{\mathit{x}}}_j(k|k)={\widehat{\mathit{x}}}_j(k|k-1)+{\mathit{K}}_j{\mathit{\nu }}_j(k)\\ {\widehat{\mathit{P}}}_j(k|k)=(\mathit{I}-{\mathit{K}}_j{\mathit{H}}_j){\widehat{\mathit{P}}}_j(k|k-1){(\mathit{I}-{\mathit{K}}_j{\mathit{H}}_j)}^{\mathrm{T}}+{\mathit{K}}_j{\mathit{R}}_j{\mathit{K}}_j^{\mathrm{T}}\end{array}$$

(13)

D. Mode Probability Update $(j=1,2)$

First, the likelihood function is calculated with the following equation.

$${\mathsf{\Lambda }}_j(k)=\mathit{N}({\mathit{\nu }}_j(k),0,{\mathit{S}}_j(k))$$

(14)

where ${\mathsf{\Lambda }}_j(k)$ is the likelihood function, $\mathit{N}({\mathit{\nu }}_j(k),0,{\mathit{S}}_j(k))$ denotes the Gaussian density function of ${\mathit{\nu }}_j(k)$ with zero mean and covariance ${\mathit{S}}_j\left(k\right)$. The updated model probabilities are denoted as:

$${\mu }_j(k)=\frac{{\mathsf{\Lambda }}_j(k){\overline{c}}_j}{{\displaystyle \sum _{i=1}^2{\mathsf{\Lambda }}_i(k){\overline{c}}_i}}$$

(15)

Step 4 Estimation fusion module.

$$\begin{array}{l}\widehat{\mathit{x}}(k|k)={\displaystyle \sum _{j=1}^2{\widehat{\mathit{x}}}_j(k|k)}{\mu }_j(n)\\ \mathit{P}(k|k)={\displaystyle \sum _{j=1}^2{\mu }_j(k)\{{\widehat{\mathit{P}}}_j(k|k)+[{\widehat{\mathit{x}}}_j(k|k)}\\ -\widehat{x}(k|k)][{\widehat{\mathit{x}}}_j(k|k)-\widehat{\mathit{x}}{(k|k)}^{\mathrm{T}}]\}\end{array}$$

(16)

The first two steps in the above steps are completed at the $k-1$ moment, thus predicting the position of the UGVs at the $k$ moment. The last two steps are performed after the completion of the vehicle IMU/co-ranging assistance at the $k$ moment to update the model data of the IMM algorithm.

3.2. Cost Functions and Path Planning Strategies

The positioning accuracy of the UAVs depend on the ranging error, the air-based reference position error, and the UAVs configuration distribution. The range error is mainly determined by the clock difference between the two vehicles, the air-based reference position error mainly depends on the GNSS positioning accuracy, and the above two points are determined by the sensor hardware performance, so the UAV needs to dynamically adjust the flight position to form different formation configurations to provide cooperative navigation services for the UGVs. After the predicted position of the UGVs at the $k$ moment, the position prediction value needs to be used to plan the position of the UAVs to achieve the optimal configuration. Path planning algorithms are mainly classified into three categories, namely traditional path planning algorithms, sampling-based path planning algorithms, and intelligent bionic algorithms, among which the A* algorithm is the mainstream algorithm in the field of path planning at present [42,43]. The advantage of the A* algorithm is its rapid response to the environment and high computational efficiency. It is a heuristic search algorithm that allows the UAV to quickly plan a route and generate maneuver control commands with known starting and ending points [44].

This paper combines the need of real-time configuration optimization and the idea of the sparse A* algorithm to propose a real-time memoryless path optimization method. Taking the current position of the UAV as the center and dividing the neighborhood space to establish a grid centered on the UAV, that is, the area to be extended, and the combination of all the UAVs’ areas to be extended, is called the search space. Traversing all the combinations of ways in the search space to find the grid position corresponding to the minimum cost, that is, the planning position of the UAV at the next moment. First, we establish the cost function on the voyage.

3.2.1. Cost Function Establishment

In the cooperative mission execution of heterogeneous air-ground vehicle formations, borrowing the A* algorithm for trajectory planning from the literature [45], the cost can generally be divided into two parts, namely the route flight cost and the GDOP cost. The route flight cost mainly includes the distance flown, as it will determine the duration of the UAV, and the route flight cost can also include the distance from the target point if there is a target point for the mission. The GDOP cost is the sum of the GDOP values corresponding to each UGV during the execution of the mission. There is a coupling relationship between the GDOP cost and the route flight cost, so the two need to be considered together.

The cost function is defined as:

$$\mathit{J}(t)=\mathit{g}(t)+\mathit{r}(t)$$

(17)

where $\mathit{g}(t)$ denotes the GDOP cost, and assuming that the number of ground vehicles is $N$, $\mathit{g}(t)$ can be designed as:

$$\mathit{g}(t)={\mathit{\omega }}_1{\displaystyle \sum _{i=1}^N{\mathrm{GDOP}}_i}$$

(18)

where $\mathit{r}(t)$ denotes the flight cost of the route, and assuming that the number of aerial vehicles is $M$, $\mathit{r}(t)$ is designed as:

$$\mathit{r}(t)={\mathit{\omega }}_2{\displaystyle \sum _{{\alpha }_n=1}^M{\mathit{D}}_{{\alpha }_n}}$$

(19)

In Equations (18) and (19), ${\mathit{\omega }}_1$ and ${\mathit{\omega }}_2$ are the weights of GDOP cost and route flight cost, respectively, which ${\mathit{\omega }}_1{\mathit{\omega }}_2$ can be adjusted and used to choose whether to give priority to guaranteeing the GDOP value or reducing the flight distance. In this system, the fixed-wing UAVs are selected as the aerial benchmarks, and the movement speed is larger than that of the rotary-wing UAVs, which can reach the preset position quickly, so ${\mathit{\omega }}_1$ is set to 1/3 and ${\mathit{\omega }}_2$ is set to 2/3. ${\mathit{D}}_{{\alpha }_n}$ denotes the distance flown by the UAV ${\alpha }_n$ from the $k-1$ moment to the $k$ moment.

3.2.2. Path Planning Strategy

When establishing the area to be extended for UAVs, the constraints of UAVs need to be considered simultaneously, including the maximum movement step $L_{\max }$, minimum movement step $L_{\min }$, maximum pitch angle ${\theta }_{\max }$, minimum flight height $H_{\min }$, and minimum collision avoidance distance $R_{\min }$ between two UAVs. According to the current position of the UAVs and the constraints, the path planning process is as follows.

A. Search space establishment

As shown in Figure 2, the region to be extended for the high-altitude UAVs is established with the current position as the center and the constraints.

Figure 2. Diagram of the UAV to be expanded area.

Split the area to be extended, as shown in Figure 2. The horizontal profile of the area to be extended is a circle, as shown in Figure 3, and the circle can be split into $l$ parts, each of which has a vertical profile of a sector ring, as shown in Figure 4.

Figure 3. Horizontal section of the area to be expanded.

Figure 4. Vertical section of the annular sector.

Divide the sector ring into $n$ copies along the radius direction and $m$ copies along the arc direction, so that the area to be expanded is divided into $m\times n\times l$ expansion nodes. The combinations of extended nodes of $M$ airborne UAVs have ${(m\times n\times l)}^M$ ways, and the combinations that do not satisfy the height constraint and the minimum collision avoidance distance constraint are removed, and the remaining combinations will constitute the search space at the $k-1$ moments.

B. Calculation of the cost function

Based on the UGVs’ location predicted by Equation (10), all node combinations in the search space are traversed, and the corresponding generation value is calculated according to Equation (17) to find the least costly node combination as the location where the UAVs should arrive at the $k$ moment.

C. Path Planning

The positions obtained in step B are only isolated coordinate points and need to be combined with the motion characteristics of the UAV to plan a motionable route, and the specific route planning algorithm can be found in the literature [46].

3.3. Inertial/Co-Ranging Value Fusion Method for UGVs

When the UAVs establish the aerial benchmarks, the UGVs complete the cooperative information interaction and distance calculation through the data chain with the UAVs, and the Kalman filter needs to be used to complete the navigation information fusion. Under the Kalman filtering framework, the system state equation is constructed by using the position and attitude information obtained from the inertial sensors as state quantities; then the best state estimate of the previous moment is combined with the equation of motion to complete the one-step prediction; finally, the relative distance is used as the observed quantity to construct the measurement update equation, and the above operations are cycled to complete the cooperative navigation and positioning solution [47]. Compared with the cooperative navigation technique based on factor graph theory, the Kalman filter has the advantages of high computational efficiency, good real-time performance, and low communication load requirement, which can be realized by engineering [48].

3.3.1. State Equation

In the process of UAV route planning, it also continuously sends range signals and position information, and after receiving this information, the UGV can fuse it with its own inertial information to make effective corrections to the inertial information.

Using the geographic coordinate system as the navigation coordinate system, the state vector of the UGV $i$ navigation system is defined as follows [49].

$$\begin{array}{l}\mathit{X}=[{\phi }_x^g{\phi }_y^g{\phi }_z^g\delta v_x^g\delta v_y^g\delta v_z^g\delta L\delta \lambda \delta h\\ {\epsilon }_{bx}{\epsilon }_{by}{\epsilon }_{bz}{\epsilon }_{rx}{\epsilon }_{ry}{\epsilon }_{rz}{\nabla }_x{\nabla }_y{\nabla }_z{]}^{\mathrm{T}}\end{array}$$

(20)

where the superscript $g$ represents the geographic coordinate system. where ${\phi }_x^g{\phi }_y^g{\phi }_z^g$ and $\delta v_x^g\delta v_y^g\delta v_z^g$ are platform angle error and velocity error of east, north, and up directions, respectively. $\delta L\delta \lambda \delta h$ are, respectively, latitude error, longitude error, and altitude error. ${\epsilon }_{bx}{\epsilon }_{by}{\epsilon }_{bz}{\epsilon }_{rx}{\epsilon }_{ry}{\epsilon }_{rz}$ are the gyro constant drift errors and the first-order Markov drift errors, respectively; ${\nabla }_x{\nabla }_y{\nabla }_z$ are the accelerometer biases.

The state equation can be constructed according to the defined state vector

$$\mathit{X}=\mathit{A}\mathit{X}+\mathit{B}\mathit{W}$$

(21)

where $\mathit{A}$ is the linearized INS error states matrix, $\mathit{B}$ is the noise transfer matrix, $\mathit{W}$ is the system process noise with multivariate mean normal distribution with variance ${\mathit{Q}}_{INS}$, whose value is determined by the accuracy of gyroscope and accelerometer.

3.3.2. Measurement Equation

The measurement equation of the filter can be defined as

$$\mathit{Z}={\mathit{H}}_{INS}\mathit{X}+\mathit{V}$$

(22)

where $\mathit{Z}$ is the observation vector related to the wireless ranging measurements, ${\mathit{H}}_{INS}$ is the observation matrix, $\mathit{V}$ is the measurement noise of wireless ranging with $R$. The observation vector and observation matrix are defined as:

$$\mathit{Z}=\left[\begin{array}{c}{\mathit{r}}_{{\alpha }_1,INS}-{\mathit{r}}_{{\alpha }_1\leftrightarrow i}\\ {\mathit{r}}_{{\alpha }_2,INS}-{\mathit{r}}_{{\alpha }_2\leftrightarrow i}\\ \cdots \\ {\mathit{r}}_{{\alpha }_n,INS}-{\mathit{r}}_{{\alpha }_n\leftrightarrow i}\end{array}\right]$$

(23)

$${\mathit{H}}_{INS}=[0_{n\times 6}{\mathit{H}}_i{\mathit{H}}_e^g{0}_{n\times 9}]$$

(24)

where ${\mathit{H}}_e^g$ is the transformation matrix that converts $\delta L\delta \lambda \delta h$ to $\delta x^e\delta y^e\delta z^e$, which satisfies the following formula:

$${\mathit{H}}_e^g=\left[\begin{array}{ccc}-(R_N+h)\sin L\cos \lambda & -(R_N+h)\cos L\sin \lambda & \cos L\cos \lambda \\ -(R_N+h)\sin L\sin \lambda & (R_N+h)\cos L\cos \lambda & \cos L\sin \lambda \\ [R_N{(1-f)}^2+h]\cos L& 0& \sin L\end{array}\right]$$

(25)

where $R_N$ is the radius of curvature in prime vertical, $f$ denotes the earth oblateness.

3.4. Description of the Cooperative Navigation Method

The structure of the heterogeneous air-ground vehicle formations cooperative navigation method proposed in this paper is given in Figure 5. Combining the methods and strategies proposed in Section 3.1, Section 3.2 and Section 3.3, the steps of the cooperative navigation method are as follows.

Figure 5. Cooperative navigation method structure.

Step 1: Initialization

Initialization of the whole cooperative navigation system according to the constraints, such as motion characteristics and task requirements of the heterogeneous air-ground vehicle formations, including the establishment of the cost function, the initial model probability, and model transfer probability assignment in the IMM algorithm.

Step 2: Location estimation of all UGVs

At the current moment, using the two steps 1 and 2 described in Section 3.1, the position estimates ${\widehat{\mathit{x}}}_i(k|k-1),i\in \mathbf{G}$ of all UGVs are obtained.

Step 3: Establishment of UAVs’ search space and selection of the minimum cost combination

According to the position estimation value ${\widehat{\mathit{x}}}_i(k|k-1)$ of the UGV and the current position ${\mathit{x}}_{{\alpha }_n}$ of the UAV, the area to be extended is constructed by combining the relevant constraints, and the area to be extended of all UAVs is partitioned and combined into the search space. The generation value of all node combinations in the search space is calculated according to Equation (17), and the location combination with the lowest cost is selected as the target location of the UAV at the next moment. The UAV uses the target position for path planning and flight control.

Step 4: Inertial/co-ranging fusion filter of UGV

The UAVs continuously broadcasts range measurement signals and position information during flight. After receiving the signals and decoding the distance, the UGVs can fuse and filter them with their inertial guidance information according to Equations (21) and (22). It is worth noting that the filtering frequency need not be consistent with the frequency of the UAV path planning, and the frequency of the UAV path planning can be reduced in order to reduce the computation.

Step 5: IMM sub-filter filtering and fusion

After the position of the ground vehicle is corrected, the model parameters and model probabilities of the IMM algorithm are updated by using the corrected position and velocity as measurements and completing the two steps (3), (4) described in Section 3.1.

Step 6: Return to Step 2.

4. Simulation Results

4.1. Sensor Configuration and Simulation Scenario

In order to verify the effectiveness of the proposed method, heterogeneous air-ground vehicle formations are simulated for the scenario shown in Figure 1. This paper gives a simulation environment with five UAVs and three UGVs with a simulation time of 1200 s. The UAVs’ initial altitude distribution is from 1000 to 1500 m, and the unmanned vehicle performs horizontal orientation maneuvers on the ground without a wide range of changes in altitude. The initial positions of the UAVs and UGVs are shown in Figure 6.

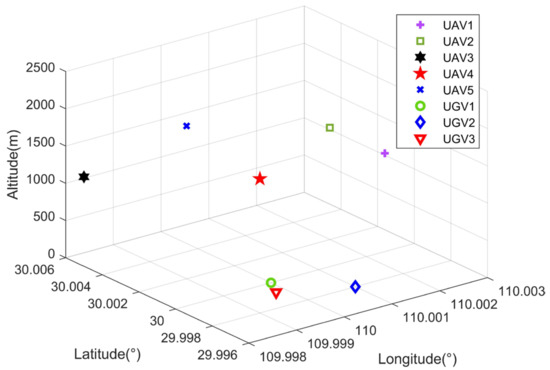
Figure 6. Initial location of air-ground vehicle formations.

All UAVs are equipped with high-precision navigation equipment, such as RTK, INS, and range and communicate with UGVs through wireless networks; UGVs are equipped with INS and use wireless range information to assist in positioning. Wireless ranging uses time division multiple access (TDMA) mode of operation, using time synchronization. In addition, signal arrival time measurement is an important means to achieve the ranging between UAVs and UGVs, and its ranging error source is mainly equipment delay. The simulation parameters of the sensors carried by the UAVs and UGVs are shown in Table 1.

Table 1. Sensor configuration and simulation parameters.

Sensor	Parameter	Value
GNSS	Position noise standard dev.	0.1 m
	Initial clock difference	40 ns
	clock drift	50 ns/s
	Update Frequency	1 Hz
Gyroscope	Random constant drift	0.1 °/h
	White noise	0.1 °/h
	First-order Markov drift	0.1 °/h
	First-order Markov correlation time	3600 s
	Update Frequency	50 Hz
Accelerometer	First-order Markov drift	10−4 g
	First-order Markov correlation time	1800 s
	Update Frequency	50 Hz
Wireless ranging	Ranging noise	10 m
	Update Frequency	1 Hz

4.2. Results and Analysis of the Simulation

Based on the above simulation conditions, the localization accuracy of the UGVs is simulated and analyzed. In order to verify the localization performance of the algorithm in this paper under the high dynamic motion state of multiple vehicles, three motion trajectories are designed for the UGVs. No. 1 and No. 3 UGVs are simulated in complex environments, such as urban alleys with high-speed, sharp turns characteristics, while the No. 2 UGV is in low-speed motion mode. The trajectories of UGVs are shown in Figure 7. To verify the effectiveness of the conversion of different motion models in the IMM algorithm, this UGV will have different motion modes, such as acceleration, uniform speed, and different time stagnation in the whole process. They are combined with the optimal configuration solution of UAVs and real-time position dynamic adjustment to complete the cooperative navigation and positioning of UGVs.

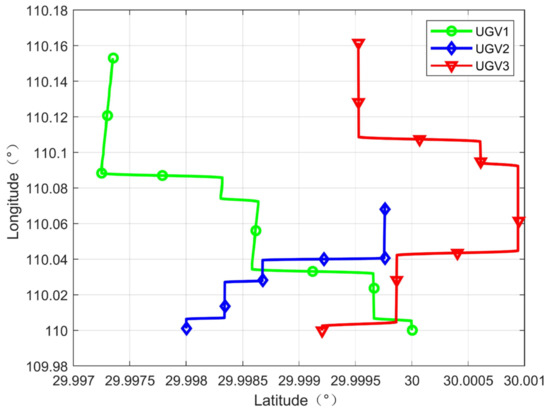
Figure 7. Trajectories of UGVs.

For the traditional space-based area cooperative navigation system, a nonlinear optimization algorithm is often used to solve the target positioning information, based on the idea of the satellite pseudo-range single-point positioning algorithm. In order to verify the representativeness of the cooperative navigation algorithm (DOC-CN) based on motion estimation and the regional real-time path planning strategy proposed in this paper, and also to verify the effect of UAVs’ configuration changes on the overall navigation and positioning performance of the formation, the text algorithm is compared with the direct localization method based on a two-step least square algorithm (TSLS) [50] and the fixed configuration cooperative navigation method (FC-CN) [51]. The GNSS, inertial sensor, and range sensor parameters are kept the same in the three algorithms. The simulation results of the positioning of UGVs are shown in Figure 8 and Figure 9.

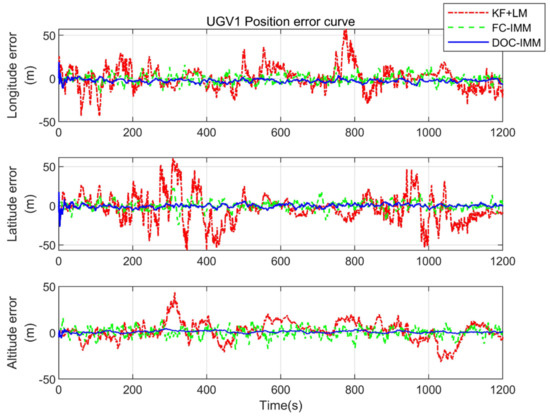
Figure 8. Position error of UGV1.

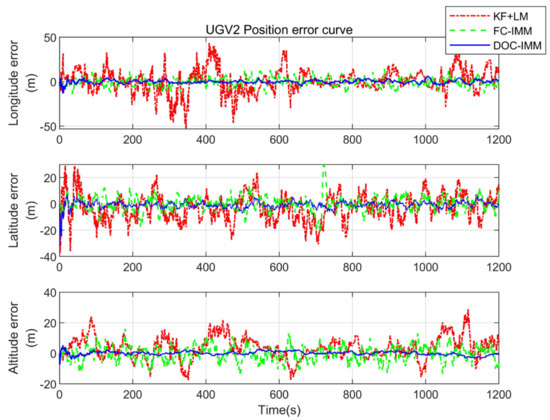
Figure 9. Position error of UGV2.

As can be seen from Figure 8 and Figure 9, the cooperative navigation algorithm based on motion estimation and the regional real-time path planning strategy proposed in this paper has been significantly improved in terms of positioning accuracy compared with the remaining two navigation and positioning algorithms. The nonlinear filtering algorithm does not require high accuracy for initial value setting and can achieve fast convergence, however, its algorithm only solves the optimal solution from spatial measurements and ignores the temporal state correlation, so the localization error fluctuates more when relying only on the range value for cooperative navigation. The fixed configuration cooperative navigation algorithm is used to reduce the influence of the convergence target maneuver, but the overall positioning accuracy is lower than that of the cooperative navigation algorithm proposed in this paper.

The flight trajectory of the UAV optimized by the DOC-CN algorithm is shown in Figure 10, and the GDOP value is kept minimum during the flight. To quantitatively analyze the positioning errors of three UGVs under different methods, the root mean square error (RMSE) was used for the UGVs, and the results are shown in Table 2. The equation for the position estimation error in Table 2 is shown in Equation (26).

$$E=\sqrt{Er{r}_E^2+Er{r}_N^2+Er{r}_U^2}$$

(26)

where $Er{r}_{E}Er{r}_N$ and $Er{r}_U$ are the estimate errors in east, north, and up (ENU) directions, respectively.

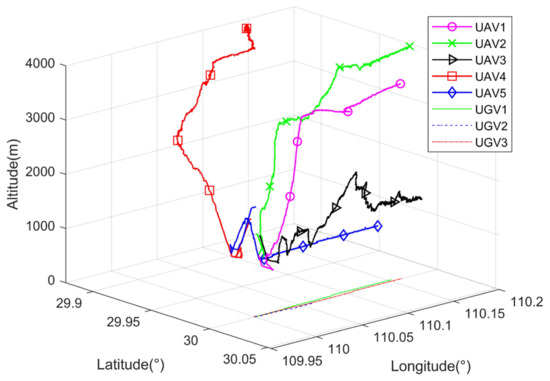
Figure 10. Optimized trajectories of UAVs.

Table 2. Statistics of position error.

Number	Position Error	RMSE/m
		TSLS	FC-CN	DOC-CN
UGV1	Longitude	13.04	4.78	3.32
	Latitude	18.61	5.74	2.48
	Altitude	10.78	5.04	1.52
	3-D	25.15	9.00	4.41
UGV2	Longitude	13.39	4.93	1.98
	Latitude	17.06	5.58	2.69
	Altitude	8.21	5.04	1.22
	3-D	23.19	8.99	3.56
UGV3	Longitude	13.38	5.08	1.87
	Latitude	17.72	5.87	2.53
	Altitude	8.10	4.80	1.01
	3-D	23.64	9.13	3.30

From Table 2, it can be seen that the UGVs only use the TSLS direct localization algorithm in 3-D localization errors of 23.19 m~25.15 m. The interactive multi-model can improve UGVs’ positioning performance in high dynamic motion mode. The UGVs use the FC-CN localization algorithm in 3-D localization errors of 8.99 m~9.13 m, and the positioning accuracy is nearly 1.78 times better than traditional methods. On this basis, the cooperative navigation algorithm based on motion estimation and regional real-time path planning strategy proposed in the text maintains a positioning accuracy of 3.30 m~3.56 m, and the overall positioning accuracy is 7.3 times better than the original algorithm.

To demonstrate the overall improvement in the level of positioning performance of all UGVs in the formation, the cumulative distribution function is used to describe the probability distribution of the magnitude of all UGVs’ positioning errors, and 50 Monte Carlo experiments are conducted in this paper in order to reflect the stability of the algorithm in this paper. Figure 11 compares the cumulative distribution of the UAVs and UGVs positioning estimation errors. Using conventional methods, only 9.8% of the positioning error is less than 5 m. The percentage of less than 5 m localization error supported by the DOC-CN algorithm can reach 91.2%.

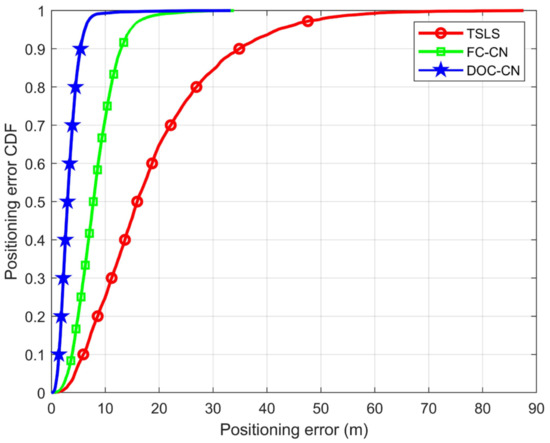
Figure 11. Positioning error CDF comparisons.

In summary, it can be demonstrated that the DOC-CN algorithm can significantly improve the positioning accuracy of UGVs in complex environments such as urban alleyways. This allows UGVs to obtain similar positioning performance as UAVs, thus improving the overall positioning performance of heterogeneous formations.

5. Conclusions

In this paper, for the situation of satellite navigation signal challenged in cities, hills, and valleys, we use the techniques of multi-dimensional sensing of navigation information, wireless ranging information interaction, and cooperative interoperability between heterogeneous air-ground vehicle formations to complete real-time navigation and positioning of UGVs. In this method, the DOC-CN algorithm is divided into three steps. First, the location of the UGV is predicted by the IMM algorithm. Then, aerial benchmarks are established by calculating cost functions and the path planning algorithm. Finally, the SINS solution platform is constructed to obtain the continuous position information of the UGVs.

The simulation shows that the DOC-CN algorithm proposed in this paper is significantly superior to that of traditional cooperative positioning methods such as TSLS and the FC-CN method. It can realize the navigation and positioning requirements of UGVs in a certain area under the GNSS-challenged environment and improve the overall formation’s positioning accuracy. Moreover, the next step is to embed the flight control program and navigation algorithm into the hardware platform and complete the practical validation.