A Novel Vegetation Index Approach Using Sentinel-2 Data and Random Forest Algorithm for Estimating Forest Stock Volume in the Helan Mountains, Ningxia, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field Data Collection
2.3. The Acquiring and Processing of Sentinel-2 Data
2.3.1. Original Band Information
2.3.2. Traditional Vegetation Indices
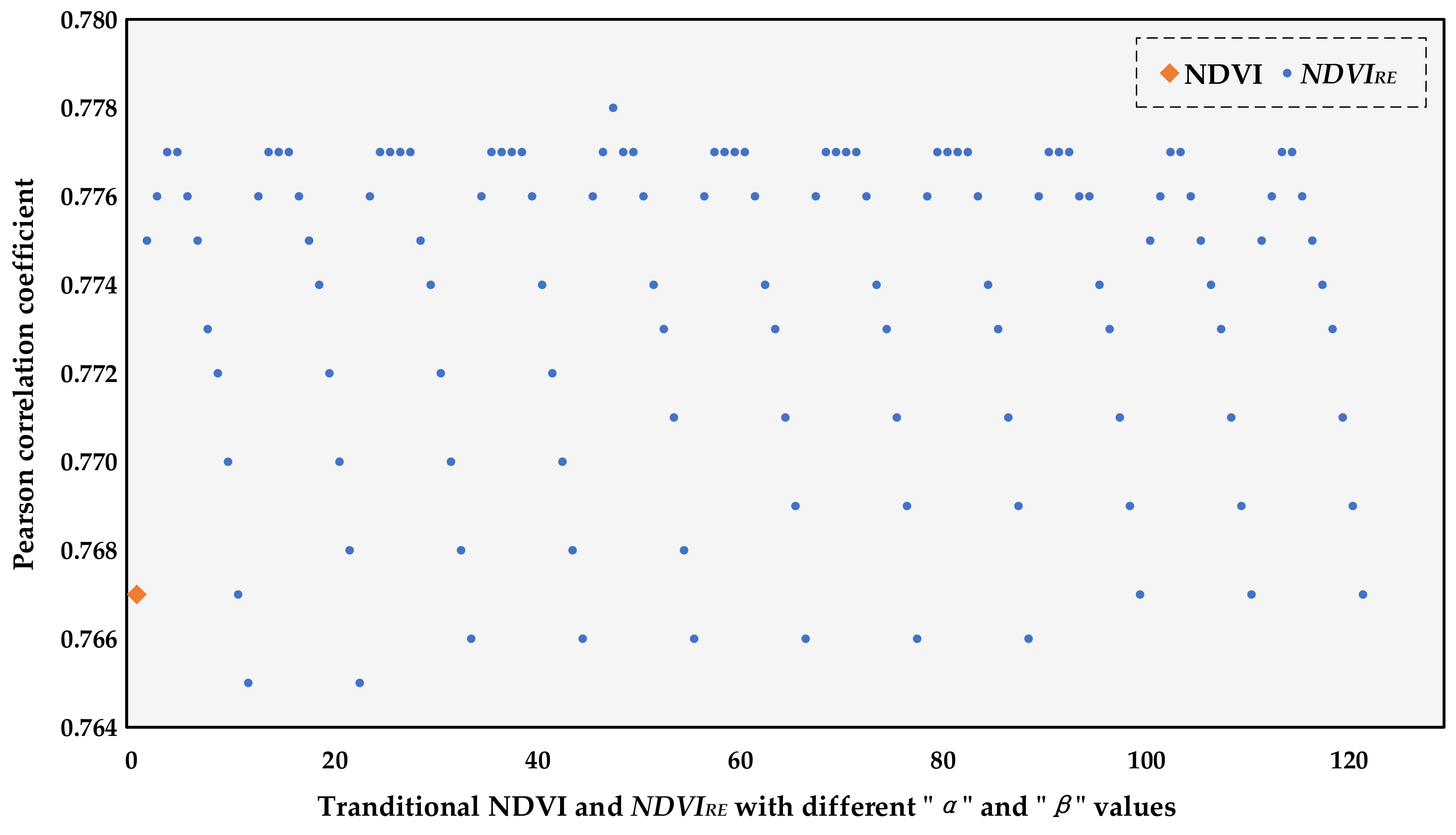
2.3.3. Novel Vegetation Index Based on Red-Edge Bands
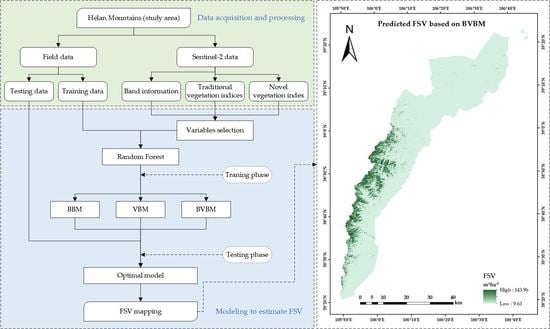
2.4. Acquisition of the Forest Distribution Pattern in the Helan Mountains
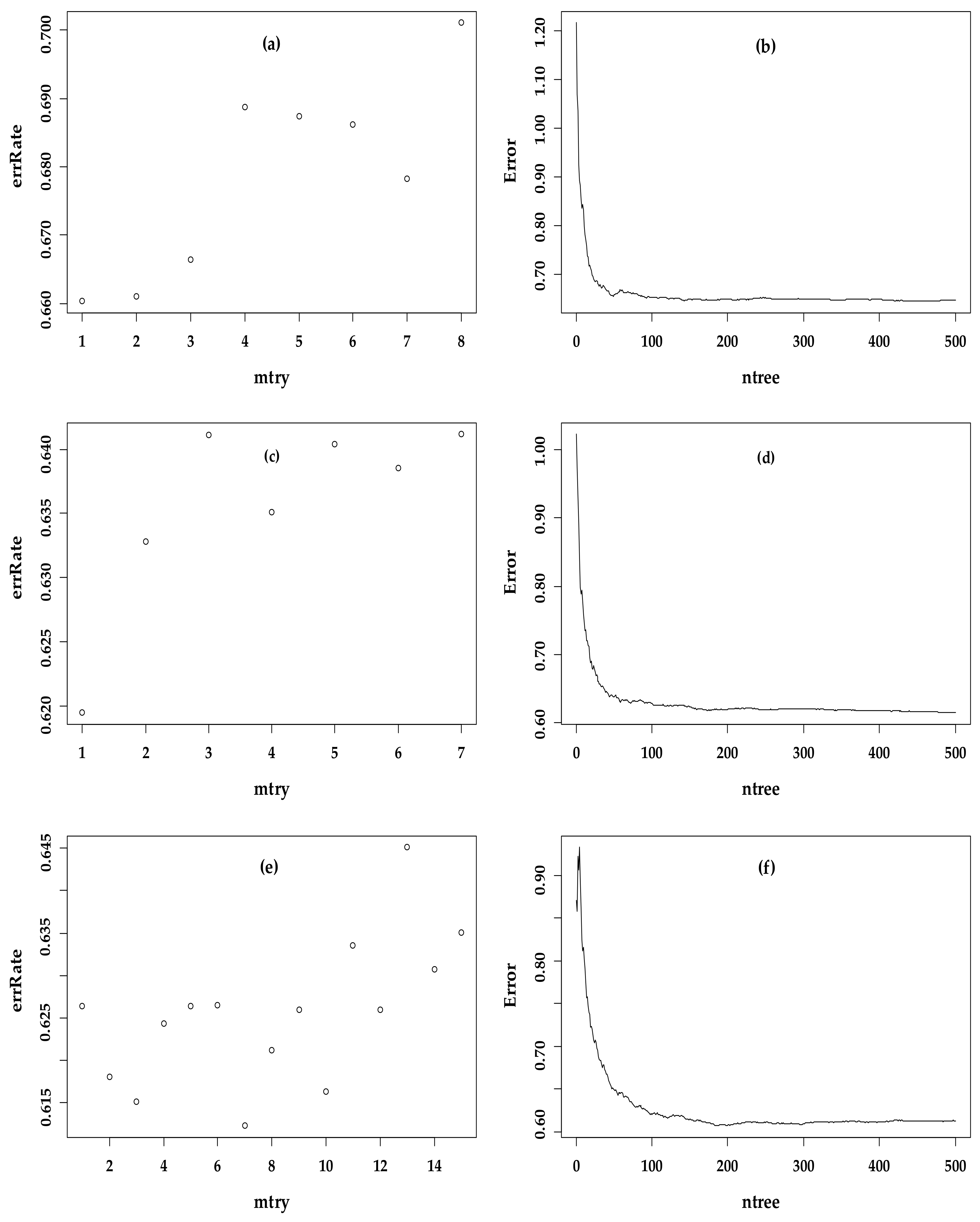
2.5. Machine Learning Algorithm of Modeling FSV
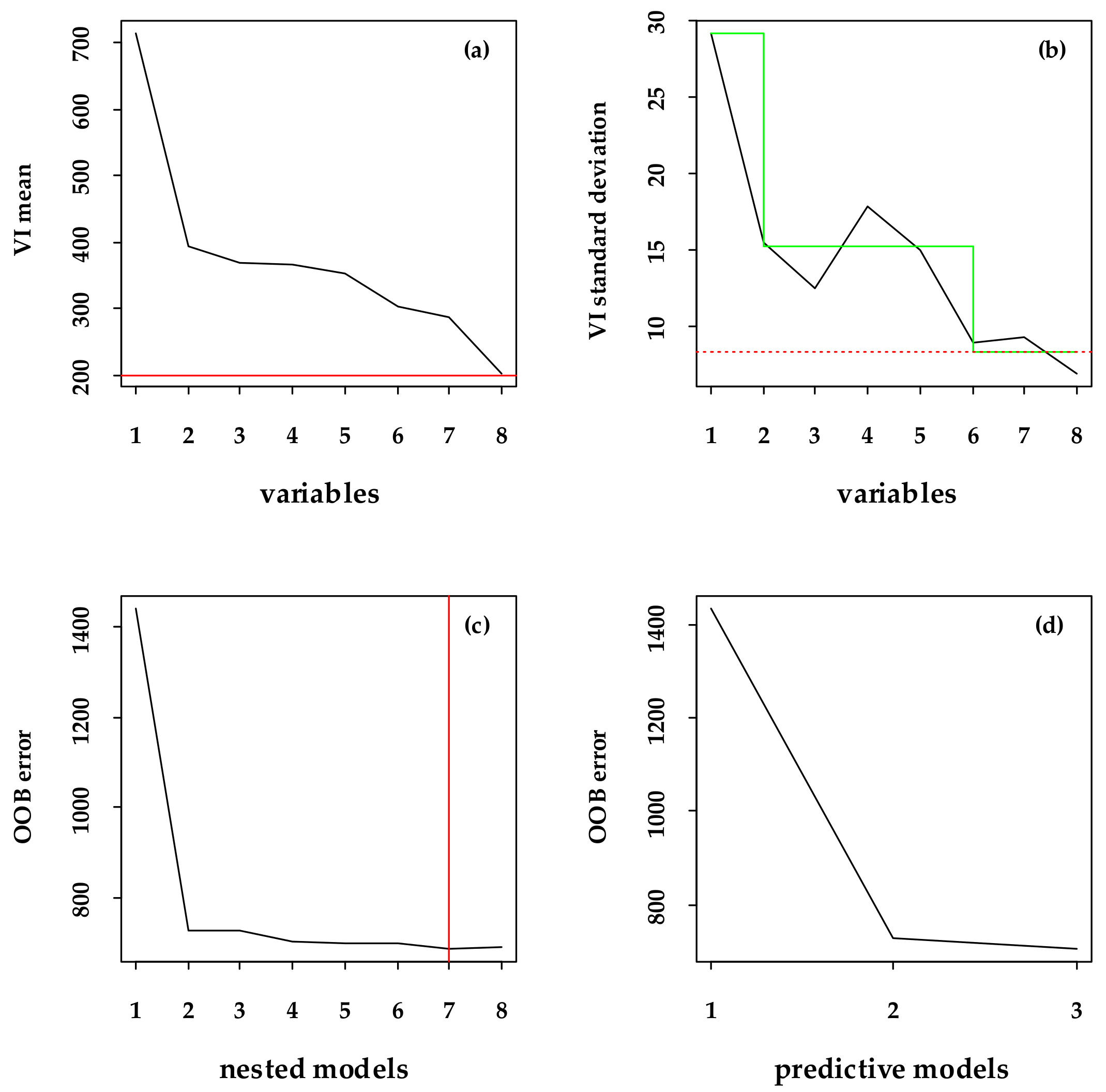
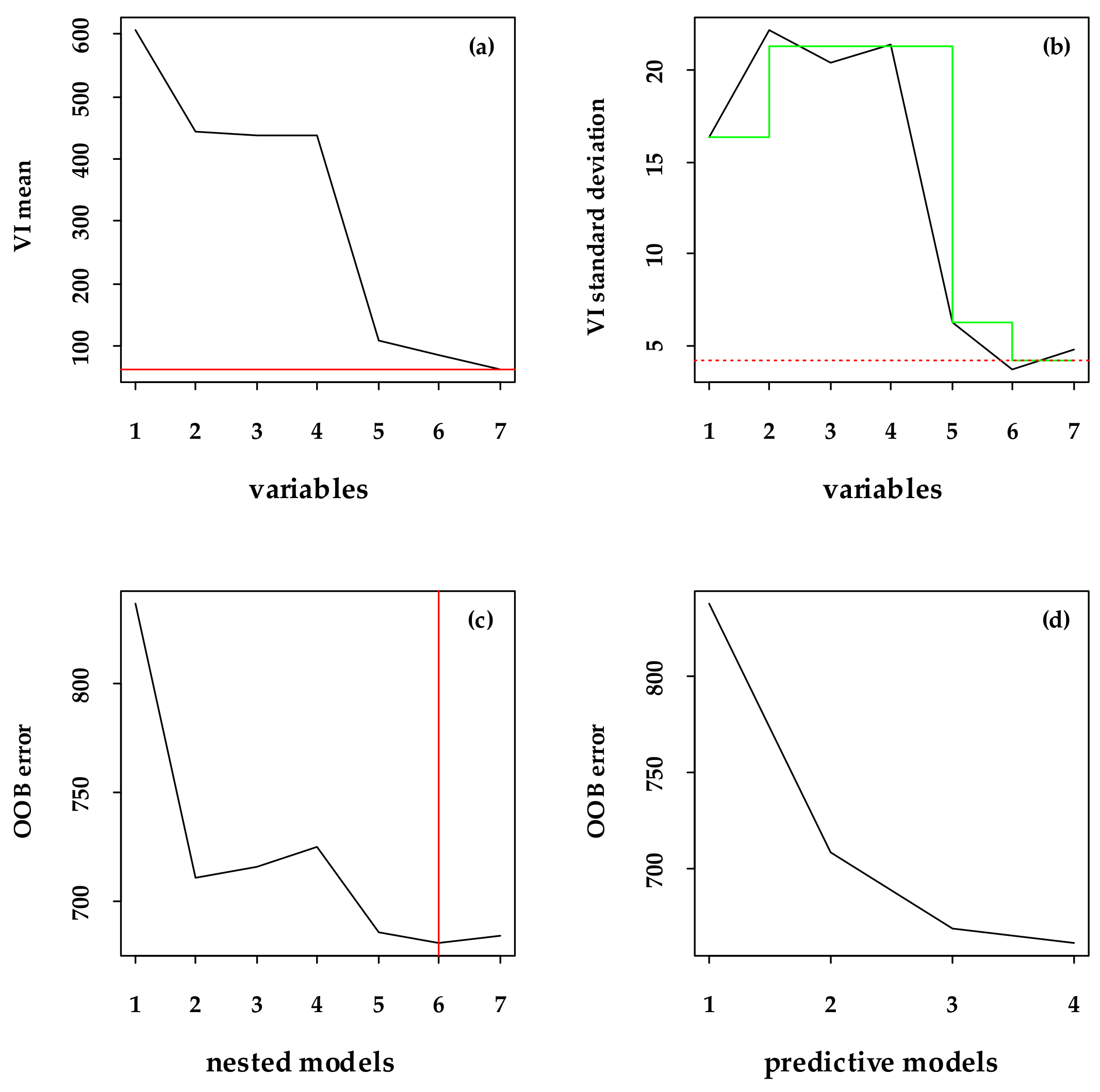
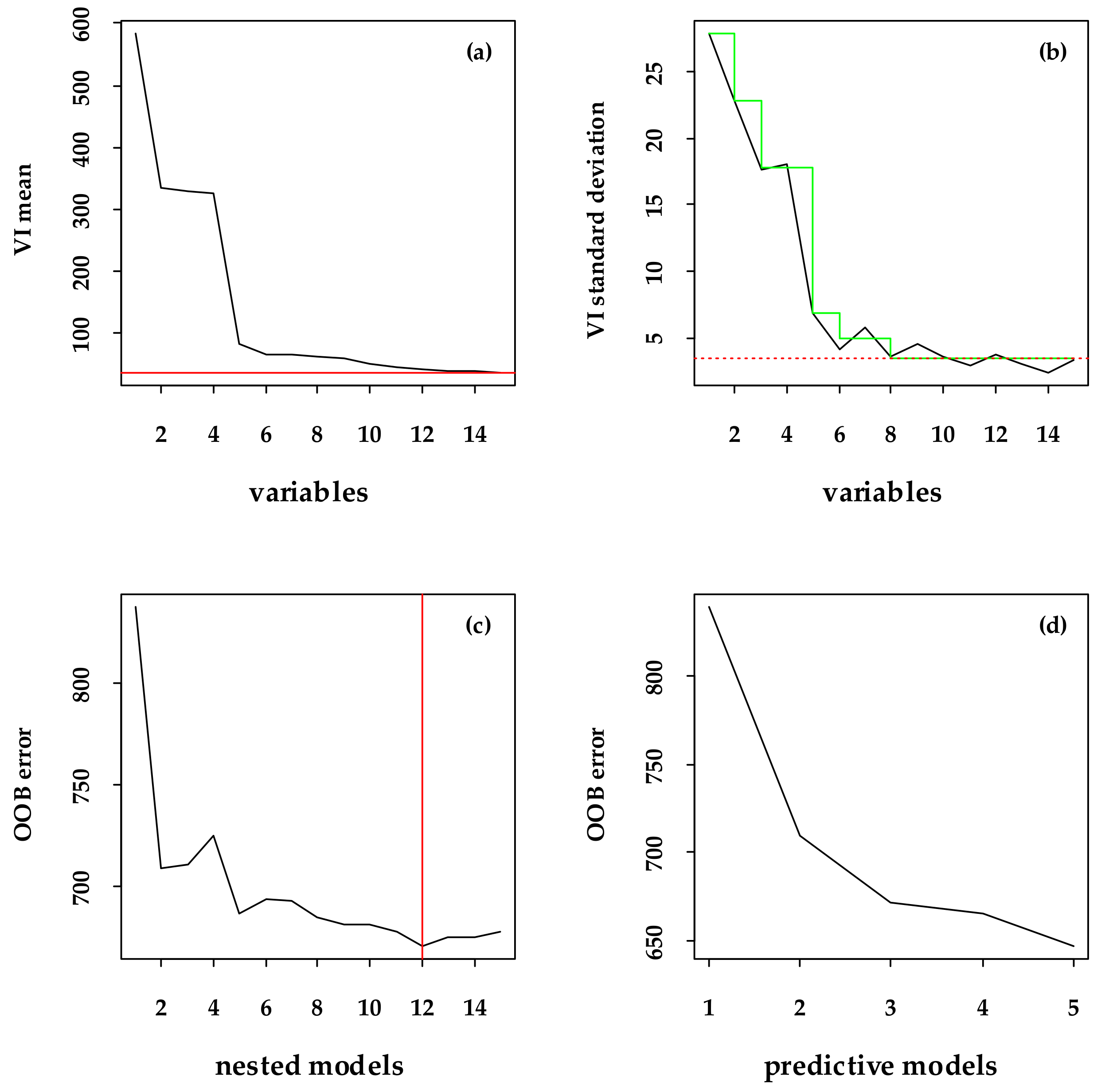
2.6. Selecting Variables Using the VSURF Package
2.7. Assessment of the Modeling Performance
3. Results
3.1. Determination of the Optimal Novel Vegetation Index
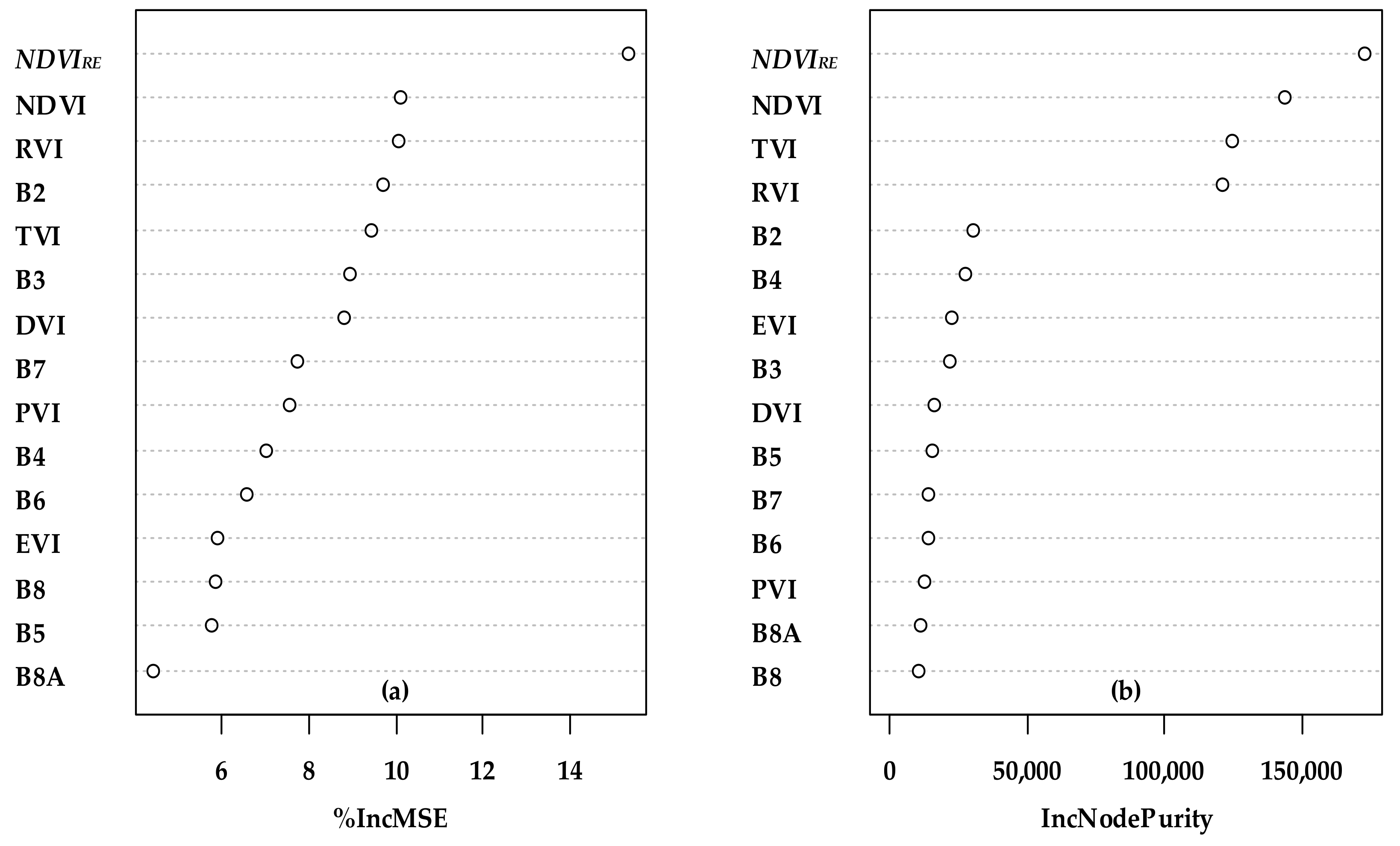
3.2. Major Variables Selection and the Importance Related to the FSV Data
3.3. Optimal Regression Model for the Three Models
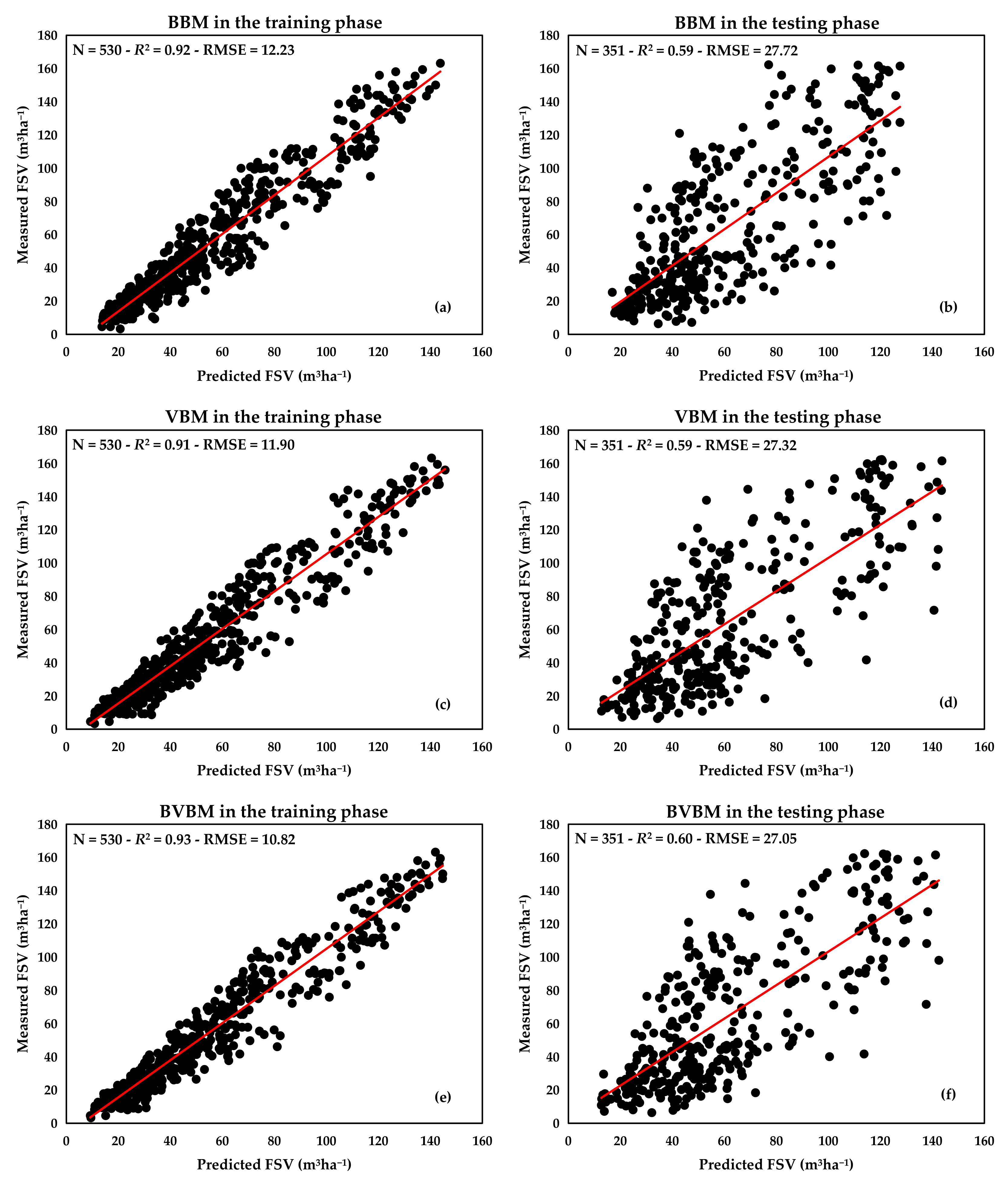
3.4. Comparison of the Three Models Predicting FSV
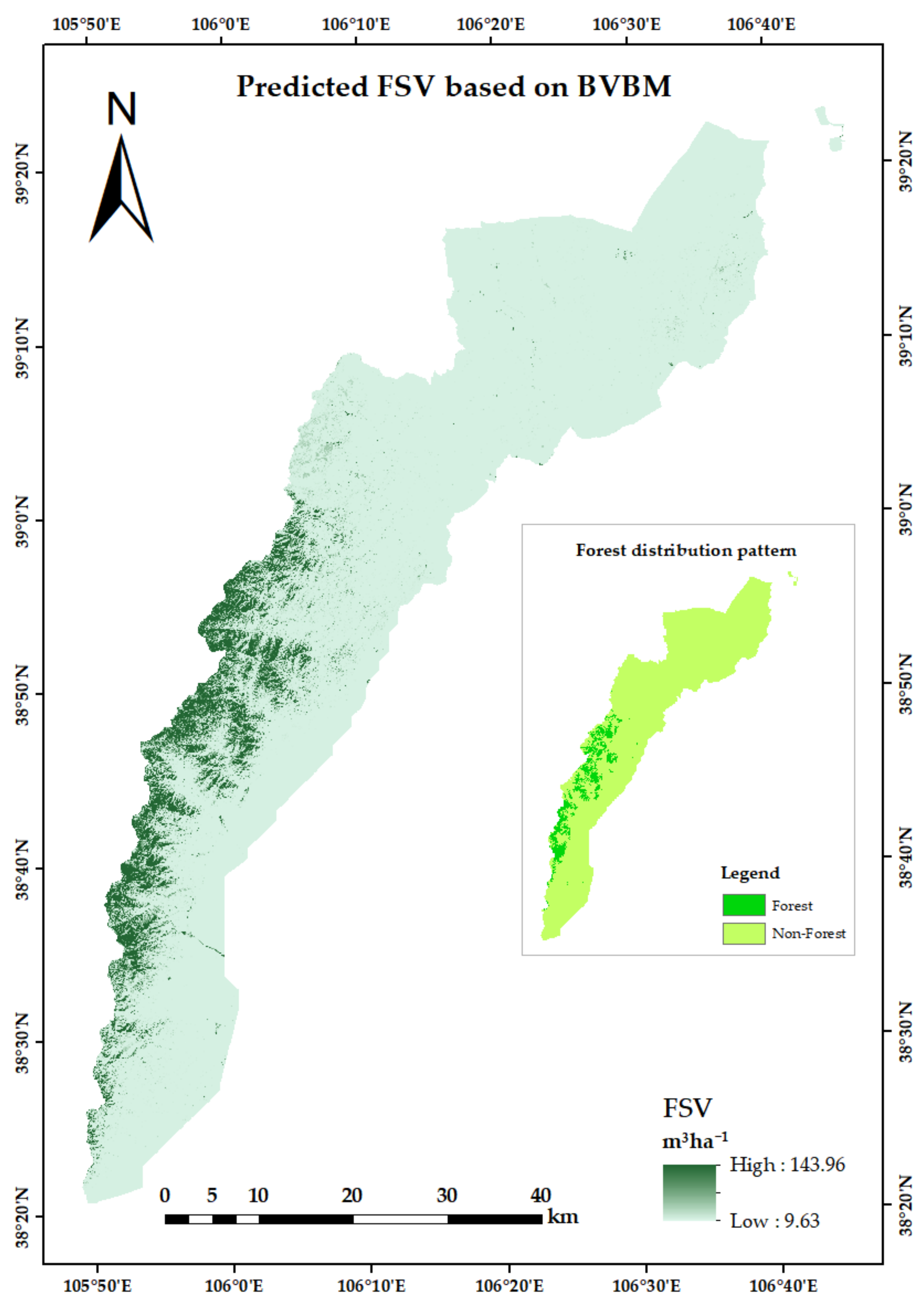
3.5. Mapping FSV Distribution of Helan Mountains
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, Y.; Xu, X.; Wu, F.; Sun, Z.; Xia, H.; Meng, Q.; Huang, W.; Zhou, H.; Gao, J.; Li, W.; et al. Estimating Forest Stock Volume in Hunan Province, China, by Integrating In Situ Plot Data, Sentinel-2 Images, and Linear and Machine Learning Regression Models. Remote Sens. 2020, 12, 186. [Google Scholar] [CrossRef]
- Fang, G.; Fang, L.; Yang, L.; Wu, D. Comparison of Variable Selection Methods among Dominant Tree Species in Different Regions on Forest Stock Volume Estimation. Forests 2022, 13, 787. [Google Scholar] [CrossRef]
- Yao, W.; Chi-Hui, G.; Xi-Jie, C.; Li-Qiong, J.; Xiao-Na, G.; Rui-Shan, C.; Mao-Sheng, Z.; Ze-Yu, C.; Hao-Dong, W. Carbon peak and carbon neutrality in China: Goals, implementation path and prospects. China Geol. 2021, 4, 720–746. [Google Scholar]
- Sun, Y.; Liu, S.; Li, L. Grey Correlation Analysis of Transportation Carbon Emissions under the Background of Carbon Peak and Carbon Neutrality. Energies 2022, 15, 3064. [Google Scholar] [CrossRef]
- Sun, L.; Cui, H.; Ge, Q. Will China achieve its 2060 carbon neutral commitment from the provincial perspective? Adv. Clim. Change Res. 2022, 13, 169–178. [Google Scholar] [CrossRef]
- Pugh, T.A.M.; Lindeskog, M.; Smith, B.; Poulter, B.; Arneth, A.; Haverd, V.; Calle, L. Role of forest regrowth in global carbon sink dynamics. Proc. Natl. Acad. Sci. USA 2019, 116, 4382–4387. [Google Scholar] [CrossRef] [PubMed]
- Astola, H.; Häme, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 imagery for forest variable prediction in boreal region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- Li, C.; Zhou, L.; Xu, W. Estimating Aboveground Biomass Using Sentinel-2 MSI Data and Ensemble Algorithms for Grassland in the Shengjin Lake Wetland, China. Remote Sens. 2021, 13, 1595. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Remote Sensing of Above-Ground Biomass. Remote Sens. 2017, 9, 935. [Google Scholar] [CrossRef]
- Lu, L.; Luo, J.; Xin, Y.; Duan, H.; Sun, Z.; Qiu, Y.; Xiao, Q. How can UAV contribute in satellite-based Phragmites australis aboveground biomass estimating? Int. J. Appl. Earth Obs. 2022, 114, 103024. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Niang Gadiaga, A.; Linard, C.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E.; Kalogirou, S. Geographical random forests: A spatial extension of the random forest algorithm to address spatial heterogeneity in remote sensing and population modelling. Geocarto Int. 2021, 36, 121–136. [Google Scholar] [CrossRef]
- Hu, Y.; Sun, Z. Assessing the Capacities of Different Remote Sensors in Estimating Forest Stock Volume Based on High Precision Sample Plot Positioning and Random Forest Method. Nat. Environ. Pollut. Technol. 2022, 21, 1113–1123. [Google Scholar] [CrossRef]
- Lister, A.J.; Andersen, H.; Frescino, T.; Gatziolis, D.; Healey, S.; Heath, L.S.; Liknes, G.C.; McRoberts, R.; Moisen, G.G.; Nelson, M.; et al. Use of Remote Sensing Data to Improve the Efficiency of National Forest Inventories: A Case Study from the United States National Forest Inventory. Forests 2020, 11, 1364. [Google Scholar] [CrossRef]
- Chave, J.; Davies, S.J.; Phillips, O.L. Ground Data are Essential for Biomass Remote Sensing Missions. Surv. Geophys. 2019, 40, 863–880. [Google Scholar] [CrossRef]
- Ou, G.; Li, C.; Lv, Y.; Wei, A.; Xiong, H.; Xu, H.; Wang, G. Improving Aboveground Biomass Estimation of Pinus densata Forests in Yunnan Using Landsat 8 Imagery by Incorporating Age Dummy Variable and Method Comparison. Remote Sens. 2019, 11, 738. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining Spectral Reflectance Saturation in Landsat Imagery and Corresponding Solutions to Improve Forest Aboveground Biomass Estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Moran, E.; Batistella, M.; Zhang, M.; Vaglio Laurin, G.; Saah, D. Aboveground Forest Biomass Estimation with Landsat and LiDAR Data and Uncertainty Analysis of the Estimates. Int. J. For. Res. 2012, 2012, 1–16. [Google Scholar] [CrossRef]
- Tilly, N.; Aasen, H.; Bareth, G. Fusion of Plant Height and Vegetation Indices for the Estimation of Barley Biomass. Remote Sens. 2015, 7, 11449–11480. [Google Scholar] [CrossRef]
- Kross, A.; McNairn, H.; Lapen, D.; Sunohara, M.; Champagne, C. Assessment of RapidEye vegetation indices for estimation of leaf area index and biomass in corn and soybean crops. Int. J. Appl. Earth Obs. 2015, 34, 235–248. [Google Scholar] [CrossRef]
- Li, C.; Chimimba, E.G.; Kambombe, O.; Brown, L.A.; Chibarabada, T.P.; Lu, Y.; Anghileri, D.; Ngongondo, C.; Sheffield, J.; Dash, J. Maize Yield Estimation in Intercropped Smallholder Fields Using Satellite Data in Southern Malawi. Remote Sens. 2022, 14, 2458. [Google Scholar] [CrossRef]
- Luo, W.; Kim, H.S.; Zhao, X.; Ryu, D.; Jung, I.; Cho, H.; Harris, N.; Ghosh, S.; Zhang, C.; Liang, J. New forest biomass carbon stock estimates in Northeast Asia based on multisource data. Glob. Chang. Biol. 2020, 26, 7045–7066. [Google Scholar] [CrossRef]
- Shen, X.; Cao, L.; Yang, B.; Xu, Z.; Wang, G. Estimation of Forest Structural Attributes Using Spectral Indices and Point Clouds from UAS-Based Multispectral and RGB Imageries. Remote Sens. 2019, 11, 800. [Google Scholar] [CrossRef]
- Xiao, C.; Li, P.; Feng, Z.; Liu, Y.; Zhang, X. Sentinel-2 red-edge spectral indices (RESI) suitability for mapping rubber boom in Luang Namtha Province, northern Lao PDR. Int. J. Appl. Earth Obs. 2020, 93, 102176. [Google Scholar] [CrossRef]
- Roy, D.; Li, Z.; Zhang, H. Adjustment of Sentinel-2 Multi-Spectral Instrument (MSI) Red-Edge Band Reflectance to Nadir BRDF Adjusted Reflectance (NBAR) and Quantification of Red-Edge Band BRDF Effects. Remote Sens. 2017, 9, 1325. [Google Scholar] [CrossRef]
- Bramich, J.; Bolch, C.J.S.; Fischer, A. Improved red-edge chlorophyll-a detection for Sentinel 2. Ecol. Indic. 2021, 120, 106876. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Alonso, L.; Moreno, J. Evaluation of Sentinel-2 Red-Edge Bands for Empirical Estimation of Green LAI and Chlorophyll Content. Sensors 2011, 11, 7063–7081. [Google Scholar] [CrossRef]
- Liu, J.; Fan, J.; Yang, C.; Xu, F.; Zhang, X. Novel vegetation indices for estimating photosynthetic and non-photosynthetic fractional vegetation cover from Sentinel data. Int. J. Appl. Earth Obs. 2022, 109, 102793. [Google Scholar] [CrossRef]
- Bilal, M.; Nichol, J.E. Evaluation of the NDVI-Based Pixel Selection Criteria of the MODIS C6 Dark Target and Deep Blue Combined Aerosol Product. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2017, 10, 3448–3453. [Google Scholar] [CrossRef]
- Asgarian, A.; Amiri, B.J.; Sakieh, Y. Assessing the effect of green cover spatial patterns on urban land surface temperature using landscape metrics approach. Urban Ecosyst. 2015, 18, 209–222. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Noor, K.; Herbert, K. Modelling Reservoir Chlorophyll-a, TSS, and Turbidity Using Sentinel-2A MSI and Landsat-8 OLI Satellite Sensors with Empirical Multivariate Regression. J. Sens. 2020, 2020, 1–21. [Google Scholar] [CrossRef]
- Warren, M.A.; Simis, S.G.H.; Martinez-Vicente, V.; Poser, K.; Bresciani, M.; Alikas, K.; Spyrakos, E.; Giardino, C.; Ansper, A. Assessment of atmospheric correction algorithms for the Sentinel-2A MultiSpectral Imager over coastal and inland waters. Remote Sens. Environ. 2019, 225, 267–289. [Google Scholar] [CrossRef]
- Huang, H.; Roy, D.; Boschetti, L.; Zhang, H.; Yan, L.; Kumar, S.; Gomez-Dans, J.; Li, J. Separability Analysis of Sentinel-2A Multi-Spectral Instrument (MSI) Data for Burned Area Discrimination. Remote Sens. 2016, 8, 873. [Google Scholar] [CrossRef]
- Jin, Y.; Yang, X.; Qiu, J.; Li, J.; Gao, T.; Wu, Q.; Zhao, F.; Ma, H.; Yu, H.; Xu, B. Remote Sensing-Based Biomass Estimation and Its Spatio-Temporal Variations in Temperate Grassland, Northern China. Remote Sens. 2014, 6, 1496–1513. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 1–17. [Google Scholar] [CrossRef]
- Liu, Z.; Ye, Z.; Xu, X.; Lin, H.; Zhang, T.; Long, J. Mapping Forest Stock Volume Based on Growth Characteristics of Crown Using Multi-Temporal Landsat 8 OLI and ZY-3 Stereo Images in Planted Eucalyptus Forest. Remote Sens. 2022, 14, 5082. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop J. 2016, 4, 212–219. [Google Scholar] [CrossRef]
- Torre-Tojal, L.; Bastarrika, A.; Boyano, A.; Lopez-Guede, J.M.; Graña, M. Above-ground biomass estimation from LiDAR data using random forest algorithms. J. Comput. Sci. 2022, 58, 101517. [Google Scholar] [CrossRef]
- Li, X.; Ye, Z.; Long, J.; Zheng, H.; Lin, H. Inversion of Coniferous Forest Stock Volume Based on Backscatter and InSAR Coherence Factors of Sentinel-1 Hyper-Temporal Images and Spectral Variables of Landsat 8 OLI. Remote Sens. 2022, 14, 2754. [Google Scholar] [CrossRef]
- Glushkova, M.; Zhiyanski, M.; Nedkov, S.; Yaneva, R.; Stoeva, L. Ecosystem services from mountain forest ecosystems: Conceptual framework, approach and challenges. Silva Balc. 2020, 21, 47–68. [Google Scholar] [CrossRef]
- Zhang, L.; Shao, Z.; Liu, J.; Cheng, Q. Deep Learning Based Retrieval of Forest Aboveground Biomass from Combined LiDAR and Landsat 8 Data. Remote Sens. 2019, 11, 1459. [Google Scholar] [CrossRef]
- Ayhan, B.; Kwan, C.; Budavari, B.; Kwan, L.; Lu, Y.; Perez, D.; Li, J.; Skarlatos, D.; Vlachos, M. Vegetation Detection Using Deep Learning and Conventional Methods. Remote Sens. 2020, 12, 2502. [Google Scholar] [CrossRef]
- Bhatnagar, S.; Gill, L.; Ghosh, B. Drone Image Segmentation Using Machine and Deep Learning for Mapping Raised Bog Vegetation Communities. Remote Sens. 2020, 12, 2602. [Google Scholar] [CrossRef]
- Liu, M.; Fu, B.; Xie, S.; He, H.; Lan, F.; Li, Y.; Lou, P.; Fan, D. Comparison of multi-source satellite images for classifying marsh vegetation using DeepLabV3 Plus deep learning algorithm. Ecol. Indic. 2021, 125, 107562. [Google Scholar] [CrossRef]
- Lees, T.; Tseng, G.; Atzberger, C.; Reece, S.; Dadson, S. Deep Learning for Vegetation Health Forecasting: A Case Study in Kenya. Remote Sens. 2022, 14, 698. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, W.; Yao, Y.; Wang, W. Estimating Aboveground Carbon Stock at the Scale of Individual Trees in Subtropical Forests Using UAV LiDAR and Hyperspectral Data. Remote Sens. 2021, 13, 4969. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, W.; Yao, Y.; Wang, W. Individual tree segmentation and tree species classification in subtropical broadleaf forests using UAV-based LiDAR, hyperspectral, and ultrahigh-resolution RGB data. Remote Sens. Environ. 2022, 280, 113143. [Google Scholar] [CrossRef]
- Dashti, H.; Poley, A.; Glenn, N.F.; Ilangakoon, N.; Spaete, L.; Roberts, D.; Enterkine, J.; Flores, A.N.; Ustin, S.L.; Mitchell, J.J. Regional Scale Dryland Vegetation Classification with an Integrated Lidar-Hyperspectral Approach. Remote Sens. 2019, 11, 2141. [Google Scholar] [CrossRef]
- Zhu, W.; Sun, Z.; Peng, J.; Huang, Y.; Li, J.; Zhang, J.; Yang, B.; Liao, X. Estimating Maize Above-Ground Biomass Using 3D Point Clouds of Multi-Source Unmanned Aerial Vehicle Data at Multi-Spatial Scales. Remote Sens. 2019, 11, 2678. [Google Scholar] [CrossRef]
- Picos, J.; Bastos, G.; Míguez, D.; Alonso, L.; Armesto, J. Individual Tree Detection in a Eucalyptus Plantation Using Unmanned Aerial Vehicle (UAV)-LiDAR. Remote Sens. 2020, 12, 885. [Google Scholar] [CrossRef]
- Santos, A.A.D.; Marcato Junior, J.; Araújo, M.S.; Di Martini, D.R.; Tetila, E.C.; Siqueira, H.L.; Aoki, C.; Eltner, A.; Matsubara, E.T.; Pistori, H.; et al. Assessment of CNN-Based Methods for Individual Tree Detection on Images Captured by RGB Cameras Attached to UAVs. Sensors 2019, 19, 3595. [Google Scholar] [CrossRef]
- Sankey, T.T.; McVay, J.; Swetnam, T.L.; McClaran, M.P.; Heilman, P.; Nichols, M.; Pettorelli, N.; Horning, N.; Pettorelli, N.; Horning, N. UAV hyperspectral and lidar data and their fusion for arid and semi-arid land vegetation monitoring. Remote Sens. Ecol. Conserv. 2018, 4, 20–33. [Google Scholar] [CrossRef]

| Statistical Category | Training Data (m3ha−1) | Testing Data (m3ha−1) |
|---|---|---|
| Minimum | 3.30 | 6.40 |
| Maximum | 163.20 | 162.30 |
| Median | 45.15 | 48.80 |
| Mean | 56.66 | 63.84 |
| Number of sample plots | 530 | 351 |
| Sentinel-2 Bands | Description | Central Wavelength (nm) | Bandwidth (nm) | Resolution (m) | Resampling Resolution (m) |
|---|---|---|---|---|---|
| B2 | Blue | 492.4 | 66 | 10 | 30 |
| B3 | Green | 559.8 | 36 | 10 | 30 |
| B4 | Red | 664.6 | 31 | 10 | 30 |
| B5 | Red Edge 1 | 704.1 | 15 | 20 | 30 |
| B6 | Red Edge 2 | 740.5 | 15 | 20 | 30 |
| B7 | Red Edge 3 | 782.8 | 20 | 20 | 30 |
| B8 | NIR | 832.8 | 106 | 10 | 30 |
| B8A | Narrow NIR | 864.7 | 21 | 20 | 30 |
| Original Vegetation Indices | Formulas | References |
|---|---|---|
| NDVI | [20] | |
| DVI | [33] | |
| RVI | [34] | |
| PVI | [34] | |
| TVI | [34] | |
| EVI | [20] |
| RF Models | Variables Selected |
|---|---|
| BBM | B4, B8, B2 |
| VBM | NDVIRE, TVI, EVI, DVI |
| BVBM | NDVIRE, NDVI, EVI, DVI, B2 |
| RF Models | mtry | ntree | Mean of Squared Residuals | % Var Explained |
|---|---|---|---|---|
| BBM | 1 | 468 | 636.68 | 56.77 |
| VBM | 1 | 494 | 612.33 | 58.42 |
| BBVM | 7 | 188 | 609.55 | 58.61 |
| Statistical Category | Training Phase (m3ha−1) | Testing Phase (m3ha−1) | ||||
|---|---|---|---|---|---|---|
| BBM | VBM | BVBM | BBM | VBM | BVBM | |
| Minimum | 13.69 | 9.27 | 9.21 | 16.88 | 12.75 | 12.66 |
| Maximum | 143.83 | 145.66 | 144.76 | 127.55 | 143.64 | 142.48 |
| Median | 48.17 | 47.75 | 47.81 | 50.52 | 52.38 | 50.51 |
| Mean | 56.71 | 56.62 | 56.88 | 60.50 | 60.68 | 60.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, T.; Hu, Y.; Wang, J.; Beckline, M.; Pang, D.; Chen, L.; Ni, X.; Li, X. A Novel Vegetation Index Approach Using Sentinel-2 Data and Random Forest Algorithm for Estimating Forest Stock Volume in the Helan Mountains, Ningxia, China. Remote Sens. 2023, 15, 1853. https://doi.org/10.3390/rs15071853
Ma T, Hu Y, Wang J, Beckline M, Pang D, Chen L, Ni X, Li X. A Novel Vegetation Index Approach Using Sentinel-2 Data and Random Forest Algorithm for Estimating Forest Stock Volume in the Helan Mountains, Ningxia, China. Remote Sensing. 2023; 15(7):1853. https://doi.org/10.3390/rs15071853
Chicago/Turabian StyleMa, Taiyong, Yang Hu, Jie Wang, Mukete Beckline, Danbo Pang, Lin Chen, Xilu Ni, and Xuebin Li. 2023. "A Novel Vegetation Index Approach Using Sentinel-2 Data and Random Forest Algorithm for Estimating Forest Stock Volume in the Helan Mountains, Ningxia, China" Remote Sensing 15, no. 7: 1853. https://doi.org/10.3390/rs15071853
APA StyleMa, T., Hu, Y., Wang, J., Beckline, M., Pang, D., Chen, L., Ni, X., & Li, X. (2023). A Novel Vegetation Index Approach Using Sentinel-2 Data and Random Forest Algorithm for Estimating Forest Stock Volume in the Helan Mountains, Ningxia, China. Remote Sensing, 15(7), 1853. https://doi.org/10.3390/rs15071853