Optimizing Wheat Yield Prediction Integrating Data from Sentinel-1 and Sentinel-2 with CatBoost Algorithm
Abstract
1. Introduction
2. Materials and Methods
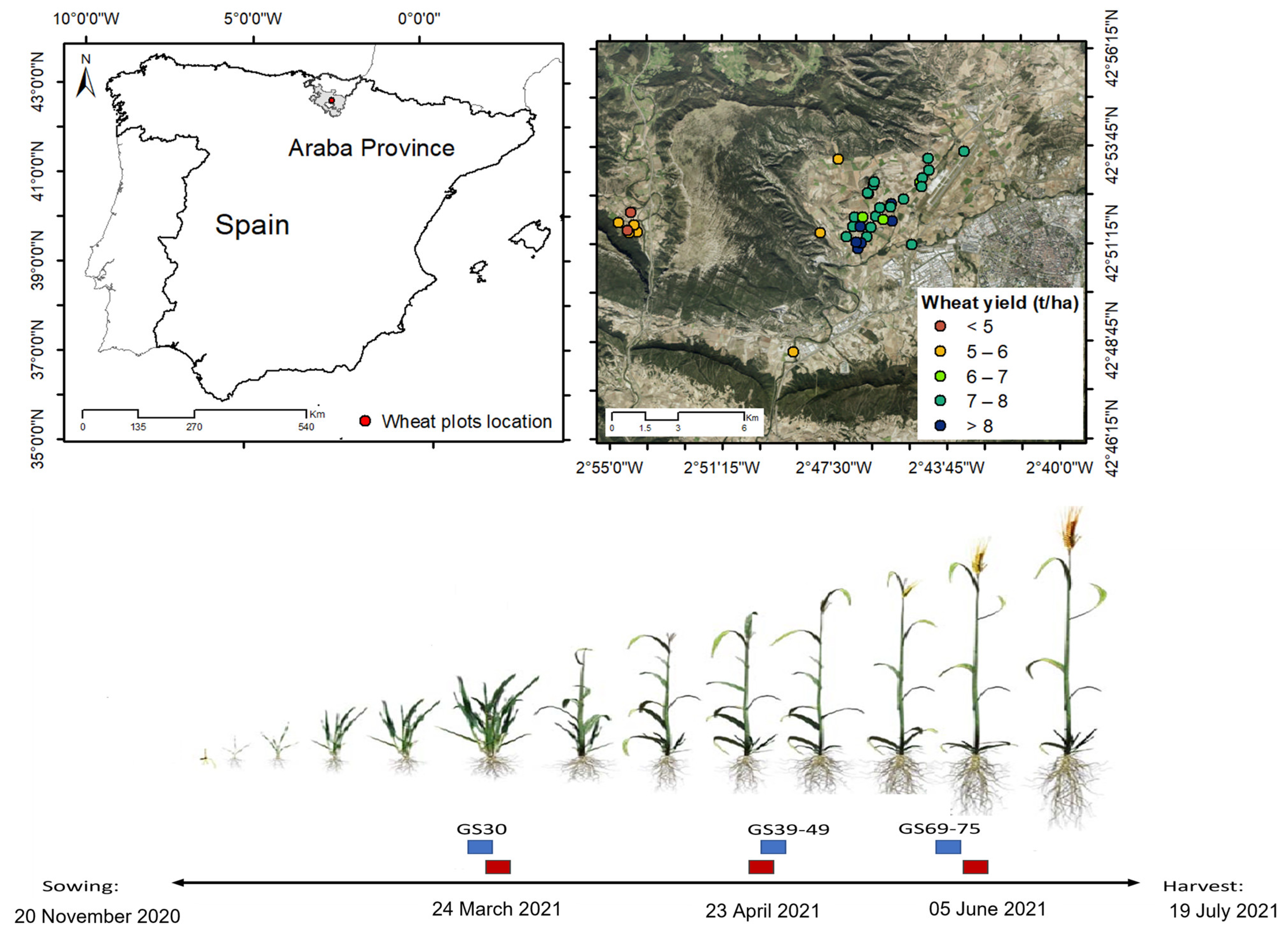
2.1. Study Area
2.2. Sentinel-2 Data and Derived Vegetation Indices
2.3. Wheat Grain Yield Acquisition, Preprocessing, and Connection with Sentinel Data
2.4. Sentinel-1 Data and Retro Dispersion Calculation
2.5. Machine Learning Algorithms
2.6. Accuracy Assessment
2.6.1. Root Mean Squared Error (RMSE)
2.6.2. Relative RMSE (rRMSE)
2.6.3. Coefficient of Determination (R2)
2.6.4. Percentage of Mean Absolute Error (%MAE)
2.6.5. Accuracy
2.6.6. Kappa Index (KI)
3. Results
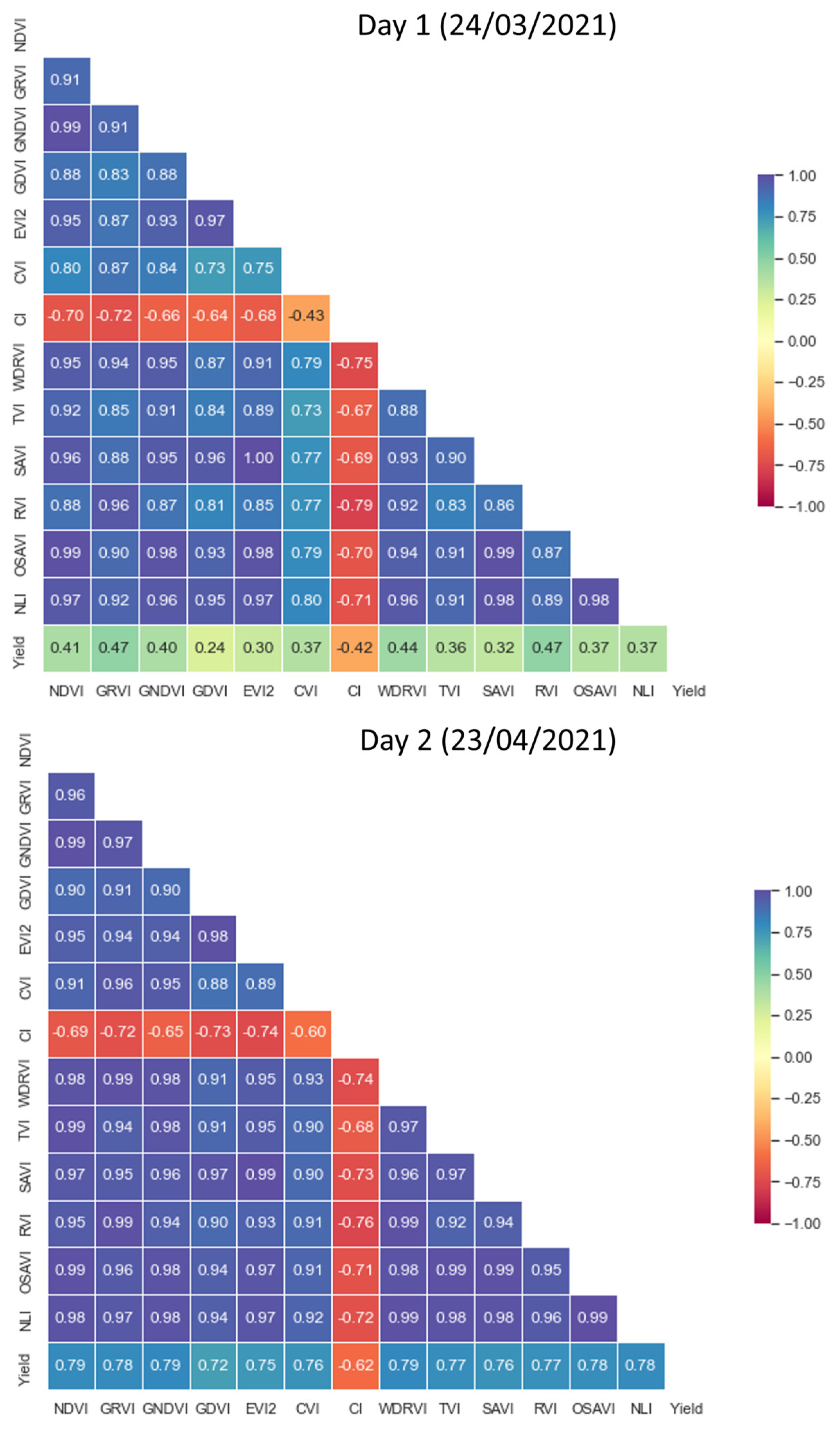
3.1. Relationship between Vegetation Indices and Wheat Yield Using Sentinel-2 Imagery
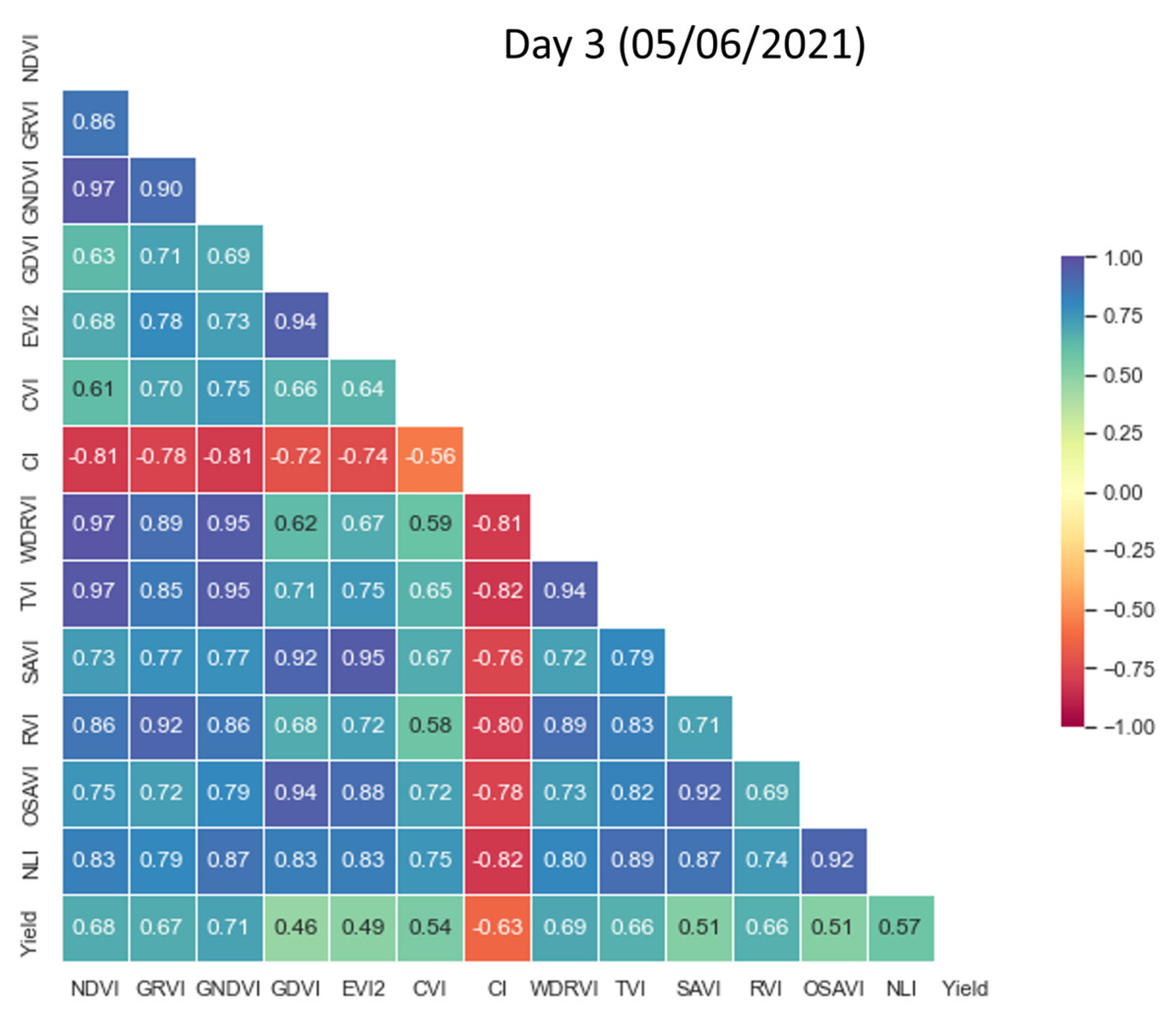
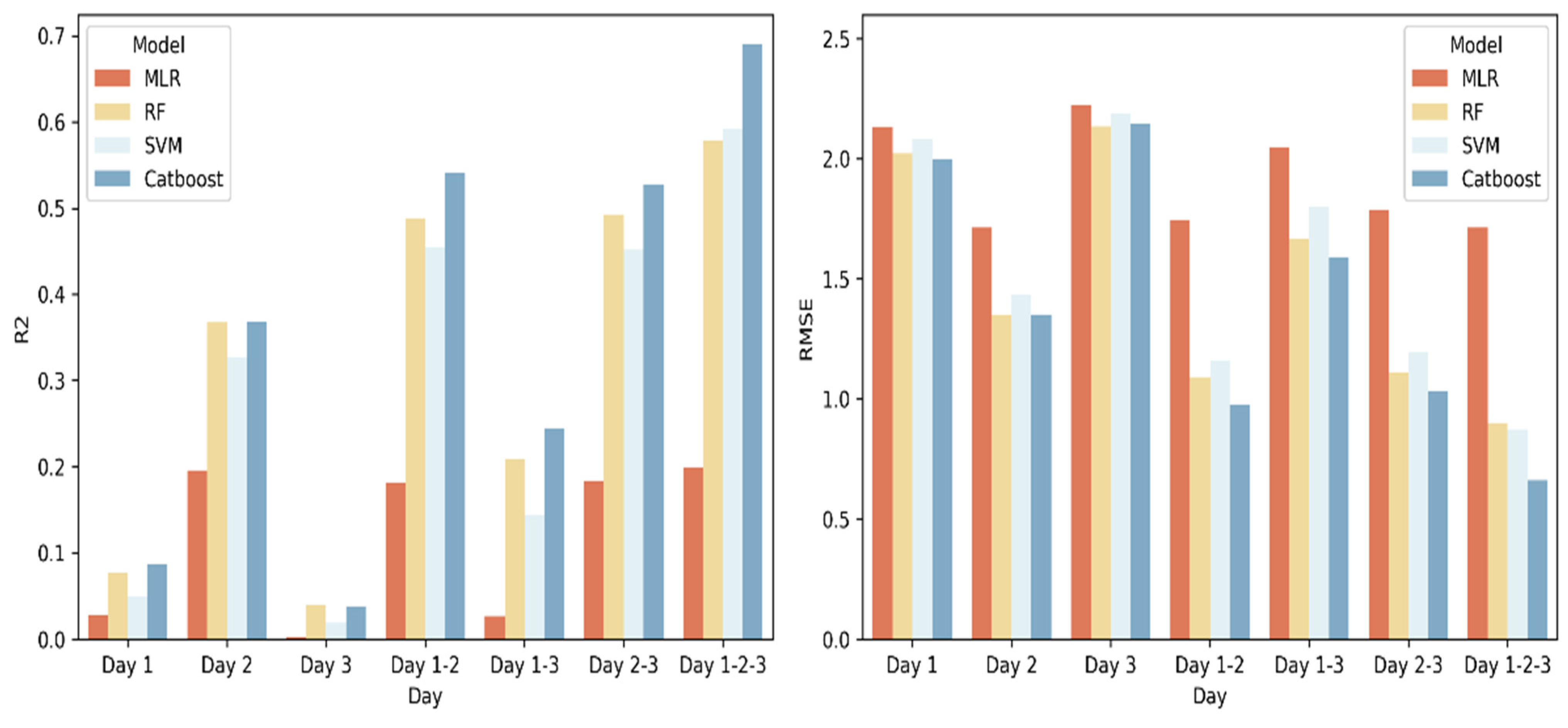
3.2. Exploring the Impact of Date Selection on Wheat Yield Prediction Using VIs Derived from Sentinel-2
3.3. Exploring the Impact of Date Selection on Wheat Yield Prediction Using Backscatter Information Derived from Sentinel-1
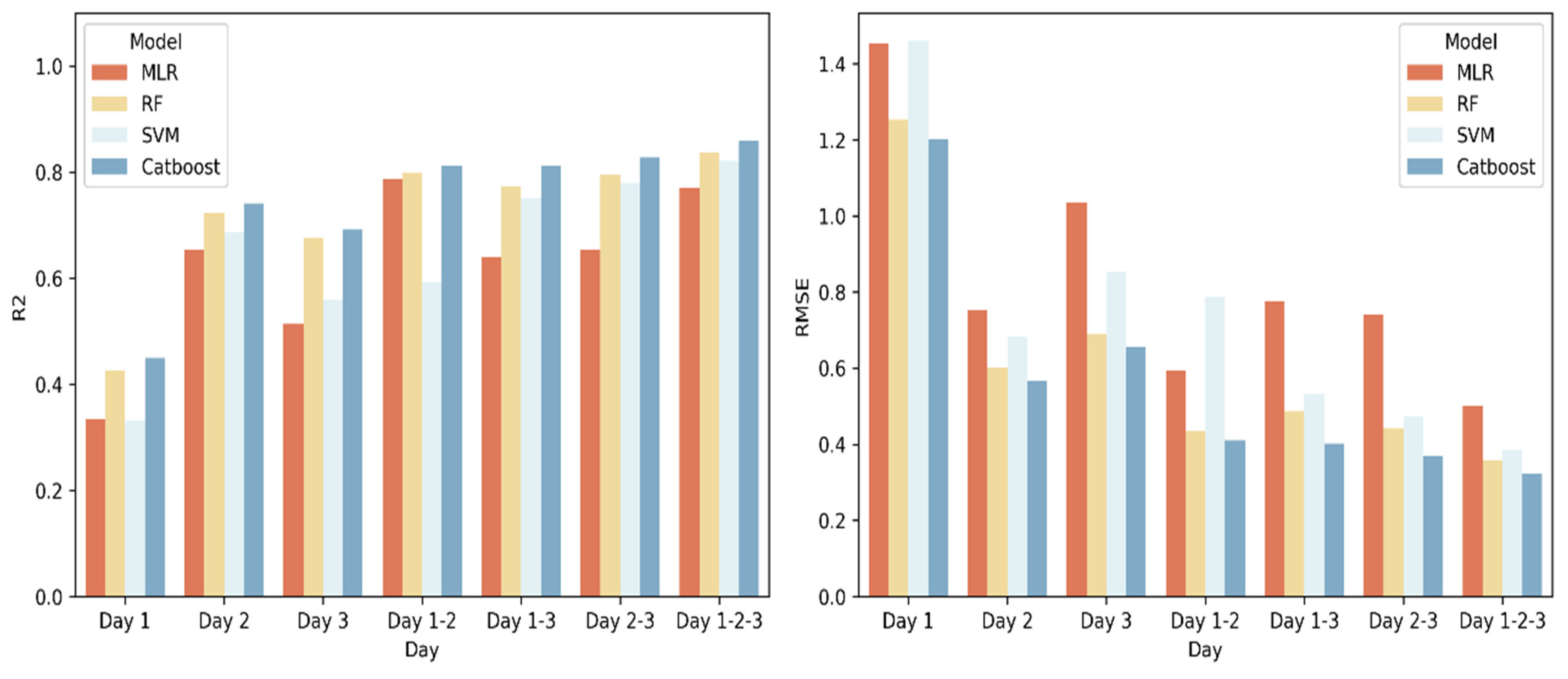
3.4. Comparison of Machine Learning Algorithms for Estimating Wheat Yield Using Multisource Data
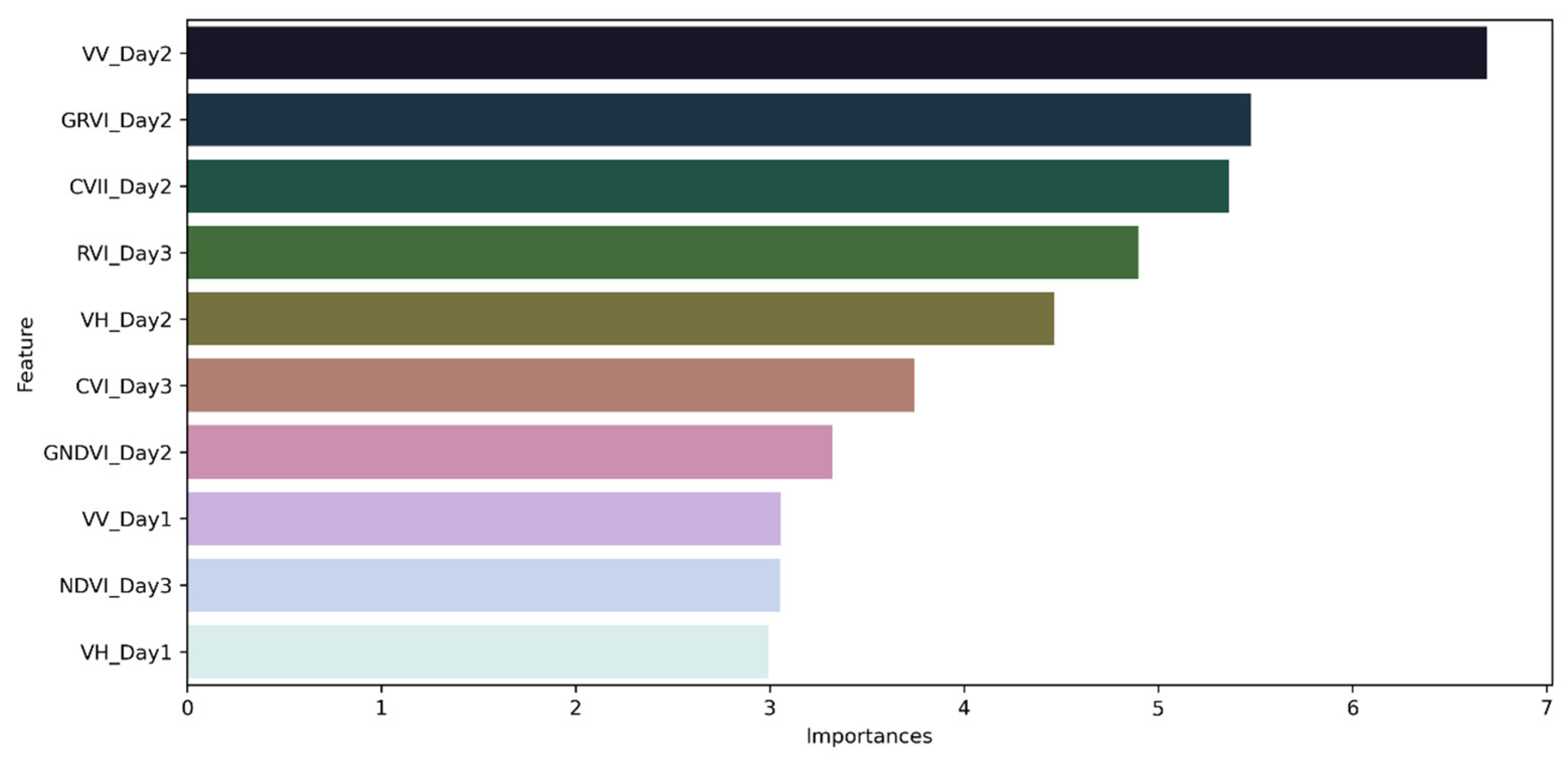
3.5. Contribution of the Variables to the Defintive Algorithm
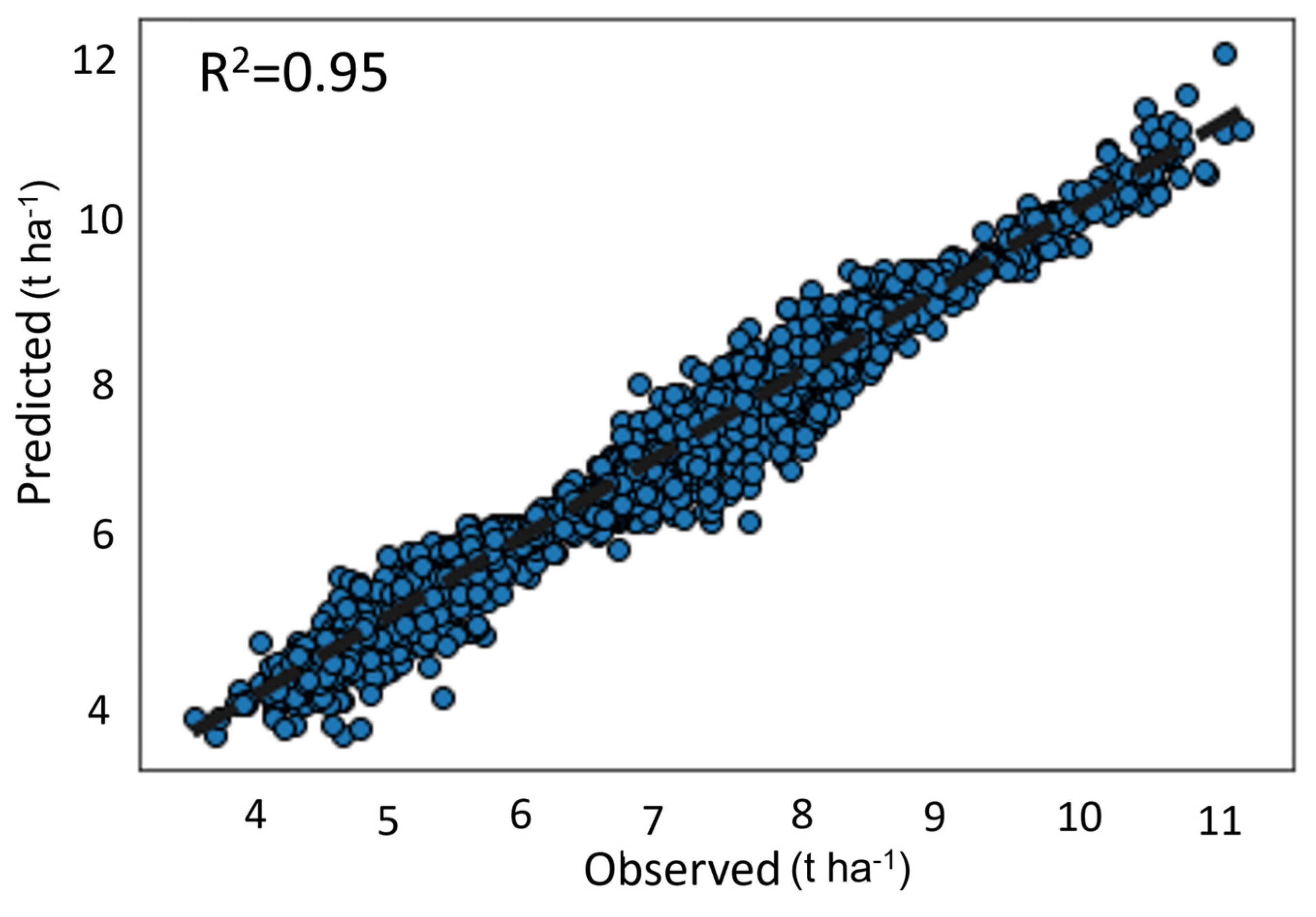
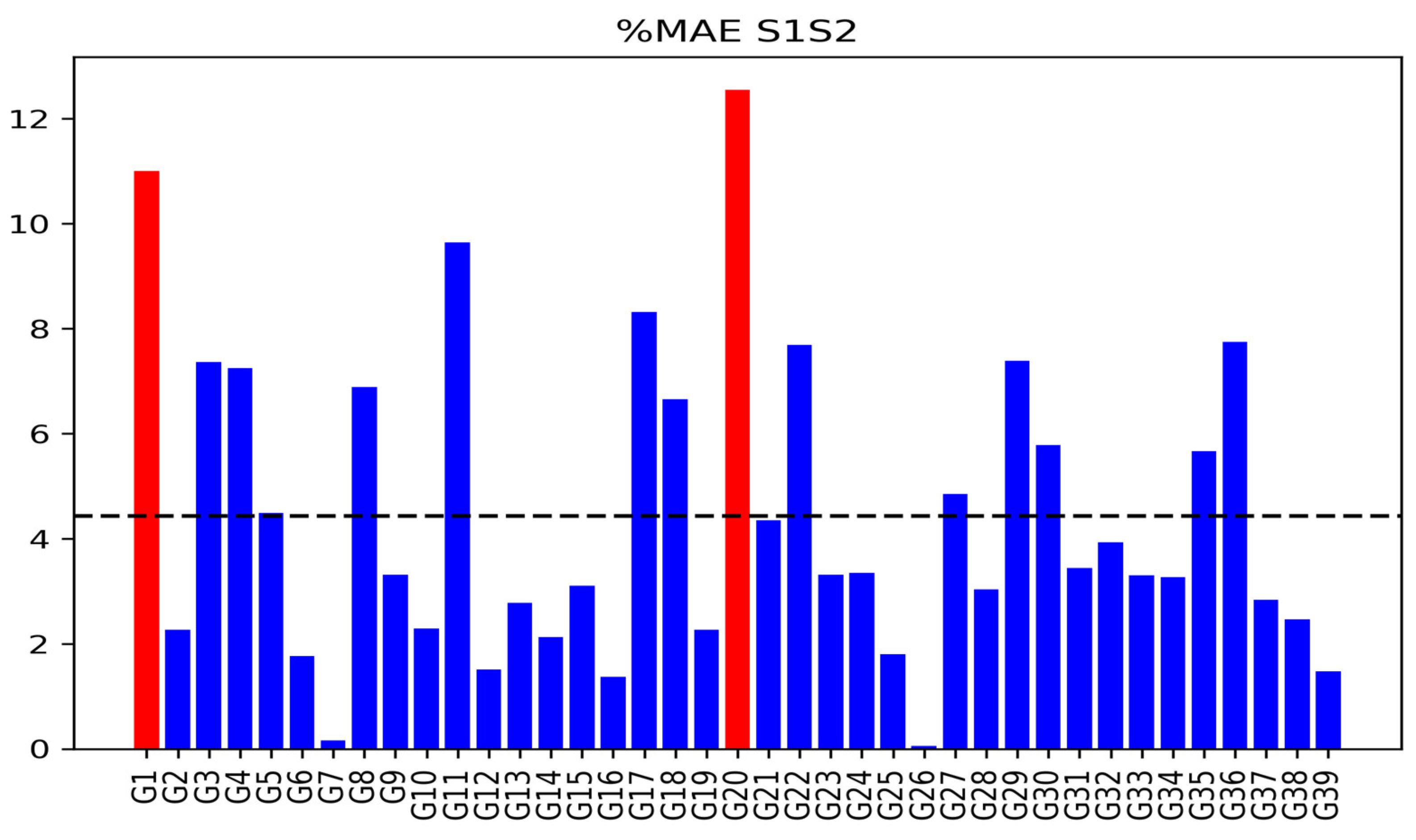
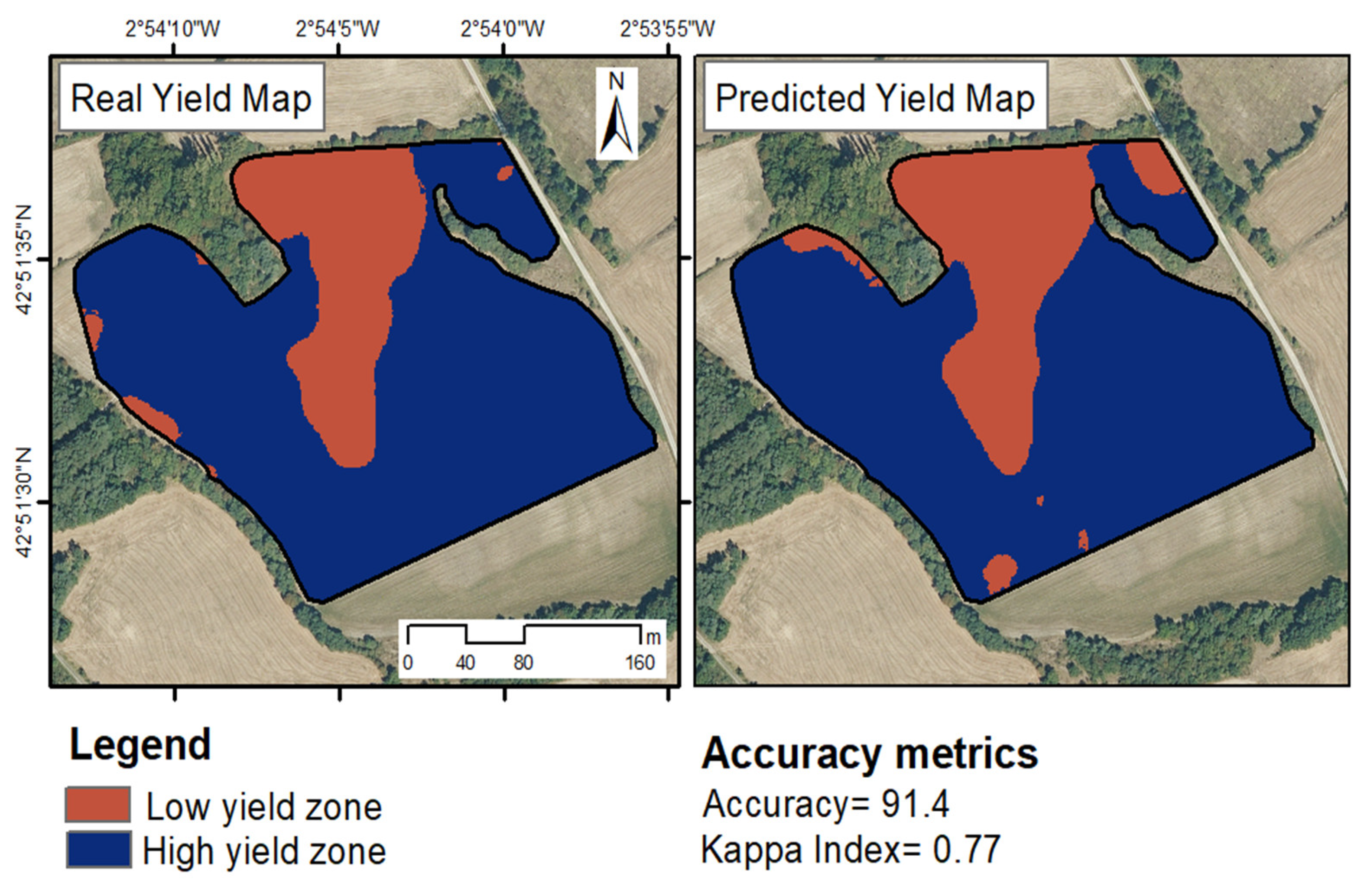
3.6. The Ability of CatBoost to Predict Yield of Entire Plots Using Data from Other Plots
4. Discussion
4.1. Inclusion of Sentinel-1 and Sentinel-2 in the Yield Estimation Model
4.2. Reasons Why the Combination of Information from Sentienel-1 and Sentinel-2 Enhances the Yield Estimation Model
4.3. Algorithm Analysis
4.4. CatBoost Algorithm as a Tool for Processing Heterogeneous Data in Precision Agriculture
4.5. Potential of S1 Backscatter and VIs for Precise Yield Mapping in Rainfed Areas Using the CatBoost Algorithm
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giller, K.E.; Delaune, T.; Silva, J.V.; Descheemaeker, K.; van de Ven, G.; Schut, A.G.; van Wijk, M.; Hammond, J.; Hochman, Z.; Taulya, G.; et al. The future of farming: Who will produce our food? Food Secur. 2021, 13, 1073–1099. [Google Scholar] [CrossRef]
- Pingali, P.L. Green Revolution: Impacts, limits, and the path ahead. Proc. Natl. Acad. Sci. USA 2012, 109, 12302–12308. [Google Scholar] [CrossRef]
- Wik, M.; Pingali, P.; Broca, S. Global Agricultural Performance: Past Trends and Future Prospects; World Bank: Washington, DC, USA, 2008. [Google Scholar]
- Hazell, P. Handbook of Agricultural Economics; Pingali, P., Evenson, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 3469–3530. [Google Scholar]
- Randall, G.; Goss, M. Nitrate Losses to SurfaceWater through Subsurface, Tile Drainage. In Nitrogen in the Environment: Sources, Problems, and Management; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Snyder, C.; Bruulsema, T.; Jensen, T.; Fixen, P. Review of greenhouse gas emissions from crop production systems and fertilizer management effects. Agric. Ecosyst. Environ. 2009, 133, 247–266. [Google Scholar] [CrossRef]
- Ziliani, M.G.; Altaf, M.U.; Aragon, B.; Houborg, R.; Franz, T.E.; Lu, Y.; Sheffield, J.; Hoteit, I.; McCabe, M.F. Early season prediction of within-field crop yield variability by assimilating CubeSat data into a crop model. Agric. For. Meteorol. 2022, 313, 108736. [Google Scholar] [CrossRef]
- Zambon, I.; Cecchini, M.; Egidi, G.; Saporito, M.G.; Colantoni, A. Revolution 4.0: Industry vs. Agriculture in a Future Development for SMEs. Processes 2019, 7, 36. [Google Scholar] [CrossRef]
- Mumtaz, R.; Baig, S.; Fatima, I. Analysis of meteorological variations on wheat yield and its estimation using remotely sensed data. A case study of selected districts of Punjab Province, Pakistan (2001–2014). Ital. J. Agron. 2017, 12, 897. [Google Scholar] [CrossRef]
- Sandonís-Pozo, L.; Llorens, J.; Escolà, A.; Arnó, J.; Pascual, M.; Martínez-Casasnovas, J.A. Satellite multispectral indices to estimate canopy parameters and within-field management zones in super-intensive almond orchards. Precis. Agric. 2022, 23, 2040–2062. [Google Scholar] [CrossRef]
- Uribeetxebarria, A.; Arnó, J.; Escolà, A.; Martínez-Casasnovas, J.A. Apparent electrical conductivity and multivariate analysis of soil properties to assess soil constraints in orchards affected by previous parcelling. Geoderma 2018, 319, 185–193. [Google Scholar] [CrossRef]
- Del-Moral-Martínez, I.; Rosell-Polo, J.R.; Company, J.; Sanz, R.; Escolà, A.; Masip, J.; Martínez-Casasnovas, J.A.; Arnó, J. Mapping Vineyard Leaf Area Using Mobile Terrestrial Laser Scanners: Should Rows be Scanned On-the-Go or Discontinuously Sampled? Sensors 2016, 16, 119. [Google Scholar] [CrossRef]
- Daberkow, S.G.; McBride, W.D. Farm and Operator Characteristics Affecting the Awareness and Adoption of Precision Agriculture Technologies in the US. Precis. Agric. 2003, 4, 163–177. [Google Scholar] [CrossRef]
- Chen, W.; Bell, R.W.; Brennan, R.F.; Bowden, J.W.; Dobermann, A.; Rengel, Z.; Porter, W. Key crop nutrient management issues in the Western Australia grains industry: A review. Soil Res. 2009, 47, 1–18. [Google Scholar] [CrossRef]
- Barnes, A.; Soto, I.; Eory, V.; Beck, B.; Balafoutis, A.; Sánchez, B.; Vangeyte, J.; Fountas, S.; van der Wal, T.; Gómez-Barbero, M. Exploring the adoption of precision agricultural technologies: A cross regional study of EU farmers. Land Use Policy 2019, 80, 163–174. [Google Scholar] [CrossRef]
- Ingram, J. Agronomist–farmer knowledge encounters: An analysis of knowledge exchange in the context of best management practices in England. Agric. Hum. Values 2008, 25, 405–418. [Google Scholar] [CrossRef]
- Segarra, J.; Buchaillot, M.L.; Araus, J.L.; Kefauver, S.C. Remote Sensing for Precision Agriculture: Sentinel-2 Improved Features and Applications. Agronomy 2020, 10, 641. [Google Scholar] [CrossRef]
- Ghosh, P.; Mandal, D.; Bhattacharya, A.; Nanda, M.K.; Bera, S. Assessing crop monitoring potential of sentinel-2 in a spatio-temporal scale. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-5, 227–231. [Google Scholar] [CrossRef]
- Yi, Z.; Jia, L.; Chen, Q. Crop Classification Using Multi-Temporal Sentinel-2 Data in the Shiyang River Basin of China. Remote Sens. 2020, 12, 4052. [Google Scholar] [CrossRef]
- Sadeghi, M.; Babaeian, E.; Tuller, M.; Jones, S.B. The optical trapezoid model: A novel approach to remote sensing of soil moisture applied to Sentinel-2 and Landsat-8 observations. Remote Sens. Environ. 2017, 198, 52–68. [Google Scholar] [CrossRef]
- Vallentin, C.; Harfenmeister, K.; Itzerott, S.; Kleinschmit, B.; Conrad, C.; Spengler, D. Suitability of satellite remote sensing data for yield estimation in northeast Germany. Precis. Agric. 2022, 23, 52–82. [Google Scholar] [CrossRef]
- Barnett, T.; Thompson, D. Large-area relation of landsat MSS and NOAA-6 AVHRR spectral data to wheat yields. Remote Sens. Environ. 1983, 4, 277–290. [Google Scholar] [CrossRef]
- Maselli, F.; Conese, C.; Petkov, L.; Gilabert, M.-A. Use of NOAA-AVHRR NDVI data for environmental monitoring and crop forecasting in the Sahel. Preliminary results. Int. J. Remote Sens. 1992, 13, 2743–2749. [Google Scholar] [CrossRef]
- Hamar, D.; Ferencz, C.; Lichtenberger, J.; Tarcsai, G.; Ferencz-Árkos, I. Yield estimation for corn and wheat in the Hungarian Great Plain using Landsat MSS data. Int. J. Remote Sens. 1996, 17, 1689–1699. [Google Scholar] [CrossRef]
- Bebie, M.; Cavalaris, C.; Kyparissis, A. Assessing Durum Wheat Yield through Sentinel-2 Imagery: A Machine Learning Approach. Remote Sens. 2022, 14, 3880. [Google Scholar] [CrossRef]
- Shen, J.; Evans, F.H. The Potential of Landsat NDVI Sequences to Explain Wheat Yield Variation in Fields in Western Australia. Remote Sens. 2021, 13, 2202. [Google Scholar] [CrossRef]
- Trombetta, A.; Iacobellis, V.; Tarantino, E.; Gentile, F. Calibration of the AquaCrop model for winter wheat using MODIS LAI images. Agric. Water Manag. 2016, 164, 304–316. [Google Scholar] [CrossRef]
- Boissard, P.; Guérif, M.; Pointel, J.-G.; Guinot, J.-P. Application of SPOT data to wheat yield estimation. Adv. Space Res. 1989, 9, 143–154. [Google Scholar] [CrossRef]
- Hunt, M.L.; Blackburn, G.A.; Carrasco, L.; Redhead, J.W.; Rowland, C.S. High resolution wheat yield mapping using Sentinel-2. Remote Sens. Environ. 2019, 233, 111410. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z.; Liu, G.; Jiang, Z.; Huang, C. Improving Winter Wheat Yield Estimation from the CERES-Wheat Model to Assimilate Leaf Area Index with Different Assimilation Methods and Spatio-Temporal Scales. Remote Sens. 2017, 9, 190. [Google Scholar] [CrossRef]
- Curnel, Y.; de Wit, A.J.W.; Duveiller, G.; Defourny, P. Potential performances of remotely sensed LAI assimilation in WOFOST model based on an OSS Experiment. Agric. For. Meteorol. 2011, 151, 1843–1855. [Google Scholar] [CrossRef]
- Rodriguez, J.C.; Duchemin, B.; Hadria, R.; Watts, C.; Garatuza, J.; Chehbouni, A.; Khabba, S.; Boulet, G.; Palacios, E.; Lahrouni, A. Wheat yield estimation using remote sensing and the STICS model in the semiarid Yaqui valley, Mexico. Agronomy 2004, 24, 295–304. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Prats, J.M.C.; Romo, A. Early prediction of crop production using drought indices at different time-scales and remote sensing data: Application in the Ebro Valley (north-east Spain). Int. J. Remote Sens. 2006, 27, 511–518. [Google Scholar] [CrossRef]
- Moriondo, M.; Maselli, F.; Bindi, M. A simple model of regional wheat yield based on NDVI data. Eur. J. Agron. 2007, 26, 266–274. [Google Scholar] [CrossRef]
- Segarra, J.; Araus, J.L.; Kefauver, S.C. Farming and Earth Observation: Sentinel-2 data to estimate within-field wheat grain yield. Int. J. Appl. Earth Obs. Geoinf. 2022, 107, 102697. [Google Scholar] [CrossRef]
- Uribeetxebarria, A.; Castellón, A.; Elorza, I.; Aizpurua, A. Intra-Plot Variable N Fertilization in Winter Wheat through Machine Learning and Farmer Knowledge. Agronomy 2022, 12, 2276. [Google Scholar] [CrossRef]
- Meraner, A.; Ebel, P.; Zhu, X.X.; Schmitt, M. Cloud removal in Sentinel-2 imagery using a deep residual neural network and SAR-optical data fusion. ISPRS J. Photogramm. Remote Sens. 2020, 166, 333–346. [Google Scholar] [CrossRef]
- Phiri, D.; Simwanda, M.; Salekin, S.; Nyirenda, V.R.; Murayama, Y.; Ranagalage, M. Sentinel-2 Data for Land Cover/Use Mapping: A Review. Remote Sens. 2020, 12, 2291. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Ulaby, F.; Moore, R.; Fung, A. Microwave Remote Sensing Active and Passive-Volume III: From Theory to Applications; Artech House: Norwood, MA, USA, 1986. [Google Scholar]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.; Santra, G.H. Applications of Machine Learning Techniques in Agricultural Crop Production: A Review Paper. Indian J. Sci. Technol. 2016, 9, 1–14. [Google Scholar] [CrossRef]
- Shao, Y.; Campbell, J.B.; Taff, G.N.; Zheng, B. An analysis of cropland mask choice and ancillary data for annual corn yield forecasting using MODIS data. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 78–87. [Google Scholar] [CrossRef]
- Bhosle, K.; Musande, V. Evaluation of Deep Learning CNN Model for Land Use Land Cover Classification and Crop Identification Using Hyperspectral Remote Sensing Images. J. Indian Soc. Remote Sens. 2019, 47, 1949–1958. [Google Scholar] [CrossRef]
- Worrall, G.; Rangarajan, A.; Judge, J. Domain-Guided Machine Learning for Remotely Sensed In-Season Crop Growth Estimation. Remote Sens. 2021, 13, 4605. [Google Scholar] [CrossRef]
- Arno, J.; Martinez-Casasnovas, J.A.; Ribes-Dasi, M.; Rosell, J.R. Clustering of grape yield maps to delineate site-specific management zones. Span. J. Agric. Res. 2011, 9, 721. [Google Scholar] [CrossRef]
- Tang, X.; Liu, H.; Feng, D.; Zhang, W.; Chang, J.; Li, L.; Yang, L. Prediction of field winter wheat yield using fewer parameters at middle growth stage by linear regression and the BP neural network method. Eur. J. Agron. 2022, 141, 126621. [Google Scholar] [CrossRef]
- Meraj, G.; Kanga, S.; Ambadkar, A.; Kumar, P.; Singh, S.K.; Farooq, M.; Johnson, B.A.; Rai, A.; Sahu, N. Assessing the Yield of Wheat Using Satellite Remote Sensing-Based Machine Learning Algorithms and Simulation Modeling. Remote Sens. 2022, 14, 3005. [Google Scholar] [CrossRef]
- Wang, J.; Si, H.; Gao, Z.; Shi, L. Winter Wheat Yield Prediction Using an LSTM Model from MODIS LAI Products. Agriculture 2022, 12, 1707. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Safaei, N.; Khaki, S.; Lopez, G.; Zeng, W.; Ewert, F.; Gaiser, T.; Rahimi, J. Winter wheat yield prediction using convolutional neural networks from environmental and phenological data. Sci. Rep. 2022, 12, 3215. [Google Scholar] [CrossRef]
- Cao, J.; Wang, H.; Li, J.; Tian, Q.; Niyogi, D. Improving the Forecasting of Winter Wheat Yields in Northern China with Machine Learning–Dynamical Hybrid Subseasonal-to-Seasonal Ensemble Prediction. Remote Sens. 2022, 14, 1707. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a New Boosting Algorithm. In Proceedings of the 13th International Conference on International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1996; pp. 148–156. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD ’16: 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. arXiv 2019, arXiv:1706.09516. [Google Scholar]
- Cai, Y.; Guan, K.; Lobell, D.; Potgieter, A.B.; Wang, S.; Peng, J.; Xu, T.; Asseng, S.; Zhang, Y.; You, L.; et al. Integrating satellite and climate data to predict wheat yield in Australia using machine learning approaches. Agric. For. Meteorol. 2019, 274, 144–159. [Google Scholar] [CrossRef]
- Folberth, C.; Skalský, R.; Moltchanova, E.; Balkovič, J.; Azevedo, L.B.; Obersteiner, M.; van der Velde, M. Uncertainty in soil data can outweigh climate impact signals in global crop yield simulations. Nat. Commun. 2016, 7, 11872. [Google Scholar] [CrossRef]
- Zadoks, J.C.; Chang, T.T.; Konzak, C.F. A decimal code for the growth stages of cereals. Weed Res. 1974, 14, 415–421. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Data descriptor: Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180–214. [Google Scholar] [CrossRef]
- Unamunzaga, O.; Aizpurua, A.; Artetxe, A.; Besga, G.; Castroviejo, L.; Blanco, F.; de la Llera, I.; Ramos, L.; Astola, G. Asistencia Técnica Para la Caracterización Agrológica del Suelo Rústico del Municipio de Vitoria-Gasteiz. Available online: https://docplayer.es/amp/152712108-Asistencia-tecnica-para-la-caracterizacion-agrologica-del-suelo-rustico-del-municipiode-vitoria-gasteiz.html (accessed on 30 January 2021). (In Spanish).
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Deering, D.W.; Schell, J.A.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (GreenWave Effect) of Natural Vegetation; NASA/GSFC Type III Final Report 5; NASA: Greenbelt, MD, USA, 1974; p. 371.
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Buschmann, C.; Nagel, M. In vivo spectroscopy and internal optics of leaves as basis for remote sensing of vegetation. In-ternational Journal of Remote Sensing. Int. J. Remote Sens. 1993, 14, 711–722. [Google Scholar] [CrossRef]
- Tucker, C.; Elgin, J.; McMurtrey, J.; Fan, C. Monitoring corn and soybean crop development with hand-held radiometer spectral data. Remote Sens. Environ. 1979, 8, 237–248. [Google Scholar] [CrossRef]
- Miura, T.; Yoshioka, H.; Fujiwara, K.; Yamamoto, H. Inter-Comparison of ASTER and MODIS Surface Reflectance and Vegetation Index Products for Synergistic Applications to Natural Resource Monitoring. Sensors 2008, 8, 2480–2499. [Google Scholar] [CrossRef]
- Vincini, M.; Frazzi, E.; D’Alessio, P. A broad-band leaf chlorophyll vegetation index at the canopy scale. Precis. Agric. 2008, 9, 303–319. [Google Scholar] [CrossRef]
- Escadafal, R. Remote sensing of soil color: Principles and applications. Remote Sens. Rev. 1993, 7, 261–279. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for Remote Quantification of Biophysical Characteristics of Vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A.R. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Goel, N.S.; Qin, W. Influences of canopy architecture on relationships between various vegetation indices and LAI and Fpar: A computer simulation. Remote Sens. Rev. 1994, 10, 309–347. [Google Scholar] [CrossRef]
- García-Escudero, L.A.; Gordaliza, A.; Matrán, C.; Mayo-Iscar, A. A general trimming approach to robust cluster Analysis. Ann. Stat. 2008, 36, 1324–1345. [Google Scholar] [CrossRef]
- Taylor, J.A.; McBratney, A.B.; Whelan, B.M. Establishing Management Classes for Broadacre Agricultural Production. Agron. J. 2007, 99, 1366–1376. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, L.; Xu, W.; Ledwith, V. Use of local Moran’s I and GIS to identify pollution hotspots of Pb in urban soils of Galway, Ireland. Sci. Total. Environ. 2008, 398, 212–221. [Google Scholar] [CrossRef]
- European Space Agency (ESA). Sentinel-1 Mission. 2021. Available online: https://www.esa.int/Applications/Observing_the_Earth/Copernicus/Sentinel-1 (accessed on 30 January 2021).
- Alpaydin, E. Introduction to Machine Learning. 2nd ed. 2010. Available online: https://books.google.nl/books?hl=nl&lr=&id=TtrxCwAAQBAJ&oi=fnd&pg=PR7&dq=introduction+to+machine+learning&ots=T5ejQG_7pZ&sig=0xC_H0agN7mPhYW7oQsWiMVwRnQ#v=onepage&q=introduction-to-machine-learning&f=false (accessed on 30 January 2021).
- Friedman, J.H.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bloniarz, A.; Liu, H.; Zhang, C.-H.; Sekhon, J.S.; Yu, B. Lasso adjustments of treatment effect estimates in randomized experiments. Proc. Natl. Acad. Sci. USA 2016, 113, 7383–7390. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, R.; Bajorath, J. Evolution of Support Vector Machine and Regression Modeling in Chemoinformatics and Drug Discovery. J. Comput. Mol. Des. 2022, 36, 355–362. [Google Scholar] [CrossRef]
- Balfer, J.; Bajorath, J. Systematic Artifacts in Support Vector Regression-Based Compound Potency Prediction Revealed by Statistical and Activity Landscape Analysis. PLoS ONE 2015, 10, e0119301. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; pp. 278–282. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Glantz, S.; Slinker, B. Primer of Applied Regression and Analysis of Variance; McGraw-Hill: New York, NY, USA, 1990. [Google Scholar]
- Magney, T.S.; Eitel, J.U.; Huggins, D.R.; Vierling, L.A. Proximal NDVI derived phenology improves in-season predictions of wheat quantity and quality. Agric. For. Meteorol. 2016, 217, 46–60. [Google Scholar] [CrossRef]
- Uribeetxebarria, A.; Castellón, A.; Aizpurua, A. A First Approach to Determine If It Is Possible to Delineate In-Season N Fertilization Maps for Wheat Using NDVI Derived from Sentinel-2. Remote Sens. 2022, 14, 2872. [Google Scholar] [CrossRef]
- Babar, M.A.; Reynolds, M.P.; van Ginkel, M.; Klatt, A.R.; Raun, W.R.; Stone, M.L. Spectral Reflectance Indices as a Potential Indirect Selection Criteria for Wheat Yield under Irrigation. Crop Sci. 2006, 46, 578–588. [Google Scholar] [CrossRef]
- Tian, H.; Wang, P.; Tansey, K.; Han, D.; Zhang, J.; Zhang, S.; Li, H. A deep learning framework under attention mechanism for wheat yield estimation using remotely sensed indices in the Guanzhong Plain, PR China. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102375. [Google Scholar] [CrossRef]
- Hosseini, M.; McNairn, H. Using multi-polarization C- and L-band synthetic aperture radar to estimate biomass and soil moisture of wheat fields. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 50–64. [Google Scholar] [CrossRef]
- Ouaadi, N.; Jarlan, L.; Ezzahar, J.; Zribi, M.; Khabba, S.; Bouras, E.; Bousbih, S.; Frison, P.-L. Monitoring of wheat crops using the backscattering coefficient and the interferometric coherence derived from Sentinel-1 in semi-arid areas. Remote Sens. Environ. 2020, 251, 112050. [Google Scholar] [CrossRef]
- Wollmer, A.-C.; Pitann, B.; Mühling, K.H. Grain storage protein concentration and composition of winter wheat (Triticum aestivum L.) as affected by waterlogging events during stem elongation or ear emergence. J. Cereal Sci. 2018, 83, 9–15. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Ratha, D.; Dey, S.; Bhattacharya, A.; Lopez-Sanchez, J.M.; McNairn, H.; Rao, Y.S. Dual polarimetric radar vegetation index for crop growth monitoring using sentinel-1 SAR data. Remote Sens. Environ. 2020, 247, 111954. [Google Scholar] [CrossRef]
- Bai, X.; He, B.; Li, X.; Zeng, J.; Wang, X.; Wang, Z.; Zeng, Y.; Su, Z. First Assessment of Sentinel-1A Data for Surface Soil Moisture Estimations Using a Coupled Water Cloud Model and Advanced Integral Equation Model over the Tibetan Plateau. Remote Sens. 2017, 9, 714. [Google Scholar] [CrossRef]
- Mercier, A.; Betbeder, J.; Baudry, J.; Le Roux, V.; Spicher, F.; Lacoux, J.; Roger, D.; Hubert-Moy, L. Evaluation of Sentinel-1 & 2 time series for predicting wheat and rapeseed phenological stages. ISPRS J. Photogramm. Remote Sens. 2020, 163, 231–256. [Google Scholar] [CrossRef]
- El Imanni, H.S.; El Harti, A.; Panimboza, J. Investigating Sentinel-1 and Sentinel-2 Data Efficiency in Studying the Temporal Behavior of Wheat Phenological Stages Using Google Earth Engine. Agriculture 2022, 12, 1605. [Google Scholar] [CrossRef]
- Chauhan, S.; Darvishzadeh, R.; Lu, Y.; Boschetti, M.; Nelson, A. Understanding wheat lodging using multi-temporal Sentinel-1 and Sentinel-2 data. Remote Sens. Environ. 2020, 243, 111804. [Google Scholar] [CrossRef]
- Vavlas, N.-C.; Waine, T.W.; Meersmans, J.; Burgess, P.J.; Fontanelli, G.; Richter, G.M. Deriving Wheat Crop Productivity Indicators Using Sentinel-1 Time Series. Remote Sens. 2020, 12, 2385. [Google Scholar] [CrossRef]
- Kamenova, I.; Dimitrov, P. Evaluation of Sentinel-2 vegetation indices for prediction of LAI, fAPAR and fCover of winter wheat in Bulgaria. Eur. J. Remote Sens. 2021, 54 (Suppl. S4), 89–108. [Google Scholar] [CrossRef]
- Sohil, F.; Sohali, M.U.; Shabbir, J. An introduction to statistical learning with applications in R: By Gareth James, Dan-iela Witten, Trevor Hastie, and Robert Tibshirani, New York, Springer Science and Business Media, 2013, $41.98, EISBN: 978-1-4614-7137-7. Stat. Theory Relat. Fields 2021, 6, 87. [Google Scholar] [CrossRef]
- Tesfaye, A.A.; Osgood, D.; Aweke, B.G. Combining machine learning, space-time cloud restoration and phenology for farm-level wheat yield prediction. Artif. Intell. Agric. 2021, 5, 208–222. [Google Scholar] [CrossRef]
- Kok, Z.H.; Shariff, A.R.M.; Alfatni, M.S.M.; Khairunniza-Bejo, S. Support Vector Machine in Precision Agriculture: A review. Comput. Electron. Agric. 2021, 191, 106546. [Google Scholar] [CrossRef]
- Heremans, S.; Dong, Q.; Zhang, B.; Bydekerke, L.; Van Orshoven, J. Potential of ensemble tree methods for early-season prediction of winter wheat yield from short time series of remotely sensed normalized difference vegetation index and in situ meteorological data. J. Appl. Remote Sens. 2015, 9, 097095. [Google Scholar] [CrossRef]
- Li, X.; Yuan, W.; Dong, W. A Machine Learning Method for Predicting Vegetation Indices in China. Remote Sens. 2021, 13, 1147. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Z.; Zheng, J. CatBoost: A new approach for estimating daily reference crop evapotranspiration in arid and semi-arid regions of Northern China. J. Hydrol. 2020, 588, 125087. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]


| Vegetation Index | Abbreviation | Formula | Reference |
|---|---|---|---|
| Normalized Difference Vegetation Index | NDVI | (B8 − B4)/(B8 + B4) | [62] |
| Green Ratio Vegetation Index | GRVI | B8/B3 | [63] |
| Green Normalized Difference Vegetation Index | GNDVI | (B8 − B3)/(B8 + B3) | [64] |
| Green Difference Vegetation Index | GDVI | B8 − B3 | [65] |
| Enhanced Vegetation Index 2 | EVI2 | 2.4 × ((B8 − B4)/(B8 + B4 + 1)) | [66] |
| Chlorophyll Vegetation Index | CVI | B8 × (B4/(B3 × B3)) | [67] |
| Color Index | CI | (B4 − B2)/B4 | [68] |
| Wide Dynamic Range Vegetation Index | WDRVI | ((0.1 × B8) − B4)/((0.1 × B8) + B4) | [69] |
| Transformed Vegetation Index | TVI | [70] | |
| Soil Adjusted Vegetation Index | SAVI | ((B8 − B4)/(B8 + B4 + 0.5)) × (1 + 0.5) | [71] |
| Simple Ratio 800/670 Ratio Vegetation Index | RVI | B8/B4 | [72] |
| Optimized Soil Adjusted Vegetation Index | OSAVI | (1 + 0.16) × ((B8 − B4)/(B8 + B4 + 0.16)) | [73] |
| Nonlinear Vegetation Index | NLI | ((B8 × B8) − B4)/((B8 × B8) + B4) | [74] |
| Algorithm | n * | Mean RMSE (t ha−1) | SD | rRMSE (%) |
|---|---|---|---|---|
| MLR | 30 | 1.1 | 0.77 | 15.25 |
| RF | 30 | 0.69 | 0.35 | 9.78 |
| SVM | 30 | 0.62 | 0.34 | 8.92 |
| CatBoost | 30 | 0.41 | 0.29 | 5.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uribeetxebarria, A.; Castellón, A.; Aizpurua, A. Optimizing Wheat Yield Prediction Integrating Data from Sentinel-1 and Sentinel-2 with CatBoost Algorithm. Remote Sens. 2023, 15, 1640. https://doi.org/10.3390/rs15061640
Uribeetxebarria A, Castellón A, Aizpurua A. Optimizing Wheat Yield Prediction Integrating Data from Sentinel-1 and Sentinel-2 with CatBoost Algorithm. Remote Sensing. 2023; 15(6):1640. https://doi.org/10.3390/rs15061640
Chicago/Turabian StyleUribeetxebarria, Asier, Ander Castellón, and Ana Aizpurua. 2023. "Optimizing Wheat Yield Prediction Integrating Data from Sentinel-1 and Sentinel-2 with CatBoost Algorithm" Remote Sensing 15, no. 6: 1640. https://doi.org/10.3390/rs15061640
APA StyleUribeetxebarria, A., Castellón, A., & Aizpurua, A. (2023). Optimizing Wheat Yield Prediction Integrating Data from Sentinel-1 and Sentinel-2 with CatBoost Algorithm. Remote Sensing, 15(6), 1640. https://doi.org/10.3390/rs15061640








