Kinematic Rupture Process and Its Implication of a Thrust and Strike-Slip Multi-Fault during the 2021 Haiti Earthquake
Abstract
1. Introduction
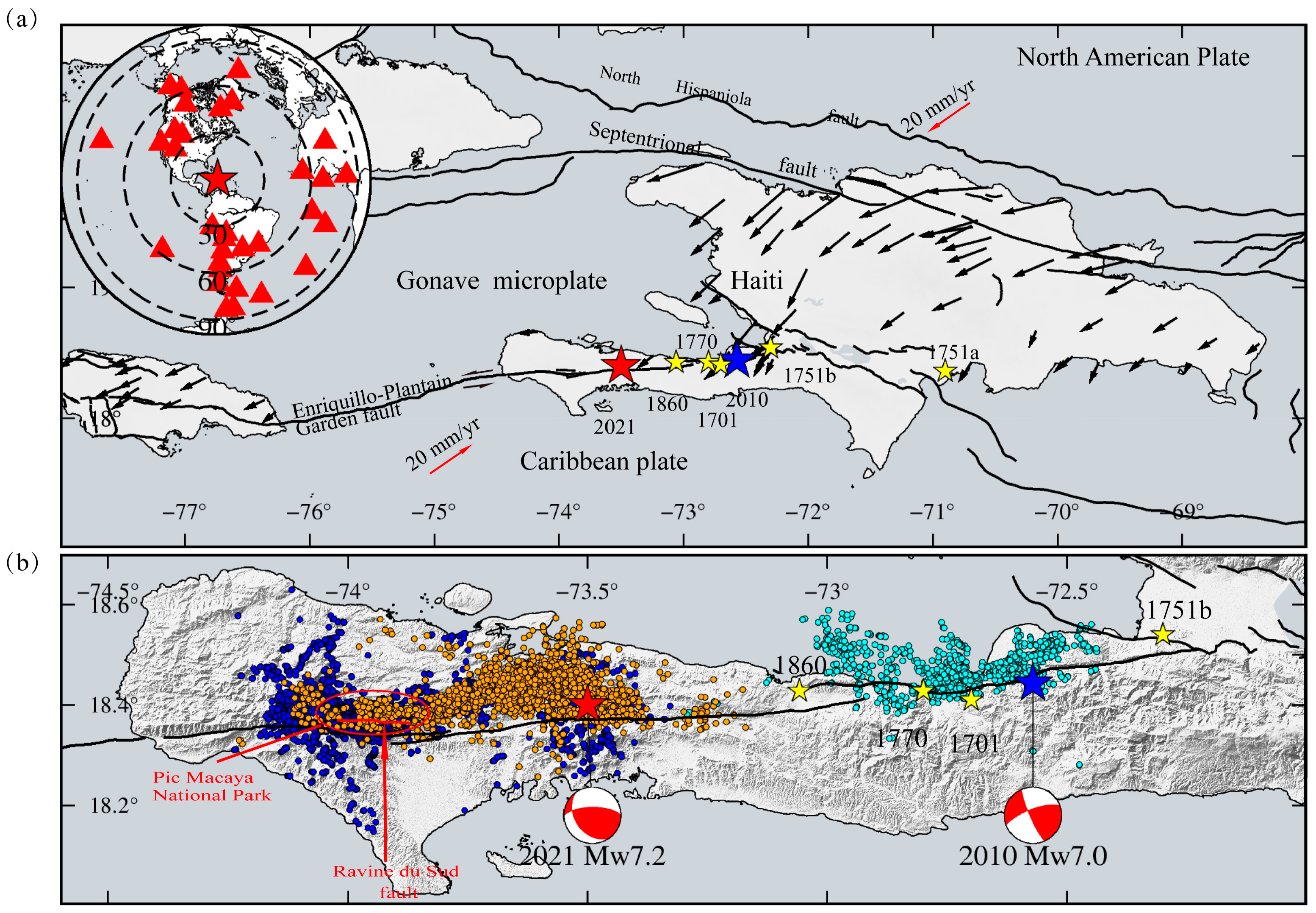
2. Materials
3. Inversion and Results
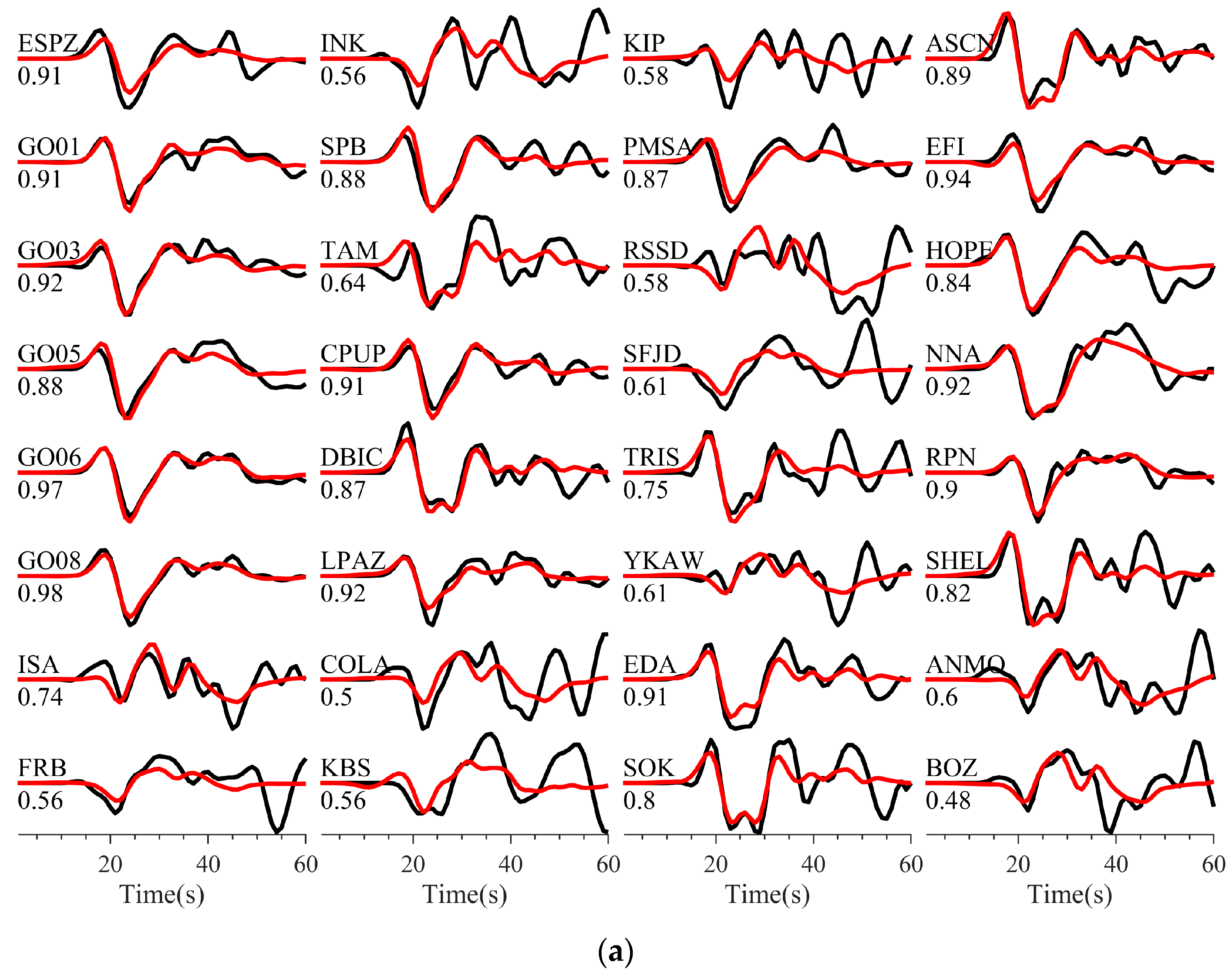
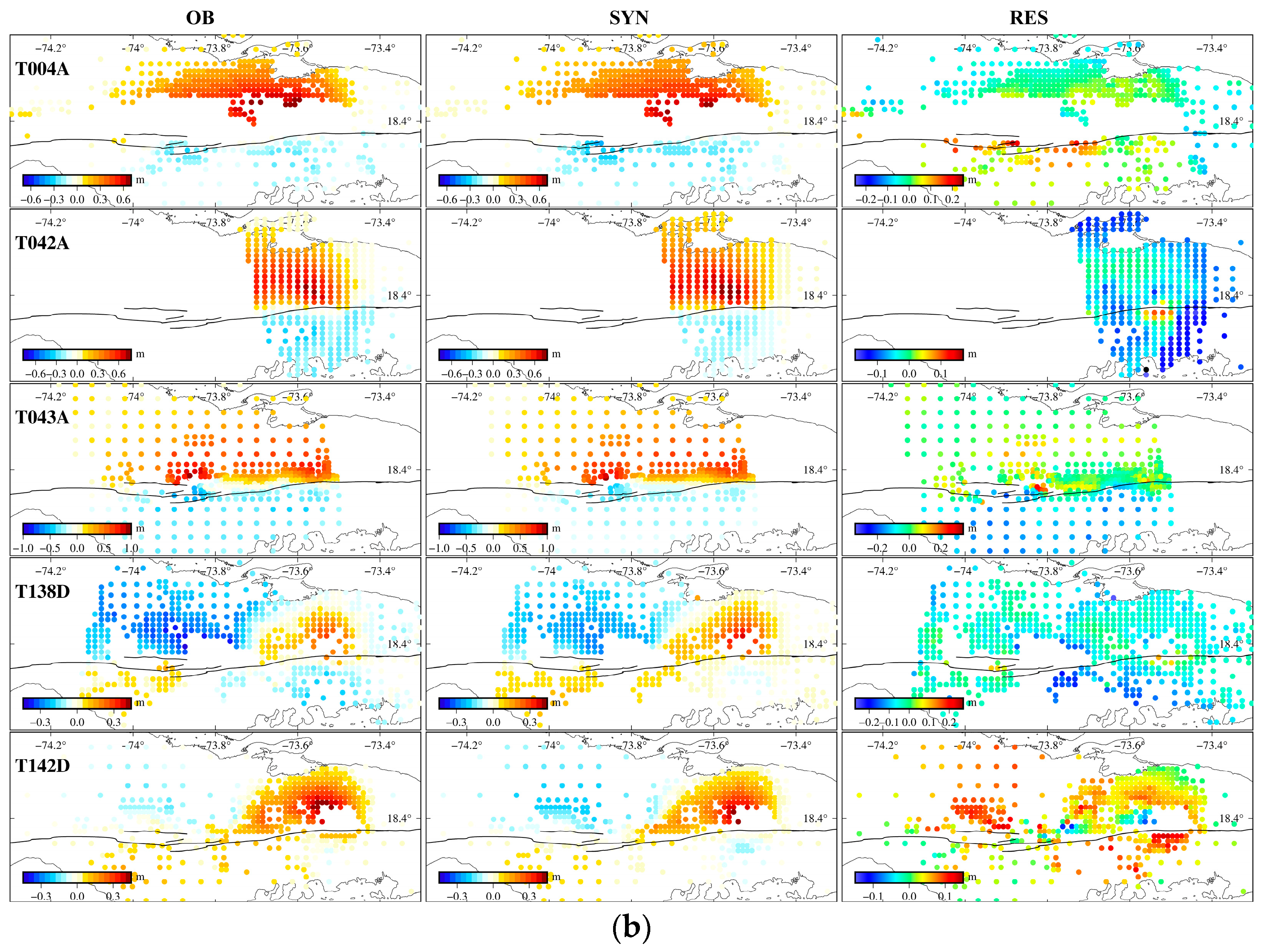
3.1. Finite-Fault Inversion
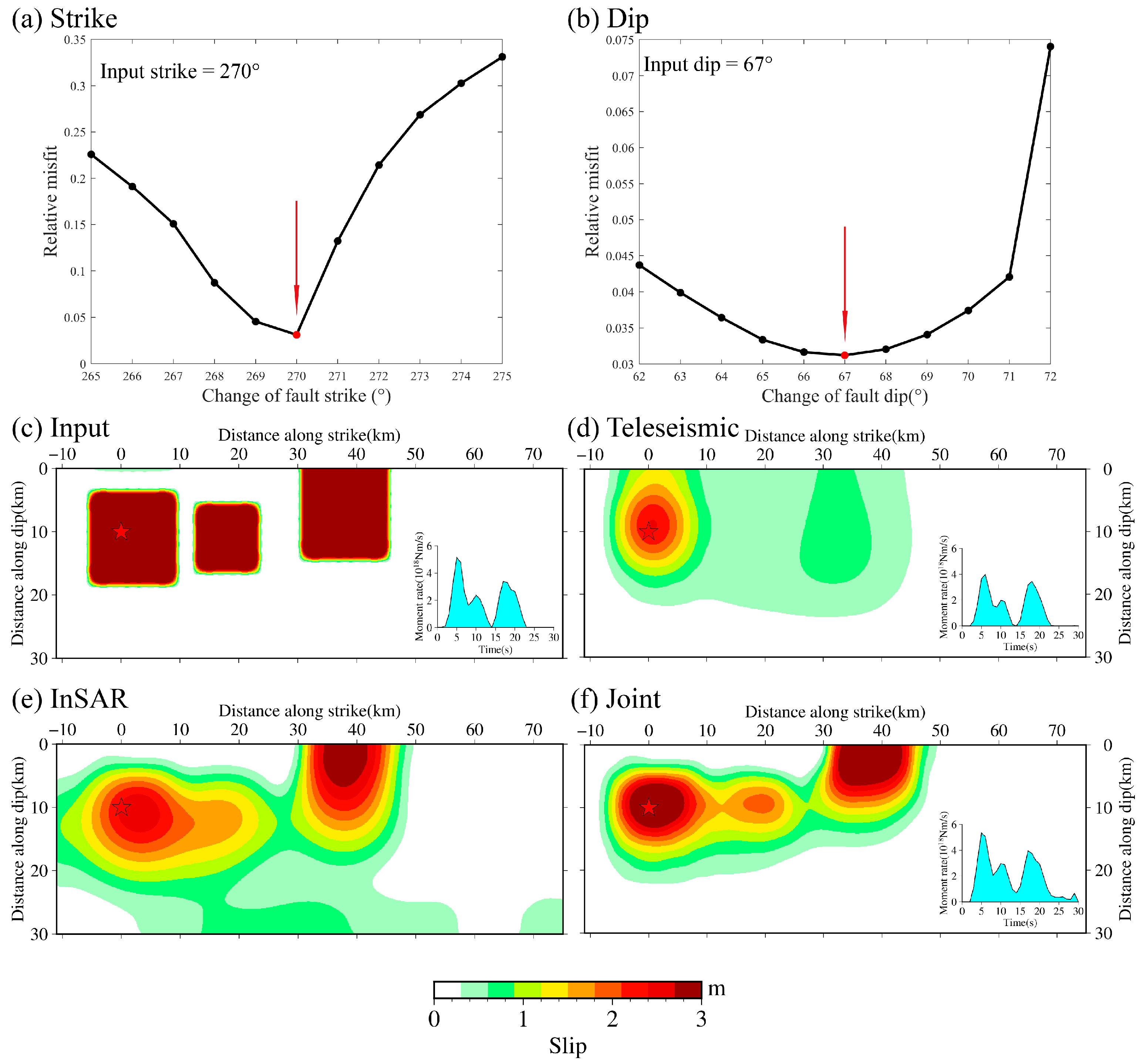
3.2. Fault Geometry
3.3. Results
4. Discussion
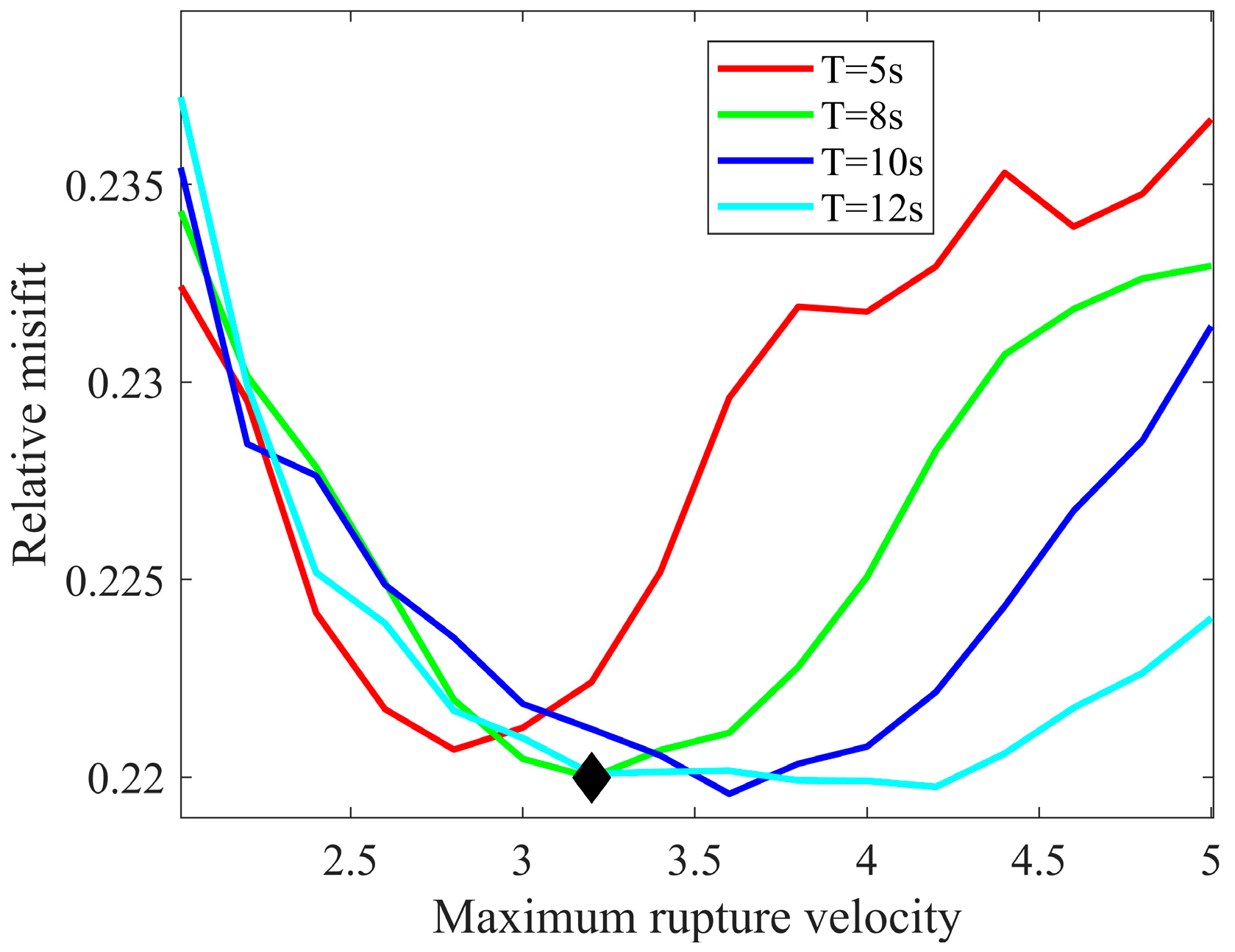
4.1. Stability of the Rupture Model
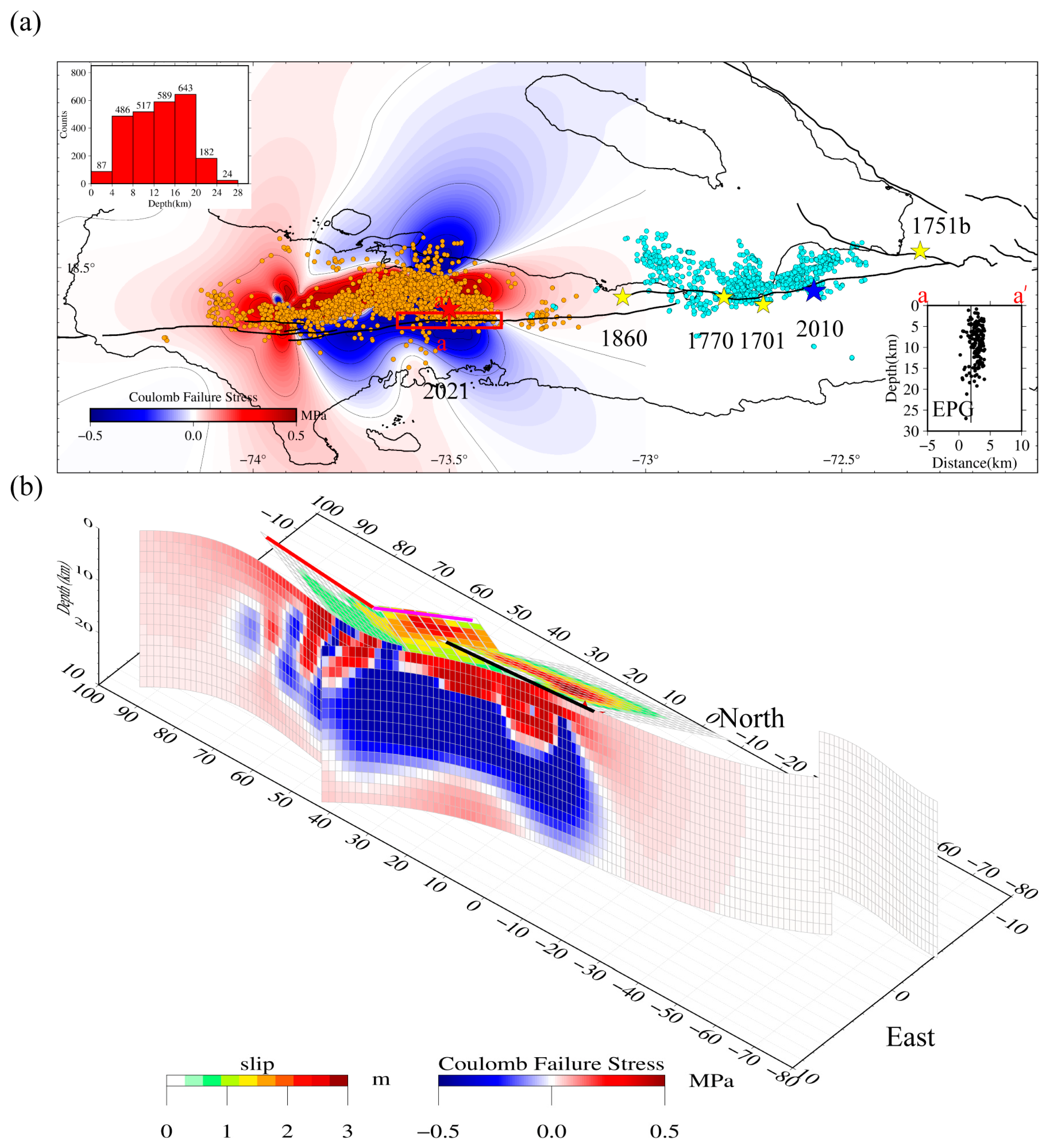
4.2. Cascading Rupture of the Multi-Fault System
4.3. Potential Seismic Hazard
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- UN Office for the Coordination of Humanitarian Affairs (UN-OCHA). Haiti: Earthquake Situation Report No. 8—Final (29 November 2021). ReliefWeb, 2021. Available online: https://reliefweb.int/report/haiti/haiti-earthquake-situation-report-no-8-final-29-november-2021 (accessed on 10 December 2021).
- Manaker, D.M.; Calais, E.; Freed, A.M.; Ali, S.T.; Przybylski, P.; Mattioli, G.; Jansma, P.; Prépetit, C.; De Chabalier, J.B. Interseismic Plate coupling and strain partitioning in the Northeastern Caribbean. Geophys. J. Int. 2008, 174, 889–903. [Google Scholar] [CrossRef]
- Benford, B.; DeMets, C.; Calais, E. GPS estimates of microplate motions, northern Caribbean: Evidence for a Hispaniola microplate and implications for earthquake hazard. Geophys. J. Int. 2012, 191, 481–490. [Google Scholar] [CrossRef]
- Fleur, N.S.; Feuillet, N.; Grandin, R.; Jacques, E.; Weil-Accardo, J.; Klinger, Y. Seismotectonics of southern Haiti: A new faulting model for the 12 January 2010 M 7.0 earthquake. Geophys. Res. Lett. 2015, 42, 10273–10281. [Google Scholar] [CrossRef]
- Calais, É.; Symithe, S.; de Lépinay, B.M.; Prépetit, C. Plate boundary segmentation in the northeastern Caribbean from geodetic measurements and Neogene geological observations. C. R. Geosci. 2016, 348, 42–51. [Google Scholar] [CrossRef]
- Mann, P.; Burke, K.; Matumoto, T. Neotectonics of Hispaniola: Plate motion, sedimentation, and seismicity at a restraining bend. Earth Planet. Sci. Lett. 1984, 70, 311–324. [Google Scholar] [CrossRef]
- Prentice, C.S.; Mann, P.; Crone, A.J.; Gold, R.D.; Hudnut, K.W.; Briggs, R.W.; Koehler, R.D.; Jean, P. Seismic hazard of the Enriquillo–Plantain Garden fault in Haiti inferred from palaeoseismology. Nat. Geosci. 2010, 3, 789–793. [Google Scholar] [CrossRef]
- Symithe, S.; Calais, E. Present-day shortening in Southern Haiti from GPS measurements and implications for seismic hazard. Tectonophysics 2016, 679, 117–124. [Google Scholar] [CrossRef]
- Bakun, W.H.; Flores, C.; Brink, U.S.T. Significant earthquakes on the Enriquillo fault system, hispaniola, 1500–2010: Implications for seismic hazard. Bull. Seismol. Soc. Am. 2012, 102, 18–30. [Google Scholar] [CrossRef]
- Martin, S.S.; Hough, S.E. The 8 April 1860 Jour de Pâques earthquake sequence in southern Haiti. Bull. Seismol. Soc. Am. 2022, 112, 2468–2486. [Google Scholar] [CrossRef]
- Hough, S.E.; Martin, S.S.; Symithe, S.J.; Briggs, R. Rupture Scenarios for the 3 June 1770 Haiti Earthquake. Bull. Seismol. Soc. Am. 2022, 113, 157–185. [Google Scholar] [CrossRef]
- Hayes, G.P.; Briggs, R.W.; Sladen, A.; Fielding, E.J.; Prentice, C.; Hudnut, K.; Mann, P.; Taylor, F.W.; Crone, A.J.; Gold, R.; et al. Complex rupture during the 12 January 2010 Haiti earthquake. Nat. Geosci. 2010, 3, 800–805. [Google Scholar] [CrossRef]
- Calais, E.; Freed, A.; Mattioli, G.; Amelung, F.; Jónsson, S.; Jansma, P.; Hong, S.-H.; Dixon, T.; Prépetit, C.; Momplaisir, R. Transpressional rupture of an unmapped fault during the 2010 Haiti earthquake. Nat. Geosci. 2010, 3, 794–799. [Google Scholar] [CrossRef]
- Douilly, R.; Haase, J.S.; Ellsworth, W.; Bouin, M.-P.; Calais, E.; Symithe, S.; Armbruster, J.G.; De Lépinay, B.M.; Deschamps, A.; Mildor, S.-L.; et al. Crustal Structure and Fault Geometry of the 2010 Haiti Earthquake from Temporary Seismometer Deployments. Bull. Seismol. Soc. Am. 2013, 103, 2305–2325. [Google Scholar] [CrossRef]
- Symithe, S.J.; Calais, E.; Haase, J.S.; Freed, A.M.; Douilly, R. Coseismic Slip Distribution of the 2010 M 7.0 Haiti Earthquake and Resulting Stress Changes on Regional Faults. Bull. Seismol. Soc. Am. 2013, 103, 2326–2343. [Google Scholar] [CrossRef]
- Geospatial Information Authority of Japan. The 2021 Haiti Earthquake: Crustal Deformation Detected by ALOS-2 Data. 2021. Available online: https://www.gsi.go.jp/cais/topic20210814-e.html (accessed on 10 December 2021).
- Yin, H.Z.; Xu, X.; Haase, J.S.; Douilly, R.; Sandwell, D.T.; de Lepinay, B.M. Surface Deformation Surrounding the 2021 Mw 7.2 Haiti Earthquake Illuminated by InSAR Observations. Bull. Seismol. Soc. Am. 2022, 113, 41–57. [Google Scholar] [CrossRef]
- Okuwaki, R.; Fan, W. Oblique Convergence Causes Both Thrust and Strike-Slip Ruptures during the 2021 M 7.2 Haiti Earthquake. Geophys. Res. Lett. 2022, 49, e2021GL096373. [Google Scholar] [CrossRef]
- Maurer, J.; Dutta, R.; Vernon, A.; Vajedian, S. Complex Rupture and Triggered Aseismic Creep during the 14 August 2021 Haiti Earthquake from Satellite Geodesy. Geophys. Res. Lett. 2022, 49, e2022GL098573. [Google Scholar] [CrossRef]
- Calais, E.; Symithe, S.; Monfret, T.; Delouis, B.; Lomax, A.; Courboulex, F.; Ampuero, J.P.; Lara, P.E.; Bletery, Q.; Chèze, J.; et al. Citizen seismology helps decipher the 2021 Haiti earthquake. Science 2022, 376, 283–287. [Google Scholar] [CrossRef]
- Douilly, R.; Paul, S.; Monfret, T.; Deschamps, A.; Ambrois, D.; Symithe, S.J.; Fleur, S.S.; Courboulex, F.; Calais, E.; Boisson, D.; et al. Rupture Segmentation of the 14 August 2021 Mw 7.2 Nippes, Haiti, Earthquake Using Aftershock Relocation from a Local Seismic Deployment. Bull. Seismol. Soc. Am. 2022, 113, 58–72. [Google Scholar] [CrossRef]
- Fleur, N.S.; Klinger, Y.; Feuillet, N. Detailed map, displacement, paleoseismology, and segmentation of the Enriquillo-Plantain Garden Fault in Haiti. Tectonophysics 2020, 778, 228368. [Google Scholar] [CrossRef]
- Styron, R.; García-Pelaez, J.; Pagani, M. CCAF-DB: The Caribbean and Central American active fault database. Nat. Hazards Earth Syst. Sci. 2020, 20, 831–857. [Google Scholar] [CrossRef]
- Martinez, S.N.; Allstadt, K.E.; Slaughter, S.L.; Schmitt, R.G.; Collins, E.; Schaefer, L.N.; Ellison, S. Landslides Triggered by the August 14, 2021, Magnitude 7.2 Nippes, Haiti, Earthquake (No. 2021-1112); U.S. Geological Survey: Reston, VA, USA, 2021. [Google Scholar] [CrossRef]
- Jonsson, S. Fault Slip Distribution of the 1999 Mw 7.1 Hector Mine, California, Earthquake, Estimated from Satellite Radar and GPS Measurements. Bull. Seismol. Soc. Am. 2002, 92, 1377–1389. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, W.; Chen, Y.; Xu, L.; Li, Z.; Forrest, D. The 2009 L’Aquila MW 6.3 earthquake: A new technique to locate the hypocentre in the joint inversion of earthquake rupture process. Geophys. J. Int. 2012, 191, 1417–1426. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, W.; Li, X.; Liu, Y.; Ning, J.; Huang, Q. Joint Inversion of Rupture across a Fault Stepover during the 8 August 2017 Mw 6.5 Jiuzhaigou, China, Earthquake. Seism. Res. Lett. 2021, 92, 3386–3397. [Google Scholar] [CrossRef]
- Wang, R.; Heimann, S.; Zhang, Y.; Wang, H.; Dahm, T. Complete synthetic seismograms based on a spherical self-gravitating Earth model with an atmosphere–ocean–mantle–core structure. Geophys. J. Int. 2017, 210, 1739–1764. [Google Scholar] [CrossRef]
- Kennett, B.L.N.; Engdahl, E.R.; Buland, R. Constraints on seismic velocities in the Earth from traveltimes. Geophys. J. Int. 1995, 122, 108–124. [Google Scholar] [CrossRef]
- Wang, R.; Lorenzo-Martín, F.; Roth, F. PSGRN/PSCMP—A new code for calculating co- and post-seismic deformation, geoid and gravity changes based on the viscoelastic-gravitational dislocation theory. Comput. Geosci. 2006, 32, 527–541. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Y.; Xu, L. Geometry-dependent rupture process of the 2015 Gorkha, Nepal, earthquake determined using a dip-varying inversion approach with teleseismic, high-rate GPS, static GPS and InSAR data. Geophys. J. Int. 2021, 229, 1408–1421. [Google Scholar] [CrossRef]
- Aki, K. Characterization of barriers on an earthquake fault. J. Geophys. Res. Atmos. 1979, 84, 6140–6148. [Google Scholar] [CrossRef]
- Kase, Y.; Day, S.M. Spontaneous rupture processes on a bending fault. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Madariaga, R.; Ampuero, J.P.; Adda-Bedia, M. Seismic radiation from simple models of earthquakes. Geophys. Monogr. 2006, 170, 223–236. [Google Scholar] [CrossRef]
- Bruhat, L.; Fang, Z.; Dunham, E.M. Rupture complexity and the supershear transition on rough faults. J. Geophys. Res. Solid Earth 2016, 121, 210–224. [Google Scholar] [CrossRef]
- Okuwaki, R.; Yagi, Y. Role of geometric barriers in irregular-rupture evolution during the 2008 Wenchuan earthquake. Geophys. J. Int. 2017, 212, 1657–1664. [Google Scholar] [CrossRef]
- Shimizu, K.; Yagi, Y.; Okuwaki, R.; Fukahata, Y. Development of an inversion method to extract information on fault geometry from teleseismic data. Geophys. J. Int. 2020, 220, 1055–1065. [Google Scholar] [CrossRef]
- Aagaard, B.T. Dynamic Rupture Modeling of the Transition from Thrust to Strike-Slip Motion in the 2002 Denali Fault Earthquake, Alaska. Bull. Seismol. Soc. Am. 2004, 94, S190–S201. [Google Scholar] [CrossRef]
- Talebian, M.; Fielding, E.J.; Funning, G.J.; Ghorashi, M.; Jackson, J.; Nazari, H.; Parsons, B.; Priestley, K.; Rosen, P.A.; Walker, R.; et al. The 2003 Bam (Iran) earthquake: Rupture of a blind strike-slip fault. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Liu-Zeng, J.; Zhang, Z.; Wen, L.; Tapponnier, P.; Sun, J.; Xing, X.; Hu, G.; Xu, Q.; Zeng, L.; Ding, L.; et al. Co-seismic ruptures of the 12 May 2008, Ms 8.0 Wenchuan earthquake, Sichuan: East–west crustal shortening on oblique, parallel thrusts along the eastern edge of Tibet. Earth Planet. Sci. Lett. 2009, 286, 355–370. [Google Scholar] [CrossRef]
- Shen, Z.-K.; Sun, J.; Zhang, P.; Wan, Y.; Wang, M.; Burgmann, R.; Zeng, Y.; Gan, W.; Liao, H.; Wang, Q. Slip maxima at fault junctions and rupturing of barriers during the 2008 Wenchuan earthquake. Nat. Geosci. 2009, 2, 718–724. [Google Scholar] [CrossRef]
- Walters, R.J.; Gregory, L.C.; Wedmore, L.N.J.; Craig, T.J.; McCaffrey, K.; Wilkinson, M.; Chen, J.; Li, Z.; Elliott, J.R.; Goodall, H.; et al. Dual control of fault intersections on stop-start rupture in the 2016 Central Italy seismic sequence. Earth Planet. Sci. Lett. 2018, 500, 1–14. [Google Scholar] [CrossRef]
- Somerville, P.G.; Smith, N.F.; Graves, R.W.; Abrahamson, N.A. Modification of Empirical Strong Ground Motion Attenuation Relations to Include the Amplitude and Duration Effects of Rupture Directivity. Seism. Res. Lett. 1997, 68, 199–222. [Google Scholar] [CrossRef]
- Stein, R.S. The role of stress transfer in earthquake occurrence. Nature 1999, 402, 605–609. [Google Scholar] [CrossRef]
- Freed, A.M. Earthquake triggering by static, dynamic, and postseismic stress transfer. Annu. Rev. Earth Planet. Sci. 2005, 33, 335–367. [Google Scholar] [CrossRef]
- Nalbant, S.S.; McCloskey, J. Stress evolution before and after the 2008 Wenchuan, China earthquake. Earth Planet. Sci. Lett. 2011, 307, 222–232. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S. Long- and Short-Term Stress Interaction of the 2019 Ridgecrest Sequence and Coulomb-Based Earthquake Forecasts. Bull. Seismol. Soc. Am. 2020, 110, 1765–1780. [Google Scholar] [CrossRef]
- He, K.; Wen, Y.; Xu, C.; Zhao, Y. Fault Geometry and Slip Distribution of the 2021 Mw 7.4 Maduo, China, Earthquake Inferred from InSAR Measurements and Relocated Aftershocks. Seism. Res. Lett. 2021, 93, 8–20. [Google Scholar] [CrossRef]
- Stein, R.; Temblor; Toda, S.; Lin, J.; Sevilgen, V. Are the 2021 and 2010 Haiti Earthquakes Part of a Progressive Sequence? Temblor: Redwood City, CA, USA, 2021. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Richards-Dinger, K.; Bozkurt, S.B. Forecasting the evolution of seismicity in southern California: Animations built on earthquake stress transfer. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Lin, J.; Stein, R.S. Stress triggering in thrust and subduction earthquakes and stress interaction between the southern San Andreas and nearby thrust and strike-slip faults. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]

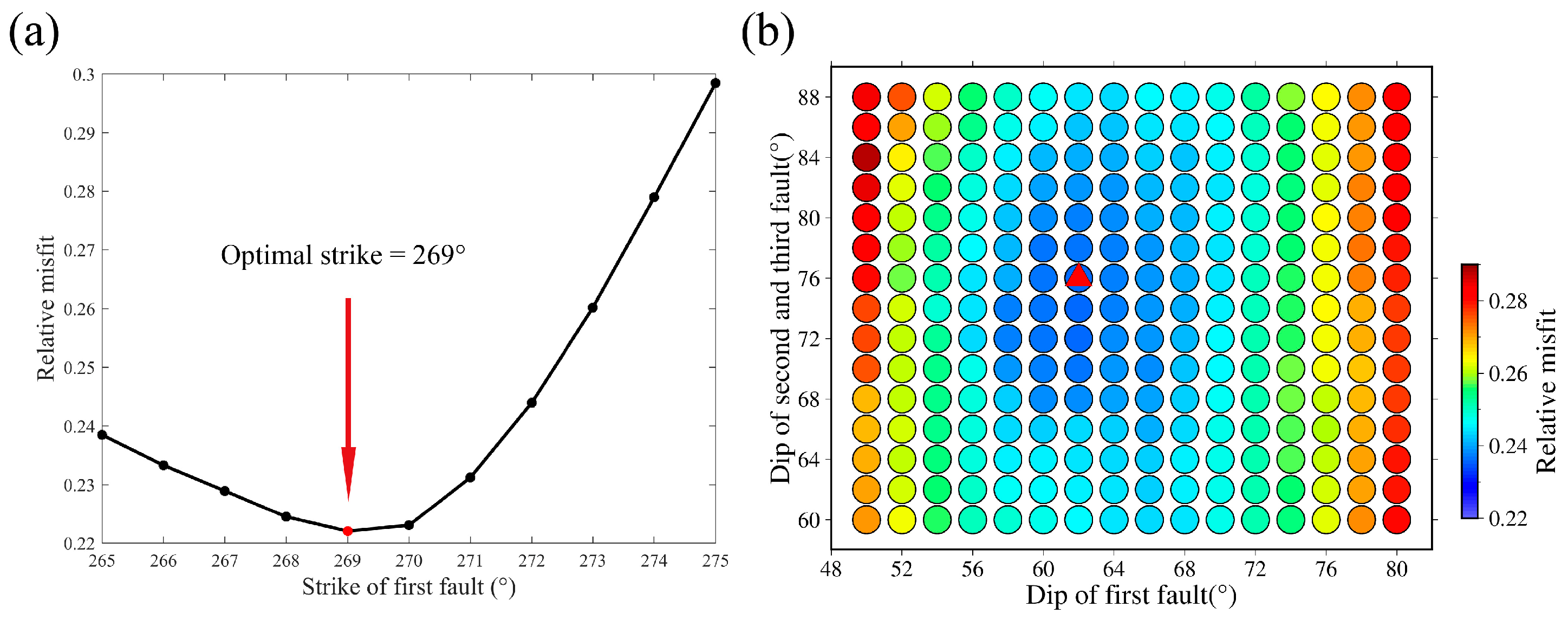


| Strike/° | Dip/° | Length/km | Width/km | |
|---|---|---|---|---|
| First segment | 269 | 62 | 38 | 30 |
| Second segment | 260 | 76 | 18 | 30 |
| Third segment | 272 | 76 | 30 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, G.; Li, X.; Zhao, Y.; Zhang, Y.; Xu, C.; Zheng, Y. Kinematic Rupture Process and Its Implication of a Thrust and Strike-Slip Multi-Fault during the 2021 Haiti Earthquake. Remote Sens. 2023, 15, 1730. https://doi.org/10.3390/rs15071730
Wen G, Li X, Zhao Y, Zhang Y, Xu C, Zheng Y. Kinematic Rupture Process and Its Implication of a Thrust and Strike-Slip Multi-Fault during the 2021 Haiti Earthquake. Remote Sensing. 2023; 15(7):1730. https://doi.org/10.3390/rs15071730
Chicago/Turabian StyleWen, Guisen, Xingxing Li, Yingwen Zhao, Yong Zhang, Caijun Xu, and Yuxin Zheng. 2023. "Kinematic Rupture Process and Its Implication of a Thrust and Strike-Slip Multi-Fault during the 2021 Haiti Earthquake" Remote Sensing 15, no. 7: 1730. https://doi.org/10.3390/rs15071730
APA StyleWen, G., Li, X., Zhao, Y., Zhang, Y., Xu, C., & Zheng, Y. (2023). Kinematic Rupture Process and Its Implication of a Thrust and Strike-Slip Multi-Fault during the 2021 Haiti Earthquake. Remote Sensing, 15(7), 1730. https://doi.org/10.3390/rs15071730





