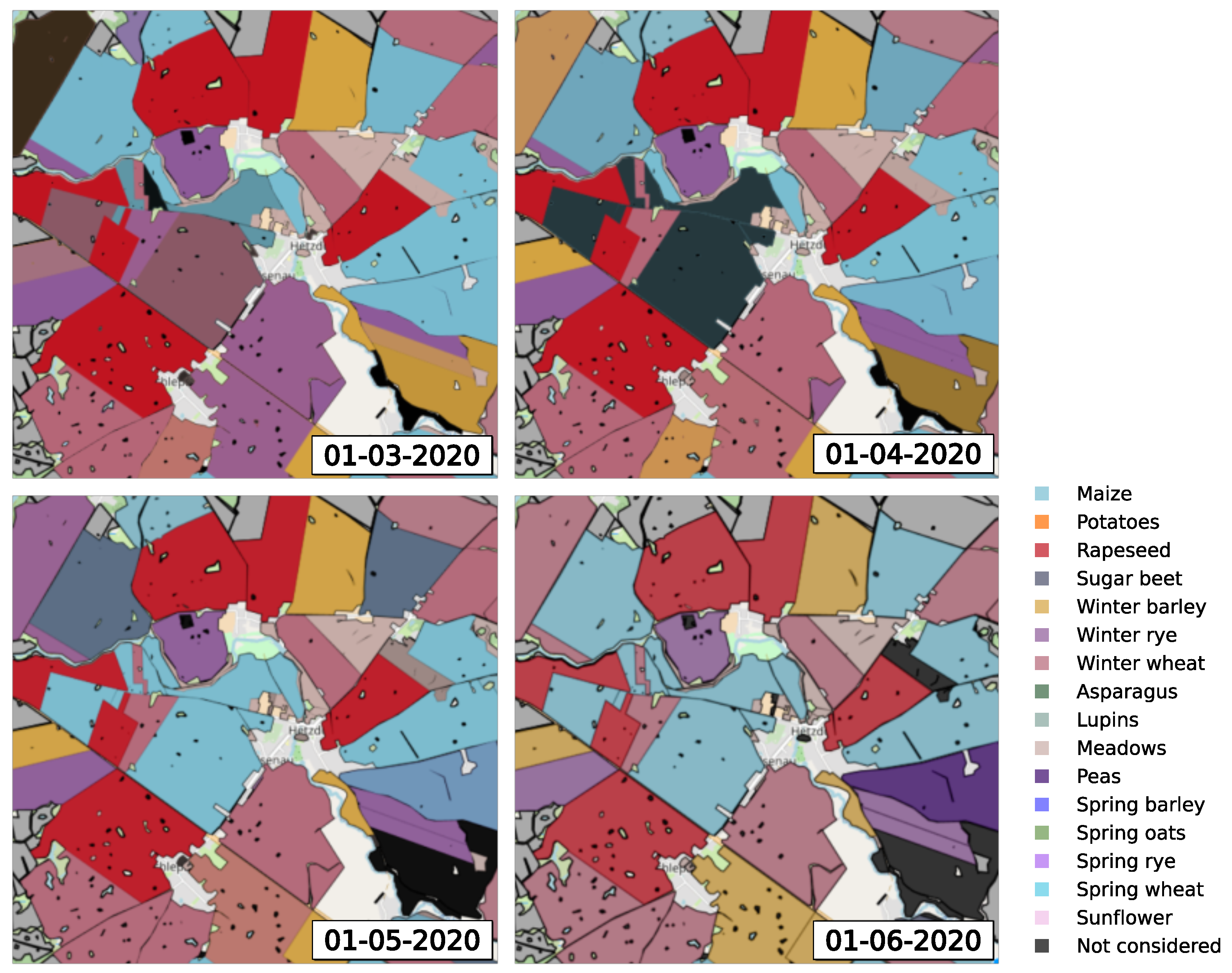
1. Introduction
The ongoing climate change, a rising world population, the increasing use of agricultural products as energy sources, as well as a growing demand for the integration of sustainable cultivation forms are evident major challenges for the agriculture of the future. For all those aspects, access to detailed area-based information is crucial, e.g., for the creation of yield forecasts, agricultural water balance models, remote sensing-based derivation of biophysical parameters or precision farming. Of particular relevance is the knowledge and monitoring of crop types. It is highly relevant for a number of user groups, such as public institutions (subsidy control, statistics) or private actors (farmers, agro-pharmaceutical companies, dependent industries). For most use cases, in fact, the respective crop type information is usually needed as early as possible, ideally several months before harvest.
The identification of crop types has a long research history in remote sensing [
1,
2,
3,
4,
5]. In the 1980s it started by using (un-)supervised classification approaches using single optical images [
3,
4,
6]. Meanwhile, studies have shown that crop-type classification benefits from integrating remote sensing time series data instead of mono-temporal information [
3,
4], combining complementary information of optical and radar data instead of single sensor approaches [
2,
7,
8,
9,
10,
11], as well as from utilizing deep learning models in favor of classical supervised approaches [
4,
12]. While during the last decade decision-based models, such as random forests, were commonly used for crop type classification [
13,
14,
15,
16,
17], subsequently deep learning models, such as convolutional, as well as recurrent neural networks, proved to be very successful [
18,
19,
20]. More recently, experimental comparisons showed that the self-attention layer as used in Transformer models [
21] yields even more precise results for crop type prediction on remote sensing data [
22,
23].
However, besides the recent methodological advancements, crop types are still often identified only retrospectively after harvest or in rather late cultivation phases. Additionally, most studies have been developed on relatively small reference datasets [
2], which is most likely also one of the main reasons why the transferability of the approaches in time and space has been hardly addressed so far [
2]. Larger reference data sets are required to exploit the full potential of deep learning approaches and to develop models that generalize well.
Another aspect concerning input data is the fusion of the multi-modal information of optical and radar remote sensing data. So far, this has been realized at different stages of the algorithm [
2,
24,
25] and a straightforward method for data integration of spatiotemporal heterogeneous data coverage of different modality keeps being a major challenge for crop-type classification approaches.
In this article, we aim to address those issues by proposing an approach for progressive intra-season crop-type classification with a seamless integration of spatiotemporal data sources. Our developments are mainly based on the self-attention-based architecture developed by [
22], which has proven to work well in the classification of crop types in satellite time series data. However, certain methodological developments are necessary in order to allow for the real world scenario of an ongoing near real-time crop classification as the growing season progresses. In particular, the model needs to be able to reliably predict crop types in time series data of arbitrary length in a year the model was not trained on. Thus, our study evaluates different strategies for early crop type classification and focuses on the ability to be transferred to unseen data in time (different years) and space (different regions). Moreover, the goal of large area crop classification requires the model to be flexible in terms of the input data type in order to ensure reliable data availability for each region and time the model is applied to. Hence, the second large focus of our work is on developing seamless data fusion techniques which shall especially be able to handle the freely available dense time series of Sentinel-1 (radar) and Sentinel-2 (optical) data. It has already been shown that using both sensors simultaneously improves prediction performance [
24,
25], however, the progressive early crop classification brings some special requirements also for the data-fusion techniques. Therefore, the data fusions need to be flexible and, in particular, be applicable to spatiotemporally inconsistent time series data of arbitrary length.
The development of our approach is based on crop data from three German federal states (Brandenburg, Mecklenburg-Vorpommern, and Thuringia) from 2018 until 2020 comprising more than million reference parcels (i.e., agricultural fields). This large and heterogeneous reference dataset allows for a well-balanced training and testing of the approach in different scenarios.
The main contributions of our work can be summarized as follows:
We propose and implement a deep learning-based method for predicting crop types during the entire year, in particular allowing for early classification.
We systematically compare model performances in different cultivation stages (from early to late season).
We present a generic way of combining input data from several different sources, in particular focusing on the fusion of data from Sentinel-1 and Sentinel-2 satellites.
We predict crop types in a year that is not available during training (temporal transfer).
We apply our method for the prediction in another region (spatial transfer).
The article is structured as follows.
Section 2 gives an overview of the used datasets and lists the most relevant crop types.
Section 3 summarizes the machine learning model and highlights our methodological improvements.
Section 4 shows the results of multiple experiments that evaluate different aspects and scenarios of the approach. It follows a step-wise procedure to support methodological decisions made towards the real world scenario of progressive early crop-type classification. The performance of the approach and its methodological aspects are discussed in the context of the relevant literature in
Section 5, followed by a final conclusion of the findings in
Section 6.
2. Data
For this study, parcel boundary information is combined with Sentinel-1/-2 data for three German federal states (Brandenburg, Mecklenburg-Vorpommern, and Thuringia), shown in
Figure 1, and three years (2018, 2019, and 2020). The regions have been chosen because of the large field sizes, therefore having high potential and relevance for large scale remote sensing based analysis. Furthermore the crop data for training and validation were openly accessible or have been provided by the federal states. The diversity of data is crucial for showing the temporal and spatial generalization of our models and especially for showing the feasibility of our methods for early classification of crops in a year not appearing in the training data.
2.1. Satellite Data
Observations from the Sentinel-1 (S1) and Sentinel-2 (S2) satellites from the Copernicus program are used.
Sentinel-1: In case of S1 backscatter coefficients (sigma nought) in decibel (dB) of two polarizations (VH, VV) from the S1 SLC product are used. The data are processed by using pyroSAR [
28,
29] to apply SNAP [
30] functionalities in a pipeline (i.e., “Apply-Orbit-File”, “ThermalNoiseRemoval”, “Calibration”, “TOPSAR-Deburst”, “Multilook”, “Speckle-Filter”, “Terrain-Correction”). During terrain correction the S1 data are aligned to the S2 data in terms of the same spatial resolution (10 m), the same map projection, and the same pixel grid. Data of the ascending orbit are used (approx. sensing time of 5 pm) to have a consistent data base and to avoid more frequent dew and rime in earlier sensing times of the descending orbit (approx. sensing time of 5 a.m.) [
31].
Sentinel-2: S2 data are provided as bottom of atmosphere Level2A data products. The atmospheric correction is performed using Scicor [
32]. Scicor enables the classification of cloud conditions and a classification into broad surface categories [
33]. Pixels representing reflectances of Earth’s surface under clear sky conditions are used for further analysis. Pixels classified by Scicor as cloud, cirrus, shadow, snow, or water are excluded and masked as no-data pixels. We use all the 10 m and 20 m bands of S2 (B2, B3, B4, B5, B6, B7, B8, B8A, B11, and B12) in their original spatial resolution.
We use data from within a hydrological year to reflect the possible phenological stages of agricultural crops. For example, when referring to the 2019 data, we use the observations acquired on days from 1 October 2018, to 30 September 2019. The acquisition dates differ between parcels and sources (for example due to cloud obstruction). This is shown for two exemplary parcels in
Figure 2.
2.2. Reference Data for Crop Types and Regions
Reference data for training and validation are based on the Integrated Administration and Control System (IACS), providing the crop type information. Data sets from three federal states of Germany, Brandenburg (BB), Mecklenburg-Vorpommern (MV), and Thuringia (TH) have been used for this study. Together, they contain information for over
million reference parcels. The data for Brandenburg are freely available [
34], the data for the other two states were provided to the authors by the corresponding authorities upon request. They are based on Shapefiles which contain polygons outlining parcels and the respective crops that farmers have declared to their agricultural administrations to be growing there for each year and state. Since each federal state has its own scheme for distinguishing crop types, we harmonized the labels using the definitions from the Joint Experiment for Crop Assessment and Monitoring (JECAM), as described in [
35] (for details about this harmonization see
Appendix F). This way, we use clear crop type definitions, allowing for the extension of the labeling scheme to other German federal states or regions in other countries.
All parcels appearing in these declarations are used, except very small parcels that do not cover at least one Sentinel-1/-2 pixel. We describe crop classes with the following four kinds of crop types:
Main crop types: maize, potatoes, rapeseed, sugar beet, winter barley, winter rye, winter wheat;
Additional crop types: asparagus, lupins, meadows, peas, spring barley, spring oats, spring rye, spring wheat, sunflower;
Not considered: any class not listed above.
Other: additional crop types and not considered.
The main crop types are the most relevant crop types in our study area. The selection has been based on statistical appearance, economic impact, and also the potential of classification for class separation, based on remote sensing expertise. We train our models on all crop types, but usually report only the metrics on the main crop types to keep the presentation concise. More precisely, we will distinguish the seven main crop types and the additional class other, comprising all the crop types which are not among the main crop types (including the crop types which are not considered).
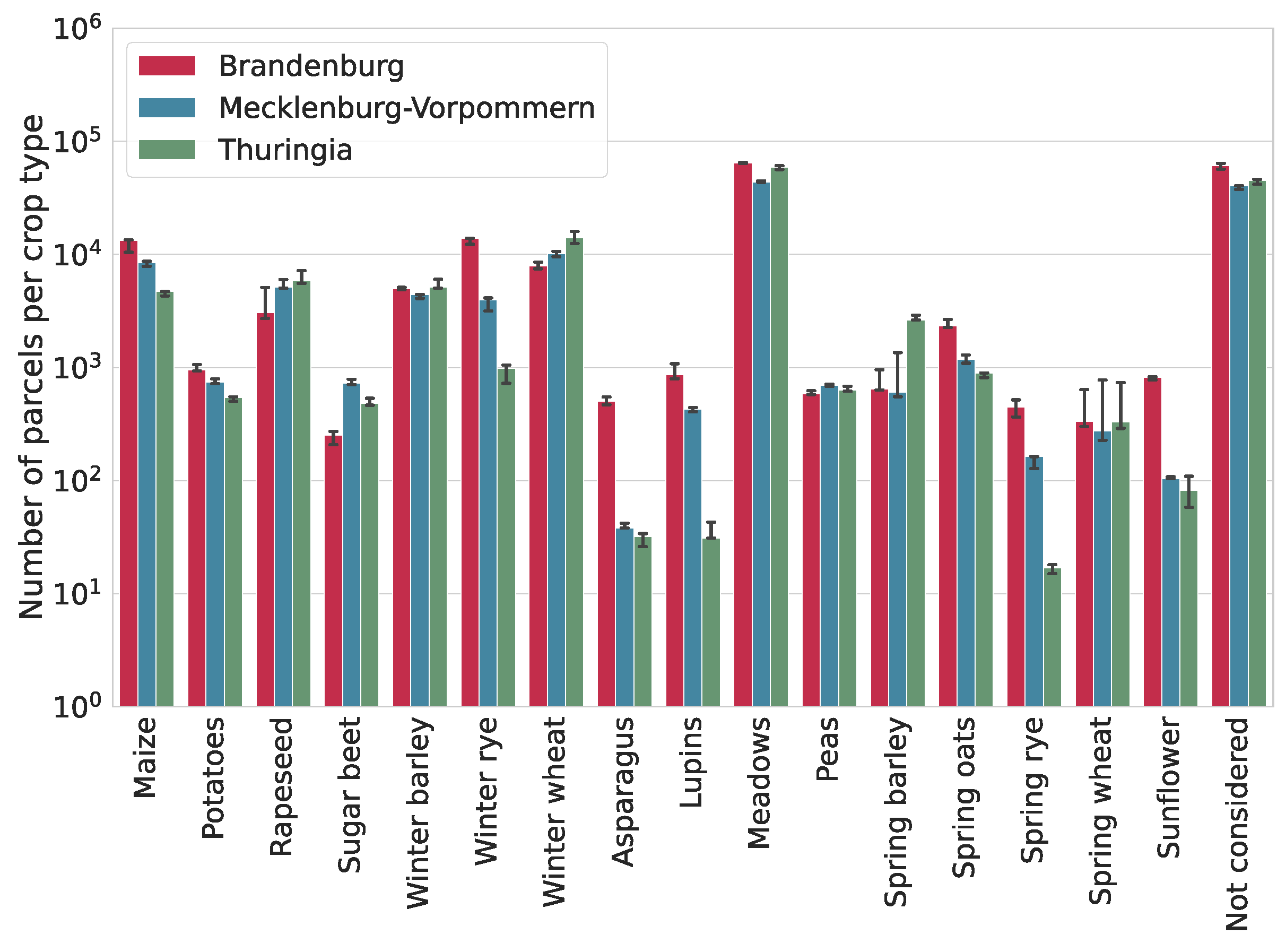
We show the amount of parcels per crop type in our dataset in
Figure 3 for all three years 2018, 2019, and 2020. These numbers do not vary much between the years for a given state, but they can vary between states. For example, asparagus is more common in Brandenburg than in the other states, and winter rye and lupins are comparatively rare in TH.
3. Methods
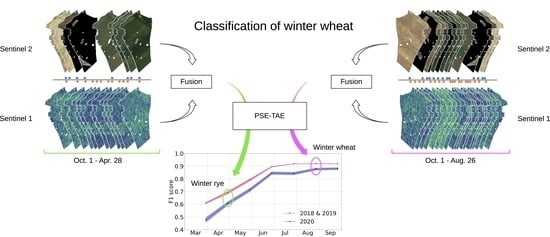
In this section, we detail the developed methods and in particular elaborate on the used machine learning model and its early classification, as well as data fusion capabilities. The model builds on previous work [
22] and leverages the
attention mechanism originally introduced in the famous Transformer architecture [
21], aiming to better exploit relevant information about crop types included in the change of satellite images over time. At the same time, certain aspects need to be modified, such as, e.g., the positional encoding, in order to be able to train and predict on regions and data sources with differing acquisition time points.
3.1. Deep Learning Model
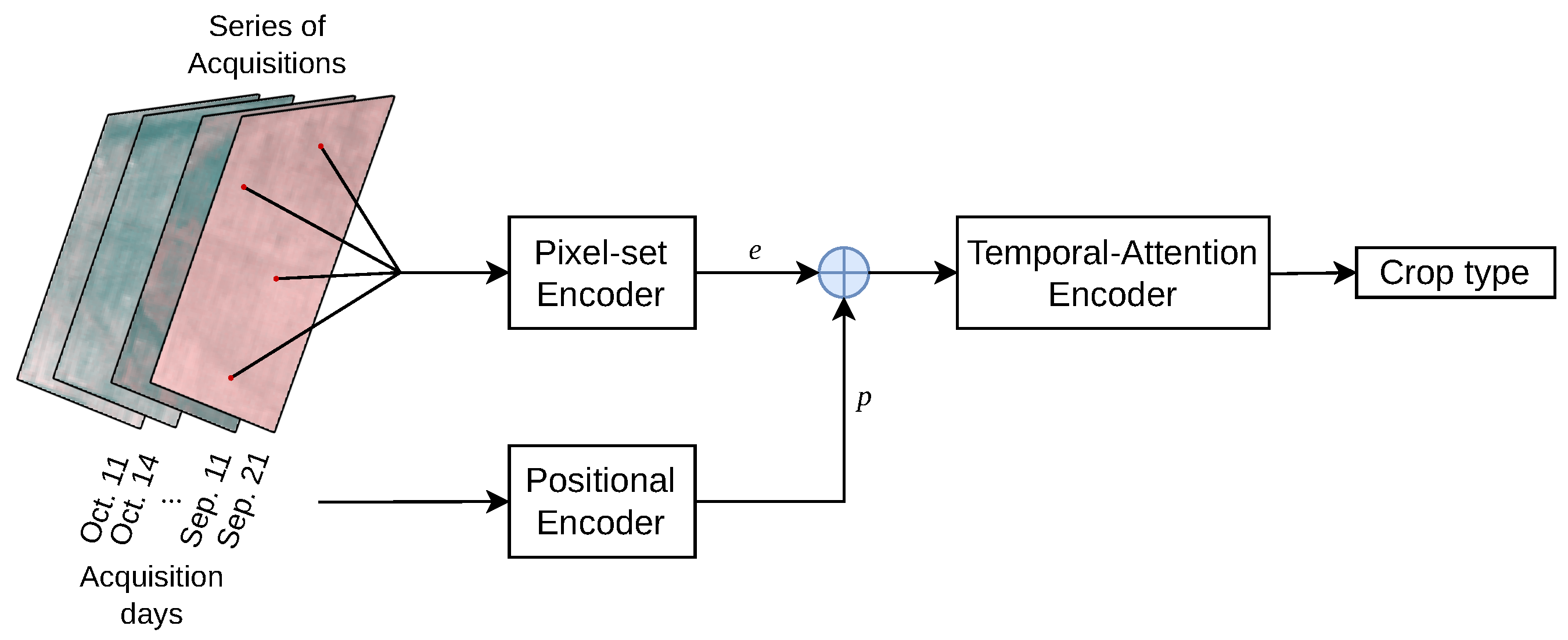
Our work mainly builds on the Pixel-Set Encoder–Temporal-Attention Encoder (PSE-TAE) model introduced in [
22]. This neural network consists of three steps which are executed for each parcel. These steps and the most important modifications to them in this study are briefly outlined in the following (see also
Figure 4):
Pixel-set encoder (PSE): fully connected neural networks are applied to a random sample of 10 pixel positions from a parcel. This yields a vector
for each index
(all input time series are padded to a common length of
). The pixel sampling is random during training, i.e., usually a different set of pixels is chosen every time a parcel is loaded. However, the random number generator is seeded during evaluation to make the predictions for a given model reproducible. We also experiment with a different encoding technique: we simply pass the averages of the selected pixels to the TAE (see
Appendix D).
Positional encoding: time information
is added to each vector
. The positional encoding mechanism thereby takes care of different temporal acquisition patterns, as it adds the information about the acquisition date directly to the parcel observation serving as an input for the next step. The specific implementation of the temporal encoding is the most important architectural change in this study compared to [
22]: In contrast to the original model, the actual acquisition day relative to the start of the growing season (e.g., “day 6”) instead of the acquisition count (e.g., “acquisition number 2”) is used to calculate
. This provides greater flexibility with regard to the temporal patterns in the input data (see also
Section 3.3). More details about the positional encoding mechanism can be found in
Appendix A.2.
Temporal-attention encoder (TAE): the main component of this step is the attention mechanism originally introduced in the famous Transformer architecture [
21] for natural language processing (NLP). There it is used to encode text as a sequence of vectors indexed by the position of each word in a sentence and specifically encourages interactions between different words, i.e., it can learn context. This allows to compute semantically meaningful representations of sentences. Based on the observation that a parcel’s development can be represented as a sequence of vectors indexed by time and that the change of a parcels appearance over time is an important factor when classifying crop types, attention is used in an analogous setting here: instead of a sequence of words, the corresponding neural network layer encodes a time series of parcel observations and their interactions, which is then used to compute the final classification.
Further details on our model and modifications with respect to [
22] can be found in
Appendix A, a description of our training parameters can be found in
Appendix C.
3.2. Normalization
Since we want to concatenate data from Sentinel-1 (S1) and Sentinel-2 (S2), first a normalization of the input data for each source needs to be completed. This usually helps a deep learning model to converge better. For each channel c, we collected the values observed in the train set for Brandenburg and Mecklenburg-Vorpommern (BB + MV) for 2019 and computed their mean and standard deviation . During data loading, each input channel is then normalized via .
3.3. Data Fusion
We deal with the varying resolution of satellite bands by converting everything to 20 m resolution. For data in 10 m resolution, we only use every other pixel along the horizontal and the vertical axis. Since we do not use texture but a set of sampled pixels, we do not expect to lose relevant information by this simple and efficient strategy. We did not try other strategies, but refer to studies such as [
36,
37] for alternatives. Note that the model itself is resolution agnostic: as we sample pixels for each parcel to be classified, it could be used with data in 10 m resolution without any changes.
We fuse the data early at the input-level before sending it to the model: this means that we concatenate the observations from S1 and S2 for each day on which there was an image acquisition from at least one of the two (concatenation along channels). For days on which there was only an acquisition from one of the data sources, the special no data value is used to fill in the missing data from the other source. Since the positional encoding includes information about the exact acquisition day for each observation, no temporal interpolation is needed to align the time series from different modalities, regardless of vastly different acquisition patterns.
3.4. Early Classification
The main objective and use case is to predict crop types early during the year. Additionally, the application of a model trained on data from earlier years on a later year, from which no data have been seen during training will be performed. Crucially, only the input data are modified in order to learn early classification, the architecture described in
Section 3.1 remains unchanged.
Temporal masking: the operation used for input data modification is the following: for a given satellite image time series
x and a date index
, we define
where
is the last observation in
x acquired at most
D days after October 1st of the preceding year, i.e.,
and
. We say the
time series x bounded by the D-th day. This means that we mask out some of the acquisition time points in order to simulate the situation in early crop classification when there is only data available up until a certain point in time. Specifically, this also means that the data fusion mechanism described in
Section 3.3 can be applied in the same way as when classifying time series from a complete growing cycle.
We try two approaches for training models:
- (S)
Train separate models for separate periods, e.g., the model to be used at the end of May is trained on the time series (end of May is approximately days after 1 October). When predicting the crop type for a parcel with data available until a certain month, we use the corresponding model.
- (U)
Train a unified model: the training data spans full hydrological years. However, during training, we apply random temporal masking, i.e., we randomly select a day D for each parcel and epoch and use only as input data. This way, we simulate having observations only until a certain date. Then we use this single trained model for all time series lengths at prediction time—no matter whether they contain only data from a few months or from the full year.
In the evaluation, we always use observations until a given date, e.g.,
contains all observations until approximately the end of February (five months counting from October). Each model from approach (S) is evaluated with data restricted to the same period it was trained for. When evaluating approach (U) for each bound
D on the days, we simply evaluate the unified model on the data bounded by
D. In practice, we run our evaluations for
, see
Section 4.3.
3.5. Train/Test Splits
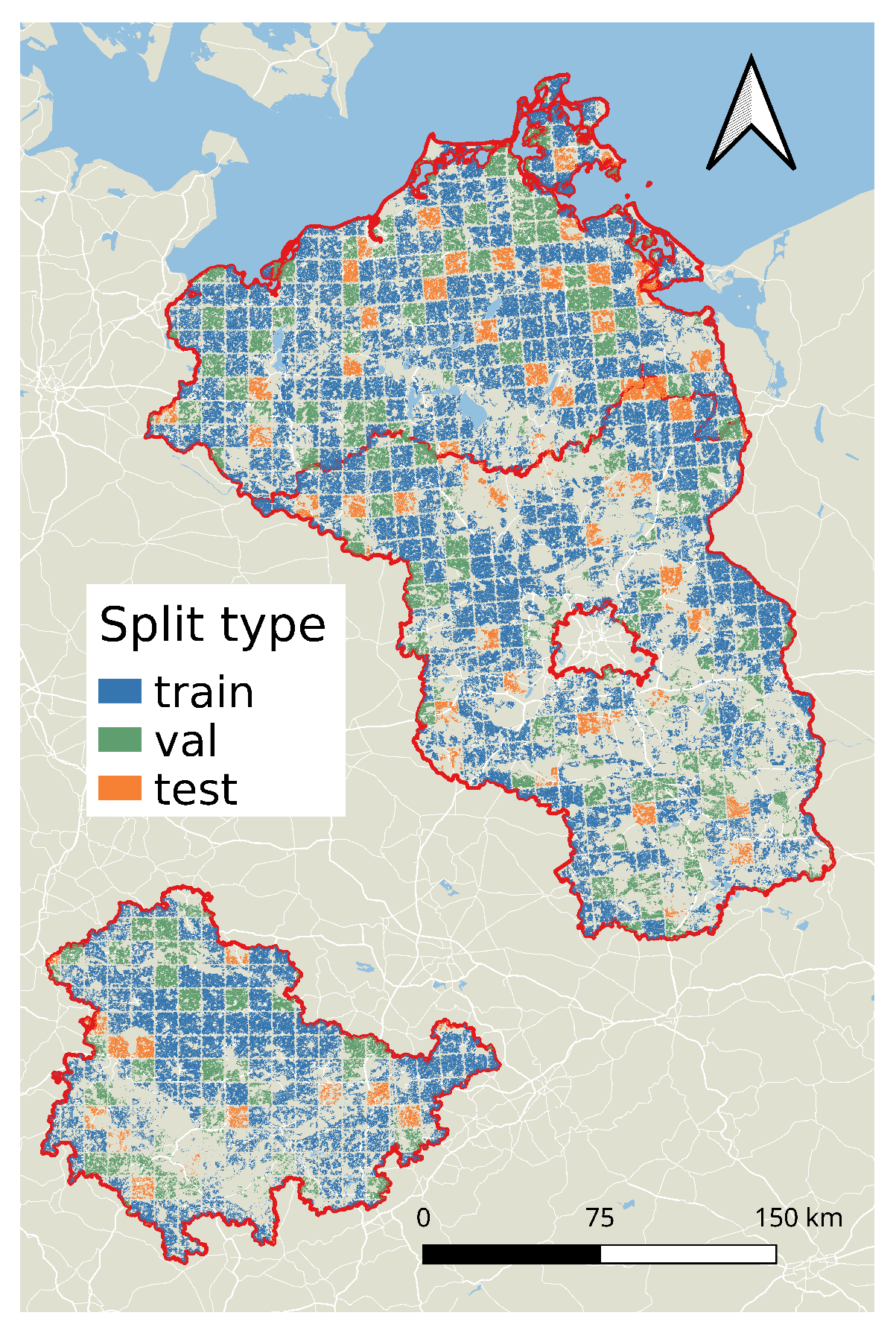
The area of interest consisting of the three states is split into train, validation, and test regions. The area is covered by grid squares from the Military Grid Reference System (MGRS, Ref. [
38]). We use the grid squares with precision
as tiles of size
which cover the area, e.g., the MGRS coordinate 33UUV85 denotes such a tile lying inside Mecklenburg-Vorpommern. We created a random split of these tiles into train, validation, and test tiles—using a ratio of 7:2:1. Each parcel is assigned to train/validation/test depending on the MGRS tile covering it. We drop the parcels whose centers lay within a margin of 250 m to the tile border, in order to avoid data leakage between splits. For example, we assign the tile 33UUV85 to the train split, hence all parcels whose centers are located at least 250 m from the border of the tile belong to the train set. We show the result of this split for Brandenburg, Mecklenburg-Vorpommern, and Thuringia in
Figure 1. This split is kept the same during all years. We took the idea for this tile-wise split from [
23].
3.6. Metrics
The dataset shows a strong class imbalance (
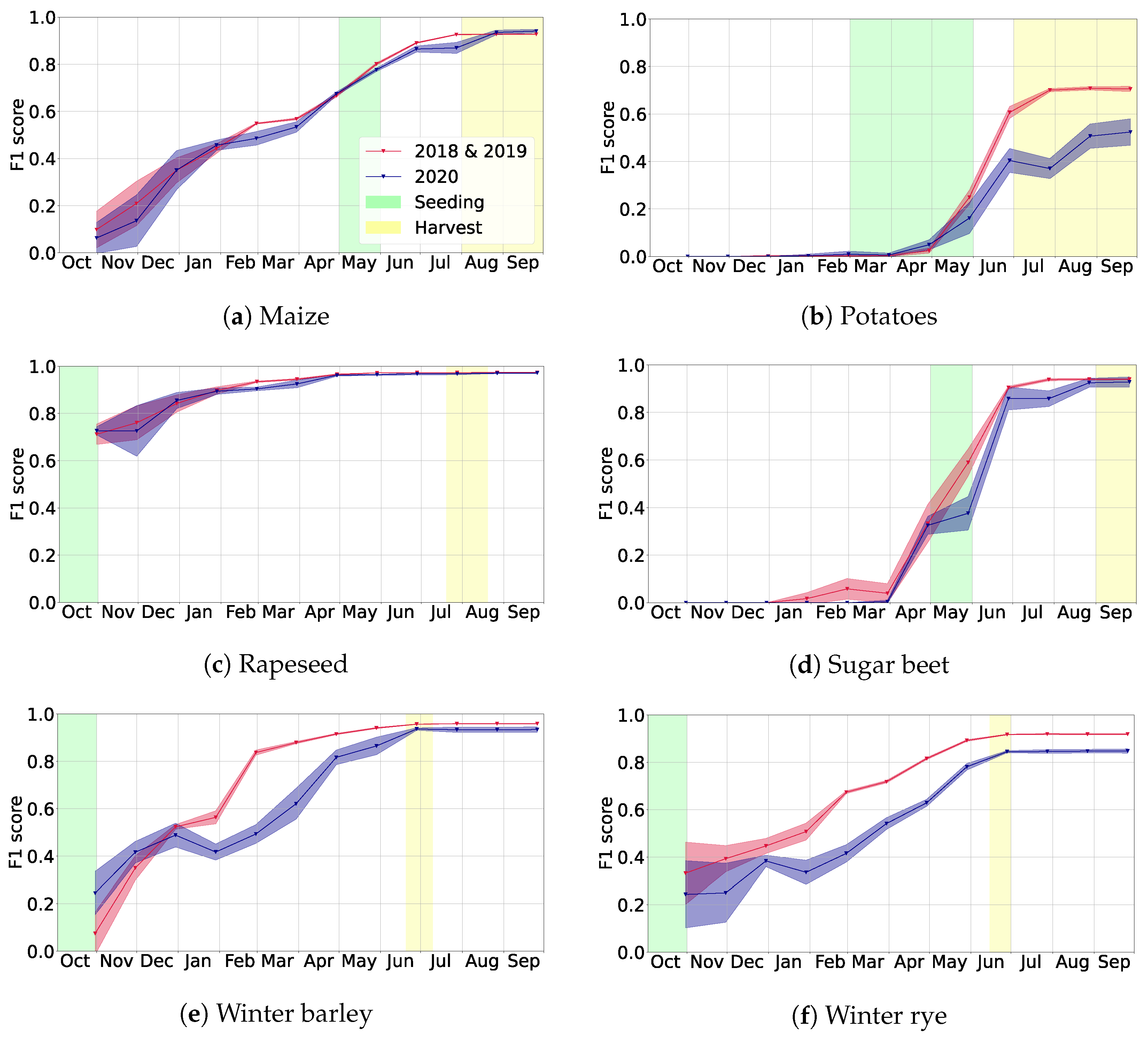
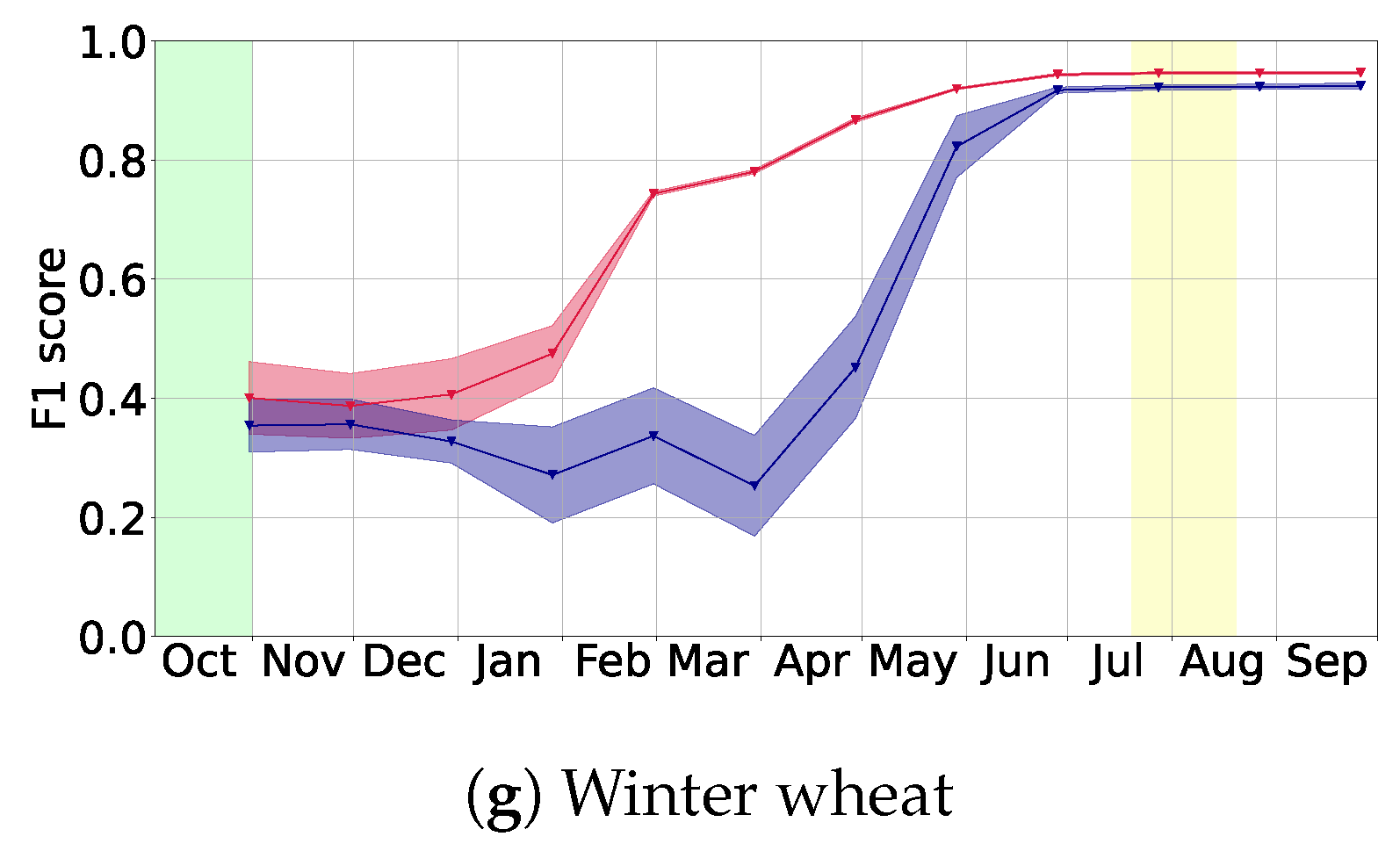
Figure 3). Hence, measuring the prediction quality using overall accuracy would mean that the most frequent crop types would dominate the computation, for example winter wheat and the irrelevant class “other”. We therefore decided to mainly report the (class-wise) F1 metric. However, we sometimes mention the overall accuracy as well. Mainly to make our results more easily comparable to related work, which often reports overall accuracy.
For every crop type, we count the number of correctly predicted parcels and incorrectly predicted parcels. This yields the usual recall (sometimes called producer’s accuracy) and precision (user’s accuracy). Their harmonic mean is the F1 score for each crop type.
We consider the arithmetic mean (macro average) of the F1 scores of the main crop types our standard measure of the prediction quality and call it main F1 score. Using this metric, each crop type has the same influence on the overall score. We always report metrics on the test set, the validation set is used for tuning hyperparameters during training and model development.
6. Conclusions
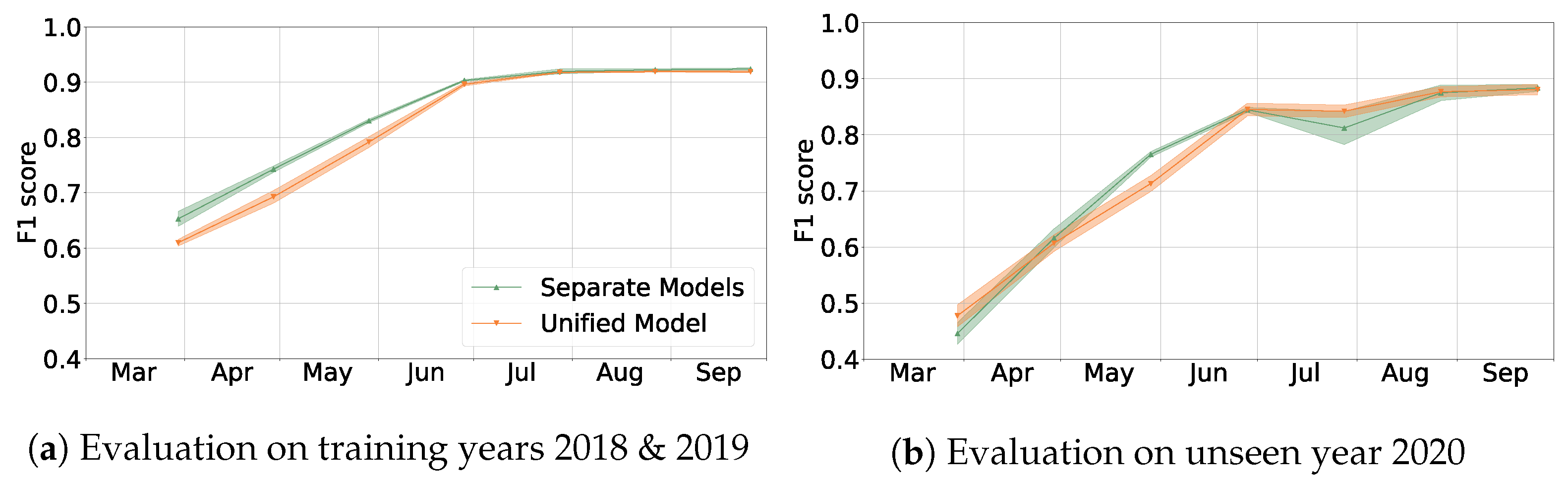
In this article, we presented a flexible deep learning based method for the classification of crop types growing on a given parcel. The corresponding model performs best when using Sentinel-1 and Sentinel-2 data together, while also leading to reasonable performance when only relying on data from Sentinel-1. We showed that it generalizes well to a new year that was not seen during training. Furthermore, we observed that using training data from several years and regions simultaneously increases prediction performance and that using additional train and validation data should be helpful for future research to analyze the generalization abilities of the approach. For both aspects, one can imagine some saturation, for example when lots of different weather conditions were used in the training years. Crucially, we may conclude that our model can conduct classification early in the year: we typically reached F1 scores above at least a month before harvest time.
Apart from the amount of data it was trained on, the two main advantages of our model are that on the one hand it can easily incorporate further data sources without the need for temporal interpolation due to its flexible data fusion mechanism, and on the other hand that a single model can predict crops at an arbitrary time point during the growing season.
In order to scale the application of the model (for example to be able to operationalize it as a service), the transferability to other regions with different growing patterns, smaller field sizes, and different crop types need to be studied.