Different Influences on “Wave Turbopause” Exerted by 6.5 DWs and Gravity Waves
Abstract
1. Introduction
2. Materials and Methods
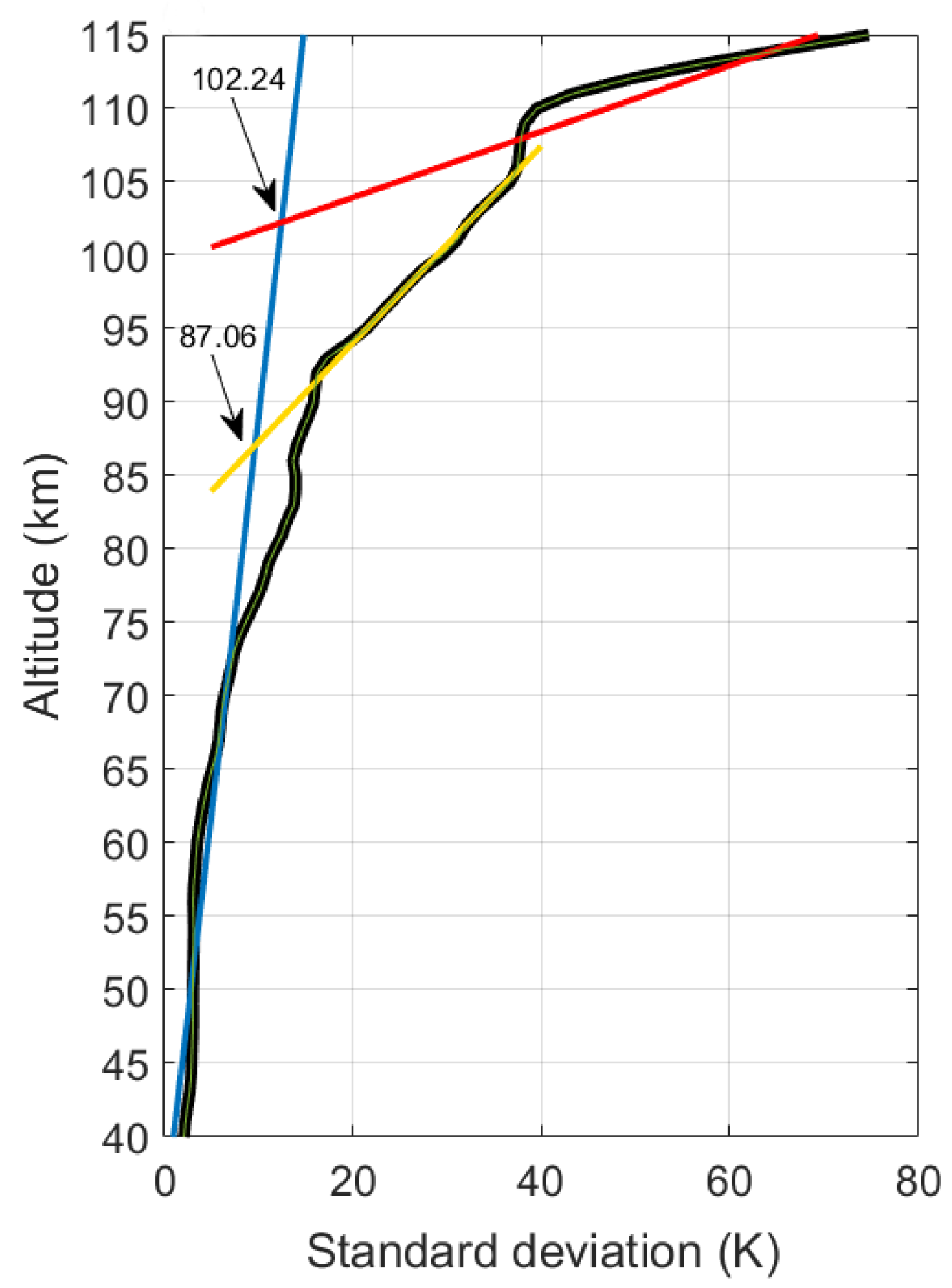
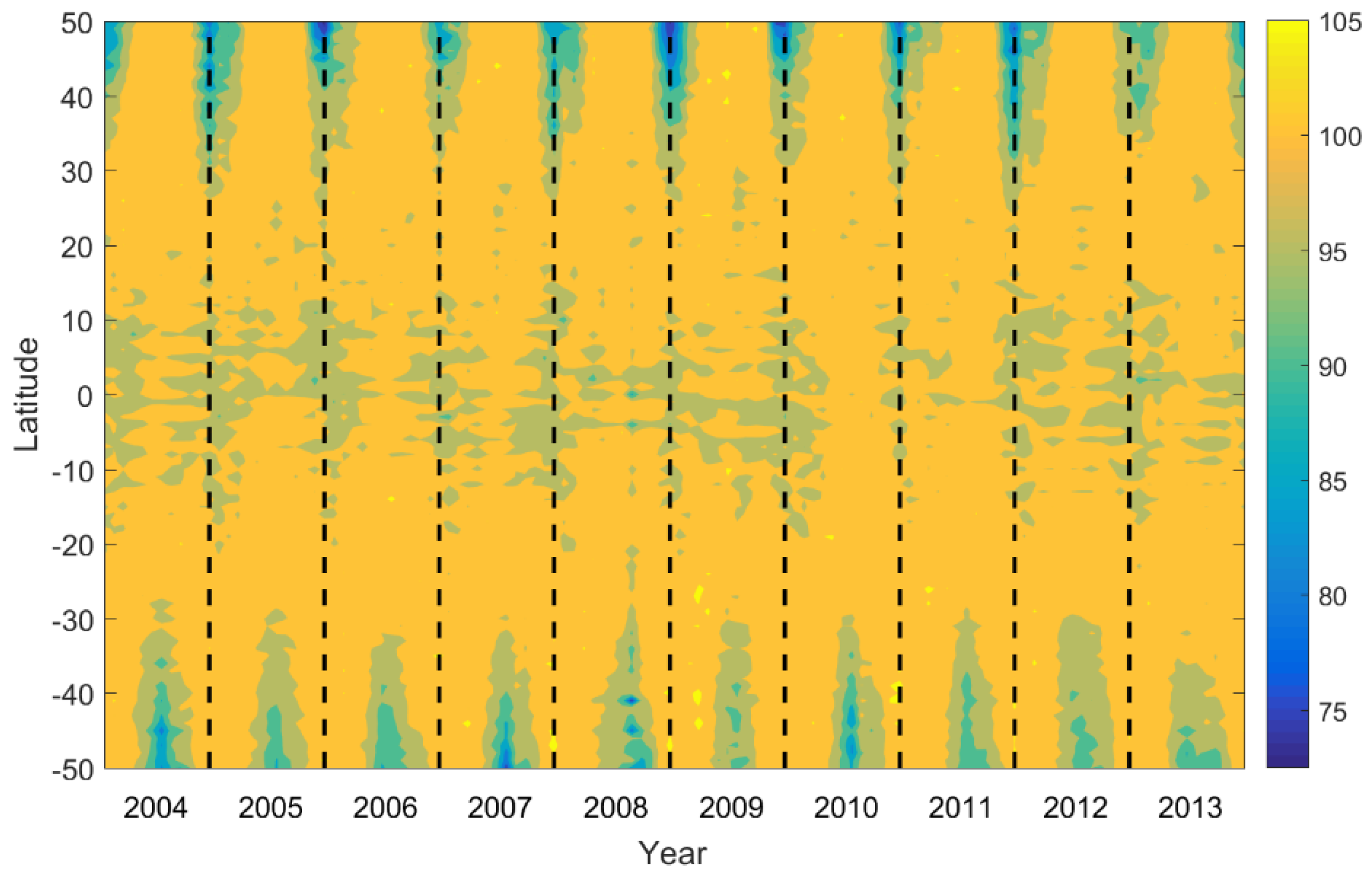
2.1. Determination of the “Wave Turbopause”
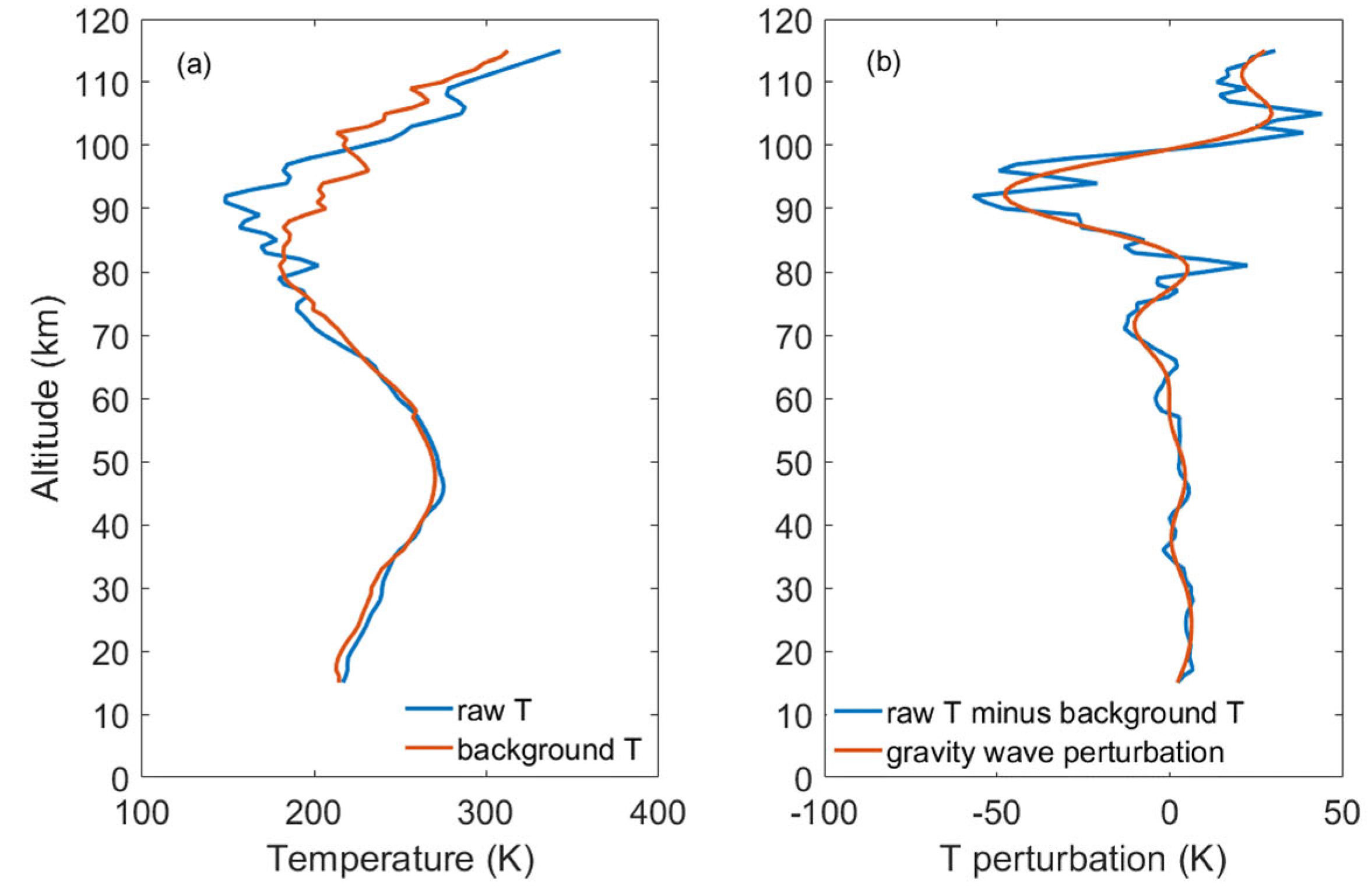
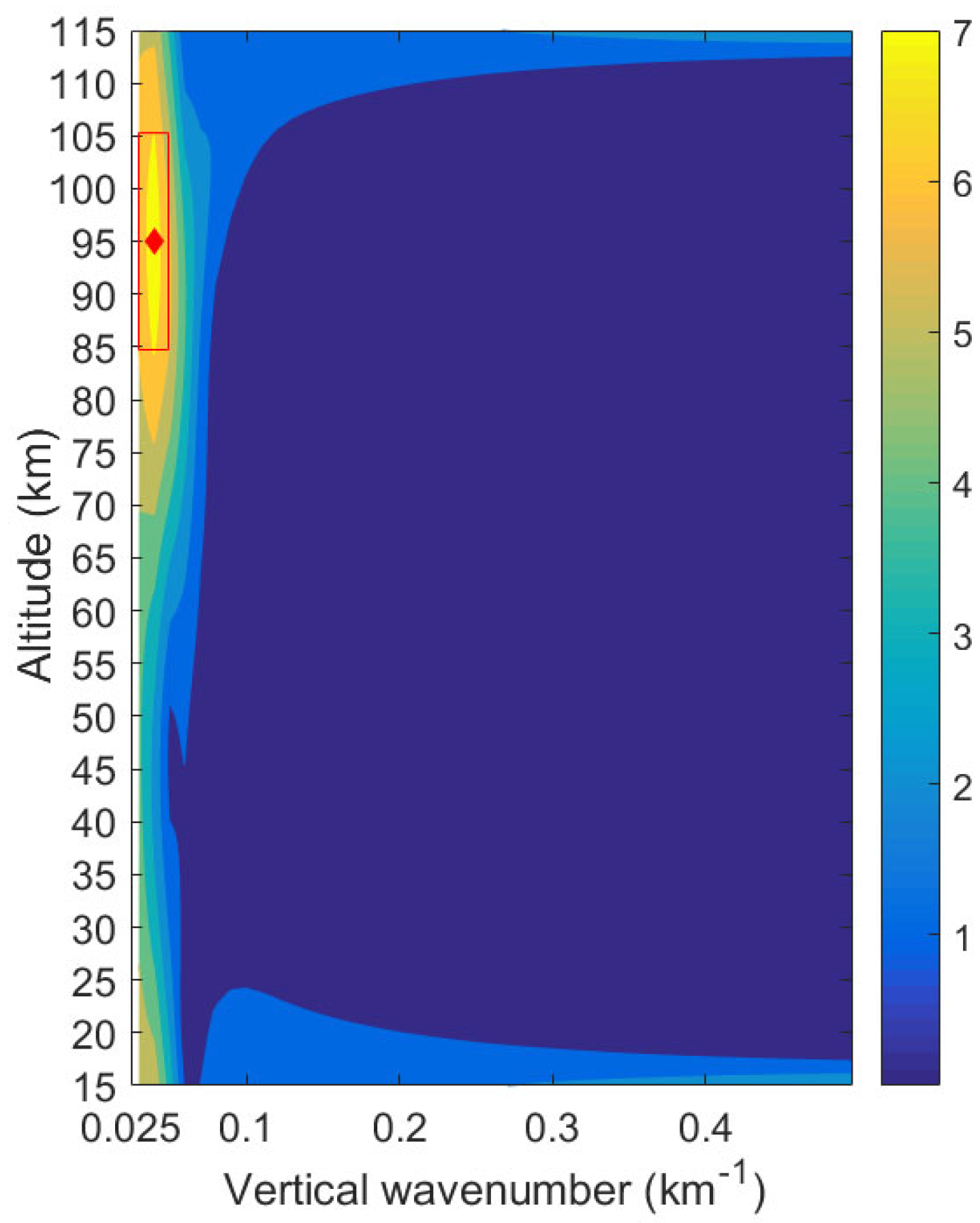
2.2. Identifying Temperature due to 6.5 DWs and Gravity Waves
3. Results
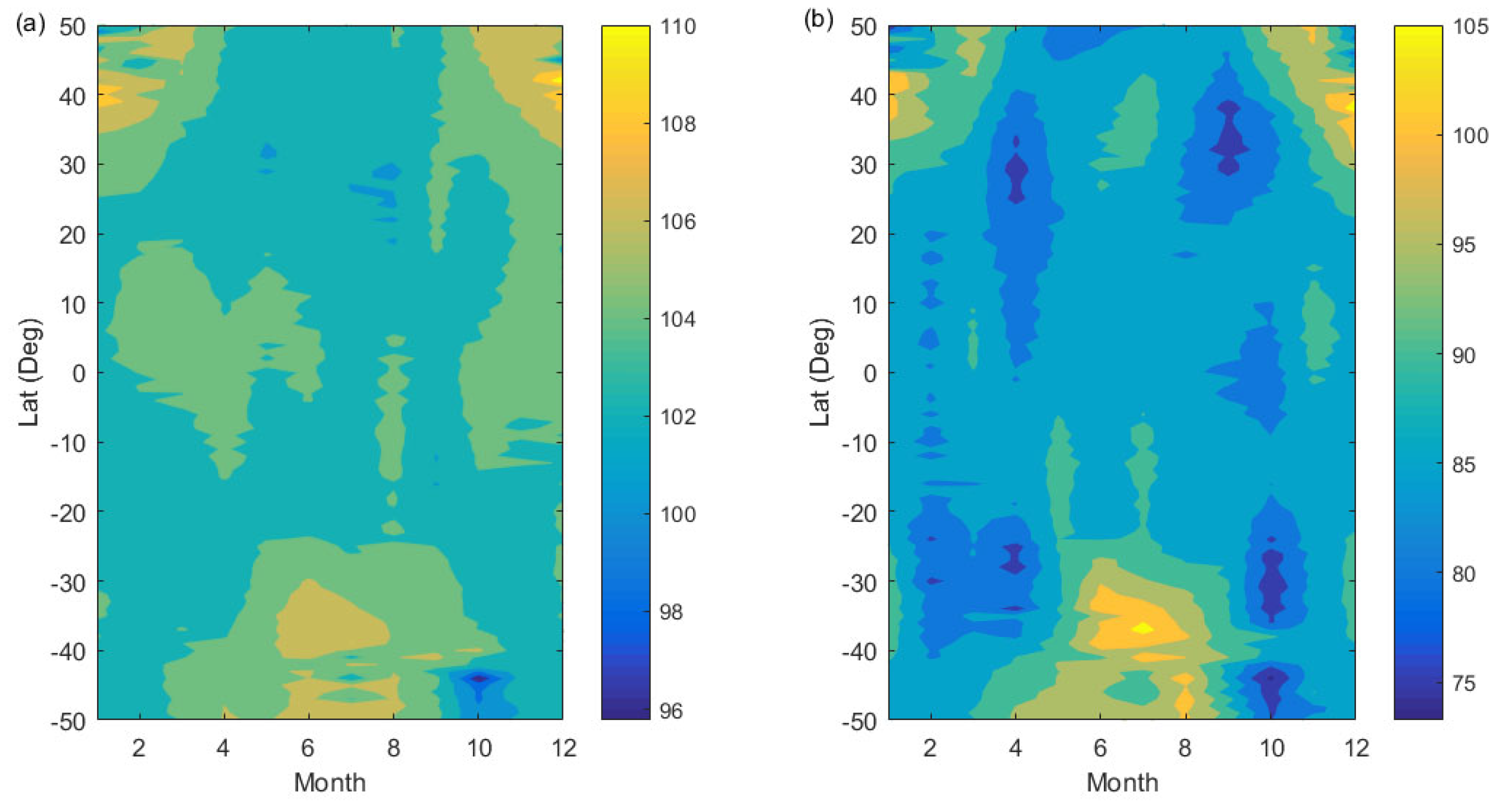
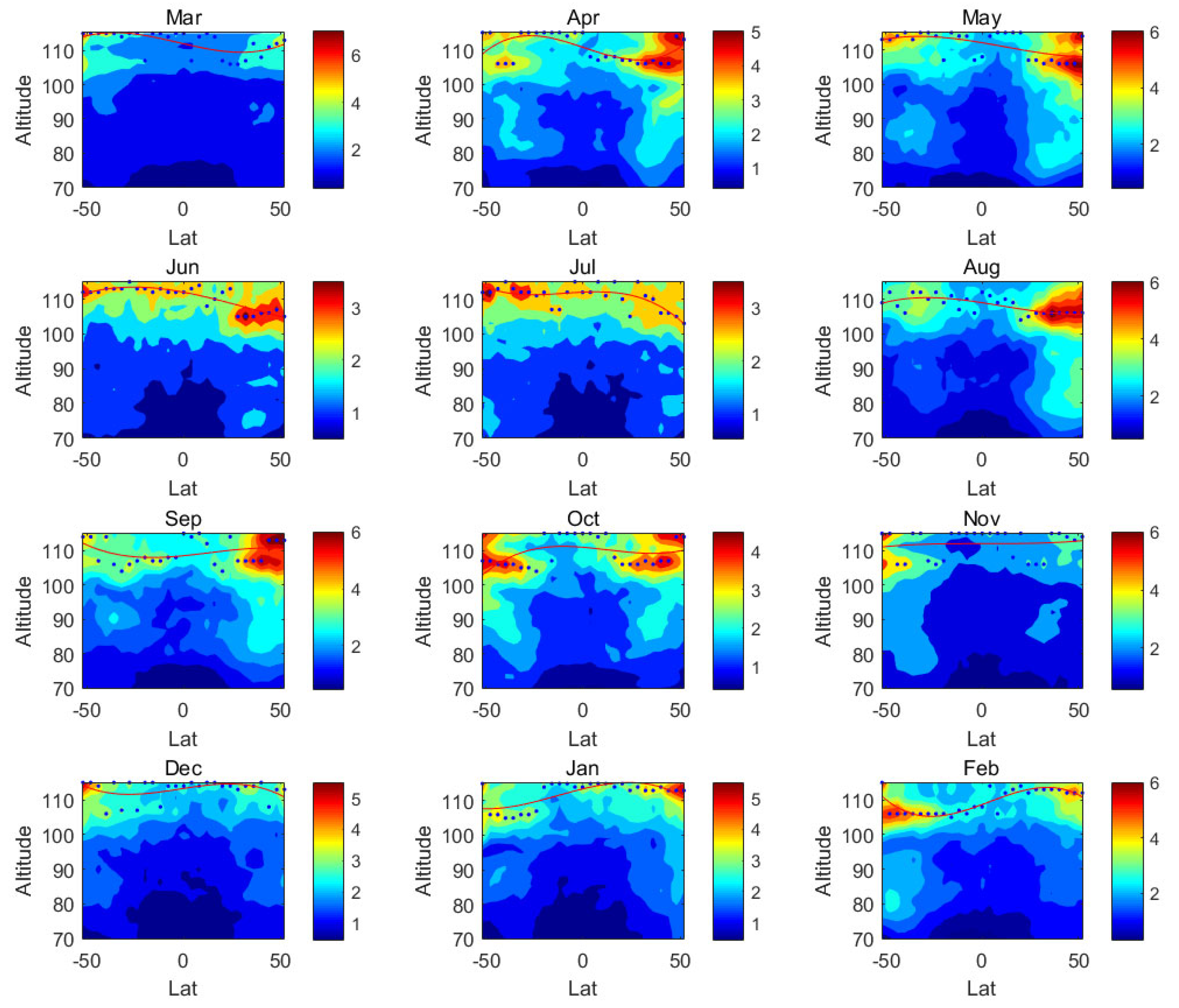
3.1. Seasonal Variation in the “Wave Turbopause” Layer
3.2. Seasonal Variations in the Peak Height of Amplitude for 6.5 DWs
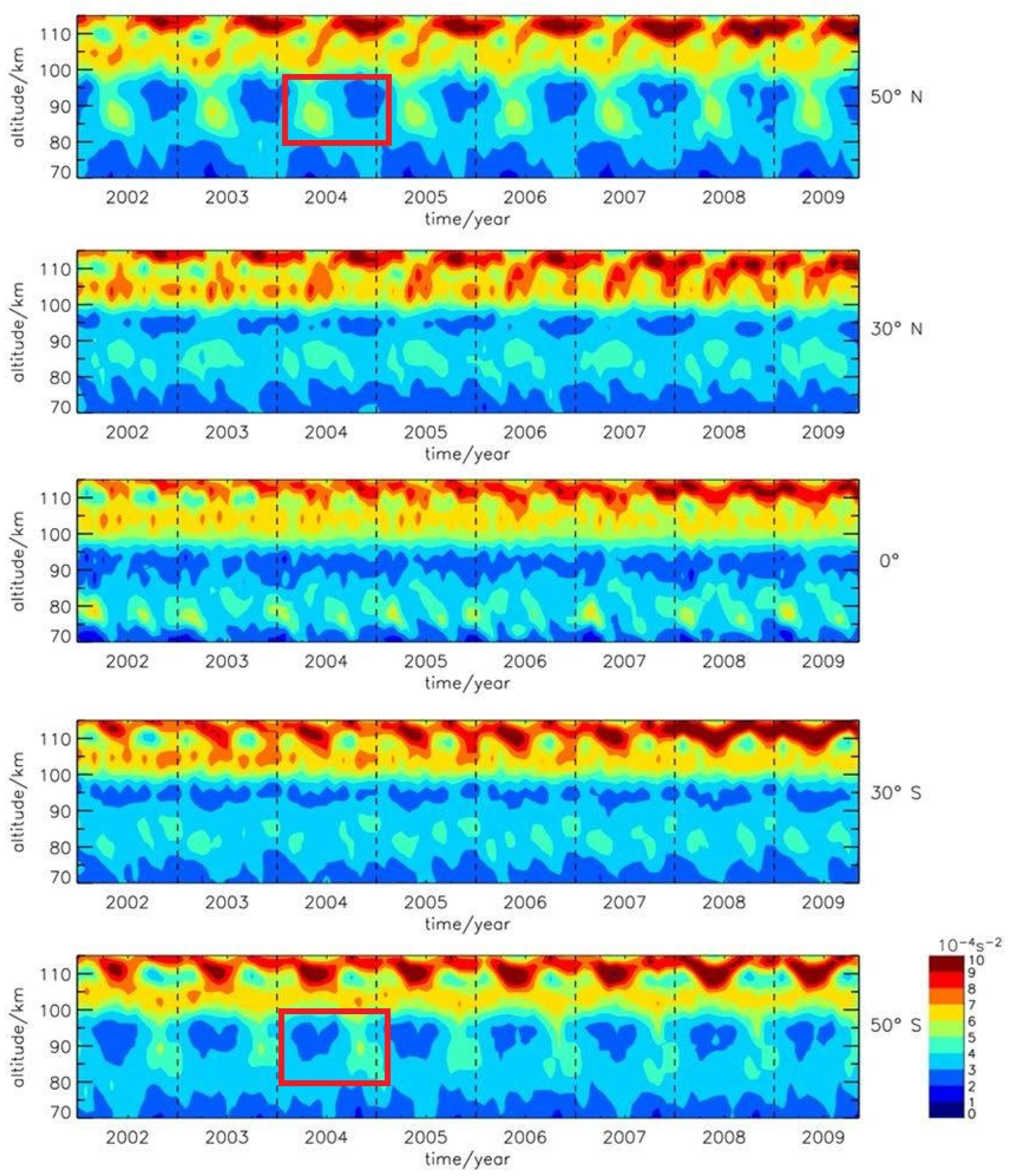
3.3. Seasonal Variations in the Peak Height of Amplitude for Gravity Waves
4. Discussion
5. Conclusions
- (1)
- Seasonal variations of the “wave turbopause” and the peak height of amplitude for 6.5 DWs are roughly the same. Both reach their maximum at the winter pole and their minimum at the summer pole.
- (2)
- Seasonal variations of the “wave turbopause” and the peak height of amplitude for gravity waves are anti-correlated. PHA for gravity waves is lower in the winter pole and higher in the summer pole.
- (3)
- A possible reason for the anti-correlation may lie on the Brunt–Vaisala frequency from 80 to 100 km. Relatively unstable atmosphere causes gravity waves to break at a lower height instead of propagating upward.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hall, C.M.; Manson, A.H.; Meek, C.E. Seasonal Variation of the Turbopause: One Year of Turbulence Investigation at 69° N by the Joint University of Tromsø/University of Saskatchewan MF Radar. J. Geophys. Res. 1998, 103, 28769–28773. [Google Scholar] [CrossRef]
- Offermann, D.; Friedrich, V.; Ross, P.; Zahn, U.V. Neutral Gas Composition Measurements between 80 and 120 Km. Planet. Space Sci. 1981, 29, 747–764. [Google Scholar] [CrossRef]
- Bishop, R.L.; Larsen, M.F.; Hecht, J.H.; Liu, A.Z.; Gardner, C.S. TOMEX: Mesospheric and Lower Thermospheric Diffusivities and Instability Layers. J. Geophys. Res. Atmos. 2004, 109, D02S03. [Google Scholar] [CrossRef]
- Lehmacher, G.A.; Larsen, M.F.; Bilén, S.; Croskey, C.L.; Mitchell, J.D.; Lübken, F.J.; Rapp, M.; Collins, R. “Where is the turbopause?” Rocket campaign: Overview and first results. In Proceedings of the 19th ESA Symposium on European Rocket and Balloon Programmes and Related Research, Bad Reichenhall, Germany, 7–11 June 2009. [Google Scholar]
- Danilov, A.D.; Kalgin, A.; Pokhunkov, A.A. Variation of the Turbopause Level in The Polar Regions—Sciencedirect. In Proceedings of the Open Meetings of the Working Groups on Physical Sciences of the Twenty-First Plenary Meeting of COSPAR, Innsbruck, Austria, 29 May–10 June 1978; pp. 173–176. [Google Scholar]
- Hall, C.M.; Meek, C.E.; Manson, A.H.; Nozawa, S. Turbopause Determination, Climatology, and Climatic Trends Using Medium Frequency Radars at 52° N and 70° N. J. Geophys. Res. 2008, 113, D13104. [Google Scholar] [CrossRef]
- Offermann, D.; Jarisch, M.; Schmidt, H.; Oberheide, J.; Grossmann, K.U.; Gusev, O.; Iii, J.M.R.; Mlynczak, M.G. The “Wave Turbopause”. J. Atmos. Sol. Terr. Phys. 2007, 69, 2139–2158. [Google Scholar] [CrossRef]
- Zhao, X.R.; Sheng, Z.; Li, J.W.; Yu, H.; Wei, K.J. Determination of the “Wave Turbopause” Using a Numerical Differentiation Method. J. Geophys. Res. D. Atmos. JGR 2019, 124, 10592–10607. [Google Scholar] [CrossRef]
- Offermann, D.; Jarisch, M.; Oberheide, J.; Gusev, O.; Wohltmann, I.; Iii, J.; Mlynczak, M.G. Global Wave Activity from Upper Stratosphere to Lower Thermosphere: A New Turbopause Concept. J. Atmos. Sol. Terr. Phys. 2006, 68, 1709–1729. [Google Scholar] [CrossRef]
- Fritts, D.C. Gravity Wave Dynamics and Effects in the Middle Atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- He, Y.; Sheng, Z.; He, M. The Interaction Between the Turbulence and Gravity Wave Observed in the Middle Stratosphere Based on the Round-Trip Intelligent Sounding System. Geophys. Res. Lett. 2020, 47, e2020GL088837. [Google Scholar] [CrossRef]
- He, Y.; Zhu, X.; Sheng, Z.; Zhang, J.; Zhou, L.; He, M. Statistical Characteristics of Inertial Gravity Waves over a Tropical Station in the Western Pacific Based on High-Resolution GPS Radiosonde Soundings. J. Geophys. Res. Atmos. 2021, 126, e2021JD034719. [Google Scholar] [CrossRef]
- He, Y.; Zhu, X.; Sheng, Z.; He, M.; Feng, Y. Observations of Inertia Gravity Waves in the Western Pacific and Their Characteristic in the 2015/2016 Quasi-Biennial Oscillation Disruption. JGR Atmos. 2022, 127, e2022JD037208. [Google Scholar] [CrossRef]
- Ji, Q.; Zhu, X.; Sheng, Z.; Tian, T. Spectral Analysis of Gravity Waves in the Martian Thermosphere during Low Solar Activity Based on MAVEN/NGIMS Observations. ApJ 2022, 938, 97. [Google Scholar] [CrossRef]
- Zhang, J.; Ji, Q.; Sheng, Z.; He, M.; He, Y.; Zuo, X.; He, Z.; Qin, Z.; Wu, G. Observation Based Climatology Martian Atmospheric Waves Perturbation Datasets. Sci. Data 2023, 10, 4. [Google Scholar] [CrossRef] [PubMed]
- Offermann, D.; Gusev, O.; Donner, M.; Forbes, J.M.; Hagan, M.; Mlynczak, M.G.; Oberheide, J.; Preusse, P.; Schmidt, H.; Russell, J.M. Relative Intensities of Middle Atmosphere Waves. J. Geophys. Res. Atmos. 2009, 114, D06110. [Google Scholar] [CrossRef]
- Remsberg, E.E.; Gordley, L.L.; Marshall, B.T.; Thompson, R.E.; Burton, J.; Bhatt, P.; Harvey, V.L.; Lingenfelser, G.; Natarajan, M. The Nimbus 7 LIMS Version 6 Radiance Conditioning and Temperature Retrieval Methods and Results. J. Quant. Spectrosc. Radiat. Transf. 2004, 86, 395–424. [Google Scholar] [CrossRef]
- John, S.R.; Kumar, K.K. The Concept of Wave-Turbopause Layer and Its Signature in the Global Mesosphere-Lower Thermospheric Gravity Wave Activity. J. Geophys. Res. Space Phys. 2012, 117, A10310. [Google Scholar] [CrossRef]
- Preusse, P.; Eckermann, S.; Oberheide, J.; Hagan, M.; Offermann, D. Modulation of Gravity Waves by Tides as Seen in CRISTA Temperatures. Adv. Space Res. Off. J. Comm. Space Res. (COSPAR) 2001, 27, 1773–1778. [Google Scholar] [CrossRef]
- Ern, M.; Preusse, P.; Gille, J.C.; Hepplewhite, C.L.; Mlynczak, M.G.; Russell, J.M.; Riese, M. Implications for Atmospheric Dynamics Derived from Global Observations of Gravity Wave Momentum Flux in Stratosphere and Mesosphere. J. Geophys. Res. 2011, 116, D19107. [Google Scholar] [CrossRef]
- Alexander, P.; Schmidt, T.; De La Torre, A. A Method to Determine Gravity Wave Net Momentum Flux, Propagation Direction and “Real” Wavelengths: A GPS Radio Occultations Soundings Case Study. Earth Space Sci. 2018, 5, 222–230. [Google Scholar] [CrossRef]
- Stockwell, B.R.; Mansinha, L.; Lowe, R. Localization of the Complex Spectrum: The S Transform, Signal Processing. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Cao, W.X. Observations of Atmospheric Mesopause and Wave Turbopause by SABER/TIMED Satellite. Doctoral Dissertation, Wuhan University, Wuhan, China, 2012. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, W.; Sheng, Z.; Huang, Y.; He, Y.; Liao, Q.; Chang, S. Different Influences on “Wave Turbopause” Exerted by 6.5 DWs and Gravity Waves. Remote Sens. 2023, 15, 800. https://doi.org/10.3390/rs15030800
Ge W, Sheng Z, Huang Y, He Y, Liao Q, Chang S. Different Influences on “Wave Turbopause” Exerted by 6.5 DWs and Gravity Waves. Remote Sensing. 2023; 15(3):800. https://doi.org/10.3390/rs15030800
Chicago/Turabian StyleGe, Wei, Zheng Sheng, Yingying Huang, Yang He, Qixiang Liao, and Shujie Chang. 2023. "Different Influences on “Wave Turbopause” Exerted by 6.5 DWs and Gravity Waves" Remote Sensing 15, no. 3: 800. https://doi.org/10.3390/rs15030800
APA StyleGe, W., Sheng, Z., Huang, Y., He, Y., Liao, Q., & Chang, S. (2023). Different Influences on “Wave Turbopause” Exerted by 6.5 DWs and Gravity Waves. Remote Sensing, 15(3), 800. https://doi.org/10.3390/rs15030800






