Individual Tree Segmentation from Side-View LiDAR Point Clouds of Street Trees Using Shadow-Cut
Abstract
1. Introduction
- (1)
- Compared with the current individual tree segmentation methods, the method proposed in this study is not limited to the information of canopy, but also takes into account the information of the undergrowth trees to achieve multi-directional segmentation of the side face of trees.
- (2)
- Due to the complex structure of 3D vegetation point clouds, we propose extracting 3D point cloud contours through the edge information in 2D images and realize the mapping from 2D edges to 3D contours, thus solving the segmentation problem of the tree point clouds in 3D space.
2. Materials and Methods
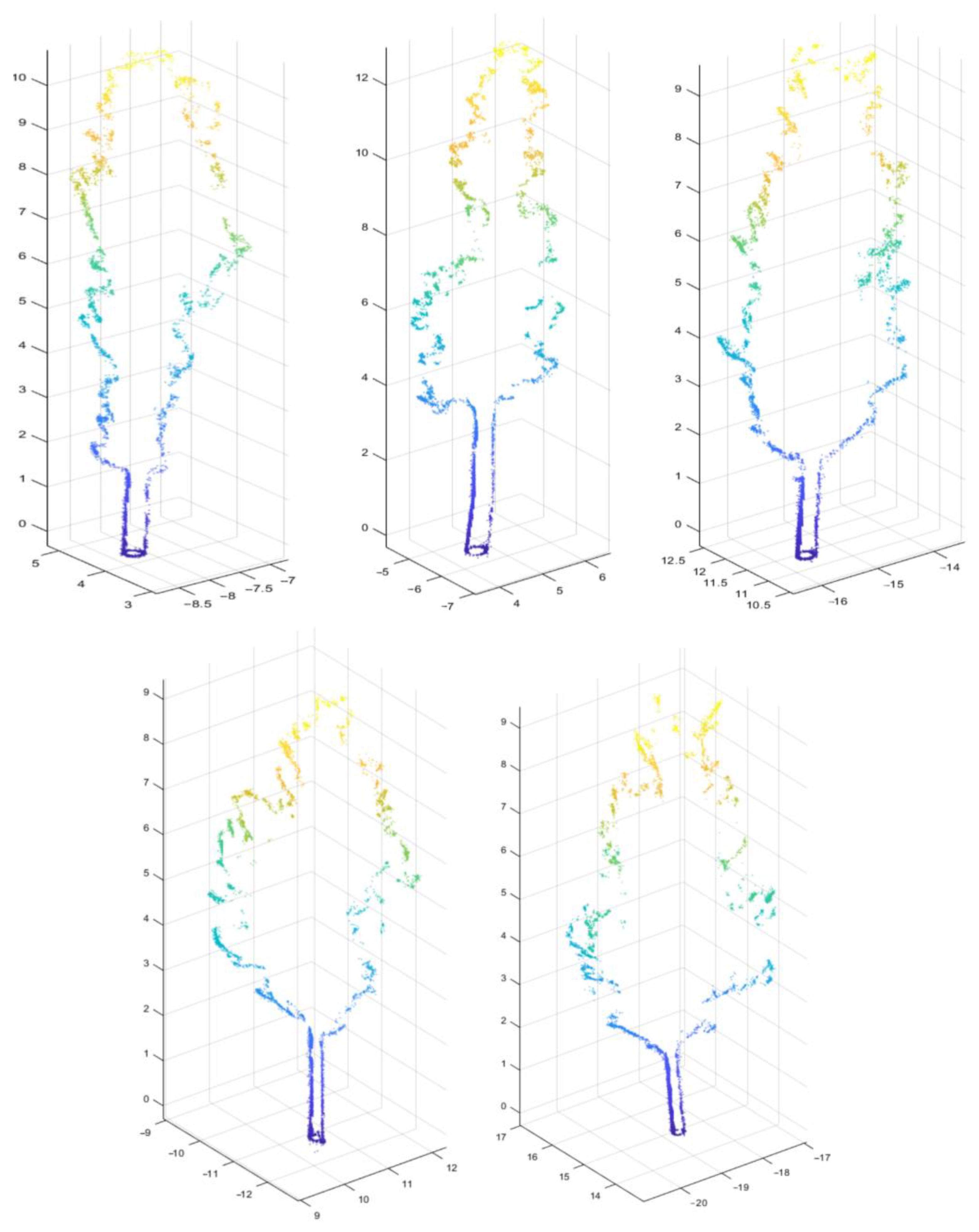
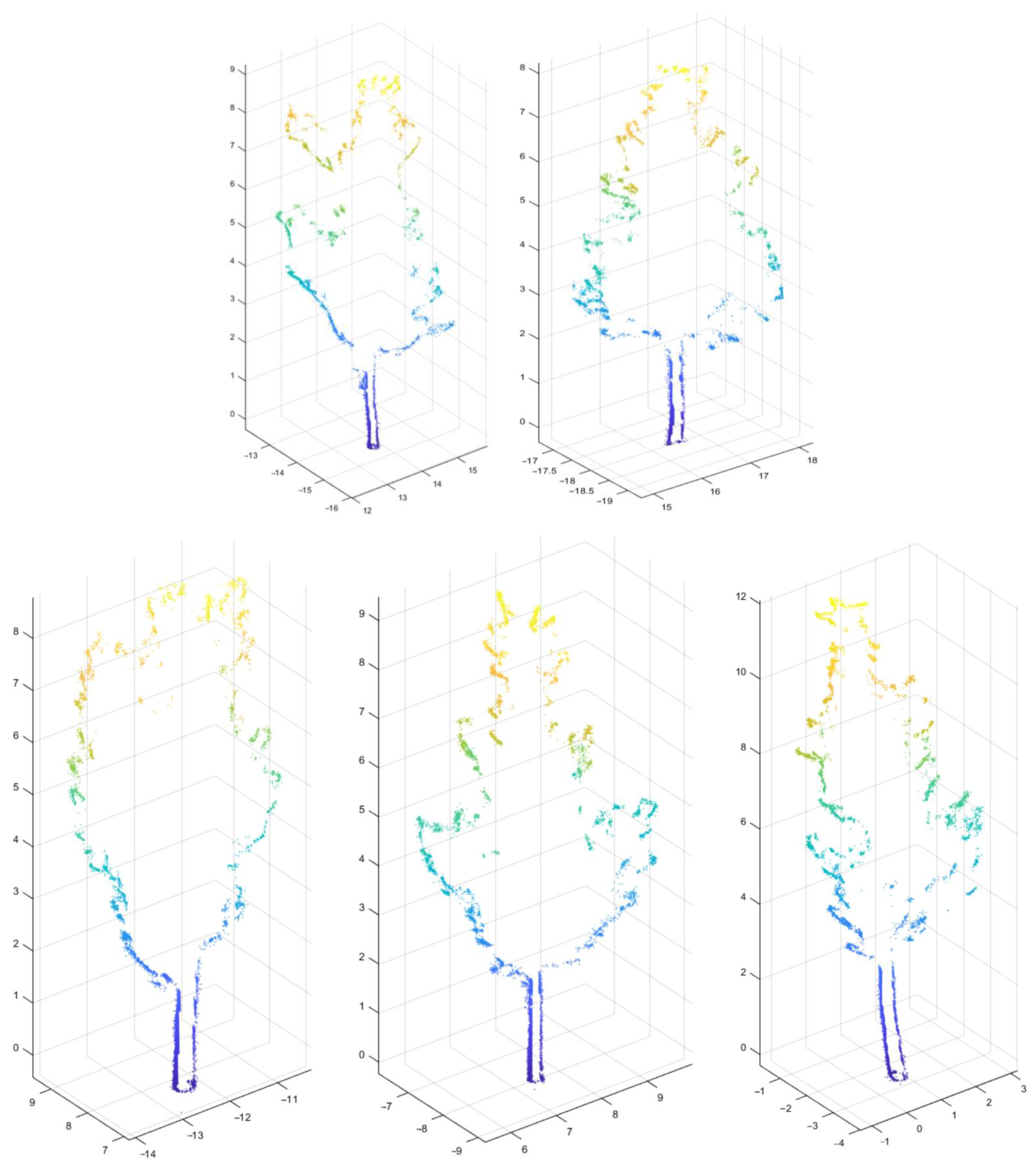
2.1. Study Area and Data Preparation
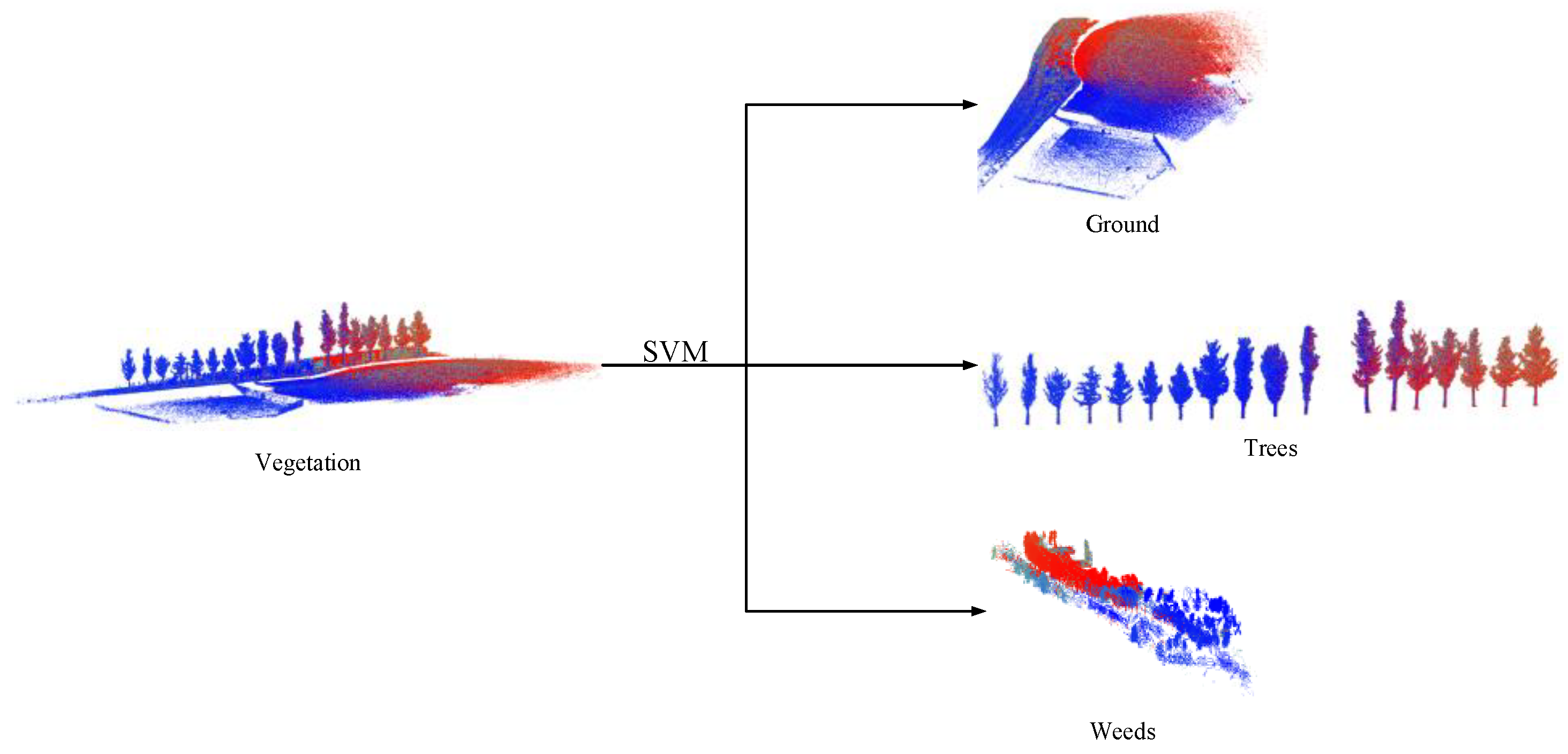
2.2. Vegetation Classification
2.3. Point Cloud Projection
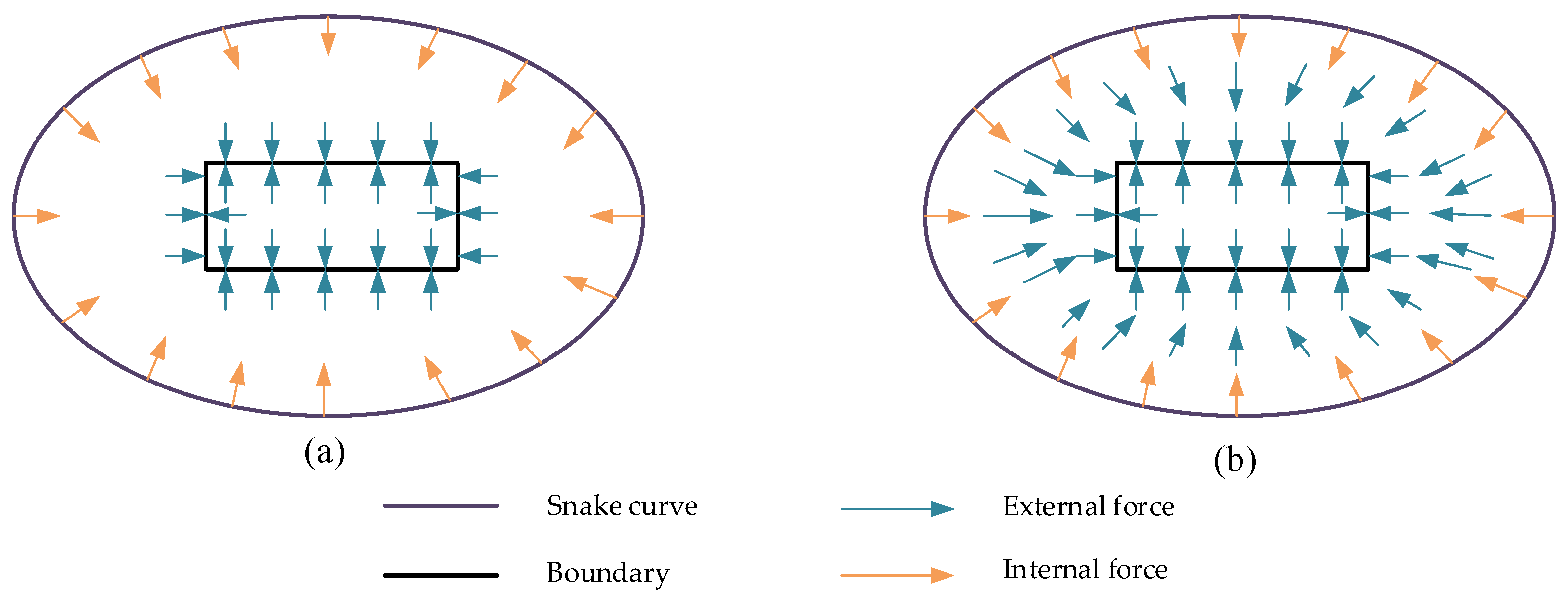
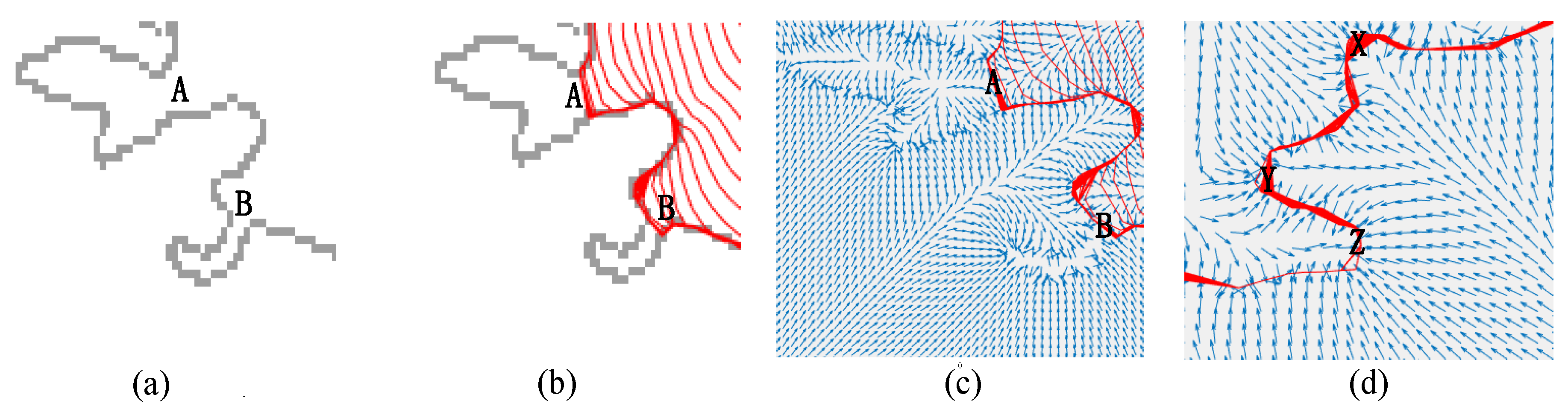
2.4. Edge Detection
2.5. Point Cloud Back-Projection
| Algorithm 1: Point Cloud Back-Projection Using Pixel Matching |
| Input: Data are the matrix of N rows and 3 columns composed of point cloud coordinates, where each row represents the coordinates of a point and N is the number of point clouds; Loc is the matrix of N rows and 2 columns formed by the corresponding pixel positions after point cloud projection, where each row represents the projection position of a point, the row number corresponds to Data, and N is the number of point clouds. Snk is a matrix of M rows and 2 columns composed of the pixel positions corresponding to the curve extracted by Snake, where M is the number of pixels.
|
3. Results and Discussion
3.1. Vegetation Classification
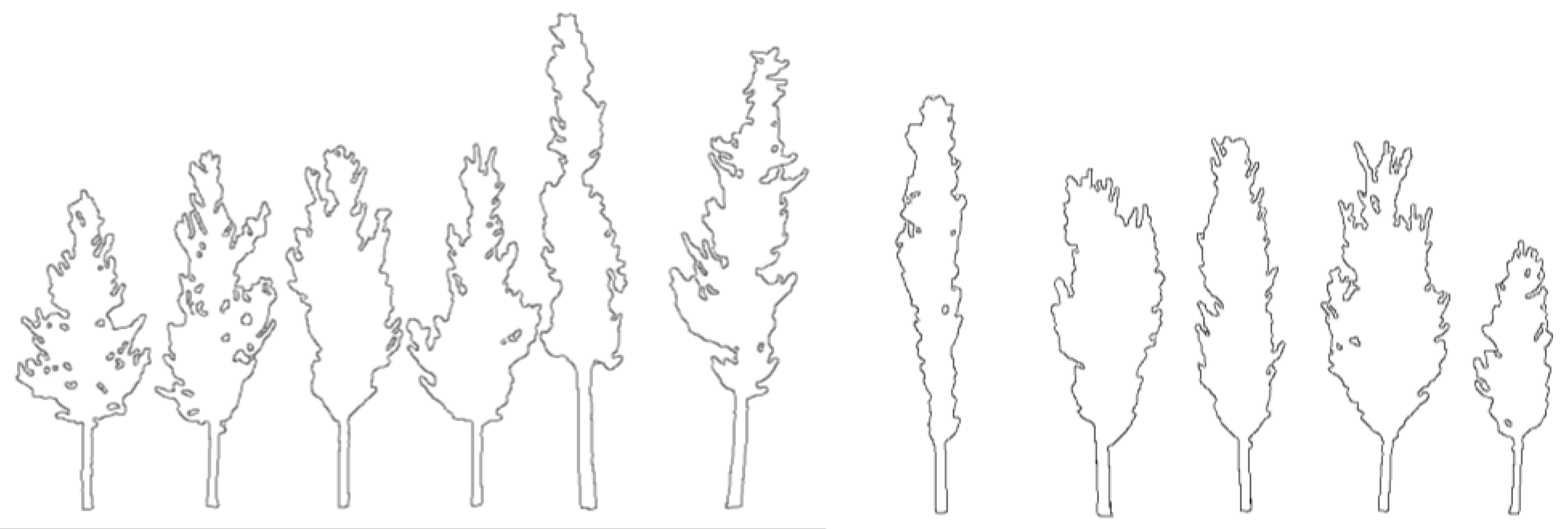
3.2. Projection and Contour Extraction
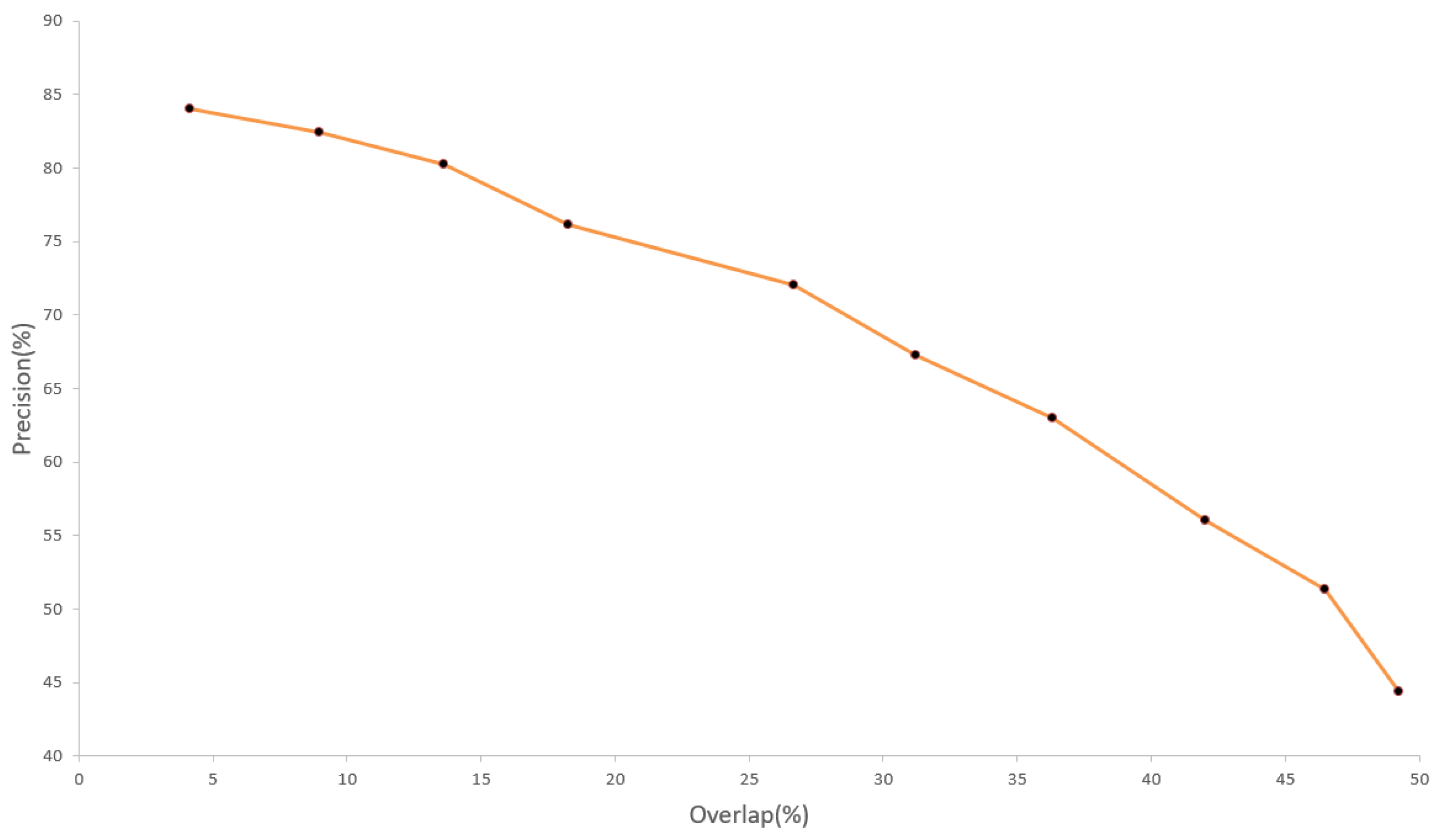
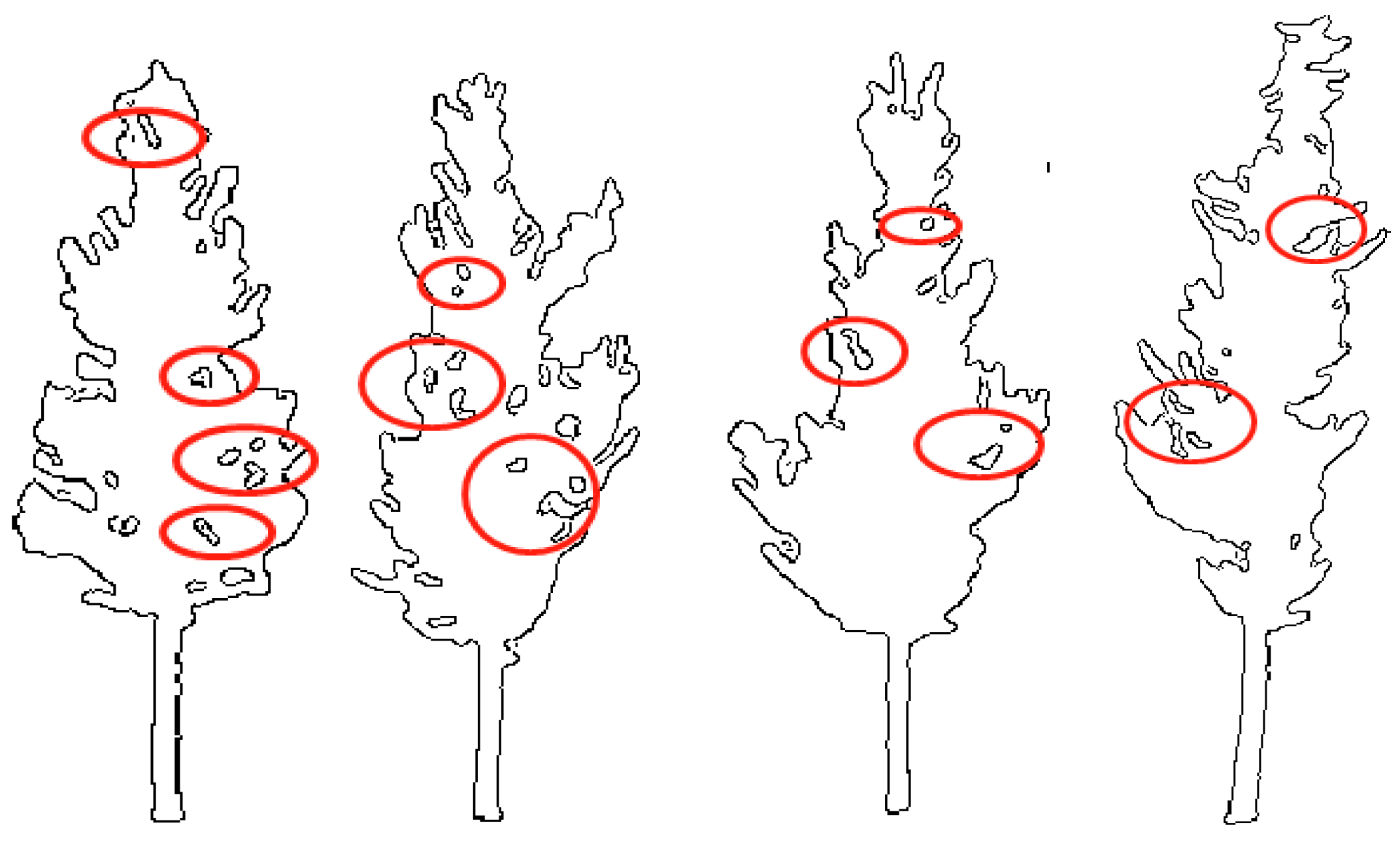
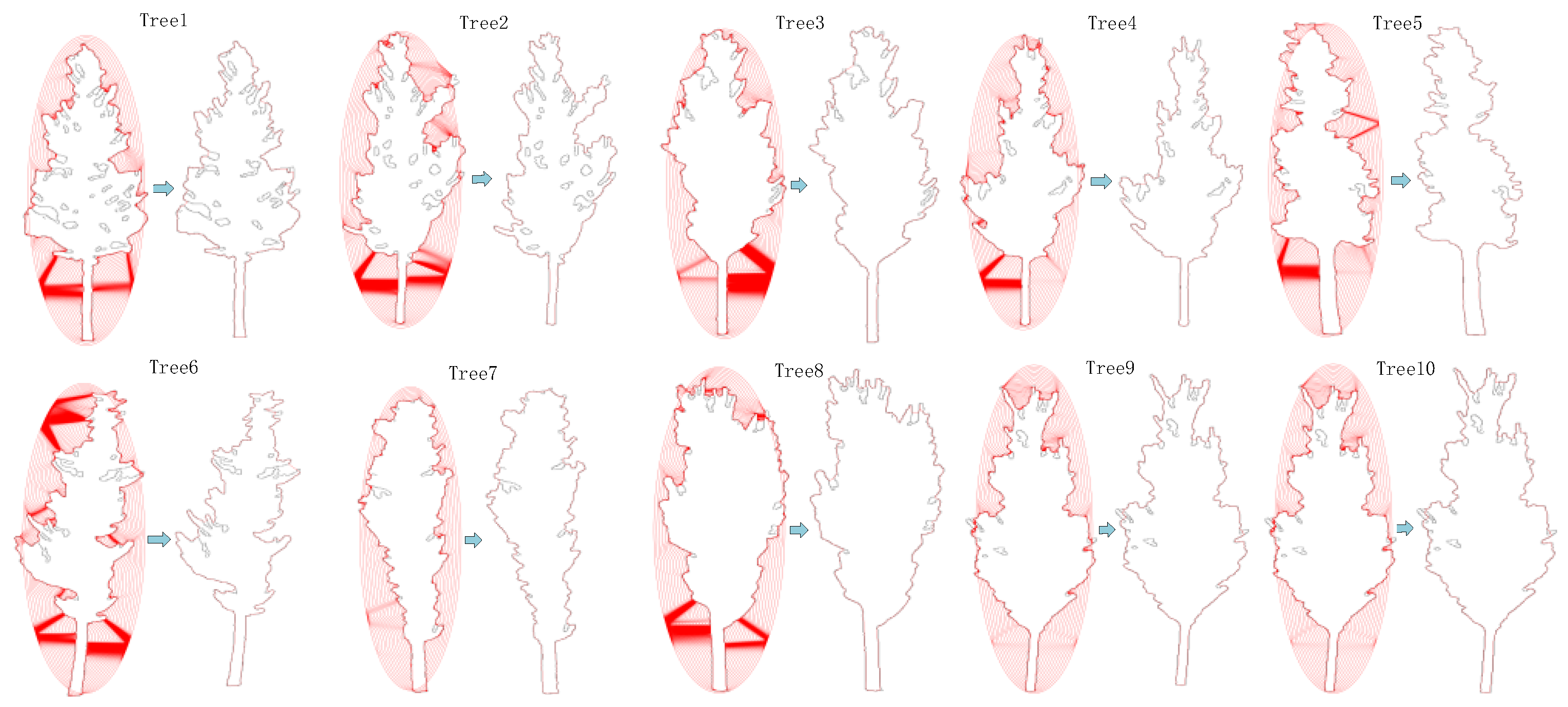
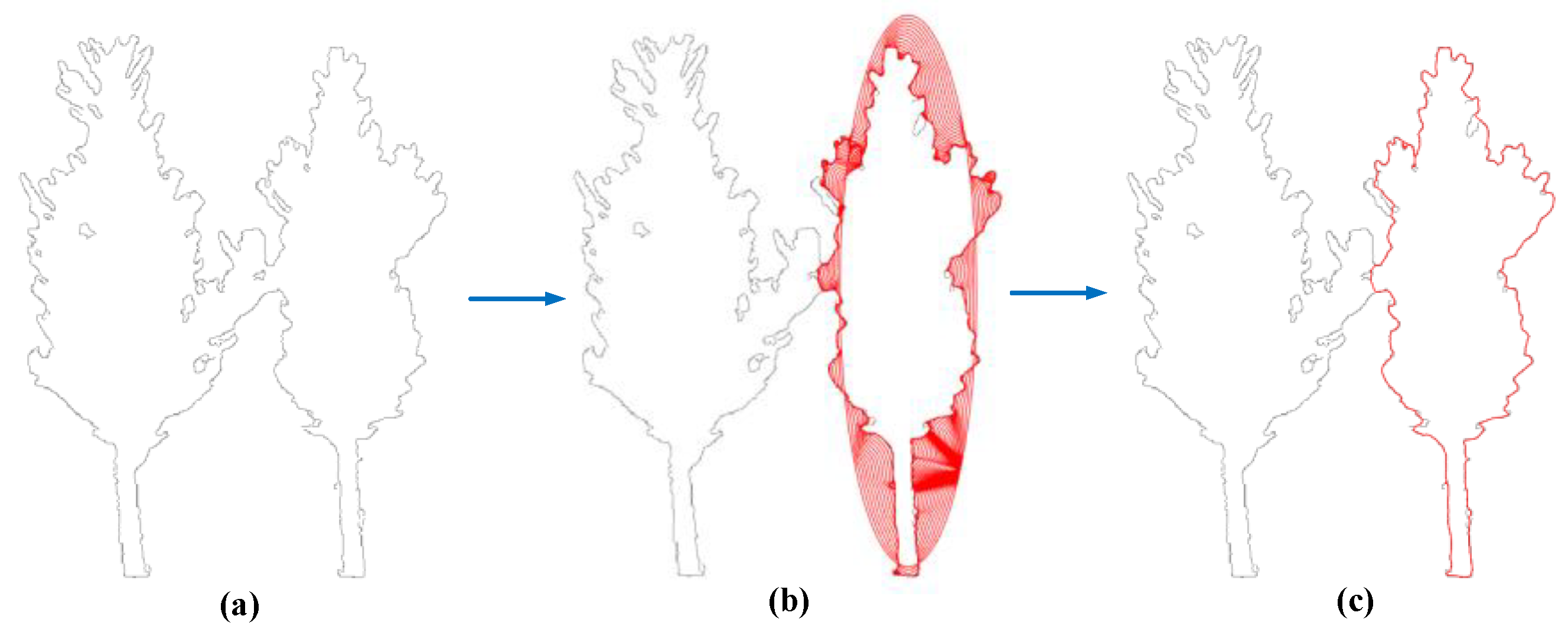
3.3. Validation Approach
3.4. Evaluation and Analysis
4. Conclusions
- (a)
- Most of the current individual tree segmentation methods are realized by using the canopy information, thus ignoring the parameters at the lower part of the canopy. The proposed method takes full account of the complex structure and irregular density of vegetation point clouds and uses point cloud projection and back-projection to verify the practicability of edge detection method in 3D point cloud segmentation.
- (b)
- Moreover, in the processing of projection images, we combined Canny algorithm and Snake to effectively avoid the influence of false edges caused by tree gaps on the experimental results. The experiment shows that, for most trees, the results obtained by Snake are better than those obtained by Canny alone. For the sample plot, p, r, and q increased by 1.39%, 3.95%, and 4.36%, respectively.
- (c)
- The segmentation accuracy of this method can reach up to 91%, so the edge of a tree can be accurately extracted. However, due to the complex shape of some trees, the Snake curve does not converge completely for some narrow concave edges, resulting in some 3D point cloud contours to break, which is the main reason that affects the segmentation accuracy of the algorithm. In the subsequent research, improving the accuracy of individual tree segmentation will be one of our priorities, and we will study the extraction of tree skeletons through the separation of branches and leaves so as to better achieve 3D reconstruction of trees.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, X.; Sun, T.; Cao, T. Study on landscape quality assessment of urban forest parks: Take Nanjing Zijinshan National Forest Park as an example. Ecol. Indic. 2021, 120, 106902. [Google Scholar] [CrossRef]
- Miao, C.; Yu, S.; Hu, Y.; Liu, M.; Yao, J.; Zhang, Y.; He, X.; Chen, W. Seasonal effects of street trees on particulate matter concentration in an urban street canyon. Sustain. Cities Soc. 2021, 73, 103095. [Google Scholar] [CrossRef]
- Caneva, G.; Bartoli, F.; Zappitelli, I.; Savo, V. Street trees in Italian cities: Story, biodiversity and integration within the urban environment. Rend. Lincei. Sci. Fis. E Nat. 2020, 31, 411–417. [Google Scholar] [CrossRef]
- Li, Q.; Yuan, P.; Liu, X.; Zhou, H. Street tree segmentation from mobile laser scanning data. Int. Ournal Remote Sens. 2020, 41, 7145–7162. [Google Scholar] [CrossRef]
- Xu, S.; Han, W.; Ye, W.; Ye, Q. 3-D Contour Deformation for the Point Cloud Segmentation. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Xia, S.; Chen, D.; Peethambaran, J.; Wang, P.; Xu, S. Point Cloud Inversion: A Novel Approach for the Localization of Trees in Forests from TLS Data. Remote Sens. 2021, 13, 338. [Google Scholar] [CrossRef]
- Næsset, E.; Økland, T. Estimating tree height and tree crown properties using airborne scanning laser in a boreal nature reserve. Remote Sens. Environ. 2002, 79, 105–115. [Google Scholar] [CrossRef]
- Xu, S.; Li, X.; Yun, J.; Xu, S. An Effectively Dynamic Path Optimization Approach for the Tree Skeleton Extraction from Portable Laser Scanning Point Clouds. Remote Sens. 2021, 14, 94. [Google Scholar] [CrossRef]
- Xia, S.; Xu, S.; Wang, R.; Li, J.; Wang, G. Building Instance Mapping from ALS Point Clouds Aided by Polygonal Maps. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Xu, S.S.; Xu, S. Identification of Street Trees’ Main Nonphotosynthetic Components from Mobile Laser Scanning Data. Opt. Mem. Neural Netw. 2020, 29, 305–316. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Stinson, G.; Hilker, T.; Kurz, W.A.; Coops, N.C.; St-Onge, B.; Trofymow, J.A. Implications of differing input data sources and approaches upon forest carbon stock estimation. Env. Monit Assess 2010, 166, 543–561. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating Individual Trees in a Savanna Woodland Using Small Footprint LIDAR Data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of Individual Tree Crowns in Airborne Lidar Data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef]
- Ayrey, E.; Fraver, S.; Kershaw, J.A., Jr.; Kenefic, L.S.; Hayes, D.; Weiskittel, A.R.; Roth, B.E. Layer Stacking: A Novel Algorithm for Individual Forest Tree Segmentation from LiDAR Point Clouds. Can. Ournal Remote Sens. 2017, 43, 16–27. [Google Scholar] [CrossRef]
- Yunsheng, W.; Holger, W.; Barbara, K. A Lidar Point Cloud Based Procedure for Vertical Canopy Structure Analysis and 3D Single Tree Modelling in Forest. Sensors 2008, 8, 3938–3951. [Google Scholar]
- Morsdorf, F.; Meier, E.; Kötz, B.; Itten, K.I.; Dobbertin, M.; Allgöwer, B. LIDAR-based geometric reconstruction of boreal type forest stands at single tree level for forest and wildland fire management. Remote Sens. Environ. 2004, 92, 353–362. [Google Scholar] [CrossRef]
- Vega, C.; Hamrouni, A.; El Mokhtari, S.; Morel, J.; Bock, J.; Renaud, J.-P.; Bouvier, M.; Durrieu, S. PTrees: A point-based approach to forest tree extraction from lidar data. Int. Ournal Appl. Earth Obs. Geoinf. 2014, 33, 98–108. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, X.; Ye, W.; Ye, Q. Classification of 3D Point Clouds by a New Augmentation Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar]
- Lee, K.H.; Woo, H.; Suk, T. Data reduction methods for reverse engineering. Int. Ournal Adv. Manuf. Technol. 2001, 17, 735–743. [Google Scholar] [CrossRef]
- Han, X.F.; Jin, J.S.; Wang, M.-J.; Jiang, W.; Gao, L.; Xiao, L. A review of algorithms for filtering the 3D point cloud. Signal Process. Image Commun. 2017, 57, 103–112. [Google Scholar] [CrossRef]
- Lin, C.H.; Chen, Y.; Su, P.L.; Chen, C.H. Eigen-feature analysis of weighted covariance matrices for LiDAR point cloud classification. Isprs J. Photogramm. Remote Sens. 2014, 94, 70–79. [Google Scholar] [CrossRef]
- Wang, D.; Hollaus, M.; Pfeifer, N. Feasibility of machine learning methods for separating wood and leaf points from terrestrial laser scanning data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, IV-2/W4, 157–164. [Google Scholar] [CrossRef]
- Guo, Y.F.; Shu, T.T.; Yang, Y.; Li, S.J. Feature Extraction Method Based on the Generalised Fisher Discriminant Criterion and Facial Recognition. Pattern Anal. Appl. 2001, 4, 61–66. [Google Scholar] [CrossRef]
- Yue, J.; Fang, L.; Ghamisi, P.; Xie, W.; Li, J.; Chanussot, J.; Plaza, A.J. Optical Remote Sensing Image Understanding with Weak Supervision: Concepts, Methods, and Perspectives. IEEE Geosci. Remote Sens. Mag. 2022, 10, 250–269. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Mongus, D.; Žalik, B. An efficient approach to 3D single tree-crown delineation in LiDAR data. ISPRS J. Photogramm. Remote Sens. 2015, 108, 219–233. [Google Scholar] [CrossRef]
- Reitberger, J.; Schnörr, C.; Krzystek, P.; Stilla, U. 3D segmentation of single trees exploiting full waveform LIDAR data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 561–574. [Google Scholar] [CrossRef]

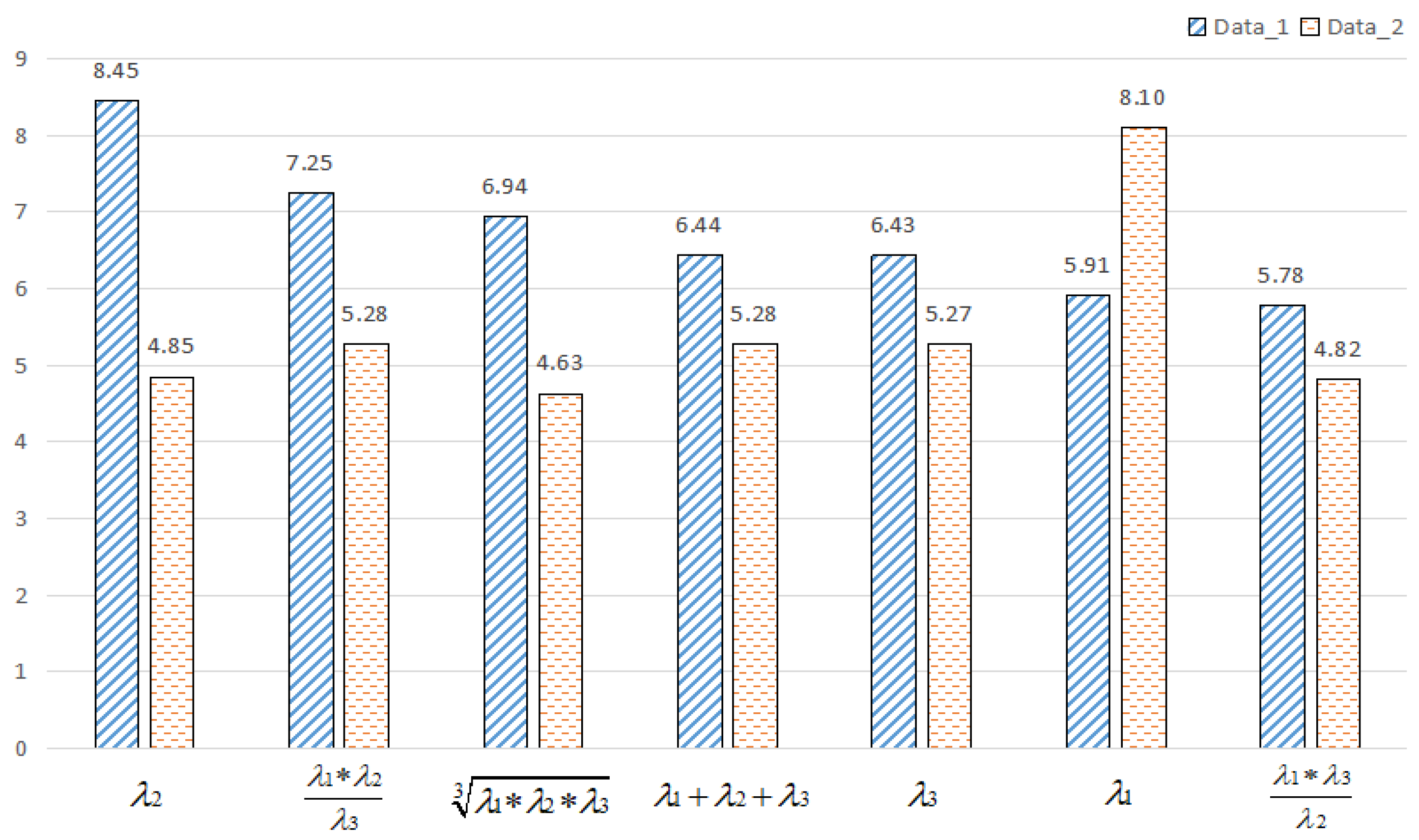



| Name | Combination Value | Name | Combination Value | ||
|---|---|---|---|---|---|
| ∑λ | Sum | Cλ | Surface Variation | ||
| Oλ | Omnivariance | Sλ | Sphericity | ||
| Aλ | Anisotropy | Vλ | Verticality | ||
| Pλ | Planarity | Jλ | Area | ||
| Lλ | Linearity | Zλ | Pointing | ||
| Method | Canny | Canny + Snake | ||||
|---|---|---|---|---|---|---|
| Accuracy Metrics | p % | r % | q % | p % | r % | q % |
| Tree 1 | 82.86 | 80.57 | 69.06 | 86.90 | 79.85 | 71.27 |
| Tree 2 | 81.71 | 78.48 | 66.76 | 86.58 | 88.62 | 77.92 |
| Tree 3 | 86.65 | 81.75 | 72.60 | 87.57 | 88.73 | 78.80 |
| Tree 4 | 85.82 | 79.65 | 70.39 | 88.48 | 83.98 | 75.70 |
| Tree 5 | 91.83 | 93.00 | 85.89 | 91.90 | 93.96 | 86.77 |
| Tree 6 | 87.08 | 88.67 | 78.36 | 85.89 | 83.58 | 73.49 |
| Tree 7 | 90.52 | 89.06 | 81.46 | 91.51 | 89.16 | 82.35 |
| Tree 8 | 89.54 | 88.95 | 80.57 | 89.40 | 83.16 | 75.70 |
| Tree 9 | 92.41 | 75.80 | 71.36 | 91.55 | 89.64 | 82.79 |
| Tree 10 | 90.83 | 81.97 | 75.70 | 91.01 | 89.11 | 81.90 |
| … | … | … | ||||
| All | 90.28 | 81.38 | 74.83 | 91.67 | 85.33 | 79.19 |
| Method | p % | r % | q % |
|---|---|---|---|
| Watershed algorithm | 88.97 | 79.14 | 72.07 |
| Point cloud-based cluster segmentation | 91.86 | 83.18 | 77.47 |
| Shadow-cut | 91.67 | 85.33 | 79.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, Z.; Xu, S.; Liu, Y. Individual Tree Segmentation from Side-View LiDAR Point Clouds of Street Trees Using Shadow-Cut. Remote Sens. 2022, 14, 5742. https://doi.org/10.3390/rs14225742
Hua Z, Xu S, Liu Y. Individual Tree Segmentation from Side-View LiDAR Point Clouds of Street Trees Using Shadow-Cut. Remote Sensing. 2022; 14(22):5742. https://doi.org/10.3390/rs14225742
Chicago/Turabian StyleHua, Zhouyang, Sheng Xu, and Yingan Liu. 2022. "Individual Tree Segmentation from Side-View LiDAR Point Clouds of Street Trees Using Shadow-Cut" Remote Sensing 14, no. 22: 5742. https://doi.org/10.3390/rs14225742
APA StyleHua, Z., Xu, S., & Liu, Y. (2022). Individual Tree Segmentation from Side-View LiDAR Point Clouds of Street Trees Using Shadow-Cut. Remote Sensing, 14(22), 5742. https://doi.org/10.3390/rs14225742






