Remote Sensing-Based Hydro-Extremes Assessment Techniques for Small Area Case Study (The Case Study of Poland)
Abstract
:1. Introduction
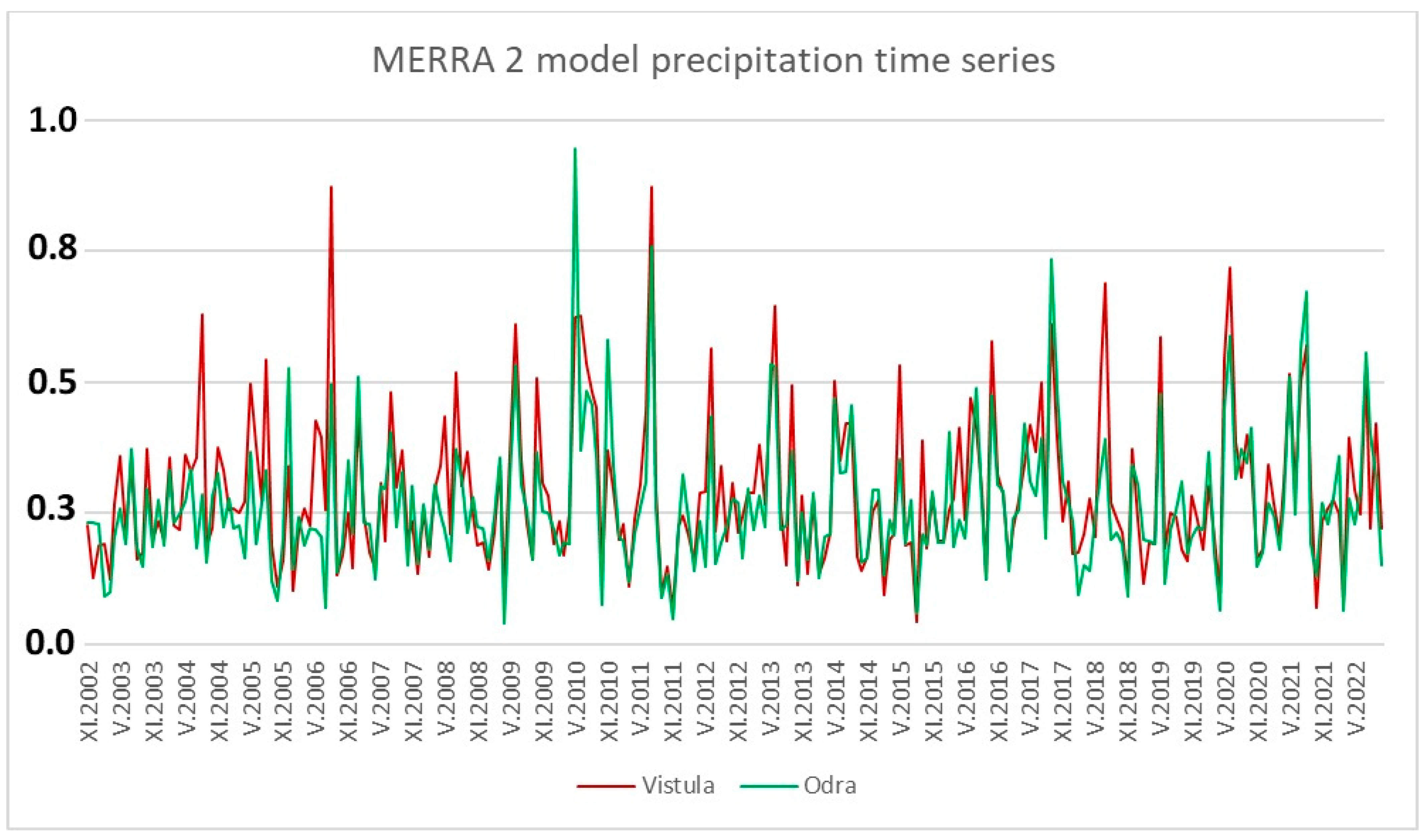
2. Data and Case Study Localization
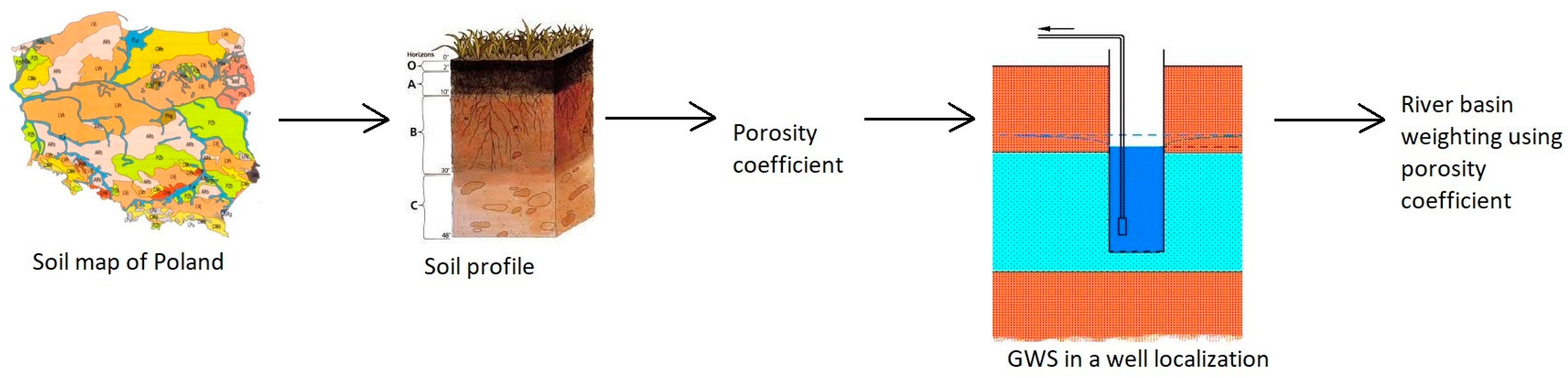
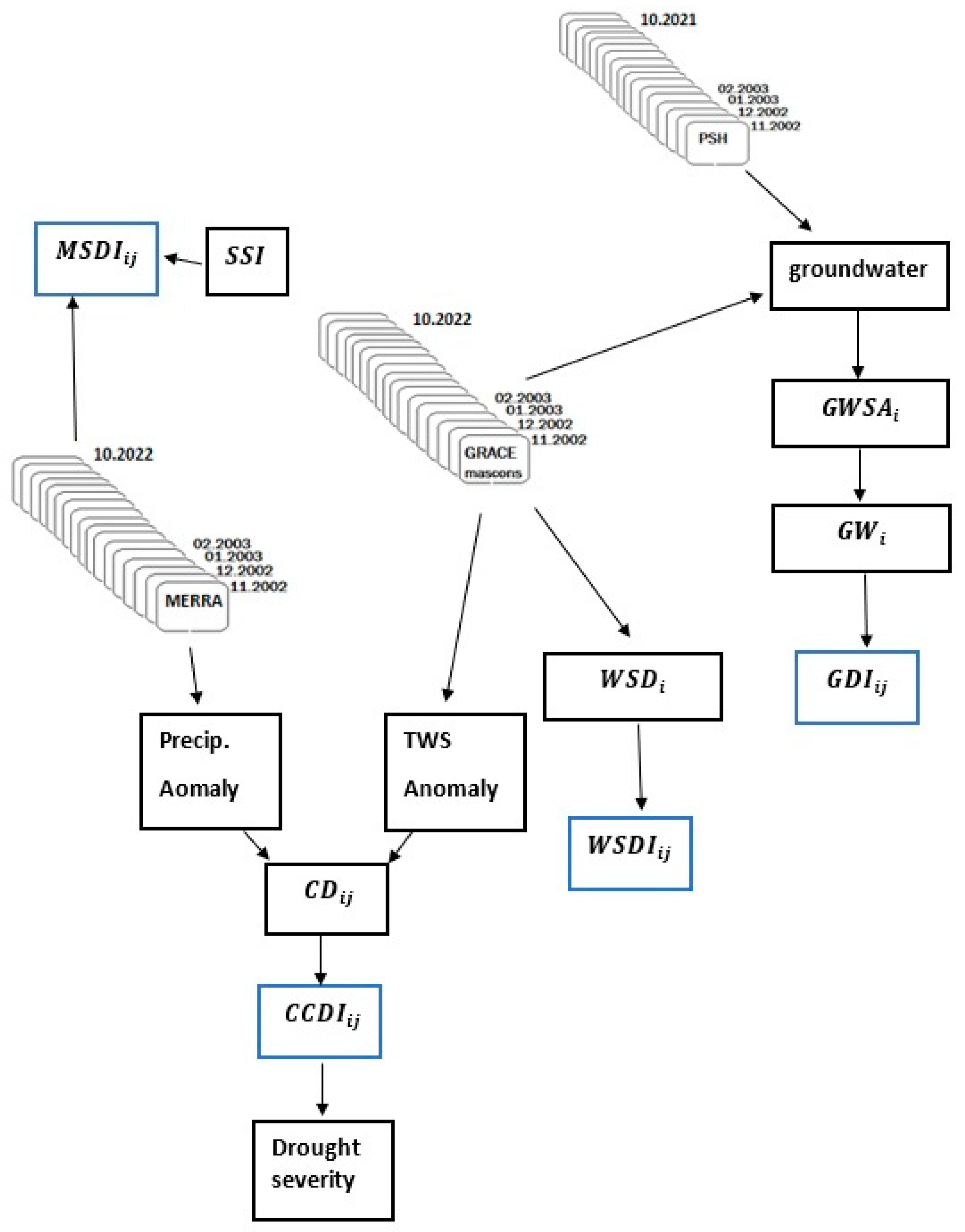
3. Methods
3.1. Combined Climatologic Deviation Index
3.2. Drought Severity
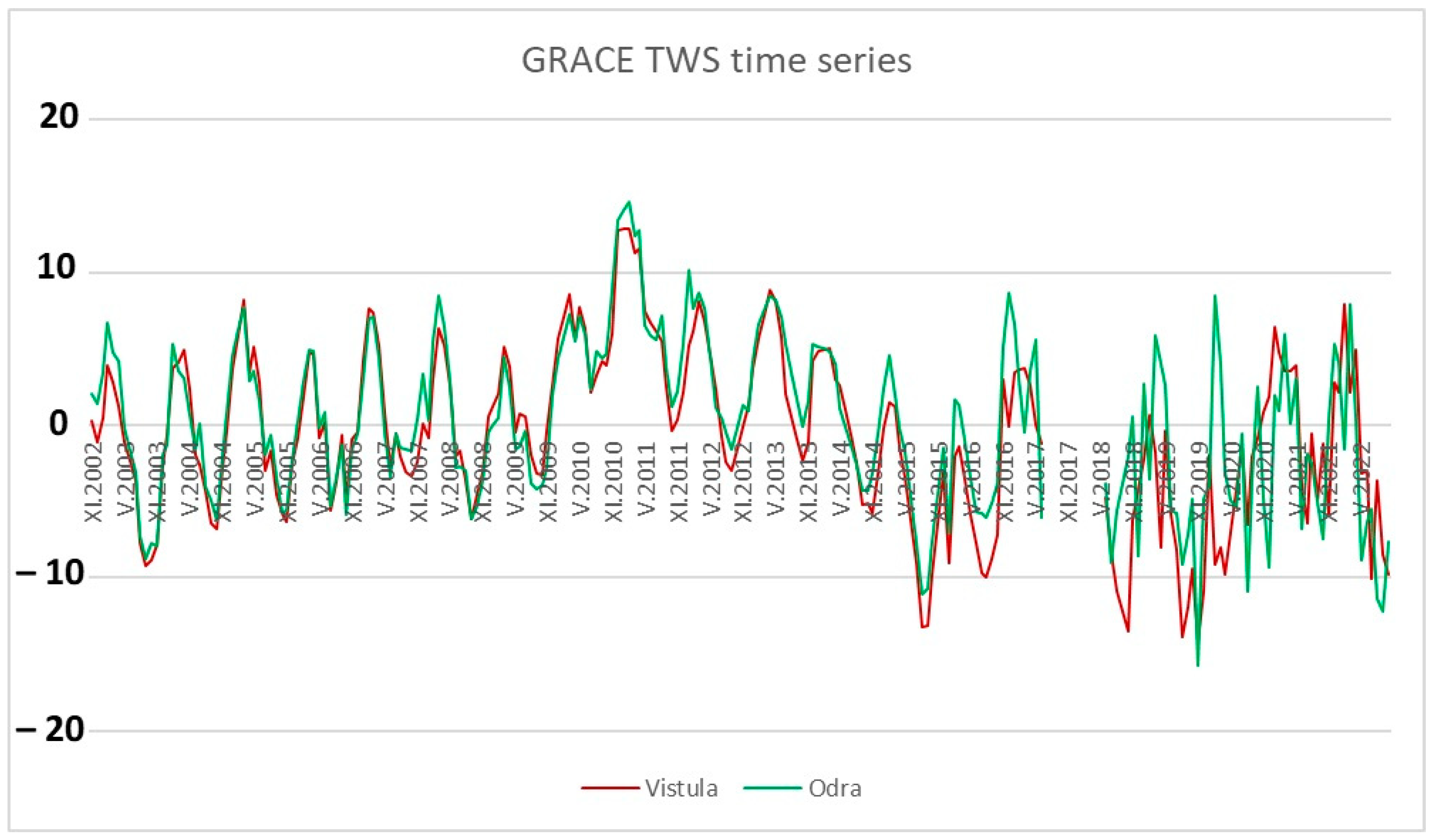
3.3. Water Storage Deficit
3.4. Multivariate Standardized Drought Index
4. Results
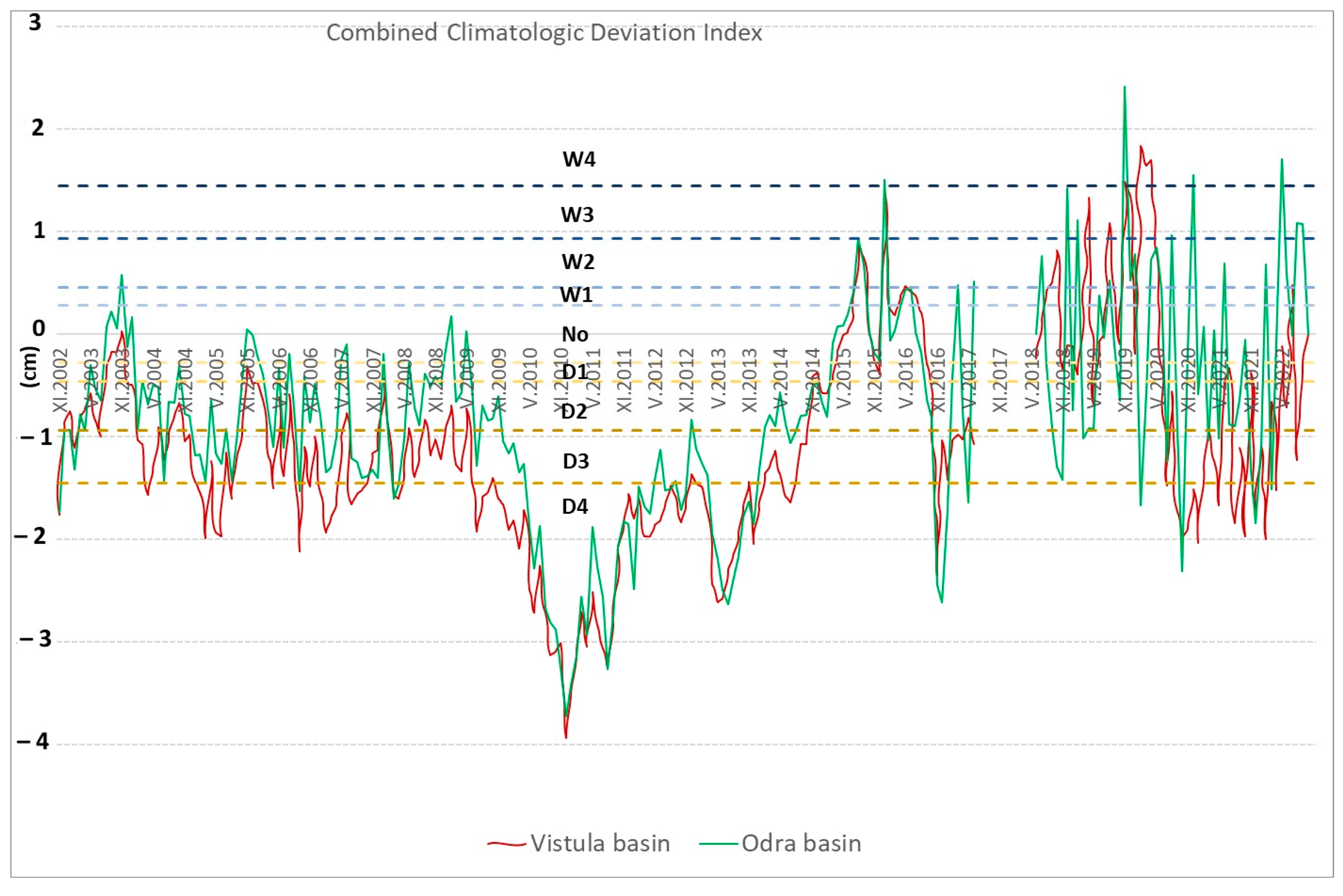
4.1. Combined Climatologic Deviation Index
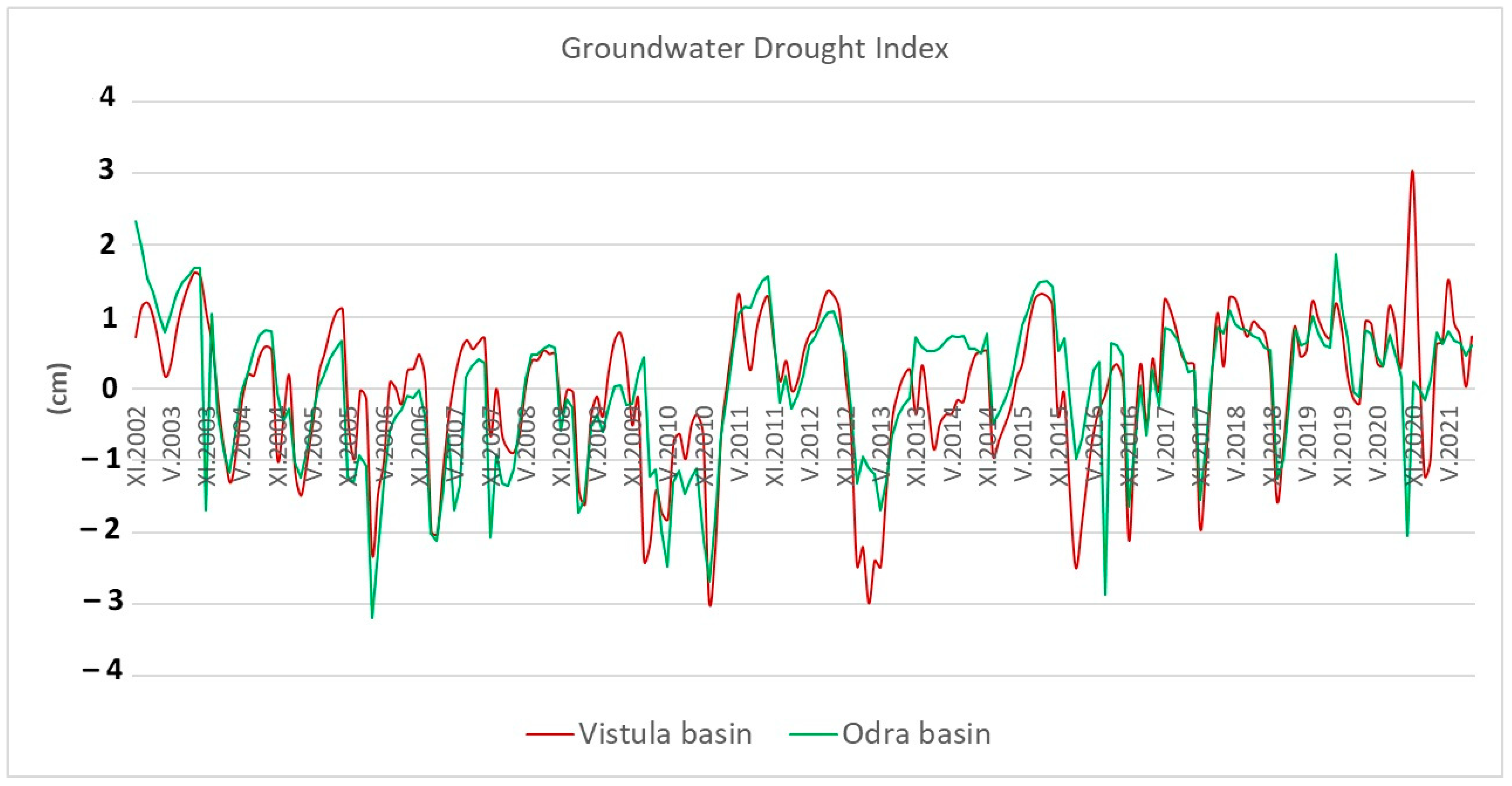
4.2. Groundwater Drought Index
4.3. Water Storage Deficit
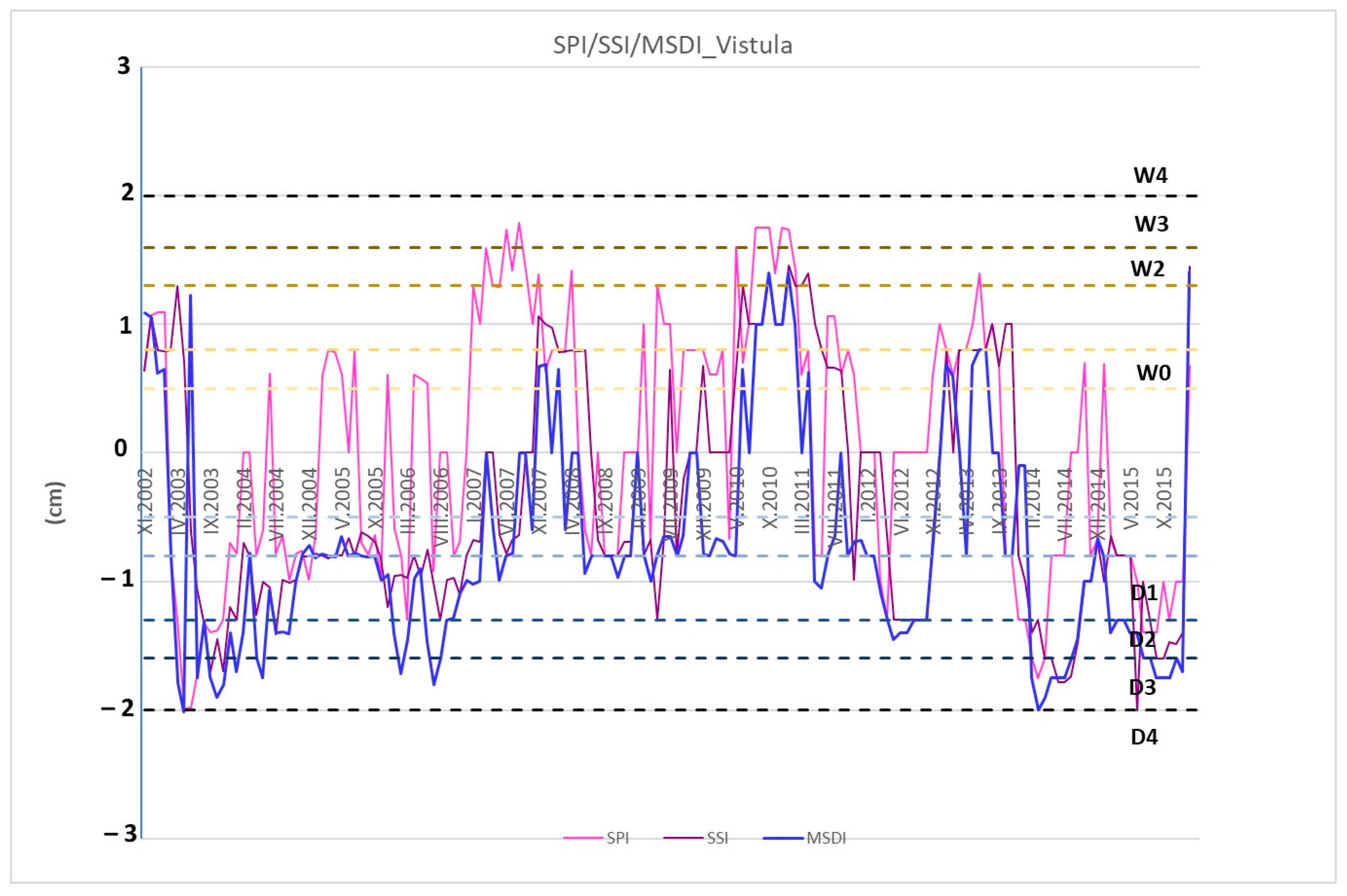
4.4. Multivariate Standardized Drought Index
5. Conclusions
- In the studied river basins, there were regular periods of drought with an intensity from D1 to above D4. The longest and most intense period of drought, extending over 3 years, is observed for both catchments in the years 2010–2013. During this period, the indicator fluctuated between D1 and below D4, never reaching the W range;
- Much smaller amplitudes of changes between the intervals D and W were observed in the period before the month-long drought of 2002–2010 (−1.5 cm–0.5 cm), after the drought, the amplitudes of the changes increased and reached a range between −2 and 1.5 cm;
- Drought in the catchments, after the analysis of the CCDI coefficient, occurs every year in the autumn and is greater in the catchment of Vistula in comparison to the Odra catchment.
- Using the GGDI coefficient, a stable groundwater level was found throughout the months under study;
- The WSDI analysis showed the deteriorating state of the total water—in the autumn, the values fell to the D2 range and from 2018 they reach D3 and D4. This shows the loss of total water, less precipitation, less water in the atmosphere, and more evaporation and evapotranspiration caused by the increase in temperature. The amount of snowfall in winter is also reduced;
- MSDI should be analyzed depending on climatic zones—Poland is a rather homogenous country in this respect; however, the division into basins is a vertical division, in contrast to the horizontal distribution of climatic zones. When analyzing the effects of meteorological and agricultural drought in the form of the MSDI index, an unfavorable situation in terms of drought was noticed in the study area, especially since 2014, when even the upper MSDI levels are at the D1 level;
- To sum up, the analysis of climate coefficients in terms of researching and identifying the phenomenon of drought using the CCDI, GGDI, WSDI, and MSDI indicators is a necessary tool. The periods of drought can be seen, especially since 2014. This is not groundwater-related drought; it seems to be due to low rainfall and snowfall.
- The proposed methods for determining the water indices can be used in almost any region. And we think it would be worth implementing them in the continuous monitoring of basin areas. Testing the resources and availability of groundwater, which is crucial for consumption, is of exceptional importance. However, the porosity coefficient should not be used in future work in the case of areas covered with ice, because the ice itself has a significant impact on the permeability there and the ice itself could be treated as a rock, which is only an additional, yet important factor.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Babre, A.; Kalvāns, A.; Avotniece, Z.; Retiķe, I.; Bikše, J.; Popovs, K.; Jemeljanova, M.; Zelenkevičs, A.; Dēliņa, A. The use of predefined drought indices for the assessment of groundwater drought episodes in the Baltic States over the period 1989–2018. J. Hydrol. Reg. Stud. 2022, 40, 101049. [Google Scholar] [CrossRef]
- Birylo, M.; Rzepecka, Z.; Nastula, J. Assessment of the Water Budget from GLDAS Model. In Proceedings of the 2018 Baltic Geodetic Congress (BGC Geomatics), Olsztyn, Poland, 21–23 June 2018; pp. 86–90. [Google Scholar]
- Wilhite, D.A.; Glantz, M.H. Understanding: The Drought Phenomenon: The Role of Definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Rawat, S.; Ganapathy, A.; Agarwal, A. Drought characterization over Indian sub-continent using GRACE-based indices. Sci. Rep. 2022, 12, 15432. [Google Scholar] [CrossRef]
- Balint, Z.; Mutua, F.; Muchiri, P.; Omuto, C.T. Monitoring Drought with the Combined Drought Index in Kenya. In Developments in Earth Surface Processes; Elsevier: Amsterdam, The Netherlands, 2013; Volume 16. [Google Scholar] [CrossRef]
- Yu, W.; Li, Y.; Cao, Y.; Schillerberg, T. Drought Assessment using GRACE Terrestrial Water Storage Deficit in Mongolia from 2002 to 2017. Water 2019, 11, 1301. [Google Scholar] [CrossRef]
- Lu, J.; Jia, L.; Zhou, J.; Jiang, M.; Zhong, Y.; Menenti, M. Quantification and Assessment of Global Terrestrial Water Storage Deficit Caused by Drought Using GRACE Satellite Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5001–5012. [Google Scholar] [CrossRef]
- Krogulec, E.; Małecki, J.J.; Porowska, D.; Wojdalska, A. Assessment of Causes and Effects of Groundwater Level Change in an Urban Area (Warsaw, Poland). Water 2020, 12, 3107. [Google Scholar] [CrossRef]
- Boczoń, A.; Kowalska, A.; Stolarek, A. The Impact of Climate Change on the High Water Levels of a Small River in Central Europe Based on 50-Year Measurements. Forests 2020, 11, 1269. [Google Scholar] [CrossRef]
- Śliwińska, J.; Birylo, M.; Rzepecka, Z.; Nastula, J. Analysis of Groundwater and Total Water Storage Changes in Poland Using GRACE Observations, In-situ Data, and Various Assimilation and Climate Models. Remote Sens. 2019, 11, 2949. [Google Scholar] [CrossRef]
- Okoniewska, M. Specificity of Meteorological and Biometeorological Conditions in Central Europe in Centre of Urban Areas in June 2019 (Bydgoszcz, Poland). Atmosphere 2021, 12, 1002. [Google Scholar] [CrossRef]
- Kalbarczyk, R.; Kalbarczyk, E. Research into Meteorological Drought in Poland during the Growing Season from 1951 to 2020 Using the Standardized Precipitation Index. Agronomy 2022, 12, 2035. [Google Scholar] [CrossRef]
- Wicher-Dysarz, J.; Dysarz, T.; Jaskuła, J. Uncertainty in Determination of Meteorological Drought Zones Based on Standardized Precipitation Index in the Territory of Poland. Int. J. Environ. Res. Public Health 2022, 19, 15797. [Google Scholar] [CrossRef] [PubMed]
- Rzepecka, Z.; Birylo, M. Groundwater Storage Changes Derived from GRACE and GLDAS on Smaller River Basins—A Case Study in Poland. Geosciences 2020, 10, 124. [Google Scholar] [CrossRef]
- Available online: http://grace.jpl.nasa.gov (accessed on 12 June 2023).
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2006; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2007. Available online: https://www.pgi.gov.pl/psh/materialy-informacyjne-psh/rocznik-hydrogeologiczny-psh.html (accessed on 12 June 2023).
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2007; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2008. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2008; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2009. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2009; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2010. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2010; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2011. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2011; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2012. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2012; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2013. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2013; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2014. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2014; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2015. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2015; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2016. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2016; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2017. Available online: https://www.pgi.gov.pl/psh/materialy-informacyjne-psh/rocznik-hydrogeologiczny-psh.html (accessed on 12 June 2023).
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2017; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2018. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2018; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2019. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2019; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2020. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2020; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2021. [Google Scholar]
- Sadurski, A. Hydrogeological Annual Reports. In Polish Hydrological Survey. Hydrological Year 2021; Polish Geological Institute—National Research Institute: Warsaw, Poland, 2022. [Google Scholar]
- Sinha, D.; Syed, T.H.; Reager, J.T. Utilizing combined deviations of precipitation and GRACE-based terrestrial water storage as a metric for drought characterization: A case study over major Indian river basins. J. Hydrol. 2019, 572, 294–307. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. Multivariate Standardized Drought Index: A parametric multi-index model. Adv. Water Resour. 2013, 57, 12–18. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A. A Nonparametric Multivariate Multi-Index Drought Monitoring Framework. J. Hydrometeorol. 2014, 15, 89–101. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Z.; Yang, H.; Di, D.; Zhao, Y.; Liang, Q. Utilizing GRAC-based groundwater drought index for drought characterization and teleconnection factors analysis in the North China Plain. J. Hydrol. 2020, 585, 124849. [Google Scholar] [CrossRef]
- Thomas, B.F.; Famiglietti, J.S.; Landerer, F.W.; Wiese, D.N.; Molotch, N.P.; Argus, D.F. GRACE Groundwater Drought Index: Evaluation of California Central Valley groundwater drought. Remote Sens. Environ. 2017, 198, 384–392. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE-based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef]
- Yirdaw, S.Z.; Snelgrove, K.R.; Agboma, C.O. GRACE satellite observations of terrestrial moisture changes for drought characterization in the Canadian Prairie. J. Hydrol. 2008, 356, 84–92. [Google Scholar] [CrossRef]
- AghaKouchak, A. A multivariate approach for persistence-based drought prediction: Application to the 2010–2011 East Africa drought. J. Hydrol. 2015, 526, 127–135. [Google Scholar] [CrossRef]


| CCDI [cm] | WSDI [cm] | Category of DS with Severity Level |
|---|---|---|
| [−1.45, −∞) | [−3, −∞) | Extreme drought (D4) |
| [−1.44, −0.94] | [–3, –2] | Severe drought (D3) |
| [−0.93, −0.46] | [−2, −1] | Moderate drought (D2) |
| [−0.45, −0.28] | [−1, −0] | Mild drought (D1) |
| [0.28, −0.44] | [−1, 1] | Normal (No) |
| [0.45, 0.28] | [0.5, 1] | Mild wet (W1) |
| [0.93, 0.46] | [1, 1.5] | Moderate wet (W2) |
| [1.44, 0.94] | [1.5, 2] | Severe wet (W3) |
| (∞, 1.45] | (∞, 2] | Extreme wet (W4) |
| MSDI [cm] | Category of DS with Severity Level |
|---|---|
| [−2, −∞) | Exceptional drought (D4) |
| [−1.6, −1.99] | Extreme drought (D3) |
| [−1.3, −1.59] | Severe drought (D2) |
| [−0.8, −1.29] | Moderate drought (D1) |
| [−0.5, −0.79] | Abnormally dry (D0) |
| [0.5, 0.79] | Abnormally wet (W0) |
| [0.8, 1.29] | Moderate wet (W1) |
| [1.3, 1.59] | Severe wet (W2) |
| [1.6, 1.99] | Extreme wet (W3) |
| (∞, 2] | Exceptional wet (W4) |
| Stat. Char. | Vistula Basin [cm] | Odra Basin [cm] |
|---|---|---|
| Max. | 1.836 | 2.412 |
| Min. | −3.935 | −3.720 |
| Mean | −1.081 | −0.810 |
| St. Dev. | 1.002 | 1.002 |
| Stat. Char. | Vistula Basin [cm] | Odra Basin [cm] |
|---|---|---|
| Max. | 3.021 | 2.327 |
| Min. | −2.986 | −3.205 |
| Mean | 0.000 | 0.000 |
| St. Dev. | 1.002 | 1.002 |
| Stat. Char. | Vistula Basin [cm] | Odra Basin [cm] |
|---|---|---|
| Max. | 2.425 | 2.685 |
| Min. | −2.455 | −2.983 |
| Mean | 0.000 | 0.000 |
| St. Dev. | 1.002 | 1.002 |
| Stat. Char. | SPI | SSI | MSDI | SPI | SSI | MSDI |
|---|---|---|---|---|---|---|
| Vistula Basin [cm] | Odra Basin [cm] | |||||
| Max. | 1.790 | 2.000 | 1.750 | 1.460 | 1.450 | 1.415 |
| Min. | −1.990 | −2.000 | −1.995 | −2.000 | −2.050 | −1.875 |
| Mean | 0.046 | 0.098 | 0.072 | −0.458 | −0.458 | −0.407 |
| St. Dev. | 0.982 | 1.028 | 0.930 | 0.908 | 0.976 | 0.859 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Birylo, M.; Rzepecka, Z. Remote Sensing-Based Hydro-Extremes Assessment Techniques for Small Area Case Study (The Case Study of Poland). Remote Sens. 2023, 15, 5226. https://doi.org/10.3390/rs15215226
Birylo M, Rzepecka Z. Remote Sensing-Based Hydro-Extremes Assessment Techniques for Small Area Case Study (The Case Study of Poland). Remote Sensing. 2023; 15(21):5226. https://doi.org/10.3390/rs15215226
Chicago/Turabian StyleBirylo, Monika, and Zofia Rzepecka. 2023. "Remote Sensing-Based Hydro-Extremes Assessment Techniques for Small Area Case Study (The Case Study of Poland)" Remote Sensing 15, no. 21: 5226. https://doi.org/10.3390/rs15215226
APA StyleBirylo, M., & Rzepecka, Z. (2023). Remote Sensing-Based Hydro-Extremes Assessment Techniques for Small Area Case Study (The Case Study of Poland). Remote Sensing, 15(21), 5226. https://doi.org/10.3390/rs15215226







